Extensive Long-Range and Nonsyntenic Linkage Disequilibrium in Livestock Populations: Deconstruction of a Conundrum

Abstract

Great interest was aroused by reports, based on microsatellite markers, of high levels of statistically significant long-range and nonsyntenic linkage disequilibrium (LD) in livestock. Simulation studies showed that this could result from population family structure. In contrast, recent SNP-based studies of livestock populations report much lower levels of LD. In this study we show, on the basis of microsatellite data from four cattle populations, that high levels of long-range LD are indeed obtained when using the multi-allelic D′ measure of LD. Long-range and nonsyntenic LD are exceedingly low, however, when evaluated by the standardized chi-square measure of LD, which stands in relation to the predictive ability of LD. Furthermore, specially constructed study populations provided no evidence for appreciable LD resulting from family structure at the grandparent level. We propose that the high statistical significance and family structure effects observed in the earlier studies are due to the use of large sample sizes, which accord high statistical significance to even slight deviations from asymptotic expectations under the null hypothesis. Nevertheless, even after taking sample size into account, our results indicate that microsatellites testify to the presence of usable LD at considerably wider separation distances than SNPs, suggesting that use of SNP haplotypes may considerably increase the usefulness of a given fixed SNP array.

THE effectiveness of whole-genome association studies (WGA) or whole-genome selection (WGS) depends on the level of linkage disequilibrium (LD) in the population. Consequently, great interest was aroused by reports, based on microsatellites, of relatively high statistically significant levels of marker–marker LD in dairy cattle and other farm animals over extended intrachromosomal regions and even between chromosomes (Farnir et al. 2000; McRae et al. 2002; Tenesa et al. 2003; Nsengimana et al. 2004; Heifetz et al. 2005). On the basis of simulation studies, Farnir et al. (2000) concluded that the observed values of their LD measure could be explained as derived from the family structure of their population. In contrast, recent studies using SNP markers report much lower levels of LD, limited to ≤100 kb (McKay et al. 2007; Khatkar et al. 2008; Sargolzaei et al. 2008). Other studies have found significant LD between microsatellite markers over larger separation distances than between SNP markers (Varilo et al. 2003), but the magnitude of difference reported above is unprecedented. Although in many applications high-density SNP arrays appear to be replacing microsatellites as the marker of choice, it is difficult to believe that microsatellites, which so beautifully embody all the desired qualities of a genetic marker, will be superceded by SNP arrays in all applications. Additionally, there is some evidence that SNP haplotypes combine the advantages of multi-allelic markers and array technology (Pe'er et al. 2006), while extension of array technology to microsatellites is certainly within the realm of possibility. Thus, it is of interest to continue to explore the properties of microsatellites as representative of multi-allelic markers in general and to search for a solution to the above conundrum in particular.

All of the microsatellite-based livestock studies cited above, with the exception of Heifetz et al. (2005), used Hedrick's multi-allelic D′ (henceforth denoted D′*; Hedrick 1987) as the measure of LD, while the SNP studies used Hill and Robertson's r² (Hill and Robertson 1968). In contrast to r², D′* does not provide a quantitative estimate of the information provided by one locus for the other (Ardlie et al. 2002; McRae et al. 2002; Flint-Garcia et al. 2003; Zhao et al. 2005). Zhao et al. (2005, 2007) found that standardized χ² (henceforth denoted χ^2′*; Yamazaki 1977) closely tracked the regression of the allelic state at a QTL on the allelic state at a multi-allelic marker and hence conveys the same information for multi-allelic markers as r² does for diallelic markers. In this study, therefore, we evaluated LD among microsatellite markers in a number of dairy and dual cattle populations using D′* and χ^2′*, and also examined the effect of population structure and sample size on LD measures and their associated P-values. On the basis of our results we conclude that at short range (<5 cM) microsatellites may indeed capture useful LD that is not captured by SNPs, but that at longer ranges, although statistically significant LD is present, its magnitude is far from sufficient for purposes of WGA or WGS.

MATERIALS AND METHODS

Populations:

Four population sample (PS) sets were constructed (Table 1). PS1 consisted of three subsets: Israel Holstein (IsH), Italian Holstein (ItH), and Italian–Austrian–German Brown Swiss (BS). Each of the subsets consisted of 10–15 daughters of each of 8–10 sires, the sires themselves, and some of the sires of the sires (grandsires). PS2 consisted of a sample of German Fleckvieh sires (also known as Simmental), part of a large granddaughter design. PS3 and PS4 were IsH samples constructed to minimize family structure. PS3 consisted of 20 daughters of each of 10 sires, chosen so that each of the 200 daughters had a different maternal grandsire (MGS); all but 17 of the daughters also had different maternal great grandsires. PS4 consisted of 27 IsH sires that, aside from two sire-son pairs and two half-brother pairs, did not have any parents or grandparents in common.

TABLE 1.

Population characteristics

						Haplotypes/markera
Acronym	Country of origin	Breed	Marker sets genotyped	No. of individuals sampled	Total haplotypes	Mean	Range
PS1-IsH	Israel	Holstein	1	95	102	69.4	43–92
PS1-ItH	Italy	Holstein	1	159	128	111.0	61–128
PS1-BS	Au/Deu/Itb	Brown Swiss	1	133	100	72.4	50–96
PS2	Germany	Fleckviehc	1, 2	600	273	186.7	80–253
PS3	Israel	Holstein	3, 4	200	147	147.0	NRe
PS4	Israel	Holstein	1, 3, 4d, 5	27	40	40.0	NRe

^aNumber of haplotypes for calculating LD for a given marker pair.

^bAustria/Germany/Italy.

^cAlso known as Simmental.

^dMarker set 4 genotyped for 39 haplotypes only.

^eNR, not relevant, all haplotypes genotyped for all markers.

Markers:

Only dinucleotide microsatellite markers were used. PS1 was genotyped for 19 markers (marker set 1: MS1) spanning 78 cM of BTA13. PS2 was genotyped for 16 of the 19 MS1 markers and for an additional 19 markers (MS2) on the same chromosome (total of 35 markers). PS3 was genotyped for 5 markers (MS3) spanning 5.0 cM of BTA6 and 4 markers (MS4) spanning 4.5 cM of BTA11. PS4 was genotyped for MS1, MS3, and MS4 and for an additional 122 (total 157) markers (MS5) distributed among 21 bovine autosomes.

Haplotypes:

Haplotypes for PS2 were constructed by the Simwalk2 software (Sobel and Lange 1996) and by the PowerMarker software (Liu and Muse 2005) with some reliance on Mendelian relationships for PS1, PS3, and PS4. Individuals with wrongly assigned parentage were removed from the study. Only haplotypes for which 50% or more of the genotypes were known were included. For the PS1 populations, each sire and grandsire haplotype was included once only. Thus, the PS1 samples consisted primarily of unselected maternal haplotypes of the daughters and are therefore considered representative of the corresponding unselected cow populations. PS2 and PS3 included only maternal haplotypes of the sons or daughters, respectively. For PS2 these maternal haplotypes represent a highly selected group of cows (dams of young sires), which may not be representative of the unselected cow population. For PS3 and PS4 all haplotypes included in the sample were independent at the MGS level. As a result of the parentage and haplotype-frequency screens, the number of haplotypes in each population sample (except for PS4) was generally less than the number of individuals (Table 1). For PS1 and PS2, about two-thirds of the available haplotypes were informative for the average marker pair (Table 1). For PS3 and PS4, all haplotypes were available for all marker pairs.

LD measures:

The measures of LD used in this study were calculated as

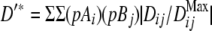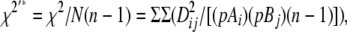where D_ij = pA_iB_j − pA_ipB_j; pA_i and pB_j are the population frequencies of alleles i and j at marker loci A and B, respectively; i = 1–n, j = 1–m; pA_iB_j is the observed frequency of the haplotype made up of alleles A_i and B_j; D_ij^Max = Min[pA_ipB_j; (1 − pA_i)(1 − pB_j)], when D_ij < 0, and Min[pA_i(1 − pB_j), (1 − pA_i)pB_j], when D_ij > 0; 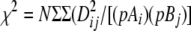; n and m are the number of alleles of the marker A or B having the lower and higher number of alleles, respectively; and N is the total sample size (number of haplotypes).

PowerMarker software (Liu and Muse 2005) provided estimates of D′* and χ² for each marker pair; χ^2′* was then calculated as χ^2′* = χ²/N(n − 1). Separation distances were binned as <5, 5–10, 10–20, 20–50, and >50 cM and nonsyntenic. LD measures were calculated separately for each population × separation distance (PD) combination.

Effect of sample size on LD:

Khatkar et al. (2008) showed that upward bias for r² and D′ was present for small samples. This can be expected to hold for χ^2′* as well. Since χ^2′* = χ²/N(n − 1), it will distribute as noncentral χ²/(n − 1) with d.f. = (n − 1)(m − 1). The sampling distribution of noncentral χ² will necessarily be skewed to the right for values of χ^2′* close to the lower boundary for this parameter (0.0) and skewed to the left for values close to the upper boundary (1.0). Consequently, the mean of the sample χ^2′* values will differ from the true population value. Since sample size in this study was relatively small, it was important to establish the effect of sample size on χ^2′* to interpret sample values in terms of population values. Following Khatkar et al. (2008), this was investigated by bootstrapping subsamples of various size from our population samples. Since each bootstrap included a large number of marker pairs, we assumed that 5 or 10 bootstraps (depending on the number of individuals sampled to the bootstrap) would be sufficient to characterize the distribution of χ^2′* values for the given sample size.

Statistical significance of LD measures:

Comparison-wise error rate P-values for each marker pair were provided by the PowerMarker statistical package using the Monte Carlo approximation to Fisher's exact P-value (henceforth, P-values). The P-values depend on the actual distribution of haplotypes for the marker pair and hence are obviously not affected by the statistic used to measure LD for that marker pair. Consequently, although D′* and χ^2′* for a given marker pair can differ widely in absolute magnitude, they will have the same P-value. For each PD combination, the statistical significance of the P-values was determined by a false discovery rate (FDR) approach (Benjamini and Hochberg 1995). FDR was controlled at a 5% level, and significance thresholds for P-values were determined accordingly.

Proportion of true LD values among all LD values:

Mosig et al. (2001) presented a histogram-based method further developed by Nettleton et al. (2006) for deconvoluting a mixture of n₁ false and n₂ true null hypotheses. The method is based on the difference between the observed distribution of the total of n P-values and the expected distribution under the null hypotheses. However, in this study, in a number of PD combinations where the proportion of P-values in the 0.00–0.50 bins (denoted P₅₀) was 0.50 or very close to 0.50 (which, as noted below, is indicative of the absence of falsified null hypotheses), the Mosig et al. (2001) procedure yielded appreciable positive estimates of n₁ for that PD combination. This led us to develop an alternative procedure for estimating n₁, which yields results virtually identical to those given by the Mosig et al. (2001) procedure when there is a significant excess of P-values in the P₅₀ bin but that does not return positive estimates of n₁ when P₅₀ ≤0.50. The new procedure is based on the conservative assumption that all P-values found in the 0.50–1.00 bins (henceforth, the P_50/100 bin) represent true null hypotheses. In this case, letting n_50/100 = the number of LD values in the P_50/100 bin, and 0.50 the expected proportion of values in the P_50/100 bin under the null hypothesis, we have n_50/100 = n₂ × 0.50, giving n₂ = n_50/100/0.50. Applying this procedure, n₂ and n₁ = n − n₂ were estimated from the histogram of P-values for each of the PD combinations, and the proportion of true LD values among all LD values was calculated as .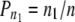

Relationship of LD values and P-values:

In normative experimental science, sample sizes are limited by considerations of expense and hence are set at the minimal size needed to uncover meaningful effects. LD analyses, however, are often based on genotyping results obtained in the course of other experiments, such as QTL mapping, that require large sample sizes. As a result, values of LD measures of very small magnitude, which are inconsequential for purposes of WGA or WGS, can have P-values that are highly significant due to the ever-present minor deviations of a typical real distribution from the theoretical distribution to which it is being compared.

Test for presence of LD across long-range intrachromosomal distances (>50 cM) and between nonsyntenic marker pairs:

Under the null hypothesis, 50% of P-values associated with LD measures should be in the P_0/50 bin and 50% in the P_50/100 bins. On this basis, following Farnir et al. (2000) we tested for the presence of true LD among long-range intrachromosomal (>50 cM) and nonsyntenic marker pairs by comparing observed to expected numbers of P-values in the P_0/50 bin, using standard chi-square goodness-of-fit test. Absence of a significant excess of values in the P_0/50 bin was taken to indicate the absence of true LD among the tested marker pairs.

Effect of population structure on LD measures:

Dairy and dual-purpose cattle populations consist for the most part of a small number of very-large sire-half-sib daughter families. This introduces an admixture component into the population structure, which can potentially generate long-range and nonsyntenic LD. To avoid this, LD studies in dairy cattle are based on maternal haplotypes of the offspring, with addition of no more than one exemplar each of the two sire haplotypes. This is the procedure followed by Farnir et al. (2000) and similar studies. However, even when this is done, there is possibility of residual family structure at the MGS level, since many of the dams of the daughters will be the progeny of a limited number of MGS. Indeed, on the basis of simulation studies Farnir et al. (2000) concluded that this was the source of the long-range LD that they observed. To evaluate possible effects of this nature, the PS3 and PS4 samples were constructed to have minimal family structure at the MGS level. In contrast, the PS1 and PS2 samples did not attempt to limit haplotype representation at the MGS level. Thus, similar LD measure distributions in PS1 and PS2 as compared to PS3 and PS4 would be an indication that population structure at the MGS level does not play a major role determining LD in these populations. PS3 and PS4 were genotyped for markers on 2 and 21 chromosomes, respectively, enabling nonsyntenic LD to be evaluated directly in these populations. PS1 and PS2 were genotyped for markers on a single chromosome only, and hence nonsyntenic LD could not be calculated directly. Instead, this was represented by intrachromosomal long-range LD (>50 cM).

RESULTS

Comparison of the two multi-allelic LD statistics:

Table 2 shows frequency distribution of the D′* and χ^2′* LD statistics between microsatellite markers for PS1 and PS2 for separation distances <5 and >50 cM. As will be shown in section Statistical significance of χ^2′* values, <5 cM represents a situation in which much true LD is present, while >50 cM represents a situation in which little if any true LD is present. At the <5 cM separation distance, mean D′* across the populations was 0.48 (range of means: 0.35–0.64). Corresponding values for χ^2′* were 0.16 (range: 0.11–0.22). For the >50-cM separation distance, mean values for D′* were 0.28 (range: 0.19–0.46) and 0.07 (range 0.04–0.10) for χ^2′*.

TABLE 2.

LD between microsatellite markers on BTA13 according to population sampled, LD statistic, and separation distance

LDa	PS1-IsH				PS1-ItH				PS1-BS				PS2 (all)
	<5 cM (n = 18)		>50 cMa (n = 14)		<5 cM (n = 18)		>50 cMa (n = 14)		<5 cM (n = 18)		>50 cMa (n = 14)		<5 cM (n = 82)		>50 cMa (n = 40)
	D′	χ2′*	D′	χ2′*	D′	χ2′*	D′	χ2′*	D′	χ2′*	D′	χ2′*	D′	χ2′*	D′	χ2′*
0.9													0.01		0.03
0.8	0.11												0.01
0.7					0.11				0.22				0.02		0.03
0.6					0.17				0.39		0.07		0.04
0.5	0.17				0.11	0.06			0.06		0.14		0.04	0.01	0.03
0.4	0.33				0.28				0.17		0.64		0.15	0.01	0.03
0.3	0.17	0.22		0.07	0.17						0.14		0.32	0.01	0.05
0.2	0.22	0.22	0.36		0.17	0.61			0.06	0.06			0.34	0.06	0.45
0.1		0.33	0.36	0.29	0	0.17	0.5			0.56		0.21	0.07	0.24	0.30	0.025
0.0		0.22	0.07	0.64	0	0.17	0.5	1.0		0.39		0.79		0.66	0.10	0.975
Mean	0.43	0.19	0.22	0.10	0.48	0.22	0.19	0.05	0.64	0.11	0.46	0.08	0.35	0.11	0.25	0.04
SD	0.15	0.10	0.08	0.09	0.17	0.11	0.05	0.02	0.18	0.05	0.07	0.02	0.15	0.09	0.18	0.02

n, number of marker pairs. PS1-IsH, Israel Holstein; PS1-ItH, Italian Holstein; PS1-BS, Austrian, German, Italian Brown Swiss; PS2, Fleckvieh. SD, standard deviation of LD values

^aBin boundaries: 0.00 = 0.000–0.099; 0.10 = 0.100–0.199, etc.

At the <5-cM separation distance, almost all D′* values but only 32% of χ^2′* values were ≥0.20; whereas at the >50 cM separation distance, 43% of D′* values were ≥0.20, but almost none of the χ^2′* values were in this range. Thus, even at the largest separation distance, which corresponds closely to the case of nonsyntenic markers (see section Analysis of nonsyntenic LD based on cumulative Fisher exact P-values), a high proportion of marker pairs show appreciable D′* values, consistent with the reports of the livestock studies cited above, which were based on microsatellites and the D′* statistic.

Effect of sample size on distribution of χ^2′*:

Table 3 illustrates the effect of sample size on the distribution of χ^2′*, according to separation distance (<5 and >50 cM) and population. For all PD combinations, decrease in sample size achieved by bootstrapping resulted in an appreciable increase in mean χ^2′* and in the proportion of LD values ≥0.20. The proportional increase in going from large to small sample size was generally twice as great for the >50-cM separation distance (mean: 105%; range: 16–166%) than for the <5-cM separation distance (mean: 60%; range: 20–110%).

TABLE 3.

Observed LD according to sample size and by population and separation distance

	PS1-IsH		PS2		PS3
χ2′*	All (69.4)	BE (40) (27.2)	All (186.7)	BE (100) (68.4)	All (147)	BE (100) (100)	BE (40) (40)
Separation distance <5 cM
0.5–0.6		0.08	0.01	0.04			0.02
0.4–0.5		0.13	0.01	0.01			0.03
0.3–0.4	0.22	0.21	0.01	0.05		0.01	0.10
0.2–0.3	0.22	0.26	0.06	0.14		0.04	0.33
0.1–0.2	0.33	0.24	0.24	0.49	0.50	0.64	0.44
0.0–0.1	0.22	0.08	0.66	0.28	0.50	0.31	0.09
n	18		82		16
Mean	0.19	0.28	0.11	0.16	0.10	0.12	0.21
>50 or nonsyntenic
0.5–0.6
0.4–0.5		0.06					0.01
0.3–0.4	0.07	0.14					0.01
0.2–0.3		0.20		0.03			0.21
0.1–0.2	0.29	0.37	0.03	0.42	0.05	0.09	0.60
0.0–0.1	0.64	0.23	0.98	0.55	0.95	0.91	0.16
n	14	70	40		20
Mean	0.10	0.19	0.04	0.09	0.06	0.07	0.16

In parentheses, the mean number of haplotypes per marker pair. n, number of marker pairs; All, all marker pairs included; BE, bootstrap estimates (BE 40, 10 bootstrap samples, each containing 40 individuals; BE 100, 5 bootstrap samples, each containing 100 individuals).

Statistical significance of χ^2′* values:

Table 4 shows the distribution of P-values associated with the χ^2′*, values according to PD combination. To enable comparison with PS1, PS2 is represented by the pooled bootstrap samples of 100 [PS2(100)] as well as by the full sample [PS2(All)]. Under the null hypothesis, we expect a uniform distribution of P-values among the P-value bins (i.e., 10% of P-values should fall into each bin). However, there was a distinct excess of P-values in the lowest P-value bin at all but the largest separation distance (>50 cM). This can most plausibly be attributed to the presence of true LD in these PD combinations. Across the three PS1 populations and the PS2(100) bootstrap, the weighted mean proportion of P-values in the 0–0.10 bin decreased from 0.67 at the <5-cM separation distance to 0.38, 0.22, and 0.12 at 5–20-, 20–50-, and >50-cM separation distances, respectively. The proportion of P-values in this bin for the >50-cM separation distance (0.12) differs only slightly from the 0.10 expected under the null hypothesis. The decrease in the proportion of P-values in the lowest bin with increased separation distance reflects a corresponding difference in the proportion of true LD values among all LD values. Estimates of the proportion of true LD values among all LD values for a given PD combination (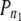) are very high at the separation distance of <5 cM (mean: 0.75), remain quite high at the separation distance of 5–20 cM (mean: 0.50), and then decrease rapidly at the separation distances of 20–50 cM (mean: 0.23) and >50 cM (mean: 0.09, and only 0.03, if an exceptionally high value for PS1-BS at this separation distance is excluded). Thus, these results indicate that a very high proportion of LD values at the <5-cM separation distance but essentially none of the LD values at the >50-cM separation distance represent true LD.

TABLE 4.

Distribution of Monte Carlo approximation to Fisher exact P-values according to population and separation distance

P	<5 cM					5–20 cM					20–50 cM					>50 cM
	PS1			PS2		PS1			PS2		PS1			PS2		PS1			PS2
	IsH	ItH	BS	All	100	IsH	ItH	BS	All	100	IsH	ItH	BS	All	100	IsH	ItH	BS	All	100
0.0–0.1	0.83	1.00	0.67	0.83	0.57	0.52	0.70	0.36	0.59	0.27	0.23	0.23	0.27	0.29	0.19	0.00	0.07	0.36	0.20	0.10
0.1–0.2	0.11	0.00	0.11	0.09	0.11	0.19	0.13	0.16	0.18	0.11	0.12	0.15	0.09	0.12	0.10	0.14	0.14	0.00	0.08	0.07
0.2–0.3	0.00	0.00	0.06	0.02	0.05	0.11	0.05	0.11	0.07	0.09	0.12	0.15	0.05	0.14	0.08	0.00	0.21	0.14	0.08	0.12
0.3–0.4	0.00	0.00	0.06	0.00	0.05	0.06	0.02	0.06	0.04	0.10	0.12	0.08	0.13	0.09	0.10	0.21	0.07	0.00	0.10	0.09
0.4–0.5	0.00	0.00	0.56	0.01	0.03	0.03	0.02	0.09	0.02	0.08	0.03	0.11	0.11	0.06	0.09	0.14	0.07	0.29	0.08	0.10
0.5–0.6	0.00	0.00	0.00	0.01	0.05	0.02	0.05	0.05	0.01	0.07	0.11	0.08	0.11	0.08	0.08	0.29	0.21	0.07	0.13	0.07
0.6–0.7	0.06	0.00	0.00	0.00	0.05	0.03	0.03	0.03	0.03	0.07	0.13	0.07	0.07	0.06	0.08	0.00	0.00	0.07	0.13	0.08
0.7–0.8	0.00	0.00	0.00	0.00	0.04	0.00	0.00	0.03	0.03	0.07	0.07	0.07	0.07	0.09	0.08	0.00	0.07	0.00	0.03	0.09
0.8–0.9	0.00	0.00	0.06	0.04	0.03	0.12	0.02	0.02	0.03	0.08	0.04	0.07	0.01	0.03	0.10	0.07	0.14	0.00	0.13	0.11
0.9–1.0	0.00	0.00	0.00	0.00	0.03	0.03	0.00	0.09	0.00	0.06	0.04	0.01	0.09	0.04	0.11	0.14	0.00	0.07	0.08	0.17
n	18	18	18	82	82	64	64	64	229	229	75	75	75	244	244	14	14	14	40	40
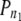	0.93	1.00	0.89	092	062	081	0.82	0.56	0.80	0.31	0.31	0.41	0.33	0.41	0.12	000	014	0.38	0.04	0.00
FDR 0.05	0.015	0.041	0.003	0.030	0.015	0.006	0.025	0.008	0.012	0.005	0.003	—	—	0.0007	0.0012	—	—	—	—	0.001
P0/50*	0.94	1.00	0.94	0.95	0.81	0.91	0.91	0.78	0.90	0.65	0.61	0.71	0.65	0.70	0.55	0.50	0.57	0.79	0.52	0.47

n, total number of marker pairs; 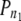, proportion of true LD values among all LD values; FDR 0.05, 0.05 FDR significance thresholds; P_0/50*, proportion of P-values in the 0.00–0.50 bin.

Table 4 also shows the FDR 0.05 thresholds for the various PD combinations. These vary according to separation distance, being least stringent for the <5-cM separation distance (range: P = 0.003–0.041) and about half this (range: 0.005–0.025) for the 5- to 20-cM separation distance. For the larger separation distances (20–50 and >50 cM), thresholds at this FDR either were very low or could not be found. The increasingly stringent thresholds with increasing separation distance are a consequence of the decrease in the proportion and possibly the magnitude of true LD at the greater separation distances.

Comparing the P-values and χ^2′* values for PS2(All) and PS2(100) illustrates clearly inflation of LD values at smaller sample sizes (Table 3) while the proportion of statistically significant LD values decreases (Table 4).

Analysis of nonsyntenic LD based on cumulative Fisher exact P-values:

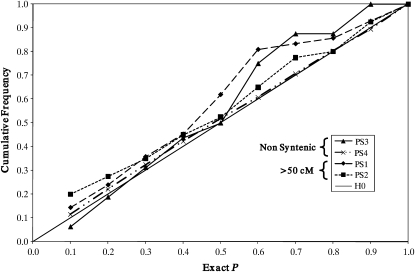
Figure 1 presents the cumulative distribution of P-values for marker pairs at a >50-cM separation distance for combined data of PS1 and PS2 (total 82 marker pairs) and for nonsyntenic marker pairs of PS3 (20 pairs) and PS4 (12,246 pairs). Both PS3 and PS4 closely track expectation under the null hypothesis. For the PS1 and PS2 combined data for long-range intrachromosomal separation (>50 cM), there is a very slight positive deviation across the lowest value bins, but the distribution of P-values did not differ significantly from expectation under the null hypothesis. Thus, these data do not support the presence of long-range or nonsyntenic LD.

Figure 1.—

Cumulative Fisher exact P-values according to population and separation distance. PS1, mixed sire and maternal haplotypes combined values for ItH, IsH, and BS; PS2, Fleckvieh sire maternal haplotypes; PS3, IsH cow maternal haplotypes; PS4, IsH sire maternal and paternal haplotypes; PS1 and PS2, marker pairs at separation distance >50 cM, independent at sire level but not at MGS level; PS3 and PS4, nonsyntenic marker pairs independent at MGS level.

Relation of χ^2′* values and Fisher exact P-values:

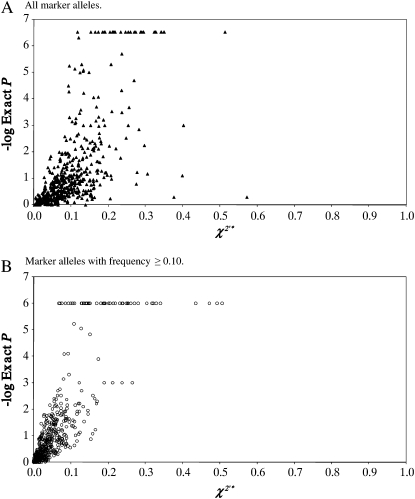
Figure 2 presents a scattergram of LD values against P-values for the combined χ^2′* values of the three PS1 populations and all separation distances. χ^2′* values based on all marker alleles (Figure 2A) and χ^2′* values limited to marker alleles with frequency ≥0.10 (Figure 2B) are shown separately. The very broad spread of P-values corresponding to the same χ^2′* value and of χ^2′* values corresponding to the same P-value is immediately apparent. Thus, when all marker alleles are included in LD calculations, LD measures tell little about P-values, and P-values tell little about LD. The spread is much less, but still present, when LD measures are limited to alleles with a frequency ≥0.10. Lack of correspondence between the absolute magnitude of LD measures and the significance of P-value is exacerbated when a sample size is large. For example, for marker pair BMS1145 and BL42 on BTA13 of PS1-IsH, we obtained χ^2′* = 0.014; i.e., useful LD at this marker pair is as low as possible. Indeed, P = 1.0 at the actual sample size of 45. Yet at sample size N = 450, for the same proportional distribution of haplotypes, P = 0.0078, which is highly significant, while χ^2′* is unchanged at 0.014.

Figure 2.—

Scattergram showing χ^2′* against Fisher exact P-values for combined marker pairs of the three PS1 populations, separately for (A) marker pairs including all marker alleles and (B) for marker pairs including only marker alleles with minor allele frequency (MAF) ≥0.10. In some cases, the PowerMarker program returns a value of 0.00 for the Fisher exact P-value. In this case, for technical reasons, the value for −log exact P was arbitrarily set at 6.0 for the P-values calculated using marker alleles with MAF ≥0.10 and to 6.5 for the P-values calculated using all marker alleles.

Distribution of χ^2′* by population and separation distance:

Table 5 presents the distribution of observed χ^2′* values for the three PS1 populations and for PS2(All) and PS2(100). Mean χ^2′* for the three PS1 populations and for PS2(100) decreased steadily with an increase in separation distance, being equal to 0.174, 0.108, 0.094, and 0.082 for the <5-, 5–20-, 20–50-, and >50-cM separation distances, respectively. The major decline (by 48%) was in going from <5 to 5–20 cM. Thereafter, declines were much less, being 13% for each of the two subsequent steps. Taking the >50-cM separation distance as roughly approximating the null condition, it is evident that most of the observed LD at the 5–20- and 20–50-cm separation distances represents the null condition, with only a slight admixture of true LD. This view is supported by consideration of the proportion of statistically significant χ^2′* values (P_s) by χ^2′* bin according to PD combination. All χ^2′* values ≥0.30 were significant, irrespective of population or separation distance. Conversely, almost all χ^2′* values ≤0.10 were not significant, irrespective of PD combination. For the χ^2′* 0.10–0.20 and 0.20–0.30 bins, however, there was a clear decline in P_s with increasing separation distance. At <5 cM, almost all χ^2′* values in both bins were significant. At 5–20 cM, almost all χ^2′* values in the 0.20–0.30 bin, but half of values in the 0.10–0.20 bin, were significant. For the two larger separation distances (20–50 and >50 cM) almost none of the χ^2′* values in these bins were significant. This is consistent with the assumption that almost all LD values at these separation distances represent the null situation.

TABLE 5.

Distribution of LD values for the three PS1 subpopulations and for PS2 (all) and PS2(100)

χ2′*	<5 cM					5–20 cM					20–50 cM					>50 cM
	PS1			PS2		PS1			PS2		PS1			PS2		PS1			PS2
	IsH	ItH	BS	All	100	IsH	ItH	BS	All	100	IsH	ItH	BS	All	100	IsH	ItH	BS	All	100
0.5		0.056		0.012	0.027					0.003	0.013				0.001
0.4				0.012	0.012						0.013
0.3	0.222			0.012	0.049	0.047			0.004	0.017	0.013	0.013			0.006	0.071
0.2	0.222	0.611	0.056	0.061	0.139	0.063	0.078	0.031	0.004	0.071	0.080	0.027	0.027		0.053					0.025
0.1	0.333	0.167	0.556	0.244	0.488	0.547	0.391	0.328	0.127	0.405	0.373	0.160	0.347	0.020	0.412	0.286		0.214	0.025	0.421
0.0	0.222	0.167	0.389	0.659	0.276	0.344	0.531	0.641	0.865	0.504	0.507	0.800	0.627	0.980	0.529	0.643	1.000	0.786	0.975	0.553
n	18	18	18	82	82	64	64	64	229	229	75	75	75	244	244	14	14	14	40	40
Mean	0.193	0.224	0.113	0.108	0.164	0.131	0.104	0.085	0.063	0.113	0.118	0.074	0.080	0.048	0.105	0.101	0.048	0.084	0.040	0.094
SD	0.102	0.102	0.051	0.091	0.114	0.067	0.062	0.058	0.040	0.071	0.095	0.057	0.051	0.024	0.058	0.091	0.021	0.025	0.024	0.051
Ps (0.2)	1.00	1.00	1.00	0.83	1.00	1.00	1.00	1.00	0.00	0.65	0.17	0.00	0.00		0.22	0.00				0.75
Ps (0.1)	0.83	1.00	0.90	1.00	0.26	0.23	0.80	0.43	0.77	0.08	0.00	0.00	0.00	0.00	0.02	0.00		0.00	0.00	0.01
Ps (0.0)	0.00	0.67	0.14	0.72	0.00	0.00	0.29	0.00	0.32	0.00	0.00	0.00	0.00	0.02	0.00	0.00	0.00	0.00	0.05	0.00

The number (n), mean, and standard deviation (SD) of LD values according to separation distance are shown. n_i, total number of LD values in the ith LD bin; P_s (i) = proportion of significant LD tests in the ith LD bin.

Effect of population structure:

For the PS3 and PS4 samples, the cumulative distribution of Fisher exact P-values for nonsyntenic marker pairs of both populations closely tracked expectation under the null hypothesis (Figure 1). Thus, at least in the IsH population, family structure deeper than grandparent level apparently did not contribute to LD. The PS1 and PS2 samples included only independent haplotypes at the sire level, but did not attempt to limit haplotype representation at the MGS level. Thus, any family structure effects on LD at the grandparent level should be expressed in these samples. Nevertheless, for these populations cumulative distribution of Fisher exact P-values for marker pairs on BTA13 at a separation distance >50 cM did not reveal any deviation from expectation on the null hypothesis (Figure 1). Thus, there is no indication in these data of grandparental or more remote population structure effects on LD.

DISCUSSION

Extent of LD in the study populations:

Comparison of the values obtained for D′* and χ^2′* clearly demonstrate the upward bias of the D′* statistic, which gave moderate-to-high values at the greatest intrachromosomal separation distances (>50 cM) and even for nonsyntenic marker pairs. In contrast, χ^2′* values dropped off rapidly with increasing separation distance and were very low for separation distances >20 cM and for nonsyntenic pairs. The tendency to high values for D′* is not unexpected. It is well known that for diallelic markers D′ tends to be strongly inflated, especially in cases of small sample size and low minor allele frequency. This tendency is undoubtedly exacerbated for microsatellite markers because of the general presence of one or more alleles at low frequency. Similar comparative results for D′* and χ^2′* have recently been reported for sheep (Meadows et al. 2008).

Working with SNP markers, Khatkar et al. (2008) found that once sample size reached 75 haplotypes, there was no further change in the sample values of r². In this study, χ^2′* continued to decrease from samples of 27 to 69 haplotypes (PS1-IsH), 68 to 187 haplotypes (PS2), or 40 to 100 to 147 haplotypes (PS3). Thus, the LD values obtained in this study may be biased upward, and sample sizes >200 haplotypes may be needed to accurately assess population LD values for multi-allelic markers.

The microsatellite results of this study indicate the absence of useful long-range intrachromosomal and nonsyntenic LD in the study populations. They do, however, suggest the presence of considerable LD at the <5-cM range. The values obtained for χ^2′* at this separation distance, although much less than those given by D′*, are still considerably greater than those reported at this separation distance in cattle for diallelic SNP markers, using the comparable r² measure (McKay et al. 2007; Khatkar et al. 2008; Sargolzaei et al. 2008). In this study, the majority of marker pairs at this separation distance show highly significant LD, and the observed magnitude of LD is at a level that would be useful for WGA and WGS applications. However, as noted, LD values showed a strong inverse relation to sample size, and it turned out that the sample sizes available in this study were not large enough to asymptotically reflect population values. Thus, we cannot extrapolate with confidence from our sample χ^2′* values to the actual underlying population values for χ^2′* at the <5-cM separation distance in the study populations. It would certainly be of interest to reexamine this question either by theoretical analysis of noncentral χ² or by examining a larger sample base. Nevertheless, it is relevant that the decrease in observed χ^2′* from smaller to larger sample size was only half as great at the <5-cM separation distance as at the other separation distances. This is what would be expected if a high proportion of the values for the <5-cM separation distance were asymptotically approaching a population value that differs appreciably from zero, while a high proportion of the values for the >5-cM separation distances were asymptotically approaching a zero population value. Thus, LD between multi-allelic markers may indeed be greater and extend over longer distances than LD among diallelic markers. This could be exploited using SNP arrays by constructing multi-allelic SNP haplotypes (Pe'er et al. 2006).

The coefficient of variation of χ^2′* (SD/mean) was very high (average 0.59 across all PD combinations). Part of this may be due to an admixture of true and false LD and part to sampling variation of small samples, but a considerable residual at the lowest separation distance apparently represents true LD. Thus, a fraction of marker pairs may present useful levels of LD at the <5-cM separation distance.

The magnitude of LD appeared to be greater and to extend over longer distances in the two Holstein populations than in the Brown Swiss population. This can be attributed to the very effective and intense long-term selection in the Holstein breed on the basis of young sire progeny testing focused on milk yield. In contrast, the Brown Swiss was originally a dual-purpose breed selected for multiple objectives and was not subject to advanced selection procedures until more recently. The Fleckvieh (PS2), which remains a dual-purpose breed selected for multiple objectives to this day, is not directly comparable to the PS1 populations, since the maternal chromosomes representing this breed were derived from a granddaughter design and hence represent a highly selected sample.

Effect of population structure on LD:

Results of this study show that, when family structure at the MGS level is removed from the population as in PS3 and PS4, the distribution of nonsyntenic LD closely follows expectation on the null hypothesis of absence of true LD. Furthermore, it appears that when LD analysis is based on independent haplotypes at the sire level—that is, of maternal haplotypes only, as in PS2, or with each of the two sire haplotypes appearing no more than once in the analysis as in PS1—residual family structure at the MGS level does not appear to be a factor affecting LD analysis. We believe that the difference between these results and those of Farnir et al. (2000) is due to the difference in sample size of the two studies. Farnir et al. (2000) employed sample sizes large enough so that deviations from expectation may have been due primarily to the inevitable deviation of real population values from those expected on asymptotic approximation of theoretical distributions. Thus, when sample size is even moderately large, many long-range or nonsyntenic marker pairs that present negligible χ^2′* values may nevertheless show highly significant P-values. In effect, when sample size is large, almost everything will be significant, and hence statistical significance does not distinguish between consequential and inconsequential effects. In this study, sample sizes were much smaller, so that deviations from expectation were primarily generated by sampling, and hence the differences between sample values and expectation distributed more or less as expected under the null hypothesis. This could be tested more stringently by increasing sample size of the PS1 populations to be comparable to that of the Farnir et al. (2000) study.

This analysis implies that the significant results over long distances of Farnir et al. (2000), although of negligible magnitude for predictive purposes, are nevertheless real and are possibly due to very small effects of population structure that become important when sample sizes are large. This has implications for WGA, which also involves large sample sizes, and may therefore present results of high significance but little value. To avoid this, it may be useful to choose a sample that limits any individual MGS to one or a small number of appearances as in the PS3 population.

Taken together, the above considerations provide a plausible explanation for the results of Farnir et al. (2000) and similar studies in which appreciable levels of LD at high statistical significance were found across large intrachromosomal distances or even across nonsyntenic chromosomes. Namely, the use of the D′* measure provided ostensibly high magnitudes of LD, and the use of large samples imparted high statistical significance to these inflated LD values.