Incorporating Desirable Genetic Characteristics From an Inferior Into a Superior Population Using Genomic Selection

Abstract

Resistance to specific diseases may be improved by crossing a recipient line with a donor line (a distantly related strain) that is characterized by the desirable trait. However, considerable losses in the total merit index are expected when crossing recipient and donor lines. Repeated backcrossing with the recipient line will improve total merit index, but usually at the expense of the newly introgressed disease resistance, especially if this is due to polygenic effects rather than to a known single major QTL. This study investigates the possibilities for a more detailed introgression program based on marker-trait associations using dense marker genotyping and genomic selection. Compared with classical selection, genomic selection increased genetic gain, with the largest effect on low heritability traits and on traits not recorded on selection candidates (due to within-family selection). Further, within a wide range of economic weights and initial differences in the total merit index between donor and recipient lines, genomic selection produced backcrossed lines that were similar or better than the purebred lines within three to five generations. When using classical selection in backcrossing schemes, the long-term genetic contribution of the donor line was low. Hence, such selection schemes would usually perform similarly to simple purebreeding selection schemes.

MANY purebred, domesticated populations may benefit from introgression of favorable alleles from wild or other inferior populations possessing some favorable heritable characteristics. As an example, here we will use two fish populations: one population of farmed fish (recipient line) characterized by high levels of productivity (e.g., growth) and one population (e.g., a wild population) characterized by high levels of disease resistance, but low productivity (donor line). Recent technological development in molecular genetics has given new opportunities for introgressing specific alleles from generally inferior populations by use of information on marker and quantitative trait loci (QTL) (Visscher et al. 1996; Hospital 2001; Wall et al. 2005). Single-gene introgression schemes have been carried out in a number of species, mainly plants, e.g., barley (Jefferies et al. 2003), and in experimental animals, e.g., mice (Koudande et al. 2005). More complex multi-gene introgression schemes have been suggested for known QTL (Hospital et al. 2000; Piyasatian et al. 2008).

In genomic selection (Meuwissen et al. 2001), marker-allele effects are estimated, and individuals are selected on the basis of the sum of marker-allele estimates across all marker loci. Combining introgression schemes with genomic selection may be a more flexible way of incorporating favorable multi-gene characteristics of donor lines into recipient lines and thereby optimize the genome of future farmed populations, without having to choose between a synthetic population or an introgression scheme aiming at minimizing linkage drag from the donor line. As individuals are selected on the basis of the sum of estimated marker effects across the entire genome, QTL positions do not need to be known in advance, and any favorable QTL allele from the donor line may be introgressed, not only the known and the most favorable ones. However, introgression of specific QTL cannot be assured as selection is for the total genetic effect across all genomic regions. Accuracy of genomic selection is likely to be higher than for classical selection (Meuwissen et al. 2001), especially for traits of low heritability and for traits that cannot be recorded on selection candidates (Dekkers and Hospital 2002), e.g., disease resistance and slaughter traits.

In this simulation study, we combine the genetic resources of two already existing populations—a recipient line, initially selected for production traits, and a donor line, (naturally) selected for disease resistance—with the aim of producing an offspring population combining favorable DNA segments from both populations. Our objective was to improve both production and disease resistance traits, where the disease trait is assumed to be recorded on sibs of the selection candidates by disease challenge testing (typical for fish-breeding schemes). We compared the following three strategies to achieve this objective: a purebred recipient line selected for both traits; a synthetic line created from crossing the recipient and donor lines, followed by selection for both traits; and a crossbred line subjected to (potentially) repeated backcrossing with the recipient line, combined with selection for both traits (introgression scheme). The different strategies were compared by computer simulations of the genomes of all involved individuals, applying both classical and genomic selection, with varying heritabilities and economic weights for the two traits.

MATERIALS AND METHODS

Population structure:

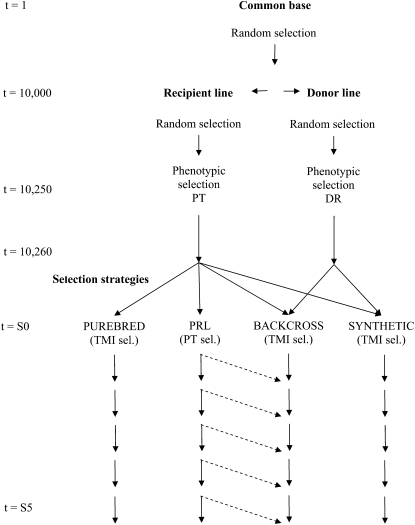
The selection experiment was designed to utilize genetic resources of two partially separated fish populations that were assumed to be readily available at the start of the selection experiment (e.g., an already existing domesticated strain and a distantly related wild strain). The two populations were generated by simulating a common base population, which subsequently was split into two lines that were separated for a number of generations. This produced two partially differentiated base populations. A general description of the base populations and selection schemes is given in Figure 1.

Figure 1.—

Structure of selection schemes.

The common base population was generated and mated for 10,000 generations (t = 1–10,000), applying random sampling with replacements of 500 sires and 500 dams (i.e., effective population size N_e = 1000, assuming the Wright–Fisher idealized population model). At t = 10,001, the base population was split into two equally sized subpopulations by random sampling with replacement of 500 males and 500 females for each subpopulation. These two populations were kept separate (with N_e = 1000 for each population) for the following 250 generations (t = 10,001–10,250). For the next 10 generations (t = 10,251–10,260), the recipient and donor lines were phenotypically selected for a production trait (PT) and disease resistance (DR), respectively, by selecting the top 10% of males and females, assuming heritabilities of 0.1 for both traits. This was done to produce a recipient line with an enhanced genetic level for productivity traits (e.g., growth) and a donor line with an enhanced genetic level for disease resistance. The resulting two lines (generation t = 10,260) were then used as base populations in the following selection experiment.

To produce the first generation of the selection experiment, randomly selected sires and dams from the recipient line (t = 10,260) were mated to produce purebred lines, and randomly selected dams from the recipient line (t = 10,260) were mated with randomly selected sires from the donor line to produce F₁ crossbreds. The resulting generation (termed S0) was then used in the different selection schemes, where five subsequent generations were generated (S1–S5). Throughout the entire simulation study, sires and dams were replaced every generation.

Selection:

Four selection strategies were used for generations S0–S5: (1) purebreeding of the recipient line, using a breeding objective with PT only (termed production line, or PRL), which may be seen as a currently available commercial line undergoing selection for improved productivity in a classical breeding program; (2) purebreeding of the recipient line, using a breeding objective with both PT and DR (termed PUREBRED); (3) creation of F₁ crossbreds of recipient and donor lines, followed by intermating selection candidates from the crossbred line (termed SYNTHETIC); and (4) an introgression strategy based on the F₁ line described above, where males from the crossbred line are backcrossed with females from the recipient (PRL) line (termed BACKCROSS). In the BACKCROSS scheme, backcrossing was done only to the extent that females from the PRL were superior to females recruited from within the BACKCROSS on the basis of their estimated breeding values (EBV). Hence, if the BACKCROSS line becomes increasingly superior (or less inferior) over time, actual use of females from the PRL reduces.

For generations S0–S5, all lines were kept at a constant size of 1000 breeding candidates within each line, and 50 sires and 50 dams were selected per line. For S0, random selection and mating with replacement were applied, while, for generations S1–S5, truncation selection on the basis of predicted EBVs was used. The selected 50 sires and 50 dams were randomly mated with replacement to create 50 full-sib families with 20 offspring each to form selection candidates for the next generation. Additionally, all families within the PUREBRED, SYNTHETIC, and BACKCROSSED lines produced 20 offspring, which were used in sib testing for DR.

Genome structure:

The genome structure was assumed to be diploid with 10 chromosomes, each with a size of 100 cM, assuming the Haldane mapping function and Mendelian inheritance of all loci. For each chromosome, 500 microsatellite marker loci were assumed, as well as 100 QTL per trait (PT and DR). Markers and QTL loci were randomly spaced throughout each chromosome. It was assumed that all loci (both marker and QTL) had two initial alleles with frequencies (in t = 1) sampled from a uniform distribution in the interval [0, 1]. Rates of mutations for marker and QTL alleles were 0.0001 and 0.00001, respectively (per allele and meiosis for each generation). All mutations generated new alleles, and all loci were thus potentially multi-allelic. The allelic effects of the QTL (both original and novel mutations) were sampled from a gamma distribution with a shape parameter of 0.40 and a scale parameter of 0.13. No pleiotropy was assumed, implying zero genetic covariance between the traits before selection. As the gamma distribution produced only positive values, each QTL effect was assumed to be either negative or positive with a probability of 0.5.

For generation t = 10,260, ∼80% of the marker loci were segregating within each subpopulation while the corresponding number for the segregating QTL was ∼15%.

Linkage disequilibrium (LD) between adjacent markers was calculated as the standardized chi-square, χ^2′ (Yamazaki 1977; Heifetz et al. 2005), which extends the usual R² to multi-allelic markers:

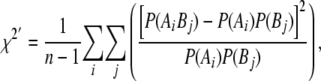where 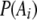is the frequency of allele i at locus A, 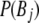is the frequency of allele j at locus B, 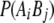is the frequency of the haplotype with allele i at locus A and j at locus B, and n is the number of alleles at the marker with the smaller number of alleles. Average 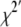and expected (Sved 1971) LD for both adjacent markers were 0.2, where the expectation was based on the actual distance within each pair.

Data:

True breeding values of an individual were defined as the sum of QTL allelic effects for the individual across all 1000 QTL loci for each trait. At generation t = 10,250, QTL effects were scaled so that the total genetic variance of both traits (before selection) equaled 1.0 within the recipient line. Phenotypes of both traits were produced by adding normally distributed error terms, sampled from 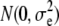, to the true breeding values of each individual. In the following, heritabilities are presented as the ratio of genetic variance (at t = 10,250) to total phenotypic variance within the recipient line. For both traits, h² ranged between 0.1 and 0.5 (by varying 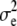). It was assumed that all individuals within the relevant lines were genotyped for the available 5000 marker loci.

PT:

The production trait was recorded on all selection candidates (1000 individuals per line and generation).

DR:

Disease resistance was recorded on full-sibs of the selection candidates, using a challenge-test type of design (1000 individuals per line and generation) except for the PRL, where only the average genetic level was assumed to be available. Individuals challenge tested for DR were not considered as selection candidates.

Breeding value estimation:

Genomic BLUP prediction:

Marker effects were estimated using the BLUP estimation procedure of marker effects (Meuwissen et al. 2001) with the statistical model

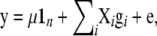where y is the data vector (PT or DR), 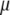is the overall mean, 1_n is a vector of n ones, g_i 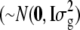is a vector of allele by base population effects associated with a marker at position i, X_i is the design matrix for the marker effect i, and e is a vector of random residuals 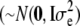. Genetic variance was assumed to be identical across loci and set to 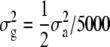, where 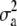is the total genetic variance (set to 1.0 at generation t = 10,250), 5000 is the number of marker loci, and the factor is because each animal has a paternal and a maternal allele. All crossbred lines (SYNTHETIC and BACKCROSS) will have marker alleles from both the originating populations. Marker alleles from the two base populations may be identical, but in LD with different QTL alleles. Consequently, a marker by base population effect was fitted, assuming that the marker alleles of each individual can be traced back to their originating base populations (i.e., the gametic phase is known). Marker effects were reestimated each generation, using data from both the current and all preceding generations (down to S0). Individual Genomic BLUP (GBLUP) values for the two traits were calculated as the sum of all estimated marker effects associated with each trait across the entire genome.

Classical BLUP prediction:

EBVs were obtained by classical BLUP (CBLUP) predicted with the model

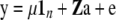(Henderson 1984), where a is a vector of random additive genetic effects of each individual 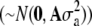, A is the additive relationship matrix, Z is a design matrix for the additive genetic effect, and the other parameters are as described above. The true total genetic (in generation t = 10,250) and residual variances were used as input parameters. The CBLUP of DR for selection candidates was calculated on the basis of sib and pedigree data, as selection candidates cannot be tested for disease.

Selection criteria:

Individuals were selected on the basis of total merit index (except for the PRL line), i.e., the sum of GBLUP or CBLUP EBVs for the two traits multiplied with their corresponding economic weights. In some of the schemes (BACKCROSS), selection was across breeding candidates having either CBLUP or GBLUP selection criteria. The expected regression coefficient of true breeding value on CBLUP equals unity. However, this is not necessarily the case for GBLUP (Meuwissen et al. 2001), and the two EBVs are hence not directly comparable. To make the two criteria comparable, GBLUP values were scaled by a factor of

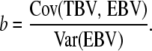In real data, the necessary scaling factors may be estimated through regression of phenotypes of offspring on mid-parent GBLUP EBVs.

Scenarios:

Two sets of economic weights were used: either 100% (2:1) or 200% (3:1) higher relative weight on PT compared with DR. Heritabilities were low (0.1) for both traits, high (0.5) for both traits, or high (0.5) for PT and low (0.1) for DR. Further, all selection schemes (except PRL) were tested using the two selection criteria (CBLUP and GBLUP).

Calculation of summary statistics:

A total of 50 replicates were produced for each combination of scenario (economic weights and heritabilities), selection strategy, and method of breeding value estimation. For a given replicate number, sires and dams for the S0 generation were recruited from identical populations (i.e., generation t = 10,260 of a given replicate is identical for all scenarios and selection methods). Average level of true breeding values (DR, PT, and TMI) and average level of inbreeding were produced for each replicate and generation and averaged over all 50 replicates. Genetic gains for PT, DR, and TMI were then calculated as differences in true genetic level from generation S0 to S5.

RESULTS

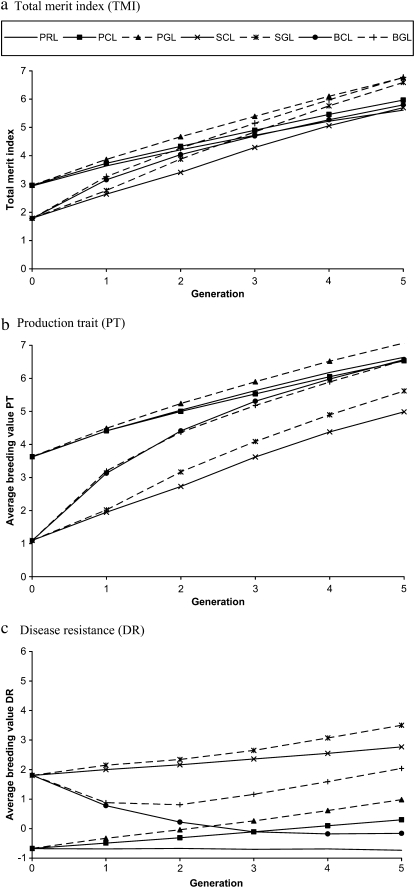
At generation S0, the average genetic differences (in genetic standard deviations) between the recipient (PUREBRED and PRL) and the F₁ crossbred lines (SYNTHETIC and BACKCROSS) were 2.5 and −2.5 for PT and DR, respectively (Figure 2, b and c). Correspondingly, the differences in TMI (Figure 2a) were 1.1 and 1.6 genetic standard deviations between the recipient and F₁ crossbred lines, assuming, respectively, 100 or 200% higher economic weight for PT (economic weights were 2:1 and 3:1). Genetic variances were identical for the two traits.

Figure 2.—

Genetic levels for (a) TMI, (b) PT, and (c) DR by generation for the different selection schemes under the scenario with low (0.1) heritabilities for both traits. The selection schemes presented are PRODUCTION LINE (PRL), PUREBRED CBLUP (PCL), PUREBRED GBLUP (PGL), SYNTHETIC CBLUP (SCL), SYNTHETIC GBLUP (SGL), BACKCROSS CBLUP (BCL), and BACKCROSS GBLUP (BGL). The relative economic weight of PT vs. DR was 2:1.

As expected, genetic variance in crossbred lines (after the F₁ cross) was larger than for the purebreds. For example, assuming no selection, the synthetic line had ∼50% higher genetic variance in generation F₂ (S1), compared with the purebred (recipient) line (not shown).

Scenario 1: low heritabilities for PT and DR:

Ratio of economic weights for PT and DR 2:1:

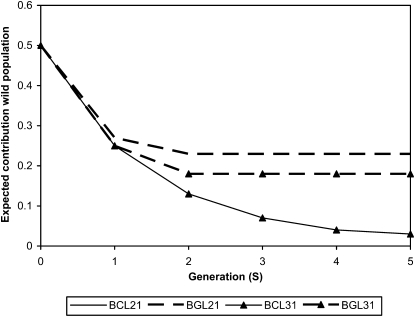
Genetic levels by generation for TMI, PT, and DR (based on true breeding values) are shown in Figure 2 (a, b, and c, respectively). Further, genetic gains for PT, DR, and TMI from generation S0 to S5 for the different selection schemes are shown Table 1. When comparing the genetic gain in TMI for the different selection strategies, genomic selection in general was favorable relative to classical selection (26, 23, and 24% higher genetic gain for TMI between S0 and S5 in PUREBRED, SYNTHETIC, and BACKCROSS, respectively), with the most profound effect on DR (70 and 75% higher genetic gain for the nonbackcrossed PUREBRED and SYNTHETIC lines, respectively). The latter may be explained by the fact that the trait cannot be recorded on breeding candidates, and the favorable effect of genomic selection is thus a consequence of moving from between-family selection (CBLUP) to individual selection (GBLUP). Both crossbred alternatives (SYNTHETIC and BACKCROSS) had generally higher genetic gains compared with the PRL and PUREBRED lines. Starting from the relatively low genetic level of the initial crossbred generation, TMI for the BACKCROSS and SYNTHETIC GBLUP lines passed the PRL at generations S2 and S3, respectively (Figure 2c), and at generation S5, the BACKCROSS GBLUP even passed the PUREBRED GBLUP. The superiority of the BACKCROSS GBLUP is likely to increase in subsequent generations due to its higher genetic gain, even without backcrossing, and the latter strategy is therefore preferred. For the BACKCROSS GBLUP, backcrossing with the PRL occurred mainly up to generation S2 (Figure 3), causing an initial drop in genetic level for DR (Figure 2). Thereafter, the BACKCROSS selection strategy was more or less shifted toward a synthetic line (with no substantial backcrossing) selected for both traits, resulting in positive genetic gain for DR. For the PUREBRED selection scheme, ratio of genetic gains of DR relative to PT was approximately equal to the ratio of their relative economic weights (2:1), despite the fact that DR was recorded on sibs only, while PT was recorded on both sibs and the selection candidate itself. Using classical selection, the ratio of genetic gains (DR vs. PT) was considerably higher (e.g., lower relative gain in DR), which may be explained by a larger disadvantage by lack of individual data on DR for selection candidates. The ratio of genetic gains (DR vs. PT) was generally higher for the SYNTHETIC scheme (for both selection methods), which can be explained by a realized negative genetic correlation between the traits (result of crossing the two base populations).

TABLE 1.

True genetic gains from generations S0 to S5 for PT, DR, and TMI for the different selection schemes in the scenarios with low (0.1) heritability for both PT and DR

	Genetic gain in generations S0–S5
Selection scheme	PT	DR	TMI
Relative economic weights: PT = 2, DR = 1
PRL	3.02 (0.09)	−0.05 (0.08)	2.67 (0.09)
PCL	2.91 (0.11)	0.97 (0.07)	3.03 (0.10)
PGL	3.44 (0.11)	1.65 (0.09)	3.82 (0.10)
SCL	3.89 (0.12)	0.97 (0.12)	3.91 (0.10)
SGL	4.52 (0.14)	1.70 (0.12)	4.80 (0.11)
BCL	5.48 (0.16)	−1.96 (0.12)	4.02 (0.14)
BGL	5.46 (0.18)	0.23 (0.15)	4.99 (0.13)
Relative economic weights: PT = 3, DR = 1
PRL	3.03 (0.10)	−0.15 (0.09)	2.83 (0.10)
PCL	3.05 (0.10)	0.69 (0.07)	3.11 (0.09)
PGL	3.50 (0.11)	1.31 (0.08)	3.74 (0.10)
SCL	3.98 (0.11)	0.50 (0.08)	3.93 (0.10)
SGL	4.73 (0.13)	0.78 (0.12)	4.73 (0.12)
BCL	5.57 (0.15)	−2.17 (0.12)	4.60 (0.14)
BGL	5.81 (0.16)	−0.73 (0.14)	5.28 (0.14)

All values are given in genetic standard deviations. Standard errors are given in parentheses. PRL, production line; PCL, purebred classically selected line; PGL, purebred genomically selected line; SCL, synthetic classically selected line; SGL, synthetic genomically selected line; BCL, backcrossed classically selected line; BGL, backcrossed genomically selected line.

Figure 3.—

Expected genetic contribution of the donor line to the backcrossed line (based on pedigree information) by generation for the low heritability (0.1 for both traits) scenarios. The recipient lines presented are BCL21, BGL21, BCL31 and BGL31 (BC, BACKCROSS CBLUP; BG, BACKCROSS GBLUP; first number, economic weight for production trait; second number, economic weight for disease resistance). The curves for BCL21 and BCL31 are overlapping.

Ratio of economic weights for PT and DR 3:1:

Genetic gains for PT, DR, and TMI from generation S0 to S5 for the different selection schemes are shown in Table 1. Results in general were similar to the preceding scenario. The initial genetic differences in TMI between the purebred recipient lines (PRL + PUREBRED) and the F₁ crossbred (SYNTHETIC + BACKCROSS) was somewhat larger than for the scenario above (1.6 vs. 1.1 genetic standard deviations). As a result, the genetic level of TMI for the BACKCROSS GBLUP line did not outperform the PUREBRED GBLUP line during the experiment, but the lines were similar at generation S5 (results not shown). Hence, the BACKCROSS GBLUP line would outperform the PUREBRED GBLUP line in the long run due to faster genetic gain. As a result of increased backcrossing and reduced relative economic weight for DR, the drop in genetic level for DR was deeper and more sustained (not shown).

Scenario 2: high heritabilities for PT and DR:

Ratio of economic weights for PT and DR 2:1:

Genetic gains for PT, DR, and TMI from generation S0 to S5 for the different selection schemes are shown in Table 2. As expected, when heritabilities of the two traits were high (0.5 for both traits), genetic gains in TMI were generally higher than in the preceding scenarios. In classical selection, the increased genetic gain in TMI due to higher heritabilities for both traits to a larger extent was explained by increased genetic gain for PT, while for genomic selection the genetic gains of the PUREBRED line were still proportional to the relative economic weights of the two traits (2:1). Thus, compared with the preceding scenarios, the relative advantage of genomic selection relative to classical selection was even more extreme for DR (average genetic gain increased 115 and 179% for the nonbackcrossed PUREBRED and SYNTHETIC lines, respectively). With respect to TMI, the BACKCROSS GBLUP was superior to all other lines from generation S4 onward.

TABLE 2.

True genetic gains from generations S0 to S5 for PT, DR, and TMI for the different selection schemes for the scenario with high (0.5) heritabilities for both PT and DR

	Genetic gain in generations S0–S5
Selection scheme	PT	DR	TMI
PRL	4.32 (0.11)	−0.06 (0.07)	3.84 (0.11)
PCL	4.07 (0.11)	1.11 (0.07)	4.14 (0.09)
PGL	4.28 (0.12)	2.38 (0.07)	4.89 (0.09)
SCL	5.53 (0.13)	0.85 (0.08)	5.32 (0.11)
SGL	5.64 (0.14)	2.37 (0.11)	6.11 (0.11)
BCL	6.74 (0.18)	−1.40 (0.13)	5.41 (0.15)
BGL	6.47 (0.19)	1.18 (0.17)	6.32 (0.13)

All values are given in genetic standard deviations. The relative economic weight of PT vs. DR was 2:1. Standard errors are given in parentheses. For abbreviations, see Table 1.

Scenario 3: high heritability for PT and low heritability for DR:

Ratio of economic weights for PT and DR 2:1:

Genetic gains for PT, DR, and TMI from generation S0 to S5 for the different selection schemes are shown in Table 3. As expected, the results were similar to the scenario above, with genomic selection having a rather extreme effect with respect to genetic gain in DR relative to classical selection (increases of 39 and 205% for the nonbackcrossed PUREBRED and SYNTHETIC lines, respectively). The BACKCROSS GBLUP line was superior to all other lines from generation S4 onward. As a result of lower heritability for DR compared with PT, the ratio of genetic gains (DR vs. PT) for the PUREBRED line was lower than the ratio of their relative economic weights, even when using genomic selection.

TABLE 3.

True genetic gains from generations S0 to S5 for PT, DR, and TMI for the different selection schemes for the scenario with high (0.5) heritability for PT and low (0.1) heritability for DR

	Genetic gain in generations S0–S5
Selection scheme	PT	DR	TMI
PRL	4.31 (0.11)	−0.08 (0.07)	3.82 (0.10)
PCL	4.17 (0.12)	0.71 (0.07)	4.05 (0.11)
PGL	4.62 (0.12)	0.99 (0.06)	4.57 (0.10)
SCL	5.63 (0.14)	0.42 (0.10)	5.22 (0.11)
SGL	6.00 (0.14)	1.27 (0.10)	5.94 (0.11)
BCL	6.82 (0.17)	−1.90 (0.12)	5.25 (0.15)
BGL	6.81 (0.19)	−0.10 (0.15)	6.04 (0.13)

All values are given in genetic standard deviations. The relative economic weight of PT vs. DR was 2:1. Standard errors are given in parentheses. For abbreviations see Table 1.

Inbreeding:

Average increases in level of inbreeding from generation S0 to S5 for the different scenarios and selection schemes are shown in Table 4. No relationship information was used for the generations prior to the initial generation in the experiment (S0). Inbreeding depression was not simulated, but would give an additional advantage of crossbreeding in real data. Generally, rate of inbreeding decreased with increasing heritability. Hence, for the scenarios assuming high heritabilities for either one or both traits, differences between selection strategies and selection methods (CBLUP, GBLUP) were rather small. However, the most striking result was that for the low heritability scenario, genomic selection generally reduced the rate of inbreeding, with the most extreme differences observed for the SYNTHETIC line (up to 44% relative reduction).

TABLE 4.

Increase of average inbreeding level from generations S0 to S5 for the selection schemes PRL, PUREBRED, SYNTHETIC, and BACKCROSS

Scenario characteristics					Increase of inbreeding level for selection schemes:
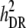		EWPT	EWDR	EBV estimating method	PRL	PUREBRED	SYNTHETIC	BACKCROSS
0.1	0.1	2	1	CBLUP	0.149	0.153	0.163	0.124
				GBLUP	—	0.122	0.092	0.099
0.1	0.1	3	1	CBLUP	0.147	0.141	0.143	0.126
				GBLUP	—	0.114	0.090	0.103
0.5	0.5	2	1	CBLUP	0.082	0.089	0.088	0.065
				GBLUP	—	0.077	0.071	0.067
0.5	0.1	2	1	CBLUP	0.081	0.082	0.090	0.067
				GBLUP	—	0.081	0.071	0.067

EW, economic weight.

DISCUSSION

Classical introgression schemes (introgressing specific QTL alleles) are most likely to be successful when combined with deliberate selection for the specific favorable alleles, known to exist in the donor line, or by selection on closely linked markers. However, the rate of success decreases for introgression of larger numbers of target QTL (Hospital 2005). Using genomic selection, all marker alleles in LD with favorable QTL alleles are potentially selected for, and this method may thus be especially relevant in situations where a number of QTL underlie the genetic variation of the trait. During the backcrossing process, donor alleles are likely to be lost or at low frequencies unless favored by selection within the crossbred line. For example, if three generations of (full) backcrossing are applied, only 6.25% (0.5⁴) of neutral alleles are expected to come from the donor line. However, by combining backcrossing with genomic selection, any favorable QTL alleles from the donor line that are rare or nonexistent in the recipient line may be preserved at a frequency much higher than the expected value, while the opposite will be true for unfavorable QTL alleles. In all purebred lines, genetic drift would have fixed a proportion of unfavorable QTL alleles. Crossing can be used for introgression of favorable novel alleles and may be worthwhile even when there are considerable differences in the genetic levels of the recipient and donor lines.

In all scenarios studied, the BACKCROSS alternative using genomic selection was similar or better than the best purebred selection scheme (PUREBRED GBLUP) with respect to TMI within four to five generations of selection, and this alternative was therefore preferred as the best way of jointly improving both traits.

Genomic vs. classical selection:

Genomic selection is expected to increase the accuracy of selection, especially for traits that cannot be recorded directly on breeding candidates and for traits with low heritabilities (Meuwissen et al. 2001; Piyasatian et al. 2007), which is confirmed in this study. Genomic selection gives a more balanced selection response in the two traits and is preferred to classical selection, both in breeding programs aiming at improving DR through purebreeding and in programs improving DR through introgression of genes from more resistant, but less productive, donor populations (Figure 2).

For the PUREBRED GBLUP selection scheme (assuming zero genetic correlation between the traits and identical heritabilities), relative genetic gains for the two traits are close to proportional with the relative economic weights of the two traits, while for classical selection, this is expected only in a situation where identical amounts of information are available for the two traits. Here, no individual information on DR was available for selection candidates. Hence, in using genomic selection, there is seemingly little to gain by including individual records on selection candidates in addition to considerable amounts of data on full-sibs (20/family). This can be explained by the fact that all alleles in a selection candidate (irrespective of population frequency) are likely to be inherited by 50% of its full-sibs in different combinations. Using genomic selection, full-sib data may completely replace individual and offspring data, which is never the case in classical selection. This explains the more balanced response for the two traits using genomic relative to classical selection.

Inbreeding is an important factor in any breeding program. Rates of inbreeding were reduced with increasing heritabilities for both CBLUP and GBLUP. Genomic selection resulted in generally lower rates of inbreeding, which can be explained by increased emphasis on within-family selection (Daetwyler et al. 2007).

Comparison of selection schemes:

Purebreeding for disease traits controlled by many loci does not result in as rapid genetic changes as with crossing, but rather gradual improvements, depending on the economic weights. If a certain level of resistance is needed to make aquaculture production feasible in a specific environment, purebreeding will thus require more generations of selection to make the population suitable for field production. Using crossbreeding, the necessary level of resistance can quickly be achieved, given that a more resistant donor line is available. However, purebreeding has some advantages; it is simpler and an initial drop in TMI level is avoided. On the other hand, crossbred populations generally would be more heterozygous, resulting in increased accuracy of selection and more rapid genetic gain.

Using classical selection, the BACKCROSS schemes gave results generally similar to purebreeding schemes; i.e., the newly introgressed donor alleles are again replaced by recipient alleles. However, with genomic selection the BACKCROSS proved to be the fastest way of producing a more resistant line that is still commercially competitive with respect to the traits included in the breeding objective. In this study, the average initial difference in TMI between the purebred and F₁ crossbred lines was 1.1–1.6 genetic standard deviations (depending on relative economic weights), but within four to five generations of selection (S4 and S5) the profitability of the BACKCROSS GBLUP was similar or better than the best purebred line (PUREBRED GBLUP), even for the largest initial difference in TMI. The favorable results of backcrossing combined with genomic selection can be explained by a generally faster genetic gain for crossbred lines caused by increased heterozygosity at the QTL level. The relative advantage of using crossbred lines with respect to increased heterozygosity and thus genetic variance depends on how much the populations have diverged and on the (historical) effective population sizes. Generally, the advantage of crossing is likely to increase with increasing genetic distance (assuming heterosis is not negative). In this study, the two populations were completely separated for 260 generations. If the separation period is considerably shorter, the relative advantage of crossing will be smaller. However, more distantly related populations may exist, e.g., European and North American Atlantic salmon (Wennevik et al. 2004) or even different species that can produce viable offspring, as in tilapia (Agresti et al. 2000). In such cases, the relative advantage of crossing may be substantial.

The ranking of the selection schemes depends partly on the initial genetic differences between the lines for the important traits and what these differences represent in TMI. If DR has a high economic value (i.e., if the donor line is not considered as “inferior” compared with the recipient line), a synthetic line may be preferred, as little or no reduction in profitability through crossing is expected. However, line differences, measured in genetic standard deviations, are actually more important than the absolute differences in TMI, as the latter criterion indicates the economic value of these lines as they are today, while the first criterion indicates how fast these differences can be eliminated through backcrossing and selection.

Effect of assumptions:

In this study, it is assumed that all marker alleles can be traced back to their originating populations. If tracing of alleles is imprecise, this is likely to reduce the accuracy of selection compared with this study. Accurate tracing of alleles will be facilitated by denser marker maps. Further, as a result of genetic drift, numerous population-specific marker alleles may exist, which (if included in the analysis) facilitates the tracing of alleles also in neighboring loci.

Genomic selection relies on the existence of population-wide LD between markers and QTL. However, LD will be reduced for populations of larger N_e, but this can be compensated for by using a marker density higher than that outlined in this study. In this study, a relatively short genome was chosen (10 M) to reduce computational costs. However, the results also apply to larger genomes, but more markers and more records will be needed to achieve similar accuracies under genomic selection.

No pleiotropic effects of the QTL were assumed; i.e., genetic correlation between the traits was zero, unless affected by selection and mating schemes. If QTL with antagonistic pleiotropic effects exist, introgression of favorable alleles for DR would be unfavorable for PT and thus reduce TMI of the population. In this study, the selection history of the founding populations will generate a temporary negative genetic correlation between the traits within the crossbred line; i.e., DNA sequences containing favorable alleles with respect to DR are more likely to come from the donor line and are thus less likely to contain favorable alleles with respect to PT. This effect will, however, be reduced over time as a result of the recombination of donor and recipient DNA sequences.

In this study, an identical recombination rate was assumed for the two genders, while in many species recombination rate is often higher in females than in males (Hedrick 2007). This is not likely to have a substantial effect on the results, as the LD in the population is more dependent on the average recombination rate rather than on which gender recombination occurs; e.g., the main effect of the reduced recombination rate in males is actually a shortening of the genome (measured in centimorgans).

Populations were selected for maximized genetic gain with no restrictions on rate of inbreeding, and the different schemes were therefore compared at different rates of inbreeding. In practical breeding programs some restrictions on inbreeding would usually be applied, limiting selection intensity. This is expected to have the largest effect on scenarios currently having the highest rates of inbreeding. Hence, for a fixed maximum rate of inbreeding, genomic selection using a crossbred line might be even more favorable than that outlined in this study. Further, in real data, crossing may generate heterosis, making the SYNTHETIC and BACKCROSS schemes even more favorable compared with the PUREBRED.

The generation interval was assumed constant for all selection criteria and selection schemes. When applying genomic selection, generation intervals may be considerably shortened (depending on the reproductive characteristics of the species), as selection can take place as soon as marker information becomes available. Short generation intervals, however, may compromise data recording (e.g., harvesting weight in farmed fish) and potentially reduce accuracy of selection.

Due to computing time considerations, marker effects were estimated using the BLUP method of Meuwissen et al. (2001), assuming a homogeneous fixed marker variance. However, the same authors also suggested more advanced Bayesian methods for estimating marker effects, i.e., the so-called BayesA and BayesB. The first method allowed different marker variances to be estimated at different loci. The BayesB method takes this to an extreme by allowing some of the marker variances to be set to zero. When applying these methods there is potential for more efficient use of genomic information as the genetic effects are more accurately assigned to markers close to segregating QTL.

The proposed selection method is not focused on reducing linkage drag around a specific QTL of interest, but would generally increase frequencies of favorable alleles at the expense of unfavorable ones (irrespective of origin) across the entire genome. This is particularly relevant when genetic variance is controlled by numerous QTL, while problems related to linkage drag are more relevant in situations where one or a few major QTL are responsible for a large proportion of the genetic variation. This will be dealt with in a future study. The results indicated that substantial genotyping is needed for successful implementation of genomic selection, but have not taken into account the cost effectiveness of such a breeding program. However, costs of genotyping will most likely be reduced in the future and genotyping may also be useful for other purposes in addition to genomic selection (e.g., parentage testing).

In this study we have used a population of farmed fish as an example. However, the results may be easily generalized to other species, such as dairy cattle, where selection for functional traits of low heritability, which are measurable only in one of the genders (e.g., mastitis), have become increasingly important in breeding programs worldwide. We assumed nonoverlapping generations, but use of overlapping generations may further improve the superiority of genomic selection schemes, as marker genotypes can be assessed at a very young age, which may reduce generation intervals. Our results also provide an additional justification for the conservation of genetic resources, since they demonstrate how favorable characteristics of generally inferior conserved populations can be utilized in commercial breeding programs. Alternatively, genomic selection may be utilized for introgression of genetic material from commercial strains into locally adapted populations, with the intent of developing more productive populations that are still adapted to the local environment, e.g., with respect to resistance to specific diseases or parasites.