Abstract
Deep brain stimulation (DBS) is an established therapy for the treatment of Parkinson’s disease and shows great promise for numerous other disorders. While the fundamental purpose of DBS is to modulate neural activity with electric fields, little is known about the actual voltage distribution generated in the brain by DBS electrodes and as a result it is difficult to accurately predict which brain areas are directly affected by the stimulation. The goal of this study was to characterize the spatial and temporal characteristics of the voltage distribution generated by DBS electrodes. We experimentally recorded voltages around active DBS electrodes in either a saline bath or implanted in the brain of a non-human primate. Recordings were made during voltage-controlled and current-controlled stimulation. The experimental findings were compared to volume conductor electric field models of DBS parameterized to match the different experiments. Three factors directly affected the experimental and theoretical voltage measurements: 1) DBS electrode impedance, primarily dictated by a voltage drop at the electrode-electrolyte interface and the conductivity of the tissue medium, 2) capacitive modulation of the stimulus waveform, and 3) inhomogeneity and anisotropy of the tissue medium. While the voltage distribution does not directly predict the neural response to DBS, the results of this study do provide foundational building blocks for understanding the electrical parameters of DBS and characterizing its effects on the nervous system.
Keywords: deep brain stimulation, voltage distribution, electrode, volume conductor, electric field, non-human primate, finite element, diffusion tensor
Introduction
Chronic electrical stimulation of subcortical structures, known as deep brain stimulation (DBS), has become an accepted surgical procedure for the treatment of movement disorders, and shows promise for the treatment of epilepsy and neuropsychiatric disorders (Perlmutter and Mink, 2006). Despite the clinical success of DBS, substantial gaps remain in the scientific characterization of the underlying biophysics and therapeutic mechanism(s) of the technology (Johnson et al., 2008). These scientific limitations are highlighted by the inability to quantify the electric field strength in specific brain regions and directly relate the stimulation parameters to changes in neural activity. This obstacle exists because experimental measurements (in vitro or in vivo) of the voltage distributions generated by DBS electrodes are lacking, and computational models that are typically used to estimate the electric fields generated by DBS have not been directly validated.
While the fundamental purpose of DBS is to modulate pathological neural activity with applied electric fields, most attempts to define the therapeutic target area for stimulation have concentrated on determining the anatomical location of the active electrode contact (e.g. Yelnik et al., 2003; Nowinski et al., 2005). Additionally clinical studies have worked to correlate stimulation parameters settings (amplitude, pulse width, frequency, polarity) with behavioral outcomes (Rizzone et al., 2001; Moro et al., 2002; Kuncel et al., 2006). However, without considering the complete system of stimulation parameters, electrode characteristics, and electrical properties of the surrounding tissue medium it is impossible to determine if the stimulation effects will be contained to the anatomical region of the active contact or if they will extend to surrounding areas (Maks et al., 2008). Therefore, the first step in predicting the stimulation effects of DBS is to characterize the voltage distribution generated in the brain.
Substantial effort has been dedicated to building volume conductor electric field models of clinical DBS (McIntyre and Thakor, 2002; Kuncel and Grill, 2004; Butson and McIntyre, 2005; Hemm et al., 2005; Butson et al., 2006; Astrom et al., 2006; Yousif et al., 2008). DBS volume conductor models have also been coupled to multi-compartment cable models of neurons to develop theoretical predictions of neural activation as a function of therapeutic stimulation parameter settings (McIntyre et al., 2004a; 2004b; Miocinovic et al., 2006; Butson et al., 2007; Sotiropoulos and Steinmetz, 2007; Maks et al., 2008). However, several aspects of these models relied on unvalidated assumptions regarding the electrical properties of the tissue medium and the electrode-electrolyte interface, principaly because the experimental data necessary to constrain the models did not exist. We undertook this study with the goal of experimentally characterizing the spatial and temporal characteristics of the voltage distribution generated by DBS electrodes. The experiments were performed by recording voltages around active DBS electrodes implanted in a saline bath, or in the thalamus and subthalamic nucleus (STN) of a non-human primate. The experimental data was then compared to volume conductor models representing the different experimental environments.
Methods
The voltages induced by DBS in a saline bath or brain tissue were recorded with microelectrodes positioned at various distances (within a radius of 7 mm) from the active DBS electrode contact. By varying the vertical and horizontal distance of the microelectrode from the DBS electrode, multiple recordings were obtained and voltage distribution maps were constructed. The temporal characteristics of the induced voltages were recorded for both constant voltage (voltage-controlled) and constant current (current-controlled) stimulation. Volume conductor models were constructed in an attempt to theoretically reproduce the voltage distributions recorded in vitro and in vivo.
Stimulation and Recording Protocols
Most of the experiments in this study were conducted with scaled-down versions of the clinical DBS electrodes, anatomically suitable for implantations into the brains of non-human primates (Hashimoto et al., 2003; Elder et al., 2005). Each monkey DBS electrode consisted of a 45 mm polyurethane shaft with four cylindrical platinum/iridium contacts wrapped around the distal end of the lead. The contacts were 0.75 mm in diameter, 0.5 mm in height and separated by 0.5 mm of insulation spacing. The monkey DBS electrodes were manufactured by the Advanced Bionics Corporation (Valencia, CA). In a subset of in vitro experiments, a human clinical DBS electrode (3387 model) was used. The contacts were 1.27 mm in diameter, 1.5 mm in height and separated by 1.5 mm of insulation spacing. The human DBS electrode was manufactured by Medtronic Inc. (Minneapolis, MN).
Both constant-voltage and constant-current pulses were used for stimulation through the DBS electrodes. Constant-voltage stimulation experiments relied on either a clinical pulse generator (IPG; Itrell II model, Medtronic Inc., Minneapolis, MN) or biphasic pulse generator (BPG-1; Bak Electronics, Mount Airy, MD) with a biphasic constant-voltage stimulus isolator (BSI-1; Bak Electronics). For constant-current stimulation we used an external pulse generator (S88; Grass Instruments, Quincy, MA) and two photoelectric constant-current stimulus isolation units (PSIU6; Grass Instruments).
Typical IPG parameters settings used in our experiments were 0.3 V, 450 μs and 20 Hz unless otherwise specified. The IPG generated an asymmetrical charged-balanced waveform with a cathodic phase defined by the inputed stimulus amplitude and pulse width followed by a low amplitude long duration anodic phase (Butson and McIntyre, 2007). While the settings used in many of our experiments were not clinically relevant, they were chosen to provide the greatest amount of information on the temporal aspects of the applied voltages. The low amplitude limited the amount of stimulation induced neural activity generated by the pulse, the long pulse width allowed for quantification of the capacitative components of the recorded waveforms, and the low frequency limited any overlap between the temporal aspects of each pulse. However, more clinically relevant settings were also tested. Additional experiments were also performed with symmetrical charge-balanced waveforms to more completely characterize the range of waveforms used in brain stimulation applications. These parameters were 0.3 V or 30 μA amplitude, 500 μs cathodic pulse, 500 μs interpulse delay, and 500 μs anodic pulse delivered at 20 Hz (Fig. 1).
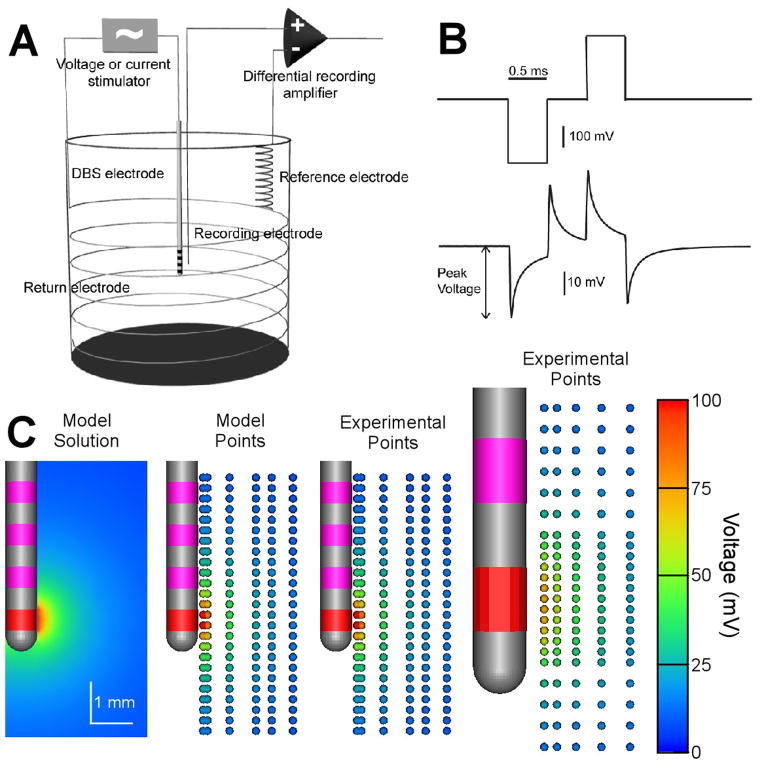
Figure 1.
In vitro voltage recordings using monkey and human DBS electrodes. A) In vitro recordings were performed with a four-electrode setup. A constant voltage or constant current stimulus was applied across the DBS electrode and a return electrode. The response voltage was measured between the microelectrode and reference electrode. B) Voltage-controlled stimulus waveform and recording from the medium. C) Voltage distribution maps. The active electrode contact is red and the inactive contacts are pink. Left: Voltage distribution map obtained from finite element model optimized to fit the in vitro recording data. Middle: Individual recording locations are marked with small spheres; sphere color indicates recorded peak voltage. Right: Experimental data recorded from human DBS electrode. Stimulus amplitude was 0.3 V. Voltage drop at the electrode-electrolyte interface limited the peak voltage recorded in the medium.
In all cases, monopolar stimulation was tested with a single active electrode contact and a distant return. Inactive electrode contacts were left open and were not connected to a defined potential. The stimulation parameter settings were chosen such that the applied fields were subthreshold for behavioral effects in the animal experiments. Stimulation was applied for 5 seconds at each DBS contact for each microelectrode recording position.
Voltages generated in the saline bath or brain tissue by the DBS electrode were measured with a microelectrode to achieve fine spatial resolution. Specific details regarding in vitro and in vivo measurements are described in subsequent sections. In both cases epoxylite-coated tungsten microelectrodes with tip lengths of approximately 50 μm (FHC, Bowdoinham, ME) were positioned at different vertical and horizontal distances from the DBS electrode using a microdrive (MO-95-lp, Narishige Scientific Instruments, Tokyo, Japan). Vertical spatial resolution was 0.25–0.5 mm while horizontal resolution was 0.5–1 mm. The recorded signal was amplified (50x) and bandpass filtered (0.1 Hz – 20 kHz) using a differential amplifier connected to a high-impedance headstage (model 3000, A–M systems, Sequim, WA). The signal was then digitally sampled at 100 kHz and stored for later offline analysis (Power 1401 and Spike2 software, Cambridge Electronic Design, Cambridge, UK). The average peak cathodic voltage was calculated by averaging peak voltage in 100 (5 sec × 20 Hz) waveform responses recorded at each microelectrode location. Voltage distribution spatial maps were constructed by plotting the average peak cathodic voltage measured at multiple locations in plane with the DBS electrode.
Monitoring electrode impedance is important both for understanding the stimulation effects and recorded responses. Existing clinical DBS systems employ voltage-controlled stimulation. Under voltage-controlled stimulation, DBS electrode impedance influences the voltage amplitude induced in the medium. And, under both voltage- and current-controlled stimulation, microelectrode impedance affects the amplitude of the recorded signal. DBS impedance recordings were performed at 1 kHz using an Autolab potentiostat (PG-STAT12, Eco Chemie, Utrecht, The Netherlands) by applying a 25 mV (rms) sine wave between the DBS electrode and the silver/silver chloride reference wire (placed in the saline-filled contralateral recording chamber) and measuring the current output. Microelectrode impedances were acquired with 1 kHz sinusoid impedance meter (IMP-1, Bak Electronics, Mount Airy, MD). Microelectrodes were regularly tested to assure their impedances remained relatively constant during a series of experimental voltage recordings (the same microelectrode was usually used for recordings in the same area repeated over several days). Initial microelectrode impedances were between 0.5–1 MΩ, and daily variations within ±0.2MΩ were tolerated.
In Vitro Experiments
In vitro experiments were performed by suspending a DBS electrode in saline. Constant voltage or constant current stimulus pulses were applied through the DBS electrode and voltages generated in the medium were recorded with a microelectrode as described in the previous section. The cylindrical glass jar was 7 cm in diameter, 7 cm in height and filled with 0.9% NaCl (conductivity 1.5 S/m). A stainless steel wire was wound around the inner wall of the container and served as the return electrode. A silver/silver chloride wire was positioned several centimeters from the recording microelectrode and it served as the reference electrode (Fig. 1A). Photographs were taken during the recordings to verify microelectrode distance from the DBS electrode.
In Vivo Experiments
Two DBS electrodes were chronically implanted into the brain of a rhesus monkey (Macacca mulatta; ID number 05-m-003; weighing 5.0 kg) following published procedures (Elder et al., 2005; Miocinovic et al., 2007) (Fig. 2). The first DBS electrode was implanted in the left thalamus, and the second electrode was implanted in the right STN. Constant voltage or constant current stimulus pulses were applied through each DBS electrode and the voltage distribution was recorded with a microelectrode as described in the previous section. All surgical and recording protocols were approved by the Cleveland Clinic Institutional Animal Care and Use Committee and complied with United States Public Health Service policy on the humane care and use of laboratory animals.
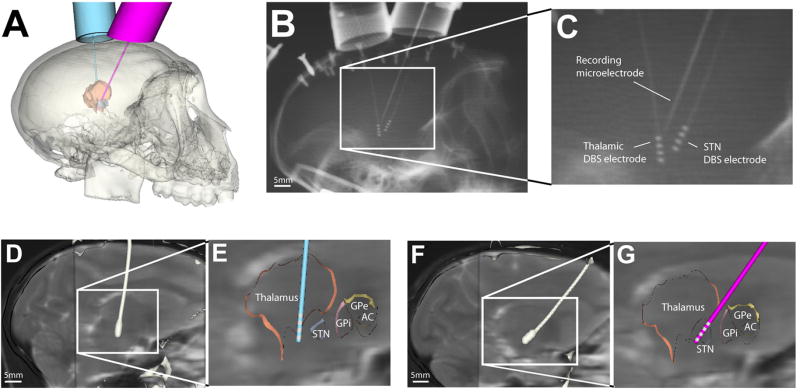
Figure 2.
Surgical planning and electrode implantation. A. Cicerone software was used to plan locations for chambers targeting thalamus (left hemisphere) and STN (right hemisphere). B. X-ray image taken during a recording session. C. Zoomed in view of figure B. In this example, the microelectrode was 2.5 mm posterior to the STN DBS electrode. D, F. the post-DBS-implantation CT was coregistered with pre-DBS-implantation MRI to define the DBS electrode location in the brain. The white structure is the contour of the electrode extracted from the post-DBS-implantation CT. E, G. Cicerone was used to visualize electrode location with respect to a brain atlas warped to match the neuroanatomy of the animal.
Imaging
Magnetic resonance imaging (MRI) was used to obtain anatomical images for surgical planning and diffusion weighted images for estimation of tissue electrical conductivity parameters. Images were acquired on Siemens Trio 3 Tesla scanner (Siemens Medical Systems, Erlangen, Germany). The animal was imaged under propofol anesthesia. T2-weighted images were acquired and consisted of twenty 2 mm thick coronal slices and twenty 2 mm thick sagittal slices (256×256 matrix, 120×120mm field of view (FOV), 0.47×0.47mm in-plane resolution). T1-weighted MPRAGE images (88 1-mm thick axial slices; 128×128 matrix; 1×1mm in plane resolution) were acquired along with the diffusion-weighted images for image co-registration.
The diffusion-weighted images, from which diffusion tensors were calculated, were acquired using a twice-refocused spin-echo pulse sequence to minimize eddy current artifacts (Reese et al., 2003). Axial images were acquired with following parameters: 15 slices of 1.5 mm thickness, 64×64 matrix, 96×96 FOV, b-value of 1000 s/mm2, partial Fourier factor 5/8, TR=2000 ms, TE=87 ms, bandwidth=1166 Hz/pixel. The diffusion gradients were encoded along 71 non-collinear orientations selected by a Coulomb repulsion algorithm (Jones et al., 1999). Eight acquisitions without diffusion weighting (b-value = 0) were acquired at equal intervals among the diffusion-weighted images. Signals were averaged after motion correction, in which images without diffusion weighting were coregistered with AFNI (Cox, 1996), and interpolated coordinates were used to reposition intervening, diffusion-weighted images. Resulting SNR0 was ~15 in the white matter in images without diffusion weighting. Diffusion-weighted data was normalized by mean b=0 signal, and the diffusion tensor components were calculated by linear regression fits to the log of the diffusion-weighted data (Basser et al., 1994). Tensors were diagonalized by a Jacobi transformation using LAPACK (Anderson et al., 1999) yielding eigenvalues and eigenvectors.
Computed tomography (CT) scans, performed with a Siemens SOMATOM Sensation, were used for surgical planning and subsequent localization of the implanted DBS electrodes (Fig. 2D, E). The CT images were acquired in the axial plane in 1 mm increments (135 slices at 512×512 pixels; 0.24mm×0.24mm in plane resolution). All of the MRI and CT images were coregistered in Analyze 7.0 (AnalyzeDirect, Lenexa, KS).
Surgical Procedure and DBS Electrode Implantation
Recording chambers were implanted on the skull in an aseptic surgical procedure under isoflurane anesthesia with the animal’s head held in a primate stereotactic frame (model 1430, Kopf Instruments, Tujunga, CA). Prior to surgery MRI and CT images were imported into our neurosurgical navigation software (Cicerone) and stereotactic chamber coordinates were calculated (Miocinovic et al., 2007) (Fig. 2A). Two craniotomies were performed and one metal chamber (16 mm inner diameter) was anchored over each hemisphere. The chamber targeting the thalamus was placed over the left hemisphere, in the sagittal plane at 5° from the vertical axis (anterior-to-posterior), 6.6 mm anterior and 5.4 mm lateral (in frame coordinates). The second chamber targeting the STN was placed over the right hemisphere, in the sagittal plane at 35° from the vertical axis (anterior-to-posterior), 0 mm anterior and 7.5 mm lateral (in frame coordinates). Postoperative CT verified that the chambers were implanted as planned. The DBS electrodes were implanted in a separate procedure after several days of neurophysiological mapping of the target brain region (Elder et al., 2005; Miocinovic et al., 2007).
Voltage Distribution Data Collection
During microelectrode voltage recordings, the animal was lightly sedated with acepromazine (1 mg/kg) and sitting in a primate chair with the head restrained (the animal was also receiving 4 mg of prednisolone daily to treat an endogenous intestinal disorder). During recordings, the animal was awake but drowsy and voluntary movement was reduced, thus minimizing recording noise and pressure exerted on the head implant. Each recording session lasted up to 4 hours.
Microelectrode voltage recordings were performed through the same chamber where the DBS electrode was implanted. The microelectrode was positioned parallel to the DBS electrode, either anterior or posterior, in the same sagittal plane (thalamus) or in the plane 1 mm lateral (STN) to the DBS electrode. The microelectrode guide tube, inserted a few millimeters below the dura, was used as a reference electrode. A chamber on the opposite hemisphere was used for stimulation current return.
X-ray images were acquired for each recording track to verify the distance from the microelectrode to the DBS electrode (Fig. 2 C, D). A portable veterinary unit (PXP-40HF; Poskom, Korea) was used with 10×12 inch film and an intensifying grid cassette. The X-ray source was set to 70 kVp and 2 mA and positioned 106 cm from the film cassette. A custom-made alignment tool was used to position the animal so that the images were taken in a sagittal plane (the same plane in which the DBS electrode and microelectrode were inserted). During a single recording session the X-ray source, film cassette, and animal were kept in the same position, so that only the microelectrode position changed. However, small variations in day to day positioning were unavoidable. Films were digitized and distance of the microelectrode to the active contact was measured in Analyze 7.0.
Modeling Studies
Finite element models (FEMs) of DBS were created to augment the analysis of our experimental recordings and evaluate their accuracy in reproducing the experimental data. A 3-dimensional, multi-resolution finite element mesh of the DBS electrode and surrounding tissue medium was constructed. A single model mesh consisting of 90,113 total elements, generated by FEMLAB 3.1 (Comsol Inc., Burlington, MA, USA), was used in all simulations (in vitro and in vivo) to allow consistent comparison of model outputs. The mesh density was highest at the electrode contact and element size increased as a function of distance from the electrode. Boundaries were defined 7 cm from the DBS electrode contacts and the outer boundary was set to ground. Nodes on the active electrode surface were used as current/voltage sources. The Poisson equation was solved to determine voltage as a function of space within the tissue medium:
where Ve is voltage, I represents injected current and σ is a complex stiffness matrix that includes the tissue conductivities. Simulations and visualization were conducted using BioPSE (Scientific Computing and Imaging Institute, University of Utah, Salt Lake City, UT). The simulation files and instructions on their use are available upon request.
Three varients of the DBS model were created. The models mimicked the in vitro DBS, in vivo thalamic DBS, and in vivo STN DBS experiments, respectively. The in vitro DBS model consisted of a single isotropic domain (σ = 1.5 S/m) representing the saline bath. The in vivo DBS models were substantially more complex incorporating a sheath of encapsulation tissue (0.25 mm thick (Haberler et al., 2000; Nielsen et al., 2007), σ = 0.18 S/m (Grill and Mortimer, 1994)) surrounding the DBS electrode and bulk tissue electrical properties derived from diffusion tensor imaging (DTI).
The DTI data from the animal was used to estimate the brain tissue conductivity. The DTI tensors were converted from diffusivity to conductivity using a scalar transform, based on the work of Tuch et al. (Tuch et al., 2001):
where D is the diffusion tensor at each individual voxel. These conductivity tensors were then mapped to their respective finite elements in the DBS model (McIntyre et al., 2004a; Butson et al., 2007). The electrical conductivity parameters describing the various sections of the models were selected to be within previously established experimental/theoretical ranges and provide voltage distributions with the best overall fit to our experimental data.
Results
In Vitro Voltage Recordings
Voltage-controlled stimulation generated a time dependent voltage waveform in the saline medium (Fig. 1B). The capacitance of the electrode-saline interface modulated the shape of the waveform, generating exponential decays and rises throughout the time course of the biphasic pulse. The peak voltage occurred at the beginning of the pulse and the response decayed over time (i.e. less current was injected over time). The time-constant (τ) for the voltage decay in vitro was on average 0.22 ± 0.04 and 0.15 ± 0.03 ms for the monkey and human electrode, respectively. These time constants were calculated using the formula: V=Voe−t/τ, where Vo is the peak voltage and τis the time constant. For current-controlled stimulation, the shape of the in vitro recorded waveform was approximately identical to the applied pulse (data not shown).
Capacitance (C=τ/Z) of the monkey electrode was calculated as 0.6 μF using the average contact impedance (Z) measured with a bipolar electrode setup (as described in Holsheimer et al., 2000). The capacitance of a human DBS electrode has been estimated at 3.3 μF (Butson and McIntyre, 2005). Given the 5.1 times smaller surface area of the monkey DBS electrode contact, its capacitance should be approximately 0.64 μF which agrees well with the above calculated value.
We created spatial maps of the peak voltage recorded during the applied waveform at different locations around the DBS electrode (Fig. 1C). The maximal voltages were recorded near the active electrode contact and decayed non-linearly as a function of distance from the active electrode contact. These spatial maps were then compared to computational models to further characterize the experimental data.
In Vitro Voltage Distribution Model
The in vitro DBS FEM generated a 3D solution of the voltage distribution in the saline medium (Fig. 1C). Coupled analysis of the theoretical and experimental results suggests a substantial voltage drop across the electrode-saline interface. This interface voltage drop has been documented in the electrochemistry literature and is related to the transition from electrons carrying the current in the electrode to ions carrying the current in the medium (Mansfield, 1967; Dymond, 1976; Geddes, 1997; Merrill et al., 2005). Ignoring the effects of the interface voltage drop resulted in models that substantially underestimated the DBS model impedance and overestimated the voltages generated in the surrounding medium. In turn, we incorporated this voltage drop by reducing the effective stimulation voltage applied to the model. For monkey DBS electrodes the drop was calculated to be 57% meaning that the 0.3 V stimulus created by the pulse generator resulted in an equivalent stimulus of 0.13 V after the interface voltage drop. The resulting in vitro DBS model impedance was 0.77 kΩ,compared to 0.75 kΩ recorded experimentally. Point-by-point comparison with the experimental voltage recordings resulted in a 1.2% average error in the model predictions (Fig. 1C).
In Vivo Voltage Recordings
Voltages generated by DBS electrodes in the thalamus and STN under constant-voltage or constant-current stimulation were recorded (Fig. 3). Similar to the in vitro recordings (Fig. 1B), the voltage-controlled waveforms decayed exponentially. However, the in vivo voltage decay occurred with a longer time constant than observed in vitro. The monkey DBS electrode exhibited a voltage decay time constant of 0.64 ± 0.27 ms in vivo. The stimulus waveform produced by the Medtronic IPG was asymmetric and the delay between the cathodic and anodic phase depended on the stimulation frequency (~1 ms for 20 Hz stimulus and ~0.25 ms for 185 Hz stimulus) (Butson and McIntyre, 2007). Interestingly, the capacitive discharge of the IPG waveform did not occur immediately after the end of the cathodic phase as observed with traditional square wave stimuli (Fig. 1B), but instead there was an ~0.25 ms delay (Fig. 3A) due to IPG electronic circuit characteristics not under our experimental control.
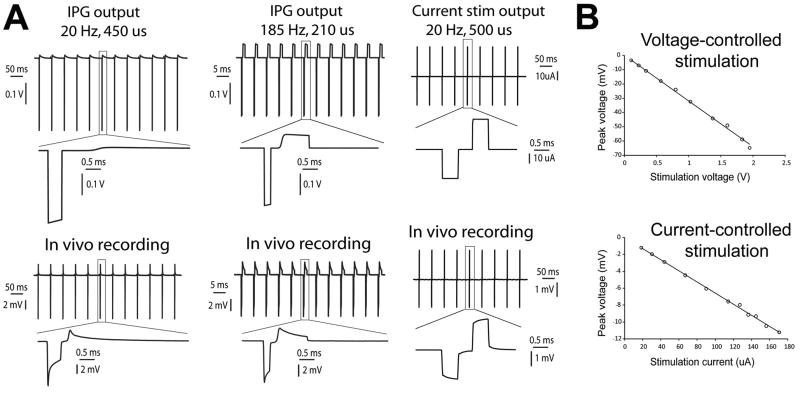
Figure 3.
In vivo stimulus waveform recordings. A. Voltage-controlled (IPG) and current-controlled stimulus waveforms at 20 Hz and 185 Hz recorded across a 1 kΩ resistor (top) and corresponding voltage responses recorded in vivo (bottom). B. The peak voltage recorded in vivo was proportional to the applied stimulus amplitude for both voltage-controlled and current-controlled stimulation.
Constant-current stimulation generated experimentally recorded waveforms that more closely resembled the output of the pulse generator (Fig. 3A). However, compared to the in vitro constant-current waveforms which reached their peak almost immediately, the in vivo recorded voltages rose throughout the pulse duration such that the peak voltage occurred at the end of the pulse. Previous theoretical analyses suggest that this phenomenon was caused by the capacitance of the tissue medium (Butson and McIntyre, 2005).
The recorded peak voltage was linearly related to the stimulus amplitude for both constant-voltage and constant-current stimulation (Fig. 3B). This was true over a wide range of stimulus amplitudes (e.g. 0.1 – 2.0 V). In turn, while sub-clinical amplitudes were used for majority of the experiments, the fundamental results of this study should be applicable across the spectrum of clinically relevant parameter settings.
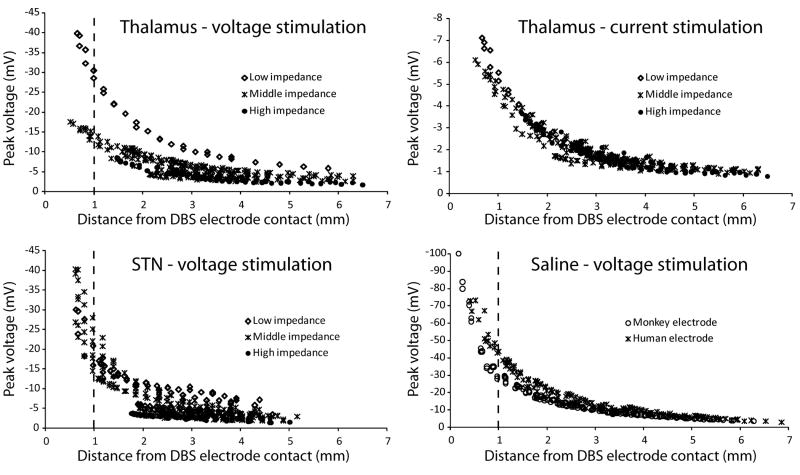
The voltage distribution generated by DBS in vivo exhibited a non-linear decay as a function of distance from the active electrode contact (Fig. 4). The power (x) of the voltage decay (1/rx), where r is the distance from the electrode, was estimated from individual recording tracks. The thalamic constant-voltage recordings exhibited an x of 0.78 ± 0.11 and 0.78 ±0.14 for thalamic constant-current stimulation. The STN constant-voltage recordings had an x of 0.88 ±0.16. These estimates were lower than the theoretical decay for a point-source electrode where x equals 1. In turn, the voltage distribution from a DBS electrode falls off more slowly in space than the voltage distribution from a point source electrode (McIntyre and Thakor, 2002).
Figure 4.
In vivo peak voltages. Individual voltage recordings plotted against the distance from the microelectrode tip to the active DBS electrode contact. The data was classified according to DBS electrode impedance. Low DBS electrode impedance was defined as less than 3 kΩ, medium impedance as 3–5 kΩ, and high impedance as more than 5 kΩ. Thalamic data included 11 recording tracks (30 recording locations in each track) collected over 4 days using the same DBS contact for stimulation. Data for thalamic voltage-controlled and current-controlled stimulation were collected at the same time so recording locations were identical. STN data includes 16 recording tracks (27 recording locations in each track) collected over 8 days. Saline data was divided according to the type of DBS electrode used (monkey vs. human – lower right plot). Monkey electrode data consisted of 7 tracks (33 locations in each track) recorded over 2 days. Human electrode data consisted of 7 tracks (23 locations in each track) recorded during 1 day. The stimulus amplitude was 0.3 V or 30 μA.
Voltages recorded during constant-voltage stimulation were influenced by the DBS electrode impedance (Fig. 4). DBS electrode impedance can vary over time (see Discussion) and as a result voltage recordings carried out over several weeks were subjected to different impedance conditions. For example, voltage recordings at the same general location relative to the DBS electrode could vary by 50% or more depending on the electrode impedance (lower impedance resulted in higher recorded voltage). On the other hand, voltages generated during constant-current stimulation were independent of DBS electrode impedance (Fig. 4). Despite the occasional variations, most of the constant-voltage recordings were acquired with the DBS electrode impedance in the middle (3–5 kΩ) range.
In Vivo Voltage Distribution Model
The in vivo DBS FEMs generated 3D solutions of the voltage distribution in the monkey brain and these results were compared to the experimental measurements (Fig. 5). Two representative sets of experimental data recorded from thalamus and STN were used to evaluate the in vivo models. The in vitro DBS FEM predicted a 57% voltage drop at the electrode-electrolyte interface and this voltage drop was included in the in vivo models. The in vivo models also accounted for the high resistance encapsulation tissue that forms around implanted foreign bodies (see Methods and Discussion). Together these features dominated the overall model impedance that closely paralleled the experimental measurements. The impedance measured through the STN DBS electrode was 3.8 kΩ for the experimental data presented in Fig. 5 and 3.8 kΩ in the corresponding model. The thalamic DBS electrode was 3.4 kΩ in the experiments and 3.7 kΩ in the model.
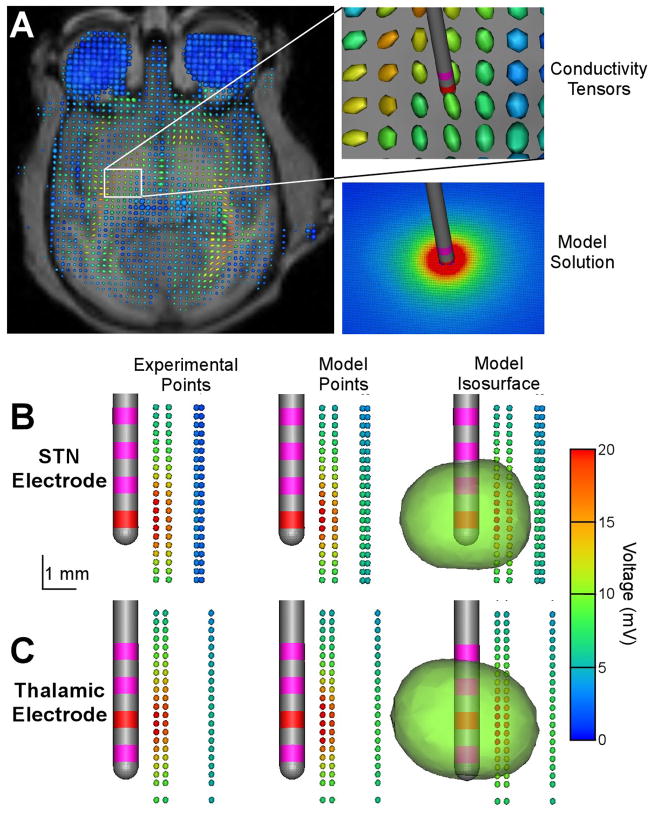
Figure 5.
In vivo voltage distribution model. A) Electrical conductivity of the brain was estimated on a voxel-by-voxel basis using diffusion tensor data. Conductivity tensors are represented as an ellipsoid with its long axis indicating the direction of highest conductivity and the color representing the degree of anisotropy (red – anisotropic, blue – isotropic). B, C) Experimental recordings, corresponding model solutions and an example model 3D voltage isosurface at 10 mV for the STN (B) and thalamic (C) DBS electrode. For both B and C the recording tracks were acquired parallel to and posterior from the DBS electrode trajectory.
The in vivo DBS FEMs accurately predicted the voltage distribution in both the STN (Fig. 5B) and the thalamus (Fig. 5C). Point-by-point comparison of the experimental recordings and model predictions showed an average model error of 6.2% in the STN and 17.4% in the thalamus within 2.5 mm of the stimulating electrode. Interestingly, the more distant recording tracks in the STN showed greater errors, with the model overestimating the voltage, while the average error of the thalamic model was independent of distance from the active contact. The more distant recording tracks of the STN electrode were presumably in the internal capsule (given the stereotactic location of the recording electrode in the brain volume). The DTI-based conductivities of the STN model did create a more dramatic voltage gradient in that highly anisotropic region, but the experimental data suggest an even stronger effect than predicted by the model.
To further evaluate the impact of tissue anisotropy and inhomogeneity we created a simplified in vivo DBS FEM that replaced the DTI-based tissue conductivities with an isotropic conductivity of 0.2 S/m (Ranck, 1963), resulting in a 3.6 kΩ model impedance. Repeating the above listed point-by-point comparison revealed an average error of 8.5% in the STN and 16.9% in the thalamus with the simplified model. These results suggest that when evaluating DBS voltage distributions within a few millimeters of an active electrode contact, an appropriately parameterized isotropic model provides similar overall predictions to a more detailed DTI-based model. However, the DTI-based models did generate quantitatively different results than the isotropic model when the complete 3D solutions were compared (data not shown). For example, the isotropic DBS model created nearly perfect spherical voltage isosurfaces while the DTI-based model voltage isosurfaces were distorted by the complex tissue electrical properties (Fig. 5B,C).
Discussion
The fundamental purpose of DBS is to modulate brain activity with applied electric fields and the goal of this study was to quantitatively characterize those fields. This study experimentally and theoretically examined features of the electrode-brain interface that dictate the spatial and temporal voltage distribution generated by DBS. Voltages generated by DBS electrodes were recorded in vitro (saline bath) and in vivo (thalamus and STN of a monkey) and the results were compared to volume conductor finite element models. Three features of the electrode-brain interface directly affected the experimental and theoretical results: 1) DBS electrode impedance, dictated by a voltage drop at the electrode-electrolyte interface and the conductivity of the tissue medium, 2) capacitive modulation of the stimulus waveform, and 3) inhomogeneous and anisotropic tissue properties. These results represent important building blocks for quantifying the neural response to DBS, and subsequently defining its therapeutic mechanisms of action.
Electrode-Brain Interface
The interface between a permanently implanted electrode and the brain is a complex entity that can dramatically affect the functioning of the clinical device. An anatomically and electrically stable interface is necessary to allow for the determination of stimulation parameters that can provide consistent therapeutic benefit. This interface is made up of many different components. At the core of this interface is the transfer of charge from the metal electrode to the ionic medium of the brain, thereby establishing a potential gradient from the cathode to the anode (Mansfield, 1967; Dymond, 1976; Geddes, 1997; Merrill et al., 2005). This potential gradient passes through the extracellular space whose electrical conductivity is inhomogeneous, meaning it changes as a function of distance from the electrode, and anisotropic, meaning it changes as a function of direction (Tuch et al., 2001; McIntyre et al., 2004a). Very close to the electrode (within a few hundred microns) the tissue medium is typically made up of glia cells and extracellular matrix proteins that form a low conductivity encapsulation layer around the foreign body (Caparros-Lefebvre et al., 1994; Haberler et al., 2000; Henderson et al., 2002; Moss et al., 2004; Nielsen et al., 2007). The periphery of this encapsulation layer transitions into the normal brain tissue which is a complex 3D volume conductor. The potential gradient established in the brain is directly affected by these different features of the electrode-brain interface.
Electrode Interface Voltage Drop
Our results suggest a relatively dramatic drop in voltage occurs in the transition from the polarization of the DBS electrode contact to the ionic medium. DBS electric field models commonly assume an ideal electrode behavior (i.e. no voltage drop across the electrode interface). However, both the in vitro and in vivo experimental recordings generated voltage measurements that were substantially lower than idealized model predictions. It was therefore necessary to include an interface layer, which we empirically modeled as percentage voltage reduction across the electrode interface. While more complicated equivalent circuit models exist for modeling the electrode interface (e.g. Cantrell et al., 2008), our method was sufficient to accurately characterize the data without increasing the overall complexity of the model. However, it should be noted that our simplistic voltage drop representation ignores the complex non-linear and frequency-dependent reactions that actually take place at the electrode-electrolyte interface.
We calculated the interface voltage drop using the in vitro recording data, as this drop was the only unknown variable (saline conductivity was known and there was no encapsulation layer or tissue anisotropy/inhomogenity). We then used this value for the in vivo models under the assumption that the extracellular fluid in immediate contact with the electrode contact is similar to saline. Clearly, this generalization does not take into account all ionic features of the actual in vivo environment. Nonetheless, our in vivo electric field model predictions matched well with our experimental recordings and the lowest model errors were achieved with the interface voltage drop defined by the in vitro model, compared to arbitrarily selected voltage drops. However, it sould be noted that the models presented in this study were parameterized to match higher frequency components of the impedance spectrum and may not be applicable for lower frequency analysis.
Tissue Influences on Electrode Impedance
The brain’s inflammatory response to the implanted DBS electrode is the creation of a tissue encapsulation sheath (Haberler et al., 2000; Henderson et al., 2002; Nielsen et al., 2007). This collection of cellular infiltrate, protein deposits, and collagen matrices increases the electrode impedance and reduces the electric field generated in the bulk tissue medium (Butson et al., 2006). As a result, the effective strength of voltage-controlled stimulation is reduced because the injected current is inversely proportional to electrode impedance. Current-controlled stimulation was not affected by the electrode impedance and similar potentials were generated for a range of electrode impedance values. Interestingly, stimulation itself reduced electrode impedance. In our experience, most of the reduction in impedance occurred within the first 10–15 minutes of acute stimulation (Lempka et al., 2007). These effects were transient and the impedance returned to baseline in a time dependent manner following cessation of stimulation. This phenomenon has been studied in cochlear (Ni et al., 1992; Newbold et al., 2004; Shepherd and McCreery, 2006), cortical (Weiland and Anderson, 2000), subcutaneous (Grill and Mortimer, 1994), and DBS (Hemm et al., 2004) electrodes. These results have important implications for voltage-controlled stimulation in that the effective spread of stimulation can change as the impedance changes.
A number of histological studies have examined the encapsulation response on and around clinical DBS electrodes (Caparros-Lefebvre et al., 1994; Haberler et al., 2000; Henderson et al., 2002; Moss et al., 2004; Nielsen et al., 2007). In most cases gliosis was observed around the electrode track (extending up to ~1 mm) and no overt neuronal damage in response to chronic stimulation has been found. The animal used in this study underwent acute stimulation only, but our preliminary results suggest that chronic impedance values would be very similar to those recorded after ~1 hour of acute stimulation (Lempka et al., 2007). It should be noted that this animal was receiving chronic steroid treatment for an intestinal disorder so its inflammatory response to the DBS electrode could have been reduced. At the writing of this manuscript, the animal was participateing in other long-term DBS research experiments so histological characterization of the encapsulation response was not possible.
Capacitive Modulation of the Stimulus Waveform
Our results show that the shape of the stimulus waveform recorded in saline or brain tissue was modified from the stimulus waveform generated by the pulse generator (Fig. 1B, 3A). The actual stimulus waveform imposed on the brain tissue directly impacts the neural response to the stimulation pulse. Previous work has explored the effects of electrode and tissue capacitance on the shape of DBS waveforms transmitted to brain tissue (Butson and McIntyre, 2005; Gimsa et al., 2006). Theoretical models postulate that the double layer capacitance at the electrode interface results in a non-linear decay of the potential during a voltage-controlled stimulus pulse. On the other hand, a current-controlled waveform is not affected by the interface capacitance and instead exhibits a non-linear rising of the voltage measured in the tissue due to the effects of tissue capacitance. The waveforms recorded experimentally confirm these theoretical predictions and highlight the importance of incorporating time-dependent capacitive components into neurostimulation models.
Tissue Anisotropy and Inhomogeneity
Brain tissue electrical conductivities are inherently complex and difficult to characterize. Further, DBS electrodes are commonly implanted in brain regions with high degrees of anisotropy (e.g. fiber tracks) and inhomogeneity (e.g. grey matter/white matter transitions). In an attempt to evaluate the effect of different brain region conductivities, we placed electrodes in a region with relatively low anisotropy and inhomogeneity (thalamus) and a region with relatively high anisotropy and inhomogenetiy (STN) (Shimony et al., 1999). The experimentally recorded voltage distributions were measurably different with a more spherically radiating field generated by the thalamic electrode, and a more distorted voltage distribution from the STN electrode (Fig. 5). Further, the in vivo DBS FEM 3D solutions exhibited voltage isosurfaces that were more distorted around the STN electrode than thalamic electrode, especially at lower voltage values (data not shown). These effects have also been predicted by previous computer models (McIntyre et al., 2004a; Butson et al., 2007; Sotiropoulos and Steinmetz, 2007), and our experimental measurements support the hypothesis that brain tissue anisotropy and inhomogeneity directly impact the stimulating field.
Implications for Neural Activation
This study describes the voltage distribution generated by DBS electrodes, but it is important to note that absolute voltage at any point in space does not determine the neural response to stimulation. Theoretical derivations demonstrate that the spatial change in the electric field, or the second-order difference of the extracellular voltage distribution, directly influences the polarization of a neural process (e.g. axon or dendrite) (McNeal, 1976; Rattay, 1989). While methods utilized in this paper do not directly address electric field gradients they do provide us with tools (i.e. realistically parametrized electric field models) that can be used to calculate the gradients and predict the spatial extent of neural activation during DBS (McIntyre et al., 2004a; 2004b; Miocinovic et al., 2006; Butson et al., 2007; Sotiropoulos and Steinmetz, 2007; Maks et al., 2008).
The temporal characteristics of the applied voltage are also important when considering the effects of stimulation on neural activation. During voltage-controlled stimulation the observed voltage decay is related to charging the electrode capacitance which increases the electrode impedance over the time course of the applied pulse, diminishing the current injection into the tissue (Mansfield, 1967; Gimsa et al., 2005). In turn, neual stimulation thresholds are dependent not only on the voltage stimulus amplitude, but also the electrode geometry, impedance, and capacitance (Butson and McIntyre, 2005; 2006; Butson et al., 2006; Gimsa et al., 2006). Even when the standard clinical DBS electrodes are used it is difficult to compare voltage-controlled stimulation thresholds across patients or experiments unless detailed measurements of the electrode impedance are available. This problem can be avoided by using current-controlled pulses which have stimulation thresholds that are effectively independent of electrode impedance.
Experimental Limitations
There exist several possible sources of error in our experimental voltage distribution recordings. Two notable inaccuracies are the distance estimates between the stimulating and recording electrodes, and the impedance variations for the DBS and microelectrodes. Recorded voltages could be under- or over-estimated because of recording distance uncertainty. This is especially true for very small distances between the stimulating and recording electrodes where the voltage distribution changes rapidly. This issue was minimized with our in vitro recordings by direct visual inspection of electrode positions and repeated measurements under the same conditions. However, the in vivo experimental conditions were more difficult to control. Both microdrive coordinates and x-ray images were used to estimate the distance between the electrodes, and while every effort was made to minimize possible errors (see Methods), submillimeter inaccuracies were possible.
As discussed above DBS electrode impedance is a continuously variable parameter and it has a measureable effect on voltages generated in the tissue during voltage-controlled stimulation. Due to our experimental setup and time constraints, impedances were measured once before and once after the voltage recording session so the exact impedance was not known for each recorded voltage value. During a related series of experiments we observed that the impedance decreased most rapidly during the first few minutes of stimulation (Lempka et al., 2007). We therefore discarded the first recording track of the day if the ‘before’ and ‘after’ impedances varied by more than 50% and considered the ‘after’ impedance to be the representative impedance for the remaining recordings.
Microelectrode impedance depends on the surface area of the exposed tip which can be increased by passing current through the electrode. However, a tip area that is too large will reduce the spatial resolution of the recordings. As a compromise we used microelectrodes with ~0.5 MΩ impedance. Point source field recordings for which analytical solution exists confirmed that appropriate voltage values could be recorded with such microelectrodes (data not shown).
The stimulation amplitude (0.3 V or 30 μA) was chosen to be low enough so that it did not induce any behavioral response in the animal. However, it should be noted that the stimulation probably excited some neurons in very close proximity to the electrode. These stimulation-induced potentials, as well as spontaneous neuronal potentials are typically in the microvolt range and could contribute to the recorded voltage in the tissue medium. In an attempt to alleviate these effects, we concentrated on voltage recordings from the beginning of the stimulus pulse and used low frequency stimulation. However, to verify that our findings were applicable to clinically relevant stimulation we also utilized higher frequency (up to 185 Hz) and higher amplitude (up to 2 V and 1 mA) stimulation. For both in vitro and in vivo experiments we observed that the recorded voltages were directly proportional to the stimulus amplitude and recorded amplitudes were not affected by the stimulation frequency (Fig. 3; all data not shown).
Conclusion
Clinical applications of DBS technology continue to grow, but limitations in scientific characterization of its interaction with the nervous system hinder the engineering design of even more efficacious devices. Computational modeling of DBS electric fields has recently emerged as a tool to predict the effects of DBS on neural tissue and design new DBS technology; however, the validity of the models has been an issue of concern. We experimentally measured the voltage distribution generated by DBS electrodes implanted in non-human primates and compared the recordings to detailed computational models. Our results show that appropriately parameterized finite element models can be used to accurately capture the generated potentials. The results of this study provide the first experimental characterization of the voltage distribution generated by DBS electrodes and substantiate the use of computational models to quantify the spread of stimulation as a function of the electrode placement and stimulation parameter settings used in an individual subject.
Acknowledgments
The authors thank Weidong Xu and Jianyu Zhang for help with the experimental preparations, Jennie Minnich for assistance in animal care, and Ashutosh Chaturvedi for assistance with the model simulations. The research was financially supported by the National Institutes of Health (T32 GM-07250, R01 NS047388, and R01 NS037019).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson E, Bai Z, Bischof C, Blackford S, Demmel J, Dongarra J, Du Croz J, Greenbaum A, Hammarling S, McKenney A, Sorensen D. LAPACK Users’ Guide. 3. Society for Industrial and Applied Mathematics; 1999. [Google Scholar]
- Astrom M, Johansson JD, Hariz MI, Eriksson O, Wardell K. The effect of cystic cavities on deep brain stimulation in the basal ganglia: a simulation-based study. J Neural Eng. 2006;3:132–8. doi: 10.1088/1741-2560/3/2/007. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. 1994;103:247–54. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Benabid AL, Deuschl G, Lang AE, Lyons KE, Rezai AR. Deep brain stimulation for Parkinson’s disease. Mov Disord. 2006;21(Suppl):168–70. doi: 10.1002/mds.20954. [DOI] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Tissue and electrode capacitance reduce neural activation volumes during deep brain stimulation. Clin Neurophysiol. 2005;116:2490–500. doi: 10.1016/j.clinph.2005.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Role of electrode design on the volume of tissue activated during deep brain stimulation. J Neural Eng. 2006;3(1):1–8. doi: 10.1088/1741-2560/3/1/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Differences among implanted pulse generator waveforms cause variations in the neural response to deep brain stimulation. Clin Neurophysiol. 2007;118:1889–94. doi: 10.1016/j.clinph.2007.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, Maks CB, McIntyre CC. Sources and effects of electrode impedance during deep brain stimulation. Clin Neurophysiol. 2006;117:447–54. doi: 10.1016/j.clinph.2005.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, Cooper SE, Henderson JM, McIntyre CC. Patient-specific analysis of the volume of tissue activated during deep brain stimulation. Neuroimage. 2007;34:661–70. doi: 10.1016/j.neuroimage.2006.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantrell DR, Inayat S, Taflove A, Ruoff RS, Troy JB. Incorporation of the electrode-electrolyte interface into finite-element models of metal microelectrodes. J Neural Eng. 2008;5:54–67. doi: 10.1088/1741-2560/5/1/006. [DOI] [PubMed] [Google Scholar]
- Caparros-Lefebvre D, Ruchoux MM, Blond S, Petit H, Percheron G. Long-term thalamic stimulation in Parkinson’s disease: postmortem anatomoclinical study. Neurology. 1994;44:1856–60. doi: 10.1212/wnl.44.10.1856. [DOI] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29(3):162–73. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Duan YY, Clark GM, Cowan RS. A study of intra-cochlear electrodes and tissue interface by electrochemical impedance methods in vivo. Biomaterials. 2004;25(17):3813–28. doi: 10.1016/j.biomaterials.2003.09.107. [DOI] [PubMed] [Google Scholar]
- Dymond AM. Characteristics of the metal-tissue interface of stimulation electrodes. IEEE Trans Biomed Eng. 1976;23:274–80. doi: 10.1109/tbme.1976.324585. [DOI] [PubMed] [Google Scholar]
- Elder CM, Hashimoto T, Zhang J, Vitek JL. Chronic implantation of deep brain stimulation leads in animal models of neurological disorders. J Neurosci Methods. 2005;142:11–6. doi: 10.1016/j.jneumeth.2004.07.007. [DOI] [PubMed] [Google Scholar]
- Geddes LA. Historical evolution of circuit models for the electrode-electrolyte interface. Ann Biomed Eng. 1997;25:1–14. doi: 10.1007/BF02738534. [DOI] [PubMed] [Google Scholar]
- Gimsa J, Habel B, Schreiber U, Rienen U, Strauss U, Gimsa U. Choosing electrodes for deep brain stimulation experiments-electrochemical considerations. J Neurosci Methods. 2005 Mar;142(2):251–65. doi: 10.1016/j.jneumeth.2004.09.001. [DOI] [PubMed] [Google Scholar]
- Gimsa U, Schreiber U, Habel B, Flehr J, van Rienen U, Gimsa J. Matching geometry and stimulation parameters of electrodes for deep brain stimulation experiments--numerical considerations. J Neurosci Methods. 2006;150(2):212–27. doi: 10.1016/j.jneumeth.2005.06.013. [DOI] [PubMed] [Google Scholar]
- Grill WM, Mortimer JT. Electrical properties of implant encapsulation tissue. Ann Biomed Eng. 1994;22:23–33. doi: 10.1007/BF02368219. [DOI] [PubMed] [Google Scholar]
- Haberler C, Alesch F, Mazal PR, Pilz P, Jellinger K, Pinter MM, Hainfellner JA, Budka H. No tissue damage by chronic deep brain stimulation in Parkinson’s disease. Ann Neurol. 2000;48:372–6. [PubMed] [Google Scholar]
- Hashimoto T, Elder CM, Okun MS, Patrick SK, Vitek JL. Stimulation of the subthalamic nucleus changes the firing pattern of pallidal neurons. J Neurosci. 2003;23:1916–23. doi: 10.1523/JNEUROSCI.23-05-01916.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemm S, Mennessier G, Vayssiere N, Cif L, El Fertit H, Coubes P. Deep brain stimulation in movement disorders: stereotactic coregistration of two-dimensional electrical field modeling and magnetic resonance imaging. J Neurosurg. 2005;103:949–55. doi: 10.3171/jns.2005.103.6.0949. [DOI] [PubMed] [Google Scholar]
- Hemm S, Vayssiere N, Mennessier G, Cif L, Zanca M, Ravel M, Frerebeau P, Coubes P. Evolution of brain impedance in dystonic patients treated by gpi electrical stimulation. Neuromodulation. 2004;7:67–75. doi: 10.1111/j.1094-7159.2004.04009.x. [DOI] [PubMed] [Google Scholar]
- Henderson JM, Pell M, O’Sullivan DJ, McCusker EA, Fung VS, Hedges P, Halliday GM. Postmortem analysis of bilateral subthalamic electrode implants in Parkinson’s disease. Mov Disord. 2002;17:133–7. doi: 10.1002/mds.1261. [DOI] [PubMed] [Google Scholar]
- Holsheimer J, Dijkstra EA, Demeulemeester H, Nuttin B. Chronaxie calculated from current-duration and voltage-duration data. J Neurosci Methods. 2000;97(1):45–50. doi: 10.1016/s0165-0270(00)00163-1. [DOI] [PubMed] [Google Scholar]
- Johnson MD, Miocinovic S, McIntyre CC, Vitek JL. Mechanisms and targets of deep brain stimulation in movement disorders. Neurotherapeutics. 2008;5(2):294–308. doi: 10.1016/j.nurt.2008.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42(3):515–25. [PubMed] [Google Scholar]
- Kuncel AM, Grill WM. Selection of stimulus parameters for deep brain stimulation. Clin Neurophysiol. 2004;115:2431–41. doi: 10.1016/j.clinph.2004.05.031. [DOI] [PubMed] [Google Scholar]
- Kuncel AM, Cooper SE, Wolgamuth BR, Clyde MA, Snyder SA, Montgomery EB, Jr, Rezai AR, Grill WM. Clinical response to varying the stimulus parameters in deep brain stimulation for essential tremor. Mov Disord. 2006;21(11):1920–8. doi: 10.1002/mds.21087. [DOI] [PubMed] [Google Scholar]
- Lempka SF, Miocinovic S, Russo GS, Zhang J, Vitek JL, McIntyre CC. In vivo deep brain stimulation electrode impedance spectroscopy. Society for Neuroscience. 2007 abstract No. 693.8/N10. [Google Scholar]
- Maks CB, Butson CR, Walter BL, Vitek JL, McIntyre CC. Deep brain stimulation activation volumes and their association with neurophysiological mapping and therapeutic outcomes. J Neurol Neurosurg Psychiatry. 2008 Apr 10; doi: 10.1136/jnnp.2007.126219. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mansfield PB. Myocardial stimulation: the electrochemistry of electrode-tissue coupling. Am J Physiol. 1967;212:1475–88. doi: 10.1152/ajplegacy.1967.212.6.1475. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Thakor NV. Uncovering the mechanisms of deep brain stimulation for Parkinson’s disease through functional imaging, neural recording, and neural modeling. Crit Rev Biomed Eng. 2002;30:249–81. doi: 10.1615/critrevbiomedeng.v30.i456.20. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Mori S, Sherman DL, Thakor NV, Vitek JL. Electric field and stimulating influence generated by deep brain stimulation of the subthalamic nucleus. Clin Neurophysiol. 2004a;115:589–95. doi: 10.1016/j.clinph.2003.10.033. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Grill WM, Sherman DL, Thakor NV. Cellular effects of deep brain stimulation: model-based analysis of activation and inhibition. J Neurophysiol. 2004b;91:1457–69. doi: 10.1152/jn.00989.2003. [DOI] [PubMed] [Google Scholar]
- McNeal DR. Analysis of a model for excitation of myelinated nerve. IEEE Trans Biomed Eng. 1976;23:329–37. doi: 10.1109/tbme.1976.324593. [DOI] [PubMed] [Google Scholar]
- Merrill DR, Bikson M, Jefferys JG. Electrical stimulation of excitable tissue: design of efficacious and safe protocols. J Neurosci Methods. 2005;141:171–98. doi: 10.1016/j.jneumeth.2004.10.020. [DOI] [PubMed] [Google Scholar]
- Miocinovic S, Parent M, Butson CR, Hahn PJ, Russo GS, Vitek JL, McIntyre CC. Computational analysis of subthalamic nucleus and lenticular fasciculus activation during therapeutic deep brain stimulation. J Neurophysiol. 2006;96:1569–80. doi: 10.1152/jn.00305.2006. [DOI] [PubMed] [Google Scholar]
- Miocinovic S, Zhang J, Xu W, Russo GS, Vitek JL, McIntyre CC. Stereotactic neurosurgical planning, recording, and visualization for deep brain stimulation in non-human primates. J Neurosci Methods. 2007;162:32–41. doi: 10.1016/j.jneumeth.2006.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moro E, Esselink RJ, Xie J, Hommel M, Benabid AL, Pollak P. The impact on Parkinson’s disease of electrical parameter settings in STN stimulation. Neurology. 2002;59(5):706–13. doi: 10.1212/wnl.59.5.706. [DOI] [PubMed] [Google Scholar]
- Moss J, Ryder T, Aziz TZ, Graeber MB, Bain PG. Electron microscopy of tissue adherent to explanted electrodes in dystonia and Parkinson’s disease. Brain. 2004;127:2755–63. doi: 10.1093/brain/awh292. [DOI] [PubMed] [Google Scholar]
- Newbold C, Richardson R, Huang CQ, Milojevic D, Cowan R, Shepherd R. An in vitro model for investigating impedance changes with cell growth and electrical stimulation: implications for cochlear implants. J Neural Eng. 2004;1:218–27. doi: 10.1088/1741-2560/1/4/005. [DOI] [PubMed] [Google Scholar]
- Ni D, Shepherd RK, Seldon HL, Xu SA, Clark GM, Millard RE. Cochlear pathology following chronic electrical stimulation of the auditory nerve. I: Normal hearing kittens. Hear Res. 1992;62:63–81. doi: 10.1016/0378-5955(92)90203-y. [DOI] [PubMed] [Google Scholar]
- Nielsen MS, Bjarkam CR, Sørensen JC, Bojsen-Møller M, Sunde NA, Østergaard K. Chronic subthalamic high-frequency deep brain stimulation in Parkinson’s disease--a histopathological study. Eur J Neurol. 2007;14:132–8. doi: 10.1111/j.1468-1331.2006.01569.x. [DOI] [PubMed] [Google Scholar]
- Nowinski WL, Belov D, Pollak P, Benabid AL. Statistical analysis of 168 bilateral subthalamic nucleus implantations by means of the probabilistic functional atlas. Neurosurgery. 2005;57(Suppl):319–30. doi: 10.1227/01.neu.0000180960.75347.11. [DOI] [PubMed] [Google Scholar]
- Perlmutter JS, Mink JW. Deep brain stimulation. Annu Rev Neurosci. 2006;29:229–57. doi: 10.1146/annurev.neuro.29.051605.112824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranck JB. Specific impedance of rabbit cerebral cortex. Exp Neurol. 1963;7:144–52. doi: 10.1016/s0014-4886(63)80005-9. [DOI] [PubMed] [Google Scholar]
- Rattay F. Analysis of models for extracellular fiber stimulation. IEEE Trans Biomed Eng. 1989;36(7):676–82. doi: 10.1109/10.32099. [DOI] [PubMed] [Google Scholar]
- Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med. 2003;49(1):177–82. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
- Rizzone M, Lanotte M, Bergamasco B, Tavella A, Torre E, Faccani G, Melcarne A, Lopiano L. Deep brain stimulation of the subthalamic nucleus in Parkinson’s disease: effects of variation in stimulation parameters. J Neurol Neurosurg Psychiatry. 2001;71(2):215–9. doi: 10.1136/jnnp.71.2.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd RK, McCreery DB. Basis of electrical stimulation of the cochlea and the cochlear nucleus. Adv Otorhinolaryngol. 2006;64:186–205. doi: 10.1159/000094652. [DOI] [PubMed] [Google Scholar]
- Shimony JS, McKinstry RC, Akbudak E, Aronovitz JA, Snyder AZ, Lori NF, Cull TS, Conturo TE. Quantitative diffusion-tensor anisotropy brain MR imaging: normative human data and anatomic analysis. Radiology. 1999;212(3):770–84. doi: 10.1148/radiology.212.3.r99au51770. [DOI] [PubMed] [Google Scholar]
- Sotiropoulos SN, Steinmetz PN. Assessing the direct effects of deep brain stimulation using embedded axon models. J Neural Eng. 2007;4:107–19. doi: 10.1088/1741-2560/4/2/011. [DOI] [PubMed] [Google Scholar]
- Tuch DS, Wedeen VJ, Dale AM, George JS, Belliveau JW. Conductivity tensor mapping of the human brain using diffusion tensor MRI. Proc Natl Acad Sci U S A. 2001;98:11697–701. doi: 10.1073/pnas.171473898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiland JD, Anderson DJ. Chronic neural stimulation with thin-film, iridium oxide electrodes. IEEE Trans Biomed Eng. 2000;47:911–8. doi: 10.1109/10.846685. [DOI] [PubMed] [Google Scholar]
- Yelnik J, Damier P, Demeret S, Gervais D, Bardinet E, Bejjani BP, Francois C, Houeto JL, Arnule I, Dormont D, Galanaud D, Pidoux B, Cornu P, Agid Y. Localization of stimulating electrodes in patients with Parkinson disease by using a three-dimensional atlas-magnetic resonance imaging coregistration method. J Neurosurg. 2003;99:89–99. doi: 10.3171/jns.2003.99.1.0089. [DOI] [PubMed] [Google Scholar]
- Yousif N, Bayford R, Wang S, Liu X. Quantifying the effects of the electrode-brain interface on the crossing electric currents in deep brain recording and stimulation. Neuroscience. 2008;152:683–91. doi: 10.1016/j.neuroscience.2008.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]