NEURAL MECHANISMS OF AUDITORY DISCRIMINATION OF LONG-DURATION TONAL PATTERNS: A NEURAL MODELING AND FMRI STUDY

Abstract

Language perception comprises mechanisms of perception and discrimination of auditory stimuli. An important component of auditory perception and discrimination concerns auditory objects. Many interesting auditory objects in our environment are of relatively long duration; however, the temporal window of integration of auditory cortex neurons processing these objects is very limited. Thus, it is necessary to make active use of short-term memory in order to construct and temporarily store long-duration objects. We sought to understand the mechanisms by which the brain manipulates long-duration tonal patterns, temporarily stores the segments of those patterns, and integrates them into an auditory object. We extended a previously constructed model of auditory recognition of short-duration tonal patterns by expanding the prefrontal cortically-based short-term memory module of the previous model into a memory buffer with multiple short-term memory submodules and by adding a gating module. The gating module distributes the segments of the input pattern to separate locations of the extended prefrontal cortex in an orderly fashion, allowing a subsequent comparison of the stored segments against the segments of a second pattern. In addition to simulating behavioral data and electrical activity of neurons, our model also produces simulations of the blood oxygen level dependent (BOLD) signal as obtained in fMRI studies. The results of these simulations provided us with predictions that we tested in an fMRI experiment with normal volunteers. This fMRI experiment used the same task and similar stimuli to that of the model. We compared simulated data with experimental values. We found that two brain areas, the right precentral gyrus and the left medial frontal gyrus, correlated well with our simulations of the memory gating module. Other fMRI studies of auditory perception and discrimination have also found correlation of fMRI activation of those areas with similar tasks and thus provide further support to our findings.

INTRODUCTION

Language perception incorporates mechanisms of perception and discrimination of auditory stimuli. However, these mechanisms remain understudied. An important component of auditory discrimination concerns auditory objects, which are those sounds that have definable and delimited boundaries and can be separated from the background [17] (also see Griffiths and Warren [9]). Examples of auditory objects are words, parts of melodies, and definable environmental sounds. Many interesting auditory objects in our environment are of relatively long-duration (e.g., several seconds long), such as multisyllabic words, short sentences, some animal calls, and melodic fragments. However, the temporal window of the auditory cortex neurons processing these objects is very limited. For example, in the primary auditory cortex of awake marmoset monkeys, this window is only 20–30 ms long [21]. Because auditory stimuli are always transient, it is necessary to make active use of short-term memory in order to store and construct long-duration auditory objects. Thus, the question arises as to what are the mechanisms by which the cerebral cortex encodes sounds whose durations are greater than the window of integration of its individual neurons? Another way of phrasing this question is: what are the brain mechanisms that enable a transient sensory memory to progress to a short-term memory in which long-duration auditory objects can be constructed and manipulated? In this paper, we attempt to address this question using a computational modeling-experimental framework. The model is a large-scale neural network that simulates a delayed match-to-sample (DMS) task using auditory long-duration tonal patterns as input. The experiment uses a similar paradigm and stimuli as the model and employs functional magnetic resonance imaging (fMRI).

The issues of perceptual discrimination, formation of auditory objects in short-term memory, and windows of integration have been addressed previously by a realistic neural model of auditory perception and discrimination proposed by Husain et al. [12]. This model was designed to put forth hypotheses concerning how the human auditory pathway in cortex processes and discriminates frequency modulated (FM) tonal patterns. The specific stimuli that were inputs to this model were tonal contours, each of which consisted of a combination of two FM sweeps interspersed with a constant tone, with total duration of approximately 350–500 ms. The Husain et al. model provided a neurally-based explanatory theory of how auditory stimuli are encoded in auditory cortex and the means by which auditory working memory handles discrimination tasks. Simulated data generated by this model generally matched human fMRI data. The model has also been tested by simulating behavioral studies of perceptual grouping [11], a necessary step in the formation of auditory objects and their separation from background.

In the present paper, we sought to investigate the mechanisms by which the brain manipulates long-duration tonal patterns (in our specific case, of up to approximately 1.5 sec), temporarily stores the segments of those patterns, and integrates them into an auditory object. Therefore, we extended Husain et al’s model of auditory recognition of short-duration tonal patterns by adding a mechanism that increased the storage capacity of the model to be able to handle long-duration tonal patterns. A major difference between the present model and Husain et al’s model is that the original model incorporated the integration of the percept in a superior temporal gyrus/sulcus area, whereas the present model performs a further integration of the segments of the auditory input in a prefrontal cortex module. Additionally, the present model maintains the order of the segments within the tonal pattern. Thus, in the present model, not only the memory of the segments is important but also the order of their presentation within the input pattern.

In order to integrate the segments into an object and to remember the order of presentation of the segments, we made two simplifying computational assumptions. First, the input patterns were assumed to be segmented and were treated as sequences of auditory segments separated by silent gaps (segmentation of auditory stimuli, including speech, has been addressed by a number of investigators; e.g., [5,14]). The second assumption was that the input patterns could have a maximum of three segments. Thus, the input patterns were modeled as a set of up to three short-duration frequency-modulated tonal contours with a silent gap between the segments.

Our strategy for implementing the storage of sequences of auditory segments could have been in one of two possible ways. The first way was as an active rehearsal circuit in which the neural activity sequentially encoding the memory traces of the subcomponents of a long-duration stimulus would circulate dynamically through a kind of “rehearsal articulatory loop” (e.g., akin to the working memory module of Baddeley [1]). The second possibility was a memory buffer with spatially allocated memory percepts. In the latter, a memory buffer would allocate multiple and distinct neural resources to the different stimulus subcomponents and would keep track of their presentation order. This would mean that the sound subcomponents would be coded in short-term memory and kept active simultaneously. Because the stimuli we used in our experimental studies did not seem to engage overt or covert articulation (as opposed to, for instance, keeping track of a telephone number), we opted for the second possibility and the original model of Husain et al. [12] was accordingly expanded by (1) extending the prefrontal cortically-based short-term memory (STM) module into a memory buffer with multiple STM sub-modules, and (2) by adding a gating module for maintaining the order of the contents of each sub-module.

The extended model handles long-duration tonal patterns consisting of up to three short-duration segments, but it can be generalized to longer sequences. Although in the model it is possible to include as much buffer space as needed to handle a large number of segments, there is evidence that the number of chunks that the human brain is capable of remembering in STM is limited (e.g., 7±2) [15,18,22].

In addition to simulating behavioral data and electrical activity of neurons, our model also generates simulated blood oxygen level dependent (BOLD) signals such as would be obtained in human functional magnetic resonance imaging (fMRI) studies. The results of these simulations provided us with predictions that we tested in an fMRI experiment with normal volunteers using the same stimuli as the model by comparing experimental to simulated values. A major difference between the present study and other fMRI studies on auditory perception is that we sought to make explicit hypotheses concerning some of the neural mechanisms underlying auditory working memory of long-duration auditory stimuli, rather than just determining the loci of brain areas activated by the stimuli. An important aspect of our experiment was that a load effect takes place when storing tonal contours of long duration. Our proposal is that when the task involves auditory percepts that are serially organized, areas higher than auditory cortex become implicated in the task, in a hierarchical manner, to handle basic auditory units and the order in which they are presented (see Rypma et al. [25] for an analogous case using visual stimuli). Since other working memory modules of the model had already been associated with brain areas by Husain et al’s study [12], the present investigation sought to associate the gating module to brain areas by comparing the model-based fMRI to experimental fMRI.

NEURAL NETWORK MODEL

The neural network model used in the present study consists of a number of modules, each representing a postulated brain region (Fig 1). The regions and the basic computational unit contained in these regions, parameter selection and input stimuli are detailed below, along with the procedure used to simulate fMRI activity. Experimental evidence supporting the hypotheses used in the model is provided as well (see also Husain et al. [12]).

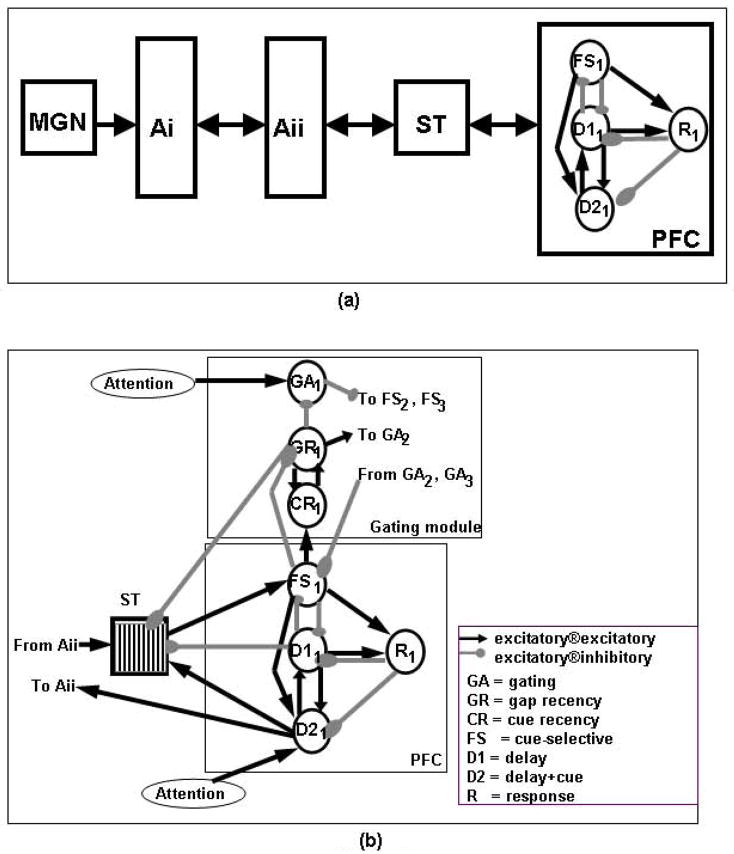
Figure 1.

(a) Simplified diagram of the Husain et al [12] model. (b) Diagram of the new model of short-term memory for long-duration tonal patterns. Key: MGN, medial geniculate nucleus; Ai, primary auditory cortex; Aii, secondary auditory cortex; ST, superior temporal gyrus/sulcus; PFC, prefrontal cortex module; FS, cue-selective units; D1, delay-selective units; D2, delay+cue-selective units; R, response units; ®, synapses onto.

Regions of the model

Our current model is an extension of the model presented by Husain et al [12]. We first briefly describe the Husain et al model and then the current extension.

Husain et al’s model incorporated four major brain regions representing an auditory object processing stream: (1) primary auditory cortex (Ai), where neurons respond in a tonotopically organized fashion to up and down frequency modulated (FM) sweeps; (2) secondary auditory cortex (Aii, which corresponds to lateral and parabelt auditory cortex), where neurons respond to longer up and down sweeps, as well as to changes in the direction of the FM sweeps; this module is also tonotopically organized; (3) an area called ST (which is in the rostral part of the superior temporal gyrus/sulcus) where a complex sound is represented in a distributed manner in the neuronal population in its entirety; and (4) a prefrontal module, which plays a key role in short-term working memory.

In particular, the prefrontal (PFC) module has four different types of neuronal units: (1) cue-sensitive units (denoted here as “FS”), which fire when a stimulus is presented, two types of delay units (denoted as “D1” and “D2”), of which the first type fires during the delay period of a DMS task and the second type fires during both stimulus presentation and the delay period; and response units (“R”), which fire if the two stimuli of a DMS trial match.

Husain et al’s model handled short-duration (about 500 msec or less in duration) FM tonal patterns. However, the short-term memory module of that model lacked a mechanism to store long-duration auditory patterns. If a pattern whose duration was longer than 350–500 ms was presented to this model, later parts of the pattern would “write over” earlier parts. To deal with this problem, we extended the model by increasing the size of the PFC memory module of the original model and by adding a gating module (Figure 1).

The gating module distributes the segments of the input pattern to separate locations of the extended PFC in an orderly fashion, allowing a subsequent comparison of the stored segments against the segments of a second pattern. Inhibition is used to handle the distribution of segments of the input pattern from ST to separate prefrontal cortex units (see Fig. 1). Other units serve as gap detectors. When these gap detectors are activated, they inhibit some gating units and excite others. This change in inhibition/excitation shifts the balance towards the next available buffer location and the next segment of the input pattern is sent to that location in prefrontal cortex.

The extended model handles long-duration tonal patterns consisting of up to three short-duration segments, three being chosen for computational convenience.

A number of features of our model are based on evidence from studies in nonhuman primates. It has been shown that cells in dorsolateral prefrontal cortex demonstrate high activation during the delay period of an auditory short-term memory task [3,16]. Also, there is evidence that inhibition and disinhibition between cells in dorsolateral prefrontal cortex might be used to link a temporal chain of events [6], and therefore might be part of a mechanism that could code complex stimuli such as long-duration sounds. Furthermore, cells in prefrontal cortex have been shown to encode order of presentation of spatial positions in a delayed saccade task [8], and the lateral prefrontal cortex of the monkey is capable of coding both object identity and presentation order of a remembered stimulus [24].

The “gating” module, which consists of several different types of neurons, uses inhibition from gating-specific neurons (GA_i) to the prefrontal cue-selective units FS_i (i=1,2,3) to handle the distribution of segments of the input pattern from ST to separate FS_i units (see Fig. 1). There also are gap-detecting units (GR_i), which, when activated, inhibit the GA_i units and excites units GA_i+1. This flips the balance and the next segment of the input pattern is sent to FS_i+1. Feedback from GR_i to ST results in ST neurons returning to baseline in preparation for the next segment of the input pattern. CR units complement GR because they form, together with the units in GR, a memory of whether a given location of PFC is currently storing a segment of the input pattern. The reverberatory circuit formed by GR and CR is identical to that formed by D1 and D2 that keeps the memory of the actual segment of the input pattern. However, the GR-CR circuit is a memory of a “state” in the sense that it indicates whether a location of the memory buffer is available or not.

Basic unit

The extended version of the model uses the same basic units as the previous model ([12]; see also [27]). Each module contains 81 basic units (this number is arbitrary), each unit representing a population of neurons (i.e., a cortical column). There is one excitatory (E) and one inhibitory (I) element per unit [30]. For details on the equations used, see Figure 2 and Husain et al [12].

Figure 2.

Equations and parameters used in the neural network model. E_i(t) and I_i(t) are electrical activities of excitatory and inhibitory units, respectively; Δ is the rate of change; K_E and K_I are gains of the sigmoid functions; T_E and T_I are the input thresholds; N(t) is the random activity term; δ is the decay rate; and w_EE, w_IE, and w_EI are the weights (excitatory-to-excitatory, inhibitory-to-excitatory, and excitatory-to-inhibitory). in_iE(t) and in_iI(t) are the total inputs coming from other areas into the excitatory and inhibitory units at time t.

Parameter selection

Two sets of factors were manipulated in the model: the parameters of the equations and the weights of the connections between the elements of the model. The values of the parameters used in the new modules of the model equations are shown in Figure 2. The parameters of the modules of the original model were kept the same (see Table 1 in Husain et al [12] for a list of these values). The weights among the excitatory and inhibitory elements of the basic units of each module added were adjusted and fine-tuned until the model made the correct responses during the required delayed match-to-sample task (see Table 1 for their values). The weights in the primary and secondary auditory areas (Ai and Aii) and perceptual integration area ST in the model remained the same as in the original model. The self excitatory-to-excitatory, excitatory-to-inhibitory and inhibitory-to-excitatory connections within a basic unit in all modules remained the same as in the original model.

Table 1.

Connectivity of gating modules.

Connectivity of the new gating units
Source	Destination	Type	Weight	Fanout
Attention	GA1	Excitatory	0.2	9 × 9
	GA2	Excitatory	0.01	9 × 9
	GA3	Excitatory	0.025	9 × 9
Attention	D21	Excitatory	0.05	9 × 9
	D22	Excitatory	0.05	9 × 9
	D23	Excitatory	0.05	9 × 9
Attention	GR1	Inhibitory	0.05	9 × 9
	GR2	Inhibitory	0.05	9 × 9
	GR3	Inhibitory	0.05	9 × 9
GA1	FS1	Inhibitory	0.2	1 × 1
	FS2	Inhibitory	0.1	1 × 1
	FS3	Inhibitory	0.1	1 × 1
	GA2	Inhibitory	0.01	1 × 1
	GA3	Inhibitory	0.01	1 × 1
GA2	FS1	Inhibitory	0.1	1 × 1
	FS2	Inhibitory	0.2	1 × 1
	FS3	Inhibitory	0.1	1 × 1
	GA1	Inhibitory	0.01	1 × 1
	GA3	Inhibitory	0.01	1 × 1
GA3	FS1	Inhibitory	0.1	1 × 1
	FS2	Inhibitory	0.1	1 × 1
	FS3	Inhibitory	0.2	1 × 1
	GA1	Inhibitory	0.01	1 × 1
	GA2	Inhibitory	0.01	1 × 1
GR1	GA1	Excitatory	3	1 × 1
	GA2	Excitatory	0.004	9 × 9
	CR1	Excitatory	0.105	1 × 1
	STG	Inhibitory	0.03	1 × 1
	GA1	Inhibitory	0.02	9 × 9
GR2	GA2	Excitatory	3	1 × 1
	GA3	Excitatory	0.005	9 × 9
	CR2	Excitatory	0.105	1 × 1
	STG	Inhibitory	0.03	1 × 1
	GA2	Inhibitory	0.02	9 × 9
GR3	GA3	Excitatory	3	1 × 1
	GA3	Inhibitory	0.02	9 × 9
	CR3	Excitatory	0.105	1 × 1
	STG	Inhibitory	0.03	1 × 1
CR1	GR1	Excitatory	0.1	1 × 1
CR2	GR2	Excitatory	0.1	1 × 1
	GR1	Excitatory	0.1	1 × 1
CR3	GR3	Excitatory	0.1	1 × 1
FS1	GR1	Excitatory	0.00015	6 × 6
	CR1	Excitatory	0.07	1 × 1
	GR1	Inhibitory	0.05	1 × 1
FS2	GR2	Excitatory	0.006	6 × 6
	CR2	Excitatory	0.07	1 × 1
	GR2	Inhibitory	0.05	1 × 1
FS3	GR3	Excitatory	0.006	6 × 6
	CR3	Excitatory	0.07	1 × 1
	GR3	Inhibitory	0.05	1 × 1

Input stimuli and task description

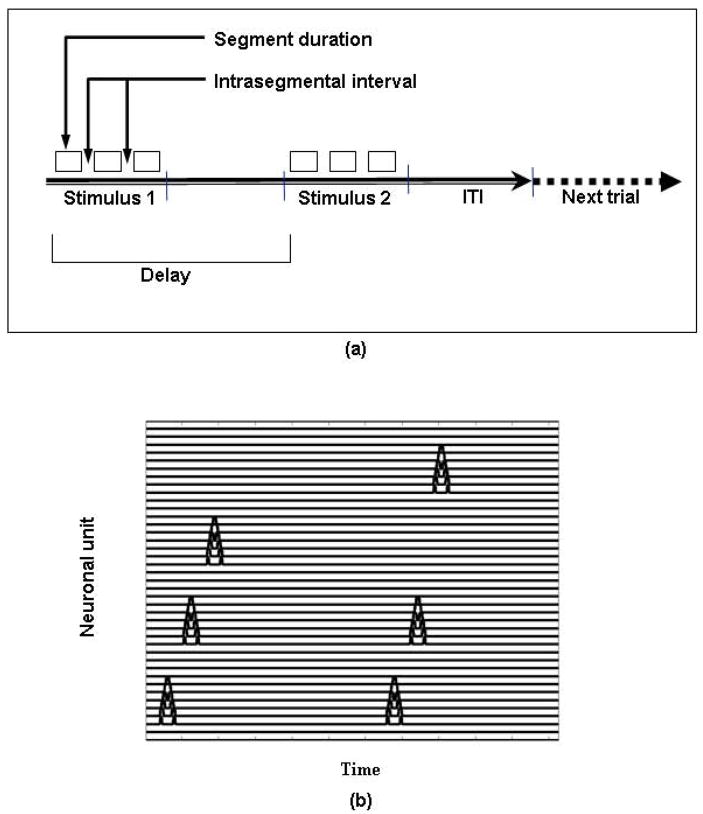
The input to our model consisted of long-duration tonal patterns, and the task performed by the model is a delayed match-to-sample (DMS) task. For computational convenience, we made two assumptions: (1) the input patterns were segmented and were treated as sequences of auditory segments separated by silent gaps; and (2) the input patterns could have a maximum of three segments. Thus, the input patterns were modeled as a set of up to three short-duration FM tonal contours with a silent gap between the segments. Every segment was 100 simulation time steps in duration (this is another computational convenience; segments need not have been of equal duration). Because each time step in the model corresponds to approximately 4 ms, each segment of the input stimuli has a duration of about 400 ms. The gaps between the segments were 60 time steps (i.e., 240 ms). The delay period of each DMS trial was 1125 time steps (i.e., 4500 ms) and the response time (which included the inter-trial interval) was 750 time steps (3000 ms). As shown in Figure 3, a trial in the simulated task consisted of presentation of an auditory stimulus, a delay, and presentation of a second stimulus, after which the model determined if the two stimuli were the same or different.

Figure 3.

Timeline of an experimental and simulated trial. (a) Delayed match-to-sample trial depiction. The value of segment duration was 400 ms for the experiments and 100 timesteps for the simulations; the intrasegmental interval was 150 ms for the experiments and 60 timesteps for the simulations; the delay period was 6±1 sec for the experiments and 1125 timesteps for the simulations; the intertrial interval (ITI) was 3+1 sec for the experiments and 750 timesteps for the simulations. (b) Graphical representation of the input for the simulated trial ABC vs ABD.

Simulated behavioral results and electrical activity

Our neural network model of short-term memory of long-duration auditory stimuli was able to simulate behavioral (match, mismatch) and electrical neuronal data during the delayed match-to-sample task.

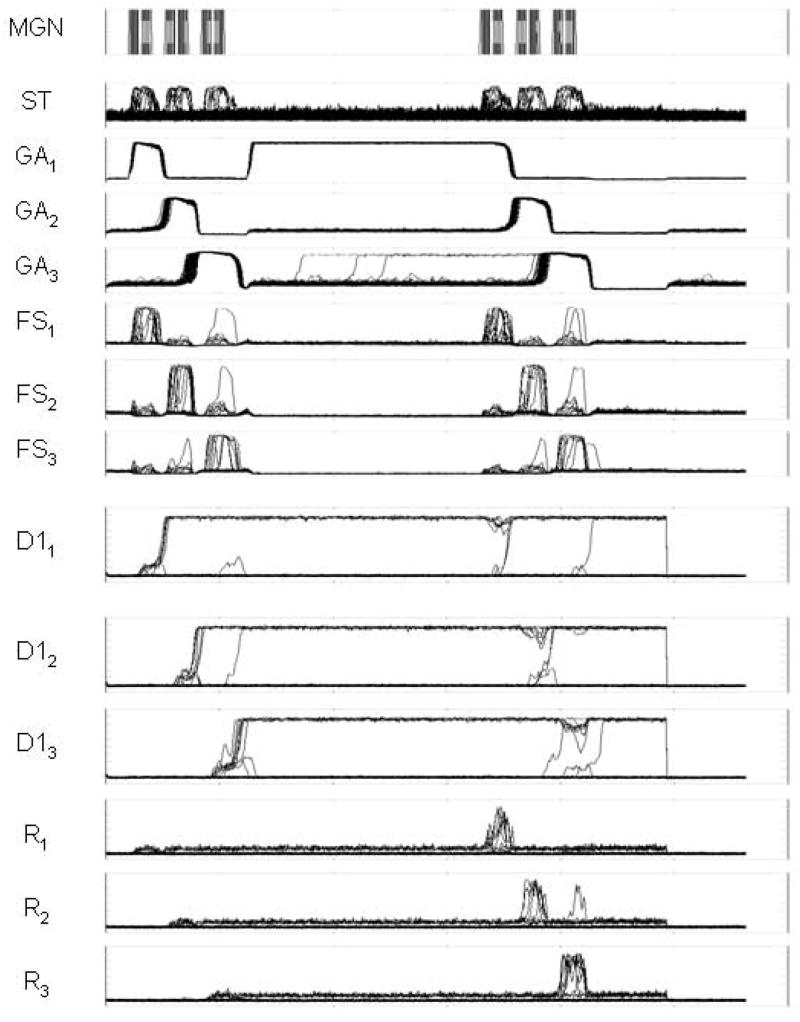
A representative example of simulated electrical neuronal activity for a single trial is shown in Figure 4. For display purposes, the activities of all eighty-one units in each module were collapsed to obtain a two-dimensional graph of electrical activity versus time for each module. The first row, labeled “MGN”, shows the input to the model. The input is cast as a sequence of three segments, with gaps between the segments.

Figure 4.

Graphical output of simulated neural activities for some of the modules for a simulated trial that uses patterns of 3 tonal contours for each stimulus. The activities of all eighty-one units in each module were collapsed to obtain a two-dimensional graph of electrical activity versus time for each module. The scale of the Y-axis is from zero to a maximum value of one, and the abscissa represents time. Key: MGN, medial geniculate nucleus; ST, superior temporal gyrus/sulcus; GA_i, gating units; FS_i, cue-selective units; D1_i, delay-selective units; R_i, response units.

The input shown in MGN is subsequently processed by a series of modules that simulate the primary and secondary auditory cortices (not shown in Fig. 4) and that decompose the input stimuli into “features” (for a detailed explanation of this auditory processing see Husain et al [12]). After the feature extraction modules have finished their processing, all of the features are integrated into an abstract representation of the input sound. The neural activity corresponding to this integrated representation is labeled “ST” in Figure 4.

The next step in the process is to separate each segment from the rest of the sequence and to store each segment in a separate compartment of short-term memory. A gating module, represented by GA₁, GA₂, and GA₃, separates each segment from the rest of the sequence. GA_1, the only one of the gating modules that is active during presentation of the first segment, exerts strong inhibition over FS₂ and FS₃ (see Fig. 1(b)) and thus prevents FS₂ and FS₃ from showing any significant activity during presentation of the first segment. However, FS₁ is strongly activated during presentation of the first segment and therefore “captures” the first segment and allows it to be registered in the D1₁–D2₁ memory module.

As shown in Figure 1(b), the activation of the module D1₁ inhibits FS₁, which in turn triggers the activation of GR₁ (not shown in Fig. 4), which, in turn, strongly inhibits GA₁ and excites GA₂. The action of GR₁ over GA₁ and GA₂ effectively shuts off GA₁ and activates GA₂, therefore closing the “gate” from ST to FS₁ and opening a gate from ST to FS₂. Note that because GA₂ exerts inhibition over FS₁ and FS₃, only FS₂ is allowed to capture the activity of the second segment of the sequence shown in ST. When FS₂ is activated by the action of the second segment in ST, the percept in FS₂ is registered in D1₂–D2₂ and the balance of the gating units is once again shifted. This time, GA₃ inhibits both FS₁ and FS₂ and allows only FS₃ to register the third segment of the sequence contained in ST. The third segment is then transferred to D1₃–D2₃.

After a delay period in which the activities of the gating modules return to their initial conditions (but the memory of the first sequence persists in D1₁–D2₁, D1₂–D2₂, and D1₃–D2₃), the second sequence is handled in the same way as the first sequence. When the matching actions are executed, every segment of the input sequence is contained in the memory modules D1₁–D2₁, D1₂–D2₂, and D1₃–D2₃ in the order in which they were presented and in separate compartments.

The results of the matching mechanism are shown in the modules R₁, R₂, and R₃. Each module represents a match for the corresponding segment of the sequence shown in ST. In the example of Fig. 4, a complete match is obtained and the order of the responses in R₁, R₂, and R₃ represents a match of the corresponding segments in the two sequences presented.

Performance in our model was measured by the number of units firing above a threshold in the response units of our model. The response modules in our model contained 81 units and their range of response of each unit was a number between 0 and 1, which indicated how well a match had been established. Because our units always have some baseline activity, we used a threshold of 0.6 to determine whether a given unit was responding to a match of the pattern. If at least 4 units surpassed this threshold, we considered that the response of the model to the input was a “match” and otherwise it was a “non-match.” Because the weights of the model were hardwired and calibrated with a number of input stimuli, our model responded with a near 100 percent certainty.

Reaction times were not simulated with the present model because we did not have a motor output module to perform the button response in the DMS task. However, the present model has been extended by Wen et al [29] to include a competitive mechanism that simulates decision making and motor output, and therefore can simulate reaction times.

In summary, our model can correctly perform the DMS task for these long-duration auditory stimuli, and the simulated electrical activities in each of the modules display appropriate behavior.

Simulating fMRI

The task simulated here was reproduced (with minor modifications) in an fMRI experiment with normal volunteers. The general hypothesis of our experiment was that a load effect takes place when storing tonal contours of longer duration. Our proposal was that when the task involves auditory percepts that are serially organized, other areas of cortex become involved in the task to handle basic auditory units and the order in which they are presented (see Rypma et al. [25] for a analogous case that used visual stimuli).

In a manner similar to our previous modeling [10,12], we simulated the fMRI signal (the blood oxygenation level dependent (BOLD) signal) by integrating the absolute value of the simulated synaptic activity over the slice acquisition time [10,20]. The resulting values of each region were convolved with a hemodynamic response function [4], which produced a smoothed time series. This time series was sampled every TR=2 sec (fMRI scanner repetition time) to generate the simulated fMRI activity.

Because an event-related experimental design was used, we estimated the simulated percentage change in BOLD signal by using the lowest memory load as a baseline. After the smoothed time series were obtained, the event-related average curves were calculated for each load of the simulation (i.e., whether the input stimulus consisted of one, two or three segments). After that, the differences were calculated for each of the points of the load’s average curves (L2, L3) minus the baseline load (L1), all divided by the baseline load L1. The averages of all the points of the two difference curves were obtained, and these were considered to be the simulated BOLD signal percentage change (L2vsL1 and L3vsL1).

A simulated experiment was conducted that assumed four different basic segments from which to construct auditory sequences: A, B, C, and D (see Fig. 3 for representations of the tonal contours corresponding to A, B, C and D). The following sequences were presented to the model: CvsC, CvsC, AvsA, ABvsAB, ABCvsABC, AvsB, ABvsAC, ABCvsABD, CvsC, CvsC. The first two and the last two sequences were entered only to allow the simulated hemodynamic signal to stabilize and were not considered for the estimation of the simulated percentage change in BOLD signal. Thus, there were six total stimuli, two for each duration (one-segment, two-segment, and three-segment stimuli). Of the two trials corresponding to a set duration of stimuli, one was a match and one was a nonmatch.

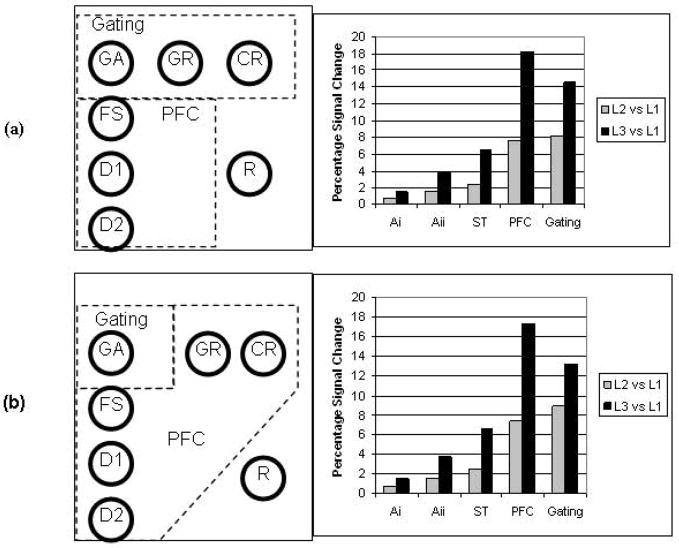
Model-based fMRI results

Our model allowed us to simulate fMRI data resulting from the delayed match-to-sample task. Because the new modules of the model did not have a specific brain area associated with them, different plausible configurations were examined. In particular, the “gating” modules, because of their different function, could possibly be located in a brain area different from the PFC module of the original model [12]. Two possibilities were selected: (1) that GR and CR are part of the gating module but distinct from the original PFC module (Fig. 5a), and (2) that GR and CR are part of the original PFC module, but the GA module is in a separate brain region (Fig. 5b). These choices were motivated by the notion that only the GA units serve directly as gating memory units, whereas the GR and CR units only assist in the gating process. Note also that we removed the response module R from the original PFC and treat it as a separate module.

Figure 5.

Diagram showing two plausible configurations of modules of the model into hypothesized brain areas. Also shown are simulated BOLD percentage signal changes for each configuration. Key: PFC, prefrontal cortex module; GA, gating units; FS, cue-selective units; D1, delay-selective units; D2, delay+cue selective units; FR, response units.

Figure 5 shows the percentage change in simulated BOLD signal for the two selected configurations of modules of the model. It is seen that the percent increase in the simulated BOLD values in each region is not simply a linear function of the load. Rather, in Ai the percent change in BOLD from L2 to L3 increased by a factor of 2.23; the corresponding numbers for the other regions were 2.59 (Aii), 2.68 (ST), and 2.38/2.34 for PFC (configurations 1 and 2).

fMRI EXPERIMENT - METHODS

An fMRI experiment was conducted to provide data to compare with the simulated results just discussed. The main purpose of the experiment was to see if we could propose brain regions that could correspond to the new modules of the model.

Stimuli and experimental design

Frequency-modulated (FM) tonal contours of 400 ms were synthesized using Sonic Foundry Sound Forge 6.0 (Sonic Foundry, Inc., Madison, Wisconsin) by modulating the frequency of a waveform (carrier) by the output of a second waveform (modulator). These FM tonal contours were then intensity normalized to −6dB using the RMS (Root-Mean-Square) and the peak level methods, and smoothed out by eliminating clicks (this was done both manually and through interpolation). The FM contours were further smoothed out by fading in the first 25 ms for the 400-ms contours, the first 50 ms for the 950-ms contours, and the first 75 ms for the 1500-ms contours of the wave form; and by fading out the last 25 ms for the 400-ms contours, 50 ms for the 950-ms contours, and 75 ms for the 1500-ms contours of the wave form. Each of the 400-ms contours used in the present experiment was similar to the tonal contours used in the Husain et al [12] experiment.

To generate 950-ms and 1500-ms stimuli, 400-ms FM contours were randomly concatenated in sequences of 2 or 3 contours by inserting a silent gap of 150 ms between contours. The silent gaps in the experimental studies were shorter than in the simulation studies because humans are better at detecting small gaps in a segmented pattern than is our model. Our neural model contains only sweep-selective neurons, whereas there are other neuronal types in the auditory cortex of mammals, including ‘gap-detection’ neurons [7]. The tonal contours were created in the 25–5140 Hz range in order to be compatible with the headphones we used. Subjects listened to the sound stimuli through headphones (Commander XG, Resonance Technology, Northridge, CA) that were attached to an electrostatic sound delivery system. The tonal contours were composed themselves of three parts: an FM sweep (up-sweep or down-sweep, 150 ms duration), a single tone (100 ms duration) and a second FM sweep (up-sweep or down-sweep, 150 ms duration). Each tonal contour started and ended at the same frequency. There were a total of 36 tonal contours, 18 were up-down contours and 18 were down-up contours. Half of the 400-ms match trials used only up-down contours and half used only down-up contours. Half of the 400-ms mismatch trials used only up-down contours and half used only down-up contours. The 950-ms match trials used equal numbers of each combination of ups and downs (3 each combination). The probe (second) stimulus in each of the 950-ms mismatches was an altered target of the same trial. This alteration occurred half the time in the first segment and half the time in the second segment of the probe stimulus (6 and 6). Of the 36 tonal contours, 24 were used for matches (with no repetition) and 36 for mismatches (with no repetition). The second stimuli in 1500-ms mismatch trials were altered in the first segment a third of the time (4 trials), in the middle segment a third of the time (4 trials), and in the final segment a third of the time (4 trials).

Stimuli were presented using the software Presentation (Neurobehavioral Systems, Inc, Albany, California) on a PC laptop computer. A trial in the experimental task consisted of presentation of an auditory stimulus, followed by a delay period, then a second stimulus after which subjects responded as to whether the two stimuli were the same or different. The delay time between the first and second stimulus was determined by an interstimulus interval of 6 sec with a jitter of ±1 sec (5–7 sec). This interstimulus interval was the time interval between the beginning of the first stimulus and the beginning of the second stimulus. The intertrial interval was 3 sec with a jitter of +1 sec (3–4 sec).

Subjects and Scanning Protocol

Fourteen subjects (13 male, 1 female, age range 23–42 yr, mean 31 yr) were scanned after obtaining informed consent according to the protocol NIH 92-DC-0178 (approved by the NIDCD-NINDS IRB). Subjects were compensated for participating in the study. All subjects were right-handed and native English speakers and reported no history of hearing loss or neurological or psychiatric problems. The scanner used was a General Electric 1.5 Tesla Signa Scanner (General Electric, Waukesha, Wisconsin). Echo planar imaging with TR=2000 ms, TE=40 ms, FA=90°, FOV=24 cm, and gap=1 mm was employed. Each volume that was acquired consisted of 23 axial slices. Prior to the functional EPI scans (voxel size 3.5 × 3.5 × 5 mm³), sagittal localizer and anatomical scans were acquired.

Subjects were allowed to give a response after the onset of the second stimulus. The response was made by pressing a button with the thumb; the left hand button was for “same” and the right hand button for “different.” Subjects underwent a short training session outside the magnet prior to the scanning session so as to become familiar with the task. There was no feedback either during training or during scanning. On 50% of the trials, the target stimulus matched the probe stimulus, and on 50% the target stimulus was different from the probe stimulus. The tonal contour sequences were intermixed with other categories of sounds (birdsongs, melodic fragments, and pseudowords that are not considered in this report), with pseudorandom presentation of the duration categories (1, 2, 3 segments) and the type of trial (match, mismatch). Thus, a total of 24 different stimulus categories were available for presentation in a single trial. A total of 48 tonal-contour trials were presented in a single session. A session was divided into four scanning runs, each lasting 528 sec (8 min 48sec). Since TR was 2 s, the number of volumes acquired per run was 264 with 23 axial slices for each volume. Trials were randomly chosen from a pool of 24 possible categories. The same runs were presented to all subjects, but the order in which the runs were presented was randomized from subject to subject. There were 5 runs available for each subject, of which one run was randomly chosen for the training session and the rest were used for the scanning session. After randomizing trial presentation in each run, each run was adjusted to fit 528 seconds. To do this, the last trial was dropped and the response time of the previous-to-the-last trial was lengthened to match 528 sec. Subjects were instructed to fixate on a visually presented “+” during the experiment. About thirty-three stimuli were used for the experiments and the rest for the training session. Behavioral pilot studies were conducted prior to the scanning experiments with 4 subjects (2 males, 2 females) in order to normalize the level of difficulty across different types of stimuli. The average performance in the pilot studies for tonal contours was 82.98% (SD=7.7%) correct responses. The average performance during the scanning sessions for tonal contours was 73.96% (SD=6.43%) correct responses.

Data Analysis

Data analysis was performed using Brain Voyager QX (Brain Innovation B.V., Maastricht, The Netherlands). The images were preprocessed with 3D motion correction, slice scan time correction, spatial smoothing (FWHM = 8 mm) and temporal smoothing (linear trend removal, high-pass filter of 5 cycles per functional run). The images were transformed into Talairach space [28] and 4D functional time series were generated. These 4D functional time z-normalized series were statistically analyzed using a multi-subject multiple regression analysis with the general linear model (GLM). A regressor was defined for each memory load, L1 (stimulus duration: 400 ms), L2 (duration: 950 ms), and L3 (duration: 1500 ms). The predictors were obtained by assuming an ideal boxcar response and shifting it 4 sec to account for the hemodynamic delay. The global level of the signal time courses in each run was taken as a confounding factor for a fixed effects analysis. The statistical maps were projected on an inflated version of the Montreal Neurological Institute template brain, downloaded from the website of the MRC’s Cognition and Brain Sciences Unit of Cambridge University (www.mrc-cbu.cam.ac.uk).

Comparing Experimental and Simulated Data

To compare the experimental and simulated data, we used a region of interest (ROI) method to determine the experimental values corresponding to each module of the model. Each ROI was a 10×10×10 voxel cube centered on a contrast local maximum. We obtained a statistical map for the areas activated during presentation of L3 stimuli contrasted with activity during presentation of L1 stimuli, as shown in Fig. 6. Based on the areas activated in this image, we tried to identify possible locations for our hypothesized “Gating area”. Once we had found a group of candidate areas, we used the voxel within that area at a relative local maximum as the center of the ROI. We also defined ROIs centered on the coordinates in Table 2 corresponding to the modules of the original model of Husain et al. [12].

Figure 6.

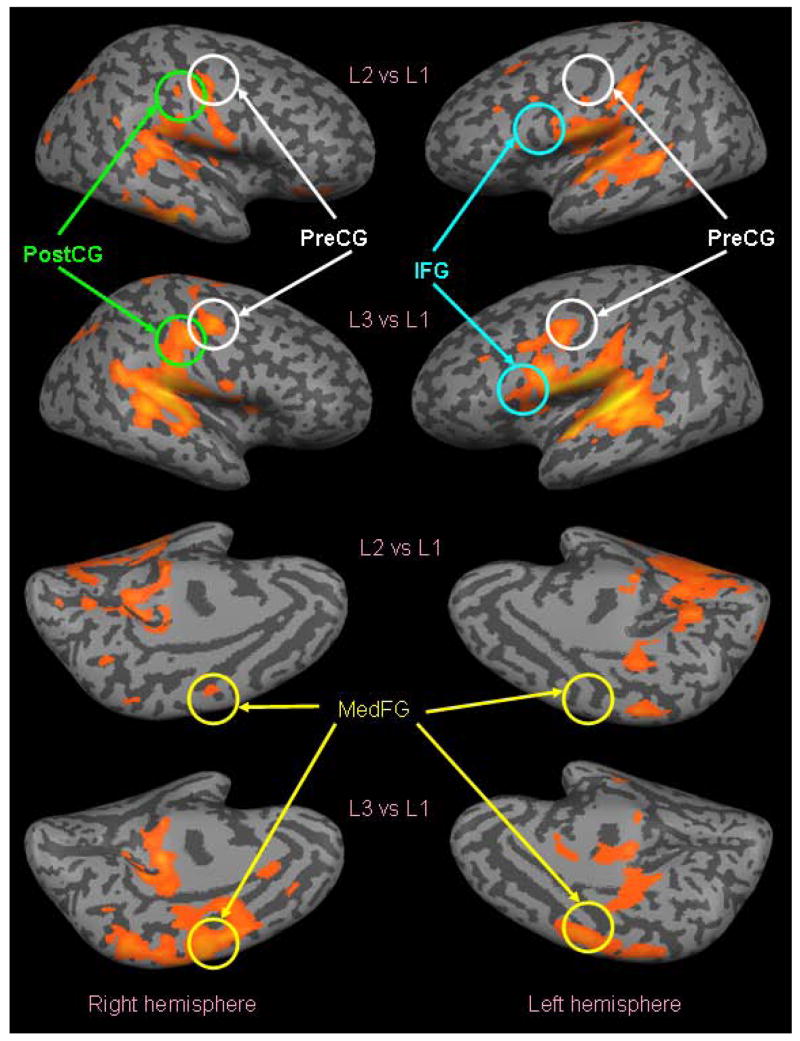
Graphical depiction of the results of the analysis of the experimental fMRI data, shown on an inflated brain version of the Montreal Neurological Institute template brain. The probability maps shown used 1-segment stimuli (L1) as a baseline, and therefore only show those areas that are more active during 2-segment stimuli (L2) than during 1-segment stimuli (first and third rows, p<0.001, uncorrected), and those that are more active during 3-segment stimuli (L3) than during 1-segment stimuli (second and fourth rows, p<0.001, uncorrected). Dark grey represents sulci and light grey represents gyri. Cortical areas chosen for ROI analysis are circled.

Table 2.

Coordinates of the center of mass of the regions of interest used by Husain et al [12] for data analysis.

		LH			RH
Region	x	y	z	x	y	z
Ai	−45	−31	15	48	−26	10
Aii	−59	−26	10	62	−32	10
ST_ant	−59	−17	4	65	−26	4
ST_post	−60	−39	12	60	−39	12
PFC	−54	9	8	56	21	5

The percentage signal change for each ROI was calculated in the same way as it was for simulated fMRI. That is, we obtained the event-related average curve for each ROI and each load condition (L2 and L3) within that ROI. After that, the differences were calculated for each of the points of the load’s average curves (L2, L3) minus the baseline load (L1), each divided by the baseline load, L1. The averages of all the points of the two difference curves were obtained, and these were considered to be the BOLD signal percentage change (L2vsL1 and L3vsL1).

fMRI EXPERIMENT - RESULTS

Experimental fMRI

The results of the analysis of the experimental fMRI data are shown on an inflated brain in Fig. 6. The probability maps shown in Fig. 6 used 1-segment stimuli (L1) as a baseline, and therefore only show those areas that are significantly more active during 2-segment stimuli (L2) than during 1-segment stimuli (first and third rows in Fig. 6, p<0.001, uncorrected), and those that are significantly more active during 3-segment stimuli (L3) than during 1-segment stimuli (second and fourth rows in Fig. 6, p<0.001, uncorrected). By visual inspection, we can see that auditory areas are active as expected, and that these auditory areas show less activation in L2 versus L1 than in L3 versus L1. In addition, L3 versus L1 shows some interesting activity that is not present in L2 versus L1. For example, in the left hemisphere of L3 versus L1 there is significant activity in medial frontal gyrus (MedFG), precentral gyrus (PreCG), inferior frontal gyrus (IFG), and postcentral gyrus (PostCG).

Tables 3 and 4 list the main clusters of activation, their center-of-mass coordinates, number of voxels, and corresponding brain areas [as found using the Talairach daemon (http://ric.uthscsa.edu/projects/talairachdaemon.html)] resulting from the GLM analysis on L2vsL1 (Table 3) and L3vsL1 (Table 4).

Table 3.

Coordinates of the center of mass of the clusters for L2vsL1.

# cluster	x	y	z	No. voxels	Brain Region
1	43	−26	−16	2398	R. fusiform gyrus
2	54	−34	15	611	R. superior temporal gyrus
3	54	−11	10	56	R. precentral gyrus
4	49	−13	36	268	R. precentral gyrus
5	30	−47	26	1600	R. parietal lobe
6	29	−37	9	176	R. caudate nucleus
7	21	−12	14	1900	R. thalamus
8	18	−65	−17	4116	R. cerebellum
9	−11	−58	−15	4119	L. cerebellum
10	−6	−31	57	227	L. paracentral lobule
11	−25	−9	11	783	Left putamen
12	−24	−54	33	111	L. parietal lobe
13	−37	−22	30	1984	L. postcentral gyrus
14	−42	−37	2	2071	L. superior temporal gyrus
15	−60	−12	9	3810	L. transverse temporal gyrus

Table 4.

Coordinates of the center of mass of the clusters for L3vsL1.

# cluster	x	y	z	No. voxels	Brain Region
1	43	−36	16	14961	R. superior temporal gyrus
2	49	−13	46	1645	R. precentral gyrus
3	22	34	22	106	R. medial frontal gyrus
4	19	−42	68	70	R. postcentral gyrus
5	19	−4	15	223	R. putamen
6	15	−15	37	301	R. cingulate gyrus
7	3	−7	57	4508	R. medial frontal gyrus
8	5	−45	56	267	R. precuneus
9	5	−29	15	380	R. thalamus
10	−25	−6	10	1122	L. putamen
11	−53	−22	11	20808	L. transverse temporal gyrus
13	−55	−2	44	2204	L. precentral gyrus

COMPARISON OF EXPERIMENTAL AND MODEL-BASED FMRI RESULTS

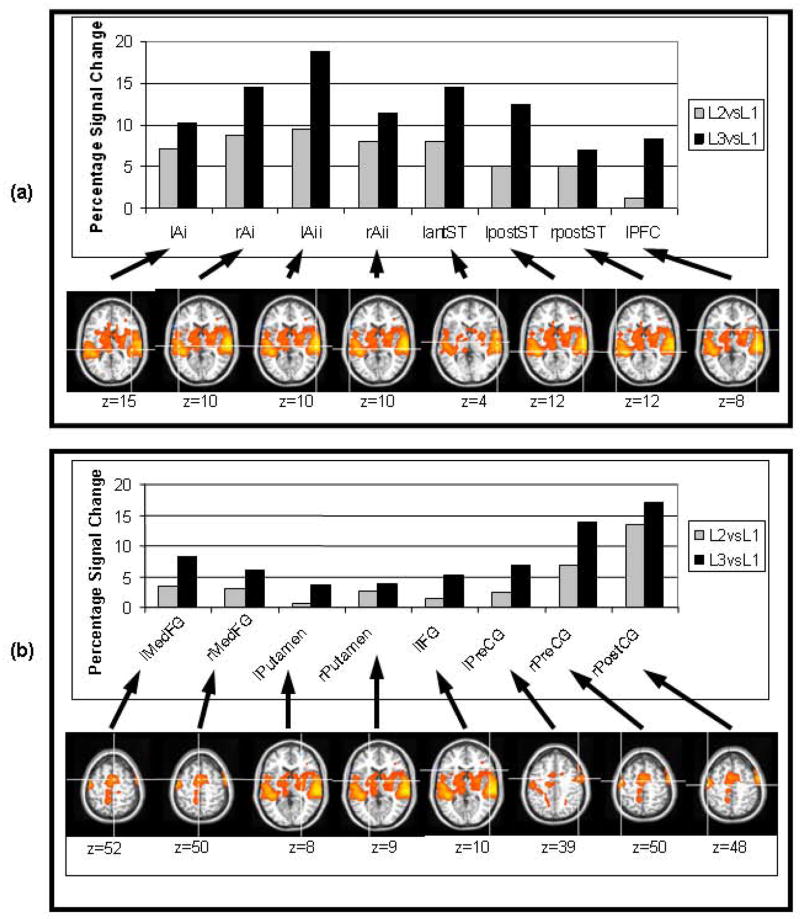
Figure 7(a) displays the percentage signal changes corresponding to the ROIs used by Husain et al [12] for L2vsL1 and L3vsL1. Table 2 lists the coordinates of the center of these ROIs. Whereas the model simulates a single brain hemisphere, we matched the simulated data with experimental values obtained from both hemispheres. As seen in Fig. 7(a) most of the areas corresponding to the modules of the original model demonstrate increased activation when the long duration (L2 and L3) auditory stimuli were used, the exceptions being right anterior ST and right PFC. A comparison of the simulated percent changes (Fig. 5) with the experimentally observed percent changes in Fig. 7(a) shows qualitative, but not quantitative, agreement between the simulated and experimental percent changes.

Figure 7.

(a) Experimental BOLD signal changes from ROIs from Husain et al (2004). The areas in which there was no activity at all were excluded (rantST and rPFC). (b) Percentage BOLD signal changes in ROIs of fMRI experiment of long-duration stimuli. The crosshairs in the brain pictures represent the center of mass of the ROIs used for the computation of BOLD signal changes. Left side of the images correspond to the right hemisphere.

Figure 7(b) shows the percentage signal changes corresponding to the ROIs selected for the current experiment as possible locations for the new modules of the model. Table 5 lists the coordinates of the centers of these ROIs.

Table 5.

Coordinates of the center of mass of the regions of interest used in the present study.

		LH			RH
Region	x	y	z	x	y	z
MedFG	−5	−2	52	4	−1	50
Putamen	−24	−2	8	20	−5	9
IFG	−52	16	10	n/a	n/a	n/a
PreCG	−52	−2	39	48	−8	50
PostCG	n/a	n/a	n/a	52	−16	48

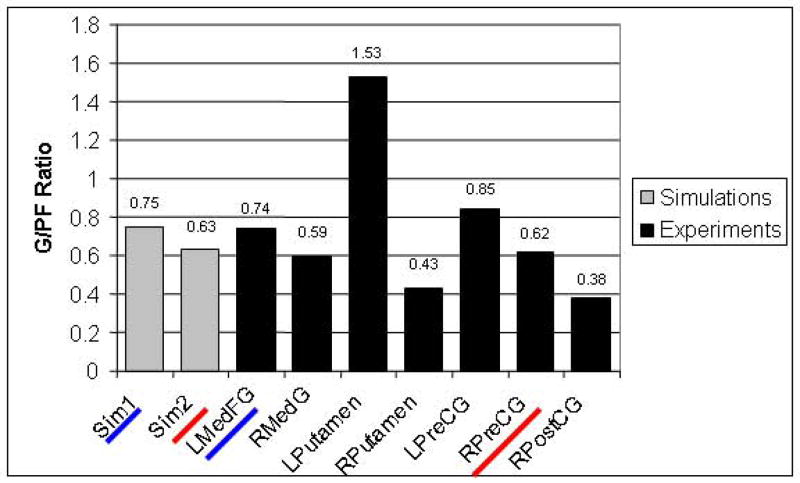
The simulated BOLD signal averages (for L2vsL1 and L3vsL1) corresponding to the “Gating” module of the proposed arrangements of the model (Fig. 5) can be compared with the estimated average of the experimental BOLD signal of the candidate Gating areas to find which area had the closest match between simulated and experimental data (Fig. 7b). However, confounding this comparison is the fact that the model PFC values differed from the experimental data. One reason for this may arise because there could be numerous cognitive processes occurring that involve PFC that are not accounted for by our model. To account for this, we normalized our simulated and experimental percent BOLD changes to those in the PFC. That is, we estimated the ratio of percentage signal changes of the Gating module to the PFC module. The ratios were evaluated for both the simulations and the experiment data (for all the candidate brain Gating areas). For the simulated percentage BOLD signal change ratios, we calculated the ratios of L3vsL1 to L2vsL1 in the Gating area. We then calculated the ratios of L3vsL1 to L2vsL1 in the PFC. We finally calculated the ratio of the Gating area ratio to the PFC area ratio for each of the arrangements of modules of the model. For the experimental percentage BOLD signal change ratios, we calculated the ratios of L3vsL1 to L2vsL1 of each one of the candidate Gating areas. We then calculated the ratio of L3vsL1 to L2vsL1 of the Left IFG (corresponding to PFC in the model). We then calculated the ratios of each of the candidate Gating area ratios to the Left IFG ratio. Each of the ratios of the candidate areas were then compared to the ratios of GA to PFC of the simulations.

Figure 8 shows the ratio of the percentage signal change of the putative Gating areas to the percentage signal change of the PFC areas for both simulated and experimental data. For the simulations, ratios for the two arrangements previously discussed (Sim1 corresponds to that shown in Fig. 5a, Sim2 to that shown in Fig. 5b) are also shown. For the experimental fMRI, ratios of the seven candidate Gating areas (GAi) are shown in Fig. 8. From this figure, it is evident that the best matches are for (1) the first configuration (Sim1, ratio=0.75) and lMedFG (ratio=0.74); and (2) the second configuration (Sim2, ratio=0.63) and rPreCG (ratio=0.62).

Figure 8.

Comparison of proportions of gating module (GA) BOLD activity to prefrontal cortex module (PFC) BOLD activity in simulated and experimental ROIs. Sim1 corresponds to the first configuration that was simulated (see Fig. 5a) and Sim2 corresponds to the second simulation (see Fig. 5b). Sim1 and lMedFG are both underlined in blue to indicate that their ratios are very similar in magnitude. Sim2 and rPreCG are both underlined in red to indicate that their ratios are very similar in magnitude.

DISCUSSION

Summary of key findings

We constructed a model based on the previous work of Husain et al [12] that simulated a delayed match-to-sample task of long-duration auditory patterns and were able to generate both simulated neuronal electrical activities and fMRI BOLD signals for the brain areas (modules) involved in the task. This allowed us to propose a mechanism for the short-term memory of long duration tonal contours and to predict the fMRI BOLD signal for the area(s) responsible for those mechanisms. Husain et al [12] found correspondence between the modules in their model and brain areas located in auditory and prefrontal cortices. In the present study, we were interested in extending those findings by seeking a short-term memory gating area, responsible for the distribution and ordering of the segments of the input pattern into short-term memory.

The addition to the model of the gating module and its interaction with the PFC module was based on monkey studies. One of those studies found evidence for inhibition and disinhibition between cells in dorsolateral prefrontal cortex, which might be used to link a temporal chain of events [6]. Thus, this might be part of a mechanism that could code complex stimuli, such as long-duration sounds. A second study found evidence that cells in prefrontal cortex encode order of presentation of spatial positions in a delayed saccade task [8]. A third study found that the lateral prefrontal cortex of the monkey is capable of coding both object identity and presentation order of a remembered stimulus [24].

Because each sub-module of our model represents a distinct neuronal population, and because we know that most cortical regions consist of multiple neuronal populations, the different modules and sub-modules in our model could be arranged in a number of ways to match specific brain areas. However, only a few of these were considered biologically plausible, and so we focused on two configurations and their corresponding fMRI BOLD signals. Configuration 1 (i.e., Sim1) (Fig. 5a) assumed that all of the new modules added to the model formed a gating area in the human brain. Configuration 2 (Sim2) (Fig. 5b) assumed that only the modules exclusively concerned with the distribution of input segments to memory formed the gating areas. In configuration 2, there were modules that represented a memory of “buffer location full” or “buffer location available,” and they were assumed to be part of the human prefrontal cortex. We found that the simulated fMRI BOLD signal of the Gating module of the two configurations of our model best matched the fMRI BOLD signal of the left medial frontal gyrus (lMedFG, Brodmann area (BA) 6) (configuration 1) and the fMRI BOLD signal of the right precentral gyrus (rPreCG, BA4/6) (configuration 2) during the auditory delayed match-to-sample task. Thus, lMedFG and rPreCG, areas most likely in medial and lateral premotor cortex (BA6), respectively, are the two most likely locations in the human brain for our hypothesized gating module.

Support for Husain et al (2004)’s model

Our study provides support for some of the hypotheses put forth by Husain et al (2004). In particular, our fMRI data showed modulation with increasing auditory size in the ROIs selected by Husain et al except in right anterior ST and right prefrontal cortex. There was no increased activity in these areas in our study. One possible explanation for the lack of activity in those areas is that whereas Husain et al’s study compared the activity during the task versus rest blocks, our study compared the activity of Load 2 and Load 3 versus Load 1. Thus, the results of analyses in the present study show activity only in those areas in which there was a change in activity with respect to load 1.

Discussion of new modules of the model

The existence of a gating mechanism in either lMedFG or in rPreCG is supported by other fMRI studies using auditory perception and discrimination tasks. Two studies have shown fMRI activity in the lMedFG during auditory discrimination [23] and during auditory working memory [26]. A third study has implicated the rPreCG in auditory segmentation, discrimination and working memory [19].

Müller et al [23] found activation in the MedFG during an fMRI experiment using an auditory discrimination task in which subjects pressed a button whenever they heard a rising tone in a sequence of three tones. The activation in MedFG bilaterally was attributed to a greater attentional demand than that required by the control condition (subjects pressing a button whenever they heard a noise burst during presentation of a sequence of three noise bursts). Stevens et al [26] found activation in the left MedFG during an fMRI experiment in an auditory working memory task, in which subjects listened to sequences of words and tones. After a delay period, subjects listened to the presentation of either one word or one tone and had to indicate their serial position within the sequence heard. Task related activation was observed in the MedFG bilaterally in schizophrenic patients and controls. In controls, the task-related activation in lMedFG during the tones task was greater than in the words task. In patients, the task-related activation in lMedFG during the tones task was smaller than in the words task. The coordinates of the center of mass for the lMedFG in this study were (−7, −8, 58) for the words task and (−8, −13, 62) for the tones task (Compare these coordinates to the approximate center of mass of the ROI labeled lMedFG in the present study: −5, −2, 52).

In the auditory working memory study of LoCasto et al [19] fMRI activation of the right PreCG was found when subjects listened to two sequences of three tones separated by a short delay period (5 ms) and had to press a button whenever the first tone of the second sequence matched the first tone of the first sequence. The control task consisted on a simple discrimination task in which two tones were used. In a comparison of sequences versus tone discriminations, rPreCG was shown to be significantly active. The coordinates of the center of mass of the rPreCG area in this study were (31, −11, 64) (Compare to the coordinates of the approximate center of mass of the ROI labeled rPreCG in the present paper: 48, −8, 50).

Comparison with other working memory models

Few models of working memory have dealt with the issue of encoding long-duration stimuli (longer than the window of temporal integration of neurons) or with the encoding of sequences (the approach used by our model). Jensen and Lisman [13] proposed a model of working memory of sequences by using the concept of theta and gamma cycles of firing of neurons. This model proposes that a way for the hippocampus to encode sequences in long term memory is by being aided by a cortical working memory buffer that encodes a sequence in short-term memory. Items in the sequence are stored in order in the gamma subcycles (of about 30–80 Hz) of theta cycles (of about 4–10 Hz). The group of neurons that represent a given item fires every theta cycle during the occurrence of the gamma subcycle during which it was encoded. When an item is presented during a trough of a theta cycle, the neurons representing that item fire during the next empty gamma subcycle.

Another model of working memory of sequences was proposed by Beiser and Houk [2]. This model is based on the known reciprocal connections between thalamus and prefrontal cortex and the connections between prefrontal cortex, the caudate nucleus, the globus pallidus, and the thalamus. Input items are represented in prefrontal cortex by “event” neurons, which form an array of connections with the caudate nucleus. Neurons in the caudate nucleus form a competitive network, from which a unique spatial pattern results that inhibits globus pallidus neurons, which in turn results in disinhibition of thalamic neurons. When a group of thalamic neurons is disinhibited, each one of these neurons fire and initiate a reciprocal excitation process with memory neurons in prefrontal cortex, thereby closing the basal ganglia – prefrontal cortex loop and encoding a representation of the input item in a spatial pattern of firing prefrontal cortex neurons. This model does not include recall of the patterns encoded in memory, but it provides a unique spatial representation for any possible input pattern to be encoded.

Conclusions

In this paper, we simulated a delayed match-to-sample task of long-duration auditory patterns and generated simulated neuronal electrical activities and fMRI BOLD signals of brain areas associated with the integrative mechanisms proposed by our model. In particular, we proposed that a gating mechanism is necessary to distribute the segments of the input pattern into different cortical locations of the working memory buffer. This gating mechanism also kept track of the order of presentation of the segments. Furthermore, we performed an fMRI experiment that used the same task and similar input stimuli to that of the simulations. We found that the model-based fMRI BOLD signal of the gating module correlated well with the experimental fMRI BOLD signal of two brain areas in premotor cortex: the left medial frontal gyrus and the right precentral gyrus. Both areas have been found by previous studies to increase fMRI activity during auditory tasks and either area, or both, is well suited for performing the gating function. A future fMRI study could be based on discerning which one of these two is the most likely gating area for auditory working memory.

The present modeling-experimental framework is important for investigating location and mechanisms of brain functions that cannot be found with either modeling or experiments alone. Whereas modeling provides explicit mechanisms for specific brain functions, it is not capable of specifying a location for those brain functions. On the other hand, fMRI experiments provide possible locations of functions that are utilized for a given task, but it does not provide an integrative mechanism responsible for mediating these functions. Only an approach that combines both is capable of providing explicit mechanisms and brain locations that correspond to those brain functions.