Computational structure-based redesign of enzyme activity

Abstract

We report a computational, structure-based redesign of the phenylalanine adenylation domain of the nonribosomal peptide synthetase enzyme gramicidin S synthetase A (GrsA-PheA) for a set of noncognate substrates for which the wild-type enzyme has little or virtually no specificity. Experimental validation of a set of top-ranked computationally predicted enzyme mutants shows significant improvement in the specificity for the target substrates. We further present enhancements to the methodology for computational enzyme redesign that are experimentally shown to result in significant additional improvements in the target substrate specificity. The mutant with the highest activity for a noncognate substrate exhibits 1/6 of the wild-type enzyme/wild-type substrate activity, further confirming the feasibility of our computational approach. Our results suggest that structure-based protein design can identify active mutants different from those selected by evolution.

Despite recent successes, enzyme design has posed significant challenges for both computational and purely experimental approaches. Until recently, computational enzyme design approaches have met with limited success (1–3), making experimental techniques, such as directed evolution, the preferred method for designing new enzymes (4–7). Advances in both algorithms and modeling recently resulted in the first computationally driven de novo structure-based design of active enzymes (8, 9). A fully automated computational approach that is applicable to general enzyme design problems, however, is yet to be developed.

A major advantage of computational structure-based protein design over the purely experimental approaches lies in its ability to efficiently (and inexpensively) search a significantly larger portion of the available space of candidate mutations. Unfortunately, computational approaches must rely on simplified models that only approximate real proteins and their interactions. Among the typical simplifying model assumptions are: a rigid protein backbone, a rotamer library of discrete side-chain conformations (10, 11), and a pairwise energy function (12, 13). To improve the accuracy of the model, some recent advances in computational protein design have incorporated continuous flexible rotamers (14) and continuous (15) or discrete (16, 17) backbone flexibility. More accurate energy functions are sometimes used as a postprocessing step to reevaluate and rerank the top-scoring predictions from the initial model (18). Despite the imperfections of the underlying models, the computational approaches have yielded successful designs of proteins with improved target properties (2, 18–21). Designing for enzyme activity, however, has proven to be far more elusive. The difficulty of designing enzymes via computational methods can be attributed to the more poorly understood catalytic enzyme machinery and the increased inability of the simplified models to represent the catalytically relevant interactions (and especially the high-energy transition states) accurately.

Here, we present a computational structure-based redesign of the 65-kDa phenylalanine adenylation domain of the nonribosomal peptide synthetase (NRPS) enzyme gramicidin S synthetase A (GrsA-PheA) for a set of noncognate substrates. NRPS enzymes are large multidomain protein complexes that work in an assembly-line manner and whose products include many peptides of pharmacological interest (including penicillin and vancomycin) (22). GrsA, in concert with GrsB, makes the decapeptide antibiotic gramicidin S (23). The crystal structure of GrsA-PheA in complex with the wild-type (WT) substrate Phe and the AMP cofactor, has been determined, thus making this domain a suitable target for structure-based redesign. Alternative methods for the redesign of NRPS enzymes include domain swapping/directed evolution (7) and various sequence-based methods (24, 25).

The results from redesigning NRPS enzymes can be divided into three categories. Category 1: switch the enzyme specificity from the WT substrate to the target substrate, so that the redesigned enzyme prefers the target over the WT substrate. Category 2: improve (but not switch) the enzyme specificity for the target substrate (in the case where the WT enzyme already has activity for the target substrate). Category 3: create activity for the target substrate (in the case where the WT enzyme has no activity for the target substrate). In previous work, we reported structure-based redesigns of the active site of GrsA-PheA that were experimentally confirmed to improve (but not switch) substrate specificity for Tyr (3) (category 2 results). Those redesigns were based on older versions of our K* algorithm (26), which computes partition functions over molecular ensembles defined by continuously flexible rotamers and/or backbones. Here, we present the application of improved versions of K* that incorporate several recently described algorithmic enhancements (14, 15, 27) to redesign the active site of GrsA-PheA to improve its specificity for a set of noncognate substrates for which the WT enzyme has little or virtually no specificity. Detailed kinetic experiments for a set of the top-ranked computational predictions confirm the desired improvement in specificity for five noncognate substrates (Leu, Arg, Glu, Lys, and Asp). Several of the Leu redesigns show a switch of specificity from Phe (category 1 results). Although the WT enzyme has virtually no activity for Arg, Glu, Lys, and Asp, the redesigns for these substrates successfully create the desired activity (category 3 results). Further algorithmic enhancements for predicting mutations outside of (both close to and far away from) the enzyme active site aiming at additional improvement in the substrate specificity are described and validated experimentally. The mutant with the highest activity for a noncognate substrate exhibits 1/6 of the WT enzyme:WT substrate activity, further confirming the feasibility of our computational approach. We experimentally tested our computational predictions and report the results below. Our results also suggest that structure-based protein design can identify active mutants different from those selected by evolution and from the predictions of other computational approaches.

Computational enzyme redesign (as opposed to de novo enzyme design) is in some ways easier (in that the catalytic machinery is present for the cognate substrate) and in some ways harder (in that the algorithm must overcome the innate specificity that presumably evolved during millions of years of natural selection). Redesign also provides an opportunity to compare enzyme performance with the WT, providing a benchmark for the desired activity. Finally, computational redesign to create biocatalysts with novel specificity can leverage the best of both worlds, by altering molecular recognition (by in silico prediction) while still exploiting the catalytic mechanisms selected by nature.

Results

The K* algorithm (14, 26) was applied to predict mutations to the active site of GrsA-PheA to switch the enzyme specificity from the WT Phe toward the target noncognate substrates Leu, Arg, Glu, Lys, and Asp. For each of the redesign targets, sets of the top computational predictions were then visualized and selected for experimental validation. For the Leu redesigns, additional mutations outside of the active site were further selected by using a computational protocol combining a self-consistent mean field (SCMF) entropy-based method (28) with our minimized dead-end elimination (MinDEE)/A* (14) algorithm. As with the active-site mutations, sets of the computationally predicted mutations outside of the active site were visualized and selected for experimental validation. Details of the computational algorithms and procedures and the experimental protocol are given in Experimental Procedures and the supporting information (SI) Appendix.

Steady-State Kinetic Analysis.

To confirm the desired improvement in specificity for the computationally predicted mutants, we performed detailed steady-state kinetic experiments on a set of top-ranked computational predictions for each of the target substrates. WT and mutant PheA were overexpressed and purified to homogeneity as shown in the SDS/PAGE (see Fig. S2 in the SI Appendix). The adenylation activity of the WT and mutant PheA was measured by monitoring the PP_i release rate by using a continuous spectrophotometric assay (29). The assay measures the degree of ATP consumption in an amino acid concentration-dependent manner, which reflects the rate of the enzyme to form and turn over aminoacyl adenylate. Among the proteins tested, all of them, except for the T278K/A301G mutant, showed typical hyperbolic curves with the initial velocity approaching saturation as the concentration of amino acid increases (see Section S3.3 and Figs. S3–S6 in the SI Appendix). A mock control experiment in the absence of the amino acid substrate showed a slow background ATP hydrolysis whose rate was subtracted from the rate in the presence of the substrate. The values of the kinetic constants k_cat, K_m, and k_cat/K_m for different proteins with different substrates are given in Table 1.

Table 1.

Mutant enzymes with experimentally observed specificity (k_cat/K_m), k_cat, and K_m for a target substrate and the WT substrate (Phe)

Redesign target	Enzyme	Rank	Target substrate			WT substrate (Phe)
			kcat min−1	Km mM	kcat/Km mM−1 min−1	kcat min−1	Km mM	kcat/Km mM−1 min−1
Leu†	T278L/A301G	1	1.16 ± 0.10	0.015 ± 0.002	79.49 ± 13.67	3.37 ± 0.08	0.097 ± 0.013	34.94 ± 4.76
	T278M/A301G	8	2.63 ± 0.24	0.130 ± 0.009	20.34 ± 3.11	4.25 ± 0.16	0.318 ± 0.009	13.35 ± 0.14
	A322V/A301G	9	4.18 ± 0.52	0.448 ± 0.019	9.34 ± 1.08	3.17 ± 0.2	0.195 ± 0.019	16.35 ± 1.3
	WT‡		28.74 ± 1.58	6.98 ± 1.00	4.15 ± 0.36	1.73 ± 0.29	0.0018 ± 0.0004	951.4 ± 111.2
Arg†	T278D/A301G	1	0.238 ± 0.007	46.43 ± 4.79	0.0051 ± 0.0004	0.50 ± 0.02	0.153 ± 0.02	3.29 ± 0.38
	WT		ND§	ND	ND
Glu†	T278H/A301G	2	0.3773 ± 0.035	25.49 ± 5.65	0.0151 ± 0.0023	0.38 ± 0.03	0.027 ± 0.006	14.7 ± 2.48
	WT		ND	ND	ND
Lys†	T278D/A301G	4	1.09 ± 0.08	78.33 ± 16.39	0.014 ± 0.003	0.50 ± 0.02	0.153 ± 0.02	3.29 ± 0.38
	WT		ND	ND	ND
Asp†	T278K/A301G	3	>0.25¶			16.19 ± 1.32	28.93 ± 1.91	0.56 ± 0.06
	WT		ND	ND	ND
Leu‖	T278L/A301G/S447N		0.85 ± 0.11	0.0054 ± 0.001	159.86 ± 14.98	3.36 ± 0.23	0.168 ± 0.027	20.38 ± 3.97
	I277L/T278L/A301G		1.52 ± 0.09	0.013 ± 0.002	119.79 ± 9.75	5.21 ± 0.22	0.306 ± 0.004	17.00 ± 0.55
	V187L/T278L/A301G		1.69 ± 0.22	0.011 ± 0.001	155.51 ± 26.71	3.24 ± 0.16	0.201 ± 0.036	16.43 ± 2.47
	I277L/T278L/A301G/S447N		0.37 ± 0.04	0.0054 ± 0.0007	69.07 ± 13.09	2.09 ± 0.10	0.282 ± 0.023	7.44 ± 0.67

^†K* active-site mutants with their respective ranks from the 2-point mutation searches for the different substrates.

^‡For clarity, the WT enzyme:WT substrate rates are shown only once.

^§ND, not detectable.

^¶K_m and k_cat/K_m cannot be determined accurately because the solubility of Asp (≈50 mM in water) limits the reaction velocity under the experimental condition, in which the velocity remains linearly dependent on the concentration of the substrate.

^‖ Bolstering mutations added to the T278L/A301G mutant with Leu as substrate.

Redesign for Leu.

The WT PheA shows a rather strong specificity to its natural substrate Phe with k_cat/K_m value ≈229-fold higher than the noncognate amino acid Leu. A previous binding study showed that without binding of ATP, the WT PheA can accommodate most of the noncognate amino acid substrates (30). Our results, however, show that the WT protein can only activate certain types of amino acids including Phe, Leu, and Val, but not charged amino acids. To switch substrate specificity of PheA from Phe to Leu, we applied the K* protein redesign algorithm (14) by using as input the crystal structure of WT PheA in complex with the Phe substrate and AMP (see Experimental Procedures and Section S1.1 in the SI Appendix). The top-ranked K* mutation sequence was T278L/A301G (Table 1). The lowest-energy T278L/A301G structure from the K* ensemble with Leu as substrate is shown in Fig. 1. The double-mutant protein showed a ≈19-fold increase of k_cat/K_m with Leu and a ≈27-fold decrease of k_cat/K_m with Phe from the WT PheA, which results in ≈2.3-fold higher k_cat/K_m for Leu than for Phe (Fig. 2). As a result, the double-mutant protein makes a ≈521-fold switch in specificity given that the k_cat/K_m ratio of Leu over Phe is only ≈0.0043 for WT PheA. The difference in the k_cat/K_m value between the WT and the T278L/A301G PheA with Leu and Phe is driven mainly by the K_m values, which have a ≈465-fold decrease with Leu and a ≈54-fold increase with Phe in the T278L/A301G mutant. As a result, the K_m value with Leu becomes ≈6-fold lower than with Phe in T278L/A301G. The switch suggests that the double-mutant protein now binds tighter to Leu than to Phe. WT PheA has a rather high k_cat value with Leu whereas it is relatively low with Phe. The k_cat value of the T278L/A301G mutant with either Leu or Phe remains at the same level as the WT PheA with Phe. The measurement of k_cat is limited by the rate of product release because of the tight binding of the aminoacyl-AMP. Therefore, the high k_cat value with Leu for the WT protein might be caused by the loose binding of the leucyl-AMP product given its high K_m value. The double mutant T278M/A301G is ranked 8th by K* for the Leu redesign. This double mutant was also previously predicted by a sequence alignment-based method and verified experimentally to activate Leu (24). We have confirmed that the T278M/A301G mutant has a k_cat/K_m value ≈5-fold higher with Leu and ≈73-fold lower with Phe than the WT PheA. The T278M/A301G mutant selects ≈1.5-fold more Leu than Phe (Fig. 2). K* also predicted the double mutant A301G/A322V, which had a k_cat/K_m value ≈59-fold lower with Phe and ≈2.2-fold higher with Leu than WT PheA.

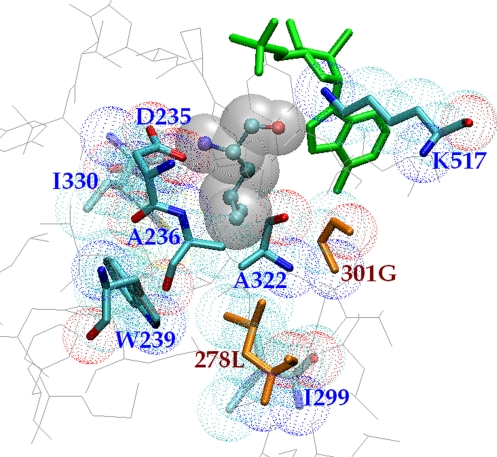
Fig. 1.

K*-predicted structure of the lowest-energy T278L/A301G conformation with Leu as substrate. Shown are the Leu substrate (CPK ball-and-stick and gray space-filling representations), the AMP cofactor (green), the two active-site mutations 278L and 301G (orange sticks and CPK dots), and the other eight active-site residues, including the remaining five mutable residues (CPK sticks and dots); C331 is hidden behind D235.

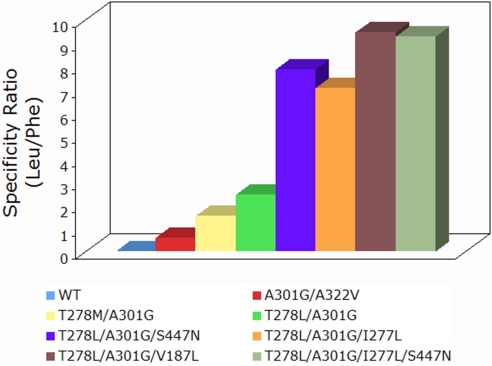
Fig. 2.

Specificity ratio $\frac{{(k_{\text{cat}}/k_{\text{m}})}_{\text{Leu}}}{{(k_{\text{cat}}/k_{\text{m}})}_{\text{Phe}}}$ for WT and mutant PheA in the Leu redesigns. The WT PheA shows a ratio of 0.0043 with its k_cat/K_m values of 4.15 (mM ⁻¹ min⁻¹) for Leu and 951.4 (mM⁻¹ min⁻¹) for Phe. A301G/A322V still prefers Phe with a ratio of 0.57. T278M/A301G prefers Leu over Phe with a ratio of 1.5, whereas T278L/A301G shows a ratio of 2.3. The three triple mutants have ratios of 7.8 for T278L/A301G/S447N, 7.0 for I277L/T278L/A301G, and 9.4 for V187L/T278L/A301G. The quadruple mutant has a ratio of 9.3.

To further improve the specificity of the double mutant T278L/A301G for Leu, we identified distal bolstering mutations outside the active site by applying the computational protocol described in Experimental Procedures and Section S1.2 in the SI Appendix. Up to 3-point bolstering mutation search (in addition to the T278L/A301G active-site mutant) was performed for the mutable positions, and the top mutations V187L, I277L, and S447N were selected and tested. All of the three triple mutants gave 1- to 2-fold additional improvement of the specificity with Leu over the T278L/A301G mutant. Among them, the T278L/A301G/S447N showed an additional ≈2-fold higher k_cat/K_m value for Leu with a ≈2.7-fold decrease of K_m and a slightly lower k_cat. The K_m values with Leu are slightly lower for both I277L/T278L/A301G and V187L/T278L/A301G with Leu compared with the T278L/A301G mutant, whereas their k_cat values are both slightly higher. All three triple mutants have a decreased specificity toward Phe from the T278L/A301G mutant. As a result, the difference of k_cat/K_m between Leu and Phe became ≈7.8-fold in T278L/A301G/S447N, ≈7-fold in I277L/T278L/A301G, and ≈9.4-fold in V187L/T278L/A301G toward a better selection of Leu (Fig. 2). These mutants gave a switch of ≈1,796-fold in T278L/A301G/S447N, ≈1,614-fold in I277L/T278L/A301G, and ≈2,168-fold in V187L/T278L/A301G from the WT PheA, exhibiting up to 1/6 of the WT enzyme:WT substrate activity (absolute values of k_cat/K_m). We next tested whether the quadruple mutant combining S447N and I277L could give additional improvement. However, although its K_m with Leu is as low as the T278L/A301G/S447N triple mutant, its k_cat is ≈2-fold lower than any of the triple mutants and the T278L/A301G mutant. Nevertheless, it showed a significant result with its K_m value of Phe close to I277L/T278L/A301G and its K_m of Leu close to T278L/A301G/S447N.

Redesign for charged amino acids.

The active site of PheA shows mainly a hydrophobic pocket and no observable activity with charged amino acids. We next tested our redesign algorithm for the activation of charged amino acids, Arg, Lys, Glu, and Asp by predicting mutations to WT PheA. As expected, the algorithm predicted mainly negatively charged side chains to bind Arg and Lys and positively charged side chains to bind Glu and Asp in the active site of PheA. The prediction resulted in the double mutant T278D/A301G, which K* ranked first to bind Arg and fourth to bind Lys. This double mutant showed small but significant activity with both Arg and Lys under the same conditions as the Leu redesign. The activity was improved when the Tris·HCl concentration was lowered to 50 mM. The T278D/A301G mutant showed substrate concentration-dependent kinetics with both the Arg and the Lys substrate (see Fig. S6 C–E in the SI Appendix). Both substrates showed much higher K_m values, which suggest a weak binding between the mutant protein and the substrates. Their k_cat values with this double mutant are also severalfold lower (≈7-fold for Arg and ≈1.5-fold for Lys) than the WT PheA with Phe. Among the top-scored sequences to bind Glu and Asp, T278H/A301G was ranked 2nd to bind Glu, and T278K/A301G was ranked 3rd to bind Asp. Both mutants showed substrate concentration-dependent kinetics with their substrates (see Figs. S5 E and F and S6 A and B in the SI Appendix). The rate of the T278K/A301G increased linearly without approaching saturation as the concentration of Asp approached its maximum solubility. As a result, only a lower bound on k_cat was determined. The three double mutants T278D/A301G, and T278H/A301G, while acquiring new substrate activity, showed decreased specificity for Phe. Unlike the increase of k_cat for Phe observed in all of the Leu-redesigned mutants, the k_cat values are significantly lower in T278D/A301G and T278H/A301G. The lower k_cat value with the natural substrate Phe suggests that introduction of charged side chains in the active site might have an influence on the enzyme catalysis. A low-energy T278D/A301G structure from the K* ensemble with Arg as substrate is shown in Fig. 3. Detailed structural analysis of T278L/A301G with Leu and T278D/A301G with Arg can be found in Section S2.1 in the SI Appendix.

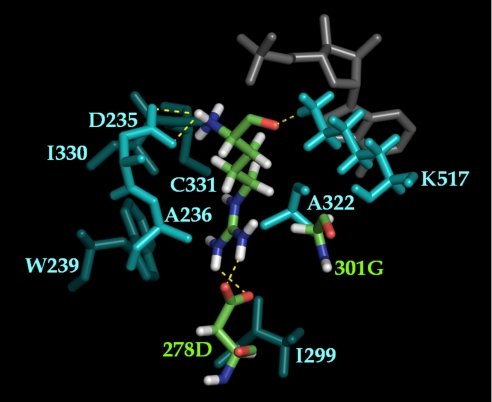
Fig. 3.

K*-predicted structure of the second lowest-energy T278D/A301G conformation with Arg as substrate. Shown are the Arg substrate and the two active-site mutations 278D and 301G (CPK), the other active-site residues (cyan), and the AMP cofactor (gray). Interactions between the substrate side chain with 278D (the distance between N_η1 (Arg) and O_δ2 (278D) is 2.92 Å; the distance between N_η2 (Arg) and O_δ1 (278D) is 3.15 Å), and the substrate backbone with D235 and K517 is shown with dashed yellow lines. The viewing angle is chosen to show side-chain interactions between Arg and 278D.

Discussion

The adenylation domain of NRPS has been known to play a major role in the recognition of the amino acid substrates (30). Several studies have shown that the substrate specificity of the adenylation domain can be modified by the mutation of the active-site residues (3, 24, 31). By using a multiple sequence alignment approach to redesign the substrate specificity of GrsA-PheA, Stachelhaus et al. (24) successfully improved the activity of the enzyme for the noncognate amino acid Leu with the introduction of a double mutation, T278M/A301G, and altered the substrate specificity of an aspartate-activating domain AspA to Asn by a single mutation H322E in the active site. The sequence-based approach identifies active-site residues important for the substrate specificity by comparing the corresponding moieties among different adenylation domains. However, its accuracy depends heavily on the number and diversity of available sequences. In contrast, our K* algorithm uses the structure of the PheA domain as well as an amino acid rotamer library and a molecular mechanics energy function as inputs. For a given amino acid substrate, the algorithm was able to search a space of thousands of sequences with hundreds of millions of conformations (see Section S1.1.3 in the SI Appendix). By computing the partition functions over the conformational ensembles, the K* algorithm scores sequences based on their approximation to the binding constant. As a result, the top-scored sequences were expected to have a lower K_d and consequently a lower K_m for the target substrate. The feasibility of the K* algorithm was shown by the lower K_m value with Leu of the top-scored mutants, T278L/A301G, T278M/A301G, and A301G/A322V.

Sequence-based methods are limited to the active-site signature motif. Hence, the sequence alignment approach can only identify regions (such as the active site) where a significant sequence homology exists. It has been suggested that distal residues outside the active site might play critical roles in stabilizing protein function (32). This idea was incorporated into our computational protocol with the identification of the bolstering mutations outside the active site. The addition of the predicted bolstering mutations in the Leu redesigns had a significant impact on the substrate specificity of the enzyme. Because residue 277 is adjacent to the active-site mutation T278L, the mutation I277L could directly affect the conformation of the enzyme active site, also affecting the substrate specificity. Residues 187 and 447, however, are distal from the ligand-binding site, and their impact is likely caused by indirect and/or long-range interactions. Interestingly, structural analysis of the lowest-energy S447N conformation predicted by the MinDEE/A* algorithm (14) shows that the Asn side chain reaches across a solvent channel inside the protein, making a hydrogen bond with backbone carbonyl oxygen of H344 (Fig. S1 in the SI Appendix). The precise effect of these distal mutations remains unclear. To understand their roles in the protein function requires further experiments, including X-ray and NMR structural studies.

The ability of the algorithm to search a large space of sequences and conformations enables us to redesign the active site for a diverse set of substrates. We tested this capability of the algorithm by predicting mutations for charged amino acids whose activity was not found in PheA. To stabilize the charged side chain of the substrates, the algorithm introduced polar or charged residues in the active site, which resulted in our successful mutations, T278D/A301G to bind Lys and Arg, T278H/A301G to bind Glu, and T278K/A301G to bind Asp. Interestingly, residue positions 278 and 301 were again chosen by the algorithm but with a different residue type at position 278. A previous report has shown that mutation at a single key position His-322 (to Glu-322) in the active site of the adenylation domain AspA from the surfactin synthetase B is sufficient to obtain the specificity switch from Asp to Asn (31). This finding, combined with our results, suggests that in GrsA-PheA, positions 278 and 301 might play key roles in the recognition of the substrate. Structural analysis of the K* models of the mutants suggests that Gly-301 might alleviate steric clashes to bind different substrates (see Section S2.1 in the SI Appendix). Residue 278 might be involved in direct interactions with the substrate side chain.

A comparison of our computationally predicted mutant active sites with a set of NRPS enzymes selected by evolution showed that although the amino acid identities at mutated positions were found as constituents of longer signature sequences, none of our exact mutant active sites could be found in that enzyme set. Moreover, a comparison with the predictions from two sequence-based methods showed that our structure-based method could identify active mutants different from the sequence-based predictions. Details of these comparisons can be found in Section S2.2 in the SI Appendix.

The mechanism of substrate recognition by the adenylation domain of NRPS has been puzzling. Luo et al. (30) claimed that the discrimination of the amino acid substrate begins when the transition state is formed during the catalysis. Stevens et al. (3) suggested that a conformational change toward a catalytically relevant intermediate occurs in the adenylation process of PheA. In our results, the double mutant T278L/A301G dramatically lowers the value of K_m for the noncognate amino acid Leu from the WT PheA, requiring changes to only two residues in the active site. It is therefore intriguing to see whether there exists any interaction between Leu-278 and Gly-301 in binding of Leu. Hence, we then investigated the double mutant T278L/A301G and the single mutants T278L and A301G by analyzing their free energy change upon binding to Phe and Leu. Detailed free energy calculations are described in Section S3.6 in the SI Appendix, and the kinetic constants as well as difference in free energy are listed in Table S8 in the SI Appendix. The result shows that the WT protein has a difference in binding energy of 3.22 kcal/mol in favor of Phe whereas the energy difference becomes 0.49 kcal/mol in favor of Leu in the T278L/A301G mutant. The free energy barrier required for the discrimination of Phe and Leu in the WT protein was decreased to favor Leu in the mutant protein. Moreover, a coupling energy (ΔΔG_int) of 1.69 kcal/mol was observed when comparing the free energy difference of the T278L/A301G mutant (ΔΔG_{WT − T278L/A301G}) and the two corresponding single mutants T278L (ΔΔG_{WT − T278L}) and A301G (ΔΔG_{WT − A301G}) in binding of Leu. The coupling energy suggests that the two active-site residues, Leu-278 and Gly-301, might interact to provide a favorable conformation for the recognition of the Leu substrate.

Using our suite of structure-based protein design algorithms, we successfully redesigned GrsA-PheA for a set of noncognate substrates. A switch of substrate specificity from Phe toward Leu was observed for several of the computationally predicted mutants. Further redesigns for Arg, Glu, Lys, and Asp were also successful experimentally and accomplished the task of creating novel substrate activity (virtually nonexistent in WT GrsA-PheA), although the preferred substrate for those mutants was still Phe. The incorporation of an explicit negative design procedure will be important for predicting active mutants that show the desired switch of substrate specificities. However, for in vitro or biotechnology applications, it would be possible to use the designed mutants for charged amino acid adenylation by controlling the input substrates to exclude Phe. More extensive investigation of the effect of bolstering mutations on the substrate specificity of the redesigned enzymes, could be an important step toward a general purely computational algorithm for predicting enzymes with high activity by identifying mutations anywhere in the protein, both proximal and distal to the ligand-binding site.

Experimental Procedures

Computational Redesign.

Active-site mutation prediction.

For a given protein–substrate complex, the K* algorithm computes partition functions over conformational ensembles, where the contribution of each conformation to the partition function is weighted by using Boltzmann probabilities. The ratio of the partition functions for the bound complex and unbound protein and ligand is then used to compute a provably accurate ε-approximation to the binding constant for the given protein–substrate complex. K* scores were computed for each candidate protein sequence with the target substrate; sequences with higher K* scores are predicted to have better specificity for the target substrate. For computational efficiency, K* uses the MinDEE (14) and the backbone dead-end elimination (BD) (15) algorithms as an initial pruning filter, and the A* branch-and-bound search (33) for the subsequent conformation enumeration (14). MinDEE and BD are DEE-based algorithms that, unlike previous DEE algorithms (34, 35), guarantee the identification of the global minimum energy conformation for, respectively, a model with continuously flexible rotamers and a flexible backbone. Combined with A*, MinDEE and BD also output conformations and sequences in the precise order in which they are ranked by the model, so that no low-energy solutions are missed by the algorithm.

Next, we describe some of the mutation search parameters used in the K* redesigns of GrsA-PheA. Complete details of the computational procedure and the algorithm parameters can be found in Section S1.1 in the SI Appendix. K* runs (with subsequent experimental validation) were performed for the following substrates: Arg, Glu, Leu, Lys, and Asp. The crystal structure of GrsA-PheA [Protein Data Bank (PDB) ID code 1amu (23)] was used in the computational redesigns. The seven active-site residues 236, 239, 278, 299, 301, 322, and 330 were modeled by using continuously flexible rotamers and were allowed to mutate. In addition, the AMP cofactor and a steric shell consisting of all residues within 8 Å from the ligand or within 3 Å from any of the seven active-site residues were included as part of the input structure. The ligand substrate was also modeled by using continuously flexible rotamers and was allowed to rotate/translate. Rotamers were obtained from the Penultimate Rotamer Library modal values (11). The energy function consisted of the Amber electrostatic, vdW, and dihedral terms (36) and the EEF1 pairwise implicit solvation energy term (37). A distance-dependent dielectric of 6 and a solvation-energy scaling factor of 0.8 were used. Conformations with an initial steric overlap of >1.5 Å were pruned. All software is available open-source upon publication.

Bolstering mutation prediction.

The K* algorithm allows us to identify mutations within the active site of an enzyme. The kinetics experiments (Results) showed these K*-predicted mutations yielded highly active mutants for Leu. We then investigated whether additional improvement in the Leu specificity could be achieved by introducing additional mutations outside of the active site. Previously, in other design protocols, this was done by performing multiple rounds of directed evolution on the active-site mutants (9). As an alternative, we applied a purely computational approach for predicting mutations outside of the enzyme active site. As a starting point for these computational experiments, we selected the highest-activity K* mutant for Leu (T278L/A301G). We then applied a SCMF entropy-based method (28) combined with our MinDEE/A* (14) algorithm to predict mutations both close to and far away from the enzyme active site to obtain further improvement in the target substrate specificity. The SCMF entropy-based method heuristically selects residue positions, anywhere in the protein, that may be tolerant to mutation. Mutations to these residue positions are then predicted by using the MinDEE/A* algorithm. We refer to these mutations as “bolstering.” The addition of the bolstering mutations aims at further stabilizing the mutant enzyme and may counteract a possible destabilizing effect from the introduction of the active-site mutations. Details of the computational redesign procedure for bolstering mutations can be found in Section S1.2 in the SI Appendix. The active-site mutations plus bolstering mutations were then tested by creating mutant proteins containing both sets of mutations, and measuring the kinetic parameters.

Experimental Redesign.

Materials.

Amino acid substrates, compounds, and enzymes for the pyrophosphate release assay were purchased from Sigma–Aldrich. Vector pQE60 and Escherichia coli strain M15 were purchased from Qiagen. Plasmid pQE60 containing WT and A301G mutant PheA genes from Bacillus brevis (GI: 39366) were obtained as described in ref. 3.

Mutagenesis of mutant PheA.

Mutagenesis was performed by using the QuikChange site-directed mutagenesis system (Stratagene) in accordance with the manufacturer's instructions with the primers summarized in the Table S6 in the SI Appendix. Preparation of the plasmid DNA was done in E. coli DH5α following standard procedures. All constructs were confirmed by DNA sequencing at Duke University DNA Analysis Facility.

Expression and purification.

Vector pQE60 containing constructs of WT or mutant PheA with a C-terminal His tag was transformed into E. coli M15 (pREP4) cells for expression. The proteins were expressed by induction of midlog cells (OD ≈0.8) with 0.2 mM IPTG and an addition of 10 mM MgCl₂ overnight at 18 °C. The double mutant T278L/A301G and the triple mutants T278L/A301G/S447N, I277L/T278L/A301G, and V187L/T278L/A301G were induced with 0.05 mM IPTG and expressed at 18 °C overnight to increase protein solubility. Double mutants T278D/A301G, T278H/A301G, and T278K/A301G and the quadruple mutant I277L/T278L/A301G/S447N were expressed at 16 °C with 0.05 mM IPTG. In a typical preparation of 2 L of culture, 7-g cell pellets were resuspended in 35 mL of buffer A [100 mM Tris·HCl (pH 7.5), 250 mM NaCl, and 5 mM Tris(2-carboxyethyl)phosphine (TCEP)] supplemented with a protease inhibitor mixture. The cells were lysed by a French press, and cell debris was removed by centrifugation at 20,000 × g for 30 min. The resulting supernatant was incubated with Ni–nitrotriacetic acid–agarose (10 mL) in buffer B [50 mM Tris·HCl (pH 8.0), 400 mM NaCl, 20 mM imidazole, 0.5 mM TCEP] at 4 °C for 1 h. The agarose was then washed extensively with buffer B. The His-tagged proteins were eluted with 400 mM imidazole (pH 6.8) and further purified by a Superdex 200 gel filtration chromatography (GE Healthcare) in buffer C [50 mM Tris·HCl (pH 7.5), 1 mM TCEP]. The purified proteins (>95% pure by SDS/PAGE) were concentrated to >20 mg/mL by using an Amicon Ultra-15 concentrator with the addition of glycerol (10% final) and rapidly frozen by liquid N₂ for storage at −80 °C.

PP_i release assay.

The rate of PP_i release was measured by using a coupled, continuous, spectrophotometric assay (29). In the reaction of 100 μL total volume, PheA or mutants (0.1–1 μM) were incubated at 25 °C with varying concentrations of amino acids (1 μM–64 mM) in buffer containing 100 mM Tris·HCl (pH 7.5), 1 mM uridine diphosphate-glucose, 375 μM glucose 1,6-bisphosphate, 1 mM β-nicotinamide adenine dinucleotide, 10 mM MgCl₂, 2 mM adenosine 5′-triphosphate, 5 mM DTT, 2 units/mL uridine-5′-diphosphoglucose pyrophosphorylase, 4 units/mL phosphoglucomutase, 4 units/mL glucose-6-phosphate dehydrogenase. Mutants T278D/A301G, T278H/A301G, and T278K/A301G were assayed in 50 mM Tris (pH 7.5). Reactions were initiated by the addition of the enzymes after a 10-min incubation to allow the removal of any contaminating PP_i. The absorbance at 340 nm (NADH_ε340 = 6,317 M⁻¹ cm⁻¹) was monitored by using an Agilent 8453 spectrophotometer. Substrate concentrations covering 0.2–5 K_m were used to determine the complete steady-state curve. The initial velocity of each substrate concentration was determined by comparison with mock-treated enzyme and fitted with the Michaelis–Menten equation to obtain k_cat and K_m.