A retinal circuit model accounting for wide-field amacrine cells

Abstract

In previous experimental studies on the visual processing in vertebrates, higher-order visual functions such as the object segregation from background were found even in the retinal stage. Previously, the “linear–nonlinear” (LN) cascade models have been applied to the retinal circuit, and succeeded to describe the input-output dynamics for certain parts of the circuit, e.g., the receptive field of the outer retinal neurons. And recently, some abstract models composed of LN cascades as the circuit elements could explain the higher-order retinal functions. However, in such a model, each class of retinal neurons is mostly omitted and thus, how those neurons play roles in the visual computations cannot be explored. Here, we present a spatio-temporal computational model of the vertebrate retina, based on the response function for each class of retinal neurons and on the anatomical inter-cellular connections. This model was capable of not only reproducing the spatio-temporal filtering properties of the outer retinal neurons, but also realizing the object segregation mechanism in the inner retinal circuit involving the “wide-field” amacrine cells. Moreover, the first-order Wiener kernels calculated for the neurons in our model showed a reasonable fit to the kernels previously measured in the real retinal neuron in situ.

Introduction

The vertebrate retina is far more than a passive visual receptor. Conventionally, higher-order visual computations are believed to be performed in visual cortices; however, it has been reported that some of the intelligent functions are found even in the retinal circuits (Masland 2003; Baccus 2007). In biological vision, one important task among those is the detection of moving objects from the visual scene. However, because of the gaze-shifting and fixational eye movements, as well as head and body movements, the visual image projected onto the retina randomly drifts at every moment, even under a perfect stationary scene. This hinders the retinal circuit to receive any static input as the background. Therefore, the visual system requires a mechanism for segregating the real movement of objects from the apparent background motion. Previous experimental studies have demonstrated that such information processing commences in the eye, and that a long-range lateral inhibition of retinal ganglion cells by amacrine cells may be involved in that processing (Olveczky et al. 2003; Roska and Werblin 2003). It has been known that the “wide-field” amacrine cells extend their multiple axonal processes toward the distant regions across the retinal horizontal plane (e.g., Dacey 1989; Famiglietti 1992a, b; Lin and Masland 2006), and can inhibit ganglion cells directly (Cook and McReynolds 1998) and/or indirectly (Shields and Lukasiewicz 2003). More recently, a study showed that such wide-field amacrine cells selectively suppress the excitatory synaptic inputs onto the ganglion cells which are sensitive to the object motion (Baccus et al. 2008). In that study, also an abstract model of the retinal circuit was proposed by employing: (1) a “linear–nonlinear” (LN) cascade model (i.e., the cascade with a linear spatio-temporal filter followed by a static nonlinearity) for the input-output dynamics of the outer retinal circuit [in turn, this determines the excitatory inputs onto ganglion/amacrine cells]; and (2) arithmetic division for the inhibitory input from the amacrine cell in the background region onto the ganglion cell in the object region. And this model could simulate the object motion sensitive (OMS) spiking behavior at the retinal output upon specific input patterns. Generally speaking, however, in such an abstract model with LN cascades, the linear filter and the nonlinearity are derived empirically, and they represent the input-output dynamics of not the cellular level but some local circuit level. Therefore, response properties of each neuron and their inter-cellular interactions are not taken into account. Unlike LN models, response dynamics of each class of retinal neurons were modeled in several previous studies. For instance, Teeters et al. (1997) introduced a spatio-temporal retinal model in which lateral inhibitory inputs onto ganglion cells from wide-field amacrine cells could eliminate visually spurious retinal outputs; but functional contribution of that inhibition to retinal visual processing was least demonstrated. In another study, Thiel et al. (2006) proposed a detailed temporal model of the turtle retina including sustained types of on and off amacrine cells together with a transient type of on-off amacrine cells; however that model assumed only spatially homogenous input patterns.

In the present study, we present a spatio-temporal computational model that implements a long-range lateral inhibition mechanism via wide-field fast-transient on-off amacrine cells. The model covers the response dynamics of all major retinal neurons in the cellular level, together with their spatio-temporal interactions. For each type of the neurons in our model, the first-order Wiener kernel of the cellular response was calculated by the white-noise analysis (Marmarelis and Naka 1973; Naka et al 1987; Sakai and Naka 1987), showing a reasonable consistency with the kernels previously measured in real retinal neurons in situ. The present model could realize the OMS retinal output, and was useful to examine the role of each neuron in such a higher-order visual computation in the retinal circuit.

Methods

Retinal circuit model

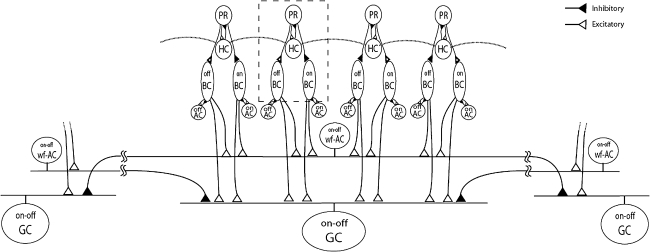
In the present model, computational elements representing the retinal neurons are divided into two groups: (1) Outer retinal elements, i.e., photoreceptors (PR), horizontal cells (HC), and on-type and off-type bipolar cells (on-BC, off-BC); (2) Inner retinal elements, i.e., on-type and off-type amacrine cells (on-AC, off-AC), wide-field fast-transient on-off amacrine cells (wf-AC) and on-off ganglion cells (GC). Figure 1 illustrates the arrangement of those elements. In the outer retinal unit (Fig. 1, dashed box), the input signal is first processed by the PR-HC circuit, and then conveyed to on-BC and off-BC. In the inner retinal unit, the outputs of on-BC and off-BC are truncated by on-AC and off-AC, respectively. Each of wf-AC and GC receives excitatory inputs from multiple BC, namely, each collects the signals from four parallel outer retinal units. Inter-unit lateral connections are also present either at outer retinal units as HC-to-HC gap junctions (Fig. 1, dotted lines) or at inner retinal units as inhibitory synapses onto GC from distantly located wf-AC. The receptive field of an outer retinal unit is assumed to be 40 μm in width and thus each of GC covers a width of 160 μm in its receptive field center without any overlap. Each of wf-AC also covers a width of 160 μm in its receptive field center, and extends its output filed of 1,600 μm in width, overlaping with neighboring wf-AC. There are 128 each of PR, HC, on-BC, off-BC, on-AC, and off-AC elements and 32 each of wf-AC and GC elements and thus the entire circuit covers the width of 5,120 μm.

Fig. 1.

Three representative circuit units of the model. Each unit includes eight neuronal elements: PR, photoreceptor; HC, horizontal cell; on-BC, on-type bipolar cell; off-BC, off-type bipolar cell, on-AC, on-type amacrine cell; off-AC, off-type amacrine cell; wf-AC, wide-field on-off amacrine cell; GC, on-off ganglion cell. Excitatory and inhibitory synaptic connections are represented with white and black triangles, respectively. Gap junctions between HC elements are indicated by dotted horizontal lines. Wide-field lateral connections are implemented between wf-AC and GC. Outer retinal units (i.e., PR, HC, on-BC, and off-BC) are enclosed with a gray dashed box constitute an outer retinal computational unit. Note that only one computational circuit unit is fully illustrated, remote units are partially shown to highlight distal connections

Spatio-temporal model

Each neuron’s membrane dynamics is governed by a differential equation (Eq. 1) which was modified from push-pull shunting models of retinal neurons (Gaudiano 1994; Thiel et al. 2006).

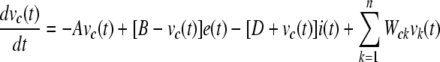1

Here, υ_c(t) stands for the membrane potential of the neuronal element of interest (the element ‘c’); A represents the rate of passive decay toward the resting potential in the dark; B and D are the saturation levels for the excitatory inputs, e(t) and inhibitory inputs, i(t), respectively; υ_k(t) is the membrane potential of the neuronal element ‘k’ which makes lateral connections via the gap junction (HC-to-HC) or the chemical synapse (wf-AC-to-GC) with the element ‘c’; W_ck determines the efficiency of the lateral connections from the element ‘k’ to ‘c’ and its value is given by a function of the distance between ‘k’ and ‘c’. As shown in Fig. 1, the excitatory inputs (i.e., e(t)) are present at the synapses from PR to HC and on-BC; from on-BC to on-AC, wf-AC, and GC; from off-BC to off-AC, wf-AC, and GC. And the inhibitory inputs (i.e., i(t)) are present at the synapses from HC to PR; from PR to off-BC; from on-AC to on-BC; from off-AC to off-BC. For the element ‘c’ of either PR, BC, on-AC, off-AC or wf-AC, W_ck is set to zero for every ‘k’ (cf. Gaudiano 1994; Thiel et al. 2006).Parameter values in the equation were calibrated so that the temporal response dynamics of every neuronal element was reproduced in accordance with previous studies. Spatial parameters of the model (e.g., wiring and W_ck) are adjusted to qualitatively meet the spatial profile of ganglion cell responses given in the previous paper (Olveczky et al. 2003).

To improve the dynamic range of PR, a compressive nonlinearity (Eq. 2) was inserted prior to the input stage as proposed by Thiel et al (2006). The PR element was fed with a hyperpolarizing input, r(t), representing the compressed form of light intensity, f(t).

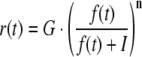2

Here, G denotes the saturation level of the hyperpolarizing input; I represents the light intensity yielding the half-maximum response and n is a constant.

All differential equations in the model were solved sequentially using the fixed-step (1 ms) Bogacki-Shampine solver of the MATLAB/SIMULINK software package (The Mathworks-Inc., Natick, MA).

Visual stimulation

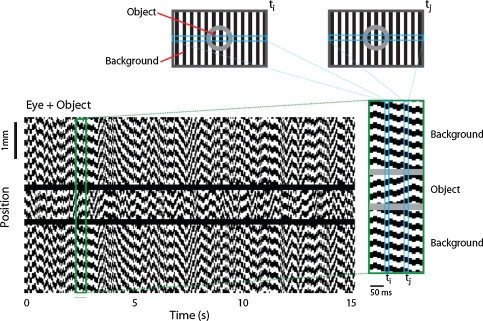
Jittered grating stimulations similar to the ones explained previously (Olveczky et al. 2003) were applied to test the present model. The grating consisted of 160-μm-wide black and white bars and the trajectory of the jitter was determined by shifting the grating randomly in one direction every 15 ms. As it is shown in Fig. 2, stimulation trajectory was separated into object (800 μm wide) and background regions by a 40-μm-wide masked (un-stimulated) region. To test the segregation mechanism, four different stimulation conditions were applied: (1) Eye + Object Condition: The object and the background gratings jittered incoherently (Fig. 2). The retinal patch corresponding to the object region experienced an incoherent motion than the eye motion, which indicated the object actually moves. (2) Eye Only: The object and the background gratings jittered coherently, indicating that the object does not move thus the object region only experiences the eye movement. (3) Object Only: The object region grating was the same as in (1) and (2), but the background region was masked. (4) Eye + Object Drift: The object and the background gratings jittered as in (2), but trajectory of the object grating was drifted by a 50-ms shift.

Fig. 2.

Spatiotemporal stimulation. Upper panels illustrate the stripe grating stimulation projected on to a 2-D retina at an instant (Olveczky et al. 2003). Stimulation trajectories are separated for object and background regions. At every 15 ms grating bars shift 40 μm in one direction depending on the trajectory. Bottom panel illustrates space–time plot of a horizontal cross section through the center of the Eye + Object stimulation (see Methods)

White-noise analysis

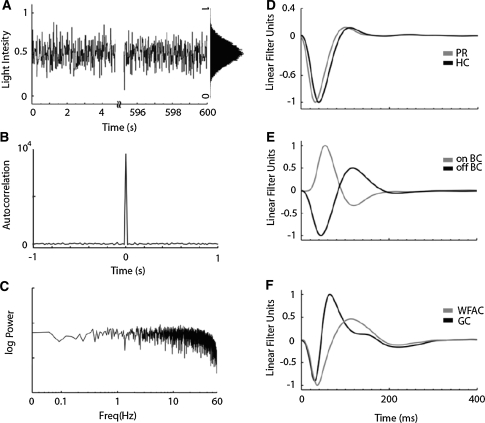
In previous studies, the white-noise analysis has been widely used to assess the transfer functions of local neuronal circuits in the vertebrate retina (horizontal cells: Sakai et al. 1997a, bipolar cells: Sakai and Naka 1987; amacrine cells: Sakai et al. 1997b; ganglion cells: Sakai et al. 1997c; Zaghloul et al. 2007). Also in the present study, we applied the white-noise analysis to our retinal model to make a comparison with the kernels previously measured in real retinal neurons in situ. Visual input was presented to the object region as a white-noise modulated pattern (Fig. 3a) with the maximum auto-correlation at the time zero (Fig. 3b) and with a flat power spectrum below a cut-off frequency of ~60 Hz (Fig. 3c). The first-order Wiener kernels were calculated by evaluating the well-known convolution integral (Eq. 3), as explained previously (Marmarelis and Naka 1973):

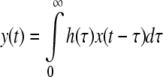3

Fig. 3.

White-noise stimulation and linear Wiener kernels. (a) Stimulus is presented as a white-noise with a Gaussian distribution in its amplitude (inset). (b) Autocorrelation of the input (without DC offset) has the maximum value at t =0 [sec]. (c) Power spectrum of the input. (d) Kernels obtained from PR (gray) and HC (black). (e) Kernels obtained from on- (gray) and off- (black) BC. (f) Kernels obtained from wf-AC (gray) and GC (black)

By cross-correlating the neural response y(t) and the white-noise input x(t), the linear transfer function h(τ) was calculated for each neuronal element. For high values of τ, h(τ) approaches to zero as determined by the lack of system memory and h(τ) is zero for negative values of τ, as the system obeys causality.

Results

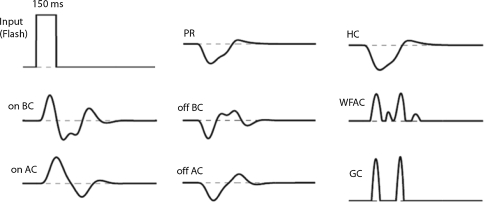
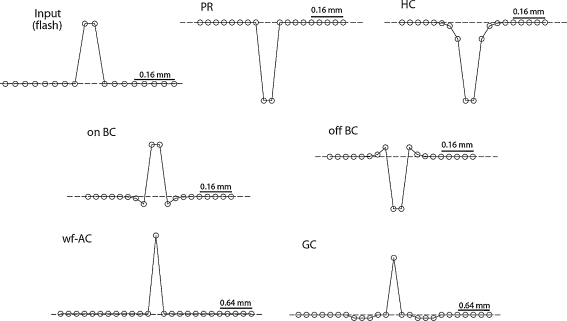
First, we confirmed whether flash-response of each cell in our circuit model agrees with the previous experimental data. Figure 4 illustrates the temporal responses of the cell elements to 150-ms-long flash of light. In the outer retinal circuit, the PR element responds with a hyperpolarization followed by a sag approaching to a plateau level, and then depolarizes after the offset of the flash with an overshoot reaching to the original resting potential. Essentially, the HC element response is a smoothened form of the PR response due to its low-pass filtering feature. The on-BC element and off-BC element depolarizes and hyperpolarizes, respectively, upon the on-set of the flash. The BC element has a negative feedback from the on-AC or off-AC element; so it has more transient dynamics in response compared to those of the PR and HC elements. Consequently, the transient dynamics are evident in the responses of the wf-AC and the GC elements as the BC element provides an excitatory synaptic input onto them. In Fig. 5, spatial profiles of the cell elements in response to a 150-ms-long and 160-μm-wide flash of light are shown. The bell-shaped and the mexican-hat profiles are present at the HC and BC levels, respectively.

Fig. 4.

Temporal responses of computational elements to a 150 ms-long full-field flash of light. Dashed horizontal lines indicate dark resting potentials. Note that the latencies of wf-AC and GC depolarizations match each other

Fig. 5.

Spatial profiles of computational elements to a 160 μm-long flash of light. Dashed horizontal lines indicate dark resting potentials. Circles represent the membrane potential levels at a specific latency depending on the cell type. Note that spatial scales are larger for wf-AC and GC cells

Figure 3 shows the first-order Wiener kernels calculated for the cell elements. The PR and HC kernels have very similar dynamics (Fig. 3d), namely, hyperpolarizing volleys peaking at 32 ms in PR and 40 ms in HC, followed by depolarizing overshoots. The kernels of on-BC and off-BC have depolarizing and hyperpolarizing transients peaking at 54 ms and 45 ms, respectively (Fig. 3e). The GC kernel has a transient hyperpolarization, peaking at 30 ms and then a depolarization, peaking at 64 ms (Fig. 3f). The wf-AC kernel is similar to the GC kernel, but has more sustained hyper- and de-polarizations with peaks at 36 ms and 112 ms, respectively (Fig. 3f).

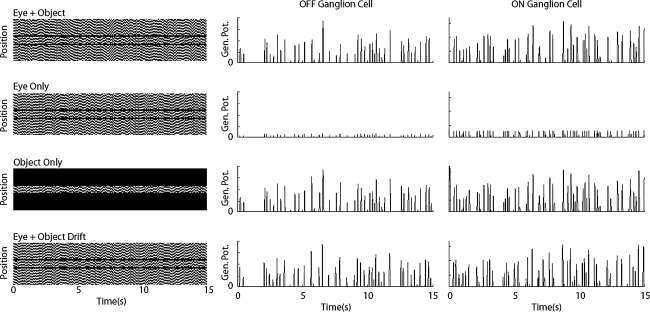
The object segregation mechanism in the present model was demonstrated by simulating the four different input conditions (the left column, Figure 6), as in the previous paper (Olveczky et al. 2003). Moreover, to be consistent with the recording conditions in the experiment (Olveczky et al. 2003), the on-off type GC element was transformed into either on-type or off-type GC by adjusting the model parameters accordingly. Figure 6 shows the generator potential of a GC element at the center of the object region, in response to the four different input patterns. As found in the figure, only upon the ‘Eye + Object’, the ‘Object Only’ and the ‘Eye + Object Drift’ conditions, the GC element shows the significant depolarizing responses with considerable frequency. However, even upon exactly the same patterns of stimulation in the object region, the same GC element is significantly suppressed, and shows only minor responses (the ‘Eye Only’ condition). The ‘Eye Only’ condition stands for the observer-induced motion such as the fixational eye movement, while under the ‘Eye + Object’ condition, the local motion of a moving object is present and thus the object and the background trajectories are incoherent. In the present simulations, the GC element strongly responds only when the latter condition of motion is presented, indicating that the proposed model is able to segregate the object local motion from the background global motion.

Fig. 6.

Responses of GC that segregate object motion from background motion. Panels on the left column illustrate space–time plots of stimulus conditions (see Methods). Panels on the second and third columns show spike generator potentials of GC units located at the center of the object region in response to 15 s jitter grating

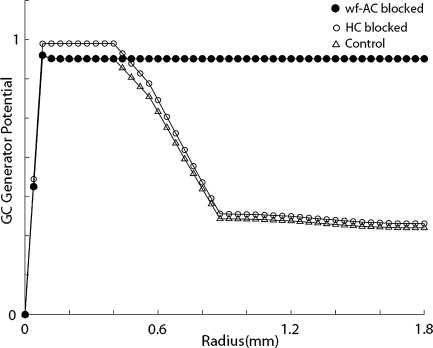
To examine spatial profile of the wide-field inhibitory mechanism, the model circuit was stimulated by flashing spots of increasing size, as similar to the experiment performed previously (Olveczky et al. 2003). Figure 7 shows that as the flash spot size increases, stimulation starts to invade the background region so that the spike generator potential of the central GC element gradually decreases out to radii of ~1,000 μm.

Fig. 7.

GC generator potentials versus object radius. Triangles indicate how GC generator potentials are inhibited as the object radius increases. Black and white circles indicate GC responses when wf-AC and HC are blocked, respectively. Note that as object radius grows, it invades background region and inhibition takes

Discussion

The present study provides a computational model including a circuitry of all major retinal cells. Resemblance of flash responses as well as first-order Wiener Kernels with those calculated from real retinal neurons in situ confirm that our model possesses well-known retinal features. Figure 5 illustrates bell-shaped spatial profile of the HC response indicating the existence of HC-to-HC gap junctions. Mexican-Hat-like receptive fields of on- and off-BC (Fig. 5) show that the model retina has well-known center-surround antagonism. As illustrated in Fig. 3, off-BC kernels have faster kinetics than the on-BC kernels in accordance with the prior experimental observations (Burkhardt et al. 1998). Main result presented in Fig. 6 demonstrates that the retinal circuitry is able to discriminate an object motion from, for example, the saccadic eye movements. As previously shown, the global background motion suppresses the central GC responses (Enroth-Cugell and Jakiela 1980; Passaglia et al. 2001; Solomon et al. 2006). However, the inhibition of GC generator potentials in segregation phenomenon cannot be simply related to the amount of the background motion. The random walk trajectories at the background regions in ‘Eye + Object’, ‘Eye Only’ conditions were generated from different seeds, yet having the same statistics. However, the inhibition was observed only for the ‘Eye Only’ condition. Under ‘Eye + Object’ condition, GC responses were almost identical to those under ‘Object Only’ condition in which there was no background stimulation at all. This indicates that the amount of background motion alone is not a decisive factor for the segregation mechanism; however the timing between the object and the background trajectories is found to be critical as experimentally observed before (Olveczky et al. 2003). Under ‘Eye Only’ condition, inhibition coming from the periphery perfectly coincides with the excitation at the centre, thus GC underlying the object region is strongly suppressed. However, under ‘Eye + Object’ condition, peripheral inhibition arrives with random timing with respect to the central excitation thus only occasional inhibition is received by GC and consequently no significant suppression takes place. When the jittered grating overlying the object region is shifted by 50 ms (‘Eye + Object Drift’), perfect match between the inhibition and the excitation under the ‘Eye Only’ condition is manually eliminated thus GC is not inhibited. Wide-field spatial profile of the inhibition phenomenon implies that wf-AC is behind the peripheral suppression, namely, the segregation mechanism of the retina. However, precise arrangement of the inhibition circuitry still remains elusive. Inhibition from wf-AC may be directly on the GC dendrites (Cook and McReynolds 1998) or presynaptically on axonal terminals of BC leading to indirect suppression (Shields and Lukasiewicz 2003). In case of indirect suppression, wf-AC would be excited by separate BC terminals as GC would receive presynaptically suppressed signal from BC terminals; because we know that wf-AC itself is not suppressed by global motion (Olveczky et al. 2003; Baccus et al. 2008; Roska and Werblin 2003). In such a case, the model BC should have been modified to have separate excitatory and inhibitory terminals that should concurrently send signals to wf-AC and GC, respectively. However, we considered simpler case in which wf-AC directly inhibits GC; and on- and off-BC terminals are not pre-synaptically inhibited.

Spatial profile of the wide-field inhibitory process is modified by the cells which can laterally process the retinal signal. As Fig. 7 illustrates, blocking HC-to-HC gap junctions slightly enhances the GC response out to radii of several hundreds of μm. This indicates the existence of lateral inhibition at HC level but this inhibition is not wide and strong enough so that HC network is not involved in the object segregation mechanism (Baccus et al. 2008). On the other hand, blocking wf-AC completely eliminates the wide-field inhibition that extends more than 2,000 μm. Similar spatial profile was observed in membrane potentials of GC in situ after wf-AC was blocked with pharmacological agents (Olveczky et al. 2003).

These results indicate that present computational model can realize object segregation mechanism specific to the retinal circuitry. Moreover, using the same parameter set, the model possesses well-known response dynamics of all major retinal neurons in the cellular level so that the role of each neuron in such a high-order computation can be understood better. In future studies, this approach could be useful to realize/model other retinal computations in which the consideration of each retinal neuron’s contribution is necessary.