Mutational spaces for leaf shape and size

Abstract

A key approach to understanding how genes control growth and form is to analyze mutants in which shape and size have been perturbed. Although many mutants of this kind have been described in plants and animals, a general quantitative framework for describing them has yet to be established. Here we describe an approach based on Principal Component Analysis of organ landmarks and outlines. Applying this method to a collection of leaf shape mutants in Arabidopsis and Antirrhinum allows low-dimensional spaces to be constructed that capture the key variations in shape and size. Mutant phenotypes can be represented as vectors in these allometric spaces, allowing additive gene interactions to be readily described. The principal axis of each allometric space reflects size variation and an associated shape change. The shape change is similar to that observed during the later stages of normal development, suggesting that many phenotypic differences involve modulations in the timing of growth arrest. Comparison between allometric mutant spaces from different species reveals a similar range of phenotypic possibilities. The spaces therefore provide a general quantitative framework for exploring and comparing the development and evolution of form.

One of the major challenges in developmental biology is to understand the molecular genetic interactions underlying growth and form. Addressing this problem requires a systematic procedure for describing mutants that affect the shape and size of organs. A prevalent approach is to classify mutants according to a combination of quantitative and qualitative descriptors. Quantitative descriptors include measures of size, such as area, and indicators of shape, such as length to width ratio (Horiguchi et al., 2006). Qualitative descriptors include terms such as rounded, pointed or elongated (Berná et al., 1999;Robles and Micol, 2001; Serrano-Cartagena et al., 1999). Although such systems have the convenience of simplicity, they suffer from several disadvantages. One is that by separating shape from size they ignore allometric relationships that arise through differential growth. A second problem is that verbal descriptions of shape can be subjective and difficult to apply to intermediate categories. Third, the effects of combining genes can be difficult to predict. To address these issues we present an alternative way of describing mutant collections that integrates mathematical methods with genetics. We illustrate the approach using a range of mutants affecting leaf development.

Leaves have the advantage that their shape and size can be readily captured to a first approximation by a two-dimensional (2D) outline. We focused on leaf mutant collections from Arabidopsis thaliana (Berná et al., 1999; Robles and Micol, 2001) and Antirrhinum majus (Hammer et al., 1990; Stubbe, 1966). Both of these species have leaves with relatively simple outlines. Several leaf shape and size genes have been isolated from these species and shown to be involved in transcription, chromatin metabolism or in hormone pathways (Barrero et al., 2007; Cnops et al., 2004; Hricová et al., 2006; Nelissen et al., 2005) (Alonso-Peral et al., 2006; Barrero et al., 2005; Clouse et al., 1996; Horiguchi et al., 2006; Pérez-Pérez et al., 2004) (Golz et al., 2002; Nath et al., 2003; Waites et al., 1998). Moreover, many mutants and transgenics have been characterized to determine the relationship between cell proliferation and size (Autran et al., 2002; Beemster et al., 2003; Desvoyes et al., 2006; Mizukami and Fischer, 2000; Tsukaya, 2003).

Previous studies have classified leaf mutant collections according to parameters such as presence∕absence of petiole, flatness, leaf index (ratio of leaf length and width), type of margin and overall size (Tsukaya, 2006). Here we use a quantitative approach based on Principal Component Analysis (PCA) (Anderson et al., 1999; Seal, 1964) of landmark positions (Horgan, 2001) to define allometric spaces that capture variation in shape and size (Langlade et al., 2005). While PCA has been used to describe variation in shape metrics such as length or width (Farris, 1984; Gilchrist et al., 2000; Strauss, 1990), the advantage of the approach described here is that it does not rely on predefined metrics. Moreover, unlike studies which employ elliptic Fourier analysis for capturing shape (Iwata and Ukai, 2002), shape and size are treated collectively, allowing allometric relationships to be defined.

We describe allometric spaces involving three or four Principal Components (PCs) for mutant collections ofArabidopsis or Antirrhinum. Each mutant can be represented as a vector in allometric space, allowing the effect of additive gene interactions to be predicted. Mutants may also be classified according to which PCs they significantly affect. The first PC for Arabidopsis and Antirrhinum (PC1) reveals a correlation between shape and size. However, the effect on shape is different in each species, paralleling the pattern of shape change during later stages of development. This suggests that many genes may influence later stages of leaf growth and highlights the close relationship between shape and size. The remaining PCs for Arabidopsis andAntirrhinum are very similar, suggesting that the species share a common range of phenotypic possibilities. The allometric approach described here thus provides a quantitative framework for analysis of genetic, developmental and evolutionary processes.

RESULTS

Capturing mutational variation in shape and size

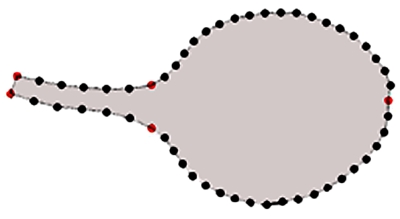
To generate a parameterized space that captures variation in leaf shape and size, leaf outlines were obtained for 91 mutants of Arabidopsis in the Landsberg erecta background (Berná et al., 1999; Robles and Micol, 2001). For each mutant line, digital images were taken of 6–8 independent mature (28 DAS) third true leaves. Plants were grown in several batches, with a wild-type accession always included. The leaf shapes and sizes were captured by placing 53 points evenly along the leaf outlines (Fig. 1). We used five “primary” landmarks (red points in Fig. 1): two points at the base of the petiole, two at the petiole to blade transition and one at the leaf tip. The other landmarks, termed “secondary” points, were placed along the outer leaf edge and evenly distributed in between the primary points by an automated process. The resulting shapes were aligned by translation and rotation (Procrustes alignment, which minimizes the mean square error between all point models and the mean point model, see Materials and Methods). From the 53 points, we obtained 106 coordinate values (two per point). The coordinates define a 106-dimensional space in which each axis represents variation in one of the coordinate values (for a secondary point, coordinate values are partly constrained by the position of neighboring points so, even for randomly positioned landmarks, variations along the 106 dimensions will not be fully independent once the secondary points have been evenly distributed). Each leaf shape can be represented as a single point in this space, and therefore all the mutant shapes define a cloud of points. The mean of each of the 106 coordinates defines the center of the cloud, corresponding to the mean leaf shape.

Figure 1. Fifty three points were used to describe the leaf shape outline, including five primary points (red dots) placed at key positions and 48 secondary points (black) spaced evenly between primary points.

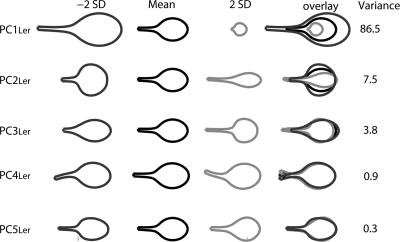
Because the points along the leaf outlines are correlated, most of the mutant leaf variation can be captured with far fewer than 106 axes. This smaller set of axes was defined through Principal Component Analysis (PCA) which uses linear correlations between data to define orthogonal axes that capture maximal trait variance. We obtained five main Principal Components (PCs) that together accounted for 99% of the total shape and size variance among the genotypes. These PCs were given a subscript Ler as they were derived from mutants within the Landsberg erecta background. Figure 2 shows the effect of varying values along PC1_Ler–PC5_Ler independently by plus or minus two standard deviations. The +∕−orientation of the PC axes is arbitrary so we standardized them such that the smallest shapes are assigned positive values. We performed a similar analysis using 19 instead of 53 points to specify the leaf outline and obtained similar PCs (data not shown).

Figure 2. Leaf shape and size of Arabidopsis mutants as described by the five main PCs from the allometry model.

For each PC, the mean leaf outline and the shape outline obtained by varying the PC value plus or minus two times the standard deviation (+2SD and −2SD) are shown. These outlines are also shown overlaid. The percentage of the variance of the model explained by each PC is shown on the right.

As no size normalization was performed in this model, it was called an “allometry model.” PC1_Ler of this model accounts for 86.5% of the total variance and affects mostly size, although there is also an effect on shape. Low values of PC1_Ler correspond to larger, more elongated leaves, whereas high values give smaller and more rounded leaves. PC2_Ler accounts for 7.5% of the variance and affects both shape and size. Low values of PC2_Ler give rounded leaves with a larger area, whereas high values give elongated leaves with a smaller area. PC3_Ler accounts for 3.8% of the variance and affects the steepness of the transition from petiole to blade—low values give a very gradual transition, whereas high values give a long petiole with a steep transition to blade. PC4_Ler accounts for 0.9% of the variance and reflected the way the petiole twisted when the leaves were flattened. Its values were not significantly different between genotypes and it was therefore excluded from further analysis. Finally, PC5_Ler accounts for 0.3% of the variance. Low values of PC5_Ler give leaves with a wide base (deltoid shape), whereas high values shift the widest point of the blade distally, to give a more obovate shape.

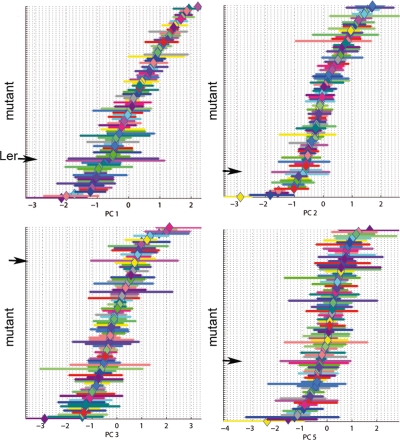
Together, PC1_Ler, PC2_Ler, PC3_Ler, and PC5_Ler define a four-dimensional allometric space that accounts for most of the variation in shape and size between the mutants. In principle, each mutant leaf outline should correspond to a point within this space. However, because of variability between different individual plants, the leaf outlines of any given genotype will not occupy identical positions but will form a small cloud of points, centered around the mean for that genotype. The projection of such a cloud onto an axis (PC) of the allometric space gives a spread of values along that axis. The range of the values of each PC for all the mutant groups is shown in Fig. 3. If a mutant has an effect on values of that PC, these projected PC values should be significantly different from those of wild-type plants grown in the same batch. As the dataset is small and might not be normally distributed, Wilcoxon’s ranked t-tests (Wonnacott and Wonnacott, 1969) were used to determine which PC values were significantly different from wild type for any given mutant (p<0.01).

Figure 3. Range of PC values obtained for each Arabidopsis mutant for the allometric Ler model.

The mean of each of the 91 mutant groups is represented by a colored diamond and the bars display the range of all the values observed for this group. The wild type (Ler) group range is indicated by an arrow. PC units are standard deviations.

As shown in Table 1, out of the 91 mutants, 19 had a significant effect on values for only one PC and were assigned to group A. Within this group, three mutants affected only PC1_Ler, with two increasing and one decreasing its value (Class A1). This included the icu6 (incurvata6) mutant which gives big leaves. Ten mutants affected only PC2_Ler values (Class A2), including the ang4 (angusta4) mutant, which gives narrow, elongated leaves. Five mutants affect PC3_Ler values only (Class A3), including the anu3angulata3) mutant. One mutant, ven6 (venosa6), affected only the values of PC5_Ler (Class A4).

Table 1.

Classification of Arabidopsis leaf shape mutants according to the combination of highly significant PC (p<0.01%) in the allometry model. Gene names are as described by Robles and Micol (2001). A Wilcoxon’s ranked t-test was performed on each PC and only the ones that were highly significant are shown; + or − sign corresponds to the way the corresponding PCs are affected in the leaf mutant (as compared to the mean, see Fig. 2). Cloned genes are shown in bold (Alonso-Peral et al., 2006; Barrero et al., 2007; Byrne et al. 2000; Cnops et al., 2004; Hricová et al., 2006; Nelissen et al., 2005; Pérez-Pérez et al., 2004; Semiarti et al., 2001).

Gene abbreviation	PC1Ler	PC2Ler	PC3Ler	PC5Ler	Class
ond2, ond3	+				A1
icu6	−
den12, icu9, api1, den5, ang4		+			A2
seal, exi6, ven2, seal, exi3		−
ron2, anu3			+		A3
api6, deal, den6			−
ven6				+	A4
sca4, anu12, anu6, anu2, anu5	+		−		B1
exi1, ond4, ero3	+		+
sca3, api4	−		−
ang2	−	−			B2
den7, ang1	−	+
sea2, hve1, icu3, icu2, exi9, elo2	+	+
rug2, exi7, anu4	+	−
ero2, ven4		−	+		B3
elo3, elo4, den16, den17, den29, elo1, ang3		+	−
ond1, ucu2	+			−	B4
tcu3, ven1, anu7			−	+	B5
den11, api3		+		+	B6
den10		−		+
den13, api5		+	−	+	C1
as3	−	−	−		C2
den1	−	+	−
orb2, ron1,	+	−	+
sea4, anu8, anu11, sea3	+	+	+
den4, den8, anu9	+	+	−
icu15, icu8,	+		−	+	C3
api7	−		−	+
den30	−	+		+	C4
tcu1	+	−		−
den14, den15	+	+		+
exi2	+	−	+	+	D1
den3	+	+	−	+
tcu2	+	−	−	+
as1	+	−	−	−
ven3, ron3, sca5, exi8, icu4, icu5, as2, api2, ero1

Most of the remaining mutants affected values for multiple PCs. Thirty nine mutants affected values for two PCs (group B), 20 affected values for three PCs (group C) and four affected values for all four PCs (group D). Nine mutants had no significant effect on the value of any PCs based on our sample of 6–8 leaves, reflecting mostly the high stringency of our t-test assay. If the p value was raised to p<0.05, only the ven3 mutant was found not to affect the value of any PCs. This might reflect the fact that ven (venosa) mutants were mainly picked out for their conspicuous venation pattern and not for their overall leaf shape effect (Berná et al., 1999; Robles and Micol, 2001). Also, our model is restricted to 2D morphological traits and cannot capture three-dimensional effects such as curvature changes.

To confirm that the classification according to PC values was sufficient to capture mutant shape and size variation, mutant shapes were recreated using only the values of the significant PCs affected in each case. This showed that the observed mean shapes and sizes of various mutants were captured effectively by only specifying the significant PC deviations (Fig. 4).

Figure 4. Eighty two Arabidopsis leaf shape mutants reconstructed using significant PCs only from the allometry model.

Mean shape as observed (in gray) is compared with the mean shape (white) reconstructed using significant PCs only (p<0.01). Leaf shapes are classified according to their PC combination as described in Table 1. Genes names are as described by (Robles and Micol, 2001). Wild type Landsberg erecta (L-er) is shown for comparison.

To test the robustness of the model, we determined its ability to classify a newly presented leaf outline. To do this, we created an allometric space for Arabidopsis mutants based on a subset of the data (five leaves from each mutant). We then used the classifications A1-D1 to define 15 regions within this allometric space. Individual mutant leaf outlines that were not involved in creating the space were then projected onto the space to determine which region they were nearest to (i.e., the most likely class they belong to). Seventy five percent of such tests returned the correct classification as the best hit. Eighty one percent returned the proper classification within the two best hits and 83% within the three best hits, using a k-neighbor method (see Materials and Methods).

We also tested individual leaf images against a classification based on the regions corresponding to the 91 different mutants (again using only a subset of data to create the allometric space). This showed that 50% of leaves could be assigned to their own mutant group and in 79% of cases the correct mutant group was in the top five hits. These results are expected as several mutants give very similar shapes.

Analysis of shape variation independently of size

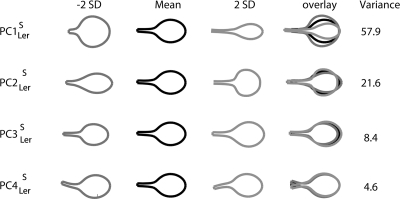
The previous analysis incorporates both shape and size differences between leaves to create an allometric space. An alternative approach is to analyze shape separately from size. To evaluate this approach, we normalized the size of leaf outlines during Procrustes alignment prior to carrying out PCA (this normalizes the average displacement of outline points from the center of the leaf). The resulting four major PCs, which account for 92% of shape variation, are illustrated in Fig. 5. These PCs are distinguished from allometric PCs described above with a superscript “s.”

Figure 5. Leaf shape variation of Arabidopsis mutants as described by the four main PCs from the shape model.

For each PC, the mean leaf outline and the shape outline obtained by varying the PC value plus or minus two times the standard deviation (+2SD and −2SD) are shown. These outlines are also shown overlaid. The percentage of the variance of the model explained by each PC is shown on the right.

$\mathrm{PC}{1}_{\mathrm{Ler}}^{\mathrm{s}}$ captures 57.9% of the total variance, with high values giving elongated leaves and long petioles and low values giving round leaves with short petioles. The effect of varying $\mathrm{PC}{1}_{\mathrm{Ler}}^{\mathrm{s}}$ values is similar to that for PC2 of the allometry model (compare Figs. 25). This is expected as most of the size variation in the allometric space is captured by PC1_Ler so the remaining variation is largely to do with differences in shape, principally captured by PC2_Ler. However, $\mathrm{PC}{1}_{\mathrm{Ler}}^{\mathrm{s}}$ is not identical to PC2_Ler as some aspects of shape that are correlated with size are also removed by PC1_Ler for the allometry model. $\mathrm{PC}{2}_{\mathrm{Ler}}^{\mathrm{s}}$ accounts for 21.6% of the shape variance and is similar to PC3_Ler of the allometry model, with high values giving wide leaves with long petioles and sharp petiole to blade transitions, whereas low values give narrow leaves with reduced petioles. $\mathrm{PC}{3}_{\mathrm{Ler}}^{\mathrm{s}}$ accounts for 8.4% of the shape variance and is very similar to PC5_Ler of the allometry model with low values giving a sharper blade to petiole transition than higher values. $\mathrm{PC}{4}_{\mathrm{Ler}}^{\mathrm{s}}$ is similar to PC4_Ler and reflects the extent to which the petiole twists to one side or the other of the leaf, accounting for 4.6% of shape variance but is not significantly affected in mutants. Thus both shape and allometry models give similar PCs with the exception of PC1_Ler of the allometry model which captures the main correlation between shape and size. The advantage of the allometry model is that it gives information about size and any associated shape variation and is therefore of more general use than the shape-only model.

Comparisons between allometric mutant spaces of different species

To compare the mutational space observed in Arabidopsis mutants to equivalent spaces for other species, we analyzed a collection of leaf shape mutants from Antirrhinum. Leaves from 53 Antirrhinum mutants from the Gatersleben collection, in the Sippe50 (S50) genetic background (Hammer et al. 1990; Stubbe 1966), were analyzed using the same model template as the one described in Fig. 1. For each mutant line six independent leaves from metamer 4 were imaged. Metamer 4 is at an equivalent position to theArabidopsis third true leaf (Mundermann et al., 2005). The main 3 PCs obtained from this allometry analysis are shown in Fig. 6.

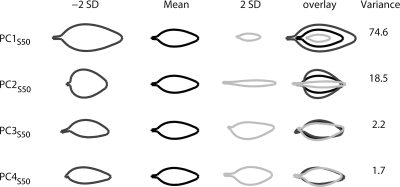
Figure 6. Leaf shape and size variation of Antirrhinum as described by the four main PCs from an allometric model.

For each PC, the mean leaf outline and the shape outline obtained by varying the PC value plus or minus two times the standard deviation (+2SD and −2SD) are shown. These outlines are also shown overlaid. The percentage of the variance of the model explained by each PC is shown on the right.

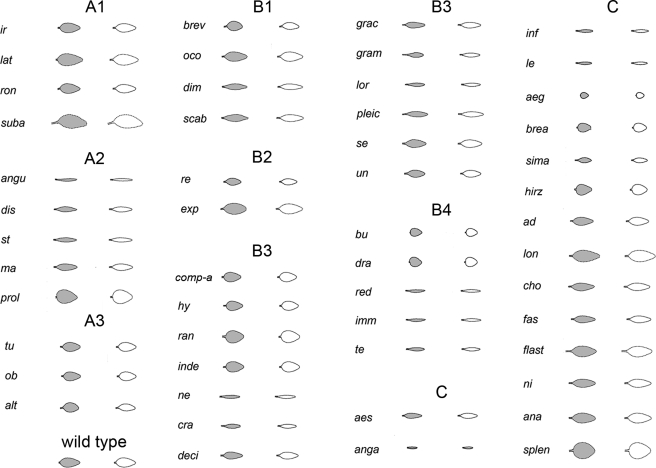
Varying PC1_S50 affects mostly size and accounts for 74.6% of the total model variance. Lower values of PC1_S50 give bigger leaves, whereas higher values give smaller leaves. PC2_S50 affects width and length and accounts for 18.5% of the total model variance. Decreasing PC2_S50 gives wide short leaves, whereas increasing PC2_S50 gives more narrow long leaves. PC4_S50 describes the petiole to blade transition (proportion of blade as compared to petiole length) and accounts for 1.7% of the total model variance. Lower values of PC4_S50 give petiole-less leaves, whereas higher values give leaves with long petiole and reduced lamina(lanceolate shape). PC3_S50 describes petiole twist but is not significantly affected in mutants. In a similar way as for the Arabidopsis analysis, Antirrhinum mutants could be classified according to the PCs that deviated significantly from wild type (Table 2). As a wild-type control, we used leaves from three independent flower mutants from the Gatersleben collection that did not affect leaf shape. Twelve mutants could be captured with only one PC only (A group), 24 with two PCs (B group) and 16 with three PCs (C group). Figure 7 shows the reconstructed and classified leaf shapes.

Table 2.

Classification of the Antirrhinum mutants according to the combination of highly significant PCs (p<0.01%) in the allometry model. Gene abbreviations are as described by Hammer et al. (1990) and Stubbe (1966). The + or − sign corresponds to the way the corresponding PCs are affected in the leaf mutant (as compared to the mean). Cloned genes are in bold (Golz et al., 2002; Golz et al., 2004).

Gene abbreviation	PC1S50	PC2S50	PC4S50	Class
ir, lat, ron, suba	−			A1
prol		−		A2
dis, angu, st, ma		+
alt, ob, tu			+	A3
brev	−	−		B1
oco, dim, scab	−	+
re	+		+	B2
exp	−		+
comp-a, hy, ran, inde		−	+	B3
ne		+	−
cra, deci, grac,gram, lor, pleic, se, un		+	+
bu, dra	+	−		B4
red, te, imm	+	+
aes, anga, inf, le	+	+	−	C
aeg, brea	+	−	−
sima	+	+	+
ad, lon, cho, fas	−	+	−
ana, flast, ni	−	+	+
hirz	+	−	+
splen	−	−	+
mus, rea

Figure 7. Fifty one Antirrhinum leaf shape mutants reconstructed using highly significant PCs only.

Mean leaf shape as observed (gray) is compared to leaf shape reconstructed (white) using significant (p<0.01%) PCs from the allometry model following a ranked t-test analysis. Wild type (averaged) is shown for comparison.

Genetic and developmental interactions

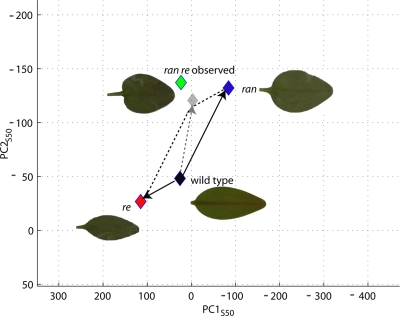
Allometric spaces can also be used to investigate the nature of gene interactions. The effect of a single mutation can be considered as a vector running from wild type to mutant locations in allometric space. If two mutants interact additively, the double mutant should be located at a position given by the sum of the two single mutant vectors (this follows from the linear nature of PCA). Figure 8 illustrates this for the double mutant of ran and re of Antirrhinum with respect to the two PCs they affect (PC1_S50 and PC2_S50). The location of ran re mutant observed is quite close to the position predicted. Hence, ran and re have mainly additive effects.

Figure 8. Projections of ran, re, and ran, re mutants of Antirrhinum as compared to averaged wild type on thePC1 _S50 andPC2 _S50 two-dimensional space.

Colored diamonds indicate the coordinates of the corresponding mean mutant shapes as observed and black diamond mean of averaged wild type. Gray diamond corresponds to predicted mean of double mutant as obtained from vector addition. Vectors corresponding to the mutant deviation from the mean are shown. Dashed line indicates the projection used for vectors addition and dashed arrow shows the resulting vector.

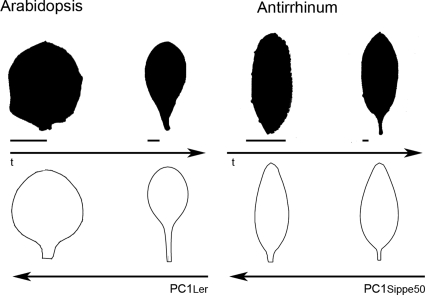
For both the Arabidopsis and Antirrhinum allometric models, PC1 captures an association between shape and size. However, the effect of varying PC1 values on shape is different for each species. Varying PC1 values to give small leaves yields a much more rounded shape for Arabidopsis than for Antirrhinum (compare effects of varying PC1 in Figs. 26). These differences between the models are mirrored in the developmental sequence of leaf shapes in each species. The top panel of Fig. 9 shows the change in shape between young (∼1 mm wide) and mature leaves of Arabidopsis or Antirrhinum leaves (leaves have been scaled to the same length). Young Arabidopsis leaves are rounder than mature leaves, whereas young Antirrhinum leaves are only slightly rounder and with a shorter petiole than mature leaves. These shape changes are similar to those obtained by varying PC1 values for each species (lower panel of Fig. 9, shapes scaled to give the same leaf length). The parallel changes between varying PC1 and developmental progression indicate that some of the mutational variation in shape and size may reflect changes in the timing of developmental arrest.

Figure 9. Comparison of developmental sequence and of PC1 effect on leaf shape of Arabidopsis and.

Leaf shape outlines from two different time points (t) are shown in black. Scale bar is 1 mm. Normalized outlines, obtained by varying PC1 +2SD (small leaves, on the left part) or −2SD (big leaves, right part) of the models, are shown in white.

DISCUSSION

Mutational variation in leaf shape and size can be described quantitatively with an allometry model involving relatively few dimensions. Mutant collections, comprising respectively 91 and 54 different genotypes, could be captured with an allometric space based on three (Antirrhinum) or four (Arabidopsis) principal components (PCs). In each case, the PC accounting for most of the variance reflects differences in size together with an associated shape change. The remaining PCs capture variation in shape together with more minor effects on size. The results have implications for genetic, developmental and evolutionary studies on leaf allometry.

Genetics

One advantage using an allometry model is that the effect of each leaf shape∕size mutation can be fully described quantitatively with a vector. The vector runs from the location of the wild-type leaf outline to the mean position for the mutant. Because PCA is based on linear correlations, additive interactions between different mutations can be captured by adding the two individual mutant vectors. The difference between the phenotype predicted by vector addition and that observed in the corresponding double mutant gives an estimate of deviation from additivity (i.e., whether epistatic interactions are involved). The allometric space also allows the position of any new mutant to be compared with all previously described mutants, making it straightforward to identify similar phenotypes and hence likely candidates for allelism tests. For example, a previously unseen individual leaf can be automatically assigned to its correct mutant group in 50% of the cases, increasing the chance of a successful first allelism test by about 50 (the chance of a leaf from the collection belonging to any mutant group at random is 1∕91=1.1%).

The allometric space can also be used to derive qualitative descriptions that provide a bridge to more traditional ontologies. For each mutant line, PC values showing significant deviation from wild type are determined and used to classify the mutants. Using this subset of PC values to reconstruct the mutant outlines shows that they are usually sufficient to capture the main features of the leaf mutant. In many cases, the classification brings together mutants previously put into a similar class. For example, several allometric classes in Arabidopsis include multiple elo or den mutants (Berná et al., 1999; Robles and Micol, 2001). Also the classification overlaps with previously defined categories such as size, leaf index (ratio of leaf length and width) and presence∕absence of petiole (Tsukaya, 2006). However, the advantage of the allometric classification described here is that it is not based on preconceptions about which characters should be considered separately. It therefore cuts across some previous categories (i.e., PC1 affects both leaf index and size), highlighting natural relationships. It also has the benefit of being quantitative, allowing mutant shapes to be specified to known accuracy through a subset of PC values. Novel mutants can therefore be automatically screened and categorized. For example, a previously unseen individual leaf can be assigned to its correct category in 75% of cases, allowing for an initial automatic categorization of mutants which could then be further refined through progeny testing.

One limitation of our analysis is that we only recorded leaf shapes in 2D. It would be interesting to extend the approach to 3D outlines to capture variations in curvature (Kaminuma et al., 2005). We also only explored one environmental condition. Many environmental factors, such as abiotic stress (Alvesa and Setterb, 2000; Farris, 1984; Housman et al., 2002), have an effect on leaf shape. Analysis of wild-type or mutant plants grown under different conditions would be a further application of the method.

Development and evolution

A striking feature of PC1 for the Arabidopsis space is the association between leaf size and shape—varying PC1_Ler values gives small round leaves in one direction and large elongated leaves in the other. This parallels the change in leaf shape during later stages of development from a round to more elongated shape. A likely explanation is that some of the mutants act by causing early growth arrest (giving small round leaves) or delayed growth arrest (giving elongated large leaves). This interpretation is consistent with the allometric model of Antirrhinum in which varying PC1_S50 values has little effect on leaf shape, paralleling a less marked developmental change in leaf shape. Similar types of explanation have been put forward to account for association between shape and size of different varieties of gourd (Sinnott, 1936). The results underscore the importance of incorporating both shape and size when considering the developmental basis of mutational effects.

Although the effect on shape associated with PC1 is different for Antirrhinum and Arabidopsis, the other PCs show qualitatively similar effects on leaf outline. In both species, PC2 mainly affects leaf width while the third PC affects petiole length. This suggests that even though the Antirrhinum and Arabidopsis lineages diverged at an early stage in eudicot evolution (Soltis et al., 2005) they may share many of the underlying developmental mechanisms controlling leaf growth.

A further implication of the similarities between theArabidopsis and Antirrhinum mutant spaces is that the developmental constraints on the evolution of leaf shape and size may be comparable. Each allometric space describes the range of phenotypes that may be reached by single mutations from the wild type. It therefore provides an estimate of the phenotypic space that could be potentially explored from a given starting point. Only a subset of this space is likely to be relevant for evolutionary change according to how the various mutations affect fitness. Nevertheless, the similarity between the spaces for Arabidopsis and Antirrhinum suggests a broadly similar range of possibilities exists in each case. However, there are also some important differences, such as the more serrated edge of Arabidopsis leaves, the more pointed tips of Antirrhinum leaves and interactions between multiple mutants. So while the allometric spaces provide a broad framework for quantification and comparison, a firm understanding will depend on a detailed analysis of the genetic mechanisms underlying developmental and evolutionary change.

NOTE ADDED IN PROOF

A similar approach to the one described here was published while our paper was under review (Weight et al., 2007).

MATERIALS AND METHODS

Plant material

Seeds were surface sterilized, sown on GM∕2 medium and stratified for two days at 4 °C. Plants were grown on plate in growth chambers with 16 h light, 70% humidity for 12–14 days. Then plantlets were transferred to soil and grown in the glasshouse (20 °C, 16 h light) until fully mature.Antirrhinum mutants came from the Gatersleben collection and were then propagated at the John Innes Centre.

Seeds were germinated on a mist bench and moved to outside benches after progressively hardening in glasshouse.

Imaging conditions

The third true leaf of each Arabidopsis plant was harvested at 28 days after stratification, flattened on a piece of double face tape and imaged with a digital camera (Kodak, DCS Pro, 14N). Metamer 4 leaves from Antirrhinum plants were harvested approximately four months after sowing when plants were flowering. Leaves were glued on paper and imaged as above.

Image processing

All images were scaled to a 200 pixels∕cm resolution for Arabidopsis leaves and to 60 pixels∕cm for Antirrhnum leaves. Leaves were properly oriented (tip always pointing to the right, and good horizontality) using Photoshop software (Adobe). Individual leaves were then processed using the AAMToolbox implemented by Andrew I. Hanna. After placing the landmarks, the secondary landmarks points were evenly spread along the leaf outline. This was achieved by taking two primary points and fitting a spline between them using the secondary points; a spline being a special function that is defined piecewise by polynomials. The secondary points were then rearranged to be equidistant from each other along the spline. Models were generated using the 6.5 version of the software, which is available on request and at http:∕∕www1.uea.ac.uk∕cm∕home∕schools∕sci∕computing∕research∕cmpbio∕Downloads.

Procrustes alignment, normalization and representation of shapes

Leaf outlines were normalized using the Procrustes method in which each shape is transformed to a mean shape using iterative translation, scaling (based on the distance of landmarks from the centroid) and rotation of the landmark data, producing a superimposition that minimizes deviations from the overall mean shape. We can represent each shape by the equations

$$x=\mathrm{Xm}+P^{*}\mathrm{b}$$

and

$$b={P^{\prime }}^{*}(x-\mathrm{Xm}),$$

where the columns of P are the principal components, Xm is the mean shape vector, and b is the vector of coefficients that represents a shape (i.e., the coordinates of the shape in PC space). Thus any shape can be related to another by comparing values of the b coefficients.

Classification of individual test outlines

Two methods were used to assign a class for a given individual leaf outline. The first was the nearest mean which looks for the shortest Euclidian distance between the tested shape and the surrounding groups. The second is a k-neighbor method, which estimates the group based on the frequency of neighbors, with K set usually to 5 (i.e., looking for the higher frequency among the five nearest neighbors). Usually, K neighbor was more accurate than using the nearest Euclidean distance.