Abstract
By exploring the folding pathways of the B1 domain of protein L with a series of equilibrium and rapid kinetic experiments, we have found its unfolded state to be more complex than suggested by two-state folding models. Using an ultrarapid mixer to initiate protein folding within ∼2–4 microseconds, we observe folding kinetics by intrinsic tryptophan fluorescence and fluorescence resonance energy transfer. We detect at least two processes faster than 100 μs that would be hidden within the burst phase of a stopped-flow instrument measuring tryptophan fluorescence. Previously reported measurements of slow intramolecular diffusion are commensurate with the slower of the two observed fast phases. These results suggest that a multidimensional energy landscape is necessary to describe the folding of protein L, and that the dynamics of the unfolded state is dominated by multiple small energy barriers.
Much of the experimental effort on protein folding of small proteins over the last 15 years has focused on two-state folders (Plaxco et al., 1998; 2000). Many small, single-domain sequences have monoexponential folding kinetics on the millisecond (or slower) time scale, and the folding rate has a Boltzmann-like dependence on temperature or denaturant concentration (Scalley and Baker, 1997). However, the experimental measurements of these two-state folders were usually limited to millisecond or longer time scales due to the limitations of stopped-flow mixing technology (Scalley et al., 1997). Evidence for kinetic processes on faster time scales is usually inferred only from the burst phase, or missing amplitude, during the mixing time. To study faster events in protein folding, researchers have investigated loop dynamics, secondary structure formation, and hydrophobic collapse on the nanosecond and microsecond time scales, which suggests that some folding steps were possible before 1 ms (Eaton et al., 2000). There has also been a lively debate on the validity and value of energy landscape theory to describe protein folding (Bicout and Szabo, 2000; Gruebele, 2002; Onuchic et al., 1997). The “new view” may allow for more complex folding paths than traditional transition state theory but seems unnecessarily complicated for describing a two-state folder.
Mixing technology has improved with the invention of continuous-flow capillary mixers which have documented intermediates in several proteins with lifetimes ∼100 μs (Capaldi et al., 2001; Park et al., 1999; Shastry and Roder, 1998; Teilum et al., 2002). A small number of extremely fast-folding proteins have also been studied on the microsecond time scale using laser temperature jump and have generally found two-state behavior, but these experiments typically cannot prompt refolding from a fully unfolded state (Kubelka et al., 2003; Qiu et al., 2002; Yang and Gruebele, 2003). Recent advances in microfluidic mixing technology have reduced the mixing time of denaturant dilution experiments to a few microseconds, which allows observation of real proteins folding from a fully denatured state on the time scale that hydrophobic collapse and secondary structure formation may be occurring (Hertzog et al., 2004; Knight et al., 1998; Lapidus et al., 2007). In this paper we have used such a mixer to follow the folding of the well-studied B1 domain of protein L and observed at least two phases before 1 ms. These results suggest a two-state model is not adequate to describe the folding of this protein. Folding intermediates could be defined to describe the observations, but the low stability relative to the major barrier has led us to choose a model of a rough landscape first described by Zwanzig (1988). For purposes of discussion, we define roughness as low (1–3 kcal∕mol) energetic barriers that retard diffusion, and intermediates as states with structural distinction and larger energetic barriers.
RESULTS
Kinetic measurements
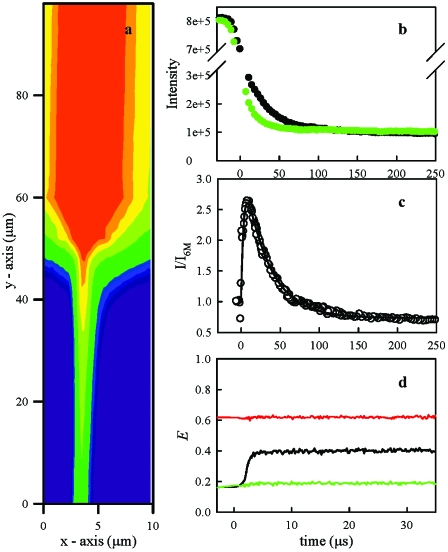
We have observed the folding kinetics of protein L in an ultrarapid, continuous-flow microfluidic mixer with a mixing time of ∼2–4 μs. The folding kinetics is monitored by the total fluorescence intensity excited at 257 nm, by time-resolved spectra of UV emission, and by visible fluorescence resonance energy transfer (FRET). Figure 1a shows a contour plot of emitted intensity near the mixing region, and Fig. 1b shows the total UV intensity as a function of time before, during, and after mixing. Because of the design of the microfluidic mixer, in which a 5 μm wide stream of protein solution is constricted to ∼100 nm jet, there is a significant decrease in the measured raw intensity in the first 2–4 μs, independent of the folding process. To correct for this effect, two measurements are made: (1) the protein in 6 M GdnHCl is mixed into 100 mM phosphate buffer without denaturant, inducing the protein to fold [black points in Fig. 1b] and (2) the protein in 6 M GdnHCl is mixed into the same 6 M GdnHCl solution, leaving it unfolded throughout (green points). The signal as a function of time is measured for each at identical flow rates and the two signals are normalized point by point, resulting in Fig. 1c. These measurements are made at three different flow rates and the normalized data are combined before fitting, which shows the measured kinetics are independent of the mixing dynamics.
Figure 1. Kinetics of protein L fluorescence after ultrarapid mixing.
(a) Contour plot of fluorescence intensity near 350 nm in the mixer. Protein L in 6 M GdnHCl flows down from the top of the figure to the mixing region, which is located at ∼45 μm in the y-axis. The folding buffer flows from either side at ∼100 times the rate of the protein channel and constricts the protein stream to a narrow jet. (b) Intensity as a function of time after mixing. The intensity is calculated as a sum over measurements over 1.25 μm across (x-axis) the jet for every y position. The position in y is converted to time using a calculated, constant flow rate. The mixing time is measured as a change in intensity of the raw data with a 90∕10 time ∼4 μs. The black points are measured after mixing into 0 M GdnHCl and the green points after mixing into 6 M GdnHCl. (c) Ratio of intensity after mixing into 0 M GdnHCl to 6 M GdnHCl. The data shown were measured at three different flow rates and combined with only the adjustment of a y-axis offset. The data for all three rates overlay seamlessly except near the mixing region, when the jet formation time will be different for different flow rates (these data not shown). The line is a fit of the data to two exponentials starting at 4.5 μs with the amplitudes constrained to be 1.0 at t=0. (d) FRET efficiency, E, as a function of time after mixing for 0 M GdnHCl (red), 6 M GdnHCl (green), and 0 M GdnHCl after dilution from 6 M GdnHCl (black). Intensities of donor and acceptor fluorophores are calculated as a sum over measurements over 0.3 μm across the jet and E is calculated using the equation in the text.
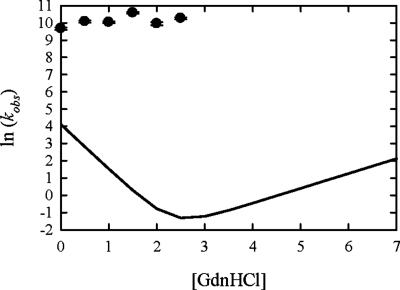
The relative UV emission [Fig. 1c] shows a significant increase in fluorescence within the mixing time, a small time-resolved increase with a rise time of 4±2 μs (which appears to be the exponential tail of the unresolved phase), and a decrease in fluorescence with a decay time 43±7 μs. Note that there is no significant change on the 1 ms time scale and that the net change in signal is negligible. Therefore, from the point of view of a stopped-flow measurement with a dead time greater than 1 ms, there is no perceptible burst phase. Figure 2 shows the rates of the slow decay at various denaturant concentrations (see Supplemental Figure S1 for raw data). In contrast to the folding rates observed by stopped-flow mixing, these rates are independent of denaturant concentration. There is also no change in rate with changing the protein concentration, changing the folding pH between 5 and 8, or increasing the viscosity of the folding buffer twofold (see Supplemental Figure S2). The early (4 μs) rise in signal is too fast to accurately measure a rate with our instrument, but within our experimental error there does not seem to be any denaturant dependence on this process either.
Figure 2. Measured rates of the slower decay in UV intensity (points) plotted as a function of final denaturant concentration.
The line is the two-state model of the rates previously measured by Scalley et al. (1997) using stopped-flow mixing.
Figure 1d shows FRET efficiency between two fluorophores at positions 16 and 64 on the folding protein chain as a function of time within the mixer. FRET efficiency, E, is defined as the relative intensity of the acceptor fluorophore E=IA∕(ID+IA) and is intrinsically normalized. The intensity of each fluorophore is observed on separate detectors and E is calculated point by point as shown in Fig. 1d (note that the data are not corrected for differences in detection between the two channels). In contrast to Fig. 1c, this plot shows only a rapid increase in E within the mixing time of 2+2 μs. This result indicates that initial collapse due to the change in solvent conditions is much faster than 106 s−1, in agreement with observations of other proteins (Lapidus et al., 2007; Nettels et al., 2007; Sadqi et al., 2003).
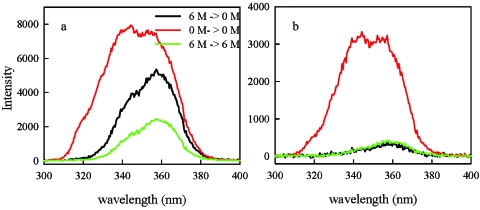
Figure 3 shows the time-resolved UV fluorescence spectra collected in three different experiments (6 M mixed into 6 M, 6 to 0 M, and 0 to 0 M GdnHCl) 22 and 118 μs after mixing. The black (6 to 0 M) and green (6 to 6 M) measurements have the same spectra, indicating the tryptophan remains exposed to solvent even as the quantum yield increases in agreement with the measurements of total intensity [Fig. 1c]. This fact, combined with the denaturant independence of the rate, indicates that there is little change in solvent-accessible surface area during this phase. Therefore, the observed fast processes are relaxations within the unfolded basin. The difference between the red and black curves shows the change in intensity and spectral shift that occurs on the millisecond time scale, beyond the time range of this mixer, as the protein folds into its native structure.
Figure 3. UV fluorescence spectra of protein L in 0 M GdnHCl (red), 6 M GdnHCl (green), and 0 M GdnHCl after dilution from 6 M GdnHCl (black).
Each spectrum was collected 12 μm (a) and 64 μm (b) below the mixing region. The solution was moving at a speed of 0.54 m∕s, which corresponds to 22 μs (a) and 118 μs (b) after mixing. The black and green spectra were recorded on the same sample. The red spectrum was recorded on a sample that had equilibrated in 0 M GdnHCl for more than 1 h and had a concentration within 10% of the other sample.
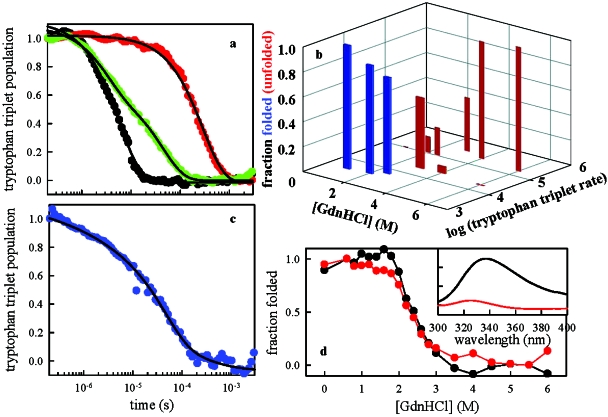
To further understand the dynamics of the unfolded state, we reexamine earlier measurements of intramolecular diffusion of denatured protein L. We have previously shown that the measurement of the tryptophan triplet lifetime in a protein L mutant with cysteine in the sequence measures the rate of intramolecular diffusion only when the protein is unfolded because cysteine acts as a close-range quencher of the triplet (Singh et al., 2007). Therefore, when the protein population is partially folded, the kinetics of triplet population exhibits two decays separated by 1–2 orders of magnitude [Fig. 4a] and the relative amplitude of the fast decay is a good measure of the fraction of unfolded molecules. However, for the protein L mutant K23C (which has similar stability to the wildtype), we observed rates in three different ranges at different denaturant concentrations; a fast rate due to intramolecular quenching by cysteine (∼105 s−1), a slow rate due to natural decay of the triplet in a hydrophobic environment (∼103 s−1), and a medium rate due to solvent quenching (∼104 s−1). In the reference Singh et al. (2007) we attributed the ∼104 s−1 rate to a well-defined intermediate. However, replotting these data [Fig. 4b] along with the relative amplitude of each decay shows that the stabilities of the protein ensembles leading to the fast and medium rates are very similar and are similar to the stability to that of the wildtype measured by fluorescence [Fig. 4d]. Since a structured intermediate usually has a different stability from the unfolded state, this suggests that both ensembles we observe lie within the unfolded basin: a rapidly diffusing state (τD+<10 μs) and a state in which intramolecular contact is too slow to observe (τD+>40 μs). This slowly diffusing state can also account for the initial rise in steady-state fluorescence emission [see Figs. 1c, 3a] because the quantum yield of tryptophan fluorescence is typically reduced by intramolecular quenching by various residues; slowing of diffusion would result in less quenching in the steady state.
Figure 4. (a) Decay kinetics of the tryptophan triplet state of the mutant K23C at various concentrations of denaturant.
The black (6 M GdnHCl) and red (1 M GdnHCl) points can be well fit to single exponentials, while the green (3 M GdnHCl) points require a two-exponential fit [fit values shown in (b)]. (b) Relative tryptophan triplet decay amplitudes for the protein mutant K23C as a function of denaturant concentration and observed rate. All kinetics was fit to two exponentials. The rates log(k)⩾5 s−1 are due to intramolecular diffusion between W47 and C23; log(k)∼4 s−1 represents a relatively rigid conformation in which the tryptophan is quenched by solvent; log(k)∼3 s−1 represents a nativelike state with the tryptophan hydrophobically buried. We designate the red bars to lie within the unfolded basin and blue bars to lie within the folded basin. (c) Decay kinetics of the tryptophan triplet state of the destabilized mutant F22A K23C in 0.1 M GdnHCl. The fit (black line) is to a stretched exponential with decay time τ=37 μs and stretching exponent β=0.56. (d) Equilibrium stability of wildtype protein as measured by fluorescence. The spectra at various concentrations of denaturant are analyzed with singlular value decomposition yielding two significant components, shown in the inset. The amplitudes of these components are normalized to the fraction folded and have a transition midpoint of ∼2.5 M GdnHCl.
Further evidence for slow diffusion in the unfolded state is shown in Fig. 4c for the mutant F22A K23C. The mutation of the phenylalanine removes one of the core hydrophobes and significantly destabilizes the folded state; it is about 60% unfolded at 0.1 M GdnHCl as monitored by single-molecule FRET (Marcus Jäger and Shimon Weiss, unpublished data). Measurement of Trp-Cys contact formation reveals highly nonexponential kinetics, which is a hallmark of glassy behavior in polymer systems (Berberan-Santos et al., 2005; Bodunov et al., 2002; Peterson and Fayer, 1986). It also resembles the distance-dependent quenching dynamics of tryptophan by cysteine embedded in a room-temperature glass, for which the diffusion constant was found to be ∼10−13cm2∕s (Lapidus et al., 2001).
DISCUSSION
The B1 domain of protein L is a common model system for studying protein folding. Mass spectrometry in conjunction with HD-exchange equilibrium experiments provided the first evidence that protein L is a two-state folder (Yi and Baker, 1996). This model was confirmed with stopped-flow mixing fluorescence and CD measurements, both of which showed single exponential decays with rates of 27.8 and ∼27 s−1, respectively, with no perceptible burst phase within the 1.7 ms dead time (Scalley et al., 1997). Plaxco et al. (1999) confirmed and expanded these findings by stopped-flow small-angle X-ray scattering (SAXS) measurements. They found no evidence of a rapid hydrophobic collapse of the unfolded protein following an abrupt change in solvent conditions to those favorable to folding, instead concluding that the collapse occurs concurrently to the folding process. Later HD-exchange experiments showed no intermediate folding state in the free energy between folded and unfolded states under native conditions (Yi et al., 1997). These data revealed a small but significant energy barrier of about 4.6 kcal mol−1 (Scalley et al., 1997) between the “unfolded” and “folded” states.
The data presented here suggest that the folding path before the major barrier has a hidden complexity. We found a significant and unresolved increase in FRET and tryptophan fluorescence within 2–4 μs, and the tryptophan fluorescence has a resolved tail that extends to ∼8 μs. Since in the absence of a significant barrier different probes may show different rates (Ma and Gruebele, 2005), the rise in tryptophan emission extending to ∼8 μs and the unresolved increase in FRET efficiency may represent the same process of relaxation of the denatured protein population in 6 M GdnHCl into unfolded equilibrium in water. After the initial rise, only the tryptophan emission decreases with ∼43 μs decay time. This rate is independent of flow rate, viscosity, and protein concentration, and extensive simulation and empirical testing of these mixers show that once the jet has formed [see Fig. 1a] (Hertzog et al., 2004), the solvent composition has reached equilibrium. That the 43 μs decay observed by tryptophan emission is not mirrored in the FRET signal suggests that this phase is not global collapse or expansion of the protein. Instead, it likely reflects local rearrangement of structure that forms during the initial collapse and may not be productive to folding.
Does the 43 μs phase represent an intermediate state? If such an intermediate exists it would certainly be off-pathway because the decay of tryptophan intensity is opposite from the increase in intensity observed during the last step of folding. However, there is no evidence that this rate depends on denaturant concentration, and there is no observable structural distinction. Based on recent theoretical work on the relaxation rate of a two-state system with a range of barriers, we estimate an upper limit on the free-energy barrier of this process of 0.5 kcal∕mol (Naganathan et al., 2007). Additionally, the lack of viscosity dependence on the rate of this process suggests that the unfolded state is dominated by internal friction. Therefore, we find little compelling evidence for a distinct intermediate rather than an ensemble of unfolded conformations. Cellmer et al. has observed no denaturant dependence on the folding rates of the N-terminal villin headpiece, but since that process leads directly to the native state, it was interpreted as a low-barrier (<2 kcal∕mol) two-state folder (Cellmer et al., 2007). Sinha and Udgaonkar also found no denaturant dependence in the early intermediate of barstar and concluded there is no significant barrier (Sinha and Udgaonkar, 2008).
The dynamics of this unfolded state ensemble after mixing may be inferred from equilibrium experiments. Measurements of tryptophan triplet quenching by cysteine in this protein show that some of the population under unfolding conditions cannot make intramolecular contact in less than 40 μs (the natural lifetime of the triplet in water), which indicates extremely slow intramolecular diffusion. A destabilized mutant, which is mostly unfolded in water, also shows a wider range of contact rates, indicating glassy dynamics, but a significant population also cannot make contact in less than 40 μs. We believe the 43 μs kinetic relaxation reflects the same conformational subpopulation that has slow intramolecular diffusion. Both have the stability of the unfolded state and neither shows any indication of native contacts such as tryptophan hydrophobic burial.
Given the glassy dynamics of unfolded protein L in water and the lack of conclusive evidence of an intermediate, we have chosen to describe the 43 μs process as diffusion on a rough potential using the formalism first developed by Zwanzig. The degree of roughness can be estimated by ΔE2=(kT)2 ln(τ∕τ0) (Zwanzig, 1988), in which τ is the observed process time and τ0 is the expected time from diffusion on a smooth potential. Szabo, Schulten, and Schulten theory for a Gaussian chain predicts the relaxation time of the unfolded state is τ0=⟨R2⟩∕3D (Buscaglia et al., 2006). Using the diffusion coefficient determined by Singh et al. (2007), D=10−8 cm2∕s and R=2.2 nm yields a relaxation time of τ0∼1.6 μs. Using τ=43 μs we calculate ΔE∼1 kcal∕mol, which is about 20% of the barrier height between the unfolded and native states. This value of ΔE is similar to that found in equilibrium unfolded cold shock protein using single-molecule FRET (Nettels et al., 2007) and somewhat higher than the lower limit set for the ultrafast- folder trpzip2 (Yang and Gruebele, 2004).
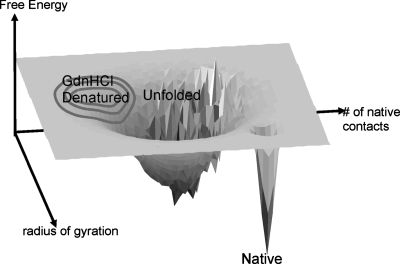
The dissimilar kinetics observed by tryptophan fluorescence and FRET and the observation of two unique diffusional populations in equilibrium strongly suggests a one-dimensional description of the folding pathway is inadequate. Therefore, we suggest a landscape such as shown in Fig. 5 more completely describes the folding dynamics before the rate-limiting step that has been well described by millisecond kinetic studies. We chose the radius of gyration and the number of native contacts as the landscape’s two reaction coordinates. The landscape features two prominent basins and the barrier between them is analogous to the energetic features of the two-state model. The specific features such as the exact positions and widths of the basins and rough patches are fairly arbitrary but it still can be used to generally describe the measured kinetics. Immediately following mixing, the state of the completely denatured protein would be deposited in the upper-left region of the landscape, where it would quickly fall into the unfolded basin. This diffusion process on a smooth portion of the landscape would correspond to rapid collapse measured within the first 2–4 μs in both FRET and fluorescence measurements, while diffusion over the rough portion would correspond to the slower relaxation of the tryptophan fluorescence. Equilibrium populations on the rough portion would have slow intramolecular diffusion. In the figure, the roughness was placed such that populations at the bottom of the unfolded well will have access to the shortest path to the folded well, thus preserving the assumed uniform nature of the transition state in phi analysis, but further experiments with other probes, such as microsecond time-resolved circular dichroism, are required to structurally discriminate multiple pathways to the major folding barrier.
Figure 5. Conceptual representation of the energy landscape under the final folding conditions.
The gray circles represent the population of fully denatured molecules that relax on the landscape during and after mixing. The depth of the unfolded and folded basins are calculated from the two-state model given by Scalley et al. (1997). The roughness in the unfolded basin is calculated by adding a normally distributed random number with a standard deviation of 1 kcal∕mol. The <10 μs rise in Figs. 1c, 1d is the downhill relaxation of the denatured state into the unfolded basin. The 43 μs decay is the diffusion on the rough part of the landscape towards the bottom of the unfolded basin. The 30 ms rise observed by Scalley et al. (1997) is the escape from the unfolded to the native basin.
MATERIALS AND METHODS
Expression and purification of protein L
The protein L plasmid (Y47W) was a generous gift from David Baker and expressed by standard methods first described by reference (Scalley et al., 1997). The K23C mutant was made and expressed as described in the reference (Singh et al., 2007). The F22A K23C (destabilized mutant) and S16C 65C (FRET labeled mutant) were mutated from the wildtype sequence using the Quikchange kit (catalog #200518) from Stratagene (La Jolla, CA). Protein expression was identical to that described in Singh et al. (2007), but after lysis and centrifugation, the destabilized protein remained in the pellet. The pellet was resuspended in 50 mM sodium phosphate, 300 mM NaCl, 6 M GdnHCl, and 0.5% triton 100X. The protein was purified from this solution as described previously (Singh et al., 2007).
Site specific labeling of protein L with a unique donor and unique acceptor molecule was accomplished using a modified sequential labeling protocol pioneered by Haas and co-workers (Ratner et al., 2002), as described in detail elsewhere (Jager et al., 2005). Two Cys residues were introduced into wildtype ProL by mutagenesis. One Cys replaced residue Ser16 at the base of the N-terminal hairpin, and a second Cys was added to the C-terminus (residue 65). The double Cys variant of ProL was comparable in protein stability to Cys-free wildtype ProL and FRET labeling did not significantly perturb the folding energetics of ProL (see Supplemental Fig. S3).
Kinetic measurements
Folding experiments were conducted through a microfluidic ultrarapid mixer of the type developed by Hertzog et al. 2006, 2004, and modified by Yao and Bakajin (2007). The mixer is made from a 500 μm thick wafer (fused silica for UV experiments and silicon for FRET experiments) with channels typically etched 10 μm deep with a second 157 μm wafer bonded on top to seal the device. All flows are in the laminar regime and the flow rates can be computed from the applied pressures by mathematical simulations (COMSOL Multiphysics, Stockholm, Sweden). The mixer used for the FRET measurements is of a highly optimized design with a mixing time of ∼2 μs, whereas the mixer used for the UV measurements, due to limitations of the fabrication process, is slightly less optimal with a mixing time of ∼4 μs. The protein, typically prepared in 6 M GdnHCl and 100 mM potassium phosphate buffer at pH 7.0, is continuously flowed through the center channel and a final folding solution is flowed through both the side channels. For the UV experiments, the typical concentration was 500 μM (concentrations as low as 100 μM were used with no change in measured kinetics); for the FRET experiments, the typical concentration was 50 nM. All experiments took place at room temperature.
Fluorescence changes can be observed at various times beyond mixing from ∼4–1500 μs using a confocal instrument described by Lapidus et al. (2007) for UV detection and Hertzog et al. (2004) for FRET detection. In order to eliminate drifts in signal due to defects in the mixing chip or diffusional broadening of the jet, all UV measurements made after mixing are normalized with a background run of the same protein sample mixed into 6 M GdnHCl. Simulations of this chip with COMSOL have shown that the presence of denaturant in the mixing buffer does not change the mixing process once the effect of viscosity is taken into account. Note that while other rapid mixing experiments have used N-actyltryptophan amide (NATA) to normalize their measurements, we have found that NATA exhibits concentration-dependent kinetics that decays on the 50 μs time scale.
Contact quenching measurements
Measurements were conducted as described in reference (Singh et al., 2007). The protein concentration was ∼30 μM.
ACKNOWLEDGMENTS
This work was partially supported by funding from NSF FIBR Grant 0623664. The research of Lisa Lapidus, Ph.D. is supported in part by a Career Award at the Scientific Interface from the Burroughs Wellcome Fund. Work at Lawrence Livermore National Laboratory was performed under the auspices of the U.S. Department of Energy under Contract DE-AC52-07NA27344 with funding from the LDRD program. This work was partially supported by funding from NSF FIBR Grant 0623664 administered by the Center for Biophotonics, an NSF Science and Technology Center, managed by the University of California, Davis, under Cooperative Agreement PHY 0120999. L.J.L., W.J.W., S.A.W., and O.B. designed the experiments. S.A.W., S.J.D., V.R.S., Y.C., M.K., S.Y., and L.J.L. took the data. S.A.W., S.Y., and O.B. designed and fabricated the mixing chips. T.B., M.J., and M.K. mutated, expressed, and labeled the proteins. L.J.L., S.A.W., and W.J.W analyzed the data and wrote the paper.
References
- Berberan-Santos, M N, Bodunov, E N, and Valeur, B (2005). “Mathematical functions for the analysis of luminescence decays with underlying distributions. 1: Kohlrausch decay function (stretched exponential).” Chem. Phys. 10.1016/j.chemphys.2005.04.006 315, 171–182. [DOI] [Google Scholar]
- Bicout, D J, and Szabo, A (2000). “Entropic barriers, transition states, funnels, and exponential protein folding kinetics: a simple model.” Protein Sci. 9, 452–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodunov, E N, Berberan-Santos, M N, and Martinho, J M G (2002). “Electronic energy transfer in polymers labeled at both ends with fluorescent groups.” J. Lumin. 10.1016/S0022-2313(01)00227-7 96, 269–278. [DOI] [Google Scholar]
- Buscaglia, M, Lapidus, L J, Eaton, W A, and Hofrichter, J (2006). “Effects of denaturants on the dynamics of loop formation in polypeptides.” Biophys. J. 10.1529/biophysj.105.071167 91, 276–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capaldi, A P, Shastry, M C R, Kleanthous, C, Roder, H, and Radford, S E (2001). “Ultrarapid mixing experiments reveal that Im7 folds via an on-pathway intermediate.” Nat. Struct. Biol. 10.1038/83074 8, 68–72. [DOI] [PubMed] [Google Scholar]
- Cellmer, T, Henry, E R, Kubelka, J, Hofrichter, J, and Eaton, W A (2007). “Relaxation rate for an ultrafast folding protein is independent of chemical denaturant concentration.” J. Am. Chem. Soc. 129, 14564–14565. [DOI] [PubMed] [Google Scholar]
- Eaton, W A, Munoz, V, Hagen, S J, Jas, G S, Lapidus, L J, Henry, E R, and Hofrichter, J (2000). “Fast kinetics and mechanisms in protein folding.” Appl. Spectrosc. 29, 327–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- See EPAPS Document No. E-HJFOA5-2-011807 for supplemental information. This document can be reached through a direct link in the online article’s HTML reference section or via the EPAPS homepage (http://www.aip.org/pubservs/epaps.html).
- Gruebele, M (2002). “Protein folding: the free energy surface.” Curr. Opin. Struct. Biol. 10.1016/S0959-440X(02)00304-4 12, 161–168. [DOI] [PubMed] [Google Scholar]
- Hertzog, D E, Ivorra, B, Mohammadi, B, Bakajin, O, and Santiago, J G (2006). “Optimization of a microfluidic mixer for studying protein folding kinetics.” Anal. Chem. 10.1021/ac051903j 78, 4299–4306. [DOI] [PubMed] [Google Scholar]
- Hertzog, D E, Michalet, X, Jager, M, Kong, X X, Santiago, J G, Weiss, S, and Bakajin, O (2004). “Femtomole mixer for microsecond kinetic studies of protein folding.” Anal. Chem. 10.1021/ac048661s 76, 7169–7178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jager, M, Michalet, X, and Weiss, S (2005). “Protein-protein interactions as a tool for site-specific labeling of proteins.” Protein Sci. 14, 2059–2068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight, J B, Vishwanath, A, Brody, J P, and Austin, R H (1998). “Hydrodynamic focusing on a silicon chip: Mixing nanoliters in microseconds.” Phys. Rev. Lett. 10.1103/PhysRevLett.80.3863 80, 3863–3866. [DOI] [Google Scholar]
- Kubelka, J, Eaton, W A, and Hofrichter, J (2003). “Experimental tests of villin subdomain folding simulations.” J. Mol. Biol. 10.1016/S0022-2836(03)00519-9 329, 625–630. [DOI] [PubMed] [Google Scholar]
- Lapidus, L J, Eaton, W A, and Hofrichter, J (2001). “Dynamics of intramolecular contact formation in polypeptides: Distance dependence of quenching rates in a room-temperature glass.” Phys. Rev. Lett. 10.1103/PhysRevLett.87.258101 87, 258101-1–258101-4. [DOI] [PubMed] [Google Scholar]
- Lapidus, L J, Yao, S, McGarrity, K S, Hertzog, D E, Tubman, E, and Bakajin, O (2007). “Protein hydrophobic collapse and early folding steps observed in a microfluidic mixer.” Biophys. J. 93, 218–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma, H, and Gruebele, M (2005). “Kinetics are probe-dependent during downhill folding of an engineered lambda6–85 protein.” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0409270102 102, 2283–2287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naganathan, A N, Doshi, U, and Munoz, V (2007). “Protein folding kinetics: Barrier effects in chemical and thermal denaturation experiments.” J. Am. Chem. Soc. 10.1021/ja0689740 129, 5673–5682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nettels, D, Gopich, I V, Hoffmann, A, and Schuler, B (2007). “Ultrafast dynamics of protein collapse from single-molecule photon statistics.” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0611093104 104, 2655–2660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onuchic, J N, LutheySchulten, Z, and Wolynes, P G (1997). “Theory of protein folding: the energy landscape perspective.” Annu. Rev. Phys. Chem. 10.1146/annurev.physchem.48.1.545 48, 545–600. [DOI] [PubMed] [Google Scholar]
- Park, S H, Shastry, M C R, and Roder, H (1999). “Folding dynamics of the B1 domain of protein G explored by ultrarapid mixing.” Nat. Struct. Biol. 10.1038/13311 6, 943–947. [DOI] [PubMed] [Google Scholar]
- Peterson, K A, and Fayer, M D (1986). “Electronic excitation transport on isolated, flexible polymer-chains in the amorphous solid-state randomly tagged or end tagged with chromophores.” J. Chem. Phys. 10.1063/1.451745 85, 4702–4711. [DOI] [Google Scholar]
- Plaxco, K W, Simons, K T, and Baker, D (1998). “Contact order, transition state placement and the refolding rates of single domain proteins.” J. Mol. Biol. 10.1006/jmbi.1998.1645 277, 985–994. [DOI] [PubMed] [Google Scholar]
- Plaxco, K W, Simons, K T, Ruczinski, I, and Baker, D (2000). “Topology, stability, sequence and length: Defining the determinants of two-state protein folding kinetics.” Biochemistry 10.1021/bi000200n 39, 11177–11183. [DOI] [PubMed] [Google Scholar]
- Plaxco, K, Millett, I, Segel, D, Doniach, S, and Baker, D (1999). “Chain collapse can occur concomitantly with the rate-limiting step in protein folding.” Nat. Struct. Biol. 10.1038/9329 6, 554–556. [DOI] [PubMed] [Google Scholar]
- Qiu, L L, Pabit, S A, Roitberg, A E, and Hagen, S J (2002). “Smaller and faster: the 20-residue Trp-cage protein folds in 4 mu s.” J. Am. Chem. Soc. 10.1021/ja0279141 124, 12952–12953. [DOI] [PubMed] [Google Scholar]
- Ratner, V, Kahana, E, Eichler, M, and Haas, E (2002). “A general strategy for site-specific double labeling of globular proteins for kinetic FRET studies.” Bioconjugate Chem. 13, 1163–1170. [DOI] [PubMed] [Google Scholar]
- Sadqi, M, Lapidus, L J, and Munoz, V (2003). “How fast is protein hydrophobic collapse?” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.2033863100 100, 12117–12122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scalley, M, and Baker, D (1997). “Protein folding kinetics exhibit an Arrhenius temperature dependence when corrected for the temperature dependence of protein stability.” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.94.20.10636 94, 10636–10640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scalley, M L, Yi, Q, Gu, H D, McCormack, A, Yates, J R, and Baker, D (1997). “Kinetics of folding of the IgG binding domain of peptostreptoccocal protein L.” Biochemistry 36, 3373–3382. [DOI] [PubMed] [Google Scholar]
- Shastry, M C R, and Roder, H (1998). “Evidence for barrier-limited protein folding kinetics on the microsecond time scale.” Nat. Struct. Biol. 10.1038/nsb0598-385 5, 385–392. [DOI] [PubMed] [Google Scholar]
- Singh, V R, Kopka, M, Chen, Y, Wedemeyer, W J, and Lapidus, L J (2007). “Dynamic similarity of the unfolded states of proteins L and G.” Biochemistry 46, 10046–10054. [DOI] [PubMed] [Google Scholar]
- Sinha, K K, and Udgaonkar, J B (2008). “Barrierless evolution of structure during the submillisecond refolding reaction of a small protein.” Proc. Natl. Acad. Sci. U.S.A. 105, 7998–8003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teilum, K, Maki, K, Kragelund, B B, Poulsen, F M, and Roder, H (2002). “Early kinetic intermediate in the folding of acyl-CoA binding protein detected by fluorescence labeling and ultrarapid mixing.” Proc. Natl. Acad. Sci. U.S.A. 99, 9807–9812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, W Y, and Gruebele, M (2003). “Folding at the speed limit.” Nature (London) 10.1038/nature01609 423, 193–197. [DOI] [PubMed] [Google Scholar]
- Yang, W Y, and Gruebele, M (2004). “Detection-dependent kinetics as a probe of folding landscape microstructure.” J. Am. Chem. Soc. 10.1021/ja0493751 126, 7758–7759. [DOI] [PubMed] [Google Scholar]
- Yao, S, and Bakajin, O (2007). “Improvements in mixing time and mixing uniformity in devices designed for studies of protein folding kinetics.” Anal. Chem. 10.1021/ac070528n 79, 5753–5759. [DOI] [PubMed] [Google Scholar]
- Yi, Q, and Baker, D (1996). “Direct evidence for a two-state protein unfolding transition from hydrogen-deuterium exchange, mass spectrometry, and NMR.” Protein Sci. 5, 1060–1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi, Q, Scalley-Kim, M L, Simons, K T, Gladwin, S T, and Baker, D (1997). “Characterization of the free energy spectrum of peptostreptococcal protein L.” Folding Des. 2, 271–280. [DOI] [PubMed] [Google Scholar]
- Zwanzig, R (1988). “Diffusion in a rough potential.” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.85.7.2029 85, 2029–2030. [DOI] [PMC free article] [PubMed] [Google Scholar]