A comparative study of biomechanical simulators in deformable registration of brain tumor images

Abstract

Simulating the brain tissue deformation caused by tumor growth has been found to aid the deformable registration of brain tumor images. In this paper we evaluate the impact that different biomechanical simulators have on the accuracy of deformable registration. We use two alternative frameworks for biomechanical simulations of mass effect in 3D MR brain images. The first one is based on a finite element model of nonlinear elasticity and unstructured meshes using the commercial software package ABAQUS. The second one employs incremental linear elasticity and regular grids in a fictitious domain method. In practice, biomechanical simulations via the second approach may be at least ten times faster. Landmarks error and visual examination of the co-registered images indicate that the two alternative frameworks for biomechanical simulations lead to comparable results of deformable registration. Thus, the computationally less expensive biomechanical simulator offers a practical alternative for registration purposes.

I. Introduction

Statistical atlases of brain function and structure have been used extensively in the brain imaging literature during the past decade [1–3] as means for integrating diverse information about anatomical and functional variability into a canonical coordinate space, often called stereotactic space, thereby better understanding, as well as diagnosing, brain diseases such as early stages of Alzheimer’s disease, schizophrenia, and others. In the case of brain tumor patients, such atlases can potentially assist in the surgical and radiotherapeutic treatment planning. However, most available brain image registration methods come short when severe deformities, such as mass effect caused by growing tumors, are present.

In order to improve the registration process, it is desirable to first construct a brain atlas that has tumor and mass effect similar to the one of a patient at study. Subsequent deformable registration is then more likely to accurately match the atlas with the patient’s images, since it has to solve a problem involving two brains that are relatively more similar, compared to matching a normal atlas with a highly deformed brain [4–7].

The purpose of this paper is not to present a new methodology for modeling brain tumor mass effect or for deformable registration of brain images. The goal is rather to compare two different modeling frameworks for mass effect, from the perspective of the registration accuracy ultimately achieved by the existing registration algorithms. The tumor growth modeling frameworks we use for registration purposes are pressure-based biomechanical [8–11].

The first framework [8, 9] models the brain tissue as a nonlinear material and approximates the expansive force exerted by the growing tumor by an outward pressure acting on the tumor boundary. This model is solved to estimate brain tissue displacements using a nonlinear finite element (FE) formulation on unstructured meshes in ABAQUS. We shall refer to this simulation framework as the Nonlinear Lagrangian (NL). Its potential advantages are: 1) more complex constitutive laws for the brain tissue/ventricles modeled by ABAQUS; 2) higher accuracy close to boundaries of interest (e.g. tumor boundary), since the underlying mesh is conformal to the anatomy. The main draw-backs are that: 1) unstructured meshes deteriorate significantly in the presence of large deformations induced by a growing brain tumor, thus frequent remeshing may be needed [8, 9]; 2) the method is computationally slow, since construction of efficient solvers for the resulting algebraic system of equations is difficult.

The second approach tested herein [10, 11] was proposed to bypass these inherent difficulties associated with the NL simulator. An incremental pressure, linear elasticity, model was developed in an Eulerian formulation, with a level-set based method for advancing fronts, and solved using regular grids in a fictitious domain method. This approach circumvents the need for mesh generation and remeshing. Thus, large deformations can be captured effortlessly and efficient solvers can be employed. This results in a fast, robust and flexible (but potentially less accurate [10, 11]) simulation framework that we shall refer to as Piecewise Linear Eulerian (PLE).

Since brain tumor images often exhibit large tumors, the biomechanical simulator needs to be robust to large deformations and also computationally efficient, particularly for registration purposes. It is therefore important to assess, if and how the differences between the two distinct biomechanical simulators affect the subsequent registration results, and thereby to determine whether potential gains in accuracy warrant the significant additional computational load imposed by the NL framework. In this paper, we compare the performance of the NL and the PLE biomechanical simulators in registering brain tumor images with a normal atlas using a deformable registration method [5, 12] based on the HAMMER algorithm [13]. For comparison purposes, we register the 3D MR images of four brain tumor patients using both biomechanical simulators and assess the registration accuracy based on landmark points manually placed by an expert neuroradiologist, as well as by visual inspection of the co-registered images.

II. Methods

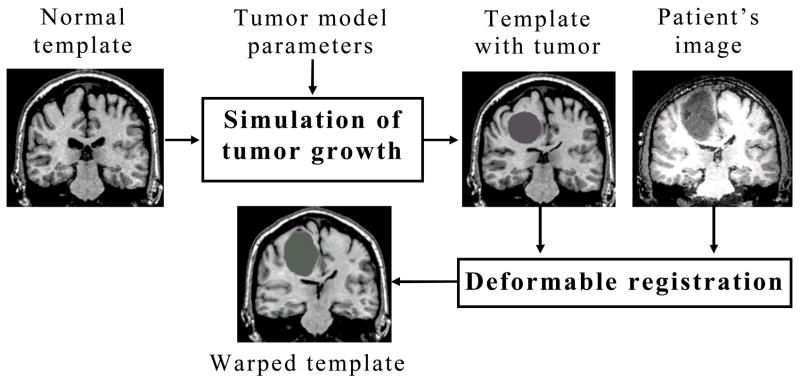
Fig. 1 illustrates the process for co-registering a normal (tumor-free) template and a tumor patient’s image. This process involves (i) insertion of a small tumor seed in the template and simulation of tumor growth, and (ii) registration of the template that is deformed by tumor growth with the patient’s image. The biomechanical simulation is initialized with a 3D segmented image of the normal brain atlas serving as template. The amount of tissue death is simulated by replacing a part of the brain parenchyma with a small tumor mass, whose location and size are parameters of the model. The initial tumor seed is expanded by the biomechanical simulators until the size of the simulated tumor in the atlas becomes close to the size of the tumor in the patient’s image. Biomechanical simulations of tumor growth are performed independently via the NL (Nonlinear Lagrangian) and PLE (Piecewise Linear Eulerian) frameworks, as described in the following.

Fig. 1.

A flowchart summarizing the basic steps for registration of a normal template (brain atlas) with a tumor patient’s image.

The NL biomechanical simulator is based on a nonlinear elastic FE formulation on tetrahedral meshes in ABAQUS (Version 6.4, 2003) [14]. A tetrahedral mesh is generated that conforms to the tumor boundary, ventricles and brain surface, respectively. The brain parenchyma is regarded as a hyperelastic homogeneous material; the ventricles are assumed void. The corresponding material properties are as in [4, 15]. The strength of the bulk tumor mass effect and the final tumor size are regulated by the pressure parameter. The imposed boundary conditions allow sliding over the brain surface except for the intersecting points with the falx, which is assumed pinned; traction is imposed on the tumor boundary, corresponding to a prescribed pressure exerted by the growing tumor onto the surrounding brain parenchyma. More details can be found in [9, 15].

In the PLE simulator, the brain is approximated as an inhomogeneous isotropic linear elastic medium, with different material properties in the white matter, gray matter and ventricles. In this framework, ventricles are treated as a soft compressible elastic material [10, 11]. For simplicity, zero displacements are imposed at the skull. The target domain (brain) is embedded in a larger computational cubic domain (box), with material properties and distributed forces chosen so that the imposed boundary conditions on the true boundary (here consisting of the brain surface and the tumor boundary, respectively) are approximated. An Eulerian formulation is employed to capture large deformations, with a level-set based approach for evolving fronts. The problem is solved using a regular grid discretization with a fast matrix-free multigrid solver for the resulting algebraic system of equations. The methodology is described in detail in [10, 11]. For the simulations in this paper, the same material properties as in [10, 11] are used.

For comparison purposes, we used the same tumor model parameters (tumor seed size and location) in both simulators. These parameter values have been estimated in [12] for the patient images used in this study via optimization of a criterion reflecting elastic stretching energy and image similarity upon registration. Specifically, the optimality criterion is defined as the combination of three normalized measures: (i) the residual volume of overlap of the co-registered atlas and patient’s images, (ii) the distance of attribute (feature) vectors which are defined similarly as in [5], and (iii) the Laplacian of the deformation field defined to reflect smoothness properties.

After simulating tumor growth in the atlas, a deformable registration method is applied to register the tumor-bearing images. The registration method is built upon the idea of the HAMMER registration algorithm [13] and follows a deformation strategy that is robust to confounded factors caused by the presence of a tumor, as described in [5].

III. Results

The registration accuracy was assessed using Magnetic Resonance (MR) images of brain tumor patients. Four T1-weighted brain datasets were selected including tumors of different types, grades and sizes. Specifically, for patient 1 to 4, the brain tumors were diagnosed as oligodendroglioma (WHO grade II/IV), anaplastic oligoastocytoma (WHO grade III/IV), anaplastic oligodendroglioma (WHO grade III/IV) and glioblastoma (WHO grade IV/IV), and reached a size of 26.3, 18.5, 80.7 and 36.9 cc, respectively. All the images were segmented and registered with a normal brain image serving as template, which consisted of 198 axial scans with image dimensions 256×256 voxels and voxel size 1×1×1 mm³.

A. Quantitative assessment based on landmarks

In order to quantitatively assess the registration accuracy, an expert neuroradiologist manually placed landmark points in each patient’s image in anatomical regions that were displaced by the tumor (13–14 landmarks) or were not displaced (7–10 landmarks). Similarly, the corresponding landmarks were manually identified in the atlas. This set of landmarks is referred to as the first set of landmarks. In order to ensure consistency in the identification of landmarks, the reverse procedure was followed a few weeks later. The same expert first looked at the selected landmarks locations in the atlas, and then identified the corresponding points in the patient’s images. This set of landmarks is labeled as the second set of landmarks. The point coordinates of manual landmarks defined in the patient’s images were mapped to the atlas space through the resulting deformation maps obtained via each of the two biomechanical simulations and registration. Then, the mapped landmarks were compared with the corresponding manually placed landmarks in the atlas. The minimum (min), average (avg), maximum (max), and standard deviation (stdev) of the landmarks error for the regions displaced or not displaced by the tumor are shown in Table I and Table II, respectively. For each patient’s image, the first row in the tables indicates the intra-rater variability in placing the two sets of landmarks. The other two rows show left and right the error statistics for each of the first and second set of landmarks, respectively.

TABLE I.

Intra-rater variability and Registration error (in mm) of the 1^st (left) and 2^nd (right) set of landmarks in areas displaced by the tumor using NL and PLE simulators, respectively.

		min	Avg	max	stdev
patient 1	Variability	1.4	7.6	16.9	4.3
	NL	1.9/3.1	11.3/10.2	26.6/31.9	7.7/7.7
	PLE	2.4/3.3	11.0/10.0	23.9/30.5	7.2/7.2
patient 2	Variability	1.0	4.8	10.0	2.9
	NL	2.5/2.3	6.0/7.1	10.2/16.7	2.4/4.2
	PLE	1.6/2.3	6.2/7.2	11.4/17.3	2.8/4.3
patient 3	Variability	1.0	6.9	17.7	5.5
	NL	1.9/1.1	8.6/8.7	16.6/17.5	4.3/5.3
	PLE	2.9/2.4	9.2/9.5	16.0/16.5	4.0/4.7
patient 4	Variability	1.4	7.1	16.9	5.5
	NL	0.6/2.9	6.0/7.2	18.9/15.1	4.4/3.5
	PLE	2.7/3.8	7.1/7.8	17.9/16.0	3.8/3.9

TABLE II.

Intra-rater variability and Registration error (in mm) of the 1^st (left) and 2^nd (right) set of landmarks in areas not displaced by the tumor using NL and PLE simulators, respectively.

		min	avg	max	stdev
patient 1	Variability	1.4	3.1	7.7	2.7
	NL	2.8/3.3	8.8/7.2	16.8/15.4	4.9/3.9
	PLE	2.7/3.2	8.8/7.2	16.9/15.5	4.9/4.0
patient 2	Variability	0.0	2.2	7.0	2.5
	NL	1.0/1.2	5.1/4.5	14.7/13.7	5.0/4.5
	PLE	0.9/1.3	5.2/4.5	15.1/13.9	5.2/4.5
patient 3	Variability	0.0	2.6	5.6	2.1
	NL	0.4/1.1	4.0/4.1	12.2/8.7	3.6/2.5
	PLE	0.4/1.0	3.9/4.1	12.7/9.1	3.8/2.6
patient 4	Variability	1.0	3.8	9.8	3.1
	NL	0.6/0.7	3.2/4.6	6.3/9.0	2.1/3.0
	PLE	0.5/1.0	3.2/4.5	7.3/8.7	2.3/3.1

The results summarized in Tables I and II indicate that the registration is not significantly affected if a PLE simulation of tumor growth is performed, instead of a NL simulation. Thus, the solution differences are minor in comparison to the inter-subject variation and the applied registration method can compensate for them. In these tests, our current version of the PLE simulator was about 10 times faster than the NL simulator: an average of around 3 minutes¹ compared to an average of around 30 minutes. This is an important aspect to be taken into account for the purpose of achieving fast integration with image registration.

In order to assess the importance of incorporating a biomechanical model of mass effect into the registration process, the registration was also performed immediately after placing the tumor seed (without modeling the mass effect). As expected, the landmark errors increased, with the maximum increase exhibited in the case of the patient with the largest tumor volume (patient 3). For this case, the average and maximum errors (averaged between the first and second set of landmarks) increased to 11.1 and 20.7 mm, as compared to 8.7 and 17.0 mm for the NL simulator and 9.4 and 16.2 mm for the PLE simulator, respectively.

B. Visual assessment

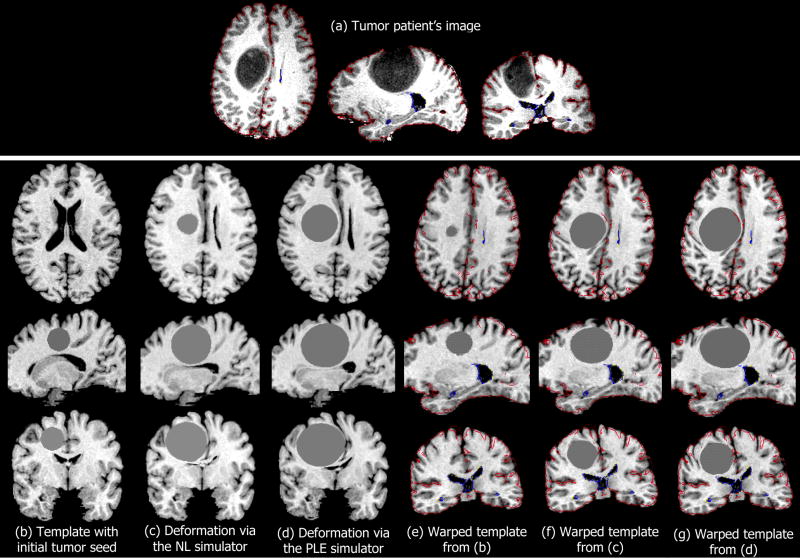
Complementary to calculating landmark errors, the registration accuracy of the proposed framework was also visually assessed for all four patients. As an illustrative example, images of the patient with the largest tumor (patient 3) are displayed in Fig.2. The tumor mass-effect simulated on the template via the NL and PLE simulators is shown in Fig. 2c and 2d, respectively. As expected, the two biomechanical simulators produce somewhat different results. On the one hand, the NL and PLE simulators employ different material constitutive laws and boundary conditions. On the other hand, the final tumor volume reached by each simulator might be slightly different².

Fig. 2.

Registration example of a normal template to a brain tumor image. The brain tumor image, which corresponds to patient 3 from Tables I and II is shown in (a). The template with the initial tumor seed is shown in (b). The template with simulated tumor using (c) the NL simulator and (d) the PLE simulator is registered as shown in (f) and (g) respectively. The registration of (b) to (a) without the application of any biomechanical model of mass effect is shown in (e). The colored curves in (e–g) represent the edges of the patient’s image, overlaid on the warped template.

The warping of the corresponding template images with simulated tumor growth to the patient’s image is shown in Fig. 2f and 2g, respectively. Edges on the cortical and ventricular boundary were extracted from the patient’s image and superimposed into the warped template with different colors. The visualization of the results shows that, although the tumor growth simulations did not produce identical images, after registration with the patient’s image, the tumor-bearing templates become highly similar (Fig. 2f, 2g). Also, the visualization of the co-registered images without the application of any biomechanical model (shown in Fig. 2e) demonstrates that the mass effect has not been captured correctly by the registration method alone and therefore the accuracy close to the tumor is poor, e.g. there is no midline shift and the cingulate sulcus is not suppressed by the tumor.

IV. Discussion and Conclusions

The need to integrate diverse information about anatomical and functional variability into the patient data space, for surgery and radiotherapy treatment planning, motivates the development of a method that registers a brain tumor image to a normal template (stereotactic atlas). However, most of the customary registration methods in neuroimaging fail around the tumor region due to large deformations and lack of clear definition of anatomical detail in the brain tumor images. Simulating the brain tissue deformation caused by tumor growth has been shown to aid the deformable registration of normal brains with brain tumor images. In this study, we use a pipeline consisting of two major components: simulation of tumor growth and image registration. We compare two alternative elasticity-based frameworks for biomechanical simulations of brain tumor mass effect in 3D MR images: Nonlinear Lagrangian (NL) and Piecewise Linear Eulerian (PLE).

A direct comparison between the NL and the PLE approaches is difficult, since both the modeling approaches and the numerical solution procedures are different. Regarding accuracy, the two frameworks have been separately assessed in [9] and [10] for NL and PLE respectively³, based on landmarks manually placed in some serial scans of a single brain tumor subject, thus avoiding the need of inter-subject registration. The reported landmark errors indicate that the NL framework can be more accurate. However, in the absence of sufficient data pertinent to a more systematic study, it is difficult to ascertain clearly how much is due to the model itself, i.e. material constitutive law (nonlinear vs. linear) and boundary conditions, or the underlying numerics, i.e. structured vs. unstructured meshes. Regarding performance, the NL approach is computationally slower and can cause significant mesh distortions and simulation failure in the case of large tumors, as those frequently appearing in brain tumor images.

Motivated by the need for a robust and computationally efficient simulator to be applied in registration of brain tumor images, in this study we compare the two alternative frameworks in respect to the final accuracy achieved. Landmark errors and visual examination of the co-registered images indicate that the registration accuracy is not significantly affected by the choice of the PLE simulator over the more complex NL simulator. The PLE biomechanical simulations are in average about ten times faster than the corresponding NL simulations, which is an important gain towards fast image registration.

Finally, it is important to note that the registration accuracy for images with tumor mass effect is increased when any of the two biomechanical models is used for simulating the brain tissue deformation prior to registration. Brain tumor images with small deformations caused by the tumor show only modest improvement (~5%) in the landmarks error, while brain tumor images exhibiting significant mass effect show significant improvement (~25%) upon using a biomechanical model in the simulation pipeline. This is not surprising, since in the cases with small mass effect, the initial tumor seed is a rough approximation of the final tumor. It must be additionally noted, that reliable landmarks can seldom be placed in areas very close to the tumor, because structure is generally not easily identifiable due to confounding effects and large deformations. Particularly in these areas, where registration accuracy is difficult to assess, physics-driven biomechanical simulators are important for simulating realistic deformation fields.