Insights into the Organization of Biochemical Regulatory Networks Using Graph Theory Analyses

Abstract

Graph theory has been a valuable mathematical modeling tool to gain insights into the topological organization of biochemical networks. There are two types of insights that may be obtained by graph theory analyses. The first provides an overview of the global organization of biochemical networks; the second uses prior knowledge to place results from multivariate experiments, such as microarray data sets, in the context of known pathways and networks to infer regulation. Using graph analyses, biochemical networks are found to be scale-free and small-world, indicating that these networks contain hubs, which are proteins that interact with many other molecules. These hubs may interact with many different types of proteins at the same time and location or at different times and locations, resulting in diverse biological responses. Groups of components in networks are organized in recurring patterns termed network motifs such as feedback and feed-forward loops. Graph analysis revealed that negative feedback loops are less common and are present mostly in proximity to the membrane, whereas positive feedback loops are highly nested in an architecture that promotes dynamical stability. Cell signaling networks have multiple pathways from some input receptors and few from others. Such topology is reminiscent of a classification system. Signaling networks display a bow-tie structure indicative of funneling information from extracellular signals and then dispatching information from a few specific central intracellular signaling nexuses. These insights show that graph theory is a valuable tool for gaining an understanding of global regulatory features of biochemical networks.

Progress in biochemistry over the past 40 years has allowed us to develop an impressive parts list of cellular components and their interactions. Such interactions give rise to functional subcellular machines such as metabolic circuits, signaling networks, and cytoskeletal structures. Each of these systems contains several hundreds to thousands of different types of components. For example, a recent comprehensive study of mitochondria in the mouse identified over 1000 different types of proteins (1). Understanding the global topological organization of such complex systems is a first step toward a holistic yet detailed functional map of the entire cell. Graph theory, a subfield of mathematics, has been a valuable tool in the past decade to gain insights into the global organization of regulatory biochemical networks as well as to develop more informed hypotheses for new experiments.

Euler's famous publication from 1736 on the Seven Bridges of Königsberg problem (2) initiated graph theory. Over 225 years later, in the late 1950s, a relevant historical development in graph theory was the analysis of random networks by Erdös and Rényi (ER graphs). In the late 1990s, it was recognized that real networks are different from ER graphs. Real-world complex systems abstracted to networks across disciplines, including biochemical networks, have a common global architecture termed small-world (3) and scale-free (4). Small-world indicates a relatively short distance from any node to any other node and a relatively high level of clustering. Clustering means that groups of nodes have many interactions with one another. Scale-free denotes a connectivity distribution that fits a power law. These two seminal observations initiated a new approach to modeling systems of biochemical reactions in a cell. Instead of viewing reactions in pathways as substrates acted upon by enzymes to produce products or as mass-action binding reactions, biochemical interactions in biochemical networks can be abstracted to nodes and links forming a graph (5). Graphs are mathematical structures that have been successfully applied to model complex systems from computer science, electrical engineering, physics, and social sciences and in recent years to represent biological networks.

There are two fundamental approaches in applying graph theory to analyze biochemical regulatory networks. The first is an attempt to understand the global organization of these networks. For this, properties and attributes computed for individual nodes, links, and/or groups of nodes and links are averaged, or the distribution of such properties is analyzed and compared with the distributions found in shuffled networks. The second approach is more practical. By using prior knowledge about biomolecules and their interactions, it is possible to place results from multivariate experiments that produce lists of genes, shown to be altered under different experimental conditions, in the context of known pathways and networks. Here, I describe a few applications and insights from graph theory analyses applied to study biochemical networks in combination with an introduction to concepts and definitions from graph theory.

Nodes and Links

Graphs are mathematical structures made of a few related sets. The first set represents entities. When modeling biochemical networks, these entities typically represent genes, proteins, or other type of biomolecules. These entities are formally called vertices and less formally nodes or components. The second set in a graph describes the relations between the entities. The elements of this set are formally termed edges for undirected graphs and arcs for directed graphs. Directed graphs, termed digraphs, can be used to represent systems in which the causal relationship between vertices is known. For example, if A is upstream of B, then there is an arc (arrow) pointing from A to B. Other less formal names to describe edges and arcs are links or interactions. In biochemical regulatory networks, these can be direct physical interactions between proteins, transcription factors binding to promoter sites, other indirect gene regulation effects, or enzymatic reactions in which enzymes are linked to their substrates. Throughout the text, the terms graph/network, vertices/nodes/components, and edges/links/interactions are used interchangeably but mostly have the same meaning.

There are different types of graphs used to represent different types of biochemical networks (6). For example, mixed graphs are graphs that are both directed and undirected. These graphs have two or more sets of relations. Typically, edges are separated from arcs. Cell signaling pathways are commonly represented using mixed graphs in which arcs represent activation or inhibition relations, whereas edges represent physical protein-protein interactions without a clear-cut directionality such as binding to anchors and scaffolds (7). Other sets in cell signaling graphs can represent other properties of edges such as interaction weights. Weights of arcs can be used to represent the kinetics of biochemical reactions (8).

Having two types of arcs, such as activation versus inhibition relations, is an example of edge coloring. Coloring is the assignment of labels to vertices or edges with some defined constraints. For example, vertex coloring can be used to distinguish transcription factors from other proteins in a protein-protein interaction graph. The Gene Ontology Consortium can be considered a graph-coloring undertaking for labeling genes and proteins based on their function, location in the cell, and involvement in biological processes (9). The Gene Ontology data set itself is stored in a hierarchical tree graph data structure in which different levels represent the detailed specific description of terms recounting properties of genes. The Gene Ontology hierarchical tree is an example of a specialized type of graph in which specific rules are used to connect vertices.

Types of Graphs

Another example of a specialized graph in which rules are used to restrict possible connections between vertices is a bipartite graph. These graphs have two sets of vertices where edges can connect only nodes in different sets, not nodes within a set. Bipartite networks are used, for example, to represent metabolic networks separating enzymes from their substrates and products, disease gene networks connecting diseases with disease genes (10), and drug networks connecting drugs with their known biomolecular targets (11, 12) or to integrate different “omics” data sets (13). Another type of graph, the planar graph, can be drawn on a plane with no edge crossings. Planar graphs are important for visualization. Acyclic graphs are graphs with no cycles. Bayesian networks reconstructed from time-series or perturbation high-throughput microarrays (14) or proteomics studies (15) are typically represented as acyclic graphs. An acyclic graph is also called a forest because it comprises a collection (union) of trees. A tree is a graph in which any two vertices are connected by only one possible path. A graph can be partitioned or cut into subgraphs or subnetworks based on different rules. Subnetworks of biochemical networks are often used to represent pathways, modules, or protein complexes. One example of a subgraph is a spanning tree. A spanning tree is a subgraph tree that connects all nodes in a network without using all links. A minimum spanning tree is a spanning tree that is formed with a minimum cost, where the “cost” is typically the total number of edges. Steiner trees are similar to minimum spanning trees but extra intermediate vertices and edges may be used to reduce the overall length/cost of the minimum spanning tree. Steiner trees can be used to connect lists of “seed” genes that were found to be altered under different experimental conditions using known protein-protein, cell signaling, and gene regulatory networks (16).

Most biochemical networks are not fully characterized. In many of them, there are interactions and components that are not connected with the rest of the network. Such networks typically have a giant connected component. It is important to consider that graphs can be alternately represented as a symmetric adjacency matrix where vertices are represented as identical row and column labels, and the matrix contents consist of the presence or absence of edges (0s and 1s) and/or the strength and/or direction between interacting biochemical entities. The matrix formulation of graphs allows manipulation and analysis using powerful tools from linear algebra.

Properties of Nodes

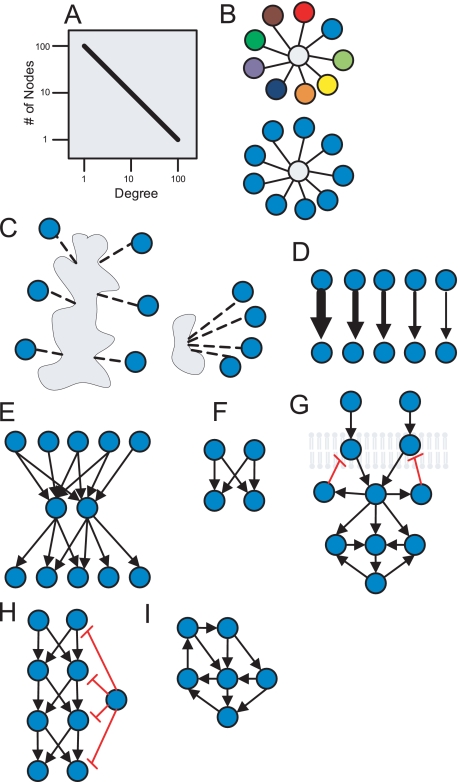
Vertices and edges in networks can have an assortment of attributes or properties. Two vertices are considered adjacent or connected if there is an edge that links them. Such vertices are also called neighbors. An important attribute/property of vertices is their vertex degree (also called valence), which is commonly denoted with k. This means that k is also the number of neighbors a vertex has. In digraphs, it is important to distinguish between in-degree and out-degree. Different types of biochemical networks across different species were found to have a connectivity degree distribution that fits a power-law function (4, 17, 18). This means that most nodes have few neighbors but that a substantial number of nodes have high degree (Fig. 1A). The power-law connectivity distribution observation can be explained by the fact the proteins in the cell are heterogeneous, serving many and different functions. Power-law distributions are commonly observed in highly heterogeneous complex systems. Vertices with high degree are informally called hubs. Analysis of protein-protein interaction networks demonstrated that hubs can be classified into “party” hubs and “date” hubs (Fig. 1B) (19). Party hubs are proteins that interact with their neighbors in the same place at the same time, whereas date hubs are proteins that interact at different times in different places within the cell. Another classification of hubs showed that hubs can be divided into single-domain or multidomain hubs (20) (Fig. 1C). Some examples of single-domain date hubs are protein kinases A and C and the phosphatase PP2A, which have many known substrates. CASK is an example of a party hub with multiple domains. Assortative mixing is when the probability for interactions between nodes is biased due to nodes' properties. For example, assortative mixing by valence is when hubs are frequently connected to one another (21). Biochemical networks in general were found not to display assortative mixing by valence as compared with other networks, for example, brain networks constructed from functional magnetic resonance images (22). On the other hand, assortative mixing by function, location, or biological process is obviously highly pervasive in regulatory biochemical networks.

FIGURE 1.

Schematics representing properties of cell signaling networks identified using the graph theory. A, the connectivity distribution of networks fits a power law (straight line on a log-log plot). B, networks consist of party and date hubs, where multiple colors represent different locations and times. C, hubs are either multisite or single-site. D, there are many pathways from some receptors to some effectors and few from most receptors to most effectors. E, signals from many receptors are converging into few cytosolic components and then fanning out to regulate many transcription factors in a “bow-tie” structure. F, the bifan motif is shown. G, negative feedback loops are more often observed in loops that include receptors; positive feedback loops are more common a few steps downstream from receptors. H, feed-forward loops are mostly coherent (positive) where negative and less regulated outgoing hubs are used to shut off signals. I, positive feedback loops are more abundant than negative feedback loops and are highly nested.

Paths in Biochemical Networks

A path in a graph represents a sequence of alternating neighboring nodes and links with no repeating nodes. Some of graph theory's most famed algorithms are those developed by Dijkstra (23) and Floyd (24) to find the shortest path (geodesic path) between two vertices in a network. Finding the shortest path between a cell-surface receptor and downstream transcription factors in a cell signaling network can be used to identify important new signaling pathways. Such an approach was useful to hypothesize potential signaling mechanisms in Neuro2A cells downstream of CB1R receptors. Cells were stimulated with a CB1R agonist, and assessment of activity for hundreds of canonical transcription factors was performed. It was found that after 20 min, CB1R activation modulates the activity of 23 transcription factors (25). Using known cell signaling and protein-protein interactions extracted from published experimental studies, new biological roles for pathways and co-regulators were identified. In another study, a global analysis of paths from receptors to effectors in a literature-based mammalian cell signaling network showed that from some receptors, e.g. the N-methyl-d-aspartate receptor, there are many paths to effectors, e.g. the transcription factor cAMP-responsive element-binding protein (CREB), whereas from other receptors, there are only a few (Fig. 1D) (26). This topological feature can be due to biased research (most data from popular proteins and pathways) but can also indicate a design that is commonly observed in learning classifier systems implemented in computer programs.

The topology of signaling networks also displays a bow-tie structure, in which signals from many receptors converge on the same intermediate components and then are directed to regulate different transcription factor effectors (Fig. 1E). This type of organization is common for Toll-like receptors sharing adaptor proteins such as MyD88 (27), G protein-coupled receptors sharing Gα and Gβγ (28), and growth factor receptors sharing adaptor proteins such as SOS1 and GRB2. The shortest path algorithm can be used to find automatically and display previously characterized interactions that “connect” genes and proteins (29) or to compute global network properties such as characteristic path length (3) or network diameter. Network diameter is simply the longest of the shortest paths among all possible shortest paths between all pairs of nodes in a network. The characteristic path length is the average shortest path across all possible pairs of nodes.

Network Motifs

Biochemical networks contain many three-node cliques. A clique is a complete subgraph in which all possible links between a subset of nodes are operational. Completing “defective cliques” was used to predict not yet observed interactions using the known protein-protein interactions of a yeast network (30). Small cliques in biochemical networks are only one kind of a possible set of small biochemical circuits. The different kinds of small biochemical circuits are collectively termed network motifs. More precisely, network motifs are subgraphs that are over-represented in real networks relative to the same subgraphs in shuffled networks (31). Shuffled networks are networks in which the edges of real networks are systematically randomized while keeping intact some general properties of the original topology such as the connectivity degree (32).

Biochemical networks such as signal transduction networks and gene regulatory networks show similar patterns of network motifs. For example, the bifan motif (33, 34) is made of two upstream regulators both regulating the same two downstream effectors (Fig. 1F). This dual regulation structure was identified statistically as the most over-represented network motif in gene regulatory networks of yeast (31) and Escherichia coli (31, 35) as well as in a mammalian neuronal cell signaling network (7). One example of a bifan motif in cell signaling networks is the regulation of transcription factors ATF2 and Elk by the kinases JNK (c-Jun N-terminal kinase) and p38 (33). The abundance of bifans is most likely due to a large number of isoforms generated through gene duplication-divergence evolution. The bifan motif and other motifs such as feedback and feed-forward loops were found to act as noise filters (33, 36, 37). Two types of network motifs, namely feedback and feed-forward loops, are very important for characterizing the dynamics of biochemical networks (38, 39). Graph analysis of a large cell signaling network suggested that negative feedback loops are more prevalent than positive feedback loops near the cell surface (7), a design that could be helpful for dampening noise while amplifying persistent extracellular signals (Fig. 1G).

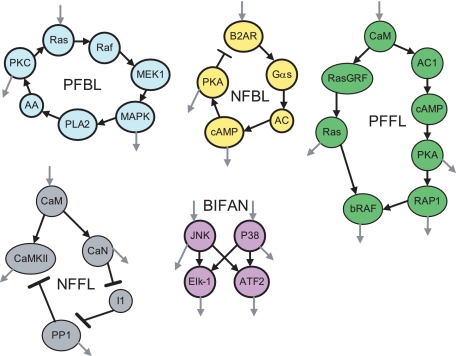
A paucity of negative feedback and feed-forward loops in yeast, E. coli, and mammalian cell signaling networks was also observed (40). This feature of the topology suggests that negative loops have not been favored through evolution because of their potential to introduce dynamical instabilities. Hence, it appears that negative regulators are less regulated outgoing hubs, examples of which are known in cell signaling networks. For instance, phosphatases such as PP1 and PP2A are enzymes that deactivate most of their effectors through dephosphorylation (Fig. 1H). On the other hand, positive feedback loops are highly nested, where the same proteins function in many positive feedback loops, a topology that also favors dynamical stability (Fig. 1I) (41). Some regulatory motifs in biochemical networks have long been known, e.g. the negative feedback loop in the synthesis of branched chain amino acid from threonine to isoleucine (42). The concept of network motifs is illustrated by several examples from cell signaling (Fig. 2).

FIGURE 2.

Example of network motifs within cell signaling networks. PFBL, positive feedback loop; NFBL, negative feedback loop; PFFL, positive feed-forward loop; NFFL, negative feed-forward loop; CaM, calmodulin; CaN, calcineurin; AC1, adenylyl cyclase I; AA, arachidonic acid; B2AR, β₂-adrenergic receptor; I1, inhibitor-1; PKA, protein kinase A; PKC, protein kinase C; PP1, protein phosphatase-1; MAPK, mitogen-activated protein kinase; PLA2, phospholipase A₂; CaMKII, Ca²⁺/calmodulin-dependent kinase II. Gray arrows represent the components in these motifs that signal to other biomolecules that are not part of the motif.

The presence of network motifs that are dense in links, like the bifan, points to the fact that biochemical networks typically have high clustering coefficients (3). A clustering coefficient measures the level of density in local connectivity around the neighborhood of a node. High clustering also suggests that biochemical networks are organized into modules. Such modules can be identified using network clustering algorithms. A popular measure for identifying clusters in networks is the betweenness centrality measure. Betweenness centrality is computed for each vertex or edge by counting the number of times the shortest paths pass through the vertex or the edge (43). If many short paths go through a vertex and if the vertex has a relatively low degree, the vertex must be connecting different modules. Such a vertex can be removed for the purpose of isolating and identifying modules/clusters.

Conclusions

One of the limitations of graph theory applications in analyzing biochemical networks is the static quality of graphs. Biochemical networks are dynamical, and the abstraction to graphs can mask temporal aspects of information flow. The nodes and links of biochemical networks change with time. Static graph representation of a system is, however, a prerequisite for building detailed dynamical models (44). Most dynamical modeling approaches, e.g. Boolean networks (45), Petri nets (46), and event ontologies (INOH Pathway Database), can be used to simulate network dynamics while using the graph representation as the skeleton of the model. Modeling the dynamics of biochemical networks provides closer to reality recapitulation of the system's behavior in silico, which can be useful for developing more quantitative hypotheses.

The challenge with building dynamical models of biochemical networks is that they require kinetic and quantity parameters, which are difficult to obtain experimentally. Another obstacle in both graph theory and dynamical modeling is that most applications are NP-hard. This means that time for execution grows exponentially with N, where N can be the number of steps in a path or the number of nodes in a graph. This computational challenge places practical limitations on calculating static and dynamical properties of large regulatory biochemical networks. To overcome this challenge, sampling (47) and parallelization of algorithms (48) can be applied.

In summary, graph analysis of biochemical networks has been useful for obtaining an overview of the organizations of different types of biochemical networks across species. In general, most networks have a connectivity distribution that fits a power law, high clustering coefficients, and relatively short average path lengths; the networks are organized in hierarchical modularity, where hubs serve as party or date hubs and can be divided into multisite or single-site hubs, and assortative mixing by valence is not common, whereas assortative mixing by function, location, or biological process is evident. Biochemical network motifs are enriched in dense substructures where the bifan motif is the most over-represented, probably due to duplication-divergence, and where negative feedback and feed-forward loops are less common than positive loops. Cell signaling networks have many paths from some input receptors and few from others, a topology reminiscent of a classification system. Signaling networks also display a bow-tie structure. These are only a handful of topological patterns out of many. Such topological properties are likely to have consequences for the dynamical behavior of a system. Initial dynamical analyses of these properties are consistent with an architecture that supports stability, noise filtering, modularity, redundancy, and robustness to failure as well as variations of kinetic rates and concentrations.

We are just starting to understand the intricate dynamics of large and complex biochemical systems in which graph theory plays an important role in organizing the accumulated knowledge. Graph theory is also useful for the analysis of multivariate data when lists of genes or proteins can be placed in the context of prior knowledge to develop more informed hypotheses about how multiple factors cooperate to produce complex phenotypes. In the new world of Big Data (massively abundant data) and Cloud Computing (data can be accessed from everywhere and processed anywhere), graph theory plays an increasingly important role in the transition from the classical approach of hypothesizing and testing experimentally to hypothesizing, modeling, and testing to measure everything, identify patterns, model, and modify (manipulate) input-output relationships (49).