Advantage of Being a Dimer for Serratia marcescens Endonuclease?

Abstract

The monomer and dimer of the bacterium Serratia marcescens endonuclease (SMnase) are each catalytically active and the two subunits of the dimer function independently of each other. Nature however chooses the dimer form instead of the monomer. In order to explain this, we performed molecular dynamics (MD) simulations of both model built complexes of a subunit of SMnase and the dimer with DNA in aqueous solution. We estimated the electrostatic binding energy, analyzed the distribution and dynamics of water around the complexes, identified water clusters in the protein, and related dynamics of water to the protein's function. We find that the dimer form has an electrostatic advantage over the monomer to associate with DNA. Although Mg²⁺ remains hexa-coordinated during the simulation, the binding pathway of DNA to Mg²⁺ changes from inner-sphere binding in the monomer to outer-sphere in the dimer, which may be more energetically favorable. In addition, two water clusters in the active site of each monomer and in the dimer complex were identified and localized in two regions, named ‘stabilizing’ and ‘working’ region. Water in the ‘working’ region in the dimer complex has larger fluctuations than that in the monomer.

Introduction

Enzymes in the family of sugar non-specific endonucleases have been isolated from a wide range of sources from bacteria to mammals [1]. They can be characterized by their abilities to hydrolyze both DNA and RNA. Although these enzymes have been extensively studied in terms of their catalytic properties and biological roles, the relationship between structure and function is still unclear. So far, only a few enzymes have been crystallized, including Staphylococcal nuclease [2], Serratia marcescens nuclease [3,4], P1 nuclease from Penicillium citrinum [5], Vvn from Vibrio vulnificus [6], and the nuclease domain of ColE7 [7] and ColE9 [8] from E. coli. Amongst them, only Vvn [6] and the nuclease domain of ColE7 [9] and ColE9 [10] have been solved with a dsDNA substrate. Of all these sugar nonspecific endonucleases, Serratia marcescens endonuclease (SMnase) is the most studied one because of its broad class of substrates, very high specific activity and wide commercial applications. Here we present a study of its structure - function relationship of the cleaving mechanism and hope this study might help us understand evolutionary aspects of this family.

SMnase is a homodimer, each with 245 amino acids (Fig.1). It is capable of cleaving single- and double-stranded DNA and RNA with a slight preference to A-form nucleic acids [11,12]. In the presence of magnesium, it produces 5'- phosphorylated and 3'-OH oligonucleotides. Since there is no structural data available for the enzyme-substrate complex, it has been of difficulty to verify the precise catalytic mechanism for SMnase. However, after comparing the three dimensional structure of the complex of I-PpoI and its cognate substrate with SMnase, a similar motif at both active sites has been identified. The motif, a ββα-Me finger, composed of two beta-strands, a helix and a metal, makes a common core of the active site for endonuclease activity [3,15]. Mutational and structural analysis propose for SMnase, Arg57, His89, Asn119 and Glu127 to play a central role in catalytic process [13,14]. During this process, oxygen atoms from the phosphate group of DNA bind to Mg²⁺ directly. His89 acts as a general base to activate the water molecule for a nucleophilic attack on the phosphorous atom, while Arg57 stabilizes the transition state and the leaving group as well [16].

Figure 1.

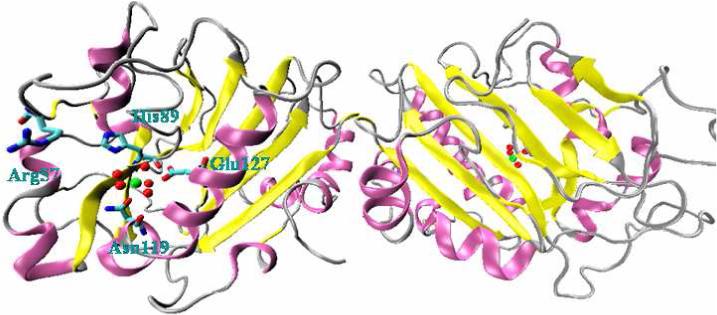
The homodimer structure of Serratia marcescens endonuclease (SMnase). Mg²⁺: green sphere; water molecules coordinating to Mg²⁺: red sphere. Arg57, His89, Asn119, and Glu127 are also shown.

One interesting feature of SMnase is that the protein functions as a dimer in nature. Experiments show that both the monomer and dimer can function with the same specific activity, and each subunit of the protein cleaves the substrate independently [17]. This does not mean that the favored dimeric state of SMnase exists without any advantage for Serratia marcescens. Kinetic studies of a series of monomer variants and the dimer [18] showed that the time course of the reaction is different between the monomer and dimer. Under the conditions of low enzyme concentration and high molecular weight DNA substrate, the dimer functions in a processive manner. This might be more effective than a monomer following a distributive mechanism, because the rate limiting step of the reaction is either the association of the protein with the substrate or the cleavage of the substrate. Nevertheless, how the monomer and dimer work in such a different manner has not been well addressed.

Our previous studies of the hydration patterns of the monomer, the dimer and one model built complex of the monomer with its DNA substrate demonstrated that the interior hydration sites identified in the averaged configuration over MD snapshots have ∼88% similarity with crystal water molecules [19,20]. Even though the general hydration pattern of the protein does not change very much on dimerization outside of the direct interface, the local dynamics of water may be affected, particularly at the active site. This might consequently influence the mechanism of the cleavage of DNA. However, whether dimerization has an effect on the association of DNA is still in question.

Nonspecific proteins binding to DNA differ from specific ones generally in that (i) association between the partners is mainly driven by electrostatic interactions with lower affinity and stronger dependence of ionic strength; (ii) the interface of protein and DNA are thought to be more hydrated and (iii) both protein and DNA have less conformational change [21,22]. As such, it is reasonable to evaluate the binding free energy assuming that the conformations of the protein and DNA taken from the complex trajectory are comparable to the free forms. In addition, we approximate the binding free energy by only considering the electrostatic contribution.

In this work, MD simulations of model built monomer-DNA and dimer-DNA complex have been carried out to further understand the effects of dimerization on the catalytic process of SMnase, such as DNA association, cleavage, transition state stabilization, leaving group protonation and DNA dissociation. By comparing the monomer-DNA with dimer-DNA complex conformers via the electrostatic contributions to the binding energy as well as in the hydration patterns, especially at the protein-DNA interface and the active site, we are able to propose a mechanism for the advantages of being a dimer for SMnase over a monomer.

Methods

MD simulation

Due to the lack of structural data for SMnase with its substrate, the protein-DNA complex system was built by superimposing the structure of I-PpoI endonuclease (PDB code: 1A73) on the subunit B of SMnase (PDB code: 1QAE) using CHARMM [23], based on the structural similarity at the active site of I-PpoI endonuclease and SMnase [16]. It has been shown that SMnase has a slight preference for A-form DNA such as in d(GGGGCGCCC)₂., therefore, a 16-mer DNA duplex, d(ATAGGGGCGCCCCTAT)₂ was first constructed in ideal A-form and then “threaded” through the backbone of the I-PpoI DNA. The details of the construction of the protein-DNA complex model were described elsewhere [19]. Protein residues 1−5, not given by the diffraction results, were also built. As for the monomer-DNA complex, the monomer was taken from the subunit B of the dimer. We used independent runs of the monomer and dimer rather than just averaging the two monomers from a dimer run so as not to bias the symmetry and outcome.

The systems were simulated using the program ESP [24] and the all-atom CHARMM 27 parameter set [25,26]. Equations of motion were integrated with a 2 fs time step in the microcanonical ensemble (NVE) with periodic boundary conditions. Electrostatic interactions were treated with an Ewald sum [27] using a fast linked-cell algorithm. The complexes were put into pre-equilibrated boxes of water using standard setup procedures (See Ref. 19). The system set-up of the monomer-DNA and dimer-DNA is summarized in Table 1. After several steepest descent energy minimization steps, the system was equilibrated at 300 K for 3.0 ns (monomer-DNA) and 6.9 ns (dimer-DNA) until geometries and energies for the complexes were stable. The trajectory was then continued to 11.1 ns for the monomer-DNA and 12.9 ns for dimer-DNA and coordinates were saved for analysis at an interval of 0.1 ps.

Table 1.

System set-up of the monomer and dimer complex systems.

	Monomer-DNA	Dimer-DNA
Box size (Å)	86.65×87.68×65.89	130.55×129.68×129.51
No. Solute atoms	4730	8448
No. TIP3P waters	15324	70896
No. Na+	55	80
No. Cl−	25	50

Analysis of contacts

In general, protein and DNA are held together by electrostatic, hydrophobic, direct hydrogen bond (H-bond), and water mediated interactions. Herein, a strong salt-bridge contact was defined between a pair of charged nonhydrogen atoms when the distance was less than 2.8 Å, and a hydrophobic interaction was defined as the distance between a pair of low charged carbon atoms (e.g. not carbonyl) was less than 4.0 Å. A hydrogen bond interaction in a donor-acceptor pair, A...H-D, satisfied a set of specified geometrical criterion, in which they are described as (i) that the distance between H (hydrogen) and A (acceptor) should be smaller than 2.3 Å, (ii) that the distance between A and D (donor) should be smaller than 3.2 Å, and (iii) that the angle between A, H and D should be between 130° and 180°. A water-mediated hydrogen bond interaction was claimed when a hydration site occupied by water molecules was in proximity to either other waters or protein/DNA.

Electrostatic binding energy calculations

The total electrostatic binding energy of a protein and DNA molecule can be expressed by

$$\Delta \Delta {\mathrm{G}}_{\mathrm{ele}}=\Delta {\mathrm{G}}_{\mathrm{ele}}\left(\text{complex}\right)-\Delta {\mathrm{G}}_{\mathrm{ele}}\left(\text{protein}\right)-\Delta {\mathrm{G}}_{\mathrm{ele}}\left(\mathrm{DNA}\right)$$ (1)

where ΔG_ele is the electrostatic potential of the molecule or complex. The electrostatic potential of a macromolecule system in a monovalent salt solution may be roughly approximated using the Poisson-Boltzmann (PB) equation [28]. Based on the thermodynamics, the total electrostatic potential can be decomposed into salt-independent ΔG_ns, and salt-dependent ΔG_s parts [29]. The salt-independent potential is composed of two terms:

$$\Delta {\mathrm{G}}_{\mathrm{ns}}=\Delta {\mathrm{G}}_{\mathrm{coul}}+\Delta {\mathrm{G}}_{\mathrm{hyd}}$$ (2)

where ΔG_coul is the Coulombic interaction in the solute's dielectric medium ε_m and ΔG_hyd is the hydration energy in the heterogeneous environment, in which the solute has the interior dielectric constant of ε_m and the solvent has ε_s. In the presence of mobile ions, the sum of ΔG_hyd and ΔG_s gives the electrostatic solvation energy. If it is assumed the electrostatic part of binding free energy entirely dominates the reaction, then the salt-dependent contribution to the total electrostatic energy should change linearly with logarithm of salt concentration M⁺,

$$-\frac{\partial \ln \left[K_{obs}\right]}{\partial \ln \left[M^{+}\right]}=\frac{1}{RT}\frac{\partial \Delta \Delta G_s^0}{\partial \ln \left[M^{+}\right]}$$ (3)

where K_obs corresponds to the observed association constant, [M⁺] represents the monovalent salt concentration, R is the gas constant, T is the absolute temperature and ΔΔG_s is the change in salt-dependent contribution to the electrostatic binding energy.

In calculation of the structurally averaged electrostatic binding energy, the coordinates of structures were extracted every 500 ps from the trajectories. The APBS package [30] was used for all the PB calculations with CHARMM 27 parameter set [25,26] for atom charges and radii. The dielectric constant of DNA and protein was set to 4, and the solvent to 78. An ionic strength of 0.1 M was used with the radius of the monovalent ion exclusion region set to 2 Å. A dielectric boundary spline was used with the window size of 0.3 Å to reduce the grid sensitivity [31]. All calculations were started with grid size at 0.6 Å, then focused to a final grid spacing of 0.4 Å. Approximately 1% difference in electrostatic binding energy was found when the higher resolution was used.

Hydration properties of the complex

Hydration properties include localization of the hydration sites, evaluation of water residence time and the dynamics of hydrogen bond interactions of water-water and water-protein at the hydration sites. Hydration sites may be defined as any local maximum in the water (oxygen) density map that satisfies certain protein proximity conditions. Obtaining the average solvent density map and localizing the hydration sites from an MD trajectory has been described in detail elsewhere [19,32]. Briefly, hydration sites were obtained using a grid spacing of 0.5 Å, a number density threshold of 1.5 per grid point, and a minimum distance of 2.8 Å which separates neighboring sites.

The dynamics of water at a hydration site can be described by water molecule residence time and lifetime of H-bond interactions which can be for water-water and water-protein/DNA residues. Water residence times can indicate how water around the protein differs from the bulk. The fluctuations of hydrogen bonds within water as well as between water and the macromolecule contribute to the mechanistic description in terms of how the dynamics of water is related to the protein's function.

The water residence time at a hydration site was evaluated from an occupation survival time correlation function C_α(t) that represents the average number of water molecules that remain in the hydration site for a duration of time [32]. The occupation survival function is defined as

$$C_{\alpha }\left(t\right)=\sum _{j=1}^{Nw}\frac{1}{T_{run}-t+1}\sum _{t_0}^{{\mathrm{T}}_{\mathrm{run}}-\mathrm{t}}{p}_{\alpha ,j}(t_0,t_0+t)$$ (4)

where p_α,_j(t₀,t₀+t) is a binary function that takes the value of 1 if the jth water molecule has occupied the α^th site from t₀ to t₀+t; otherwise, the function is 0. Also in here, N_w is the total number of water molecules and T_run is the length of simulation. Previous work [20] from the survival function for the hydration sites around the active site indicated that most sites were not well fit by a single exponential. We found the relaxation time behavior is better approximated with two terms using a stretched exponential for the long time decay (a Kohlraush-Williams-Watts model [33]), and a single exponential for the short time decay,

$${\mathrm{C}}_{\alpha }\left(\mathrm{t}\right)={\mathrm{W}}_0\{(1-x)\exp [-\mathrm{t}∕{\tau }_{\mathrm{f}}]+x\exp [-{(\mathrm{t}∕{\tau }_{\mathrm{s}})}^{\beta }]\}$$ (5)

where W₀ is the occupancy of the α^th site, τ_f and τ_s are the fast and slow residence time, respectively, x is the weight of the slow relaxation, and β is a stretching parameter between 0 and 1, which reflects the extent to which the relaxation process deviates from exponential behavior and provides us additional information upon the heterogeneity of the water dynamics around the molecule. Such nonexponential behavior has commonly been found in both amorphous and glassy condensed phase systems as well [34,35].

The dynamics of hydrogen bond interactions of water-water and water-protein/DNA at the hydration sites was investigated by calculating the average life time of the hydrogen bonds. The decay was evaluated by calculation of a hydrogen bond lifetime correlation function [36,37],

$${\mathrm{S}}_{\alpha }\left(\mathrm{t}\right)=\frac{<\mathrm{h}\left({\mathrm{t}}_0\right)\mathrm{H}({\mathrm{t}}_0+\mathrm{t}){\mathrm{p}}_{\alpha }\left({\mathrm{t}}_0\right)>}{<\mathrm{h}>}$$ (6)

where function p_α (t₀) is unity when a particular water molecule occupies the α^th hydration site at original time t₀, otherwise it is 0; h(t) is a hydrogen bond indicator, which is unity when the water molecules inside the α^th hydration site forms a pair with another molecule by hydrogen bonding at time t, otherwise it is 0; H(t₀+t) is 1 if the tagged pair remains continuously hydrogen bonded during time t₀ + t, otherwise it is 0; and <···> denotes an average over all hydrogen bonds that are present at t₀ for the α^th site. With this construct, S_α(t) describes the probability that a water pair, which occupies the α^th hydration site, is continuously hydrogen bonded during time from t₀ to t. Similar to water residence times at the hydration sites, the decay of S_α(t) around the active site is also expected to obey a KWW model.

Results and discussion

Protein-DNA contacts

Protein and DNA molecules generally utilize their chemical and geometrical properties to facilitate their recognition and association. The protein and DNA are held together by a mix of salt-bridges, water mediated and direct hydrogen bond interactions between the protein and DNA backbone, as summarized in Table 2. That almost no DNA bases are directly involved in the contacts is consistent with the reduced specificity of the enzyme in recognition of its substrate. However, these DNA contacts slightly reorganize from the monomer to dimer simulations, as shown in Fig. 2A and 2B. Particularly, in the monomer one non-bridging oxygen atom from Gua25 directly binds to Mg²⁺ with 100% of strength. Arg57 interacts with Cyt27 with a frequency of 0.15 by salt-bridge, 0.55 by direct H-bond and 0.10 by water mediated hydrogen bond. While in the dimer, DNA binds to Mg²⁺ indirectly with a frequency of 0.90 between one bridging oxygen atom 3'-O of Cyt24 and a water molecule coordinating to Mg²⁺. Arg57 interacts with Cyt26 with a frequency of 0.66 by salt-bridge, 0.96 direct H-bond and 0.31 by water mediated H-bond, much more strongly than those happening in the monomer.

Table 2.

Primary contacts between protein and DNA. (only contacts with frequencies larger than 0.10 are shown)

	Monomer-DNA			Dimer-DNA
	H-bond	Salt-bridge	Water-med.	H-bond	Salt-bridge	Water-med.
Mg2+		1.00 (G25,O2P)				0.90 (C24,O3S)
Ser53	--	--	--	0.43 (G23,O2P)
Thr56	0.82 (A3,O1P)			0.62 (G4,O1P)
Arg57	0.46 (C27,O1P)	0.15 (C27,O1P)	0.10 (C27,O1P)	0.96 (C26,O1P)	0.66 (C26,O1P)	0.31 (C26,O1P)
Asn58	0.39 (A3,O1P)			0.45 (G4,O1P)		0.20 (G4,O1P)
Lys60	--	--	--	0.33 (A3,O2P)
Asn80			0.15 (C26,O2P)	0.79 (C26,O2P)
Asp86			0.48 (C26,O2P)
			0.22 (G25,O3S)
Arg87	0.21 (C27,O1P)	0.15 (C27,O1P)	0.25 (C26,O1P)	0.65 (C26,O2P)	0.20 (C26,O2P)	0.58 (G25,O2P)
His89			0.22 (C26,O1P)			0.19 (G25,O2P)
Gln120	0.44 (G9,H22)
Arg125	0.86 (C11,O3S)	0.64 (C12,O2P)		0.15 (C13,O2P)	0.22 (C13,O2P)
	0.90 (C12,O2P)
Asp128			0.20 (C24,O2P)			0.25 (C12,O3S)
Lys196	0.37 (C10,O4S)			0.68 (C11,O2P)	0.53 (C11,O2P)
Asp199			0.15 (C12,O2P)	--	--	--

Figure 2.

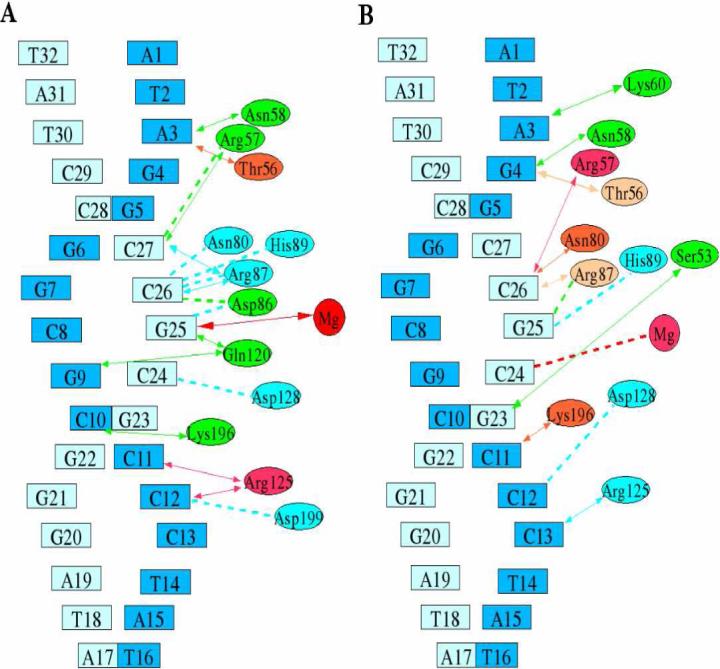
Diagram of primary contacts between protein and DNA. A: monomer-DNA complex; B: dimer-DNA complex. ↔: direct contacts; ---: water-mediated contacts. The contact strengths in different levels of color are red (100%), light red (> 90%), orange (> 70%), pink (> 50%), green (> 30%) and cyan (>10%).

Previous studies of the free protein systems [14,20] showed that Mg²⁺ has an octahedral coordination with 5 water molecules and OD1 from the side chain of Asn119. The distance between Mg²⁺ and each oxygen atom of the ligands is 1.97 ± 0.06 Å on average during the entire simulation, close to the value in the crystal structure which is in the range of between 2.01 and 2.13 Å [4]. However, in the complex systems, although Mg²⁺ maintains a hexa-coordinated structure, ligand exchange for Mg²⁺ occurs on the simulation time scale (Fig. 3A for the monomer-DNA, and 3B for the dimer-DNA). For the monomer, upon DNA binding to the protein, the contact of Asn119 with Mg²⁺ is taken place by one carboxylic oxygen atom, OE1 from Glu127. The distance between OE1 and Mg²⁺ is shortened to 1.87 ± 0.05 Å. The other carboxylic oxygen, OE2 from Glu127, and one non-bridging oxygen atom, O2P from Gua25 of DNA, substitute two water molecules for inner-sphere coordination to Mg²⁺, giving a distance of 1.90 ± 0.06 Å and 1.84 ± 0.04 Å, respectively. As for the dimer, DNA takes a different binding mode to Mg²⁺. Substitution involving Asn119B is the same as in the monomer, but five water molecules remain unchanged. One bridging oxygen atom, 3’- O from Cyt24, binds to Mg²⁺ via one ligand water with more than 90% frequency. As a result, DNA binding to Mg²⁺ changes from the inner sphere in the monomer to the outer sphere in the dimer.

Figure 3.

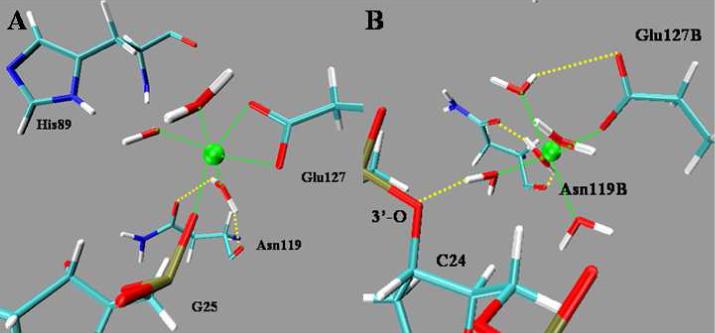
Mg²⁺ coordinations at the active site. A: monomer-DNA complex; B: dimer-DNA complex. Mg²⁺: green sphere.

SMnase is sugar-nonspecific endonuclease with only slight sequence specificity, whereas I-Ppol is a highly sequence specific homing endonuclease. Although the similar motif at their active sites suggests a similar cleaving action, it does not require that the same binding mode to the substrate should obtain. Therefore, it is necessary to investigate the association of the protein with DNA both structurally and energetically. Structurally, new models based on sugar-nonspecific endonuclease-DNA complex are required. Although it is difficult to co-crystallize such protein with its substrate because of the weaker binding affinity and less ordered association, the sugar-nonspecific endonuclease of Vvn (Vibrio vulnificus) with its short 8-base-pair DNA substrate has been refined (PDB code: 1OUP) [6]. Around their active sites, superposing residue 85−89 and 111−123 from SMnase on residue 76−80 and 119−131 from the Vvn-DNA complex gives backbone rmsd of 1.2 Å. In the procedure of building new models on Vvn, water molecules coordinated to Mg²⁺ in the crystal structure were either kept or removed. Therefore, for both the monomer and dimer state, four new complex models were built. As described in Methods, the same simulation procedure was performed on these four models. It was found that after the equilibration phase, unlike the models built on I-Ppol, Asn119 remains coordinated to Mg²⁺ in all the four models. However, regardless whether Mg²⁺ is unhydrated or hydrated in its initial structure, the monomer models have the same inner sphere binding mode, while the dimer models have the same outer sphere binding mode, as observed above.

It is well known that magnesium plays a central role as a metal cofactor in nucleic acid biochemistry. Mg²⁺ possesses special properties, including small size, high charge density and extensive hydrated state, which distinguish it from other alkali and alkaline earth metals, such as Na⁺, K⁺, and Ca²⁺ [38] in biological activity. In the current potential energy function (PEF), interactions between Mg²⁺ and its ligands are often described by electrostatic and van der Waals (vdW) forces with appropriate vdW parameters. A full +2e charge is constant for Mg²⁺. This model allows the flexible movements of ligands at the metal-binding site. Although the current PEF does not explicitly include charge transfer and local polarization effects, it is plausible because Mg²⁺, being a hard cation, is less polarizable than soft cations and interacts mainly electrostatically with its ligands. Thus the use of a mean field model of polarizability in this case is not obviously unreasonable.

The MD simulations of the free SMnase systems [20] reproduced the experimentally observed the metal coordination number and structural geometry of Mg-ligand cluster [14]. Theoretical studies of hydration properties of Mg²⁺ [39,40] showed that in water it takes18.4 kcal/mol to remove one water molecule from a hexa-hydrated Mg²⁺. For a penta-hydrated Mg²⁺, 27.4 kcal/mol energy is needed for the dehydration to form a tetra-hydrated Mg²⁺. If more water molecules are removed, the corresponding dehydration energy increases. As a consequence, in the case of SMnase, in the monomer the hydrated Mg²⁺ has to partially exchange its one or two coordinated water molecules in order to coordinate with DNA or OE2 of Glu127, which appears to be energetically costly. In addition, both experimental and theoretical studies [38,41,42] supported the propensity of magnesium to interact with oligonucleotides in an outer sphere mode. Considering that association of the substrate to the protein is rate limiting, it is reasonable to hypothesize that the favorable binding energy of DNA to Mg²⁺ in the dimer might be one advantage of dimerization of SMnase.

Electrostatic contributions to the binding energy

As shown in Fig. 4, the electrostatic surface potentials from the proteins and DNA are very complementary. On the face of the active site (Fig. 4A for the dimer and 4B for the monomer), a strong positively electrostatic field attracts DNA molecule, whereas on the opposite side of the active site (Fig. 4C for the monomer) or in the region of dimeric interface (Fig. 4A), the strong negative field repels DNA and orients it toward the active site for binding [3].

Figure 4.

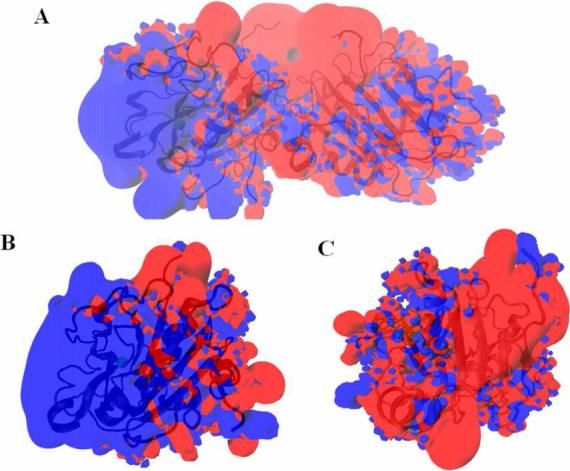
± 2 kT/e electrostatic potential isocontours of SMnase (blue: + and red: −) in a monovalent salt concentration of 0.1 M. A: in the face of the active site of the subunit B from the dimer; B: in the face of the active site of the monomer; C: on the opposite side of the active site of the monomer.

Table 3 presents contributions to the electrostatic binding energy estimated with the Poisson-Boltzmann equation with ionic strengths of 0 and 0.1 M respectively. Overall, the long-range Coulombic energy dominates the electrostatic binding. With ε_m = 4, the salt-independent component ΔΔG_ns favors the binding for both the monomer and dimer, but the salt-dependent component ΔΔG_s compensates in the opposite direction. The dimer state has a more negative ΔΔG_ns, −60.0 ± 5.9 kJ/mol than that of the monomer, −48.8 ± 7.6 kJ/mol. In addition, the dimer state has less positive ΔΔG_s of 25.3 ± 4.4 kJ/mol than 39.4 ± 3.5 kJ/mol found for the monomer. Therefore, in terms of the electrostatic binding energy, the dimer appears to associate more favorably with DNA than the monomer. As the net charge of the monomer as modeled here is zero, dimerization does not increase the net charge of the system. As a consequence, the total electrostatic binding energy is affected by the distance between the partners and/or the charge distribution within the protein.

Table 3.

The contributions to the calculated electrostatic binding energy of SMnase-DNA complex in the salt concentration of 0.1 M with ε_m at 4, 8 and 20. (Energy in kJ/mol)

	Mono-DNA	Dimer-DNA
	εm = 4.0
<ΔΔGcoul>	−1642.5 ± 110.7	−1453.0 ± 77.2
<ΔΔGhyd>	1592.7 ± 104.6	1392.5 ± 74.5
<ΔΔGns>	−48.8 ± 7.6	−60.0 ± 5.9
<ΔΔGs>	39.4 ± 3.5	25.3 ± 4.4
<ΔΔGele>	−9.4 ± 6.0	−34.7 ± 3.7
	εm = 8.0
<ΔΔGcoul>	−821.2 ± 55.3	−727.5 ± 40.1
<ΔΔGhyd>	753.1 ± 49.1	660.9 ± 36.0
<ΔΔGns>	−67.6 ± 6.7	−66.3 ± 5.5
<ΔΔGs>	40.2 ± 3.2	26.5 ± 4.2
<ΔΔGele>	−28.3 ± 4.1	−39.8 ± 2.6
	εm = 20.0
<ΔΔGcoul>	−328.5 ± 22.1	−290.6 ± 15.4
<ΔΔGhyd>	249.5 ± 15.9	220.2 ± 11.1
<ΔΔGns>	−78.8 ± 6.4	−70.3 ± 4.8
<ΔΔGs>	41.5 ± 2.7	27.1 ± 6.3
<ΔΔGele>	−37.3 ± 4.1	−43.2 ± 5.7

The exact binding value calculated from the PB method strongly depends on the parameters used in the calculations, especially the solute-solvent boundary and the interior dielectric constant. A uniform dielectric constant of 2 or 4 for the solute is routinely used to account for the effect of electronic polarizability or small dipolar fluctuations that may accompany structural transitions in proteins [43]. However, with the solvent surface definition, these values are found to overestimate desolvation cost of charges and the strengths of charge-charge interactions when pKa values are predicted. Antosiewicz et al. [44] proposed using a higher value of ε_m = 20, which effectively produces better agreements with the experimental pK_a's. Dong et al. [51] studied the contributions of electrostatic interactions to the binding stability of barnase and barstar using three protocols to define the dielectric boundary and ε_m. They found that the vdW surface with ε_m = 4 is most consistent with the experiment. The solvent exclusion (SE) surface with ε_m = 20 is qualitatively similar to the vdW surface with ε_m = 4. In contrast, the SE surface with ε_m = 4 destabilizes the binding. Although their studies do not consider the structural relaxation and sampling of protein conformation, their conclusion is a caveat to the electrostatic contributions sensitivity to a particular PB protocol.

In the past two decades, considerable theoretical work has been done to estimate ε_m. Making use of the extended Fröhlich-Kirkwood theory of solute dielectric properties, van Gunsteren and his co-workers [52,53] showed that the static dielectric constants of proteins are in the range between 17 and 40 at 300 K. ε_m is about 2 ∼ 4 in the protein core, but increases when one extends to the protein surface where the charged group most frequently occur. Therefore, charged surface residues are the dominating components of the higher dielectric permittivity estimates. Yang et al. [54] studied a system of a DNA molecule in the salt solution and found that the phosphate parts are the primary determinant of overall DNA dielectric constant which is ∼16. In addition, the dielectric constant of water in that high salt system was ∼41, smaller than 71 for pure SPC/E water [55] in part due to the well known saline dielectric decrement [56]. It appears the dielectric constant of a solute is somewhat system-dependent. A lack of universality for ε_m presents a challenge for continuum methods.

In the case of SMnase, Antosiewicz et al. [45] found that pKa values of His89, Asp86 and Asp128 are increased by 1 upon DNA binding for both the monomer and dimer state. In the current MD simulations and studies, the ionized state of the residues is not considered, and a uniform dielectric constant for the solute is used in the PB calculations with the non-optimized atomic radii for the dielectric spline-based boundary. The current work is not designed to define better PB parameters for the complex system, but to compare two protein states with reasonable parameter sets and under the same conditions. Because the interface of the protein and DNA is full of charged side chains, such as Arg57, Arg87, Arg125, Arg196, and Mg²⁺, it is reasonable to increase the dielectric constant to higher values in the range of 8 to 20 for comparison. In 0.1 M salt, higher dielectric constant of 8 and 20 reduces ΔΔG_ele,mp of the monomer state markedly by 19 kJ/mol and 28 kJ/mol, respectively, while for the dimer, by only about 5 kJ/mol and 8 kJ/mol in both cases. One possible reason explaining these differences is the direct binding of DNA to Mg²⁺ in the monomer.

When the monomer is moved away from the DNA along the direction of the center of each molecule by 1.5 Å, ΔΔG_ele,mp (in color of black) becomes more negative and relatively close to the ΔΔG_ele,dp for the dimer (in color of red), shown in Fig. 5. As for the dimer state, moving the protein away from the DNA by 1.5 Å does not influence the total electrostatic binding energy very much. When the distance between the DNA and the protein is longer than 1.5 Å, having the higher ε_m with 8 or 20 has little effect on the electrostatic binding energy for either state. As expected, the total electrostatic binding energy increases when the distance becomes longer. It seems that this configuration of the monomer and DNA with the distance at 1.5 Å is the most favorable one when comparing other configurations at a longer distance. Indirect binding to Mg²⁺ appears to be favorable.

Figure 5.

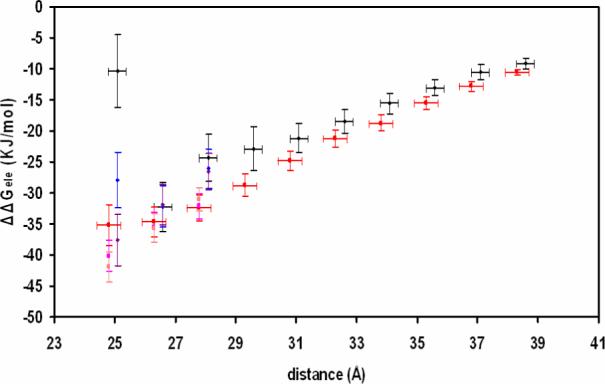
Calculated total electrostatic binding energy versus distance between the protein and DNA in 0.1 M salt solution with ε_m = 4. ΔΔG_ele and distance is averaged over the set of the snapshots from the trajectory. Distance is defined between the center of DNA and the center of the monomer or subunit B of the dimer. For the monomer, with ε_m = 4, black; ε_m = 8, blue; ε_m = 20, purple. For the dimer, with ε_m = 4, red; ε_m = 8, magenta; ε_m = 20, pink.

As for the salt-dependent electrostatic binding energy, the monomer and dimer have the ΔΔG_s of 39.4 ± 3.5 and 25.3 ± 4.4 kJ/mol, respectively, in the 0.1 M salt. Overall, ΔΔG_s destabilizes the protein-DNA complex, and it is independent of the protein's dielectric constant. In order to estimate the dependence of the electrostatic binding energy on the salt concentration, the electrostatic binding energy was calculated for the monomer and dimer state in the range of the monovalent salt from 0.05 to 0.4 M and the plot of ΔΔG_s/RT versus log[M⁺] is shown in Fig. 6. As expected, ΔΔG_s increases linearly with the salt concentration. According to the studies by Record et al. [46], the salt dependence of association follows −∂(lnK_obs)/∂(ln[M⁺]) = m'ψ, where m’ is the number of ion pairs formed with DNA and ψ is the fraction of counterions bound to each DNA phosphate. ψ = 0.88 for double stranded DNA, while ψ = 0.64 when short double stranded DNA is considered [47]. For the sequence-nonspecific binding proteins with DNA, experiments give m'ψ about 4 ∼ 7 if ψ = 0.64 [22]. In the case of SMnase, the slope of the fitted line of ΔΔG_s/RT versus log[M⁺] is about 3.2 ± 0.3, the same for both the monomer and the dimer. The calculated m'ψ is in reasonable agreement with the experimental data [22] on other systems.

Figure 6.

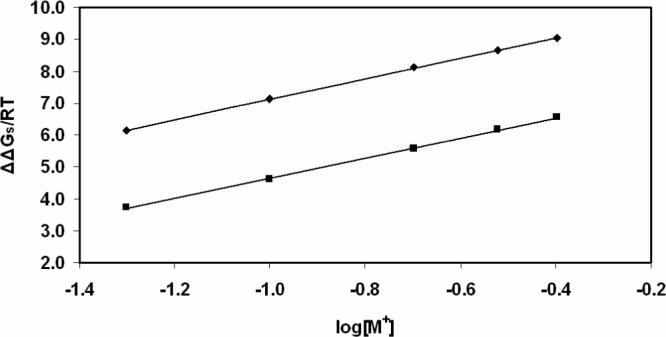
Calculated salt-dependence of electrostatic binding energy of SMnase in a monovalent salt solution with ε_m = 4. ◆: monomer-DNA complex; ■: dimer-DNA complex.

The kinetic studies found that the rate limiting step of the reaction is the association of the protein and DNA or the cleavage of DNA [18]. When the association is rate limiting, the experimental finding [18] that the dimeric form cleaves the DNA substrate more processively than the monomer can be explained by the estimated electrostatic binding energy. In the processive manner, the dimer stays associated with its substrate after the cleavage and cleaves the adjacent phosphodiester bonds. With the stronger binding affinity to DNA, one subunit of the dimeric state tends to be more effective than the monomer which dissociates from the DNA after cleavage. When the cleavage is rate limiting, the Michaelis-Menten constant K_m is approximately related to the association constant of the enzyme and the substrate. In such a situation, at least in the perspective of the binding process, from the electrostatic calculations we find the dimer is more favorably associated with the DNA than the monomer. The cleavage chemistry controls the entire reaction and in the experiment the advantage of the dimeric state is not obvious as observed.

Water dynamics in the protein-DNA interface

The process of the recognition and binding not only involves two partners, but also involves water, ions and other solvent. Water molecules are often observed in the protein-DNA interface. They may act as a buffer to reduce the electrostatic repulsion between DNA and protein, a packing element in recognition, a hydrogen bonding linker and a contributor to the stability and specificity of DNA binding, i.e. trp repressor and restriction enzyme BamH1 [48-50]. In both complex systems of SMnase, the interfacial region is highly hydrated with an average of 27 hydration sites in the monomer (Fig. 7A) and 31 sites in the dimer (Fig. 7B), respectively. These hydration sites were only considered where water contacts or mediates the protein and DNA simultaneously.

Figure 7.

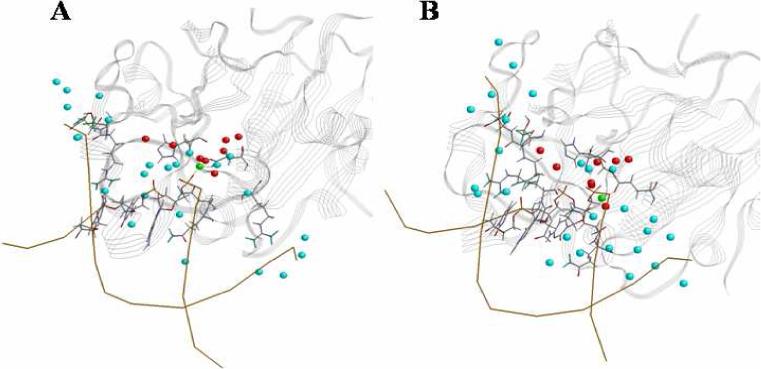
Hydration sites residing in the protein-DNA interface, shown in cyan sphere. A: monomer-DNA complex; B: dimer-DNA complex. Mg²⁺: green sphere. Some hydration sites at the active sites are shown in red sphere.

Such a wet interface is common for protein-DNA interfaces, especially for less specific complexes. About 65% of the interfacial hydration sites in the monomer-DNA interface and 70% in the dimer-DNA interface have residence time longer than 1.0 ps, the value for bulk water. In the monomer-DNA interface, relatively ordered water mainly mediates Asp86 and Cyt26 with residence times of hundreds of pico-seconds. That means water molecules act more to screen the electrostatic region between the monomer and DNA. While in the dimer-DNA interface, water with similar residence times mainly mediates the backbone oxygen of Arg87B and Gua25 and the side chain of Arg57B and Cyt26. This indicates that in the dimer system water plays more as a glue to provide the structural adaptability with the protein and DNA.

In addition to the water residence time, the stretching parameter of the H-bond relaxations between water and water, β_HB-WW, is about the same in both regions with the value averaged at 0.77 ± 0.01. The H-bond lifetime of water-water, τ_HB-WW, is about 1.03 ± 0.03 ps in the monomer complex and 0.71 ± 0.01 ps in the dimer complex, respectively. That the water-water H-bond lifetime in the dimer-DNA interface appears slightly shorter than that in the monomer-DNA interface might indicate that water in the dimer-DNA interface is less ordered and may better help facilitate DNA binding to the dimer.

Water dynamics at the active site

After analyzing site-site and site-protein interactions around the active site, two water clusters were identified and distinguished according to their positions (Fig. 8A for the monomer and 8B for the dimer complex).The water cluster colored in red is located in the deep cleft of the active site and mainly interacts with Glu127, His89 and Mg²⁺. The stretched beta value from the occupational relaxation, β_res, was estimated to be 0.67 ± 0.01 in the monomer and 0.79 ± 0.01 in the dimer complex system, respectively. Both values are smaller than 0.96 evaluated from the bulk, and β_res is lower in the monomer than that in the subunit B of the dimer. Such differences clearly demonstrate that water in this area in the subunit B of the dimer is less affected by both the protein and DNA, which is the same phenomenon observed in the protein systems [20].

Figure 8.

Water clusters at the active site. A: monomer-DNA complex; B: dimer-DNA complex. Mg²⁺: green sphere. Cluster 1, ‘stabilizing cluster’, is in red and Cluster2, ‘working cluster’ in yellow, respectively. H-bond interactions are shown in dash lines.

For the dynamics of H-bonds of water in this area, little system dependent difference was found. The lifetime, τ_HB-WW, was estimated to be 1.64 ± 0.02 ps in the monomer and 1.53 ± 0.07 ps in the subunit B of the dimer, respectively. In addition, β_HB-WW, was calculated to be 0.80 ± 0.01 in the monomer and 0.81 ± 0.02 in the dimerB. As a result, we propose the role of this water cluster is to help stabilize Mg²⁺ and below it is referred to as the ‘stabilizing cluster’.

Another water cluster in yellow in Fig. 8 is located around His89, Arg57 and the DNA phosphate group. Because of participation of His89 and Arg57 in the cleavage of DNA described by experiments, this cluster is defined as the ‘working cluster’. β_res, 0.70 ± 0.01, from occupational decay in the monomer is lower than that, 0.83 ± 0.01, in the dimer complex. This is the same trend as in the stabilizing region. Although β_HB-WW is similar in the monomer (0.76 ± 0.01) and in the subunit B of the dimer (0.78 ± 0.01), the lifetime, τ_HB-WW, is 1.32 ± 0.02 ps higher than that of 0.84 ± 0.03 ps in the dimer complex, which indicates that water might have relatively stronger interactions among each other in the working region of the monomer complex and/or interact with water in the stabilizing region as well. We verified that interactions between the working cluster and the stabilizing one in the monomer system have a frequency of more than 25% but little in the dimer system.

In addition to the H-bond life time of water, the lifetimes of hydrogen bonds between water and protein were also analyzed. Particularly, for NE2 of His89, τ_HB-WP, was estimated to be 3.34 ± 0.01 ps in the monomer complex and only 0.97 ± 0.02 ps in the dimer complex, respectively. Thus, water in the working region is more active in the subunit B of the dimer-DNA than in the monomer-DNA. This difference in water distribution and dynamics at the working region of the monomer and dimer complexes might be caused by the flexibilities of the side chains of key residues in the protein, such as His89 and Arg57.

Analysis of the interactions between His89 and other residues nearby showed that in the monomer-DNA complex, during the first two 2-ns time blocks, ND1 of His89 is directly hydrogen bonded with O of Arg87 with a frequency of about 0.13. In the following 2-ns time block, rare interactions happen. In the last 2-ns time block, ND1 is hydrogen bonded to O from Leu105 with 0.12 of frequency. However, in the dimer-DNA complex, ND1 of His89B interacts with ND1 of Asn110B with about the same frequency of 0.13 in all time blocks. It is noteworthy that Arg87 and Leu105/Asn110 are located in the opposite side of His89, shown in Fig. 9A (monomer-DNA) and 9B (dimer-DNA). So it is evident that the imidazole ring of His89 in the monomer-DNA complex rotates during the simulation. Such rotation can also be observed in the monomer system in the absence of DNA molecule. Therefore, given the time scale of the simulation, flexibility of His89 resulted from dimerization might influence the dynamics of water which consequently affects the catalytic process of the enzyme.

Figure 9.

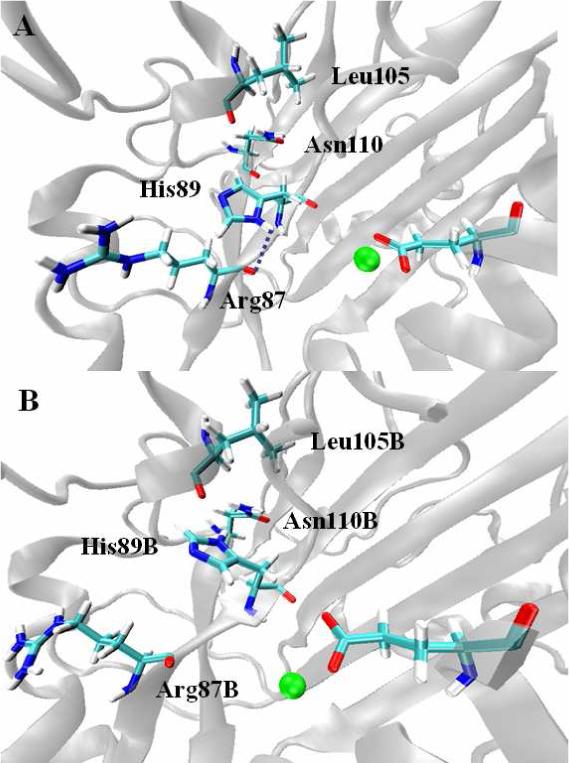
Interactions between His89 and other residues nearby. A: monomer-DNA complex; B: dimer-DNA complex.

Mechanism of the cleavage of DNA

Although only the protein-substrate complex in binding was simulated in this work, the results above enable us to rationalize the likely mechanism of the cleavage of DNA via the resulting average structures. Generally, the complementary electrostatic potentials from protein and DNA and water residing in the protein-DNA interface facilitate DNA recognition and binding to the enzyme. However, dimerization leads to different contacts between DNA and protein residues, especially to Mg²⁺. For the dimer form of the enzyme (Fig. 10B), Asn119 loses its contact with Mg²⁺ to Glu127. Ligand waters remained constant. 3’-O of Cyt24, which is in the target scissile phosphodiester bond, binds to Mg²⁺ via a ligand water molecule. His89 plays the role of a general base to activate water molecules for a nucleophilic attack on the phosphorous atom of Gua25. The phosphoanion transition state would be stabilized by water and the Mg²⁺ water cluster[13,14]. After the cleavage of the scissile phosphodiester bond, the 5'-leaving group is in position to be stabilized by Arg57. The protonation of the 3'-leaving group is then able to occur at the expense of an Mg²⁺ bound water molecule.

Figure 10.

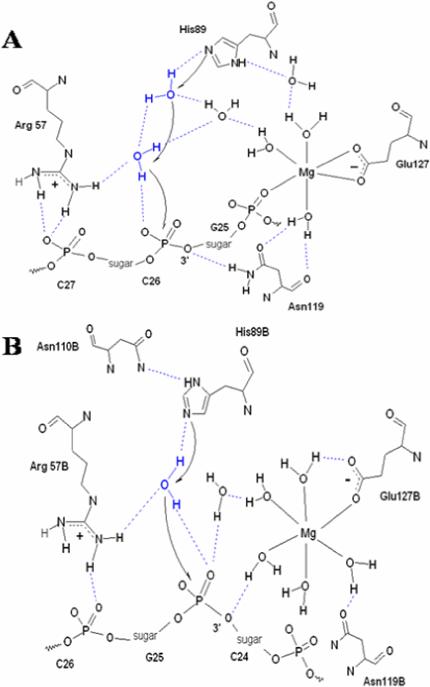
Proposed cleaving mechanism of SMnase. A: monomer; B: dimer.

However, in the monomer (Fig. 10A), several differences are found. First, one non-bridging oxygen atom of Gua25 from DNA binds directly to Mg²⁺ in an inner sphere pathway. Second, because of the flexibility of His89 and Arg57, more water molecules are involved in the working region, which seems to play multiple roles in the catalytic process. Water from that region would then be stabilizing His89 and Arg57, activated by His89, attacking the phosphorus atom, as well as stabilizing the transition state and the 5'- leaving group. Finally, although ND2 of Asn119 interacts with 3’-O weakly in the simulation, it is considered a potential general acid candidate to protonate the 3’-leaving group.

One of the more remarkable aspects of our protein-DNA complex simulations is the finding that Asn119 does not remain chelated at all times to Mg²⁺ and further that Glu127 directly coordinates this divalent cation. These results display an equilibrium between structures one of which is the published protein crystal structure [14], but they may be relevant if this enzyme has plasticity in its active site configuration. We note that the simulations are based on the models built on a highly sequence specific endonuclease I-Ppol. Thus different sequences for the protein and nucleic acid may shift the possible structures. Furthermore, our simulations of the proteins per se [20] show that the active site Mg²⁺ configuration is consistent with the experiments, as do the short simulations of the models which are built on Vvn, a sugar-nonspecific endonuclease. Even though different active site configurations are formed in the models built on I-Ppol and Vvn, simulations all give the inner sphere binding mode in the monomer while the outer sphere one in the dimer. The DNA binding mode is considered to be the main cause of the different mechanisms proposed by us and others. Given the findings in our simulation it is possible to speculate how an alternate mechanism from that previously proposed might be constructed. Of course choosing definitively between this mechanistic picture and others will require further study.

Conclusions

The catalytic process of an enzyme generally involves recognition, association, transition state stabilization, cleavage of the substrate, and dissociation of the product. As for the SMnase homodimer, steady-state kinetics demonstrated that two subunits can function independently of each other [17]. In addition, the gross activity of a series of monomer variants and the dimer are averaged to be the same although SMnase attacks natural DNA in different sites with different rates [11,17]. Under the condition of low enzyme and polynucleotide concentration, likely to be in the natural habitat of the bacterium, the course of the reaction is different. The dimer form cleaves macromolecular nucleic acids processively, while the monomer works distributively [18].

We found in our previous work on the protein systems [20], the monomer and two subunits of the dimer differ in flexibility/dynamics of residues and water locally in the active site. In this work, we considered the effect of dimerization of SMnase simulation on model-built complexes of DNA with the monomer and dimer by molecular dynamics. By calculating the electrostatic binding energy of a 16-base-pair DNA duplex with the proteins and analyzing the hydration pattern around the systems, we found the advantage enzyme has in being a dimer in the process of association and cleavage. Specifically, dimerization leads to the rearrangement of primary contacts of DNA from the monomer to the dimer due to changes in the electrostatic field. This results in the binding pathway of DNA with the hydrated Mg²⁺ changing from an inner-sphere coordination in the monomer to an outer-sphere one in the dimer. Our results imply the outer-sphere binding pathway might be energetically favorable. Electrostatic calculations indicate that the dimer form has a more favorable association with DNA. In addition, water is observed to be more mobile in the working region of the dimer than in the monomer. Since the catalytic process is water-assisted, this leads to a more effective dimer to cleave DNA.