Competition between Reversible Aggregation and Loop Formation in Denatured Iso-1-cytochrome C

Abstract

The competition between intramolecular histidine-heme loop formation and ligand-mediated oligomer formation in the denatured state is investigated for two yeast iso-1-cytochrome c variants, AcH26I52 and AcA25H26I52. Besides the native His 18 heme ligand, both variants contain a single His at position 26. The AcA25H26I52 variant has Pro 25 mutated to Ala. The concentration dependence of the apparent pK_a for His 26-heme binding in 3 M gdnHCl indicates that the P25A mutation disfavors oligomerization mediated by intermolecular heme ligation by 10-fold. Single and double pH jump stopped-flow experiments with the AcH26I52 variant show that fast phases for His-heme bond formation and breakage are due to intramolecular loop formation and slow phases for His-heme bond formation and breakage are due to intermolecular aggregation. The presence of two closely-spaced slow phases in the kinetics of loop formation for both variants suggests that intermolecular His 26-heme ligation results in both dimers and higher order aggregates. The P25A mutation slows formation and speeds breakdown of an initial dimer, demonstrating a strong effect of local sequence on aggregation. Analysis of the kinetic data yields equilibrium constants for intramolecular loop formation and intermolecular dimerization at pH 7.1 and indicates that the rate constant for intermolecular aggregation is very fast at this pH (10⁷ to 10⁸ M⁻¹s⁻¹). In light of the very fast rates of aggregation in the denatured state, comparison of models involving reversible or irreversible oligomerization steps suggest that equilibrium control of the partitioning between folding and aggregation is advantageous for productive protein folding in vivo.

Slow phases in protein folding are usually associated with proline isomerization (1). However, slow folding phases can also be caused by aggregation (2–4). Interest in protein aggregation and its causes is high due to its role in a number of human diseases characterized by irreversible aggregation (5, 6). Several recent studies demonstrate reversible aggregation during folding (2, 3, 7–10). The state that mediates aggregation during folding varies. In some cases, the denatured state is implicated (2, 7, 8) and in other cases partially folded intermediates (10). The reversibility of aggregation during folding can depend on protein concentration (9). Studies on the dynamics of denatured proteins have shown that proline residues can dramatically affect the conformational properties of the denatured state (11, 12). In the case of iso-2-cytochrome c, proline isomerization has been shown to modulate non-native His-heme ligation (12). In this study, we investigate the effects of proline on aggregation in the denatured state of iso-1-cytochrome c (iso-1-cytc;¹ we note that iso-1 and iso-2 cytochromes c are naturally occurring variants of cytochrome c in Saccharomyces cerevisiae with ~80 sequence identity).

To probe the conformational properties of the denatured state, we have developed methods to measure His-heme loop formation using variants of iso-1-cytc containing a single histidine capable of loop formation (13, 14). In general, we find that loop formation in the denatured state is independent of protein concentration (15–17). Similarly, the kinetics of His-heme loop formation and breakage are consistent with two-state intramolecular binding of histidine to heme (18). However, when the histidine is <10 amino acids from the point of attachment of the heme to the polypeptide chain, we observe significant concentration dependence for equilibrium loop formation (15–17). The AcH26I52 variant of iso-1-cytc has a histidine at position 26, which is nine residues from the nearest point of attachment to the heme (His 18). There is also a proline at position 25. Equilibrium loop formation is strongly dependent on protein concentration for this variant (15), consistent with intermolecular His-heme binding. Interestingly, when the histidine is at position 27 (AcH27 variant), such that it is not immediately adjacent to Pro 25, equilibrium loop formation is not significantly concentration dependent (17). This result suggests that the position of proline relative to histidine in short loops can have a dramatic effect on intermolecular aggregation.

Studies with a variant of iso-2-cytc having a single histidine at position 26 (N26H, H33N, H39K) show that denatured state loop formation is slowed by a factor of 140 relative to the wild type protein (12). The lifetime of 800 ms for His 26-heme loop formation suggested that loop formation was gated by trans to cis isomerization of the Gly 24-Pro 25 peptide bond in this iso-2-cytc variant. Thus, it appears that both intermolecular aggregation and proline isomerization could influence the properties of the denatured state of cytc when only a small number of residues separate the histidine from the heme.

To probe the effects of Pro 25 on the denatured state of iso-1-cytc, we use two variants, AcH26I52 (19) and AcA25H26I52. Both have a histidine at position 26 capable of forming a 9-residue His-heme loop in the denatured state. In the latter variant, Pro 25 has been mutated to Ala. We characterize denatured state His-heme bond formation using both equilibrium and kinetic methods. The equilibrium data demonstrate that replacement of Pro 25 diminishes intermolecular His-heme binding. Kinetic data show that the rate of intramolecular loop formation and breakage is not strongly influenced by this mutation. However, in the absence of Pro 25, the bimolecular rate constant for intermolecular His 26-heme binding is decreased and the unimolecular rate for breakage of the intermolecular His 26-heme bond is increased. Thus, Pro 25 acts primarily to promote intermolecular interactions in the denatured state of iso-1-cytc.

We also develop an equilibrium model to analyze amplitude data from our kinetics experiments and contrast it to a previous kinetic model (20) for predicting yields of intramolecular (folding or loop formation) versus intermolecular (aggregation) products. The comparison suggests that equilibrium control of folding versus aggregation may be more adaptive than kinetic control in vivo.

EXPERIMENTAL PROCEDURES

Preparation of the AcH26I52 and AcA25H26I52 variants

The AcH26I52 variant of iso-1-cytc, which contains the T(-5)S and K(-2)L mutations (horse cytc numbering is used, thus the first five amino acids of iso-1-cytc are numbered −5 to −1) to give an acetylated N-terminus (eliminates competition between the N-terminal amino group and histidine for binding to the heme under denaturing conditions, see ref. 21), the H33N and H39Q mutations so that His 26 is the only histidine capable of denatured state loop formation, the N52I mutation for stability (22) and the C102S mutation to prevent disulfide dimerization during physical studies, was prepared and purified from S. cerevisiae as previously described (19). The AcA25H26I52 variant adds the P25A mutation to the AcH26I52 variant. It was prepared using single-stranded pRS/C7.8 vector DNA containing the AcTM variant (T(−5)S, K(−2)L, H26N, H33N, H39Q and C102S relative to wild type) of iso-1-cytc (16) as template for the unique restriction site elimination method (23). The SacI+II− and SacI−II+ selection oligonucleotides (16) were used, as appropriate. The SacI+II− oligonucleotide eliminates a unique SacII site and creates a SacI restriction enzyme site upstream from the iso-1-cyt c gene (CYC1, see ref. 24). The SacI−II+ oligonucleotide does the opposite. The Asn 52→Ile mutation was introduced using the N52I oligonucleotide, 5′-d(TTTCTTGATGATGCCATCTGTGT)-3′ (site of mutation is underlined), and the SacI+II− selection oligonucleotide. The Pro 25→Ala mutation was then added using the P25A oligonucleotide, 5′-d(CAACCTTGTTGGCGCCACCCTTT)-3′ and the SacI−II+ selection oligonucleotide. Finally, the Asn 26→His mutation was added using the A25H26 oligonucleotide 5′-d(AACCTTGTGGGCGCCACCCTT)-3′ and the SacI+II− selection oligonucleotide. All mutations were confirmed by dideoxy sequencing. The pRS/C7.8 vector containing the AcA25H26I52 variant was transformed into the GM-3C-2 S. cerevisiae cell line (ref. 25, cytochrome c deficient) and the transformants characterized, as described previously (21). Expression and purification were carried out as for the AcH26I52 variant.

Protein stability measurements

The stability of the AcA25H26I52 variant was monitored as a function of gdnHCl concentration using an Applied Photophysics Chirascan circular dichroism spectrometer coupled to a Hamilton MICROLAB 500 Titrator using methods described previously (26). Data were acquired at 25 °C and pH 7.0 in the presence of 20 mM Tris, 40 mM NaCl as buffer. The data were fit to a linear free energy relationship, as described previously (21), to extract the free energy of unfolding in the absence of denaturant, ΔG^o′_u(H₂O), and the m-value. We use a constant native state baseline in fitting our data, as discussed previously (21). Reported parameters are the average and standard deviation of three independent trials.

Equilibrium His-heme binding in the denatured state

pH titrations to monitor His-heme binding in the denatured state (3 M gdnHCl, 5 mM Na₂HPO₄, 15 mM NaCl) of the AcA25H26I52 variant at 1, 3, 7.5 and 15 μM protein concentration were carried out with a Beckman DU800 UV-Vis spectrometer. Titrations were carried out at room temperature (22 ± 1 °C). Spectra from 350 to 450 nm were acquired at each pH. Titration procedures have been described previously (15). Data at 398 nm versus pH were fit to a modified form of the Henderson-Hasselbalch equation allowing extraction of the apparent pK_a for His-heme binding, pK_a(obs), and the number of protons, n, involved in the process. Reported parameters are the average and standard deviation of three independent trials.

The concentration dependence of pK_a(obs) was fit to a model that assumes a competition between intramolecular His-heme loop formation, K_C, and His-heme dimerization, K_A (eq 1, see

$$p{K}_a(\mathit{obs})=-log\left(\frac{K_C+\sqrt{{K_C}^2+4K_A{[\mathit{Cytc}]}_t}}{2}\right)$$ (1)

Figure 2 in Results). A derivation of this equation is provided in Supporting Information.

Figure 2.

Reaction scheme for intramolecular loop formation in competition with intermolecular dimerization.

pH dependent stopped-flow kinetic measurements

In order to monitor the breakage and formation of the His-heme bond in the denatured state of the AcH26I52 variant, stopped flow mixing methods were used, and reactions were monitored by absorbance spectroscopy (Applied Photophysics PiStar 180 spectrometer) at 398 nm and 25 °C to observe the Soret band shift resulting from His-heme bond formation or breakage (15). For pH dependent His-heme bond formation reactions, a 2 mm pathlength and 2 μL flow cell were used, and the final reaction mixture was obtained from 1:1 mixing of 30 μM AcH26I52, 3 M gdnHCl, 5 mM acetate pH 3.10, with 3 M gdnHCl, 100 mM buffer to achieve the desired ending pH (MES, pH 5.5–7.0; MOPS, pH 6.5–8.0). The loop breakage reaction, using a pathlength of 10 mm and a 20 μl flow cell, was initiated by 1:1 mixing of 6 μM AcH26I52, 3 M gdnHCl, 5 mM MOPS, pH 7.10 with 3 M gdnHCl, 100 mM buffer to achieve the desired ending pH (acetate, pH 3.7–5.5). Final reaction pH was determined by collecting the product of the mixing reaction and immediately measuring pH. Using the method of reduction of 2,6-dichlorophenolindophenol (27), 0.7 ms and 1.2 ms dead times were determined for the 2 μl and 20 μL flow cells, respectively, under our mixing conditions.

Continuous flow measurements as a function of pH

The rates of denatured state His-heme bond formation for the AcH26I52 variant were on the edge of the range accessible to stopped-flow mixing methods at higher pH. Therefore, continuous flow mixing methods were used to confirm stopped-flow mixing results. Continuous flow mixing methods with an efficient capillary mixer have been described in detail previously (28–31). Briefly, stock solutions of the AcH26I52 variant at 50 μM were prepared in 3 M gdnHCl and 5 mM acetate buffer, pH 4.0. The loop formation reaction was initiated by a five fold dilution of the protein stock solution by 200 mM buffer, 3 M gdnHCl, to reach a final reaction mixture of 3 M gdnHCl, 10 μM protein at the desired ending pH (MES pH 6.0; MOPS pH 7.75). Final reaction pH was determined by collecting the product of the mixing reaction and immediately measuring the pH. Reactions were monitored using continuous flow ultrafast mixing absorbance spectroscopy (28, 30) with a 0.9 mL/s flow rate at 395 nm and 25 °C to observe the Soret band shift which indicates His-heme bond formation. A dead time of 60 ± 10 μs was measured using ascorbate reduction of 2,6-dichlorophenolindophenol as a test reaction (27, 31). Data reduction and analysis were carried out as described previously (18).

Sequential stopped-flow mixing methods

Due to the presence of a double exponential with 1:1 stopped flow mixing, sequential mixing (Applied Photophysics PiStar 180 spectrometer) was used to separate the slow and fast phases in both the formation and breakage reactions. The initial “pre-mix” reaction was a 1:1 mix of 60 μM protein, 3 M gdnHCl, 1 mM MOPS, pH 7.0 (formation), or 1 mM acetate, pH 3.75 (breakage), with 10 mM acetate, pH 4.1 (formation), or 10 mM MOPS, pH 7.1 (breakage), 3 M gdnHCl. This “pre-mix” was held for a range of aging times (5 – 5000 ms). After the appropriate aging time, another 1:1 mixing reaction was carried out with the “pre-mix” (30 μM protein, 3 M gdnHCl, pH 4.1 or 7.1) and 3 M gdnHCl, 100 mM buffer at the desired ending pH (acetate, pH 3.75, for breakage; MOPS, pH 7.1, for formation). The final product is 15 μM protein, 3 M gdnHCl at the desired ending pH. Reaction pH is measured by immediately taking the final product and measuring the pH. Pathlength was 2 mm and the volume of the flow cell was 2 μl. The dead time for the reaction was measured by the instrument during the experiment and was approximately 1 ms. Data were fit to double exponential decay or rise to maximum equations, as appropriate.

Stopped-flow mixing as a function of protein concentration

In order to monitor the concentration dependence of breakage and formation of the histidine-heme bond in the denatured state for the AcH26I52 and AcA25H26I52 variants, stopped-flow mixing methods were used, and reactions were monitored by absorbance spectroscopy (Applied Photophysics SX20 stopped-flow spectrometer) at 398 nm and 25 ºC to observe the Soret band shift (15). A 5 μL flow cell was used for both His-heme bond formation and breakage reactions. The 5 mm pathlength of the flow cell was used for low protein concentrations (2, 3.75 and 7.5 μM), while the 1 mm pathlength was used for higher protein concentrations (15, 30, 45 and 60 μM). The starting buffer for His-heme bond formation reactions was 10 mM acetate, pH 4.10, in 3 M gdnHCl. The ending buffer was 100 mM MOPS, pH 7.10, in 3 M gdnHCl. Final reaction mixtures for His-heme bond formation reactions were obtained by a 1:1 mixing of starting buffer (with a 2X protein concentration) and ending buffer. The 3 M gdnHCl concentration was verified by refractive index measurements (32). The starting buffer for His-heme bond breakage reactions was 10 mM MOPS, pH 7.1, in 3 M gdnHCl. The ending buffer was 100 mM acetate, pH 3.75, in 3 M gdnHCl. For both upward and downward pH jump experiments, final reaction pH was determined by collecting the product of the mixing reaction and immediately measuring pH. The starting and ending pH values for these experiments were selected based on the pH dependent loop formation kinetics such that loop formation or breakage would go to completion. Reduction of 2,6-dichlorophenolindophenol by ascorbate (27) gave a 0.7 ms dead time for the 5 μl flow cell, under our mixing conditions. The time axis of the data was adjusted for the dead time prior to fitting to triple or quadruple exponential functions. The appropriateness of the fitting function was judged by comparing residuals (for details see Supporting Information).

RESULTS

Global stability of the AcA25H26I52 variant

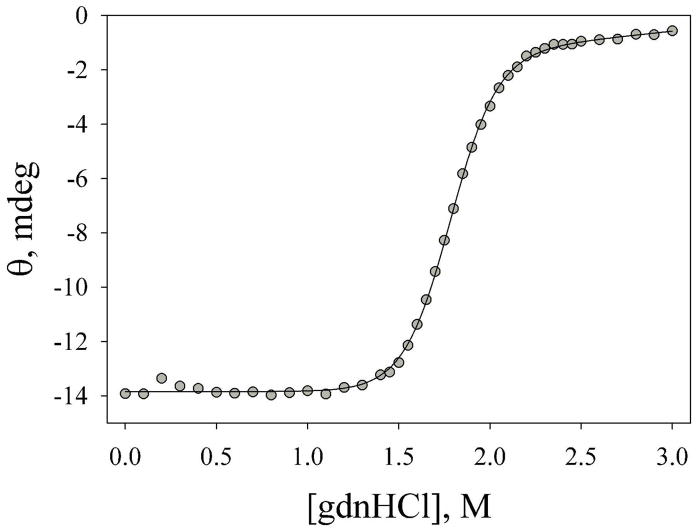
The global stability of the AcA25H26I52 variant was measured by gdnHCl denaturation yielding ΔG^o′_u(H₂O) = 7.8 ± 0.5 kcal/mol (Figure 1). The P25A mutation destabilizes the AcA25H26I52 variant by ~1.5 kcal/mol relative to the AcH26I52 variant (ΔG^o′_u(H₂O) = 9.37 ± 0.24, see ref. 19). It is clear from Figure 1 that the AcA25H26I52 is fully unfolded in 3 M gdnHCl, the conditions used for denatured state His-heme bond formation and breakage experiments.

Figure 1.

Plot of ellipticity versus gdnHCl concentration for the AcA25H26I52 variant at 25 °C. The solid line is a fit of the data to a two state model assuming a linear dependence of ΔG^o′_u on gdnHCl concentration. The fit yields m = 4.4 ± 0.3 kcal/(mol×M) and C_m = 1.79 ± 0.02 M. ΔG^o′_u(H₂O) is reported in the text. The errors are the standard deviation of parameters from three experiments.

Denatured state His-heme bond formation for the AcA25H26I52 variant

Intramolecular His-heme bond formation in the denatured state (3 M gdnHCl) leads to a nine residue loop when a histidine is at position 26 of iso-1-cytc (Figure 2). Spectroscopically monitored pH titrations yield an apparent pK_a, pK_a(obs), and the number of protons, n, involved in the process (inset to Figure 3, Table S1). For intramolecular loop formation, the pK_a(obs) should be independent of protein concentration. However, if there is an intermolecular component (Figure 2), His-heme bond formation will be favored by mass action as cytc concentration increases. Thus, intermolecular His-heme bond formation will cause the pK_a(obs) to decrease as cytc concentration increases.

Figure 3.

Plot of pK_a(obs) versus concentration for the AcA25H26I52 (●) and AcH26I52 (▲) variants and two other previously reported variants, AcH22 (□) and AcH27 (△). Error bars are the standard deviation of pK_a(obs) from three independent experiments. All data were acquired at 22 ± 1 °C in 3 M gdnHCl containing 5 mM Na₂HPO₄ and 15 mM NaCl. Data for the AcH22, AcH26I52 and AcH27 variant are from refs. 15 and 17. Solid (AcH26I52 and AcA25H26I52) and dashed lines (AcH22 and AcH27) are shown for fits to the equilibrium model in Figure 2 (Eq 1, Experimental Procedures). Inset: pH titration of AcA25H26I52 at 7.5 μM protein concentration in 3 M gdnHCl. The solid curve is a fit of the data to the Hendersen-Hasselbalch equation with the number of protons released allowed to vary. The values of pK_a(obs) and the number of protons, n, for the AcA25H26I52 variant at concentrations ranging from 1 to 15 μM are collected in Table S1 (Supporting Information).

Figure 3 shows the concentration dependence of the denatured state pK_a(obs) (3 M gdnHCl) for the AcA25H26I52 variant and the AcH26I52 variant. Data for two other variants (17), AcH22 (His 22, 5 residue intramolecular loop) and AcH27 (His 27, 10 residue intramolecular loop) are provided for comparison. For the AcH27 variant, the concentration dependence of pK_a(obs) is slight. The pK_a(obs) is strongly concentration dependent for the AcH26I52 and AcH22 variants and moderately so for the AcA25H26I52 variant. The data fit well to the equilibrium model in Figure 2 (Eq 1, Experimental Procedures), yielding apparent binding constants (Table 1) for intramolecular His-heme loop formation (K_C) and intermolecular His-heme binding (K_A). For the AcH27 variant the apparent pK_a extrapolated to 0 M protein concentration, pK_a(obs)₀ (Table 1) is identical to the pK_a(obs) at 1 μM protein concentration (17), consistent with the minor intermolecular component observed for this variant. K_A varies over two orders of magnitude (Table 1). Surprisingly, the single site mutation P25A in the AcA25H26I52 variant versus the AcH26I52 variant decreases K_A for His 26 as the heme ligand by ~10-fold, indicating that aggregation in the denatured state can be strongly dependent on local sequence.

Table 1.

Apparent intramolecular and intermolecular His-heme binding constants in the denatured state for iso-1-cytochrome c variants.^a

Variant	Intramolecular loop size	KC (M)	KA (M)	pKa(obs)0b
AcH22	5	–c	2.3 ± 0.3 × 10−5	–c
AcH26I52	9	– c	7 ± 13 × 10−5	–c
AcA25H26I52	9	4.4 ± 2.4 × 10−7	2.6 ± 0.3 × 10−6	6.35 ± 0.24
AcH27	10	1.9 ± 0.2 × 10−6	1.3 ± 0.7 × 10−7	5.72 ± 0.04

^aData were acquired in 3 M gdnHCl at 22 ± 1 °C.

^bApparent pK_a extraplated to 0 M cytochrome c concentration.

^cMeaningful values could not be obtained for these variants from the fit to eq 1.

In the sections that follow, we use kinetic methods to probe the factors that cause this difference in denatured state aggregation between the AcH26I52 and AcA25H26I52 variants due to the mutation of Pro 25 to Ala. We first probe the pH dependence of His 26-heme bond formation and breakage as an initial step in characterizing intramolecular versus intermolecular kinetic phases using the AcH26I52 variant. We then confirm these assignments for the AcH26I52 variant with double jump stopped-flow experiments. Finally, we characterize the concentration dependence of the kinetics for both variants over a 30-fold concentration range.

His 26-heme bond formation and breakage kinetics as a function of pH for the AcH26I52 variant

Rates of His 26-heme bond formation and breakage in the denatured state (3 M gdnHCl) as a function of pH were measured by both stopped-flow and continuous flow mixing methods. Fast and slow phases were observed for both upward and downward pH jump experiments (Table S2). The rate constant for the fast phase increases with increasing pH (Figure 4) as observed for intramolecular loop formation with other single histidine variants of iso-1-cytc (18). The fit of the data in Figure 4 to the mechanism in the inset to Figure 4 yields k_f = 930 ± 60 s⁻¹ and k_b = 280 ± 10 s⁻¹. These values of k_f and k_b give K_loop = k_f/k_b = 3.3 ± 0.3. The pK_a obtained from the fit, 6.1 ± 0.1, is reasonably consistent with deprotonation of His 26 prior to loop formation. Thus, the fast phase appears to be attributable to intramolecular His-heme loop formation in the denatured state of this protein.

Figure 4.

Plot of k_obs versus pH for the fast phase of His 26-heme bond formation and breakage for the AcH26I52 variant. The stopped flow data for downward (●) and upward (▲) pH jumps are shown with error bars corresponding to one standard deviation. For continuous flow upward pH jump data (□) the error is smaller than the size of the symbol. The inset shows the mechanism for loop formation used to fit the pH dependence of k_obs (see ref. 18). The solid curve is a fit of the data to this mechanism. As previously (18), the k_b reported in the text is the average and standard deviation of the four lowest pH data points.

Sequential stopped-flow mixing

If the fast His 26-heme bond formation and breakage phases in the denatured state are truly linked to the same reaction and are distinct from the slow phases, double jump stopped-flow experiments should confirm this assignment. Based on the data in Figure 4, we have used a pH of 7 to form His-heme bonds and a pH of 4 to break His-heme bonds in the denatured state (3 M gdnHCl).

Double jump experiments for His 26-heme bond formation (pH 7 to 4 to 7) were carried out with aging times from 5 to 5000 ms at pH 4 (Figure S1, Table S3). At short aging times, a fast (1000–2000 s⁻¹) His 26-heme bond formation phase dominates. At short aging times the amplitude of the slow phase (~1 s⁻¹) is initially small and negative. The amplitude of the slow phase goes through zero at an aging time of ~75 ms and then becomes positive (Figure 5A). A fit of the amplitude versus time data yields a rate constant ~5.5 s⁻¹ (see caption to Figure 5A).

Figure 5.

(A) Plot of amplitude versus aging time for the slow phase formation of the histidine-heme bond for two separate experiments (●, ○) for the AcH26I52 variant. The lines are fits to a single exponential rise to maximum equation. The rate constant for the growth of the slow phase amplitude for each data set is k = 5.2 ± 0.8 (●, solid line) and k = 5.8 ± 0.5 (3, dashed line). (B) Plot of amplitude versus aging time for the slow (○) and fast (●) phases for breakage of the His 26-heme bond for the AcH26I52 variant. Solid lines are fits to a single exponential equation and give rate constants of k = 2.8 ± 0.4 s⁻¹ and 1.9 ± 1.2 s⁻¹ for the slow and fast phase amplitudes, respectively.

The negative amplitude observed for the slow phase at short aging times can be explained by a reversal of intermolecular His 26-heme binding as the protein concentration is rapidly decreased from 60 to 15 μM in the sequential mixing experiment. Double-jump mixing experiments with an aging time of 2000 ms demonstrate that the fast phase is independent of protein concentration whereas the slow phase is concentration dependent and thus must be intermolecular (Table S4).

In double-jump His-heme bond breakage experiments (pH 4 to 7 to 4, Figure S2, Table S5), a fast phase (300–400 s⁻¹) dominates at short aging times. The amplitude for the slow phase (~5 s⁻¹) increases as aging time increases in parallel with a decrease in the fast phase amplitude (Figure 5B). The rate constants for the growth of the slow phase amplitude and the reduction of the fast phase amplitude are within error the same (~2.5 s⁻¹, see caption Figure 5B).

We note that the observed rate constant of 5.0 ± 1.2 s⁻¹ for the slow phase in the double jump His 26-heme bond breakage experiments (Table S5) matches the rate constant of ~5.5 s⁻¹ at which the slow amplitude grows in double-jump His-heme bond formation experiments. Similarly, the rate constant for slow His 26-heme bond formation at 30 μM protein concentration (2.1 ± 0.02 s⁻¹, see Table S4) is similar to the rate constant of ~2.5 s⁻¹ for the growth of the slow phase amplitude in double-jump His 26-heme bond breakage experiments (aging at pH 7 is done at 30 μM AcH26I52 in the double-jump His 26-heme bond breakage experiments). Thus, growth of the amplitude of slow His 26-heme bond breakage requires formation of the His 26-heme bonds that form at a slow rate and growth of the amplitude of slow His 26-heme bond formation requires breakage of the His 26-heme bonds that break at a slow rate. Therefore, double-jump experiments establish that slow His 26-heme bond formation is linked to slow His 26-heme bond breakage and fast His 26-heme bond formation is linked to fast His 26-heme bond breakage.

The effect of Pro 25 on the concentration dependence of the rates of denatured state His 26-heme bond formation and breakage

The equilibrium data in Figure 3 and Table 1 show that simple mutation of Pro 25→Ala diminishes the intermolecular component of His 26-heme bond formation in the denatured state (3 M gdnHCl). To probe the basis for this difference, the concentration dependence of both His 26-heme bond formation and breakage was examined using pH jump experiments in 3 M gdnHCl for both the AcH26I52 and AcA25H26I52 variants. The observed kinetics is complex, requiring 3 to 4 exponential components to provide satisfactory fits to the data (Tables S6 to S9 and Figures S5 to S8).

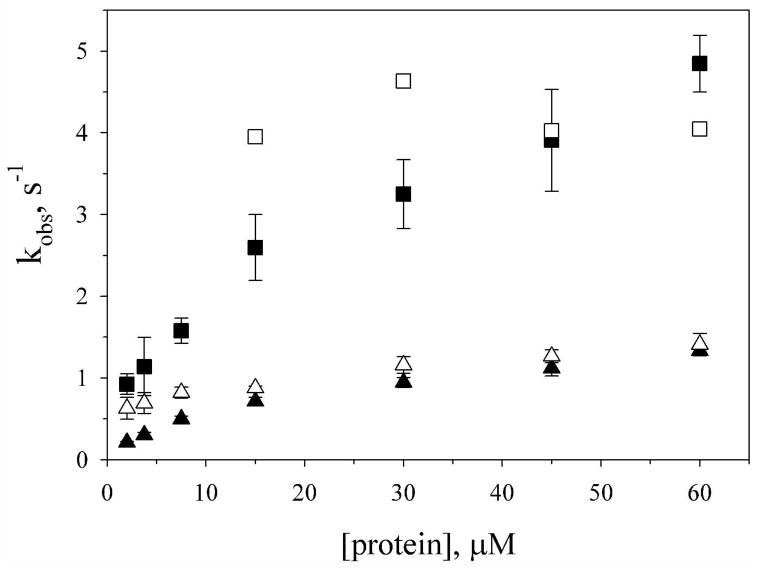
For upward pH jump data (His-heme bond formation), the best fit for both variants is obtained using a quadruple exponential function. The fractional amplitudes of three of the phases are nearly invariant with protein concentration (Figures S3 and S4). The fourth phase diminishes in fractional amplitude as concentration increases and is likely due to a small artifact observed in absorbance data near 2 ms (see Supporting Information). Disregarding this phase, a fast phase with a rate constant near 1600 s⁻¹ (AcH26I52, 1650 ± 350 s⁻¹; AcA25H26I52, 1580 ± 200 s⁻¹) and two slow phases are observed. The ability to discern two slow phases in these experiments versus the double jump experiments likely results from the superior signal to noise of the SX20 stopped-flow spectrometer used in the single jump experiments. Both slow phases are concentration dependent for the AcH26I52 variant (Figure 6), with k_obs leveling off at higher protein concentration. For the AcA25H26I52 variant, the faster of the two slow phases is not observed at lower protein concentration and within error is independent of protein concentration (4 ± 1 s⁻¹, Figure 6). The slower of the two phases is concentration dependent.

Figure 6.

Concentration dependence of the slow phase rate constants for His-heme bond formation from upward pH jump experiments with the AcH26I52 (■, ▲) and AcA25H26I52 (□, △) variants. Concentration is final concentration after mixing. Data were acquired at 25 °C in 3 M gdnHCl as described in the Experimental Procedures. The error bars are one standard deviation of the mean. For clarity, errors bars of ~ ±1 s⁻¹ are omitted for the faster of the two slow phases (□) for the AcA25H26I52 variant.

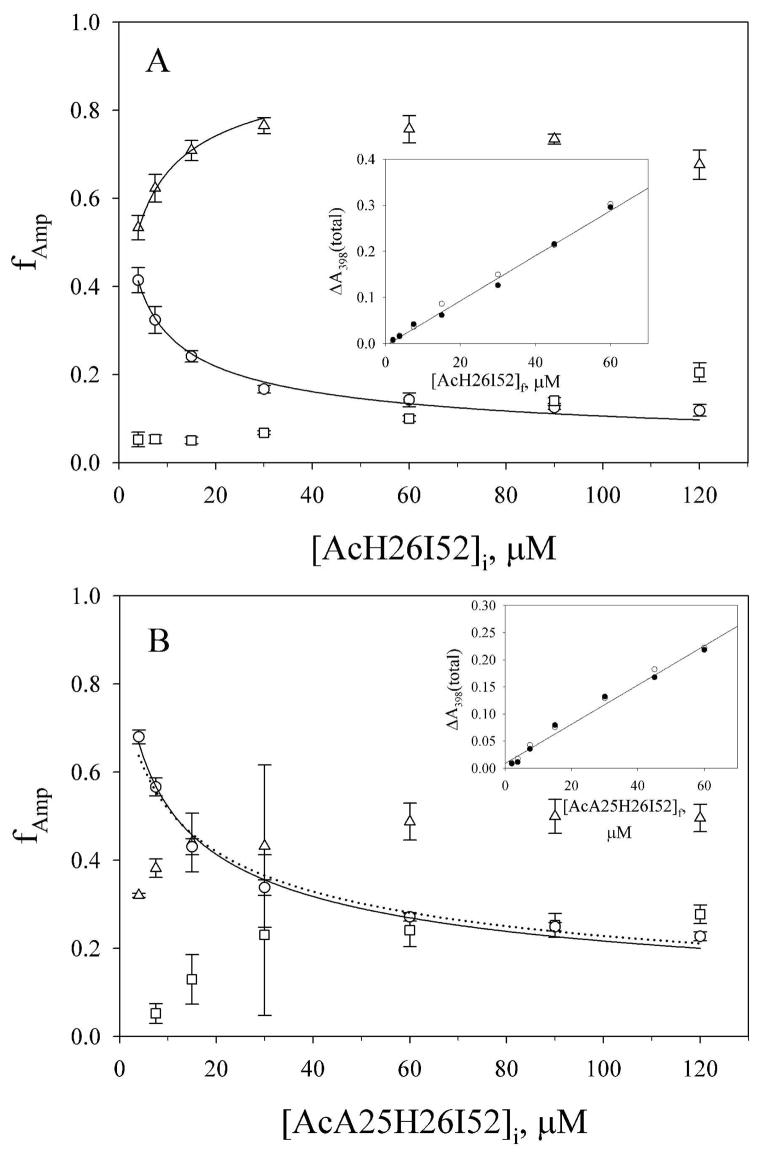
For downward pH jump data (His-heme bond breakage), three kinetic phases are observed for both proteins. The rate constants for these phases appear to be independent of protein concentration (AcH26I52, 254 ± 27 s⁻¹; 36 ± 12 s⁻¹ and 6.5 ± 0.3 s⁻¹; AcA25H26I52, 243 ± 10 s⁻¹; 40 ± 7 s⁻¹ and 20.7 ± 1.5 s⁻¹). At the lowest concentration of protein used, the intermediate phase is not discernible for the AcA25H26I52 variant. For both variants, at low protein concentration, the fractional amplitude, f_Amp, for the fast phase for loop breakage is similar to or larger than f_Amp for the slow phase (Figure 7). At higher concentration of protein, the slow phase dominates the amplitude for the breakage reaction, although the concentration dependence of the fractional amplitudes of the three phases saturates above ~ 30 μM initial protein concentration. The total amplitudes for His 26-heme bond breakage and His 26-heme bond formation are similar to each other and are linearly dependent on protein concentration (insets in Figure 7) indicating that the full reaction is being detected in both directions and at all protein concentrations.

Figure 7.

Concentration dependence of the fractional amplitudes, f_Amp, of the kinetic phases for His 26-heme bond breakage in downward pH jump experiments for the (A) AcH26I52 and (B) AcA25H26I52 variants of iso-1-cytc. Data were acquired at 25 °C in 3 M gdnHCl as described in Experimental Procedures. The f_Amp for the fast phase (○), the intermediate phase (□) and the slow phase (△) are shown with error bars derived from standard propagation of the error in the observed amplitudes. The concentrations prior to mixing, [AcH26I52]_i and [AcA25H26I52]_i, are plotted on the x-axes, since f_Amp reflects the equilibrium distribution of species prior to mixing. The solid lines are fits to the equilibrium model in Supporting Information as described in the Discussion. The dotted line in panel B is a fit to Eq 2 (Discussion) with the K_loop(obs) constrained to 4.65. The inset in each panel shows the total amplitude, ΔA₃₉₈(total), versus protein concentration after mixing, [AcH26I52]_f and [AcA25H26I52]_f, for the His 26-heme bond formation (●) and breakage (○) reactions. The solid line is a linear fit to ΔA₃₉₈(total) versus protein concentration for the His 26-heme bond formation amplitudes.

Comparison of the fast phases due to intramolecular loop formation and breakage from these concentration dependent kinetic experiments with the fast phases from the pH-dependent His 26-heme bond formation/breakage experiments in Figure 4 shows that the rate constants obtained for loop formation, k_f, and loop breakage, k_b, are similar. The magnitudes of k_b obtained for His 26-heme bond breakage at pH 3.75 for the AcH26I52 and AcA25H26I52 variants (~250 s⁻¹) are similar to k_b ~ 280 s⁻¹ obtained for the AcH26I52 variant in Figure 4. Based on the mechanism in the inset to Figure 4, k_f for intramolecular loop formation from the protein concentration dependent kinetic experiments can be approximated as the difference between the fast rate constant for His 26-heme bond formation at pH 7.1 and the fast breakage rate constant at pH 3.75. This approximation yields k_f of 1400 ± 380 s⁻¹ and 1340 ± 210 s⁻¹ for the AcH26I52 and AcA25H26I52 variants, respectively. Again, these values are reasonably similar to k_f = 930 ± 60 s⁻¹ observed with the pH dependent data for the AcH26I52 variant in Figure 4.

DISCUSSION

Our equilibrium data on the effect of protein concentration on His-heme bond formation in the denatured state of iso-1-cytc demonstrate that the contribution of the intermolecular reaction drops off rapidly with the distance of the histidine from the heme (Table 1). His 22, which is 5 residues from the heme, has a 100-fold larger intermolecular equilibrium constant, K_A, than His 27 which is 10 residues from the heme. We also find that the intermolecular reaction is very sensitive to local sequence. The Pro→25 Ala mutation decreases K_A for His 26 by ~10-fold. Comparison with data for iso-2-cytc also supports this sensitivity to local sequence (12). For iso-1-cytc, pK_a(obs) = 5.3 at 60 μM protein concentration, much higher than would be expected if an intermolecular reaction was occurring. Thus, the small sequence differences between iso-1- and iso-2-cytc for the residues in between His 26 and the heme (Val 20→Ile and Lys 22→Glu) clearly affect intermolecular aggregation as is observed for the Pro 25 Ala mutation. Aggregation is also strongly dependent on solution conditions. Data for the AcH26I52 variant in 6 M gdnHCl (15) yield K_A = 1.3 ± 1.0×10⁻⁶ M, an order of magnitude lower than in 3 M gdnHCl. Thus, the intermolecular aggregation we observe here is likely to be more prominent under folding conditions.

An interesting feature of our concentration dependent kinetic data is that the amplitudes of His 26-heme bond formation phases are independent of protein concentration (Figures S3 and S4), whereas the amplitudes of His 26-heme bond breakage phase are strongly concentration dependent (Figure 7). For His 26-heme bond formation, the fast intramolecular phase always dominates. By contrast, for His 26-heme bond breakage the fast intramolecular phase diminishes in importance rapidly as protein concentration increases. Thus, it is evident that aggregation is under equilibrium control. Previous models for the outcome of aggregation versus folding are based on kinetic partitioning between irreversible folding and aggregation reactions (20). We develop a model for equilibrium control of partitioning between folding (or loop formation) and aggregation, compare the predictions of the two models and discuss the implications for evolution of proteins. First we discuss the nature of the slow aggregation phases and then we use our data to extract equilibrium and kinetic parameters necessary to compare kinetically irreversible and equilibrium models for aggregation.

Nature of the slow phases for loop formation and breakage

The concentration dependence of the slow phases for His 26-heme bond formation clearly indicates an intermolecular process. For the AcH26I52 variant, adequate fits of the data are obtained with two exponential decays of similar amplitude with rate constants that differ by a factor of ~3 (Fig. 5, Table S6). This method of fitting the data is clearly an over-simplification. However, attempts to fit the data to a simple 2^nd order rate process produced worse fits. The two slow phases for His 26-heme bond formation are matched by two slow phases for His-heme bond breakage. In Fig. 7, the amplitude of the slowest His 26-heme bond breakage rate (6.5 ± 0.3 s⁻¹) starts to lose amplitude to the intermediate breakage rate (36 ± 12 s⁻¹) at high concentration of the AcH26I52 variant. This observation suggests that at high concentration, higher order (less kinetically stable) aggregates have formed. It is also possible that the two different slow phases represent intermolecular His 26-heme bond formation and breakage with the Gly 24-Pro 25 peptide bond in cis versus trans conformations. However, this is inconsistent with the observed decrease in the amplitude of the slower breakage rate at higher concentrations of the AcH26I52 variant. Thus, the data support a mechanism involving His-heme dimerization at lower protein concentrations with contributions from higher order aggregation at higher concentrations.

For the AcA25H26I52 variant, two slow phases for His 26-heme bond formation and breakage are also observed. The rate of the dominant slow phase (0.6 – 1.4 s⁻¹) for His 26-heme bond formation depends on the concentration of the AcA25H26I52 variant, whereas the lower amplitude slow phase (~4 s⁻¹), which only appears at =15 μM final concentration, does not. The reason for the lack of concentration dependence is unclear (although the large error bars on this rate constant may obscure concentration dependence). The rate constants for the two slow His 26-heme bond breakage phases are too similar (40 ± 7 s⁻¹ and 20.7 ± 1.5 s⁻¹) to be fully resolved.

Comparing AcH26I52 to AcA25H26I52, both have a slow phase for His 26-heme bond breakage with a rate near 40 s⁻¹. However, the slower of the two His 26-heme bond breakage phases is ~3-fold faster for the AcA25H26I52 variant. Thus, both have intermolecular processes attributable to dimerization and higher order aggregation. The higher order aggregates appear to have similar kinetic stability.

Extraction of equilibrium parameters from the kinetics of intramolecular loop formation

For both variants, the fractional amplitudes of the fast and slow phases of His 26-heme bond formation are nearly invariant with protein concentration (Figures S3 and S4) indicating that the amplitudes are controlled by the relative rates of the individual processes. The average fractional amplitude of the fast His 26-heme bond formation phase, f_fast, across all protein concentrations studied is 0.70 ± 0.04 for the AcH26I52 variant and 0.79 ± 0.04 for the AcA25H26I52 variant. Thus, the fractional amplitude of the fast phase assigned to intramolecular loop formation can be used to obtain an apparent equilibrium constant for loop formation, K_loop(obs) = f_fast/(1−f_fast), at pH 7.1 (Table 2). The values are similar to the intramolecular equilibrium constant for the AcH26I52 variant derived from the pH dependence of k_obs (Figure 4).

Table 2.

Equilibrium parameters for intramolecular and intermolecular His 26-heme bond formation at pH 7.1 and 25 °C.

Parameter and Method of Evaluation	Variant
	AcH26I52	AcA25H26I52
Kloop(obs)
pH dependent kinetics	3.3 ± 0.3a	–
ffast: His-heme bond formation amplitudes	2.3 ± 0.3	3.8 ± 0.8
kf(fast)/kb(fast)	5.5 ± 1.6	5.5 ± 0.9
ffast: His-heme bond breakage amplitudes	8.7 ± 0.3	16.1 ± 0.9
fslow: His-heme bond breakage amplitudes	10.6 ± 0.3	–b
Kinter(obs)
ffast: His-heme bond breakage amplitudes	3.00 ± 0.08×107 M−1	2.1 ± 0.2×107 M−1
fslow: His-heme bond breakage amplitudes	3.00 ± 0.07×107 M−1	–b

^aK_loop(obs) is for fully deprotonated His 26 in this case, ie., K_loop. Correcting to pH 7.1 with K_loop(pH) = K_loop/(1 + 10 ^{(pK_a − pH)}) using pK_a = 6.6 for His 26 (15) yields K_loop(obs) ~ 2.5.

^bThe data deviate too strongly from simple dimerization in competition with intramolecular loop formation equilibrium to fit f_slow to this model.

K_loop(obs) at pH 7.1 can also be estimated from the measured rate constants for the fast forward and back reactions (k_f(fast)/k_b(fast)) for intramolecular loop formation obtained from our kinetic studies on the AcH26I52 and AcA25H26I52 variants versus protein concentration. The values for K_loop(obs) obtained in this way are similar to those obtained from the fast amplitude data, f_fast, for His 26-heme bond formation (Table 2).

Extraction of equilibrium properties for intermolecular association from the kinetics of His 26-heme bond breakage

The fractional amplitude data for loop breakage as a function of protein concentration (f_Amp for the fast phase in Figure 7) provides information about the relative contributions of intra- and intermolecular His 26-heme bond formation, since these species are at equilibrium prior to the downward pH jump. Since all downward pH jump experiments start at pH 7.1, we can evaluate apparent equilibrium constants, K_loop(obs) and K_inter(obs), for denatured state intramolecular loop formation and intermolecular association, respectively, at this pH. We approximate the equilibrium with the simplest possible model: His-heme dimerization in competition with intramolecular loop formation. The fraction of protein which forms an intramolecular loop, f_loop, is given by eq 2 for this model (see Supporting Information). This equation was used to fit to fit the fast phase amplitude for the loop breakage reaction as a function of

$$f_{\mathit{loop}}=\frac{-\left(1+\frac{1}{K_{\mathit{loop}}(\mathit{obs})}\right)+\sqrt{{\left(1+\frac{1}{K_{\mathit{loop}}(\mathit{obs})}\right)}^2+8\left(\frac{K_{\text{inter}}(\mathit{obs})}{K_{\mathit{loop}}{(\mathit{obs})}^2}\right){[\mathit{Cytc}]}_t}}{4\left(\frac{K_{\text{inter}}(\mathit{obs})}{K_{\mathit{loop}}{(\mathit{obs})}^2}\right){[\mathit{Cytc}]}_t}$$ (2)

[Cytc]_i (open circles in Figure 7 A/B) to obtain K_loop(obs) and K_inter(obs) (Table 2). K_inter(obs) is of the same order of magnitude for both variants, in contrast to the results from the concentration dependence of pK_a(obs) (Table 1). However, the parameters obtained from fits to eq 2 are sensitive to small errors in the data. If we constrain K_loop(obs) to 4.65 (the average value from amplitude and rate constant data for the fast phase of His-heme bond formation/breakage for the AcA25H26I52 variant), the quality of the fit is only slightly diminished (dotted line Figure 7B) and we obtain K_inter(obs) = 1.5 ± 0.1×10⁶ M⁻¹ which is more in line with the results from the concentration dependent pK_a(obs) data. The poorer separation of dimerization and higher order aggregation for the AcA25H26I52 variant relative to the AcH26I52 variant (Figure 7) probably also affects the accuracy of K_inter(obs) obtained for the AcA25H26I52 variant.

For the AcH26I52 variant, the rise in the fractional amplitude of the slow breakage phase, f_slow (open triangles, Fig. 7A), can be fit to the equilibrium model (for equations see Supporting Information) out to 30 μM protein concentration. The values for K_loop(obs)and K_inter(obs) are similar to those obtained by fitting eq 2 to f_fast (Table 2). Thus, our simple dimerization model is adequate to describe the data at relatively low concentrations of AcH26I52. For the AcA25H26I52 variant, dimerization and higher order aggregation are poorly separated. Thus, f_slow cannot be fit to a model involving simple loop formation in competition with dimerization.

How fast is bimolecular aggregation in the denatured state?

Reversible intermolecular aggregation has been found to affect the folding kinetics of a number of proteins (2, 3, 7–10). In these cases, aggregates accumulate during folding and are not pre-existing in the denatured state in strong denaturant. Although, for the proteins CI2 and U1A aggregation is believed to occur from the denatured state under folding conditions (2, 7, 8). The bimolecular rates for association of denatured protein molecules under folding conditions can be very fast, ranging from 3×10⁵ M⁻¹s⁻¹ to 4×10⁷ M⁻¹s⁻¹ for CI2 and U1A, respectively (2, 7, 8). We can estimate the bimolecular association rate constant, k_inter, for His 26-heme bond formation at pH 7.1 using K_inter(obs) and the slowest rate constant for His-heme bond breakage. For the AcH26I52 variant, we find k_inter = 2.0 ± 0.2 ×10⁸ M⁻¹s⁻¹. For the AcA25H26I52 variant, we find k_inter = 3.0 ± 0.3 ×10⁷ M⁻¹s⁻¹ (using K_inter(obs) = 1.5 ± 0.1 ×10⁶ M⁻¹). Thus, as for the U1A protein (2, 8), intermolecular association in the denatured state of these variants of iso-1-cytc is very fast.

Equilibrium versus irreversible kinetic control of aggregation

The impact of pathological protein aggregation in living cells depends on the competition between productive intramolecular folding and deleterious intermolecular aggregation. As seen here and in previous studies, the bimolecular rate for reversible intermolecular association can be very fast. Thus, competition between protein folding and protein aggregation has the potential to be problematic in living cells particularly if one or both processes are irreversible and thus kinetically-controlled. Therefore, it is instructive to compare the advantages and disadvantages of kinetic versus equilibrium control of this competition.

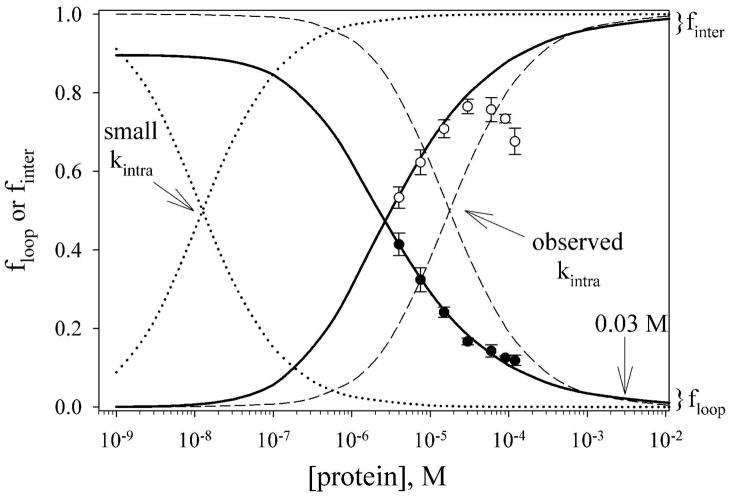
For the iso-1-cytc variants studied here, both intermolecular His 26-heme bond formation and intramolecular loop formation are reversible, and thus under equilibrium control. We examine this competition with the data for the AcH26I52 variant. Using the intramolecular loop formation/intermolecular dimerization equilibrium model described above and the parameters K_intra(obs) and K_inter(obs) obtained from the fits to the data in Fig. 7A we show the relative proportions of intramolecular loop formation versus intermolecular aggregation as a function of protein concentration (Figure 8, solid lines). For comparison, the predictions of an irreversible kinetic model (eq 3) for the competition between folding and aggregation (20) are shown (Figure 8, dashed line). Since k_intra(obs) at pH 7.1 is large for loop formation (~1400 s⁻¹),

Figure 8.

Comparison of equilibrium versus kinetic control for the production of intramolecular loops, f_loop, versus intermolecular His-heme dimers, f_inter, for the AcH26I52 variant. Curves for f_loop decrease as protein concentration increases and curves for f_inter increase as protein concentration increases. The solid curves show f_loop (eq 2) and f_inter (see Supporting Information) for the equilibrium model of intramolecular versus intermolecular competition using the parameters from the fit of f_fast for His-heme bond breakage to this model given in Table 2. Experimental data for intramolecular loop breakage (●, f_fast in Fig. 7A) and breakdown of intermolecular His-heme dimers (○, f_slow in Fig. 7A) for the AcH26I52 variant are shown against these curves. The deviation of these data from the solid curves at higher concentration is due to higher order aggregation. The calculated concentration dependencies for f_loop (eq 3) and f_inter (1−f_loop) assuming kinetic control of the partitioning between intramolecular and intermolecular reactions are shown with dashed curves. The pH 7.1 values, k_intra(obs) = 1400 s⁻¹ and k_inter(obs) = 2.0 × 10⁸ M⁻¹ s⁻¹ for the AcH26I52 variant, were used to generate these curves. The effect of reducing k_intra(obs) to 1 s⁻¹ on the concentration dependencies of f_loop and f_inter using the kinetic control model is shown with dotted curves.

$$f_{\mathit{loop}}=\frac{k_{\text{intra}}(\mathit{obs})}{{[\mathit{Cytc}]}_t\times k_{\text{inter}}(\mathit{obs})}\times ln\left(1+\frac{{[\mathit{Cytc}]}_t\times k_{\text{inter}}(\text{obs})}{k_{\text{intra}}(\mathit{obs})}\right)$$ (3)

in fact, irreversible kinetic control would have led to a considerably higher yield of the intramolecular product for the AcH26I52 variant over the concentration range of our experiments (Figure 8).

However, for many protein folding reactions, the rate of folding is considerably slower than the millisecond time scale (33). For comparison, the outcome for irreversible kinetic control is shown in Figure 8 (dotted line) if loop formation occurs on a 1 s time scale (k_intra = 1 s⁻¹) in competition with the very fast bimolecular His 26-heme reaction observed here. Clearly, kinetic control is highly disadvantageous if the intramolecular reaction is slow. Another aspect of equilibrium control is that the square root dependence of f_loop on [Cytc]_t for equilibrium control versus the logarithmic dependence of f_loop on [Cytc]_t for the kinetic model leads to a less abrupt fall-off in f_loop at higher protein concentrations (see Fig. 8). This would be advantageous for the yield of folded versus aggregated protein, as well.

In vivo, proteins must fold and operate in crowded environments, where concentrations of macromolecules approach 350 mg/mL (34). For a small protein like cytc this corresponds to a concentration of ~0.03 M. Under these conditions, fast folding kinetics (~1000 s⁻¹) will not permit competition with the very fast bimolecular aggregation we observe in the denatured state (see Fig. 8). However, if intermolecular interactions are kept modest and reversible (similar to K_inter(obs) = 3 × 10⁷ M⁻¹ observed for the AcH26I52 variant, Table 2) a protein of average stability (~5 kcal/mol) would form less than 0.1% aggregate even at 0.1 M concentration of macromolecules if the partitioning between folding and aggregation is under equilibrium control.

Thus, there are advantages for the folding versus aggregation competition to have evolved with equilibrium rather than kinetics controlling this partitioning in vivo. The observation that aggregation during folding can be reversible (2, 3, 7–10) and that protein sequences appear to have evolved to minimize aggregation prone sequences (6) supports this contention. The very fast bimolecular rate constants seen for oligomerization of denatured states (2, 7, 8) indicate that it would be difficult for folding to prevail over aggregation if kinetic control of this partitioning operated in the crowded environment of a cell. Clearly, chaperones have evolved to assist in making aggregation reversible when necessary and thus allow for productive folding for protein sequences that are not optimized for reversible aggregation (35).

Aggregation during the folding of cytochrome c

For horse heart cytochrome c reversible aggregation occurs during folding at high protein concentration (3). Given the results on intermolecular His 26-heme binding presented here, it is possible that the aggregation is mediated through His 26, although the presence of lysine at position 25 in the horse protein appears to make this process much less favorable than for Pro 25 or Ala 25, since aggregation is observed only above 30 μM protein concentration during folding. At the highest concentrations used in the horse cytc study (500 μM), irreversible kinetic control would have decreased the yield of folded protein to ~50%. With weak reversible aggregation, all of the protein reached the native state.

CONCLUSION

We have shown that reversible His 26-heme aggregation competes with intramolecular His 26-heme loop formation in the denatured state of iso-1-cytc. The bimolecular step in aggregation is very fast, indicating that intermolecular contacts between denatured proteins occur rapidly even in dilute solution. The thermodynamics of intermolecular His 26-heme binding depends strongly on the sequence proximity of the histidine to the heme and on the identity of residues adjacent to the histidine. For His 26, Pro 25 strongly enhances the intermolecular interaction relative to Ala 25, primarily by slowing breakdown of what appears to be an intermolecular dimer. We have developed an equilibrium model to analyze aggregation in the denatured state of these variants. Comparison of the predictions of this model with a previous irreversible kinetic model for aggregation shows that equilibrium control has evolutionary advantages in terms of productive partitioning between folding and aggregation.

Supplementary Material

1_si_001. SUPPORTING INFORMATION AVAILABLE.

Table S1 providing pK_a(obs) values as a function of concentration for the AcA25H26I52 variant, Table S2 providing pH dependent His-heme bond formation/breakage rate constants and amplitudes for the AcH26I52 variant, Tables S3 and S4 providing rate constants and amplitudes for double-jump His-heme bond formation experiments, Figure S1 showing double jump His-heme bond formation data, Table S5 providing rate constants and amplitudes for double-jump His-heme bond breakage experiments, Figure S2 showing double jump His-heme bond breakage data, Tables S6 to S9 providing rate constants and amplitudes for concentration dependent His-heme bond formation and breakage for the AcH26I52 and AcA25H26I52 variants, Figures S3 and S4 showing amplitudes for His-heme bond formation phases as a function of protein concentration for the AcH26I52 and AcA25H26I52 variants, Figures S5 to S8 showing typical kinetic data and data fits for concentration dependent His-heme bond formation and breakage for the AcH26I52 and AcA25H26I52 variants, derivations of equations 1 and 2 in the text and other equations used to fit data to the model for equilibrium competition between loop formation and aggregation by dimer formation are all provided as supporting information. This material is available free of charge via the Internet at http://pubs.acs.org.