Kinetic Analysis of Sequential Multi-step Reactions

Abstract

Many processes in biology and chemistry involve multi-step reactions or transitions. The kinetic data associated with these reactions are manifested by superpositions of exponential decays that are often difficult to dissect. Two major challenges have hampered the kinetic analysis of multi-step chemical reactions: (1) Reliable and unbiased determination of the number of reaction steps, (2) Stable reconstruction of the distribution of kinetic rate constants. Here, we introduce two numerically stable integral transformations to solve these two challenges. The first transformation enables us to deduce the number of rate-limiting steps from kinetic measurements, even when each step has arbitrarily distributed rate constants. The second transformation allows us to reconstruct the distribution of rate constants in the multi-step reaction using the phase function approach, without fitting the data. We demonstrate the stability of the two integral transformations by both analytic proofs and numerical tests. These new methods will help providing robust and unbiased kinetic analysis for many complex chemical and biochemical reactions.

1. Introduction

The multi-step reaction models are central to the mechanistic understandings of various fields of chemistry: organic,¹ atmospheric,² biophysical,^3–5 etc. For instance, an enzymatic reaction may be described by several sequential steps, including substrate binding, catalytic reaction, and product release;⁴ an ion channel may change its conformation through multi-step allosteric transtions;⁵ the movement by molecular motors requires ATP binding, ATP hydrolysis, and ADP release, with one of these steps linked to the powerstroke of a motor;³ proteins^6,7 and RNA molecules^8–10 may fold/unfold themselves via complicated multi-stage pathways on a rugged energy landscape. A broad spectrum of experimental methods has been devised for probing into these complex chemical reactions, and these methods can be loosely classified as either ensemble measurements or single-molecule measurements. In the former case, one tracks the time course of the concentration of a certain chemical in the bulk; in the latter case, one tracks the reaction course of individual molecules one by one. The experimental data arising from these measurements often encode the kinetic information in the form of a superposition of many exponential decay modes, and the decay rate constants and the coefficients of these decay modes contain information about the underlying chemical reaction scheme.

It is often critical to dissect the multi-step reaction kinetics quantitatively from experimental data, to determine the rate constant distribution of each step and to investigate the dependence of these rate constants on external conditions. For example, the rate constants can be affected by the concentration of substrates targeting a specific enzyme; the trans-membrane potential acting on an ion-channel; the force load on a molecular motor etc. Such dependence may elucidate the mechanism of the biological systems of interest. As individual biological molecules were brought to close scrutiny in recent single-molecule experiments, their kinetic behaviors were often found to invoke non-trivial distributions of reaction (or transition) rate constants. (See for example refs. ^{7–9,11–15}) These experiments suggest that biological processes may not only consist of multiple steps but a seemingly two-step reaction may also involve heterogeneous kinetics that are better described by a distribution of, instead of a single, kinetic rate constants, further complicating the analysis of biological processes that exhibit complex chemical kinetics.

The analysis of multi-step reaction kinetics is challenging in two aspects. The first aspect is to reliably determine the number of reaction steps from kinetic data. The number of reaction steps have been previously estimated by computing the “randomness parameter” ^16–19 from the kinetic data, or fitting the data to a Γ-distribution function.^18,20 The “randomness parameter” approach, however, generally estimates a lower bound of the total number of rate-limiting steps, and the estimates become exact only when all reaction steps involve nearly identical rate constants.^16–18 Similarly, the validity of a Γ-distribution fit also draws on identical rate constants or a Hill function response,²¹ which may not hold for general cases. The second challenge involves stable determination of the distribution of kinetic rate constants. Technically, this means to solve an inverse Laplace problem, which involves a well-known numerical instability (i.e. hypersensitivity to input noise).²² As a general practice, a discrete distribution of rate constants has typically been deduced from Levenberg-Marquardt fitting or Hidden Markov modeling,^5,23,24 although these methods may suffer from a relatively arbitrary choice of the number of fitting parameters. Continuous distributions of rate constants have often been dealt with by stabilizing the numerical inversion of Laplace transform. The Tikhonov regularization^25,26 and maximum entropy method^27,28 are two popular stabilization methods, which stabilize the inverse Laplace transform by penalizing the curvature²⁶ or information entropy^27,28 of the continuous distribution profile and may distort the rate constant distribution especially when the distribution function does not exhibit uniform ruggedness. We have recently developed a phase function method to overcome the instability of the inverse Laplace problem, handling both discrete and continuous distributions of rate constants without prior knowledge input or artificial penalization.²⁹ Nonetheless, the phase function method derives its viability and numerical stability from a strong constraint: the combination coefficients of multiple decay modes must be all non-negative real numbers, which implies single-step reaction kinetics.

To address the aforementioned challenges in the kinetic analysis of multi-step reactions, we introduce two numerically stable integral transformations in this paper. The first integral transformation enables us to reliably recover the number of reaction steps from noisy kinetic data. This method applies to general multi-step reactions, in which the rate constants of individual reaction steps can take arbitrary, non-identical distributions. The second integral transformation allows us to convert a multi-step kinetic data set to a corresponding single-step kinetic data set with a distribution of rate constants. We can thus utilize the “phase function method”²⁹ to handle multi-step reaction kinetics as well.

The paper is organized as follows. In section 2, the mathematical formulation of data analysis is presented, with detailed descriptions of the two aforementioned integral transformations. In section 3, the numerical implementations of the theory and related discussion are presented. The paper is concluded by section 4. Although examples presented in this paper are motivated by biophysical/biochemical processes, with a particular emphasis on interpreting single-molecule experiments which have been shown recently to reveal rich kinetics and dynamics of biological systems, we expect the numerical methods present here to be generally applicable to the analysis of multi-step reaction kinetics arising from many other chemical processes.

2. Theoretical Methods

2.1 Kinetic Data in Sequential Processes with m Reaction Steps

A typical m-step chemical reaction takes the following scheme:

$$A_1\stackrel{k_1}{\to }{A}_2\stackrel{k_2}{\to }\cdots A_m\stackrel{k_m}{\to }B.$$ (1)

According to eq 1, any molecule that starts from the “A₁ state” has to experience (m − 1) intermediate states A₂, …, A_m before it is turned to a “B state”. The m-step reaction involves m sequential tasks in a sequel, fulfilled with a set of rate constants k₁, k₂, …, k_m. Often, the observable properties of the A states are experimentally indistinguishable, i.e. the states A₁,…, A_m may give similar fluorescence/mechanical signals in a single-molecule experiment. This degeneracy makes it difficult to fully dissect the reaction kinetics by experimental means.

An accessible quantity for a molecule that starts from the A₁ state is how long it takes to finish all the m tasks and reach the B state. Defining this as “reaction time” t (referring to the dwell time in all the A-like states), t will be the sum of m random durations t_dt = t₁ + t₂ +···+t_m, where t_i is the dwell time that the molecule spends in the A_i state. Here, the random variable t_i is governed by the reaction rate constant k_i and thus follows the exponential decay law Prob{t_i > t} = e^−k_it, t ≥ 0. The probability density for t_i is thus given by $p_{t_i}(t)\equiv {lim}_{\mathrm{\Delta }t\to 0^{+}}\frac{\text{Prob}\{t\le t_i<t+\mathrm{\Delta }t\}}{\mathrm{\Delta }t}=k_i{e}^{-k_{i}t}$, t > 0. The probability density for t = t₁ + t₂ +···+ t_m then becomes a convolution of m factors:

$$p(t)=p_{t_1}(t)\ast \cdots \ast p_{t_m}(t)=k_1{e}^{-k_{1}t}\ast \cdots \ast k_m{e}^{-k_{m}t}$$ (2)

where the convolution operation “*” is defined as $f(t)\ast g(t)\equiv {\int }_0^{t}f(t^{\prime })g(t-t^{\prime })\text{d}{t}^{\prime }$. This probability density function p(t) will henceforth be referred to as the “overall kinetic data” or “kinetic data”, from which we will try to dissect the multi-step reaction kinetics and determine the number of reaction steps m, as well as the rate constants for each step k₁, k₂, … and k_m.

A specific case of eq 1 is the situation where k₁ = k₂ = ··· = k_m = k:

$$A_1\stackrel{k}{\to }{A}_2\stackrel{k}{\to }{A}_3\stackrel{k}{\to }\cdots \stackrel{k}{\to }{A}_m\stackrel{k}{\to }B.$$ (3)

In this case, the kinetic data p(t) is simply the well-known Γ-distribution:

$$p(t)=\underset{\text{convolution}\text{of}m\text{copies}}{\underbrace{p_{t_1}(t)\ast \cdots \ast p_{t_m}(t)}}=\frac{k^m{t}^{m-1}}{(m-1)!}{e}^{-kt}.$$ (4)

This functional form is widely used in homogeneous sequential kinetic models in physical chemistry. Two notable examples are photon counting process and the reaction of processive enzymes. In the latter context, the enzyme exhibiting a reaction scheme as shown in eq 3 is often referred to as a “Poisson enzyme”.¹⁶ Hence, we will refer to the reaction scheme eq 3 as “Poisson enzyme reaction” hereafter.

Despite the apparent difference between the reaction schemes eq 1 and eq 3 (and their respective kinetic data eq 2 and eq 4), they are intrinsically connected. eq 2 is related to eq 4 through a weighted superposition:

$$k_1{e}^{-k_{1}t}\ast k_2{e}^{-k_{1}t}\cdots \ast k_m{e}^{-k_{m}t}=\frac{t^{m-1}}{(m-1)!}\int k^m{e}^{-kt}\text{d}{\mu }_{k_1{k}_2\cdots k_m}(k),$$ (5)

where μ_{k1 k2···km} (k) is a non-decreasing function of k, bounded by 0 and 1. Physically speaking, this means that the prototypical m-step reaction $A_1\stackrel{k_1}{\to }{A}_2\stackrel{k_2}{\to }\cdots A_m\stackrel{k_m}{\to }B$ can always be realized by superposing many “Poisson enzyme reactions” $A_1\stackrel{k}{\to }{A}_2\stackrel{k}{\to }\cdots A_m\stackrel{k}{\to }B$, with a weighted distribution of k.

We defer the rigorous derivation of eq 5 and the explicit form of μ_k1k2···km (k) to Supporting Information A.1. Here, we will only illustrate the validity of eq 5 for the specific case m = 2, where we have the following result:

$$\begin{array}{l}{p}_{k_1{k}_2}(t)=k_1{e}^{-k_{1}t}\ast k_2{e}^{-k_{2}t}\\ =\{\begin{array}{cc}\frac{k_1{k}_2}{k_2-k_1}(e^{-k_{1}t}-e^{-k_{2}t}),& k_1\ne k_2\\ {(k\ast )}^{2}t{e}^{-k\ast t},& k_1=k_2=k\ast \end{array}.\end{array}$$ (6)

Noting that the identity $e^{-k_{1}t}-e^{-k_{2}t}=t{\int }_{k_1}^{k_2}{e}^{-kt}\text{d}k$ is valid for both k₁ = k₂ and k₁ ≠ k₂, we can cast p_k1k2 (t) in eq 6 into the unified form as

$$p_{k_1{k}_2}(t)=t\int k^2{e}^{-kt}\text{d}{\mu }_{k_1{k}_2}(k),\text{with}{\mu }_{k_1{k}_2}(k)=\text{Prob}\{\xi /k_1+(1-\xi )/k_2>1/k\}.$$ (7)

Here, ξ is a random variable uniformly distributed on the closed interval [0,1].

We can generalize eq 5 to reaction schemes that are more complex than shown in eq 1. For instance, we may allow the rate constant k_i of the ith step to sort from a random distribution, instead of taking a fixed value. In the reaction scheme

$$A_1\underset{F_1(k)}{\overset{k_1}{\to }}{A}_2\underset{F_2(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F_m(k)}{\overset{k_m}{\to }}B,$$

the random variable k_i obeys the cumulative distribution F_j (k) ≡ Prob{k_j < k}. In this case, the corresponding kinetic data will take the form:

$$p(t)=[\int k{e}^{-kt}\text{d}{F}_1(k)]\ast \cdots \ast [\int k{e}^{-kt}\text{d}{F}_m(k)]=\frac{t^{m-1}}{(m-1)!}\int k^m{e}^{-kt}\text{d}\mu (k),$$ (8)

Here, μ(k) = ∫dF₁ (k₁)··· ∫dF_m (k_m)μ_k1···km (k) is still a non-decreasing function of k, bounded by 0 and 1. Therefore, the “Poisson enzyme reactions” $A_1\stackrel{k}{\to }{A}_2\stackrel{k}{\to }\cdots A_m\stackrel{k}{\to }B$ are elementary building blocks of arbitrarily complicated m-step sequential reactions.

From eq 8, we make two observations:

1. The analysis of m-step sequential reactions boils down to the reconstruction of a bounded and non-decreasing function μ(k).

2. The number of reaction steps m is imbedded in the t → 0⁺ behavior of p(t): for any non-decreasing function μ(k), we have p(t) ∝ t^m−1 as t → 0⁺.

Motivated by these observations, we propose to analyze the sequential kinetic data with four sequential steps:

1. Performing a “heat capacity transform” Ĉ to the kinetic data p(t), and deducing the number of reaction steps m by exploiting the asymptotic behavior p(t) ∝ t^m−1, t → 0⁺;

2. Applying an “m-to-1 transformation” Ĵ_m to the kinetic data, and casting it into the form ℘(t) = (Ĵ_m p)(t) = ∫ke^−kt dμ(k);

3. Reconstructing the non-decreasing function μ(k) from the 1-step kinetic data ℘(t) = ∫ke^−kt dμ(k) using the “phase function approach”;²⁹

4. Extracting kinetic information from the reconstructed μ(k).

2.2 Deriving the Number of Reaction Steps through the “Heat Capacity Transform”

In the following, we will develop a method to deduce the number of reaction steps m from kinetic data as shown in eq 8.

The function p(t) has a universal asymptotic behavior p(t) ∝ t^m−1, t → 0⁺, so one may naively guess that m can be deduced by computing the limiting behavior of d ln p(t)/d ln t, as t → 0⁺. In reality, however, the estimate of d ln p(t)/d ln t can encounter the “ln0” instability when noise is superimposed on the kinetic data p(t). Here, we will suppress such instability by applying an integral transform to the kinetic data p(t).

Before presenting the integral transform, we first quantify the noise source that affects the detection of p(t). Taking single molecule experiments as examples, the kinetic data derived from single-molecule experiments are often described as a histogram, where the histogram count n_τ (t) in the bin [t, t +τ) describes the number of molecules that reach the final state B in the time interval [t, t +τ). The count n_τ (t) asymptotically scales with the probability density p(t):

$$n_{\tau }(t)\sim N\tau p(t),\text{for}N\gg \gg 1.$$ (9)

Here, N = Σ^(τ) n_τ(t) is the total number of molecules counted and “Σ^(τ)” denotes summation over all the time bins (i.e. over the entire observation time window). The uncertainty in p(t) arises from the Poisson counting noise and thus the variance of n_τ(t) is equal to its mean:

$$\langle {[\delta n_{\tau }(t)]}^2\rangle =\langle n_t(t)\rangle \approx N\tau p(t).$$ (10)

From this, it is clear that we cannot naively estimate m~d ln p(t)/d lnt, t → 0⁺, due to the numerical uncertainty $\mid \delta lnp(t)\mid =\mid \frac{\delta n_{\tau }(t)}{n_{\tau }(t)}\mid \sim 1/\sqrt{n_{\tau }(t)}\to +\infty$ (Note: n_τ(t) ∝ p(t) ∝ t^m−1 → 0, as t → 0⁺ for multi-step reactions where m > 1).

To overcome this numerical instability, we exploit the following transform:

$$(\widehat{C}{n}_{\tau })(k)\equiv \sum {{}^{(\tau )}n}_{\tau }(t)\frac{{(kt)}^2{e}^{kt}}{{(e^{kt}-1)}^2},$$ (11)

which is the discretized version of the integral transform for p(t), $(\widehat{C}p)(k)\approx {\int }_0^{+\infty }p(t)\frac{{(kt)}^2{e}^{kt}}{{(e^{kt}-1)}^2}\text{d}t$. The integral transform Ĉ significantly suppresses the noise in δn_τ (t) and the asymptotic behavior of (Ĉn_τ)(k) is given by

$$(\widehat{C}{n}_{\tau })(k)\approx N\tau {\int }_0^{+\infty }p(t)\frac{{(kt)}^2{e}^{kt}}{{(e^{kt}-1)}^2}\text{d}t\propto \frac{1}{k^m},k\to +\infty .$$ (12)

(Supporting Information B provides an analytic derivation of eq 12.) Therefore, we can derive the number of reaction steps, m, from a numerical estimate of the following limit:

$$\underset{k\to +\infty }{lim}\frac{\text{d}ln(\widehat{C}{n}_{\tau })(k)}{\text{d}ln(1/k)}.$$ (13)

Due to Poisson noise 〈[δn_τ (t)]²〉 = 〈n_t(t)〉 ≈ Nτp(t), the uncertainty in (Ĉn_τ)(k) is given by:

$$\mid \delta (\widehat{C}{n}_{\tau })(k)\mid \le min\left\{\sqrt{N},7.21\sqrt{{\int }_0^{+\infty }\frac{N(t)}{t}{e}^{-kt}\text{d}t}\right\}.$$ (14)

(See Supporting Information B for a proof of eq 14.) Here, $N(t)\equiv \sum {{}_{t^{\prime }<t}{}^{(\tau )}n}_{\tau }(t^{\prime })$ is the cumulative count for molecules with reaction time smaller than t.

One may get more physical insights into the transform Ĉ by comparing it to Debye’s formula that links the phonon spectrum D(ν) of a solid to its heat capacity C_V:

$$C_V=k_B{\int }_0^{+\infty }\text{d}\nu D(\nu )\frac{{(h\nu /k_{B}T)}^2{e}^{h\nu /k_{B}T}}{{(e^{h\nu /k_{B}T}-1)}^2}$$

where h is the Planck constant, ν is the phonon frequency, k_B is the Boltzmann constant, and T is the absolute temperature. For an m-dimensional solid, the phonon spectrum is D(ν) ∝ ν^m−1 in the low frequency limit ν → 0⁺ (which is analogous to p(t) ∝ t^m−1 as t → 0⁺), and accordingly the heat capacity goes as C_V ∝ T^m in the low temperature limit T → 0⁺ (which is analogous to the asymptotic behavior (Ĉp)(k): (Ĉn_τ)(k) ∝1 k^m as k → +∞). Just like the observation that the often rugged phonon spectrum is transformed into a smooth heat capacity curve as a function of temperature, the relatively noisy p(t) will be transformed into a relative smooth (Ĉn_τ)(k), due to the low-pass filtering property of the transformation³⁰. Hence, we referred to the integral transform Ĉ as the “heat capacity transform”.

2.3 Reducing Multi-Step Kinetics to 1-Step Kinetics by the Integral Transform Ĵ_m

Once the number of reaction step m is deduced, we will further extract the kinetic information for a multi-step reaction by reconstituting the non-decreasing distribution function μ(k), which relates to the kinetic data p(t) through eq 8:

$$p(t)=\frac{t^{m-1}}{(m-1)!}\int k^m{e}^{-kt}\text{d}\mu (k).$$

The distribution function μ(k) can further provide chemical information after we combine it with additional inputs about sequential reaction schemes. For the m = 1 case, one can stably reconstruct μ(k) from p(t) using the phase function method.²⁹ To reconstruct μ(k) in the m > 1 case, we need to transform p(t) to the form of “1-step kinetics”.

Such an “m-to-1 transform” Ĵ_m can be realized as follows:

$${\widehat{J}}_{m}p(t)\equiv (m-1)!{\int }_t^{+\infty }\text{d}{t}_{m-1}\cdots {\int }_3^{+\infty }\text{d}{t}_2{\int }_2^{+\infty }\text{d}{t}_1\frac{p(t_1)}{t_1^{m-1}}.$$ (15)

This linear transform convert p(t) to ℘(t) = (Ĵ_m p)(t) ≡ ∫ke^−kt dμ(k). The integral transform Ĵ_m is a numerically stable transformation, i.e. any small perturbation f(t) = δp(t) to the kinetic data p(t) will remain small after being transformed to (Ĵ_m f)(t). Quantitatively, one can verify the following inequality (See derivations in Supporting Information C): g

$${\int }_0^{+\infty }{[({\widehat{J}}_{m}f)(t)]}^2\text{d}t\le c_m^2{\int }_0^{+\infty }{[f(t)]}^2\text{d}t$$

and the noise amplification ratio c_m satisfies

$$c_m<\sqrt{\pi \left(m-\frac{1}{2}\right)\sqrt{\frac{m-\frac{1}{2}}{m+\frac{1}{2}}}}{\left(1-\frac{1}{4m^2}\right)}^{-\frac{m}{2}}\sim \sqrt{\pi \left(m-\frac{1}{2}\right)}.$$ (16)

We note that the reconstruction of μ(k) from the 1-step kinetic data also has a finite amplification ratio $2+\sqrt{3}$ (See Ref. 29). Thus, the mapping from the m-step kinetic data to the non-decreasing function μ(k) is numerically stable, the overall noise amplification ratio being $(2+\sqrt{3})c_m<+\infty$.

2.4 Reconstructing μ(k) from the Kinetic Data p(t) Using the “Phase Function Approach”

We have previously developed a “phase function method” to reconstruct a non-decreasing μ(k) from 1-step reaction kinetics ℘(t) = (Ĵ_m p)(t) ≡ ∫ke^−kt dμ(k).²⁹ Now that we have reduced the m-step reaction kinetics to 1-step reaction kinetics by the “m-to-1 transform” Ĵ_m, we can use the phase function approach to deduce μ(k). The main idea was to regard exponential decay e^−kt as an oscillation e^iωt in purely imaginary frequency ω = ik. We can thus decompose the kinetic data as superposition of oscillation modes by using Fourier transform and then converts information on the Reω-axis to the Imω-axis (k-axis).²⁹

The “phase function approach” reconstructs a non-decreasing μ(k) in three steps as outlined below:²⁹

1. Perform a Fourier transform to the data ℘(t) for complex-valued frequency ω = Reω + i Imω satisfying Imω ≤ 0, and determine the phase function

   $$\phi (\omega )=arg[{\int }_0^{+\infty }\wp (t)e^{-i\omega t}\text{d}t];$$

2. Since $\phi (\omega )=Imln[{\int }_0^{+\infty }\wp (t)e^{-i\omega t}\text{d}t]$ is the imaginary part of an analytic function $ln[{\int }_0^{+\infty }\wp (t)e^{-i\omega t}\text{d}t]$, it must satisfy the two-dimensional Laplace equation ∂²φ(ω)/∂(Reω)² + ∂²φ(ω)/∂(Imω)² = 0. We can thus numerically solve this Laplace equation to deduce φ(ω) for all Reω ≠ 0, which satisfies²⁹

   $$0\le \phi (\omega )<\pi ,\text{for}Re\omega <0;$$ (17)

3. We can then obtain the phase function on the imaginary axis φ(ik) ≡ lim_ε→0⁺φ(ik − ε), which contains all the information necessary for the reconstruction of μ(k) and allows μ(k) to be derived using the following transform R̂:

   $$\mu (k)=(\widehat{R}\phi )(k)\equiv \underset{\epsilon \to 0^{+}}{lim}{\int }_0^k\text{d}{k}^{\prime }\left\{\frac{sin\phi (i{k}^{\prime }-\epsilon )}{\pi k^{\prime }}exp\left[-\int ln\mid 1-\frac{k^{\prime }+i\epsilon }{k^{″}}\mid \frac{\text{d}\phi (i{k}^{″})}{\pi }\right]\right\}.$$ (18)

The non-decreasing property of μ(k) and the boundedness of the associated phase function 0 ≤ φ(ik) ≤ π ensure the numerical stability of this algorithm against noise in the time domain data.²⁹ The uncertainty in μ(k) = (R̂φ)(k) is estimated by:

$$\mid \delta \mu (k)\mid \sim (2+\sqrt{3}){\epsilon }^{\#}\sqrt{\mu (k)},$$ (19)

where ε^# is the noise level (t-domain relative error) in the kinetic data ℘(t).

2.5 From μ(k) to Kinetic Information of Interest

From μ(k), we can compute a frequency spectrum of the kinetic data p(t) as:

$$\stackrel{\sim }{p}(\omega )=({\widehat{\mathrm{\Omega }}}_m\mu )(\omega )\equiv \int {\left(1+\frac{i\omega }{k}\right)}^{-m}\text{d}\mu (k),Re\omega \ne 0.$$ (20)

The function p̃(ω) is referred to as the “frequency spectrum” because it coincides with the Fourier transform of $p(t)=\frac{1}{(m-1)!}\int k^m{t}^{m-1}{e}^{-kt}\text{d}\mu (k)$:

$$\stackrel{\sim }{p}(\omega )=({\widehat{\mathrm{\Omega }}}_m\mu )(\omega )={\int }_0^{+\infty }p(t)e^{-i\omega t}\text{d}t,Im\omega \le 0.$$

This spectral representation p̃(ω) = (Ω^_m μ)(ω) can help reveal kinetic information that is implicitly imbedded in the non-decreasing function μ(k), as shown below.

Consider the m-step sequential reaction scheme $A_1\underset{F_1(k)}{\overset{k_1}{\to }}{A}_2\underset{F_2(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F_m(k)}{\overset{k_m}{\to }}B$, where the rate constant k_j obeys the probability distribution F_j (k) = Prob{k_j < k} for j = 1,2,…, m. The scheme invokes no further branched pathways. Chemically speaking, in this scenario, we assume that the molecule has to challenge an energy barrier with distributed barrier height at each reaction step, but the distributions of barrier heights in distinct reaction steps are independent. From the kinetic data in the t-domain p(t) = [∫ke^−kt dF₁ (k)]* ··· *[∫ke^−kt dF_m (k)], which is a convolution of m factors, one can get the frequency spectrum in the ω-domain as the product of m single-step reaction frequency spectra:

$$\stackrel{\sim }{p}(\omega )=\left[\int {\left(1+\frac{i\omega }{k}\right)}^{-1}\text{d}{F}_1(k)\right]\times \cdots \times \left[\int {\left(1+\frac{i\omega }{k}\right)}^{-1}\text{d}{F}_m(k)\right]=\prod _{j=1}^m\int {\left(1+\frac{i\omega }{k}\right)}^{-1}\text{d}{F}_j(k).$$ (21)

Because the function p̃(ω) given in eq 21 satisfies 0 < |p̃(ω)| < +∞ for Reω < 0, it is possible to define a single-valued phase function ψ(ω) = Imln p̃(ω) as

$$\psi (\omega )\equiv Im{\int }_0^{\omega }\text{d}ln\stackrel{\sim }{p}({\omega }^{\prime })=arg\stackrel{\sim }{p}(\omega )=arg\int {\left(1+\frac{i\omega }{k}\right)}^{-m}\text{d}\mu (k),Re\omega <0.$$ (22)

(See Supporting Information A.2 for a proof of the above statement.) According to eq 21, the phase ψ(ω) further decomposes to the sum of m terms:

$$\begin{array}{l}\psi (\omega )=arg\stackrel{\sim }{p}(\omega )=\sum _{j=1}^m{\phi }_j(\omega ),Re\omega <0,\text{where}\\ 0\le {\phi }_j(\omega )=arg\left[\int {\left(1+\frac{i\omega }{k}\right)}^{-1}\text{d}{F}_j(k)\right]\le arg\frac{1}{i\omega }\le \pi .\end{array}$$

As we bring ψ(ω) to the limit Reω → 0⁻, we obtain:

$$\psi (ik)={\phi }_1(ik)+\cdots +{\phi }_m(ik)=\sum _{j=1}^m{\phi }_j(ik),0\le {\phi }_j(ik)\le \pi ,\text{for}j=1,2,\dots ,m.$$

Evidently, this algebraic sum in the k-domain is a mathematically more convenient form than the original m-term convolution in the t-domain: p(t) = [∫ke^−kt dF₁ (k)]*···*[∫ke^−kt dF_m (k)]. Here, we note that the crucial bridge between k- and t-domains builds on the condition 0 < | p̃(ω)| < +∞ for Reω ≠ 0, but such a bound on | p̃(ω)|, while being rigorously true for sequential reactions following the form $A_1\underset{F_1(k)}{\overset{k_1}{\to }}{A}_2\underset{F_2(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F_m(k)}{\overset{k_m}{\to }}B$, may not necessarily hold for branched reaction schemes. For a more general reaction, it is possible that p̃(ω) vanishes for some Reω ≠ 0, leading to singularities with ln p̃(ω) = ln 0 = ∞ and ill-defined phase functions.

Naturally, the next question is how to determine the distributions of rate constants F_j(k) = Prob{k_j < k} (j = 1,2,…, m) from the phase function decomposition $\psi (ik)={\sum }_{j=1}^m{\phi }_j(ik)$ ? Clearly, once we know each individual φ_j(ik), we can unambiguously reconstruct F_j(k) = (R̂φ_j)(k) (using eq 18). However, with the mere knowledge of one kinetic data set p(t), the best one can obtain is just the sum of m phase functions φ_j(ik), j = 1,2, …, m, and the problem of recovering the m individual summands is underdetermined. To fully characterize the kinetics, we usually need additional inputs.

Here, we will discuss two often encountered circumstances in which additional knowledge can help us fully dissect the multi-step reaction kinetics using ψ(ik).

Situation 1: The distributions of k_j for each step are identical

This is often assumed for the movement kinetics of motor proteins (such as kinesins³¹ and myosins¹⁴) and nucleic acid-translocating enzymes (such as polymerases¹⁵ and helicases³²) where the elementary motion steps adopt approximately identical rate constants. Under this assumption, we can model the kinetic data p(t) by the convolution of m identical copies of single-step reaction kinetics:

$$p(t)=\underset{\text{convolutions}\text{of}m\text{copies}\text{in}\text{total}}{\underbrace{\left[\int k{e}^{-kt}\text{d}F(k)\right]\ast \cdots \ast \left[\int k{e}^{-kt}\text{d}F(k)\right]}}.$$

Accordingly, the phase function of the overall sequential reaction is given by $\psi (ik)={\sum }_{j=1}^m{\phi }_j(ik)$, with all individual phase functions to be identical: φ_j(ik) = ψ(ik)/m. Therefore, we can determine F(k) using the reconstruction formula eq 18: F(k) = (R̂φ_j)(k).

Situation 2: The distributions of k_j scale independently with external experimental conditions

In many cases, the distribution of rate constants of each step of a multi-step process can be independently tuned by external conditions. A simple example is that the rate constant of enzyme-substrate binding process scales linearly with respect to concentration of the substrate. In these cases, we are not only able to determine a single phase function

$$\psi (ik)={\phi }_1(ik)+\cdots +{\phi }_m(ik)$$

but can also determine the scaled phase function

$${\psi }^{(s_1,\cdots ,s_m)}(ik)={\phi }_1(ik/s_1)+\cdots +{\phi }_m(ik/s_m)$$

from experimentally measured p(t) functions at the scaled experimental conditions. Here, s₁, …, s_m are sets of scaling factors for these conditions (substrate concentration etc.). By choosing a sufficient number of different sets of (s₁, …, s_m) (i.e. a sufficient number of independent kinetic experiments), we can uniquely determine the functional forms of individual phase functions φ₁, …,φ_m and thus the rate constant distributions of F_j(k) = (R̂φ_j)(k).

To flesh out this idea, we illustrate the case m = 2 with the enzymatic reaction:

$$\text{E}+\text{S}\stackrel{k_1={\kappa }_1[S]}{\to }\text{ES}\stackrel{k_2}{\to }\text{E}+\text{P}\text{.}$$

Here, the enzyme (E) binds a substrate (S) to form an enzyme-substrate complex (ES) with a distributed binding rate constant k₁ = κ₁[S], where [S] is the concentration of the substrate. The enzyme-substrate complex (ES) then undergoes a catalytic step, executed with a distributed rate constant k₂ (F₂(k) = Prob{k₂ < k}) to release the product (P). Suppose that we conduct two experiments: the first for [S] = [S]₀, and the second for [S] = s[S]₀, where s > 1 is a scaling factor. The resulting kinetic data sets are p^[1](t) and p^[2](t), respectively. If the distribution of $k_1^{[1]}={\kappa }_1{[\text{S}]}_0$ in the first experiment is denoted by $F_1^{[1]}(k)=\text{Prob}\{k_1^{[1]}<k\}$, then the distribution of $k_1^{[2]}={\kappa }_{1}s{[\text{S}]}_0$ in the second experiment is given by $F_1^{[2]}(k)=\text{Prob}\{k_1^{[2]}<k\}=F_1^{[1]}(k/s)$. Now we can reconstruct, from p^[1](t) and p^[2](t), two phase functions

$$\begin{array}{l}{\psi }^{[1]}(ik)={\phi }_1(ik)+{\phi }_2(ik)\\ {\psi }^{[2]}(ik)={\phi }_1(ik/s)+{\phi }_2(ik),\end{array}$$

respectively. We can compute the difference between these two phase functions to get a function

$$g(k)\equiv {\psi }^{[1]}(ik)-{\psi }^{[2]}(ik)={\phi }_1(ik)-{\phi }_1(ik/s),$$

from which we can fully recover the phase function φ₁(ik) as

$${\phi }_1(ik)=[{\phi }_1(ik)-{\phi }_1(ik/s)]+[{\phi }_1(ik/s)-{\phi }_1(ik/s^2)]+\cdots =\sum _{q=0}^{\infty }g(k/s^q).$$ (23)

Such a series actually terminates after finite terms, because when k < k ( k is the slowest detectable rate constants due to the finite time duration of the experiment), φ₁(ik) = 0 and thus g(k)=0. Therefore, we can fully determine φ₁ (ik) and φ₂ (ik), from which we can directly determine the rate constant distributions governing the two steps of the enzymatic reaction using $F_1^{[1]}=\widehat{R}{\phi }_1$, F₂ = R̂φ₂ where R̂ is again given by eq 18. This m = 2 example can be generalized to any reaction form $A_1\underset{F_1(k)}{\overset{k_1}{\to }}{A}_2\underset{F_2(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F_m(k)}{\overset{k_m}{\to }}B$ with m > 2 as long as the rate constant at all but one step can be scaled independently (for example, by tuning the concentration of (m−1) distinct substrates that bind to an enzyme in a sequential manner).

3. Numerical Results and Discussion

Here, we shall numerically illustrate the above theories and address several practical problems in the analysis of multi-step reaction kinetics:

1. Determine the number of reaction steps from noisy kinetic data;

2. Deduce the probability distribution of rate constants in each reaction step based on the assumption that the distribution is identical for all steps;

3. Determine the probability distributions of individual reaction steps in “enzymatic reactions” where the rate constant of each step can be independently scaled.

3.1 Finding the Number of Reaction Steps

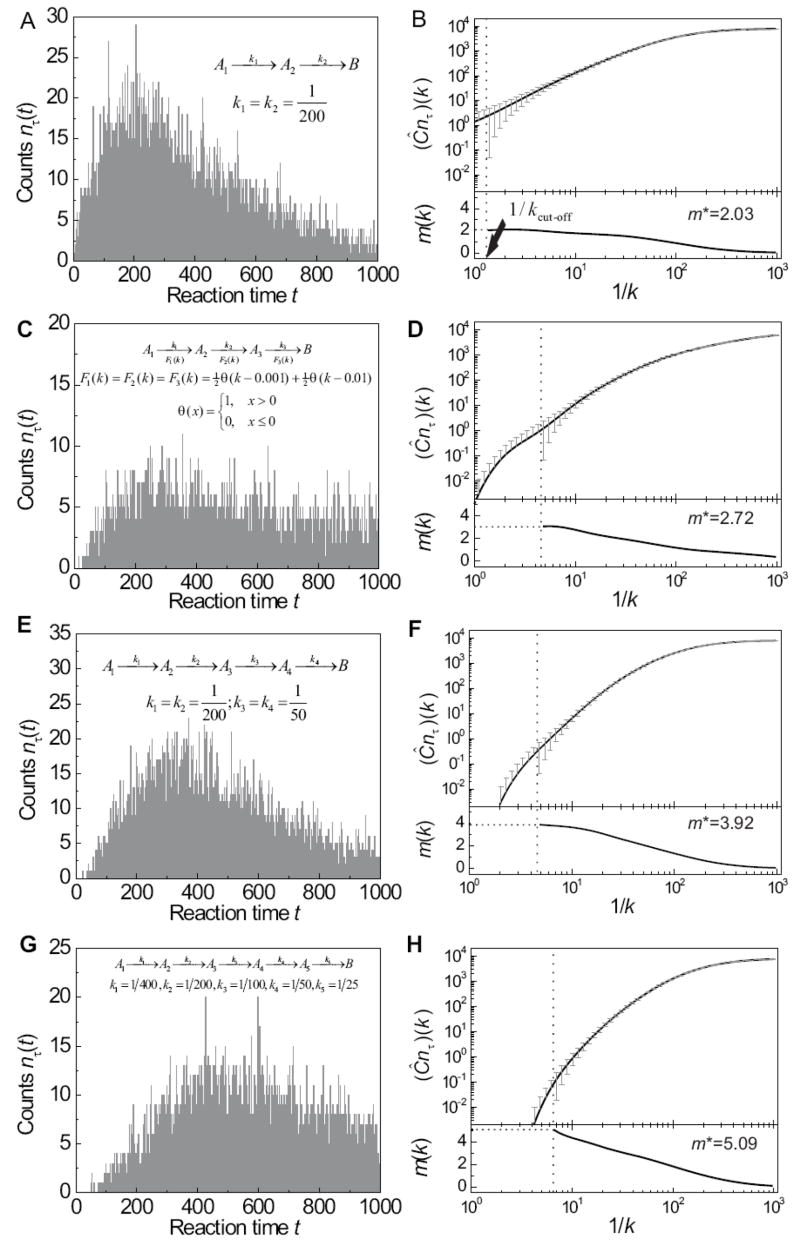
To simulate kinetic data with realistic experimental noise (such as the noise level carried by single-molecule experiments), we used Monte Carlo simulations to construct the histograms of overall reaction times for a variety of reaction schemes in the form of $A_1\underset{F_1(k)}{\overset{k_1}{\to }}{A}_2\underset{F_2(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F_m(k)}{\overset{k_m}{\to }}B$ (m = 2, 3, 4 and 5) (Figures 1a, 1c, 1e and 1g). Here the overall reaction time of each molecule is defined as the dwell time in all the A states (“reactant” and “intermediate” states) before the molecule reach the “product” state B. Each reaction step may take a fixed rate constant (Figures 1a, 1e and 1g) or sort from a non-trivial distribution (Figure 1c). The distributions of rate constants may be identical (Figures 1a and 1c) or distinct (Figures 1e and 1g) among the different reaction steps.

Figure 1.

The “heat capacity transform” Ĉ determines the number of reaction steps. Multi-step processes (m = 2, 3, 4, and 5) with various reaction schemes are analyzed by the transform Ĉ (eq 11). Panels a, c, e and g show Monte Carlo simulations of the reaction time histograms n_τ (t) from multi-step reactions (schematically shown in insets). The time resolution is set to τ = 1. The total number of events simulated is 8000. Panels b, d, f and h show numerical analyses of the histograms in a, c, e and g, respectively. The upper panels show the numerical computation of the “heat capacity transform” (Ĉn_τ)(k) with vertical error bars δ(Ĉn_τ)(k) estimated by eq 14. Lower panel plots m(k), where m(k) is the estimate of the derivative d ln(Ĉn_τ)(k)/d ln(1/k) using eq 24. The limit m* = lim_k→kmax m(k) (k_max is determined from eq 25 and marked by the dashed vertical line) provides quantitatively good estimates the number of reactions steps in all five cases.

In more details, for a given reaction scheme $A_1\underset{F_1(k)}{\overset{k_1}{\to }}{A}_2\underset{F_2(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F_m(k)}{\overset{k_m}{\to }}B$, a random reaction time was simulated as the sum of m random integers R = R₁ + R₂ + ··· + R_m, where R_j follows the distribution Prob{R_j > t} = ∫e^−kt dF_j (k). A total of N = 8000 such random integers R are simulated for each reaction scheme. The 8000 reaction times are then binned to construct a histogram, n_τ (t) (Figures 1a, 1c, 1e and 1g), with the bin size equal to the time resolution τ, which is taken as τ = 1 in all examples shown in this paper. Such a Monte Carlo approach was designed to reflect realistic noise arising from finite time resolution and finite total counts present in single molecule experiments.

We then tested the “heat capacity transform” approach with these simulated kinetic data (Figures 1b, 1d, 1f, and 1h). First we performed the transform Ĉ on the simulated histogram n_τ (t):

$$(\widehat{C}{n}_{\tau })(k)\equiv \sum _{t/\tau =0,1,2,\dots }{n}_{\tau }(t)\frac{{(kt)}^2{e}^{kt}}{{(e^{kt}-1)}^2}.$$

As shown in Figures 1b, 1d, 1f and 1h, the transform yields (Ĉn_τ)(k) ≈ N = 8000 in the small k limit as expected. To obtain a numerically stable estimate of the number of reaction steps using the large k limit, $m=\underset{k\to +\infty }{lim}\frac{\text{d}ln(\widehat{C}{n}_{\tau })(k)}{\text{d}ln(1/k)}$, we took the following procedure to estimate the derivative and limit: (1) We estimated the derivative with a dynamic window size ε_k = ln | (Ĉn_τ)(k)+ | δ(Ĉn_τ)(k) || − ln(Ĉn_τ)(k) where | δ(Ĉn_τ)(k) | is noise level in (Ĉn_τ)(k) as given in eq 14. As a result,

$$m(k)\equiv \frac{\text{d}ln[(\widehat{C}{n}_{\tau })(k)]}{\text{d}ln(1/k)}\approx \frac{ln[(\widehat{C}{n}_{\tau })(k{e}^{-{\epsilon }_k})]-ln[(\widehat{C}{n}_{\tau })(k)]}{{\epsilon }_k}.$$ (24)

(2) To properly estimate the limit at large k, we note that the rate constant k > 1/τ cannot be determined by an experiment with time resolution of τ and that the estimate of ln[(Ĉn_τ)(k)] is reliable only when (Ĉn_τ)(k)± | δ(Ĉn_τ)(k) |> 0. Bearing these two facts in mind, we set a maximum value for k in the evaluation of $\underset{k\to +\infty }{lim}[\text{d}ln(\widehat{C}{n}_{\tau })(k)/\text{d}ln(1/k)]$, i.e.

$$k_{max}\equiv min\{1/\tau ,k_{\text{cut}-\text{off}}\},$$ (25)

where k_cut-off ≡ max{k: |δ( Ĉn_τ)(k)| ≤ (Ĉn_τ)(k)}. Rather than literally pursuing k → +∞, we calculate the number of steps as the nearest integer to m* = lim_k→kmax m(k).

As shown in Figure 1, the m* values recover the correct numbers of reaction steps to within an error of ± 10%. This is not only true for multi-step reactions with identical rate constant distribution at each step (Figures 1a–1d) but also true for reactions with disparate rate constants at different steps (Figures 1e–1h). This method applies to reactions with a single rate constant in each step (Figures 1a, 1b, and 1e–1h) as well as reactions with a broad distribution of rate constants (Figures 1c and 1d). The number of reaction steps as high as m = 5 can be faithfully recovered (Figures 1g and 1h) when the noise level for the t-domain kinetic data is ~1% (Poisson counting noise corresponding to N = 8000). We expect that with lower noise in the kinetic data, even high numbers of the reaction steps can be accurately deduced (See Supporting Information D). In comparison, the “randomness parameter” defined by

$$r=\frac{\langle t^2\rangle -{\langle t\rangle }^2}{{\langle t\rangle }^2}=\frac{\langle {(t-\langle t\rangle )}^2\rangle }{{\langle t\rangle }^2}$$ (26)

gives r = 0.51, 0.75, 0.34 and 0.35 for the kinetic data shown in Figures 1a, 1c, 1e and 1g, respectively. Here 〈·〉 denotes an average weighted by the reaction time histogram n_τ (t). The lower bound of the number of reaction steps is then given by m = 1/r, corresponding to ~2, 1.3, 3 and 3 steps for the 4 cases. Indeed, when each reaction step has a single and identical rate constant k, as shown in Fig. 1a, this lower bound accurately describes the actual number of reactions steps as expected. However, for the other cases, 1/r significantly deviated from the number of reactions steps as well as rate-limiting steps.

The “heat capacity transform” thus provides a more general and precise approach to derive the number of reaction steps from kinetic data. However, for fixed data precision in the time domain, the “heat capacity transform” may also fail when the number of reaction steps m or the dispersion of rate constants is too large (See Supporting Information D for more quantitative discussion).

3.2 Reconstructing Identically Distributed Rate Constants for Sequential Multi-Step Reactions

The major concern of this subsection is to fully determine the reaction scheme $A_1\underset{F_1(k)}{\overset{k_1}{\to }}{A}_2\underset{F_2(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F_m(k)}{\overset{k_m}{\to }}B$ from kinetic data p(t), provided that k₁, ···,k_m are identically distributed: F₁(k) = ··· = F_m (k). This type of kinetic scheme can approximate many processive biomolecular processes. For instance, we may wish to characterize the kinetic profile of an RNA polymerase molecule that transcribes a piece of DNA or a helicase molecule that unwinds a DNA or RNA duplex. The typical kinetic data often provides information about how long it takes the polymerase molecule to transcribe DNA with a certain number of nucleotides or how long it takes the helicase to unwind a duplex of a certain number of base-pairs without directly revealing the actual translocation step-sizes of these molecules. If we neglect the sequence dependence, the kinetics of these processive biochemical reactions can be approximated by the scheme $A_1\underset{F(k)}{\overset{k_1}{\to }}{A}_2\underset{F(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F(k)}{\overset{k_m}{\to }}B$. Using the “heat capacity transform” Ĉ, we may deduce the number of reaction steps m required for translocating across n nucleotides. Subsequently, the step-size of the molecule of interest can be computed as n/m and then the probability distribution of rate constants for an elementary translocation step can be deduced.

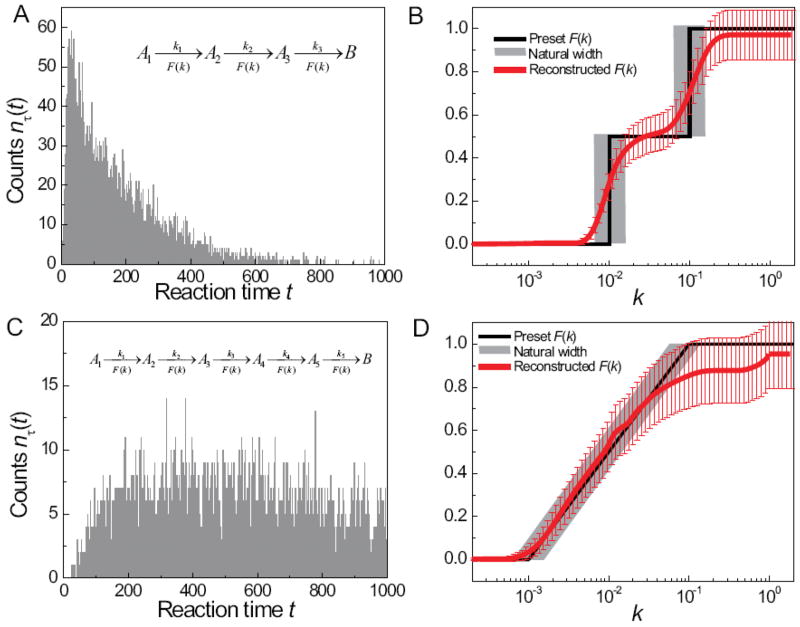
In Figure 2, we simulated the situation for m = 3 or 5 with dispersed kinetic rate constants. The distributions of the rate constants were identical but independent of each other. The reaction times in Figure 2 were simulated as the sum of random integers R= R₁ + ··· + R_m, m = 3 or 5. For the m = 3 case (Figure 2a), the rate constants were allowed to take two discrete values with equal probability, mimicking the scenario that the molecule has two distinct conformation each with a distinct reaction rate (as depicted by the black curve in Figure 2b). For the m = 5 case (Figure 2c), the reaction barriers for each step (i.e. ln k ) were taken to be uniformly distributed on an interval (as depicted by the black curve in Figure 2d).

Figure 2.

Analysis of multiple-step reaction kinetics that involve identically distributed rate constants in each step. Panels a and c show the simulated reaction time distributions n_τ (t) with the reaction schemes shown in insets. The total number of counts in each histogram is 8000. The preset rate constant distributions F(k) used to simulate the n_τ (t) in panels a and c are shown as black curves in panels b and d, respectively. The rate constant distributions F(k) reconstructed from n_τ (t) using the phase function approach are shown as red curves. The reconstructions of F(k) are achieved by computing F(k) = (R̂φ)(k) using eq 18, where the phase function φ(ik) = ψ (ik)/m is determined from μ(k), which in turn is deduced from the corresponding t-domain kinetic data n_τ (t) in panel a and c. The vertical error bars are estimated by eq 19. The uncertainties in the horizontal direction (“natural width” due to finite sampling effect) are marked as grey zones in panels b and d.

We used four steps to deduce the number of reaction steps and the underlying F(k) for each step from the simulated overall kinetic data given in Figures 2a and 2c.

1. We deduced the number of reaction steps by applying the “heat capacity transform” Ĉ to the simulated histogram n_τ (t). Taking the limit of m* = lim_k→kmax m(k) with m(k) given by eq 24, the simulated histogram shown in Figure 2a leads to an estimate m* = 3.21, which rounds off to m = 3, agreeing quantitatively with the preset number of reaction steps. Similarly, when data in Figure 2c were analyzed by transform Ĉ, the result is m* = 4.61, which rounds off to m = 5, also agreeing with the preset number of reaction steps.

2. We applied the “m-to-1” transformation Ĵ_m to the raw data n_τ (t). After Ĵ_m transformation, the kinetic data took the form ∫ke^−ktdμ(k), where the non-decreasing function μ(k) can be reconstructed via the “phase function approach” (data not shown).

3. We computed the frequency spectrum p̃ (ω) = (Ω̂_mμ)(ω) ≡ ∫(1+iω/k)^−m dμ(k) from μ(k), and deduced the phase function. The phase function for individual reaction steps were then deduced from φ(ik) = ψ (ik)/m.

4. We reconstructed the rate constant distributions F(k) from φ(ik) using the R̂ transform as shown in eq 18.

The reconstructed rate constant distributions are shown as the red curves in Figures 2b and 2d, with the vertical error bars given by $\mid \delta F(k)\mid \sim (2+\sqrt{3}){\epsilon }^{\#}\sqrt{F(k)}$ (eq 19). The reconstruction result compares quantitatively well (within error) with the preset distribution of rate constants (black curves) in both cases. The horizontal error bars on the preset F(k) (depicted by the grey zones) arise from finite sampling error in the simulated data (i.e. at the noise level (~1%) corresponding to the Poisson counting error for N = 8000, a single exponential decay cannot be distinguished from the superposition of exponential decay modes with a range of rate constants defined by Δln k = ±0.4.)

3.3 Reconstructing Michaelis-Menten Kinetics with Distributed Rate Constants

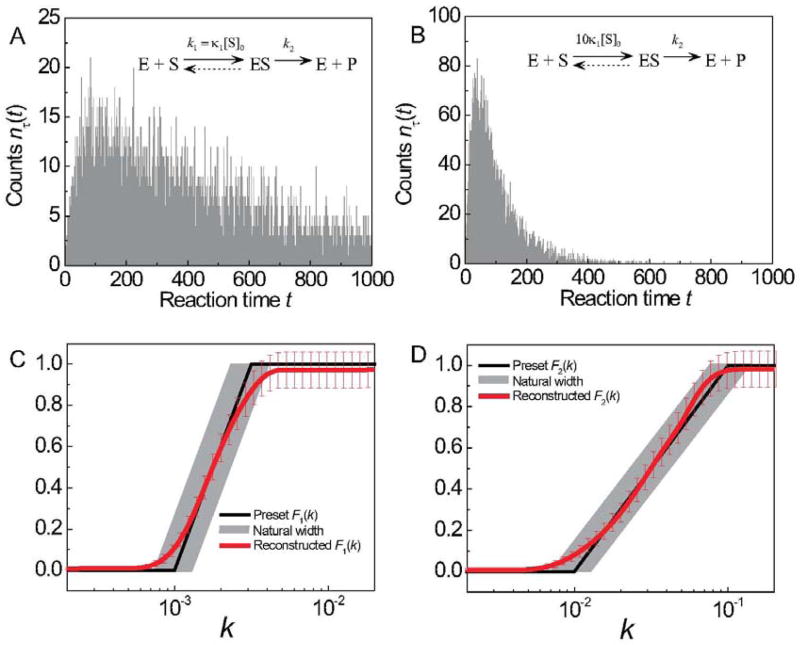
In this subsection, we dissect a 2-step enzymatic reaction $\text{E}+\text{S}\stackrel{k_1={\kappa }_1[S]}{\to }\text{ES}\stackrel{k_2}{\to }\text{E}+\text{P}$. The rate of the substrate-binding step is tunable by substrate concentration [S]. We aim to reconstruct the probability distribution of rate constants in both the substrate-binding step and the catalysis step.

In Figure 3 we simulated two enzymatic reactions:

$$\text{E}+\text{S}\stackrel{k_1={\kappa }_1{[S]}_0}{\to }\text{ES}\stackrel{k_2}{\to }\text{E}+\text{P}(\text{Figure}3a)$$

$$\text{E}+\text{S}\stackrel{k_1=10{\kappa }_1{[S]}_0}{\to }\text{ES}\stackrel{k_2}{\to }\text{E}+\text{P}(\text{Figure}3b)$$

Figure 3.

Analysis of Michaelis-Menten enzymatic kinetics with dispersed kinetic rate constants. Panels a and b show the simulated data for 2-step enzymatic reactions n_τ (t) with two different substrate concentrations [S]₀ and 10[S]₀. The kinetic data n_τ (t) were simulated using the preset rate constant distributions F₁(k) and F₂(k) shown as black curves in panels c and d. Reconstructed rate constant distributions shown in red curves compare quantitatively with the preset distributions within error. The vertical error bars were estimated by eq 19 and the horizontal errors bars marked in grey zones arise from finite sampling effect. The total number of counts per substrate concentration is 8000.

(Here, the unidirectional reaction schemes are approximations to the Michaelis-Menten scheme that involves one reversible step:

$$\text{E}+\text{S}\underset{{\kappa }_{-1}}{\overset{{\kappa }_1[\text{S}]}{\rightleftarrows }}\text{ES}\stackrel{k_2}{\to }\text{E}+\text{P},$$

under the conditions κ₋₁ ≪ k₂ and κ₋₁ ≪ κ₁[S]. The unidirectional approximation is often valid as κ₋₁ ≪ k₂ is satisfied for a wide class of enzymes and it is also possible to achieve κ₋₁ ≪ κ₁[S] by properly tuning the substrate concentration [S].) Two independent numerical simulations for the two conditions [S] = [S]₀ and [S] = 10[S]₀ were conducted to obtain the reaction time histograms in Figures 3a and 3b, with the preset rate constant distributions for k₁ = κ₁[S]₀ and k₂ as shown in Figures 3c and 3d (black curves).

The numerical reconstruction of F₁(k) = Prob{k₁ = κ₁[S]₀ < k} and F₂(k) = Prob{k₂ < k} was achieved in the following four steps.

1. We applied the “2-to-1 transformation” Ĵ₂ to both histograms in Figures 3a and 3b, and reconstructed two non-decreasing functions μ^[1] (k) and μ^[2] (k) (not shown) using the phase function method.

2. We computed the phase functions ψ^[1] (ik) = arg[(Ω̂₂μ^[1])(ik)] and ψ^[2] (ik) = arg[(Ω̂₂μ^[2])(ik)] using eqs 20 and 22.

   From ψ^[1] (ik) = φ₁ (ik) + φ₂ (ik), and ψ^[2] (ik) = φ₁ (ik/10) + φ₂ (ik), we deduced the phase function corresponding to the each reaction step, φ₁ (ik) and φ₂ (ik), using eq 23.

3. We reconstructed the distribution of rate constants for each step as F₁ (k) = (R̂φ₁)(k) and F₂ (k) = (R̂φ₂)(k) using eq 18.

The reconstructed cumulative distributions F₁ (k) = Prob {κ₁[S]₀ < k} and F₂ (k) = Prob{k₂ < k} (red curves in Figures 3c and 3d) both agree well with the preset distribution (black curves) within the finite sampling error depicted by the grey zones in the figures, arising from the finite number reaction times simulated (N = 8000). Here, the rate constant distributions in a 2-step reaction were uniquely determined by simultaneous analysis of two experimental data sets and did not invoke fitting the raw data to subjective models of the distributions. In contrast, typical fitting methods are not adequate to determine such arbitrary distributions of rate constants as shown in Figures 3c and 3d.

4. Conclusions

It is a challenging task to dissect the kinetics of a multi-step chemical reaction. This is especially true if the totally number of reaction steps are unknown a priori or if some of the reaction steps cannot be described by a single rate constant. In this work, we introduced two numerically stable integral transforms, the “heat capacity transform” Ĉ and the “m-to-1 transform” Ĵ_m, to help analyzing the general m-step reaction kinetics $A_1\underset{F_1(k)}{\overset{k_1}{\to }}{A}_2\underset{F_2(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F_m(k)}{\overset{k_m}{\to }}B$ using the phase function approach.

The “heat capacity transform” Ĉ maps the overall kinetic data, which typically follows the form $p(t)=\frac{1}{(m-1)!}\int k^m{t}^{m-1}{e}^{-kt}\text{d}\mu (k)$, to $(\widehat{C}p)(k^{\prime })={\int }_0^{+\infty }p(t){(k^{\prime }t)}^2{e}^{k^{\prime }t}/{(e^{k^{\prime }t}-1)}^2\text{d}t$. It allows us to reliably infer the number of reaction steps m from noisy kinetic data, by tracking the asymptotic behavior (Ĉp)(k′) ∝ 1/k′^m, k′ → +∞. The “heat capacity transform” method is applicable to general m-step reactions in which the rate constants can follow arbitrary distributions and/or are different among distinct steps. It should be noted, however, that the performance of the “heat capacity transform” is still subject to the numerical quality of the input data, i.e., it cannot resolve two reaction models, this distinction of which lie within the experimental noise. For example, while a single-molecule experiment with N = 2000 events may be sufficient to distinguish the 4-step and 5-step reaction models, experiments with N = 200 events could barely resolve 2-step versus 3-step reactions. (See Supporting Information D for a quantitative argument for this fundamental limitation.)

The “m-to-1 transform” Ĵ_m maps the overall kinetic data, p(t) to $(m-1)!{\int }_t^{+\infty }\text{d}{t}_{m-1}\cdots {\int }_3^{+\infty }\text{d}{t}_2{\int }_2^{+\infty }\frac{p(t_1)\text{d}{t}_1}{t_1^{m-1}}$. It effectively converts an m-step kinetic data set to a 1-step kinetic data set ℘(t) = ∫ke^−ktdμ(k), allowing the “effective” rate constant distribution μ(k) to be stably reconstructed using the “phase function approach”, a method we recently developed for stabilizing the inverse Laplace transform.²⁹ The breakdown of a unique multi-step reaction scheme is, however, usually an underdetermined problem with a single kinetic data set p(t) in spite of a full determination of μ(k). As we have demonstrated in this paper, the “effective” rate constant distribution μ(k), when combined with additional input of kinetic information offers a powerful and straight forward strategy to fully dissect the m-step reaction kinetics $A_1\underset{F_1(k)}{\overset{k_1}{\to }}{A}_2\underset{F_2(k)}{\overset{k_2}{\to }}\cdots A_m\underset{F_m(k)}{\overset{k_m}{\to }}B$.

Although we have presented our method in the context of sequential multi-step reactions with all irreversible steps, the same quantitative analysis applies to many non-sequential, partially reversible reactions as well. The classical Michaelis-Menten mechanism offers a telling example of how a partly reversible reaction is isomorphic to a sequential reaction with all irreversible steps. The reaction kinetics for

$$\text{E}+\text{S}\underset{{\kappa }_{-1}}{\overset{{\kappa }_1[\text{S}]}{\rightleftarrows }}\text{ES}\stackrel{k_2}{\to }\text{E}+\text{P}$$

is identical to the 2-step reaction $A_1\stackrel{k_1^{\prime }}{\to }{A}_2\stackrel{k_2^{\prime }}{\to }B$, where $k_1^{\prime }+k_2^{\prime }={\kappa }_1[\text{S}]+{\kappa }_2+{\kappa }_{-1}$ and $k_1^{\prime }{k}_2^{\prime }={\kappa }_1{\kappa }_2[\text{S}]$.^3,19 For the general kinetic correspondence between partly-reversible and totally-irreversible reaction schemes, we refer the readers to ref 33, where an algebraic approach was introduced for “reducing” complex reaction schemes (that involve reversible steps and loops) to more familiar paradigms.

In this paper, we mainly discussed the analysis of dwell time histograms that involve complex superpositions of exponential decays and introduced a model-independent method for analyzing these reaction kinetics. Many other statistical descriptions for kinetics in complex systems also manifest themselves as multi-exponential decays, especially in systems with a wide spectrum of time-scales. Notably, the decays of reactant concentration in bulk measurements (such as the drug metabolism and toxin degradation in pharmacokinetics³⁴), the stochastic switching kinetics between molecular states (such as the random blinking of a quantum dot³⁵), and the fluctuations of certain physiological responses (such as the polarization and depolarization of a nerve impulse³⁶) all fall into this category. We anticipate that the method presented in this work would be helpful toward quantitative analysis of the complex kinetics of these processes. As we aimed at extracting maximum information from least assumptions, our model-independent method does not adapt itself to additional knowledge inputs automatically. In the case where such input is available (such as connectivity between multiple nodes in a reaction scheme^37,38), our method may be complemented by other kinetics analysis approaches, such as the hidden Markov modeling^24,38 to provide a fuller picture of the reaction kinetics.

Supporting Information Available

Sections A–D of the Supporting Information provide additional mathematical details that are omitted in the main text. This material is available free of charge via the Internet at http://pubs.acs.org.