On the assumptions underlying milestoning

Abstract

Milestoning is a procedure to compute the time evolution of complicated processes such as barrier crossing events or long diffusive transitions between predefined states. Milestoning reduces the dynamics to transition events between intermediates (the milestones) and computes the local kinetic information to describe these transitions via short molecular dynamics (MD) runs between the milestones. The procedure relies on the ability to reinitialize MD trajectories on the milestones to get the right kinetic information about the transitions. It also rests on the assumptions that the transition events between successive milestones and the time lags between these transitions are statistically independent. In this paper, we analyze the validity of these assumptions. We show that sets of optimal milestones exist, i.e., sets such that successive transitions are indeed statistically independent. The proof of this claim relies on the results of transition path theory and uses the isocommittor surfaces of the reaction as milestones. For systems in the overdamped limit, we also obtain the probability distribution to reinitialize the MD trajectories on the milestones, and we discuss why this distribution is not available in closed form for systems with inertia. We explain why the time lags between transitions are not statistically independent even for optimal milestones, but we show that working with such milestones allows one to compute mean first passage times between milestones exactly. Finally, we discuss some practical implications of our results and we compare milestoning with Markov state models in view of our findings.

INTRODUCTION

Milestoning, introduced in Ref. 1 and further developed in Refs. ^{2, 3, 4, 5}, is a procedure to analyze the progress in time of complicated processes such as barrier crossing events between predefined states or slow diffusive motion from an initial state toward a target state. Milestoning coarse grains the temporal and spatial description of the system by reducing the dynamics into a succession of independent transition events between intermediates (the milestones), which are hypersurfaces in the configuration space of the system. The necessary information about the probability of occurrence of these transitions and the time lags between them is obtained by collecting local kinetic information from straightforward and short trajectories between the milestones. By reducing the dynamics this way, milestoning allows one to simulate the overall kinetics of the system for time scales which are much beyond what is accessible by standard molecular dynamics (MD) simulations. Milestoning, however, rests on the assumptions that such a reduction of the dynamics to transitions between milestones is legitimate and that it is possible to retrieve the right kinetic information using short simulations between these milestones. The aim of this paper is to analyze under which conditions these assumptions are valid.

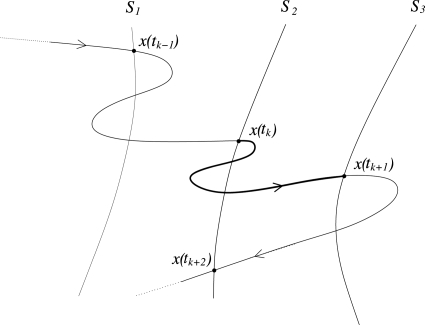
To introduce the issues that this question brings up and recall the details of the milestoning procedure, it is useful to consider a thought experiment in which one is given an infinitely long unbiased trajectory of a MD system which, assuming ergodicity, visits a given set of milestones infinitely often. Denoting these milestones by S₁,S₂,…,S_N and by x(t) with t⩾0 the instantaneous position of the system along the trajectory, let S_i0,S_i1,S_i2,S_i3,… with i_k∊{1,2,…,N}, k=0,1,2,… be the infinite sequence of successive milestones that x(t) crosses [thus we do not count recrossings of the same milestone until another milestone has been crossed in the meantime, i.e., i_k≠i_k−1 for all k=1,2,… (see Fig. 1 for an illustration)]. Let also 0⩽t₀<t₁<t₂<⋯ be the times at which these crossings occur, i.e., t₀ is the first time⩾0 such that x(t₀)∊S_i0 and for k=1,2,…, t_kis the first time such thatx(t_k)∊S_ikafter the trajectory crossedS_ik−1.

Figure 1.

Schematic of a piece of a long ergodic trajectory crossing a set of three milestones: S₁, S₂, and S₃. In this example, S_ik−1=S₁, S_ik=S₂, S_ik+1=S₃, and S_ik+2=S₂. The part of the trajectory highlighted in bold contributes to one event counted in p₂₃ and the time t_k+1−t_k contributes to the statistics of f₂₃(s). The figure also shows the previous transition event from S₁ to S₂, which contributes to p₁₂ with the time t_k−t_k−1 contributing to f₁₂(s), and the next one from S₃ to S₂, which contributes to p₃₂ with the time t_k+2−t_k+1 contributing to f₃₂(s).

The sequence {(S_i0,t₀),(S_i1,t₁),…}≡{(S_ik,t_k)}_k=0,1,… gives a coarse-grained picture of the MD trajectory, but one which, with a suitable choice of milestones, will still contain useful information about the kinetics of this trajectory. The main objective of the milestoning procedure is to generate this sequence and to analyze its statistical properties in a way which is computationally cheaper than running a long MD trajectory and waiting that it visits all the milestones as in the thought experiment above to gather its statistics.

To see how this objective is realized and the conditions this entails, let us introduce the following two statistical quantities which play a central role in milestoning. First, by going back to the sequence {(S_ik,t_k)}_k=0,1,… obtained from the long ergodic MD trajectory and recording the proportion of times along this sequence that S_j is the milestone crossed next after S_i, we can define the probability p_ij that this event occurs,⁶

$$p_{ij}=\underset{n\to \infty }{\lim }\frac{{\sum }_{k=1}^n{\delta }_{i,i_{k-1}}{\delta }_{j,i_k}}{{\sum }_{k=1}^n{\delta }_{i,i_{k-1}}}=\left(\begin{array}{l}\text{probability}\text{that}{S}_j\text{is}\text{the}\text{milestone}\\ \text{crossed}\text{next}\text{after}{S}_i\end{array}\right),$$ (1)

where δ_i,j=1 if i=j and δ_i,j=0 otherwise. (Thus, by definition p_ii=0 and ${\sum }_{j=1}^N{p}_{ij}=1$ for all i=1,…,N.) Second, by recording the time it takes for the trajectory to go to S_j next after S_i each time this event happens, we can define the probability density f_ij(s) of the lag time between these crossings conditional on them occurring: for any pair i,j such that p_ij≠0, f_ij(s) is such that

$${\int }_0^{\Delta t}{f}_{ij}\left(s\right)ds=\underset{n\to \infty }{\lim }\frac{{\sum }_{k=1}^n{\delta }_{i,i_{k-1}}{\delta }_{j,i_k}{\mathbf{1}}_{[0,\Delta t]}(t_k-t_{k-1})}{{\sum }_{k=1}^n{\delta }_{i,i_{k-1}}{\delta }_{j,i_k}}=\left(\begin{array}{l}\text{probability}\text{that}\text{the}\text{trajectory}\text{takes}\\ \text{less}\text{that}\Delta t\text{to}\text{reach}{S}_j\text{after}\text{crossing}\\ S_i\text{given}\text{that}{S}_j\text{is}\text{the}\text{milestone}\\ \text{crossed}\text{next}\text{after}{S}_i\end{array}\right)$$ (2)

where 1_[0,Δt](s)=1 if s∊[0,Δt] and 1_[0,Δt](s)=0 otherwise. [Thus, f_ij(s) is only defined if p_ij≠0 and in this case ${\int }_0^{\infty }{f}_{ij}\left(s\right)ds=1$.]

As discussed below, the quantities 1, 2 can, in principle, be computed more efficiently than via a long MD trajectory. Before explaining how to do so, however, one should wonder how useful these quantities are. Indeed, in general (i.e., for an arbitrary set of milestones), Eqs. 1, 2 contain only partial information about the statistical properties of the sequence {(S_ik,t_k)}_k=0,1,… [for instance, we could be interested in the probability that S_j is crossed after S_i and S_k after S_j, which is not given by p_ijp_jk in general, or the average time it takes to go from S_i to S_j, which is not expressible in terms of p_ij and f_ij(s) alone in general]. However, all the statistical properties of the sequence {(S_ik,t_k)}_k=0,1,… could be deduced from Eqs. 1, 2 alone if the following two properties were true. The first makes an assumption about the way successive transitions between milestones occur.

(P1) The probability that after crossing S_j0, the system successively visits n milestones in the sequence S_j1,S_j2,S_j3,…,S_jn is for any n∊N given by

$$p_{j_0{j}_1}{p}_{j_1{j}_2}{p}_{j_2{j}_3}\cdots p_{j_{n-1}{j}_n},$$ (3)

where the probability is again defined by recording the proportion of times this sequence of transitions is observed along the sequence {S_{ik}k=0,1,2,…}.

This property guarantees that the statistical properties of the sequence {S_ik}k=0,1,… are identical to those of a discrete-time Markov process (here the “time” is the index k) with transition probability p_ij. The second property makes an assumption about the statistics of the lag times between crossings of successive milestones.

(P2) Denoting by t_j0j1,t_j1j2,…,t_jn−1jn the lag times between successive crossings of the milestones along any sequence S_j0,S_j1,S_j2,…,S_jn, these lag times are statistically independent, i.e., if we compute the joint probability density function that t_j0j1=s₁,t_j1j2=s₂,…,t_jn−1jn=s_n, for any n∊N it reduces to the product

$$f_{j_0{j}_1}\left(s_1\right)f_{j_1{j}_2}\left(s_2\right)\cdots f_{j_{n-1}{j}_n}\left(s_n\right).$$ (4)

Together with (P1), this property guarantees that the statistical properties of the sequence {(S_{ik,tk)}k=0,1,…} are those of a discrete-time Markov process (where the time stands again for the index k, whereas the physical time t_k is part of the state variables of the chain⁷) with transition probability

$$\left(\begin{array}{l}\text{probability}\text{that}{S}_{i_{k+1}}=S_j\text{and}{t}_{k+1}⩽\\ t+\Delta t\text{given}\text{that}{S}_{i_k}=S_i\text{and}{t}_k=t\end{array}\right)=p_{ij}{\int }_0^{\Delta t}{f}_{ij}\left(s\right)ds.$$ (5)

This says that given that milestone S_i is crossed at time t_k, with probability p_ij, the next milestone to be crossed is S_j and given that this event occurs, it happens at time t_k+1=t_k+t_ij, where t_ij is a random time distributed according to Eq. 2.

The key assumption made in the milestoning procedure is that properties (P1) and (P2) do hold true, thereby guaranteeing that the statistical properties of the sequence {(S_{ik,tk)}k=0,1,…} obtained from the MD trajectory are identical to those of the Markov chain with transition probability Eq. 5. This chain is fully specified if one knows the quantities in Eqs. 1, 2 and it can be analyzed using the tools developed in Refs. ^{1, 2, 3, 4, 5}. Of course, this still leaves us with the important question of how to compute Eqs. 1, 2 in practice. A key component of milestoning is to do so by reinitializing the MD simulation on each milestone S_i. In principle, this reinitialization must be done using the probability density of the position at which a long ergodic trajectory first hits milestone S_i after crossing another one [i.e., the density of the points x(t_k) with k such that i_k≡i], but since this density is not known a priori, we are left with the question: What is the expression of the first hitting point probability density on the milestones that should be used to reinitialize the short MD runs in order to compute Eqs. 1, 2?

If we can answer this question, then Eqs. 1, 2 can be computed by performing relatively short MD runs until the trajectories initiated on a given milestone reach another milestone. This allows one to bypass the need to wait that the system actually reaches this milestone on its own (i.e., the need to use a long unbiased trajectory) and, in effect, it is the reason why milestoning offers a computational gain over direct MD. Indeed, with an appropriate choice of the milestones, the individual transition times between them can be made relatively short even though overall transition times between milestones which are far apart can be very long.

This finally brings us back to the aims of this paper. Our main objectives are to analyze the validity of properties (P1) and (P2) and to derive an expression for the first hitting point probability density that must be used to reinitialize the trajectories on the milestones. In Sec. 2 we will first analyze systems in the overdamped limit and show that there exist sets of milestones for which property (P1) is satisfied exactly. Property (P2), in general, will not hold exactly for this set of milestones, but we will show that this property is, in fact, not necessary to compute exactly certain quantities such as mean first passage times [in order to do such calculations exactly, only property (P1) is required]. For this reason, we shall refer to the milestones in sets such that property (P1) holds as “optimal milestones.” Using the results from transition path theory (TPT),^{8, 9, 10} we will show that these sets of optimal milestones involve the isosurfaces of the so-called committor function. We also derive the probability density of first hitting of these surfaces, from which one needs to initiate trajectories to compute Eq. 1 in the milestoning procedure. These results are illustrated in Sec. 3 via simple examples. In Sec. 4 we then consider systems with inertia, for which the situation is more complex. Optimal milestoning and the exact calculation of mean first passage time are, in principle, possible using again the isosurfaces of the committor function, but this function now depends on both the system position and momentum. In addition, for reasons that we will explain, an explicit expression for the probability density of first hitting of these surfaces is not available for systems with inertia, which complicates matters even more. How to deal with these issues, in practice, is explained in Sec. 5 where, among other things, we discuss how to identify optimal milestones in practice by combining milestoning with the string method.^{11, 12, 13, 14, 15, 16} Finally, a few concluding remarks are given in Sec. 6 where we compare milestoning with other strategies that use short runs between intermediates to deduce the overall kinetics. These include, in particular, Markov state models (MSMs) (e.g., Refs. ^{17, 18, 19, 20, 21, 22, 23, 24, 25}), transition interface sampling^{26, 27} (TIS) and forward flux sampling (FFS).²⁸ For the reader’s convenience, some background material on TPT (in particular on the committor function) and some technical derivations are deferred to two appendixes.

OPTIMAL MILESTONING IN THE OVERDAMPED LIMIT

In this section, we focus on systems governed by the overdamped (Smoluchowski) equation

$$\gamma \dot{\mathit{x}}\left(t\right)=-\nabla V\left(\mathit{x}\left(t\right)\right)+\sqrt{2{\beta }^{-1}\gamma }\mathbf{\eta }\left(t\right).$$ (6)

Here x(t)∊R^d denotes the position of the system, γ is the friction coefficient, V(x) is the potential, β is the inverse temperature, and η(t) is a white noise, i.e., a Gaussian process with mean zero and covariance ⟨η_i(t)η_j(t^′)⟩=δ_ijδ(t−t^′). The case of systems with inertia governed by the Langevin equation will be considered later in Sec. 4.

In Sec. 2A we first establish that optimal sets of milestones which satisfy property (P1) exactly exist and involve the isosurfaces of the committor function. Then in Sec. 2B we derive the probability density of first hitting points on these optimal milestones. Finally, in Sec. 2C we discuss why, in general, property (P2) does not hold exactly even for optimal milestones, but we show that mean first passage times can nonetheless be computed exactly with these milestones.

Isocommittor surfaces as optimal milestones

Successive transitions between milestones are not independent, in general, and property (P1) does not always hold because typically, the position where the trajectory crossed milestone S_i influences whether it will cross next S_j rather than another milestone. In other words, the probability that x(t_k)∊S_j given that x(t_k−1)∊S_i depends on where x(t_k−1) is located on S_i [if we knew x(t_k−1), we could deduce the probability that x(t_k)∊S_j since x(t) is a Markov process, but the exact location of x(t_k−1) is precisely what milestoning aims at coarse graining]. This issue, however, obviously disappears and property (P1) will hold if one can find sets of milestones such that the following property holds:

(P1^′) the probability to reach first S_j from S_i is the same from any starting point on S_i. The main result of this section is to show that such sets of optimal milestones satisfying property (P1^′) and, hence, (P1), exist.

To see why this is the case, suppose that we start with a first and a last milestone in a set of N milestones, i.e., two nonintersecting but otherwise arbitrary smooth dividing surfaces in configuration space, respectively, denoted by S₁ and S_N. We wish to complete this set with S₂,S₃,…,S_N−1 in such a way that property (P1^′) hold exactly for this set. To do so, let us introduce the following function:

$$q\left({\mathit{x}}_0\right)=\left(\begin{array}{l}\text{probability}\text{that}\mathit{x}\left(t\right)\text{reaches}\text{first}{S}_N\\ \text{rather}\text{that}{S}_1\text{given}\text{that}\mathit{x}\left(0\right)={\mathit{x}}_0\end{array}\right).$$ (7)

Here and below, the probability is defined with respect to the realizations of the noise in Eq. 6. The function q(x) is the so-called committor function introduced in TPT to describe the reaction between a reactant state A⊂R^d and a product state B⊂R^d, which are here the two sets whose respective boundaries are S₁ and S_N and leave out the region in between S₁ and S_N (note that since S₁ and S_N can be chosen arbitrarily, in the present context the labels “reactant” and “product” are somewhat void of content). As we recall in Appendix A, the committor function q(x) is the solution of the partial differential equation given in Eq. A7 and the isosurfaces of q(x) foliate the region in between S₁ and S_N (i.e., they are nonintersecting smooth dividing surfaces in this region). The key idea behind optimal milestoning is to use some of these surfaces as milestones. Specifically, letting z₁=0<z₂<z₃<⋯<z_N=1, we define

$$S_i=\{\mathit{x}:q\left(\mathit{x}\right)=z_i\},i=1,\dots ,N.$$ (8)

This definition is consistent with S₁ and S_N since q(x)=0 on S₁ and q(x)=1 on S_N by construction, and we claim that these surfaces are optimal milestones. To see this, look at the reaction from the extended reactant state at the left of S_i−1, i.e., the set {x:q(x)⩽z_i−1}, to the extended product state at the right of S_i+1, i.e., the set {x:q(x)⩾z_i+1}, and note that the surface S_i={x:q(x)=z_i} also is an isocommittor surface for this reaction. Indeed, the committor function for this reaction is related to the original q(x) as (q(x)−z_i−1)∕(z_i+1−z_i−1) since, by construction, this function satisfies Eq. A7 with the correct boundary conditions that it be 0 on S_i−1 and 1 on S_i+1. Since q(x)=z_i on S_i by definition, this shows that the probability to reach first S_i+1 rather than S_i−1 starting from any point on S_i is equal to (z_i−z_i−1)∕(z_i+1−z_i−1) for any i=2,…,N−1 (obviously the probability to reach first S₂ from S₁ and the one to reach first S_N−1 from S_N are both 1). This implies that properties (P1^′) and (P1) are indeed satisfied and gives the following expression for Eq. 1: p₁₂=p_NN−1=1 and, for i=2,…,N−1,

$$p_{ij}=\{\begin{array}{ll}\frac{z_{i+1}-z_i}{z_{i+1}-z_{i-1}}& \text{if}j=i-1\\ \frac{z_i-z_{i-1}}{z_{i+1}-z_{i-1}}& \text{if}j=i+1\\ 0& \text{otherwise}.\end{array}\phantom{\}}$$ (9)

The conclusions above rely on the properties of the exact q(x), which we can only hope to compute from Eq. A7 in systems of low dimensions. We note however that there are algorithms (see, e.g., Refs. ^{12, 15, 29, 30}) to effectively approximate the committor surfaces in systems with much higher dimensions under suitable assumptions (more on this in Sec. 6 below).

First hitting point density and the issue of reinitialization

As explained earlier, using optimal milestones such that property (P1) holds exactly is not enough to make milestoning practical. Indeed, since we typically do not have at our disposal an infinitely long ergodic trajectory, we also need to know how to reinitiate MD trajectories from the milestones to compute the lag-time density 2 [which is the only thing left to compute with optimal milestones since Eq. 1 is given by Eq. 9 for these milestones]. This is the issue that we discuss next.

Denote by ρ_ij(x) the probability density of the first hitting point on S_j given that the infinitely long ergodic trajectory generated by Eq. 6 crossed S_i last before S_j. As demonstrated in Appendix B, a key property of the optimal milestones defined in Eq. 8 is that ρ_ij(x) depends only on j and not on i, i.e., we have ρ_ij(x)≡ρ_j(x) with ρ_j(x) given by³¹

$${\rho }_j\left(\mathit{x}\right)=Z_j^{-1}{e}^{-\beta V\left(\mathit{x}\right)}\mid \nabla q\left(\mathit{x}\right)\mid .$$ (10)

Here Z_j is a normalization factor given by the surface integral

$$Z_j={\int }_{S_j}{e}^{-\beta V\left(\mathit{x}\right)}\mid \nabla q\left(\mathit{x}\right)\mid d{\sigma }_{S_j}\left(\mathit{x}\right),$$ (11)

where dσ_Sj(x) denotes the surface element on S_j (i.e., the Lebesgue measure on this surface). Because property (P1) holds with optimal milestones, one can compute the lag-time density 2 by reinitializing MD trajectories on these milestones, and the correct probability density to perform this reinitialization on S_j is ρ_j(x).

The proof that Eq. 10 is the correct density of first hitting point on the optimal milestones is somewhat technical, and we defer it to Appendix B. Here let us simply stress that Eq. 10 is not the equilibrium density on S_j, which would be proportional to e^−βV(x). The extra factor ∣∇q(x)∣, which appears in Eq. 10, can be understood within the framework of TPT upon noting that the probability current of reactive trajectories is proportional to e^−βV(x)∇q(x), and so the probability flux induced by this current through the surface S_j is precisely given by Eq. 11. The first hitting point density is related to this probability flux, and this is consistent with Eq. 10 rather than with the equilibrium density. How different the density 10 is with respect to the equilibrium one will be illustrated via examples in Sec. 3. In Sec. 4 we also discuss how to deal with Eq. 10 in practice.

Exact calculation of mean first passage times

As we have mentioned earlier, property (P2) is independent of (P1). In particular, even the set of optimal milestones made of isocommittor surfaces introduced in Sec. 2A will not, in general, be such that the lag times between successive transitions between milestones are statistically independent (why this is the case will be illustrated via an example in Sec. 3). This means that the reduction of the dynamics used in milestoning will not be exact in general. However, optimal milestones allow one to compute exactly certain important quantities, such as the mean first passage time from any milestone to any other one. Next we discuss why this is the case and give an explicit expression for these mean first passage times.

Consider the various instances when a long ergodic trajectory visits the milestones S_j0, S_j1,…,S_jn successively in this sequence. The duration of any one of such sequences is given by a sum of times, t_j0j1+t_j1j2+⋯+t_jn−1jn, each of which is the lag between the crossing times of two successive milestones, t_jkjk+1=t_k+1−t_k with x(t_k)∊S_jk. If one builds the statistics of these times, one will observe that, in general, they are correlated, i.e., rather than Eq. 2 what one needs to describe their statistical properties in full is their joint probability density

$$f_{j_0{j}_1\cdots j_n}(s_1,s_2,\dots ,s_n)=\left(\begin{array}{l}\text{probability}\text{density}\text{that}{t}_1-t_0=s_1,\\ t_2-t_1=s_2,\dots ,\text{and}{t}_n-t_{n-1}=\\ s_n,\text{given}\text{that}\mathit{x}\left(t_k\right)∊S_{j_k}\text{for}k=\\ 0,\dots ,n\end{array}\right)\ne f_{j_0{j}_1}\left(s_1\right)f_{j_1{j}_2}\left(s_2\right)\cdots f_{j_{n-1}{j}_n}\left(s_n\right).$$ (12)

However, regardless of whether the times t_j0j1,…,t_jn−1jn are statistically independent or not, Eq. 2 remains the marginal of the density 12 for any t_jkjk+1, i.e., for any k=1,…,n we have

$$f_{j_{k-1}{j}_k}\left(s_k\right)=\int f_{j_0{j}_1\cdots j_n}(s_1,s_2,\dots ,s_n)d{s}_1\cdots d{s}_{k-1}d{s}_{k+1}\cdots d{s}_n.$$ (13)

As a result, the average duration of such sequence is given exactly by

$${\tau }_{j_0{j}_1}+{\tau }_{j_1{j}_2}+\cdots +{\tau }_{j_{n-1}{j}_n},$$ (14)

where τ_ij is the first moment of Eq. 2,

$${\tau }_{ij}={\int }_0^{\infty }s{f}_{ij}\left(s\right)ds.$$ (15)

In essence, evaluating the mean first passage time amounts to summing up the mean duration of sequences of transitions between milestones weighed by their probability of occurrence [an explicit expression for the mean passage time is given as the solution of Eq. 21 below]. As a result, what is required to compute these times is Eq. 15 and, as long as one uses optimal milestones [in order that property (P1) holds and to get the correct Eq. 9] and one reinitializes the trajectories according to Eq. 10 [to compute the first moment 15 correctly], it does not matter whether property (P2) holds or not. This is good news also because measuring the first moment τ_ij rather than the full density f_ij(s) is easier.

Let us now give an explicit expression for the mean first passage time to a given milestone. Without loss of generality, we can assume that this milestone is the last one S_N since we can always make it so by relabeling the milestones index. Let us define

$$T_i=\left(\begin{array}{l}\text{mean}\text{first}\text{passage}\text{time}\text{from}\\ \text{milestone}{S}_i\text{to}\text{milestone}{S}_N\end{array}\right).$$ (16)

Thus T_i>0 for i≠N and T_N=0. To compute this mean first passage time, we need to sum up the average lengths in time of all the sequences leading to S_N weighed by their probability of occurrence. This is easy to do with the help of a little trick which consists in introducing a modified p_ij, denoted as ${\widehat{p}}_{ij}$ and defined as

$${\widehat{p}}_{ij}=\{\begin{array}{ll}{p}_{ij}& \text{if}i\ne N\\ {\delta }_{jN}& \text{if}i=N.\end{array}\phantom{\}}$$ (17)

The modified ${\widehat{p}}_{ij}$ turns the milestone S_N into a so-called cemetery state: unlike with the original p_ij, with the new ${\widehat{p}}_{ij}$ the process stays at milestone S_N forever if it ever reaches this milestone. Therefore the average length in time of a path starting from S_i and moving from milestones to milestones for up to n transitions but staying in S_N if ever it reaches this state can be expressed as

$$T_i^{\left(n\right)}=\sum _{j_1,\dots ,j_n}({\tau }_{i{j}_1}+{\tau }_{j_1{j}_2}+\cdots +{\tau }_{j_{n-1}{j}_n})\times {\widehat{p}}_{i{j}_1}{\widehat{p}}_{j_1{j}_2}\cdots {\widehat{p}}_{j_{n-1}{j}_n},$$ (18)

where τ_ij is the first moment of f_ij(s) defined in Eq. 15 and we have set τ_ii=0: since the only nonzero ${\widehat{p}}_{ii}$ is ${\widehat{p}}_{NN}=1$, only τ_NN enters the sum in Eq. 18, and the choice of τ_NN=0 guarantees that the length in time of a path stops growing as soon as it reaches S_N. The mean first passage time T_i is the limit of Eq. 18 as n→∞, $T_i={\lim }_{n\to \infty }{T}_i^{\left(n\right)}$ since this then takes into account paths of all possible length to reach S_N. Thus expression 18 confirms that the mean first passage time to a given milestones will be exact if property (P1) is satisfied (which ensures that p_ij and, hence, ${\widehat{p}}_{ij}$ contains the exact statistical information about probability of transitions between milestones), but regardless of whether (P2) holds or not.

To compute the limit of Eq. 18 as n→∞, let us introduce some notations and denote by ${\mathit{T}}^{\left(n\right)}={(T_1^{\left(n\right)},T_2^{\left(n\right)},\dots ,T_n^{\left(n\right)})}^T$ the vector with entries $T_i^{\left(n\right)}$, by 1=(1,1,…,1)^T the unit vector in R^N, by $\widehat{P}$ the matrix with entries ${\widehat{p}}_{ij}$, and by Q the matrix with entries ${\tau }_{ij}{\widehat{p}}_{ij}$. Then, Eq. 18 can be expressed as

$${\mathit{T}}^{\left(n\right)}=\sum _{m=1}^n{\widehat{P}}^{n-m}Q{\widehat{P}}^{m-1}\mathbf{1}=\sum _{m=1}^n{\widehat{P}}^{n-m}Q\mathbf{1},$$ (19)

where we used $\widehat{P}\mathbf{1}=\mathbf{1}$ which follows from $\widehat{P}$ being a transition probability matrix to get the second equality. Left multiplying by $\widehat{P}$, we obtain the following recurrence relation for T⁽ⁿ⁾

$${\mathit{T}}^{(n+1)}=\widehat{P}{\mathit{T}}^{\left(n\right)}+\widehat{\mathbf{\tau }}$$ (20)

where $\widehat{\mathbf{\tau }}=Q\mathbf{1}$: explicitly ${\widehat{\tau }}_i={\tau }_i$ for i≠N and ${\widehat{\tau }}_N=0$ where ${\tau }_i={\sum }_{j=1}^N{p}_{ij}{\tau }_{ij}$. We can now take the limit as n→∞ to obtain

$$(\mathrm{Id}-\widehat{P})\mathit{T}=\widehat{\mathbf{\tau }},$$ (21)

where T=(T₁,T₂,…,T_N)^T is the vector with entries T_i and Id is the identity matrix. This equation may seem problematic because $\det (\mathrm{Id}-\widehat{P})=0$ since $\mathrm{Id}-\widehat{P}$ has a zero eigenvalue associated with the eigenvector 1. However, since by definition the Nth component of the vectors $(\mathrm{Id}-\widehat{P})\mathit{T}$ and $\widehat{\mathbf{\tau }}$ are both zero, we can remove the last equation in the set [Eq. 21], which leads to a regular set of N−1 equations for the N−1 unknown T₁,…,T_N−1 which can easily be solved (and we already know that T_N=0 by definition). Equation 21 agrees with the one for T derived in Refs. ^{2, 3} using different methods.

We conclude this section with a comment. From Eq. 21, the only quantities required to compute mean first passage times are p_ij and the mean time τ_i. As a result it does not matter what the actual shape of f_ij(s) is, and we could approximate this function by

$${\tilde{f}}_{ij}\left(s\right)={\tau }_i^{-1}\exp (-s∕{\tau }_i).$$ (22)

without changing Eq. 21. Since this approximation amounts to assuming that the dynamics of the transitions between successive milestones is a continuous-time Markov process,⁷ it was referred to as Markovian milestoning in Ref. 3. In general, the approximation of f_ij(s) by Eq. 22 is invalid, but we stress again that, when used with optimal milestones, it gives the correct mean first passage times. We will come back to this observation in Sec. 6 when we compare milestoning to MSMs.

ILLUSTRATIVE EXAMPLES

Let us now illustrate the results in Sec. 2 on a few simple examples. In Fig. 2, we analyze a two dimensional example with potential

$$V(x_1,x_2)=\frac{1}{4}{(1-x_1^2)}^2+\frac{1}{2}{(x_2+\frac{1}{2}{x}_1^2)}^2$$ (23)

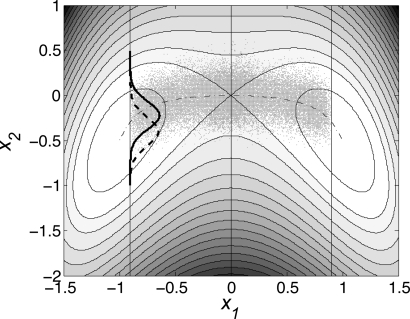
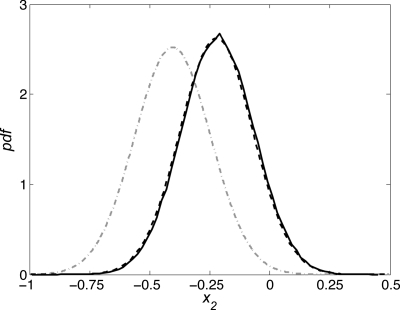
in a situation where β=40 and γ=1 in Eq. 6. First we consider an extreme case in which we only take three milestones, S₁={x₁=−0.9}, S₂={x₁=0}, and S₃={x₁=0.9}. Thus S₁ and S₃ mark the boundary of the reactant set A={x₁<−0.9} and the product set B={x₁>0.9} [i.e., S₁ is also the isocommittor surface where q(x)=0, while S₃ is the one where q(x)=1], and by symmetry, S₂ is the isocommittor surface where q(x)=0.5 for this reaction. These three surfaces are shown in Fig. 2 atop the contour plot of the potential 23. Also shown as gray dots are snapshots every δt=0.05 of 10³ trajectories generated from S₂ according to Eq. 10 in which we used a numerical approximation of ∇q(x) obtained by solving Eq. A7 by finite elements (see Ref. 10 for details). The predicted density 10 of hitting points on S₁ is also shown (thick black line) and compared to the equilibrium density on S₁, i.e., the density proportional to e^{−βV(−0.9,x₂)} (dashed line). Clearly, these two densities are different, and Eq. 10 rather than the equilibrium density is the correct first hitting point density. This was also confirmed by computing this density directly from a long MD trajectory (not shown). The difference between Eq. 10 and the equilibrium density is also apparent from Fig. 3 where we compare the density of hitting points obtained by binning the location where 10⁵ trajectories hit S₁ (black solid curve), with Eq. 10 (black dashed curve) and the equilibrium density (gray dot-dashed curve).

Figure 2.

Contour plot of the potential 23 with the three milestones S₁={x₁=−0.9}, S₂={x₁=0}, and S₃={x₁=0.9} (S₁ and S₃ are the boundaries of the reactant set {x₁<0.9} and product set {x₂>−0.9} where q(x)=0 and q(x)=1, respectively, and S₂ is the isocommittor surface q(x)=0.5 for this reaction). The minimum energy path is also shown (dot-dashed line). The gray dots are snapshots every δt=0.05 along 10³ trajectories starting from points distributed on S₂ according to Eq. 10, and the predicted density 10 of first hitting points on S₁ (thick black line) is compared to the equilibrium density on S₁ (dashed line).

Figure 3.

Comparison of the probability density of first hitting points obtained by binning the location where 10⁵ trajectories started from points in S₂ distributed according to Eq. 10 hit S₁ (black solid curve) with the density [Eq. 10] (black dashed curve) and with the equilibrium density (gray dot-dashed curve). We also computed the first hitting point density using a long unbiased trajectory and, up to statistical errors, it coincides with the solid curve shown in the figure.

It should be stressed that working with three milestones only is an extreme case, and it is the reason why the density 10 on S₁ and S₃ is so different than the equilibrium one. Indeed, S₁ and S₃ are the boundary of sets A and B which are arbitrary. As a result, we should not expect Eq. 10 to agree with the equilibrium density on S₁ and S₃. If, however, we include more milestones, then one can expect that the ones away from the boundaries of A and B will bend in the right direction in such a way that Eq. 10 and the equilibrium density may become more alike if ∣∇q(x)∣≈cst in the region in q(x)=z_j, where e^−βV(x) is peaked. This approximation will be valid if one can locally approximate the isocommittor surfaces by planes and neglect curvature effects along the reaction channel. A situation where this approximation is valid is illustrated in Figs. 45. In general, however, the extra factor ∣∇q(x)∣ in Eq. 10 compared to the equilibrium density restricted to S_j will matter (as shown, e.g., in our second example below). How to account for it will be discussed some more in Sec. 6.

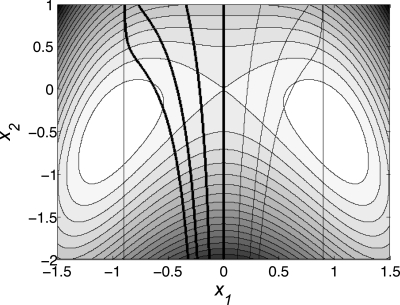
Figure 4.

Contour plot of the potential 23 with superimposed isocommittor surfaces used as milestones: from left to right, these surfaces are q(x)=0, q(x)=0.001, q(x)=0.01, q(x)=0.1, q(x)=0.5, q(x)=0.9, q(x)=0.99, q(x)=0.999, and q(x)=1.

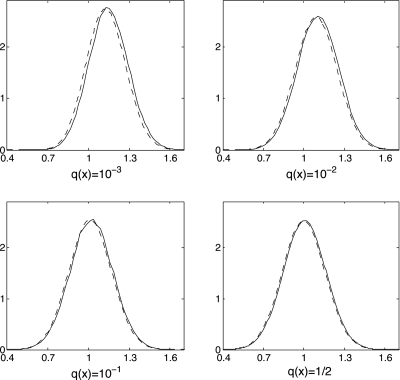
Figure 5.

Comparison of the probability density 10 (solid line) on the four milestones shown as thick lines in Fig. 4 with the equilibrium probability density (dashed line). The probability densities are plotted as functions of the arc length along the milestones.

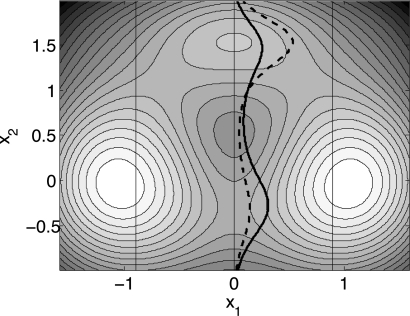
As a second illustration, let us consider an example originally proposed in Ref. 32 in which there are two reaction channels. The potential is shown in Fig. 6 and has been analyzed in detail in Ref. 10. This example shows why the time lags between transitions can be correlated even though these transitions are not. Indeed, because there are two channels (the upper and the lower ones), and the upper one contains a dynamical trap around the shallow minimum centered at (0, 1.5), the time lags between transitions in the upper channel tend to be longer than between the ones in the lower one. Hence, a long lag between transition is more likely to be followed by a long one (indicating that the process goes through the upper channel), and a short lag by a short one (indicating that the process goes through the lower channel). Therefore, this is a situation where property (P1) holds but (P2) does not. It should also be stressed that this is an example where the factor ∣∇q(x)∣ matters again. This is because there are two channels for the reaction, i.e., the Boltzmann factor e^−βV(x) is peaked in two different regions in q(x)=z_j, and even though ∣∇q(x)∣ is approximately constant in these two regions, these constants are different. This is illustrated in Fig. 6. Using the equilibrium density on q(x)=0.5 would suggest that the preferred channel is the upper one, whereas using Eq. 10 clearly shows that the lower one is preferred. This effect should be accounted for in the milestoning procedure. We come back to this point in Sec. 6.

Figure 6.

Contour plot of the three-hole potential. We use three milestones, shown as vertical lines and corresponding to (from left to right) q(x)=0, q(x)=0.5, and q(x)=1. The density 10 (thick solid line) on the surface q(x)=0.5 shows that the lower channel is the preferred one, even though the equilibrium density (thick dashed line) is peaked in the upper channel.

OPTIMAL MILESTONING IN SYSTEMS WITH INERTIA

In this section, we discuss what happens in systems with inertia, e.g., when we replace the overdamped Eq. 6 by the Langevin equation

$$\dot{\mathit{x}}\left(t\right)=\mathit{v}\left(t\right),$$ (24)

$$m\dot{\mathit{v}}\left(t\right)=-\nabla V\left(\mathit{x}\left(t\right)\right)-\gamma \mathit{v}\left(t\right)+\sqrt{2{\beta }^{-1}\gamma }\mathbf{\eta }\left(t\right),$$

where v(t) denotes the velocity, m the mass matrix, and γ the friction coefficient. Let us revisit the results of Sec. 2 in the context of Eq. 24. Much of the discussion below can be generalized, at least formally, if the Langevin terms $-\gamma \mathit{v}\left(t\right)+\sqrt{2{\beta }^{-1}}\mathbf{\eta }\left(t\right)$ in Eq. 24 are replaced by another thermal bath, possibly consistent with another ensemble than NVT.

Isocommittor surfaces as optimal milestones

Given any two nonintersecting smooth dividing surfaces in phase-space (x,v), henceforth denoted as S₁ and S_N, the committor function associated with these surfaces can be defined as [cf. Eq. 7]

$$q({\mathit{x}}_0,{\mathit{v}}_0)=\left(\begin{array}{c}\text{probability}\text{that}(\mathit{x}\left(t\right),\mathit{v}\left(t\right))\\ \text{reaches}\text{first}{\mathcal{S}}_N\text{rather}\text{than}{\mathcal{S}}_1\\ \text{given}\text{that}(\mathit{x}\left(0\right),\mathit{v}\left(0\right))=({\mathit{x}}_0,{\mathit{v}}_0)\end{array}\right).$$ (25)

As recalled in Appendix A, q(x,v) satisfies the partial differential Eq. A9, and the isosurfaces of this function are nonintersecting smooth dividing surfaces foliating the region between S₁ and S_N. As a result, we can take as milestones the generalization of Eq. 8, i.e.,

$${\mathcal{S}}_i=\{(\mathit{x},\mathit{v}):q(\mathit{x},\mathit{v})=z_i\},i=1,\dots ,N,$$ (26)

where z₁=0<z₂<z₃<⋯<z_N=1, and these milestones will satisfy properties (P1) and (P1^′) exactly with the transition matrix p_ij given in Eq. 9. This shows that optimal milestoning is possible, at least in principle, even for systems governed by Eq. 24.

There are, however, two caveats with this result. The first is that the optimal milestones are now nontrivial dividing surfaces in phase space rather than the simpler lift up in phase space of surfaces defined primarily in configuration space. The second, discussed next in Sec. 4B, is that, unlike in the case of systems in the overdamped limit, the first hitting point density associated with these optimal milestones is not available in closed form. (Practical considerations regarding both these issues are given in Sec. 5.)

First hitting point density and the issue of reinitialization

To understand the issue which arises with the Langevin Eq. 24 when one tries to derive the first hitting point density for this equation, it is useful to recall some results of TPT. TPT can be applied to Eq. 24, but in this case the statistical properties of the reactive trajectories depend on two committor functions: the forward one, which was defined in Eq. 25, and the backward one. The forward committor function gives the probability to reach first a product rather than a reactant state starting from point (x,v); the backward committor function gives the probability to arrive at (x,v) coming last from a reactant state rather than a product state. Unlike in the overdamped case, the backward committor function is not simply one minus the forward one: rather it is given by 1−q(x,−v), where q(x,v) is the forward committor function defined in Eq. 25.

As discussed in Sec. 4A, optimal milestones having property (P1^′) and, hence, (P1) can be defined using the isosurfaces of the forward committor function. This is consistent with properties (P1) and (P1^′) dealing with what happens after the process leaves a milestones, i.e., forward in time. However, when one tries to derive an explicit expression for the first hitting density of the milestones, one deals with the way the process reaches these surfaces, i.e., one must look backward in time. As a result, while it is possible to give an explicit expression for the first hitting point density of milestones defined as isosurfaces of the backward committor function (see Appendix B), such an explicit expression is not available for the optimal milestones defined in Eq. 26. To avoid confusions, let us stress that this negative conclusion does not mean that milestoning (or even optimal milestoning) is not viable in systems with inertia such as the ones governed by Eq. 24. Simply, it means that the exact probability density to reinitiate the MD trajectories on the milestones is not available in closed form, and one needs either to resort to approximations or find ways to bypass the need of this density altogether to perform milestoning. These practical issues are discussed further in Sec. 5.

Exact calculation of mean first passage times

Provided that one uses the optimal milestones defined in Eq. 26 and one uses the proper density to reinitialize the MD trajectories on these milestones to compute the first moment 15, the results given in Sec. 2C apply to the present situation, i.e., Eq. 21 remains the exact equation for the mean first passage time from any milestone to the last.

SOME PRACTICAL CONSIDERATIONS

To make the results presented in this paper practical, two main issues must be addressed. The first is how to identify the isosurfaces of the committor function to be used as optimal milestones. The second is how to reinitialize the MD trajectories on these surfaces to compute the density 2 or its first moment 15.

The first issue suggests to combine milestoning with the string method,^{11, 12, 13, 14, 15, 16} which is a technique to calculate the committor function and its isosurfaces from scratch, at least in situations where the reaction channels are localized either in the original Cartesian space or when viewed in suitable collective variables. The string method can be applied either to the overdamped Eq. 6 or to the Langevin Eq. 24. In the latter case, however, it makes the approximation that the committor function q(x,v) can be approximated by a function of x only, q(x,v)≈q(x) or, more generally, by a function of some suitable collective variables θ(x)=(θ₁(x),θ₂(x),…,θ_N(x))^T such as dihedral angles and bond distances: q(x,v)≈Q(θ(x)) [this second approximation can also be used for the overdamped Eq. 6]. The output of the method is one or more curves, the hyperplanes perpendicular to which are local approximations near the curve of the isosurfaces of the committor function (see Refs. ^{5, 16} for details). The accuracy of these approximations depends on the validity of both the assumptions above: that the reaction channels are localized and that the committor function can be approximated by a function of x only. The latter assumption is difficult to justify on general grounds, but we note that a sufficient condition for it to be valid is that the overdamped Eq. 6 be a good approximation of Eq. 24 on longer time scales where the velocities have had time to decorrelate. This suggests to use milestones that are separated enough so that the typical travel time between milestones will be longer than the velocity decorrelation time. For instance, it was observed empirically in Ref. 3 on the example of solvated alanine dipeptide that the milestones must be sufficiently separated to allow for accurate rate determination. This limits somewhat the efficiency gain achievable by milestoning, but may not be a serious issue in practice since the velocity decorrelates in MD simulations on the subpicosecond time scale while we are interested in time scales that are at least a million times longer. For instance, termination times of picoseconds between milestones yield computational speed up of about 1000 for Scapharca hemoglobin.⁴

Considering now the issue of how to reinitialize the MD trajectories on the milestones, for overdamped systems at least, the results of the string method can also be used to estimate the extra factor ∣∇q(x)∣ to be included in Eq. 10. The problem, however, is that such an approximation can be rather poor (approximating the gradient of a function is typically harder than approximating the function itself) and, in addition, this procedure is not an option for systems with inertia for which the equivalent of Eq. 10 is not available in closed form. One way to get around these difficulties in overdamped systems is to assume that ∣∇q(x)∣ is approximately constant on the isosurfaces of q(x). As was illustrated in Sec. 3 via examples, this approximation is sometimes valid but not always. Another way, which is applicable also for systems with inertia, is to use milestones sufficiently separated so that decorrelation effects along the trajectory make the influence of the density used to initiate the trajectories on the milestones less stringent. This is the procedure which was used in the original milestoning papers,^{1, 2, 3, 4} where MD trajectories are generated on the milestones using the equilibrium density restricted to these milestones. Yet another way, applicable again both to overdamped systems and to those with inertia, is to come up with a sampling procedure that bypasses the need of the first hitting point density altogether. Such a sampling procedure will be presented in Ref. 5 and we refer the reader to this reference for details.

CONCLUDING REMARKS

In this paper, we have analyzed the assumptions underlying milestoning, namely, properties (P1) and (P2), whose specific roles and importance are different. Property (P1) states that transitions between successive milestones are statistically independent and one of the main results in this paper was to establish that property (P1) is satisfied exactly provided that one uses isocommittor surfaces as milestones. Property (P2), on the other hand, does not hold exactly in general, i.e., it is not true that the time lags between successive transitions between milestones are statistically independent. However, we showed that the importance of this property is less than that of (P1). In particular, it was established that mean first passage times from any milestone to any other one can be calculated exactly if one uses milestones satisfying property (P1) and computes the first moment 15 exactly, even if (P2) does not hold. This leads to what we called optimal milestoning. Optimal milestoning requires one to use isocommittor surfaces as milestones, which in practice suggests to combine milestoning with the string method, as mentioned in Sec. 5. Optimal milestoning also requires one to know the probability density of hitting points on the milestones. This density is the one to use to reinitiate the trajectory on the milestones in order to compute the key quantities 1, 2. For systems in the overdamped limit, we derived an explicit expression for this density. We also explained why such a density is not available for the optimal milestones associated with system with inertia such as the ones governed by the Langevin Eq. 24 but, as discussed in Sec. 5, there are various ways to address this issue in practice.

The fact that, in principle at least, optimal milestoning allows one to compute exactly quantities such as mean first passage times is, we believe, a great advantage of the method. It should be stressed, however, that milestoning can remain useful even in situations where property (P1) is not satisfied exactly. In fact, the way milestoning was originally implemented in Refs. ^{1, 2, 3, 4, 5} is not optimal in the sense above, and yet it was demonstrated in this paper that the method does give accurate predictions of the long-time kinetics of various complicated MD systems. While it is difficult to give a precise assessment of why this is the case, this seems to be related to the use of well-separated milestones. The separation must be such that the trajectory decorrelates as it travels between successive milestones in such a way that properties (P1) and (P2) are approximately satisfied even though the milestones are not optimal. Clearly, using optimal milestones should remain the preferred solution, but it shows that things do not necessarily go wrong if this option is not available.

We now conclude this paper with quick comparisons of (i) milestoning versus MSMs, and (ii) milestoning versus TIS and FFS.

Milestoning versus MSM

It is useful to compare milestoning with MSMs in light of our results. MSMs have recently become popular to analyze the kinetics of complicated processes by gathering information about these processes either via short MD runs, or sometimes even in situations where the thought experiment described in the Introduction is realized, i.e., one actually has a very long MD trajectory at one disposal. The basic idea in MSM is to reduce the dynamics to a Markov jump process between the appropriately chosen states in such a way that this reduced dynamics be consistent with the actual one. Thus, at first sight, MSM seems quite similar in spirit to the Markovian milestoning procedure described at the end of Sec. 2C. There is, however, an important difference, namely, that the states used in MSM typically form a partition of phase space, whereas those used in Markovian milestoning are hypersurfaces in phase space (e.g., the states in MSM could be the regions between the milestones rather than the milestones themselves). A consequence of this is that it is hard to justify when MSMs of this type are valid and, in particular, it is not obvious how to choose the time lag at which to compute the transition probability matrix from the MD data in these models. There have been recent studies to address this issue (see, e.g., Refs. ^{23, 24}), but to the best of our knowledge, there are no rigorous results as to when MSMs are accurate. This situation is to be contrasted with milestoning which, provided that optimal milestones are being used, permits to compute exactly mean first passage times. We believe that this is an important advantage of milestoning (Markovian or not) over standard MSM that makes the former preferable to the latter for the analysis of the kinetics of complicated MD processes.

Milestoning versus TIS and FFS

Finally, our results show that milestoning is an interesting alternative to techniques such as TIS^{26, 27} or FFS.²⁸ TIS and FFS allow one to compute exactly the flux of reactive trajectories through a given set of interfaces and thereby the mean first passages between these interfaces. The interfaces used in TIS and FFS are, in principle, arbitrary (i.e., they do not need to be the isocommittor surfaces as in optimal milestoning). In practice, however, the efficiency of these methods will drop if one does not use appropriate surfaces. Ideally, one would like to choose these surfaces so as to optimize the computational gain offered by TIS or FFS, but how to do so is not clear. The isocommittor surfaces seem again a natural choice but, to the best of our knowledge, there is no rigorous proof that this choice is the best one. In addition, TIS and FFS are not as straightforward to parallelize as milestoning and as a result they will typically offer lesser computational gains. It would be interesting to investigate these questions further but we will leave this for future work.

APPENDIX A: THE COMMITTOR EQUATION

Here, we give the equations for the committor function associated with the overdamped Eq. 6 and the Langevin Eq. 24. This is a standard material which can be found in any textbook on stochastic processes, e.g., Sec. 5.7.B in Ref. 33. We start by deriving the equation for the committor function associated with Eq. 6. If x(t) satisfies Eq. 6, given a function u(x), Itô's change in variable formula (e.g., Sec. 3.3 in Ref. 33) asserts that

$$\dot{u}\left(\mathit{x}\left(t\right)\right)=\left(Lu\right)\left(\mathit{x}\left(t\right)\right)+\sqrt{2{\left(\beta \gamma \right)}^{-1}}\nabla u\left(\mathit{x}\left(t\right)\right)\cdot \mathbf{\eta }\left(t\right).$$ (A1)

Here L denotes the infinitesimal generator of the diffusion associated with Eq. 6, i.e.,

$$\left(Lu\right)\left(\mathit{x}\right)=-{\gamma }^{-1}\nabla V\left(\mathit{x}\right)\cdot \nabla u\left(\mathit{x}\right)+{\left(\beta \gamma \right)}^{-1}\Delta u\left(\mathit{x}\right),$$ (A2)

where Δ denotes the Laplacian. Suppose that we consider Eq. 6 in a domain Ω⊂R^d, and denote by τ the first exit time of Ω, i.e.,

$$\tau =\min (t:\mathit{x}\left(t\right)∊\partial \Omega ),$$ (A3)

where ∂Ω denotes the boundary of the set Ω. Integrating Eq. A1 up to time τ and taking the expectation using the property that the noise term has zero expectation, we obtain

$$⟨u\left(\mathit{x}\left(\tau \right)\right)⟩=u\left({\mathit{x}}_0\right)+⟨{\int }_0^{\tau }\left(Lu\right)\left(\mathit{x}\left(t\right)\right)dt⟩,$$ (A4)

where x₀=x(0) is the initial condition of Eq. 6. So far, u was an arbitrary function. Now, let us assume that it is the solution of

$$\left(Lu\right)\left(\mathit{x}\right)=0\text{if}\mathit{x}∊\Omega ,$$ (A5)

$$u\left(\mathit{x}\right)=f\left(\mathit{x}\right)\text{if}\mathit{x}∊\partial \Omega ,$$

where f(x) is some given function defined on the boundary of Ω. Then Eq. A4 reduces to

$$⟨f\left(\mathit{x}\left(\tau \right)\right)⟩=u\left({\mathit{x}}_0\right),$$ (A6)

where we used that x(τ)∊∂Ω, and so u(x(τ))=f(x(τ)) from the boundary condition in Eq. A5. Equation A6 is known as (an instance of) Feynman–Kac formula which gives an expression for the solution of the elliptic partial differential Eq. A5 in terms of an expectation involving the solution of the stochastic differential Eq. 6. An interesting special case is when Ω is the whole configuration space minus the union of sets A and B, Ω=R^d\(A∪B), and one sets f(x)=0 if x∊∂A and f(x)=1 if x∊∂B. Denoting by q(x) instead of u(x) the solution of Eq. A5 in this special case, one sees that Eq. A5 reduces to

$$\left(Lq\right)\left(\mathit{x}\right)=0\text{if}\mathit{x}∊{\mathbb{R}}^d\backslash (A\cup B),$$ (A7)

$$q\left(\mathit{x}\right)=1\text{if}\mathit{x}∊\partial B$$

$$q\left(\mathit{x}\right)=0\text{if}\mathit{x}∊\partial A,$$

and, from Eq. A6, the solution of this equation gives the probability that x(τ) belongs to ∂B rather than ∂A, i.e., it is the committor function defined in Eq. 7 provided that we set ∂A=S₁ and ∂B=S_N. Note that, using the time-reversal symmetry of the overdamped equation, q(x) also is the probability to arrive at x coming last from B rather than A, i.e., 1−q(x) is the backward committor function.

The case of the Langevin Eq. 24 can be treated similarly, the main difference is that all calculations must now be done in phase space rather than configuration space. The generator of the diffusion associated with Eq. 24 is [cf. Eq. A2]

$$\left(\mathcal{L}u\right)(\mathit{x},\mathit{v})=-\mathit{v}\cdot {\nabla }_{x}u(\mathit{x},\mathit{v})-\nabla V\left(\mathit{x}\right)\cdot {\Delta }_{v}u(\mathit{x},\mathit{v})-\gamma \mathit{v}\cdot {\nabla }_{v}u(\mathit{x},\mathit{v})+{\beta }^{-1}\gamma {\Delta }_{v}u(\mathit{x},\mathit{v})$$ (A8)

and the equation for the committor function is [cf. A7]

$$\left(\mathcal{L}q\right)(\mathit{x},\mathit{v})=0\text{if}(\mathit{x},\mathit{v})∊{\mathbb{R}}^{2d}\backslash (\mathcal{A}\cup \mathcal{B})$$ (A9)

$$q(\mathit{x},\mathit{v})=1\text{if}\mathit{x}∊\partial \mathcal{B}$$

$$q(\mathit{x},\mathit{v})=0\text{if}\mathit{x}∊\partial \mathcal{A},$$

where A and B are sets in phase space defining the reactant and the product states, respectively, and ∂A and ∂B are the boundaries of these sets. The only additional caveat with Eq. A9 compared to Eq. A7 is that the local vector normal to the boundaries ∂A and ∂B must have a nonzero velocity component everywhere on ∂A and ∂B except possibly on a set of zero Lebesgue measure on these sets. This condition is required in order to be able to impose the Dirichlet boundary conditions in Eq. A9 because the Laplacian term in Eq. A9 involves only v.

Finally, we note that the function q(x,v) is the forward committor function, i.e., it gives the probability to first reach B rather than A forward in time starting from point (x,v). The backward committor function, giving the probability to arrive at point (x,v) coming last from A rather than B is given by 1−q(x,−v) [and not simply 1−q(x,v)] as a result of the symmetry by time reversal of the Langevin Eq. 24.

APPENDIX B: FIRST HITTING POINT DENSITY

Here we show that the first hitting point density on milestone S_j is given by Eq. 10. Specifically, we show that if a solution of Eq. 6 is initially distributed on S_j according to ρ_j(x) (consistent with this density being assumed to be the one of the first hitting point on this surface), then the probability density of the first hitting point on S_j+1 (S_j−1) conditional on the process hitting this surface first is given by ρ_j+1(x) [ρ_j−1(x)]. Since this argument can be repeated to all the milestones, this is consistent with Eq. 10 being the first hitting point density on milestone S_j.

To get the probability density of the first hitting point on S_j+1 and S_j−1, we consider the probability density at time t of the solution of Eq. 6 in the region Ω_j between S_j−1 and S_j+1, i.e., Ω_j={x:z_j−1<q(x)<z_j+1} (if j=1,N, we simply set Ω₁={x:q(x)<z₂} and Ω_N={x:z_N−1<q(x)}). Denoting by p_t(x) the probability density that the particle be at x at time t, p_t(x) satisfies

$${\partial }_t{p}_t\left(\mathit{x}\right)={\gamma }^{-1}\nabla \cdot (\nabla V\left(\mathit{x}\right)p_t\left(\mathit{x}\right)+{\beta }^{-1}\nabla p_t\left(\mathit{x}\right))$$ (B1)

for x∊Ω_j, and p_t(x)=0 if x∊S_j−1 or x∊S_j+1. As initial condition for Eq. B1, we take the distribution in R^d whose density on S_j is ρ_j(x),³¹

$$p_{t=0}\left(\mathit{x}\right)=Z_j^{-1}{e}^{-\beta V\left(\mathit{x}\right)}{\mid \nabla q\left(\mathit{x}\right)\mid }^2\delta (q\left(\mathit{x}\right)-z_j).$$ (B2)

We also set absorbing boundary conditions at S_j−1 and S_j+1, i.e., p_t(x)=0 if x∊S_j−1 or x∊S_j+1. Due to the presence of these absorbing boundaries, we have that p_t(x)→0 for x∊Ω_j as t→∞, and this decay is associated with escape events by the boundaries S_j−1 and S_j+1. Writing Eq. B1 as

$${\partial }_t{p}_t\left(\mathit{x}\right)=-\nabla \cdot J_t\left(\mathit{x}\right),$$ (B3)

where J_t(x) is the probability current

$$J_t\left(\mathit{x}\right)=-{\gamma }^{-1}\nabla V\left(\mathit{x}\right)p_t\left(\mathit{x}\right)-{\left(\gamma \beta \right)}^{-1}\nabla p_t\left(\mathit{x}\right),$$ (B4)

we see that the probability flux density at point x∊S_j−1∪S_j+1 and time t is given by

$${\gamma }^{-1}\widehat{n}\left(\mathit{x}\right)\cdot (\nabla V\left(\mathit{x}\right)p_t\left(\mathit{x}\right)+{\beta }^{-1}\nabla p_t\left(\mathit{x}\right)),$$ (B5)

where $\widehat{n}\left(\mathit{x}\right)$ denotes the unit vector pointing outward Ω_j at x∊S_j−1∪S_j+1: explicitly, $\widehat{n}\left(\mathit{x}\right)=\nabla q\left(\mathit{x}\right)∕\mid \nabla q\left(\mathit{x}\right)\mid$ for x∊S_j+1 and $\widehat{n}\left(\mathit{x}\right)=-\nabla q\left(\mathit{x}\right)∕\mid \nabla q\left(\mathit{x}\right)\mid$ for x∊S_j−1. We are interested in the time-integrated probability flux density at the point x∊S_j−1∪S_j+1 since this time-integrated flux density gives the overall probability density that the particle escapes by this point (the hitting density). To calculate this flux density, let

$$P\left(\mathit{x}\right)={\int }_0^{\infty }{p}_t\left(\mathit{x}\right)dt.$$ (B6)

Using the initial condition B2 as well as lim_t→∞p_t(x)=0, by integrating Eq. B1 in time from 0 to ∞, we arrive at the following equation for P(x):

$$-{\rho }_j\left(\mathit{x}\right)={\gamma }^{-1}\nabla \cdot (\nabla V\left(\mathit{x}\right)P\left(\mathit{x}\right)+{\beta }^{-1}\nabla P\left(\mathit{x}\right))$$ (B7)

for x∊Ω_j, and P(x)=0 if x∊S_j−1 or x∊S_j+1. We claim that the solution of Eq. B7 is

$$P\left(\mathit{x}\right)=\{\begin{array}{cc}{C}_L(q\left(\mathit{x}\right)-z_{j-1})e^{-\beta V\left(\mathit{x}\right)}& \text{if}{z}_{j-1}⩽q\left(\mathit{x}\right)<z_j\\ C_R(z_{j+1}-q\left(\mathit{x}\right))e^{-\beta V\left(\mathit{x}\right)}& \text{if}{z}_j⩽q\left(\mathit{x}\right)⩽z_{j+1},\end{array}\phantom{\}}$$ (B8)

where

$$C_L=\gamma Z_j^{-1}\frac{z_{j+1}-z_j}{z_{j+1}-z_{j-1}},$$ (B9)

$$C_R=\gamma Z_j^{-1}\frac{z_j-z_{j-1}}{z_{j+1}-z_{j-1}}.$$

Using Eq. A7, it is easy to see that Eq. B8 solves Eq. B7 in the region Ω_j\S_j in which ρ_j(x)=0, that it satisfies the right boundary condition on S_j+1 and S_j−1, and that it is continuous (though not differentiable) on S_j. Thus it simply remains to establish that Eq. B8 also satisfies Eq. B7 on S_j in some appropriate sense. Specifically, we need to show that if we take δ>0 and an arbitrary test function f(x), multiply Eq. B7 by f(x), integrate the resulting equation on the region z_j−δ⩽q(x)⩽z_j+δ, and finally let δ→0, we get an equation which is satisfied with P(x) given by Eq. B8. Performing this calculation and using integration by parts at the right-hand side, the result is

$$-Z_j^{-1}{\int }_{S_j}f\left(\mathit{x}\right)e^{-\beta V\left(\mathit{x}\right)}\mid \nabla q\left(\mathit{x}\right)\mid d{\sigma }_{S_j}\left(\mathit{x}\right)=-{\gamma }^{-1}(C_L+C_R){\int }_{S_j}f\left(\mathit{x}\right)e^{-\beta V\left(\mathit{x}\right)}\mid \nabla q\left(\mathit{x}\right)\mid d{\sigma }_{S_j}\left(\mathit{x}\right),$$ (B10)

which is indeed satisfied for every f(x) in view of Eq. B9. Having established that Eq. B8 is the solution of Eq. B7, we can calculate the time-integrated flux at x∊S_j−1∪S_j+1 which gives the probability density that the particle exits at this point. Time-integrating Eq. B5 and using Eq. B6, this hitting density can be expressed in terms of P(x) as

$${\gamma }^{-1}\widehat{n}\left(\mathit{x}\right)\cdot (\nabla V\left(\mathit{x}\right)P\left(\mathit{x}\right)+{\beta }^{-1}\nabla P\left(\mathit{x}\right)),$$ (B11)

which, using Eq. B8, can be expressed, on S_j−1 and S_j+1, as

$${\rho }_L\left(\mathit{x}\right)={\gamma }^{-1}{C}_L{e}^{-\beta V\left(\mathit{x}\right)}\mid \nabla q\left(\mathit{x}\right)\mid \text{if}\mathit{x}∊S_{j-1}$$ (B12)

$${\rho }_R\left(\mathit{x}\right)={\gamma }^{-1}{C}_R{e}^{-\beta V\left(\mathit{x}\right)}\mid \nabla q\left(\mathit{x}\right)\mid \text{if}\mathit{x}∊S_{j+1},$$

which, according to Eq. 10, are indeed proportional to ρ_j−1(x) and ρ_j+1(x), respectively. In fact, the integrals of ρ_L(x) on S_j−1 and of ρ_R(x) on S_j+1 give the probabilities that the particle exits by S_j−1 or S_j+1, respectively,

$${\int }_{{\mathbb{R}}^d}{\rho }_L\left(\mathit{x}\right)d\mathit{x}=\frac{z_{j+1}-z_j}{z_{j+1}-z_{j-1}}\equiv p_{jj-1},$$ (B13)

$${\int }_{{\mathbb{R}}^d}{\rho }_R\left(\mathit{x}\right)d\mathit{x}=\frac{z_j-z_{j-1}}{z_{j+1}-z_{j-1}}\equiv p_{jj+1},$$

where we used Eqs. 11, B9 as well as the property (shown below) that for any j,k=1,…,N, we have

$${\int }_{S_j}\mid \nabla q\left(\mathit{x}\right)\mid e^{-\beta V\left(\mathit{x}\right)}d{\sigma }_{S_j}\left(\mathit{x}\right)={\int }_{S_k}\mid \nabla q\left(\mathit{x}\right)\mid e^{-\beta V\left(\mathit{x}\right)}d{\sigma }_{S_k}\left(\mathit{x}\right).$$ (B14)

Eq. B13 is consistent with Eq. 9, and we see that ρ_j−1(x)=ρ_L(x)∕p_jj−1 and ρ_j+1(x)=ρ_L(x)∕p_jj+1. This shows that the hitting probability on S_j−1 conditional on exiting through S_j−1 is indeed ρ_j−1(x), and similarly for S_j+1.

Finally to show that Eq. B14 holds, consider

$$I\left(z\right)={\int }_{q\left(\mathit{x}\right)=z}{e}^{-\beta V\left(\mathit{x}\right)}\mid \nabla q\left(\mathit{x}\right)\mid d{\sigma }_{\{q\left(\mathit{x}\right)=z\}}={\int }_{{\mathbb{R}}^d}{e}^{-\beta V\left(\mathit{x}\right)}{\mid \nabla q\left(\mathit{x}\right)\mid }^2\delta (q\left(\mathit{x}\right)-z)d\mathit{x}.$$ (B15)

We claim that I(z) is independent of z, which implies Eq. B14. To see this, use

$$\frac{dI\left(z\right)}{dz}=-{\int }_{{\mathbb{R}}^d}{e}^{-\beta V\left(\mathit{x}\right)}{\mid \nabla q\left(\mathit{x}\right)\mid }^2{\delta }^{\prime }(q\left(\mathit{x}\right)-z)d\mathit{x}=-{\int }_{{\mathbb{R}}^d}{e}^{-\beta V\left(\mathit{x}\right)}\nabla q\left(\mathit{x}\right)\cdot \nabla \delta (q\left(\mathit{x}\right)-z)d\mathit{x}=\beta \gamma {\int }_{{\mathbb{R}}^d}{e}^{-\beta V\left(\mathit{x}\right)}\left(Lq\right)\left(\mathit{x}\right)\delta (q\left(\mathit{x}\right)-z)d\mathit{x}=0,$$ (B16)

where we integrated by parts to get the third equality and we used Eq. A2 to get the fourth.

Similar calculations can be done for the Langevin Eq. 24 but, as explained in Sec. 4B, we can only get a closed form expression for the first hitting point density if we use as milestones the isosurfaces of the backward committor function rather than the forward one. For economy, let us omit these calculations since they are similar to the one presented above and simply state the result: the first hitting point density of the surface $S_j^b=\{(\mathit{x},\mathit{v}):q(\mathit{x},-\mathit{v})=z_j\}$ [not to be confused with Eq. 26] is given by

$${\varrho }_j(\mathit{x},\mathit{v})={\mathcal{Z}}_j^{-1}\mid {\nabla }_{v}q(\mathit{x},-\mathit{v})\mid e^{-\beta H(\mathit{x},\mathit{v})}.$$ (B17)

Here Z_j is the following normalization factor:

$${\mathcal{Z}}_j={\int }_{{\mathcal{S}}_j^b}\mid {\nabla }_{v}q(\mathit{x},-\mathit{v})\mid e^{-\beta H(\mathit{x},\mathit{v})}d{\sigma }_{{\mathcal{S}}_j}(\mathit{x},\mathit{v}),$$ (B18)

where $d{\sigma }_{S_j^b}(\mathit{x},\mathit{v})$ denotes the surface element on $S_j^b$, and H(x,v) is the Hamiltonian of the system.