Abstract
The influence of flow separation location on eigenmode synchronization and phonation onset was investigated in a two-dimensional, aeroelastic, continuum model of phonation. A linear stability analysis showed that flow separation played a critical role in initiating eigenmode synchronization and phonation. For a given glottal configuration, a small variation in the flow separation location along the vocal fold surface may lead to a qualitatively different eigenmode-synchronization pattern, and different phonation threshold pressure and frequency. This high sensitivity suggests a need for phonation models to be capable of accurate prediction of the flow separation location. Analysis with different glottal channel geometries showed that a minimum phonation threshold pressure existed for a rectangular glottal channel, consistent with previous experiments. However, in contrast to previous theoretical analyses, this study showed that phonation was facilitated, rather than prohibited, by the upstream movement of the flow separation point within a divergent glottis.
INTRODUCTION
A recent theoretical analysis (Zhang et al., 2007) showed that phonation onset occurred as two eigenmodes of the vocal fold synchronized due to a cross-mode coupling effect of the glottal flow. The details of the eigenmode synchronization process and the condition at which phonation onset occurs depend on both vocal fold biomechanics and the ability of the glottal flow to synchronize two or more structural eigenmodes. The biomechanical properties of the vocal folds determine the natural frequencies of the vocal fold structure, the initial state of the coupled system in the eigenmode synchronization process. The strength of the cross-mode coupling effect of the glottal flow depends on the intraglottal pressure distribution and how it varies with the vocal fold surface motion. It is generally accepted that airflow through the glottis remains laminar until the flow separates from the vocal fold surface. Downstream of the flow separation point, a jet forms, which eventually transitions into a turbulent flow, accompanied by a slight pressure recovery toward the supraglottal pressure. The exact flow separation location therefore determines the intraglottal pressure distribution and, for a given glottal configuration, the nature and strength of the eigenmode-synchronizing effect of the glottal flow.
The flow separation location is highly dependent on both the vocal fold geometry and the glottal flow field. Studies on steady flow through orifices of various configurations (Scherer et al., 2001; Zhang et al., 2004; Kucinschi et al., 2006) showed that airflow separated around the superior edge of the medial surface for a convergent or straight glottis. For divergent glottis, the flow separation location moved upstream to a location inside the glottis. With increasing Reynolds number, the flow separation point is generally expected to move further upstream along the divergent medial surface. During phonation, the glottis changes alternately from convergent, straight, to divergent. The flow separation location may vary accordingly during one cycle of vocal fold oscillation. For example, numerical simulations on unsteady flow through forced-oscillating glottis (Zhao et al., 2002; Alipour and Scherer, 2004) showed that the flow separation point moved upstream when the glottal divergence angle exceeded a certain threshold value, and persisted upstream into the convergent phase of the cycle. Recent numerical simulation (Sciamarella and Le Quere, 2008) also showed that the flow separation process during phonation was highly unsteady and the vocal fold motion had a significant influence on the flow separation location.
Accurate prediction of the flow separation location requires solving the full three-dimensional flow equations (e.g., Zhao et al., 2002), and is computationally expensive. For practical applications, simplified models are often used. Early models of phonation generally assumed the airflow to separate from the glottal wall at a fixed location. For example, the two-mass model (Ishizaka and Flanagan, 1972; Ishizaka, 1981) assumed flow separation occurred at the sharp edge of the superior medial surface. Pelorson et al. (1994) proposed a quasisteady flow separation model in which the flow separation location was predicted based on boundary layer theory. The flow separation point was allowed to move upstream when the glottis became divergent. A separation constant was also used in many models, which assume flow separation to occur at a point downstream of the minimum glottal constriction with a cross-sectional area equal to the minimum glottal area multiplied by the separation constant [e.g., 1.2, see Lous et al. (1998)]. Although these simplifications greatly reduce the computational costs, it is unclear how they might affect the predicted phonation characteristics. It would be useful to understand the sensitivity of phonation to slight variation in the flow separation location. In other words, how accurate does a prediction of the flow separation location have to be to reasonably capture the major dynamics of the fluid–structure interaction?
The study is a sensitivity study, with the objective of investigating how changes in the flow separation location affect eigenmode synchronization and the resulting phonation onset. A two-dimensional self-oscillating continuum model of phonation as in Zhang et al. (2007) was used. Continuum models of phonation allow more realistic reproduction of the complex fluid–structure interaction within the glottis. As in that study, phonation onset characteristics were calculated from a linear stability analysis. We will show that flow separation plays a central role in initiating phonation, and, for a given glottal geometry, a slight variation of the flow separation point may have a significant influence on the resulting phonation onset characteristics. We will also show that, in contrast to previous understanding, phonation is facilitated, rather than prohibited [as discussed by Lucero (1998), see below], by the upstream movement of the flow separation point within a divergent glottis.
MODEL DESCRIPTION
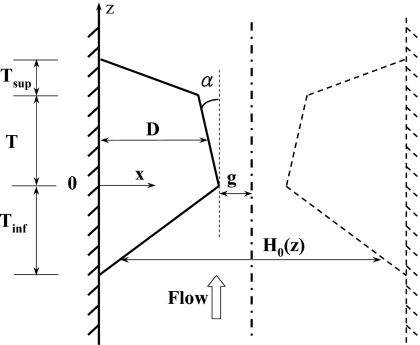
Consider a continuum vocal fold model coupled with a one-dimensional potential flow, which separates at a certain location along the vocal fold surface (Fig. 1). The vocal folds were modeled as a two-dimensional, isotropic, plane strain, elastic layer of Young’s modulus and density . No vocal tract was considered and the flow rate at the glottal entrance was assumed to be constant. For simplicity, left–right symmetry in the flow and vocal fold vibration about the glottal channel centerline was imposed and only half the system was considered. A nondimensional formulation of system equations was used. The vocal fold thickness , vocal fold density , and the wave velocity of the vocal fold structure were used as the reference length, density, and velocity scales, respectively. The nondimensional variables are defined as follows:
| (1) |
where ρf is the density of air, Uj is the mean jet velocity, Ps is the mean subglottal pressure, and f is phonation frequency. Symbols without overbars denote nondimensional variables. The physical values can be recovered by multiplying nondimensional values by the corresponding reference scales. All variables in the following are in nondimensional forms unless otherwise stated.
Figure 1.
Two-dimensional vocal fold model and the glottal channel. The flow direction is along the positive z axis. The coupled vocal fold-flow system was assumed to be symmetric about the glottal channel centerline so that only the left-hand half of the system was considered in this study. D is the vocal fold depth in the medial-lateral direction at the midpoint of the medial surface; T, Tinf, and Tsuf are the thicknesses of the entrance, medial surface, and exit sections of the vocal fold in the flow direction, respectively; H0 is the prephonatory glottal channel width; g is the minimum prephonatory glottal half-width of the glottal channel; The divergence angle α is the angle formed by the medial surface of the vocal fold with the z axis.
The linear stability analysis as in Zhang et al. (2007) was applied to the coupled fluid–structure system, from which the phonation threshold pressure and frequency and vocal fold vibration characteristics at phonation onset were calculated. A brief description of the linear stability analysis procedure is given in this section. Readers are referred to the original paper for a detailed derivation of system equations. The system equations were derived from Lagrange’s equations (Zhang et al., 2007):
| (2) |
where q is the generalized coordinate vector. The three matrices M, C, and K represent the mass, damping, and stiffness matrices of the vocal fold structure, respectively. A proportional structural damping was assumed for the vocal fold material so that the structural mass and damping matrices were related by C=σωM, where σ is the constant structural loss factor and ω is the angular frequency. For human vocal folds, the loss factor is in the range of 0.4–1.0 at low frequencies and 0.2–0.6 at high frequencies (10–15 Hz) (Chan and Titze, 1999). The term in Eq. 2 is the generalized force associated with the fluctuating flow pressure along the vocal fold surface induced by vocal fold vibration. The fluctuating flow pressure was obtained as follows. First, Bernoulli’s equation and the continuity equation of airflow were linearized around the mean state of the coupled airflow–vocal fold system (Zhang et al., 2007). As boundary conditions for the flow domain, a zero fluctuating flow velocity was imposed at the glottal entrance and a zero fluctuating pressure at the flow separation location, assuming a zero pressure recovery downstream of the flow separation location. The fluctuating pressure was then obtained by solving the linearized flow equations with these boundary conditions. The flow pressure can be decomposed into a flow-induced stiffness term, which is proportional to vocal fold displacement and represented by matrix Q0, a flow-induced damping term, which is proportional to vocal fold velocity and represented by matrix Q1, and a flow-induced mass term, which is proportional to vocal fold acceleration and represented by matrix Q2. All three matrices are functions of the jet velocity Uj, which was used as the primary control parameter. The jet velocity Uj was related to the subglottal pressure Ps by
| (3) |
where Hs and Hin are the glottal width at the flow separation location and the glottal inlet, respectively. The mass, stiffness, and structural damping matrices were symmetric matrices whereas the three generalized force matrices were in generally asymmetric (Zhang et al., 2007). Assuming q0=q0est, Eq. 2 was solved for the eigenvalues s and eigenvectors q0 as a function of the jet velocity. Phonation onset occurs at the jet velocity for which the growth rate (or real part) of one eigenvalue first becomes positive (Zhang et al., 2007).
Zhang et al. (2007) showed that the primary mechanism of phonation onset was the eigenmode-synchronizing effect of the flow-induced stiffness. The flow-induced damping and flow-induced mass generally play a minor role in phonation onset, particularly at moderate to high structural damping. To better illustrate the effect of flow separation on phonation onset, results will be presented first for cases in which the flow-induced mass, flow-induced damping, and structural damping matrices were excluded from Eq. 2, yielding
| (4) |
The results will be then discussed for the full system Eq. 2, in which all three components of the fluid pressure and structural damping are included.
Note that the mean state of the coupled system, around which the flow equations are linearized, is a function of the driven subglottal pressure or airflow. Therefore, for each given jet velocity, a nonlinear steady-state problem has to be solved to obtain the mean state of the coupled system, based on which the matrices in Eq. 2 are evaluated and the linear stability analysis is performed. In this study, as in Zhang et al. (2007), the mean state of the coupled system corresponding to each given jet velocity was not solved for. Instead, it was assumed that, for each given jet velocity, the statically deformed geometry of the vocal fold and the glottal channel remained the same as that given at rest, and the linear stability analysis was performed on this same vocal fold∕glottal channel geometry.
RESULTS
For the results presented in the following, the following nondimensional values for the model parameters were used (see definition in Fig. 1):
| (5) |
where ν is the Poisson’s ratio of the vocal fold material. Equation 5 corresponded to the following physical values (the first four are the scaling variables):
| (6) |
Coupled-mode flutter and eigenmode synchronization
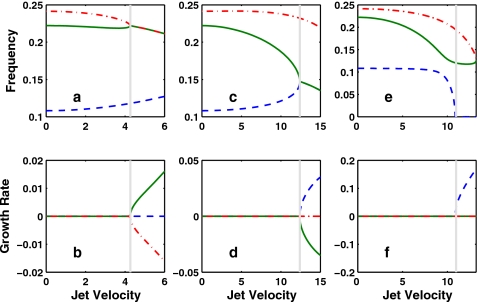
Equation 4 may exhibit two types of instabilities: static divergence and coupled-mode flutter. For a conservative system, which corresponds to symmetric matrices M, K, and Q0 in Eq. 4, the system loses stability first to static divergence (zero frequency) instability as the jet velocity increases from zero. For a nonconservative system for which the flow-induced stiffness matrix Q0 is asymmetric (e.g., due to flow separation), the system may lose stability first to a coupled-mode flutter (nonzero frequency instability and therefore phonation onset), due to a cross-mode coupling effect of the asymmetric Q0 matrix. An example is given in Figs. 2a, 2b, which shows the frequencies and growth rates of the first three eigenvalues of Eq. 4 as the jet velocity increases, for a uniform glottal channel (divergence angle α=0) and a flow separation location at z=1.0 (superior edge of the medial surface). In this case, coupled-mode flutter occurred due to the synchronization of the second and third eigenmodes.
Figure 2.
(Color online) Frequencies and growth rates of the first three eigenvalues [First (---); second (—); and third (-⋅-)] of the coupled fluid–structure system [Eq. 4] as a function of the jet velocity. The vertical line indicates the point of phonation onset. Straight glottal channel (α=0), model parameters specified in Eq. 5 were used. Only the flow stiffness term Q0 of the three flow-induced terms was included [Eq. 4], and σ=0. Flow separation location (a and b) at z=1.0 (superior edge of the medial surface); (c and d) z=0.2 (inferior part of the medial surface); and (e and f) z=1.2 (superior surface).
Effects of flow separation location
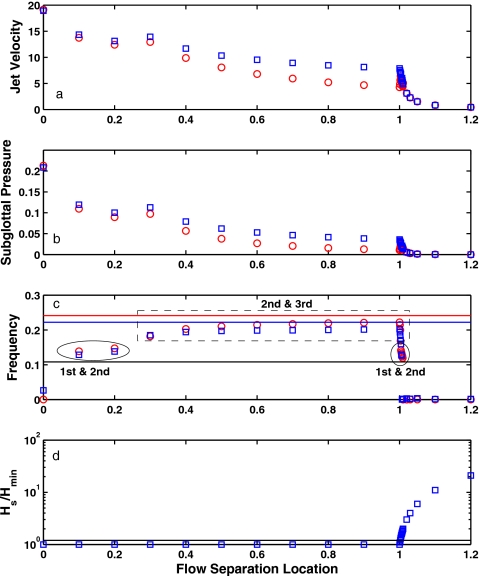
To illustrate the effects of flow separation location on phonation onset, the flow separation location was artificially manipulated along the vocal fold surface. A vocal fold with a parallel medial surface (α=0) was used, with model parameters given by Eq. 5. Figure 3 shows the phonation threshold jet velocity, threshold pressure, and onset frequency (circle symbols) as a function of the flow separation location. Also shown in Fig. 3 is the ratio between the glottal widths at the flow separation location and the minimum glottal constriction, or the separation constant as used in Lous et al. (1998).
Figure 3.
(Color online) (a) Phonation threshold jet velocity, (b) threshold pressure, (c) onset frequency, and (d)glottal width ratio Hs∕Hmin as a function as the flow separation location, for a straight glottal channel (α=0). Model parameters are given in Eq. 5. Only the flow-induced stiffness Q0 of the three flow components was included, and σ=0 (○) and all three flow components (Q0, Q1, and Q2) were included, and σ=0.3 (◻). The three horizontal lines in (c) indicate the first three in vacuo eigenfrequencies. The horizontal line in (d) indicates a constant glottal width ratio of 1.2.
Figure 3 shows that the flow separation location, which affects the intraglottal air pressure distribution, had a significant impact on the eigenmode-coupling effect of the flow-induced stiffness, which is the primary mechanism of phonation onset. As the fixed flow separation location varied along the vocal fold surface, the mode-coupling strength of the flow-induced stiffness also varied, leading to a different eigenmode-synchronization pattern. The system lost stability to different types of instabilities: both static divergence (z>1.01 and z<0.1, for a weak eigenmode-coupling effect) and coupled-mode flutter (0<z<1.01, for a strong eigenmode-coupling effect) were observed. For coupled-mode flutter instability, as the flow separation location was moved downstream, phonation onset may also occur due to eigenmode-synchronization involving different pairs of eigenmodes. For example, the second and third eigenmode synchronized for a flow separation location at z=1.0, as shown in Figs. 2a, 2b. As the flow separation location moved either downstream or upstream along the vocal fold surface, the eigenmode-synchronizing pair changed to the first and second eigenmodes, as shown in Figs. 2c, 2d for a flow separation location at z=0.2. For very superior or inferior flow separation locations, the eigenmode-coupling effect was so weak that the system lost instability to a static divergence [Figs. 2e, 2f], indicating no phonation onset based on linear stability theory. For the case shown in Fig. 3, such change in the eigenmode-synchronization pattern occurred in two regions along the medial surface: One close to the inferior edge of the medial surface (0<z<0.2), and the other around the superior edge of the medial surface (around z=1.0). Note that the second transition region around z=1.0 is in a region where flow separation would be predicted to occur in many simplified models of flow separation.
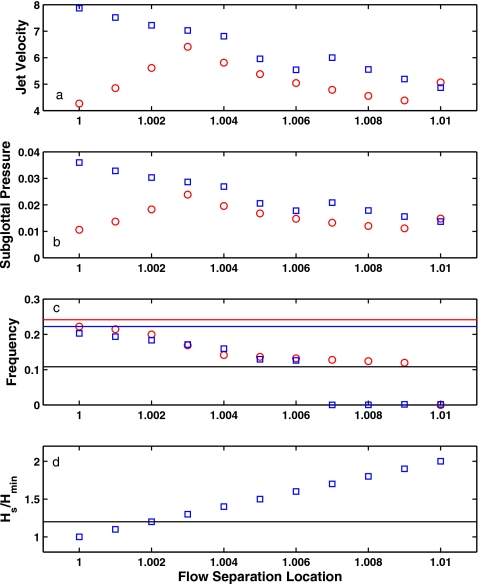
Figure 4 shows the same results as in Fig. 3, but for a small range of flow separation locations around the superior edge of the medial surface (z=1.0), where flow separation would be predicted to occur in many simplified models of flow separation. In this region, eigenmode synchronization was highly sensitive to changes in the flow separation location. If a separation constant was used to determine the flow separation location, a slightly different separation constant in the range of (1, 1.9) would lead to quite a different phonation threshold pressure and phonation frequency. For even larger separation constants, phonation would not be even possible.
Figure 4.
(Color online) Close-up view of Fig. 3 for flow separation locations in the range of (1, 1.01).
For synchronizations involving the same pair of eigenmodes, the vocal fold vibration pattern gradually varied with the flow separation location, but generally remained qualitatively similar. However, significant changes in the vocal fold vibration pattern occurred when eigenmode synchronization changed to a different pair of eigenmodes. For example, when the flow separation location moved from z=0.2 to z=0.3, the vibration pattern changed from a more in-phase medial-lateral motion to a more out-of-phase medial-lateral motion.
Figures 34 also show the phonation threshold jet velocity, threshold pressure, and onset frequency (square symbols) for Eq. 2, in which all three components (flow-induced stiffness, damping, and inertia) of the flow pressure were included, and with a constant structural loss factor of 0.3. The result was similar to that when only the flow-induced stiffness and no structural damping were included. It is noted that, for a lower structural damping, the flow-induced damping introduced a destabilizing effect, which eventually destabilized the coupled system before the emergence of static divergence for flow separation locations (z>1.01) in which static divergence was predicted in Fig. 3. For larger values of the structural loss factor (as in Fig. 3), this destabilizing effect was delayed and occur at a higher jet velocity than the static divergence, and the coupled system still lost linear stability to static divergence.
Effects of glottal channel geometry
For a given vocal fold geometry, movement of flow separation location as discussed in the previous section is highly unrealistic. However, flow separation may occur at different locations for different vocal fold geometry. During one cycle of the vocal fold oscillation, the glottal channel alternately changes from convergent, straight, and divergent. Accordingly, the flow separation location may oscillate along the vocal fold surface. In particular, the flow separation location may move abruptly upstream when the glottis takes a divergent shape. In the following, the influence of flow separation within a divergent glottis is discussed.
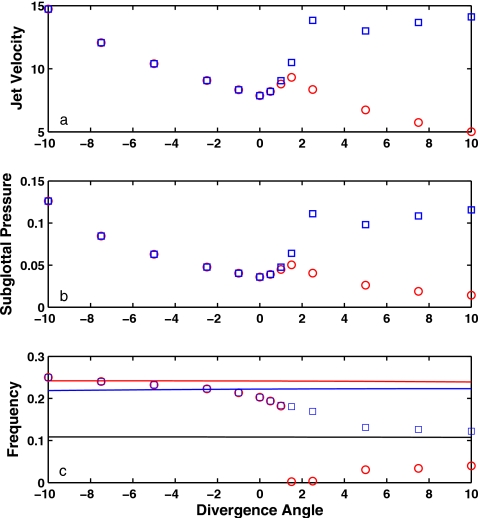
Figure 5 shows the phonation threshold jet velocity, threshold pressure, and frequency as a function of the divergence angle of the glottal channel, as predicted from solving Eq. 2. Model parameter values are given in Eq. 5, and σ=0.3. Note that the vocal fold depth at the midpoint of the medial surface was kept constant to be D=1.43 as the divergence angle was varied. This helped to maintain a nearly constant in vacuo eigenspectrum of the vocal fold, thereby minimizing the influence of vocal fold natural frequencies on phonation threshold jet velocity. Similarly, the minimum static glottal half-width was also kept constant for different vocal fold divergence angles, excluding the effect of the glottal opening on phonation threshold jet velocity. The flow separation location was determined as follows: For convergent, straight, or slightly divergent glottal channels, flow separation was assumed to occur at the superior edge of the medial surface (z=1.0); for glottal channels of large divergence angle (tan α>0.2g), the flow separation location was assumed to be a location downstream of the minimum glottal constriction with a glottal width H=1.2Hmin, where Hmin is the glottal width at minimum constriction.
Figure 5.
(Color online) (a) Phonation threshold jet velocity, (b) threshold pressure, and (c) onset frequency as a function of the divergence angle. Negative values of the divergence angle indicate convergent glottal channels. Model parameters are given in Eq. 5. All three flow components (Q0, Q1, and Q2) were included, and σ=0.3. Flow separation location fixed at the superior edge of the medial surface (z=1.0) (○) and flow separation location dependent on the divergence angle (◻). The three horizontal lines indicate the first three in vacuo eigenfrequencies.
Figure 5 shows that the minimum phonation threshold jet velocity (square symbols) occurred for nearly straight glottal channel geometry. In this case, the phonation threshold jet velocity increased slightly with increasing convergence of the glottal channel, whereas it increased rapidly when the glottal channel changed from convergent to divergent. Further increase in the glottal channel divergence angle led to only slight increase in the phonation threshold jet velocity. For convergent glottal channels, phonation onset occurred due to the synchronization of the second and third eigenmodes, whereas for large divergence angles, phonation occurred due to the synchronization of the first and the second eigenmodes. Consequently, the phonation threshold frequency decreased monotonically when the glottal channel changed from convergent to divergent, changing from being close to the second in vacuo eigenfrequency to being close to the first in vacuo eigenfrequency. For even large divergence angles (e.g., a>15°, not shown in Fig. 5), the eigenmode-coupling effect of the flow-induced stiffness was so weak that the system lost linear stability to static divergence instability.
Also shown in Fig. 5 are the phonation threshold pressure and frequency for the same vocal fold geometries, but for flow separation fixed at the superior edge of the medial surface (z=1.0), independent of the vocal fold geometry. For convergent glottal channels, as expected, the results were the same as in cases in which the flow separation location was allowed to vary with vocal fold geometry. However, for large divergence angles (α>1.5), with flow separation fixed at z=1.0, the linear stability theory predicted static divergence and no phonation onset was possible. This contrasted with the coupled-mode flutter instability as predicted when the flow separation was allowed to move upstream. For even larger divergence angles, a low-frequency oscillation was induced by the flow-induced damping. However, the corresponding frequency was much lower than that of the coupled-model flutter when the flow separation was allowed to move upstream.
DISCUSSION
The analysis was repeated for a few different vocal fold geometries. Although some details differed from those in Figs. 35 depending on the exact vocal fold geometry, structural damping, and glottal half-width used, the general features remained qualitatively similar. For example, a minimum phonation threshold pressure existed for a near-rectangular glottal configuration. Variation of the flow separation location along the vocal fold surface affected the eigenmode synchronization, which may enhance or reduce coupling in general or selectively affect coupling between certain modes. The mode-coupling effect was generally weaker for a divergent glottal configuration.
The results shown in Fig. 5 are consistent with previous experimental results in Chan et al. (1997). Their experimentally measured phonation threshold pressure showed a similar trend with varying glottal divergence angle (Fig. 4 in Chan et al., 1997) as shown in Fig. 5 of this study. They observed that the lowest phonation threshold pressure was obtained for a rectangular or near-rectangular prephonatory glottis, which is consistent with the observation of this study. The measured phonation threshold pressure in Chan et al. (1997) in most cases increased at a faster rate with increasing divergence angle than with increasing convergence angle, which was qualitatively reproduced in Fig. 5 of this study.
The existence of an optimal glottal configuration associated with the lowest phonation threshold pressure was also predicted by Lucero (1998). However, some differences in the results between that study and the present study can be noted. First, Lucero showed that, for flow separation fixed at the superior edge [referred to as “no flow separation” in Lucero (1998)], no optimal glottal configuration existed and the phonation threshold pressure increased monotonically with decreasing divergence angle. However, this study showed that an optimal glottal channel configuration existed even when the flow separation was fixed at the superior edge, indicating its existence may be mostly due to a geometrical effect. Second, Lucero showed that allowing the flow separation location to move upstream for divergent glottal shapes increased the phonation threshold, prohibiting phonation. However, our results show that phonation was facilitated by this upstream movement of the flow separation location at large divergence angles, at which phonation otherwise would not be possible if the flow separation location was fixed at the superior edge of the medial surface. Further, our results clarified that, in this case, phonation was facilitated by a change in the eigenmode synchronization pattern as the glottal shape changed from slightly divergent to highly divergent. Note that at least three degrees-of-freedom are required to capture this change of synchronization pattern, which is not possible in a two degrees-of-freedom system. Future experimental investigations are needed to clarify these discrepancies.
CONCLUSIONS
In this study, we showed that, for a given glottal configuration, the phonation threshold pressure and frequency were highly sensitive to the location of flow separation. Although the actual movement of the flow separation point may be limited in real phonation, this high sensitivity to the flow separation location still points to the need for phonation models to be capable of accurate prediction of flow separation and the flow separation location. This is particularly important for modeling pathological phonation, in which flow may separate at different locations from the two vocal folds. Due to the large vocal fold-airflow density ratio, the vocal fold motion may have a large impact on the glottal flow field and the flow separation location (Sciamarella and Le Quere, 2008). Therefore, such phonation models may require a better and realistic representation of the vocal fold biomechanics and the glottal fluid–structure interaction.
ACKNOWLEDGMENTS
The author would like to thank Dr. Juergen Neubauer for many discussions and comments on the manuscript. This study was supported by research Grant Nos. R01 DC009229 and R01 DC003072 from the National Institute on Deafness and Other Communication Disorders, the National Institutes of Health.
Portions of this work were presented at the 153rd Meeting of the Acoustical Society of America, Salt Lake City, Utah, June 2007.
References
- Alipour, F., and Scherer, R. C. (2004). “Flow separation in a computational oscillating vocal fold model,” J. Acoust. Soc. Am. 10.1121/1.1779274 116, 1710–1719. [DOI] [PubMed] [Google Scholar]
- Chan, R. W., and Titze, I. R. (1999). “Viscoelastic shear properties of human vocal fold mucosa: measurement methodology and empirical results,” J. Acoust. Soc. Am. 10.1121/1.427947 106, 2008–2021. [DOI] [PubMed] [Google Scholar]
- Chan, R. W., Titze, I. R., and Titze, M. R. (1997). “Further studies of phonation threshold pressure in a physical model of the vocal fold mucosa,” J. Acoust. Soc. Am. 10.1121/1.418331 101, 3722–3727. [DOI] [PubMed] [Google Scholar]
- Ishizaka, K. (1981). “Equivalent lumped-mass models of vocal fold vibration,” in Vocal Fold Physiology, edited by Steven K. N. and Hirano M. (University of Tokyo, Tokyo: ), pp. 231–244. [Google Scholar]
- Ishizaka, K., and Flanagan, J. L. (1972). “Synthesis of voiced sounds from a two-mass model of the vocal cords,” Bell Syst. Tech. J. 51, 1233–1267. [Google Scholar]
- Kucinschi, B. R., Scherer, R. C., DeWitt, K. J., and Ng, T. T. M. (2006). “Flow visualization and acoustic consequences of the air moving through a static model of the human larynx,” J. Biomech. Eng. 10.1115/1.2187042 128, 380–390. [DOI] [PubMed] [Google Scholar]
- Lous, N. J. M., Hofmans, G. C. J., Veldhuis, R. N. J., and Hirschberg, A. (1998). “A symmetrical two-mass vocal-fold model coupled to vocal tract and trachea, with application to prosthesis design,” Acust. Acta Acust. 84, 1135–1150. [Google Scholar]
- Lucero, J. C. (1998). “Optimal glottal configuration for ease of phonation,” J. Voice 10.1016/S0892-1997(98)80034-9 12, 151–158. [DOI] [PubMed] [Google Scholar]
- Pelorson, X., Hirschberg, A., van Hassel, R. R., Wijnands, A. P. J., and Auregan, Y. (1994). “Theoretical and experimental study of quasi-steady flow separation within the glottis during phonation. Application to a modified two-mass model,” J. Acoust. Soc. Am. 10.1121/1.411449 96, 3416–3431. [DOI] [Google Scholar]
- Scherer, R. C., Shinwari, D., DeWitt, K. J., Zhang, C., Kucinschi, B. R., and Afjeh, A. A. (2001). “Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees,” J. Acoust. Soc. Am. 10.1121/1.1333420 109, 1616–1630. [DOI] [PubMed] [Google Scholar]
- Sciamarella, D., and Le Quere, P. (2008). “Solving for unsteady airflow in a glottal model with immersed moving boundaries,” Eur. J. Mech. B/Fluids 27, 42–53. [Google Scholar]
- Zhang, Z., Mongeau, L., Frankel, S. H., Thomson, S. L., and Park, J. B. (2004). “Sound generation by steady flow through glottis-shaped orifices,” J. Acoust. Soc. Am. 10.1121/1.1779331 116, 1720–1728. [DOI] [PubMed] [Google Scholar]
- Zhang, Z., Neubauer, J., and Berry, D. A. (2007). “Physical mechanisms of phonation onset: a linear stability analysis of an aeroelastic continuum model of phonation,” J. Acoust. Soc. Am. 10.1121/1.2773949 122(4), 2279–2295. [DOI] [PubMed] [Google Scholar]
- Zhao, W., Zhang, C., Frankel, S. H., and Mongeau, L. (2002). “Computational aeroacoustics of phonation, Part I: Computational methods and sound generation mechanisms,” J. Acoust. Soc. Am. 10.1121/1.1506693 112, 2134–2146. [DOI] [PubMed] [Google Scholar]