On the Mechanism of Nitrosoarene-Alkyne Cycloaddition

Abstract

The thermal reaction between nitrosoarenes and alkynes produces N-hydroxyindoles as the major products. The mechanism of these novel reactions has been probed using a combination of experimental and computational methods. The reaction of nitrosobenzene (NB) with an excess of phenyl acetylene (PA) is determined to be first order in each reactant in benzene at 75° C. The reaction rates have been determined for reactions between phenyl acetylene with a set of p-substituted nitrosoarenes, 4-X-C₆H₄NO, and of 4-O₂N-C₆H₄NO with a set of p-substituted arylalkynes, 4-Y-C₆H₄C≡CH. The former reactions are accelerated by electron-withdrawing X-groups (ρ = + 0.4), while the latter are faster with electron-donating Y groups (ρ = − 0.9). The kinetic isotope effect for the reaction of C₆H₅NO/C₆D₅NO with PhC≡CH is found to be 1.1 (± 0.1) while that between PhC≡CH/PhC≡CD with PhNO is also 1.1 (± 0.1). The reaction between nitrosobenzene and the radical clock probe cyclopropylacetylene affords 3-cyclopropyl indole in low yield. In addition to 3-carbomethoxy-N-hydroxyindole, the reaction between PA and o-carbomethoxy-nitrosobenzene also affords a tricyclic indole derivative 3, likely derived from trapping of an intermediate indoline nitrone with PA and subsequent rearrangement. Computational studies of the reaction mechanism were carried out with density functional theory at the (U)B3LYP/6-31+G(d) level. The lowest energy pathway of the reaction of PhNO with alkynes was found to be stepwise; the N-C bond between nitrosoarene and acetylene is formed first, the resulting vinyl diradical undergoes cis-trans isomerization, and then the C-C bond forms. Conjugating substituents Z on the alkyne, Z-C≡CH, lower the calculated (and observed) activation barrier, Z=-H (19 kcal/mol), -Ph (15.8 kcal/mol) and -C(O)H (13 kcal/mol). The regioselectivity of the reaction, with formation of the 3-substituted indole, was reproduced by the calculations of PhNO + PhC≡CH; the rate-limiting step for formation of the 2-substituted indole is higher in energy by 11.6 kcal/mol. The effects of –NO₂, -CN, -Cl, -Br, -Me, and -OMe substituents were computed for the reactions of p-X-C₆H₄NO with PhC≡CH and of PhNO and/or p-NO₂-C₆H₄NO with p-Y-C₆H₄C≡CH. The activation energies for the set of p-XC₆H₄NO vary by 4.3 kcal/mol and follow the trend found experimentally, with electron withdrawing X-groups accelerating the reactions. The range of barriers for the p-Y-C₆H₄C≡CH reactions is smaller, about 1.5 kcal/mol and 1.8 kcal/mol in the cases of PhNO and p-NO₂-PhNO, respectively. In agreement with the experiments, electron donating Y-groups on the alkyne accelerate the reactions with p-NO₂-C₆H₄NO, while both ED and EW groups are predicted to facilitate the reaction. The calculated kinetic isotope effect for the reaction of C₆H₅NO/C₆D₅NO with PhC≡CH is negligible (as found experimentally) while that for PhC≡CH/PhC≡CD with PhNO (0.7) differs somewhat from the experiment (1.1). Taken together the experimental and computational results point to the operation of a step-wise diradical cycloaddition, with ratelimiting N-C bond formation and rapid C-C connection to form a bicyclic cyclohexadienyl-Noxyl diradical, followed by fast tautomerization to the N-hydroxyindole product.

Introduction

The widespread occurrence of the indole skeleton in natural products and bioactive synthetic compounds¹ has long stimulated efforts at its efficient construction.² Among the numerous approaches and synthetic methods developed, one of the earliest, the Fischer indole synthesis, still stands as one of the most useful, because it proceeds from convenient precursors, aromatic hydrazines and ketones, yet does not require a pre-existing ortho substituent to direct cyclization.³ Nonetheless, limitations of the Fisher reaction and the need for alternative synthetic approaches invite the development of new, efficient indole-forming reactions.

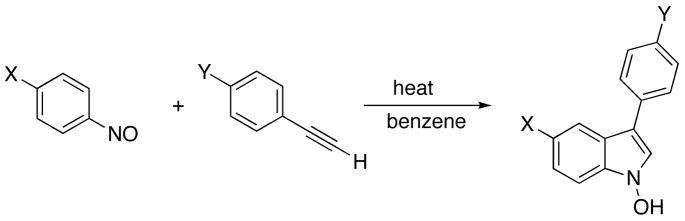
As part of our research program to develop transition metal-mediated nitrogenation reactions of unsaturated hydrocarbons⁴ we recently reported the novel reductive cycloaddition reaction between nitroarenes and alkynes catalyzed by [CpM(CO)₂]₂ derivatives (M=Fe, Ru), which produces indoles in moderate yields (Scheme 1).⁵ Subsequently, Ragaini and coworkers reported a similar palladium-catalyzed reaction.⁶ The directness of this indole construction from commercial reactants and its high regioselectivity, producing 3-substituted indoles from terminal alkynes, has prompted us to explore the synthetic potential of the reaction and its mechanistic pathway. A follow-up investigation in our group established that nitrosoarenes react with conjugated alkynes without a catalyst to produce N-hydroxyindoles (Scheme 1) in moderate to good yields and comparable regioselectivity.⁷ Curiously, early reports of 1:1 and 1:2 alkyne/nitrosoarene reactions identified acyclic nitrones and diimines⁸ and the polycyclic kabutanes⁹ as products (Scheme 2). The efficiency of the ArNO/alkyne cycloaddition can be improved significantly by alkylative trapping of the labile N-hydroxyindoles with K₂CO₃-Me₂SO₄,¹⁰ providing access to a variety of N-methoxyindoles from substituted nitrosoarenes and arylacetylenes.¹¹ The comparable regioselectivity of these reactions to the metal-catalyzed nitroarene reactions and the ready reductive conversion of the hydroxyindoles to indoles (Scheme 1) suggests that the Cp₂M-catalyzed reaction of the nitroarenes could proceed via metal-promoted nitroarene deoxygenation¹², followed by an uncatalyzed nitrosoarene/alkyne cycloaddition, and conclude with a second Cp₂M-promoted deoxygenation of the N-hydroxyindole. The unprecedented nature of the nitrosoarene/alkyne cycloaddition itself has led to the present study that seeks to elucidate the mechanism of this transformation.

Scheme 1.

Scheme 2.

The nitrosoarene (NA)-alkyne to N-hydroxyindole (NHI) conversion involves the net scission of N-O, C-C and C-H bonds and the formation of C-N, C-C and O-H bonds. The fundamental mechanistic issues of interest include the timing of these steps, i.e. the stepwise or concerted timing of bond-breaking/making, and the possible involvement of discrete intermediates, be they neutral, polar or radical. In our initial survey of the reaction’s scope and selectivity three mechanistically relevant observations were noted.⁷ First, the yields are relatively insensitive to the electronic character of the nitrosoarene, being comparatively efficient with both electron-rich and -poor NA. Second, representative terminal alkynes with conjugating substituents (R=-Ar, -CO₂R) react most efficiently and regioselectively, placing the alkyne substituent at the 3-position. Third, the reaction solvent polarity/proticity (e.g. benzene, toluene, dioxane, isopropanol) has little effect on the course or efficiency of the reaction. Together, these features seemed to render unlikely a reaction pathway involving highly polar or ionic intermediates.

Results and Discussion

1. Kinetics

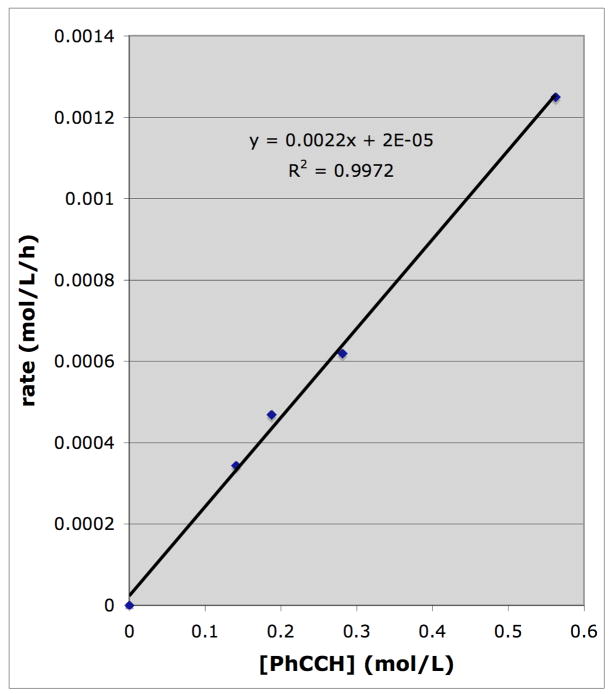
To establish the rate law for the nitrosobenzene (NB)/phenyl acetylene (PA) reaction kinetic studies were conducted on reactions in which phenyl acetylene (5.6–22.5 mM) was taken in excess at 75° C with benzene as the solvent. Under these temperature/concentration conditions the monomeric nitrosoarene is virtually the exclusive form present in solution (95–100%).¹³ The use of excess alkyne minimizes (<10–30 %) the formation of non-indole products, including azo- and azoxybenzene, kabutanes⁹ and nitrones.¹⁴ The initial rate method¹⁵ was employed, monitoring the disappearance of NB spectrophotometrically (λ=750 nm) at 0–15% conversion. Reactions were conducted with various PA/NB ratios, holding the PA concentration fixed at various NB concentrations and vice versa. Plots of rate vs. varied reactant concentrations are linear and are given in Figs. 1 and 2. From these data it can be seen that the reactions are first order each in NB and in PA.

Fig. 1.

Rate dependence on the PhNO concentration for the PhNO/PhC≡CH reaction. [PhC≡CH] = 0.28 M in benzene, 75 °C. Each data point is the result of a linear least squares fit to the [PhNO] vs time plot for at least six different times at ≤ 15% conversion; the line drawn is the least-squares fit to the experimental data points with the indicated correlation coefficient (R²) and slope.

Fig. 2.

Rate dependence on the PhC≡CH concentration. [PhNO] = 0.0094 M in benzene, 75 °C. Each data point is the result of a linear least squares fit to the [PhNO] vs time plot for at least six different times at ≤ 15% conversion; the line drawn is the least-squares fit to the experimental data points with the indicated correlation coefficient (R²) and slope.

2. Substituent Effects on Reaction Rate

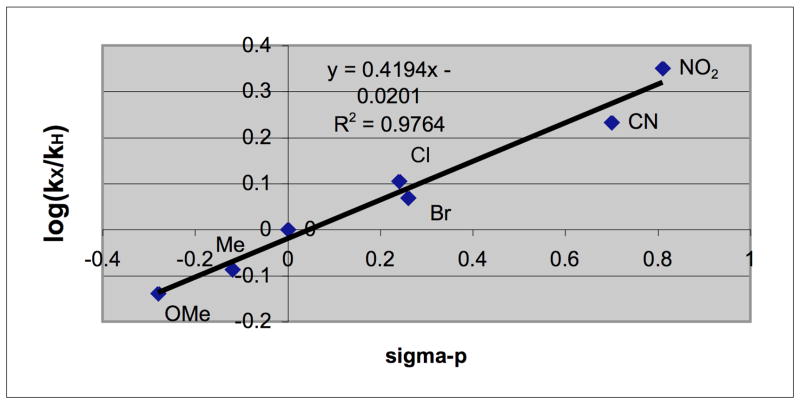
The electronic effects on the NA/AA reaction were systematically probed by comparing the rates for two sets of reactants with electronically varied substituents, p-X-C₆H₄NO and p-Y-C₆H₄C≡CH with X,Y= NO₂, CN, Cl, Br, H, Me, and OMe (Scheme 3).¹⁶ The substrates were prepared by established methods, nitrosoarenes by oxidation of the corresponding anilines¹⁷ and the arylacetylenes by Sonogashira-type reactions.¹⁸ The reactions of the various p-X-C₆H₄NO with PhC≡CH were carried out as above (benzene, 75° C) by the initial rate method (10–15% conversion) by monitoring the disappearance of p-XC₆H₄NO spectrophotometrically (λ = 750 nm). The observed rates were found to correlate reasonably well to the Hammett σ_p parameter as illustrated graphically in Fig. 3. The ρ value found (slope of Fig. 3) was + 0.45, showing a modest accelerating effect of electron-withdrawing groups. This result suggests some negative charge development on the ArNO unit in the transition state for the cycloaddition.

Scheme 3.

Fig. 3.

Correlation of relative rates of reaction of p-X-C₆H₄NO with PhC≡CH (log k_X/k_H) vs. Hammett sigma-para values.

Likewise, the reactions of the various p-Y-C₆H₄C≡CH with 4-NO₂-C₆H₄NO were conducted and their rates were determined. A Hammett plot of the rates vs. σ_p (Fig. 4) again gave a good correlation (R²= 0.96) and yielded a ρ value of −0.88, showing that electron-donating Y groups on the alkyne moderately accelerate the reaction. This is consistent with the development of some positive charge on the alkyne unit in the transition state. The opposite-signed ρ values for the nitrosoarene and alkyne reactants are noteworthy and to be expected for a reaction in which some dipolar character is developed in the rate-limiting step. The magnitude of the ρ values found for these reactions are relatively small compared to ones that involve fully charged intermediates.¹⁶ Although a somewhat polar transition state is indicated, either a concerted asynchronous cycloaddition or one with diradical character could be involved since either can exhibit sizable polar effects.¹⁹ Relevantly, sizable polar effects have been demonstrated in additions of electrophilic radicals to alkynes using two parameter LFE equations that include both polar (σ_p) and radical delocalization (σ_jj) constants.¹⁶ Obtaining definitive evidence for (or against) a radicaloid transition state from such LFE equations was judged unlikely given the already satisfactory fit with the single polar substituent constants σ_p and the need for rate data from a larger number of substituted reactants.²⁰

Fig. 4.

Correlation of relative rates of reaction of p-Y-C₆H₄C≡CH with p-O₂N-C₆H₄NO (log k_X/k_H) vs. Hammett sigma para values.

3. Kinetic Isotope Effects

Insight into the transition state for the cycloaddition reaction possibly could be obtained from kinetic isotope effects since several bonds are broken/made and a number of hybridization changes occur in the process. The bonds broken overall are N-O and C-C pi and aromatic C-H while C-N, C-C and O-H bonds are formed; the extent of these changes in the rate-limiting step could be probed via primary kinetic isotope effect.²¹ Overall hybridization (geometry) changes, potentially detectable through secondary H/D kinetic isotope effects,²² include sp --> sp² at the alkyne carbons, while a sp² --> sp³ --> sp² change could intervene at the ortho aromatic carbon in a step-wise addition/tautomerization process.

With these considerations in mind two KIE determinations were made (Scheme 4). In the first a competition reaction between phenyl acetylene and 1.0:1.0 C₆H₅NO/C₆D₅NO was carried out to 15–20 % conversion under the standard conditions. The isotopic composition of recovered NB and 3-phenylindole were determined by direct MS analysis; the unstable N-hydroxy-3-phenylindole was converted to 3-phenylindole isotopomers by catalytic hydrogenation (1 atm H₂/Pd-C). The ratio protio- to perdeutero-ratio for these three components, essentially the kinetic isotope effect, was determined to be 1.04, 1.18 and 1.35, respectively. Since some limited D/H exchange could potentially occur in the hydrogenation step (though none was detected in the hydrogenation of d₅-PhNO₂ to d₅-PhNH₂), the data from the first two analyses are likely more reliable, providing a KIE of approximately 1.1 ± 0.1. This small normal or negligible KIE clearly rules out rate-limiting aromatic C-H(D) bond-breaking. A rate-limiting step in which substantial bond formation is occurring between the NB aromatic carbon and the alkyne is also deemed unlikely since the accompanying sp² --> sp³ hybridization change would likely result in an inverse KIE of about 0.6–0.9.²³

Scheme 4.

A competition reaction was also carried out between PhNO and excess 1:1 PhC≡CH/PhC≡CD under the standard conditions. At 30–50% conversion the isolated mixture of N-hydroxyindole isotopomers was hydrogenated and the resulting 3-phenyl indole analyzed by MS to obtain a KIE of 1.1 ± 0.1. This small (negligible), normal value is the result of a secondary KIE. Since bonding and geometry changes occur at both acetylenic carbons, both α and β effects should operate, the former (if rate-limiting) is expected to be inverse, ca. 0.7–0.9 for a sp--> sp² change, while the latter should be normal in the range of ca. 1.4–1.5 giving a combined effect of ca. 1.1–1.3.²⁴ The observed value of 1.1 is thus consistent with developing N-C1 bond formation in the transition state but does not rule out rate-limiting C(arom)-C2 bond formation; the latter, however, is unlikely based on the above PhNO/d5-PhNO result.

4. Trapping/Byproduct Studies

The modest substituent and solvent effects observed in the NA-PA cycloadditions are more consistent with a radical or asynchronous concerted reaction pathway than one involving ionic transition states or intermediates. To probe for the intervention of radical intermediates two types of trapping experiments were conducted. In the first the reaction between NB and a radical clock type substrate, cyclopropyl acetylene²⁵ was examined (Scheme 5). If an intermediate with significant radical character at C-2 were to be generated, ring-opened products would be formed if cyclopropyl ring-opening is fast relative to intramolecular C-C bond formation. To facilitate the potential isolation of typically labile N-hydroxy products the NB-cyclopropyl acetylene reaction was carried out under alkylating conditions (1:10 NB-CPA, K₂CO₃-Me₂SO₄, benzene, 80° C) in a Fischer-Porter bottle under 50 psi of N₂. A complex mixture of products was produced from which it was possible to isolate and identify only one derived from the NA-CPP combination in low yield (12–15 %), 3-cyclopropyl indole (1, Scheme 5). Formation of the non-ring-opened 1 could be considered to rule out the intervention of a C-2 radical intermediate, but the result is mechanistically ambiguous because the rate of cyclopropyl ring-opening (1.6 × 10¹⁰ sec⁻¹)²⁵ may not compete with intramolecular C-C vinyl-aryl formation. Additionally, it is possible that cyclopropane ring-opened products may have formed but simply could not be isolated.

Scheme 5.

Experiments designed to test for radical intermediates with the established radical trap TEMPO²⁵ also proved to be inconclusive. When the reaction between NB and excess PA was conducted in the presence of TEMPO (6 equiv relative to NB), a complex mixture of products was produced. MS analysis of fractions obtained from preparative TLC analysis of the product mixtures suggested the formation of 1:1:1 TEMPO-NB-PA adducts, but NMR-pure compounds could not be obtained nor unambiguously identified.

During the course of our survey of the NA/alkyne reactions we isolated an unexpected byproduct from the reaction between phenyl acetylene and o-carbomethoxy nitrosobenzene that sheds some additional light on the mechanism of the cycloaddition (Scheme 6). The reaction was carried out under the standard alkylating conditions and afforded the expected 7-carbomethoxy-N-hydroxy-3-phenylindole 2, as well as a product 3 (21 %) whose NMR and mass spectra indicated the incorporation of two PA units and one NA unit; compound 3 was the major product under non-alkylating conditions. The structure of 3 was established definitively by X-ray diffraction (Fig. 5) to be 6-carbomethoxy-6-phenyl-6, 6a-dihyro-1H-1a-aza-cyclopropa[a]indeny-1-yl]phenylmethanone, featuring a 6,5,3-tricyclic skeleton with a cyclopropane ring fused to an indoline core. The PA units in 3 are incorporated in a tail-to-tail fashion (C-2, C-2) and the carbomethoxy unit has migrated from the aromatic carbon to C-1 of a PA unit. Although the tricyclic structure of 3 was surprising, a literature search for the skeleton revealed other examples and suggested a pathway for its formation. Analogs of 3 have been obtained from the reactions of indoline nitrones with alkynes14a,b, which proceed via dipolar cycloaddition followed by electrocyclic rearrangement of the intermediate isoxazoline. The formation of 3 from the reaction between ortho-carbomethoxy nitrosobenzene and PA, therefore suggests the intermediacy of nitrone 4 (Scheme 7). This species, in turn, may be derived from migratory rearrangement of a non-aromatic precursor such as nitrone 5a or a diradical equivalent 5b.

Scheme 6.

Fig. 5.

X-ray structure of adduct 3.

Scheme 7.

5. Computational Studies

All geometries and energies were calculated with the (U)B3LYP DFT functional²⁷ with the 6-31+G(d) basis set using Gaussian 03.²⁸ Minima and transition states were fully optimized and characterized by harmonic vibrational frequency analysis and verified intrinsic reaction coordinate (IRC) calculations. All calculations were validated at the UB3LYP level using the broken-symmetry wave function (guess=mix, always) to assess the expectation value of the <S²> operator. The reactants and final products are pure singlet species, with S² = 0. Radical-pair-like species between the N-C and C-C bonds formation showed typical diradical character, i.e. S² = 1, and thereby the unrestricted method was used for geometry optimization.

a. Energy profile and mechanism

The lowest energy pathway for the reaction of PhNO with HC≡CH is plotted in Figure 6. Various concerted cycloaddition pathways, e.g. 3+2, 2+2, 4+2, were considered, but attempts to locate transition states for these always converged to the N-C transition structure TS1. Based on the reaction energy profile the N-C bond formation between PhNO and HC≡CH is rate-limiting. Acetylene undergoes attack on the nitroso group to give a diradical intermediate, with the largest spin density (0.54) on the terminal vinyl carbon. The value of S² = 0.47 indicates substantial spin-contamination which is quite common for diradicals treated by unrestricted calculations. Natural Bond Orbital (NBO) analysis²⁹ indicates that a small amount of charge (0.056) migrates from PhNO to HC≡CH in the N-C forming transition state, with the largest unpaired electron density on the carbon atom that is developing into the vinyl radical. The resulting vinyl diradical intermediate undergoes cis-trans isomerization, with a calculated barrier of 3.1 kcal/mol, followed by C-C bond formation to give the hydroindole intermediate. The barrier for cyclization disappeared, which was 4.7 kcal/mol above the vinyl radical intermediate before the spin projection; the reaction is exothermic by 38.4 kcal/mol. A series of hydrogen shifts cause formation of the final, thermodynamically stable, product. This H-tautomerization could be accelerated by other mechanisms, via dimers or by acidic or basic solvents. In summary, the reaction of PhNO and HC≡CH to N-hydroxyindole is computed to be exothermic by 59.6 kcal/mol, with an overall barrier of 19.1 kcal/mol, via the vinyl radical intermediates.

Figure 6.

Calculated minimum energy pathway and stationary structures for the reaction of PhNO with HC≡CH to give N-hydroxyindole at the (U)B3LYP/6-31+G(d) level of theory (in the gas-phase; S² = 0 for the structures not explicitly labeled).

b. Regioselectivity

With a mono-substituted alkyne, two regioisomeric indoles can form. The two transition structures lead eventually to the 2- or 3-substituted hydroxyindole product. The transition structures for the first step are shown in Figure 7.

Figure 7.

The transition state structures for reaction of phenyl acetylene with nitrosobenzene at the UB3LYP/6-31+G(d) level of theory.

Transition state (TS1) is calculated to be 11.6 kcal/mol more stable, since the more stable phenyl-substituted vinyl radical is formed. TS1 has a partial N-C bond length of 1.876 Å, slightly longer by 0.03 Å than that for the TS in the parent reaction of PhNO + HC≡CH. In the following calculations, only the lower energy transition state (TS1) was considered for the KIE and p-substituent electronic effects.

It has been shown experimentally that alkynes with conjugating electron withdrawing groups (EWGs), such as ethyl propiolate (HC≡CCO₂Et), are privileged substrates for the nitroso-alkyne indolization.^7,10 This appears at first glance to be paradoxical when compared to the cyclizations with para-substituted phenylacetylenes, for which EDGs on the alkyne accelerate the reaction and EWGs slow it. Given the pathway deduced for the reactions of PhNO with HC≡CH and PhC≡CH, we determined by analogy the lowest energy pathway for the model reaction between PhNO and propynal (HC≡CCHO). Assuming that the first step, formation of the N-C bond, is rate-limiting, the transition state and intermediate structures and energies were calculated and are plotted in Figure 8.

Figure 8.

Energy profile for first (rate-limiting) step in the reaction between PhNO and propynal.

Propynal is calculated to react with nitrosobenzene via a transition state with an activation energy of only 13 kcal/mole, substantially lower than that calculated for the reaction with acetylene (19 kcal) and somewhat less than with phenyl acetylene (15.8 kcal). In the TS the largest spin density appears on the α-vinyl carbon (0.19) and is delocalized onto the oxygen (0.10) of the carbonyl. The stabilization of the singlet diradical character by the carbonyl group thus substantially lowers the energy barrier of the reaction. In the intermediate the delocalization of the vinyl radical is reflected in the nearly linear, allene-like geometry of the three carbon side chain and the orientation of the conjugating oxygen.

c. Kinetic isotope effects

The reaction barriers were recomputed for 348.15 K as in the experiments. The calculated results are listed in Table 1.

Table 1.

Calculated zero point energies (ZPEs, in kcal/mol) of reactants and reaction barriers (enthalpy, kcal/mol) at the UB3LYP/6-31+G(d) level of theory (gas phase, 348.15 K, 1.0 atm).

Reactant/Transition State	ZPEs	ΔH‡	ΔE
C6H5C≡CH	68.67	--
C6H5C≡CD	66.90	--
C6H5NO	61.07	--
C6D5NO	50.75	--
TS1-C6H5C≡CH-C6H5NO	130.19	15.27	0.00
TS1-C6H5C≡CD-C6H5NO	128.26	15.09	−0.18
TS1-C6H5C≡CH-C6D5NO	119.87	15.28	+0.01

The calculations indicate that the kinetic isotope effect (with the assumption of pseudo equilibrium at the top of the energy barriers) for the reaction of C₆H₅NO/C₆D₅NO with PhC≡CH should be negligible (KIE = 1.01; ΔE = 0.01 kcal), as expected if the phenyl C-H of PhNO is not appreciably perturbed in the rate-limiting step. However, deuteration of the alkyne, PhC≡CH/PhC≡CD, is calculated to cause an inverse KIE (~ 0.77), because the terminal sp-hybridized carbon of the alkyne rehybridizes toward sp²-in the TS. However, this type of calculation does not consider the dynamic differences of the activated complexes crossing the barriers. TS-1-C₆H₅C≡CH-C₆H₅NO, TS-1-C₆H₅C≡CD-C₆H₅NO, and TS1-C₆H₅C≡CH-C₆D₅NO were computed to be imaginary frequencies of 561.93, 561.44, and 560.71 cm⁻¹, respectively, at the UB3LYP/6-31+G(d) level. Accordingly, the activated complex, TS1-C₆H₅C≡CH-C₆D₅NO, with the lowest frequency (v_i), is likely to have larger effective partition to cross the barrier at the same temperature, and vice verse. However, for computational simplification the ZPE corrections ignore contributions from these imaginary frequencies, the ≡C-H(D) bending vibrational specifically. Thus, the inverse KIE expected from geometry change at the CH(D) (alpha effect) could be counterbalanced by a normal secondary beta-KIE from so-called “hyperconjugation”, resulting in an intermediate KIE of ca. 1–1.5, as found experimentally. This magnitude of KIE has been observed in other addition reactions of PhC≡CH(D).²⁴

d. Para-Substituent effects

Substituent effects of -NO₂, -CN, -Cl, -Br, -H, -Me, and -OMe groups at the para-positions of PhNO and PhC≡CH in the reactions were computed with the same level of theory. The reactants and rate-determining transition states were fully optimized and then the resulting stationary points were confirmed by harmonic vibrational frequency analysis. The calculated results are listed in Table 2.

Table 2.

Calculated activation energies (enthalpy, in kcal/mol) for para-substituted ArNO and ArC≡CH at the (U)B3LYP/6-31+G(d) level (gas phase at room temperature). <S²> of the calculated transition states are 0.34–0.39.

Reactions	ΔH‡ (kcal/mol)
p-O2N-C6H4NO + PhC≡CH →	13.1
p-NC-C6H4NO + PhC≡CH →	13.8
p-Cl-C6H4NO + PhC≡CH →	15.5
p-Br-C6H4NO + PhC≡CH →	14.7
PhNO + PhC≡CH →	15.8
p-Me-C6H4NO + PhC≡CH →	16.4
p-MeO-C6H4NO + PhC≡CH →	17.4
p-O2N-C6H4NO + p-O2N-C6H4C≡CH →	13.4
p-O2N-C6H4NO + p-NC-C6H4C≡CH →	13.3
p-O2N-C6H4NO + p-Cl-C6H4C≡CH →	12.8
p-O2N-C6H4NO + p-Br-C6H4C≡CH →	12.2
p-O2N-C6H4NO + PhC≡CH →	13.1
p-O2N-C6H4NO + p-Me-C6H4C≡CH →	12.6
p-O2N-C6H4NO + p-MeO-C6H4C≡CH →	11.6

The calculated reaction barriers for the substituted-PhNO reactions are qualitatively consistent with the experiments, despite the larger calculated effects of X-groups (4.3 kcal/mol) than Y-groups (1.8 kcal/mol). Nevertheless, electron withdrawing groups on PhNO and electron donating groups on PhC≡CH accelerate the reactions in both experiment and theory. Comparably, note that the reactions of PhNO + p-Y-PhC≡CH benefit from both the EW and ED groups in the calculations (shown in the supporting information), implying complications between spin-delocalization and polar substituent effects.¹⁶

G. Conclusions

In summary, the combined experimental and computational probes of the nitrosoarene/alkyne cycloaddition provide strong evidence of the operation of a step-wise mechanism which is initiated by rate-limiting bond-formation between N- and the alkyne terminal carbon to generate a polar diradical intermediate. This intermediate can cyclize rapidly via C-C bond formation to produce an intermediate cyclohexadienyl nitroxyl radical. Tautomerization of the latter produces the N-hydroxyindole. Computational and experimental studies are continuing to expand the scope of these and related nitroarene/nitrosophile cycloadditions.

Experimental

Preparative methods

Nitrosobenzene, phenylacetylene, cyclopropylacetylene, potassium carbonate, dimethyl sulfate, 4-ethynyltoluene, deuterium oxide, nitrobenzene-d₅, n-BuLi were obtained commercially and used as received. 4-X-C₆H₄-NO (X=NO₂ ^17b, CN^17f, Br^17f, Cl^17f, CH₃ ^17d,f, OCH₃ ^17c were prepared as reported. The 4-Y-C₆H₄-C≡CH derivatives were also prepared following literature procedures.¹⁸ PhC≡CD was prepared by a reported method.²⁹

PhNO-d₅ was prepared by a two-step procedure. The reduction of PhNO₂-d₅ to PhNH₂-d₅ was carried out by hydrogenation using Pd/C (10%) as catalyst at room temperature in EtOH. After 5 hr monitoring the reaction by TLC the disappearance of pentadeutero-nitrobenzene was detected with the formation of a single product. After the filtration and evaporation of the solvent the isotopic purity of PhNH₂-d₅ was checked by ¹H-NMR. The oxidation of PhNH₂-d₅ to PhNOd₅ was conducted by a literature procedure.^17f

Kinetic experiments for determination of the reaction order

Experiments for the determination of the reaction order in nitrosoarene were carried out from four different reactions using 11.25 mmol of phenylacetylene and different quantities of nitrosobenzene (0.375, 0.750, 0.188, 0.563 mmol) in 40 mL benzene at 75 °C, monitoring the absorbance at λ = 750 nm to measure the concentration of nitrosobenzene at different times as the reaction proceeds. Determination of the reaction order in phenylacetylene was carried out using four different reactions with 0.375 mmol of nitrosobenzene and different quantities of phenylacetylene (5.63, 7.50, 11.25, 22.5 mmol) in 40 mL of benzene monitoring the absorbance at λ = 750 nm.

Kinetic experiments for study of the Hammett relationship

Reactions of 4-X-C₆H₄-NO with phenylacetylene

4-X-C₆H₄-NO (0.375 mmol) and phenylacetylene (11.25 mmol) were heated in 40 mL of benzene at 75 °C monitoring the absorbance at λ = 750 nm to determine concentrations of the nitrosoarene over time.

Reactions of 4-nitro-nitrosobenzene in competition experiments with 4-Y-C₆H₄-C≡CH and PhC ≡CH in alkylating conditions

4-NO₂-C₆H₄-NO (0.375 mmol), 4-Y-C₆H₄-C≡CH (5.63 mmol), PhC≡CH (5.63 mmol), K₂CO₃ (1.5 mmol) and Me₂SO₄ (1.5 mmol) were heated in 40 mL of benzene at 75° C monitoring the absorbance at λ = 750 nm. All the reactions were conducted for 30 minutes to achieve about 15% conversion of 4-NO₂-C₆H₄-NO. After flash-chromatography the fraction that contained the mixture of the two different N-methoxyindoles was collected, solvent evaporated and the residue analyzed by ¹H-NMR. The integration of appropriate signals gave the ratio of the products. The reference N-methoxyindoles were synthesized by reactions with the procedure reported in previously.¹⁰

Trapping studies with TEMPO

Nitrosobenzene (107 mg, 1.0 mmol), phenylacetylene (2.46 mL, 20 mmol) and TEMPO (625 mg, 4.0 mmol) were refluxed in 80 mL of benzene. The reaction was monitored by TLC until the nitrosobenzene had disappeared. The solvent was evaporated to dryness and the products were purified by flash-chromatography.

Trapping studies with Cyclopropylacetylene

Nitrosobenzene (80 mg, 0.75 mmol) and of cyclopropylacetylene (1.97 g, 30 mmol) were heated at reflux in 80 mL of benzene in a Fischer-Porter bottle after charging with 50 psi of N₂. After 20 h the reaction mixture was allowed to cool and the complete conversion of nitrosobenzene was observed by TLC. The solvent was evaporated to dryness. The products were isolated and purified by flash-chromatography (eluant. In addition to azoxybenzene 3-cyclopropylindole (Rf= 0.26) was isolated in 20% yield. mp 59–61 °C. ¹H-NMR (400 MHz, CDCl₃): 7.82 (1H, d, J = 7.8 Hz), 7.76 (1H, s, br), 7.35 (1H, d, J = 7.8 Hz), 7.27 (1H, t, J = 7.8 Hz), 7.21 (1H, t, J = 7.8 Hz), 6.89 (1H, apparent singlet), 2.02 (1H, m), 0.97 (1H, m), 0.72 (1H, m). GC-MS (EI, m/z): 157, 156, 130, 129, 77, 65. ¹³C-NMR (100 MHz, CDCl₃): 136.44(C), 128.23(C), 122.18(CH), 120.68(CH), 119.38(CH), 119.32(CH), 119.10(C), 111.34(CH), 6.33(CH), 6.21(CH₂).

Synthesis of 3

o-Carbomethoxy-nitrosobenzene (0.323 g, 2.00 mmol) was dissolved in 80 mL of benzene and 3 mL of phenylacetylene (28 mmol) was added. The reaction mixture was refluxed while magnetically stirred for 2 h. After rotary evaporation of the solvent the product was isolated and purified by flash-chromatography using CH₂Cl₂/AcOEt 95/5 as eluent (Rf = 0.28). ¹H-NMR (400 MHz, CDCl₃): 7.57 (1H, d, J = 7.8 Hz), 7.51 (1H, d, J = 7.6 Hz), 7.44 (1H, t, J = 7.6 Hz), 7.31–7.25 (4H, m), 7.10 (2H, t, J = 7.7 Hz), 7.06 (2H, t, J = 7.7 Hz), 6.89 (2H, t, J = 7.6 Hz), 6.75 (1H, t, J = 7.4 Hz), 4.63 (1H, d, J = 7.0 Hz), 3.71 (3H, s), 3.67 (1H, d, J = 7.0 Hz).

¹³C-NMR (100 MHz, CDCl₃): 192.86, 173.41, 154.12, 137.45, 136.62, 134.40, 132.94, 129.42, 128.81, 128.12, 127.99, 127.76, 127.70, 127.27, 125.28, 122.63, 68.02, 54.91, 53.58, 50.19. MS (CI): 370 (M+1). IR (cm⁻¹): 1732, 1687.

X-ray structure determination of 3

Crystals suitable for X-ray analysis were obtained by slow diffusion of hexane into a dichloromethane solution of 3. The data were collected at 120(2) K on a Bruker Apex diffractometer using MoKα (l =0.71073 Å) radiation. Intensity data, which approximately covered the full sphere of the reciprocal space, were measured as a series of ω oscillation frames each 0.3° for 25 sec/frame. The detector was operated in 512 × 512 mode and was positioned 6.12 cm from the crystal. Coverage of unique data was 97.3 % complete to 56.6° (2θ). Cell parameters were determined from a non-linear least squares fit of 6011 reflections in the range of 2.3< θ < 28.2°. A total of 22184 reflections were measured. The structure was solved by the direct method using SHELXTL system (Version 6.12, Bruker AXS, Madison, Wisconsin), and refined by full-matrix least squares on F² using all reflections. All the non-hydrogen atoms were refined anisotropically. All the hydrogen atoms were included with idealized parameters. There are four molecules in the unit cell. Final R1 = 0.0411 is based on 3629 “observed reflections” [I>2s(I)], and wR² = 0.1075 is based on all reflections (4435 unique reflections). Details of the crystal data are given in Table 3. Thermal ellipsoids are drawn at 50% level for Figure 5.

Table 3.

Crystal data and structure refinement for 3.

Identification code	kn4145m
Empirical formula	C24 H19 N O3
Formula weight	369.40
Temperature	103(2) K
Wavelength	0.71073 Å
Crystal system	Monoclinic
Space group	P2(1)/c
Unit cell dimensions	a = 10.8771(11) Å α= 90°.
	b = 15.4698(16) Å β= 94.3230(10)°.
	c = 10.8948(11) Å γ = 90°.
Volume	1828.0(3) Å3
Z	4
Density (calculated)	1.342 Mg/m3
Absorption coefficient	0.089 mm−1
F(000)	776
Crystal size	0.28 × 0.12 × 0.10 mm3
Theta range for data collection	1.88 to 28.27°.
Index ranges	−14<=h<=14, −20<=k<=20, −14<=l<=14
Reflections collected	22184
Independent reflections	4435 [R(int) = 0.0236]
Completeness to theta = 28.27°	97.3 %
Absorption correction	None
Max. and min. transmission	0.9912 and 0.9756
Refinement method	Full-matrix least-squares on F2
Data/restraints/parameters	4435/0/254
Goodness-of-fit on F2	1.020
Final R indices [I>2sigma(I)]	R1 = 0.0411, wR2 = 0.0998
R indices (all data)	R1 = 0.0530, wR2 = 0.1075
Largest diff. peak and hole	0.345 and −0.193 e.Å−3

Kinetic isotope effect determination

The kinetic isotopic effect was investigated from two reactions: (1) PhNO (0.188 mmol), PhNO-d₅ (0.188 mmol) and PhC≡CH (11.3 mmol) were heated in 40 mL of benzene at 75° C monitoring the reactions until ca. 15% conversion of the nitroso derivatives was achieved and analyzing the crude mixture by GC-MS after evaporation of the solvent. (2) PhNO (0.375) was heated in 40 mL of benzene with 5.63 mmol of PhC≡CH and 5.63 mmol of PhC≡CD. Monitoring of the reaction was carried out by the absorbance at λ = 750 nm. After evaporation of the solvent the crude mixture was analyzed by GC-MS.

Computational Studies

All geometries and energies were calculated with the (U)B3LYP DFT functional²⁷ with the 6-31+G(d) basis set using Gaussian 03.²⁸ Minima and transition states were fully optimized and characterized by harmonic vibrational frequency analysis and verified by intrinsic reaction coordinate (IRC) calculations. All calculations were validated at the UB3LYP level using the broken-symmetry wave function (guess=mix, always) to assess the expectation value of the S² operator. The reactants and final products are pure singlet species, with S² = 0. Radical-pair-like species between the N-C and C-C bonds formation showed typical diradical character, i.e. S² = 1, and thereby the unrestricted method was used for geometry optimization. The spin contamination, due to admixture of high spin states into the singlet, can be eliminated using the spin projection method.³⁰ Investigations of reaction regioselectivity between 2- and 3-substituted indole formation and p-substituent effects were conducted on the rate-determining step of N-C bond formation.

Supplementary Material

1_si_001. Supporting Information Available.

Kinetic data for PhC≡CH/PhNO reactions; X-ray data collection and crystal data, selected bond-lengths and angles for 3; the computationally optimized structures and calculated reaction barriers of PhNO + p-Y-C₆H₄C≡CH; complete reference ²⁷. These materials are available free of charge via the internet at <http://pubs.acs.org>http://pubs.acs.org.

Scheme 8.