Mathematical modeling of molecular diffusion through mucus

Abstract

The rate of molecular transport through the mucus gel can be an important determinant of efficacy for therapeutic agents delivered by oral, intranasal, intravaginal/rectal, and intraocular routes. Transport through mucus can be described by mathematical models based on principles of physical chemistry and known characteristics of the mucus gel, its constituents, and of the drug itself. In this paper, we review mathematical models of molecular diffusion in mucus, as well as the techniques commonly used to measure diffusion of solutes in the mucus gel, mucus gel mimics, and mucosal epithelia.

1. Introduction

Mucus gels with distinct properties of thickness and composition are found in tissues throughout the body. The appearance, mechanical properties, and chemical constituents of the mucus layer vary among tissues, change in response to the fluctuations of the body's chemistry, for example in the hormonal cycles. In the context of drug delivery through mucosal tissues, such as in oral, intranasal, intravaginal/rectal, and intraocular drug delivery, the mucus layer is one of the primary obstacles that the therapeutic agent must overcome. Molecules that can quickly penetrate the mucus layer are available to be transported through underlying epithelial cells layer and potentially distributed inside the body.

In this review, we examine the nature of solute transport through mucus. Relevant mathematical models, as well as experimental systems used for obtaining data to test and validate these models are introduced. The discussion is limited to natural and synthetic solutes shown to have some efficacy or potential in applications, such as drugs, antibodies, globular proteins, nucleic acids, flexible linear polymers and nano- and micro-scaled polymeric particles.

1.1 Physical properties of mucus

A typical mucus sample is, by mass, 90-95 % water. The remaining mass consists of glycoprotein fibers, oligosaccharides, lipids, migrating or sloughed cell and cell contents, enzymes, antibodies, DNA and electrolytes. In addition to commensal microorganisms, which are non-pathogenic and tolerated by the host, the mucus gel also plays host to a constant stream of foreign species ranging from dust and reactive chemicals, to invading bacteria and viruses[1]. The thickness of the mucus barrier is dependent on its location. Gastrointestinal mucus is reported to be 50-600 μm in the stomach and 15-450 μm in intestine and colon[2-4]. A number of excellent reviews on the properties and function of mucus have been published[4-7].

The three-dimensional structure of mucus gel is sustained by a network of randomly interwoven flexible protein fibers called mucin. The density of mucin scaffolding fibers and the high concentration of soluble constituents which increase viscosity of the medium (ie. secreted hormones, enzymes, commensal microorganisms, and cell debris), help maintain an unstirred environment within the mucus gel layer. Convection is also inhibited by formation of a lipid-rich mucin layer at the surface of the gel[8]. Since there is little fluid movement within the gel, solutes are thought to penetrate purely by diffusion.

The physical size and arrangement of mucin fibers contribute significantly to the kinetics of the diffusion process. A major structural component of mucus, mucin fibers are polydisperse molecules of 2-40 mDa MW and 0.5-10 μm in length, with a linear topography[9]. Mucin fibers consist of 80 % proteoglycans that are attached to the primary backbone in clusters, resulting in a flexible fiber with diameter 3-10 nm (backbone glycosylation is 0.5-5 nm from the fiber core with length 50-200 nm) with persistence length 1-15 nm depending on glycosylation and charge[10]. For a more complete description of mucin structure and properties, see a review by Thornton et al[11].

A heterogeneous charge profile along the length of mucin fibers, caused by alternating glycosylated and cysteine-rich regions, enables weak interaction of mucin with other fibers and a wide range of molecules in the mucus layer. Each mucin fiber intersects on average 10-100 times with other fibers[8]. SEM analysis reveals an interwoven fibrous network with spacing of ∼500 nm between fibers and ∼100 nm spacing among additional finer structures (Figure 1.1)[12]. The lack of branched cross-linking in mucin is evident in the lubricating ability of mucus that allows it to accommodate planar shear stress: weak interactions between fibers are broken and reformed to sustain the mucus structure during shearing. It has been shown that mucin fibers alone can produce a viscoelastic gel with the same rheological properties as secreted mucus. Non-mucin components are reported to contribute to “weakening” of this gel, as they interrupt fiber associations and also play a role in impeding solute transport[13-15].

Figure 1.1.

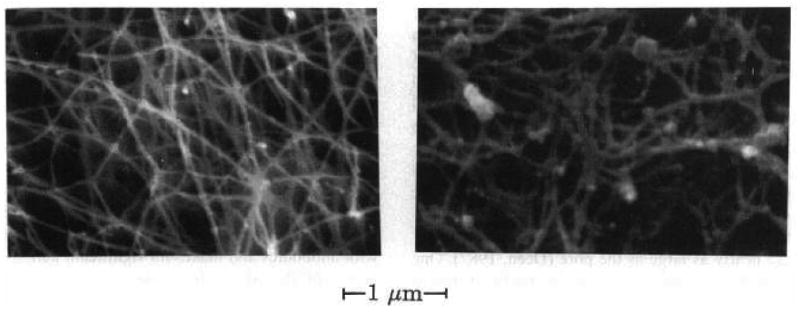
Scanning electron micrographs of human midcycle cervical mucus[12].

1.2 Translation of physical parameters to mathematical models

Creation of a mathematical model of transport through mucus requires a physical description of the complex geometry of the mucus gel. Some mathematical models depict the gel as an array of regular or randomly oriented overlapping fibers with radius r_f. The volume fraction occupied by fibers limits the free-diffusion space, which directly affects rate of solute movement. Alternately, the entire structure is sometimes depicted as a fibrous mesh, with the space between fibers forming ‘pores’ through which the solutes travel. The physical dimensions of these pores can hinder diffusion for solutes larger than a certain size. The relationship between solute radius, r_s, and pore diameter, a, is factored into mathematical models that regard the mucus layer as a molecular-sieve. The mesh produced by overlapping mucins could be represented as an array of hollow cylinders, or a network of pores in a three-dimensional environment (Figure 1.2)[16-25]. Viscosity of the fluid medium within the mucin scaffold can also significantly limit solute diffusion. Hydrodynamic models of mass transport take into account this feature by calculating the drag force upon the diffusing species as it moves through the mucus gel.

Figure1.2A-D.

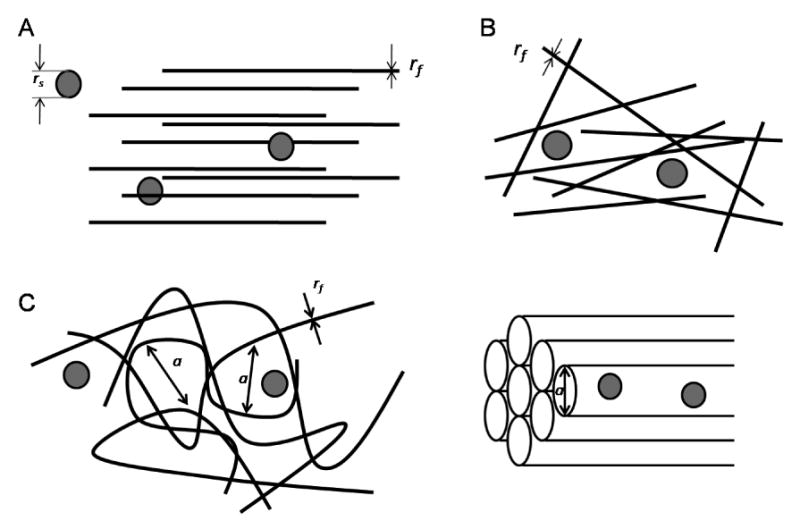
Geometric presentation of mucus gel as an array of regular (A) and overlapping fibers (B) with diameter r_f. Alternately, the mucus gel three-dimensional scaffold is modeled as a network of connected pores with diameter a(C) or an array of hollow cylinders (D). The solute is depicted as a sphere with diameter r_s.

The mucus gel is not a rigid structure. Orientation and spacing between fibers are maintained by weak, non-covalent interaction of the fibers to one another. Fiber displacement, thus, can easily occur as a result of applied mechanical force (ie. muscle contractions in stomach), thermal fluctuation, hydration, or presence of the solute itself. Having a single constant parameter to describe thickness, pore size, and viscosity of the mucus gel, in this case, may not be entirely accurate. Instead, these parameters may need to be evaluated at each state of perturbation to best describe the biological sample.

1.3 Other properties that impact diffusion through mucus

Mucin fibers exhibit ionic interactions with solutes. Early studies showed aggregation of fibers around foreign molecules of a wide range of size, composition and surface charge [26-28]. In addition, Anderson et al. reported a significant effect of solute surface charge on its transport in mucus[29]. This is likely a result of strong ionic interactions of the solute to oppositely charged mucus constituents. To circumvent the mucus barrier, some highly infectious microorganisms such as HIV virus have evolved hydrophilic protein coatings with net-neutral charge, to enhance permeability by minimizing interaction with mucus components[8]. Efforts to study and mimic virus diffusion in mucus have been made using surface-modified polymer particles of varying size[30, 31].

The mucus layer also contains a native pH value or pH gradient. The pH of mucus gel in the female reproductive tract is dependent on stage of development (pH=7 in prepubescent, pH=4-7 in pre and post-menopausal women). For women who are ovulating, cervical mucus pH also changes during the oestral cycle in response to hormone fluctuations[32]. In the gastrointestinal tract where the gradient in pH from the stomach lumen to the epithelial cell surface varies from 4 to 7, respectively, the mucus gel offers a barrier against H+ diffusion to protect the underlying tissue[33]. Change in the pH environment can cause mucus constituents, such as sugar and proteins anchored on mucin fibers, to adopt a different net charge. As the (ionic) interaction between these molecules are altered in response to pH, the macroscopic properties (ie. pore size, fiber density and medium viscosity) of the mucus gel can also change[5, 34-36].

The presence of cations can also alter mucus gel structure, via protonation of negatively charged glycosylic groups on mucin fibers. At certain critical concentrations of Na+ and Ca++, this protonation effectively reduces the negative expulsion force between glycosylic groups needed to maintain the three-dimensional structure of the mucus gel, causing the gel to collapse[6]. The net charge of a therapeutic agent, depending on its composition, can be similarly affected by the pH and ionic strength of the mucus gel environment.

In the body, the mucus lining is continually shed and replaced. The sloughed off mucus carries away contaminants from the external environment and wastes produced by the body. Unfortunately, this protective function would also physically eliminate any applied therapeutic agents still embedded in the layer. Successful delivery is, therefore, a race against time. Although the urgency depends on the tissue site, the rate of mucus clearance in the body is on the order of hours (ranging from 8.8min for nasal mucus[37] to 24-48hr in the gut[38]).

Despite the inherent obstacles to diffusion in mucus (ie. steric hindrance, ionic ‘traps’, harsh environments, and clearance), net conduction through mucus can still be achieved. The driving force behind mucus penetration is the concentration gradient across the layer. The latter is a combined effect of solubility, stability and extent of interaction with mucus, as well as the size and shape of the molecule of interest. These are quantifiable parameters, and are critical components in mathematical models, to be described in the following section.

2. Mathematical interpretations of solute diffusion in mucus: Concept, parameters, and models

To model the transport of a solute through mucus, it is helpful to observe the entire system and its components—including solute and medium—in a defined context with simplified geometry, quantifiable parameters, and stable boundary conditions. In a typical arrangement for measuring the rate of drug transport through mucus in living systems, the molecule of interest is applied to a mucus gel at a high concentration by implant or deposition. Upon leaving the source, the agent must traverse the entire thickness of the mucus layer to arrive at the underlying cell layer, from which it is transported into the body. The number of molecules successfully taken up is dependent upon predictable factors that ultimately determine diffusion speed and stability of molecule within the mucus environment.

2.1 Diffusion coefficient and flux

The degree to which a molecule, which we call “A”, can freely move in a solvent environment is described by its diffusion coefficient (D). The importance of this parameter, with units L²/t, can be argued from two different approaches: in terms of the hydrodynamic drag on the molecule, or as a result of a random walk. Both of these approaches originate from notable contributions by Einstein[16].

The first approach states that the diffusion coefficient of a molecule is determined by a hydrodynamic drag force f, produced by interactions with its environment:

$$D_o=\frac{k_{B}T}{f_o}$$ (1)

where k_B is Boltzmann's constant, T is absolute temperature, and f_o is the frictional drag coefficient. The subscript ‘o’ is used to emphasize the validity of the relationship for conditions in which the concentration of A, denoted C_A, is very low (ie. the solution is dilute). This relationship is, however, often assumed to apply in mathematical models for a wide range of C_A, as discussed in section 2.3.

By analyzing the forces on a spherical particle moving through a continuous liquid, Stokes found that the frictional drag coefficient (f) is a function of the hydrodynamic radius of the diffusing molecule (r) and medium viscosity (μ):

$$f_o=6\pi \mu r$$ (2)

which, in combination with (1), gives rise to the Stokes-Einstein equation, which provides a means to estimate the diffusion coefficient (D_o) from its physical size, r:

$$D_o=\frac{k_{B}T}{6\pi \mu r}$$ (3)

The second approach states that Brownian motion of the molecule, caused by thermal fluctuations in the system, result in an average molecular displacement (χ) in a random direction. The magnitude of displacement after time (t) can be expressed as a function of the diffusion coefficient:

$$\chi =\sqrt{2D_{o}t}$$ (4)

rearranging the equation to solve for D_o yields:

$$D_o=\frac{{\chi }^2}{2t}$$ (5)

The random walk is a probability-based process in which a single particle can take a step of defined unit-length in any direction over a fixed small time interval. According to the above equation, molecules of higher diffusivity will be displaced further from the origin, on average, than a less diffusive species after some time. When there is a difference in the local concentration of agents, the non-directionality of the stochastic walk of individual molecules can still result in net movement of the population. Provided at a concentrated point source, molecules will gradually spread out until this gradient dissipates, and a homogeneous concentration (equilibrium) throughout the defined space is reached. This distribution of molecules, in fact, follows a Gaussian spread from the point source[39]. Both concepts for describing the diffusion coefficient, in terms of hydrodynamic or random walk process, have been applied in the development of solute diffusion models in mucus. For example, hydrodynamic approach was adopted in a diffusion model by Kosar and Phillips, where the presence of fibers contribute to the effective hydrodynamic drag upon the diffusing solute[40]. In contrast, Ogston's “hindered diffusion” model was developed from the stochastic random walk theory where diffusion of solute is limited by physical dimensions of fibers which occupies available “walking” space [16].

2.2 Concentration dependency of diffusion coefficient

The effective diffusion coefficient (D) can be approximated by D_o when the concentration of the diffusing species is very low. Though a single diffusion coefficient D_o is commonly used in mathematical models with the underlying assumption that this value holds true over most physiologically relevant conditions, the diffusion coefficient for many species has been found to vary with concentration and solvent states. For example, the diffusion coefficient of A often depends on C_A. At high concentrations, the ‘crowded’ environment limits the degree of freedom for movement of a molecule, or in hydrodynamic terms, the molecule experiences an additional drag caused by interaction with other molecules. Thus, the assumptions for equations (1) and (2) must be modified.

Although studies of the concentration dependence of diffusion in mucus have not been reported, concentration dependent diffusion has been measured in other polymer solutions. Anderson et al. reported that the diffusion coefficient of polystyrene and BSA in aqueous medium varies with solution ionic strength and concentration, the latter defined by the relationship: D = D_o (1 + kC_A), where k is a concentration coefficient that depends on particle size and solution ionic strength[29]. Similarly, other studies have shown that the diffusions coefficient for albumin[41] and polystyrene particles[42] decrease with concentration. Diffusion of flexible polymers such as linear DNA oligonucleotides (8-20bp) was also found to be concentration dependent, where

$$D_A(C_A)=D_{A,0}(1+k{\phi }_A+\dots )$$ (6)

This equation was found valid over a range of C_A = 0 to C_A = 450 μg/mL, where k is the concentration coefficient, and φ_A is the volume fraction of the solute (DNA)–which is a function of concentration (C_A), partial molar volume of DNA (N_AV), and molecular weight (M_w)[43]:

$${\phi }_A=\frac{N_{AV}{C}_A{V}_h}{M_w}$$ (7)

2.3 Fick's law and mass balance

The concepts needed to describe mass transport in a finite medium are proceeded in a number of detailed sources[39, 44, 45], but summarized in this section.

The concentration of molecule A in a volume over time is a culmination of various processes, including the fluxes of A throughout the defined volume. For a finite cubic volume with side of length dx, dy and dz in rectangular coordinate system (Figure 2.1), the concentration of A in this volume is dependent upon diffusive and convective mass transport, generation and clearance of the molecule by some chemical reaction. A mass balance for A that encompasses all of these events is:

Figure 2.1.

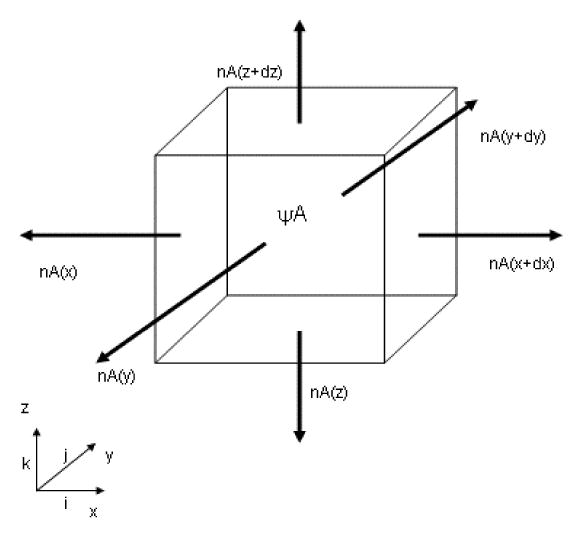
Three dimensional schematic of mass conservation in a finite volume

$$\left[\text{Total mass}\right]=[\text{molecules in}-\text{molecules out}]+\left[\text{generation}\right]-\left[\text{clearance}\right]$$ (8)

The first term represents the net rate of molecular flux in the entire volume, which is a sum of flux over the total surface area and is a vector quantity (∇n_A). In most cases, molecules are not generated in the mucus. Clearance of molecules is possible, and depends on the chemical makeup of the solute. (ie. immobilization by protein-protein interactions or degradation.)

A more rigorous description for mass flux (n_A) incorporates both diffusive and convective contributions to the overall flux. For binary systems, in which the speed of molecule (A) is measured in relation with another species (B), which we can assume to be the solvent, the convective flux is represented by the mass fraction of A (ω_A) and the mass flux of A and B: ω_A(n_A + n_B) [39]. For systems such as mucus, where convection is negligible, the diffusive flux is the sole estimate for mass transport[8].

The net rate of molecules (A) diffusion per unit cross-sectional area of some volume in space is referred to as diffusive flux (J_A). An expression that relates the diffusion coefficient, and the spatial distribution of A to J_A can be derived from the random walk model[39].

$$J_A=-D\frac{\partial C_A}{\partial x}$$ (9)

Equation 9 states that the diffusive flux of A, J_A, is proportional to its concentration gradient in the x-direction, and that the constant of proportionality is the diffusion coefficient (D). This equation is often referred to as Fick's first law, because it was first proposed by Fick based on empirical evidence. It is applied to steady state conditions, where boundary conditions do not change as function of time, for one-dimensional diffusion (ie. diffusion). The unit of diffusive flux is matter, expressed as mass or moles, over area and time (M/L²t). This expression can be extended to describe diffusive flux in more than one dimension, by expressing it as a vector quantity:

$$J_A=-D\nabla C_A$$ (10)

where ∇ is the usual gradient function ( $\nabla =\overrightarrow{i}\frac{\partial }{\partial x}+\overrightarrow{j}\frac{\partial }{\partial y}+\overrightarrow{k}\frac{\partial }{\partial z};$; i⃗ j⃗ and k⃗ are direction vectors in the x, y and z direction).

2.4 Geometry and approaches to diffusion modeling through mucus

Mucus is a viscoelastic gel sustained by a network of entangled flexible mucin fibers. The pores that exist between the fibers are swollen with fluid, the medium through which the molecule is transported. To diffuse through a medium such as this, the diffusing molecule must negotiate around the fiber obstacles. The movement of solutes through this three-dimensional mesh is hindered by steric factors, created by fibers which occupy volume, reducing space for diffusion, and serving as size-selective molecular sieves[16, 17, 23-25, 46, 47]. In addition, the interaction between molecules and fibers can result in higher hydrodynamic drag, which decreases permeability through the porous medium[18, 19, 48]. A comparison and discussion on these models as well as those based on integrated theories can be found in several reviews[22, 49, 50].

Diffusion characteristics vary predictably with the size and shape of molecules. Solutes, whether they are globular or chain-like, will adapt a three-dimensional conformation in a fluid environment. The hydrodynamic radius (r_H) of a globular solute such as polymeric particles (spheres), antibodies and proteins (a chain polymer with a singular tight-packed tertiary conformation) or a small organic drug molecule is given by equation 3, where it is represented by r_s. This parameter can be determined empirically by x-ray diffraction or calculated from the diffusion coefficient of each solute using equation 3.

For a linear or branched polymers, the size of the three dimensional complex in solution is dictated by the chain length and nature of linkage between monomers. The extent of diffusion for flexible chain polymers is primarily defined by the size of the random coil formed in solvent[45, 50-52]. Depending on the size of the chain's tertiary structure in solvent compared to matrix pore size, the diffusion process can fall into one of two regimes: the Zimm-Rousse or the reptation regime. In the section below, we will introduce and discuss mathematical models used for study of macromolecule diffusion through polymer matrix.

2.5 Models

The diffusion of molecules of type A through a hydrated gel or polymer matrix (p) is described as D_A,p. The extent of diffusion is often normalized to its diffusion in a homogeneous medium (∞) to yield a ratio, $\frac{D_{A,p}}{D_{A,\infty }}$, Where D_A,∞ is usually equal to D_o defined earlier.

Pure occlusion models are based on the theory of steric inhibition in polymer gels due to the physical presence of fibers, which occupy volume within the diffusion medium. An early occlusion model developed by Ogston considers the hindered diffusion of a spherical molecule of radius r_s as a process of stochastic random walk, limited by the available fractional volume (φ) caused by presence of straight cylindrical polymer chains with radius r_f. For this case, the diffusion ratio is:

$$\frac{D_{A,p}}{D_{A,\infty }}=\text{exp}\left(-{\phi }^{\stackrel{1}{}/\underset{2}{}}\sigma \right)$$ (11)

where $\sigma =\frac{(r_s+r_f)}{r_f}$

The assumptions of this model are 1) the diffusing molecules follow a stochastic walk, which moves the molecules either a full unit step in a random direction or not at all; 2) each unit step is related to the mean radius of spaces in fiber system; 3) the effective collision radius is the sum of the sphere (solute) and cylinder radius (r_s + r_f); and 4) fiber spatial distribution is independent of thickness of gel layer or particle movement[16]. This principle—solute size occlusion caused by matrix geometry as a principal factor in governing diffusion—was further developed by Johansson et al. and later reported to correlate well with experimental data. In contrast to Ogston's geometrical assumption, Johansson's model is based on transport of solute through of an array of cylindrical cells where a single cylinder rod is surrounded by diffusing solute[47, 53].

Giddings[54] developed a model similarly based on size-exclusion transport for spherical particles and rigid rods in matrix of cylindrical pores, where the normalized diffusion coefficient in polymer gel is closely approximated by the partitioning coefficient, K, which is related to the matrix pore radius a, and molecule hydrodynamic radius r_H. (note that for globular solutes, r_s = r_H)

$$K=\left(1-\phi \right)•{(1-\frac{r_H}{a})}^2$$ (12)

This relationship is valid for molecules with dimensions smaller than the matrix pore, $\frac{r_H}{a}\le 0.6$. In addition, the validity of this model requires that the matrix pore concentration is smaller than the pore volume, due to the geometric restriction for solutes molecules that approach the pore wall.

A semi-empirical model based on hindered transport and molecular sieving was developed by Renkin, based upon the work of Pappenheimer et al.[55, 56], to depict size-based filtration of solutes of various diameter (2 to 6 Å) through thick cellulose membranes[24]. The complexities of the actual pore arrangement were simplified, and approximated as close-packed cylinders of uniform diameter:

$$\frac{D_{A,\text{membrane}}}{D_{A,\infty }}={(1-\lambda )}^2[1-2.1044\lambda +2.089{\lambda }^3-0.948{\lambda }^5]$$ (13)

The parameter λ is a characteristic ratio of solute diameter to average pore diameter, $\frac{r_H}{a}$. In a recent study, Pluen et al. showed that the Ogston and Renkin polymer theory models produce a lower estimation of diffusion coefficient than empirical results[50]. Application of both of these models requires an estimation of matrix average pore size. In actual mucus gels, the average pore diameter is largely unknown, but probably has a wide distribution. Using solutes such as globular proteins and antibodies diffusing in several types of fibrous gel medium, Saltzman et al. were able to estimate pore size for collagen, cervical mucus and gelatin gels, using equation 13, to be >1000nm, 150nm, 12nm respectively. The pore size for mucus gel was confirmed by SEM imaging (Figure 1.1)[12].

Hydrodynamic models are based on assumptions of a modified drag force (f), from equation 2, that includes the effect of medium constituents on diffusion coefficient. It has been shown that hydrodynamic interactions of solute and matrix fibers also contribute significantly to diffusion[21]. For example, an effective medium model, derived from the Stokes-Einstein (equation 2) using Brinkman's relationship for f, yields the expression[57] [18]:

$$\frac{D_{A,p}}{D_{A,\infty }}=1+{\frac{a^2}{\kappa }}^{\stackrel{1}{}/\underset{2}{}}+\frac{1}{3}{\frac{a^2}{\kappa }}^{-1}$$ (14)

This model assumes a constant fluid flow through a medium filled with straight, rigid and randomly oriented fibers, with non-slip boundary condition at the solute surface. The validity of this model is only assumed for solutes with high diffusion velocity relative to the fiber diffusion velocity; that is, the solute is diffusing while the fibers are stationary. However, this result has been shown to provide satisfactory estimates of BSA diffusion in dextran, in which BSA and dextran have comparable diffusion velocities[40]. The hydrodynamic permeability (κ), or Darcy's permeability coefficient, is a parameter dependent on fluid flow rate, applied hydrodynamic pressure, and fluid dynamic viscosity. Whereas hindered diffusion and molecular sieving models only consider the effects of physical attributes of polymer and solute, it is possible to incorporate ionic and other effect on solute diffusion into this coefficient[29]. This model was evaluated and validated by later studies[18, 50].

A mathematical form derived empirically and frequently used to estimate diffusion from parameters such as polymer concentration (C_P), and constants associated with solute and polymer geometry and interactions (α and υ) is given by: [58]

$$\frac{D_{A,p}}{D_{A,\infty }}=\text{exp}\left({-\alpha C_P}^v\right)$$ (15)

The typical values for α and υ are compiled from various sources, as cited from [39]. (Table 2.1)

Table 2.1.

Typical value for coefficients to equation 14[39]

Probe/polymer solution	a	n
Proteins/water:dextran or water:hyaluronic acid	∼a-1	0.5
Polystyrene spheres/dextran:water	independent of a	1.0
Probes/PEO:water	--	2/3
Polystyrene spheres/BSA:water	0.0044-0.008	0.96-0.99
FITC-BSA/DNA solutions (0 to 35 mg/mL)	0.018 to 0.024 mL/mg	∼1.0

Consideration of other interactions and parameters in the system can be incorporated in the general form of this stretched exponential:

$$\frac{D_{A,p}}{D_{A,\infty }}=\text{exp}\left({-\alpha C_P}^v{M_W}^{\gamma }{I}^{\beta }{r_s}^{\delta }\right)$$ (16)

which makes it possible to account for molecular weight (M_W), geometry (solute radius r_s) and ionic strength (I) factors in the system. The coefficients range from 0.5-1 for ν, ∼0.8 for β for polyelectrolytes and 0 for non-electrolytes, and δ is ∼0.3-0.5 for polyelectrolytes and 0 for non-electrolytes; γ is ∼0.8[59].

The combined effects of steric and hydrodynamic forces have been depicted in some models[60], which were validated experimentally. Johnson et al. proposed the multiplication of steric (S) and hydrodynamic (F) effects in a study of globular proteins and Ficoll in agarose gels, such that $\frac{D_{A,p}}{D_{A,\infty }}=F\times S$ [20]. In this ‘effective medium model’, equation 14 was expressed in combination with a obstruction model obtained through data regression for spherical molecules in random overlapped polymer array by Johansson et al.[46]

$$\frac{D_{A,p}}{D_{A,\infty }}=\text{exp}\left(-0.84\phi {(\sigma )}^{1.09}\right)$$ (17)

to yield a model with better predictive value than either of models based on a single theory.

$$\frac{D_{A,p}}{D_{A,\infty }}=\frac{\text{exp}\left(-0.84\phi {(\sigma )}^{1.09}\right)}{\left[1+{\left(\frac{a^2}{\kappa }\right)}^{\stackrel{1}{}/\underset{2}{}}+\frac{1}{3}\left(\frac{a^2}{\kappa }\right)\right]}$$ (18)

Similarly, Clague and Phillips et al. used an obstruction model developed by Tsai and Streider et al. in combination with a hydrodynamic based stretched exponential relationship to yield the following expression:

$$\frac{D_{A,p}}{D_{A,w}}={(1+\frac{2}{3}\alpha )}^{-1}\text{exp}(-\pi {\phi }^{0.174\text{ln(59}\text{.6}{r}_p/r_s\text{)}})$$ (19)

where α expresses the fluctuation of polymer-solute interaction, and r_p and r_s are polymer and solute radius, respectively[19, 61]. Amsden et al. provides further discussion of these models[22].

2.6. Diffusion of flexible chain-like solutes

Unlike rigid globular molecules, flexible chain polymers can adopt a range of three dimensional conformations in solvent. Imagine a linear polymer chain made up of rigid subunits with some length (l) and containing certain degree of freedom of rotation between each unit. The rotation angle and length between these monomers, represented by the direction vector r⃑, are assumed to be independent, according to the Markov chain theory[62]. The summation of these processes result in a three-dimensional, globular shape that the linear chain adopts in solution (Figure 2.2).

Figure 2.2A-C.

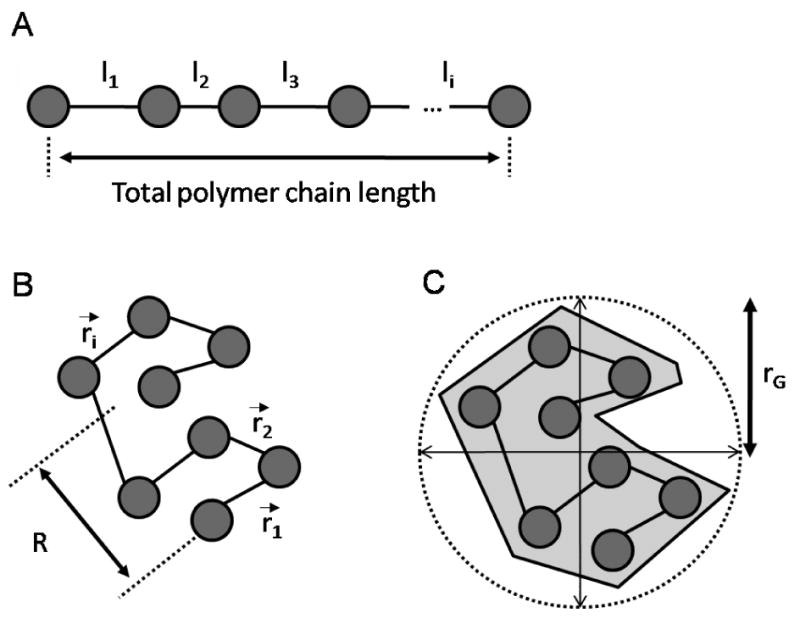
Topologically linear polymer chain (A) can adapt a three-dimensional configuration (B) due to the freedom of rotation between each subunit. The end-to-end length R is the sum of individual directional vectors, and can be correlated to r_G, the gyration radius (C).

The sum of individual direction vectors, R, is the end-to-end displacement of the polymer chain.

$$R=\sum _{i=1}^n\overrightarrow{r}$$ (20)

This value is related to the mean radius of gyration (r_G), which is defined as the average root-mean-square distance of the chain segments from the center of mass, by the following relationship:

$${6r_G}^2=R^2$$

The radius of gyration is used for approximation of the size of random coil formed by polymer chain. The relationship between r_G and r_H for linear and branched solutes has been established for a number of solvents. It was observed that the ratio r_H/ r_G decrease slightly as molecular weight increase[63].

Diffusion for long flexible polymer chains such as DNA can occur by a number of mechanisms depending on the ratio between effective size of solute (estimated by r_G or r_H) and matrix pore. The radius of gyration (r_G) for DNA is a function of the polymer persistence length p (=50nm for double stranded linear DNA), interbase spacing b₀ (0.34nm for DNA) and N₀ is the number of base pairs (or monomer unit number for other flexible polymers made by linking of rigid monomers).

$${r_G}^2=\frac{N_o{b}_{o}p}{3}\cdot \left(1-3\frac{p}{N_o{b}_o}+6{\left(\frac{p}{N_o{b}_o}\right)}^2-6{\left(\frac{N_o{b}_o}{p}\right)}^3\cdot \left\{1-exp\left(\frac{N_o{b}_o}{p}\right)\right\}\right)$$ (21)

The diffusion mechanism for molecules with r_G smaller than half of the mesh pore size (a) in medium of viscosity (μ), fall within the Ogston regime[51]. In this case, the hydrodynamic radius (r_H) can be used to approximate the solute dimension. In this case, the diffusion coefficient is expressed by the Zimm model:

$$D_G=\frac{0.196k_{B}T}{\mu r_H}$$ (22)

which is a close approximation to the square root of the base pair number:

$$D_G\cong N^{-0.5}$$

In this model, the pores are of fixed size and location (ie. stationary fibers). For cases with larger r_G, it becomes necessary for the polymer chain to unravel as the entire molecule ‘snakes’ through the overlapping pores in the matrix. This is the reptation or ‘tube’ model proposed by deGennes:

$$D_G=\frac{k_{B}T{a}^2}{{3N_{\kappa }}^2{\zeta }_{\kappa }{b}^2}\cong N^{-2.0}$$ (23)

where a is the pore radius, N_K is the number of Kuhn segments, or linked units in the chain, b is the Kuhn length, and ζ the frictional coefficient of the segments. This expression for D_G has a scaling exponent of N = −2.0. Pluen et al. showed that linear DNA conform to these models in agarose gel[50] (Figure 2.3). It must be noted that r_G and r_H are dimensions taken over the average of factors such as monomer distance and density, and the ratio r_H /r_G is found to vary with chain length[63].

Figure 2.3.

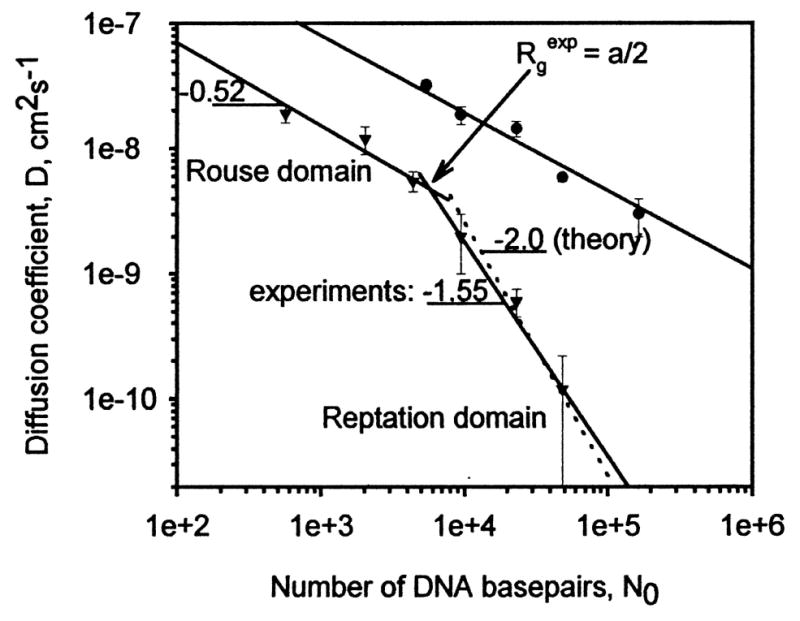
Diffusion characteristics of flexible polymer solute (DNA). The diffusion domains (Zimm-Rouse and reptation) are clearly influenced by chain length (N_o), an indicator of solute gyration radius[50].

To relate these findings to diffusion in mucus, Shen et al. measured diffusion of linear and supercoiled DNA in cervical mucus, whereas linear DNA diffusion more closely followed the Zimm-Rouse model (with a scaling factor −0.8) and that of supercoiled DNA diffusion was better described by reptation (with a scaling factor −1.3). In addition, while the absolute diffusion coefficient of supercoiled DNA was higher, it was also more susceptible to hindrance at larger MW, possibly due to steric factors. These findings suggest a different diffusion behavior for DNA in mucus compared to other medium such as agarose gel[52].

2.7 Section conclusion

Perhaps the most important parameters directly affecting diffusion through the mucus are those related to physical dimensions of the barrier (mucin fiber and pore size and density) and the chemical or biological factors within this barrier (charge, degradation, binding of solute). The latter is often not explicitly included in mathematical models.

The development of mathematical models and their application to understanding and evaluating drug delivery through mucus is an on-going process (Figure 2.4). A mathematical model is formulated based upon analysis of the diffusion process, utilizing reasonable assumptions of diffusion mechanism, geometry of the gel medium and solute, valid size or concentration range, boundary conditions, and other known or estimated parameters. Values pertaining to the system of interest (solute, medium properties) are acquired through previous studies or estimated from a similar material, and input into the model. A simulated result is returned: for example, the diffusion coefficient of a solute in a particular gel system as a function of its radius. The predictive power of the mathematical model for the specific hypothetical scenario is then tested against empirical data, where diffusion coefficient in a gel medium is obtained for solutes of various sizes. Results of several competing models can be fitted over the same data set to determine whether a single model, their combination, or some physical range in which a model is valid can be determined. The model development process can work in reverse as well, for example, where the coefficient of a general form is derived by fitting of experimental data.

Figure 2.4.

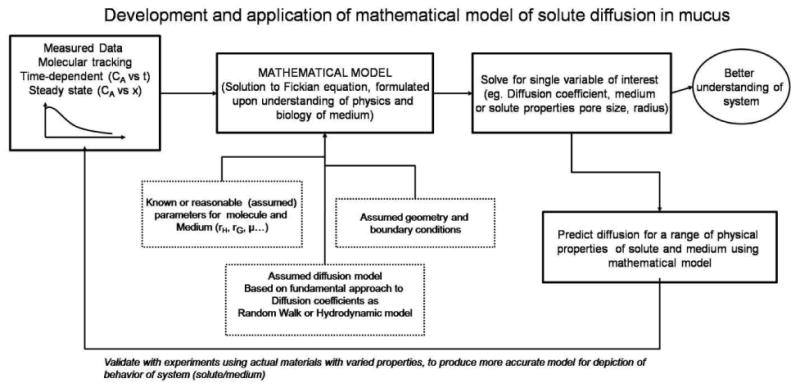
Development and application of mathematical model of solute diffusion in mucus.

One can also obtain a better estimate of physical parameters in the system with the mathematical model. For example, Saltzman et al. estimated pore diameters for fibrous gels (collagen, gelatin, and cervical mucus) by observation of diffusion behavior. In this case, by varying pore size to find the best fit to empirically obtained diffusion coefficients of various solutes (antibodies and proteins, hydraulic diameter 0.86-28nm), an estimate/average value was determined, which was confirmed by SEM imaging (Figure 1.1)[12].

Diffusion data from a variety of studies were collected by Olmsted et al. and fitted to an obstruction-scaling model developed by Amsden et al. (Figure 2.5)[23]. The general trend for this model shows a different correlation for the given range of solute hydraulic diameters than that obtained by Saltzman et al. While providing poor estimates for smaller solutes, this model can predict with reasonable accuracy the diffusion coefficients of solutes up to ∼180 nm diameter.

Figure 2.5.

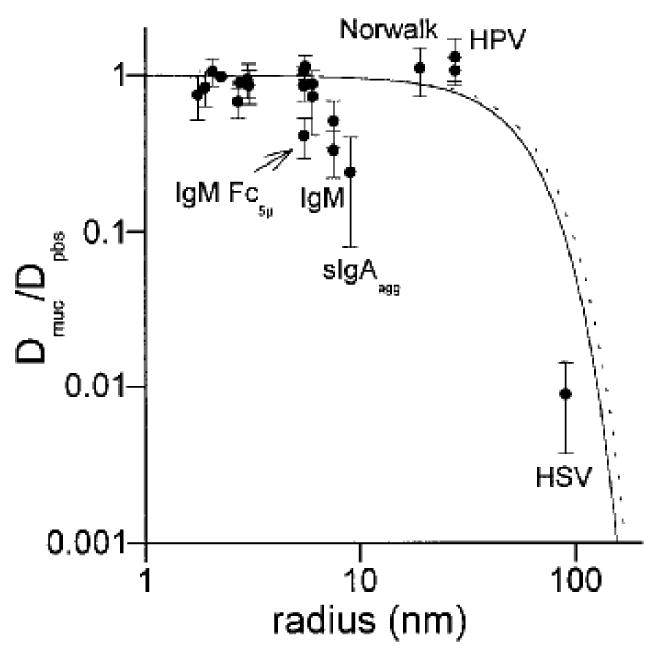
Diffusion of solutes fitted to mathematical model that predicts diffusion as a function of solute size[23].

3. Measuring diffusion coefficients: Materials, methods and their evaluations

3.1 Materials

The ideal medium for observing diffusion through mucus is a native mucus gel harvested from the particular organism or organ of interest. However, a source of fresh mucus is not always readily available; these samples may be particularly difficult to handle and store for a long period of time. The most significant complications arise from the ‘fragility’ of the native material due to lack of covalent linkage of structural components. Mechanical forces introduced by sample collection or prolonged incubation in buffers can lead to disintegration of the gel glycoprotein matrix and compromise its properties as a diffusion barrier[64]. These concerns with the native mucus gel have led to the exploration of other media as models for mucus diffusion.

Purified mucus, commercially synthesized mucin, porous membranes and non-cross linking polymer gels have been employed as alternatives to native mucus. In addition, research into cell lines secreting mucus, and recent effort to produce an ex vivo epithelium-mucus model help open new possibilities for transmucosal delivery models[65-71]. Table 3.1 provides a brief summary of relevant studies of diffusion of macromolecules through mucus or porous medium. In many respects, working in a controlled environment allows for better quantification of the macromolecular diffusion process by limiting the number of variables associated with the real system. These systems also allow for systematic alteration of the environment, to assess the impact each factor plays on mucus diffusion[13, 72, 73].

Table 3.1.

Studies of macromolecule diffusion through mucus and other porous medium

Set up	Medium	Author	Summary
Chamber	Native and purified mucus	Bhat et al.[113]	small drugs diffusion in native and purified porcine gastric mucus
		Broghton et al.[72]	200 nm fluorescent nanospheres diffusion through respiratory mucus
		Desai et al.[76, 92]	diffusion of radioactive solutes of various MW and charge
	Mucin	Norris et al.[77]	fluorescent polystyrene particles with functional groups, diameter 124-560 nm
	Polymer	Kosto et al.[101, 102]	fluorescent conjugated Ficoll diffusion in composite dextran/agarose membrane
Diffusion through gel	Native, purified, or artificial mucus	Radomsky et al.[79]	protein and antibody diffusion in capillary tube by fluoresence microscopy
		Olmsted et al.[31]	antibody virus and macro (polymeric and viral) particles fluorescent with FRP and multispeed particle tracking (MIP)
		Saltzman et al.[12]	antibody and proteins in a capillary system using FRAP and epi-fluoresence microscopy
		Shen et al.[52]	measurement of fluorescent DNA molecule by FRAP
		Park et al.[85]	holographic spectrometry of BSA migration in polyacrylamide gels
		Larhed et al.[13]	diffusion of radioactive solute in artificial mucus
		Lai et al.[30]	high-speed tracking of surface modified fluorescent polymer particles in fresh cervical mucus
		Lafitte et al.[89, 90]	diffusion of probes and PEG in non-commercial purified porcine gastric mucus with NMR
		Dawson et al.[73]	diffusion of fluorescent 100-500 nm polystyrene by rapid particle tracking
	Polymer	Amsden et al.[84]	albumin diffusion alginate gel quantitation
	Agarose	Berk et al.[81]	protein (MW 14-600kDa) and Dextran diffusion in agarose and cell mixture by FRP
		Dykstra et al.[114]	radioactive small drugs in agarose
		Gustafsson et al.[115]	ethanol by holographic laser interferon
		Pluen et al.[50]	of globular and flexible molecules by FRAP
		Gosnell et al.[51]	tracking of DNA migration by UV dye in agarose gels
	Dextran	Kosar et al.[40]	tracking diffusion of protein in Dextran solution by holographic interferometry
	Actin	Liedl et al.[82]	tracking of quantum dots in actin solution with FCS
	Commercial fibrous membrane	Gibbs et al.[88]	NMR detection of protein movement through membrane
		Bohrer et al.[100]	diffusion of flexible polymers (Dextran and Ficoll) detection by FCS
	Comparative studies of medium	Henry et al.[83]	Epi-fuorescence imaging of solute through agar, carbopol and mucus
		Johnson et al.[20, 80]	FRP analysis of protein and Ficoll
		Larhed et al.[93]	diffusion of small radioactive solutes in native and purified gastric mucus
Other studies	in vivo	Szentkuti et al.[95]	delivery of luminal dye, fluorescent Dextran and polystyrene beads 14-500 nm to rat colon
	Combined diffusion and epithelial cell uptake	Tolo et al.[116]	diffusion of radioactive125I-albumin through rabbit oral and colon mucus epithelial
		Osth et al.[94]	uptake of fluorescent ovalbumin coated starch microparticles by pig respiratory mucus and cell layer

3.2 Apparatus, experimental setup and methods of data acquisition and analysis

Diffusion studies through gel have been described extensively by Westrin[74]. A review of the general methods used in imaging solute diffusion through mucus and other biological fluids and gels have been described in detail by Saltzman et al. [39] and in a mini-review by Sanders et al.[64]. Here, we summarize briefly the methods currently used for study of diffusion through mucus, and provide some examples of their applications.

With regards to studying diffusion through a porous medium, which is a fitting description for semi-permeable membranes and gel layers, two types of experimental setups are commonly used: 1) Diffusion through chamber/reservoir and 2) Diffusion within a finite gel volume. In the first case, the molecule of interest is introduced at some concentration in a well-stirred homogeneous isotonic fluid compartment, and its transport across the diffusion limiting medium (i.e. mucus or gel slab) to the opposing compartment is observed. Determination of diffusion coefficient can be carried out in a number of ways. A finite initial concentration can be provided, and its depletion from the source and appearance in the sink is observed over time, in a pseudo-steady state mode. The solute can be provided as an “infinite” source, by maintaining a constant concentration over time, which allows measurement of steady state mass transfer. Alternatively, the lag time for solutes to appear in the second chamber can also be used to quantify diffusion coefficient[64, 74, 75]. The experimental and analytical methods required for these methods are well-developed.

For example, using a diffusion chamber (Figure 3.1), Desai et al. tracked the diffusion of radioactive-labeled solutes ranging from 126-14,4000Da through gastric mucus layer. A steady state condition to Fick's second law was assumed, where

Figure 3.1.

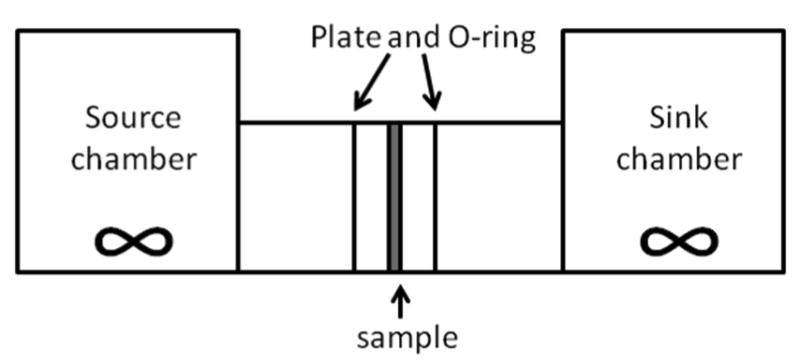
The diffusion chamber. Membrane sample is secured between two sets of plate and O-rings. The reservoir and sink is located on either side of the assembly.

$$D\frac{{\partial }^{2}C}{\partial x^2}=\frac{\partial c}{\partial t}=0$$ (24)

with a fixed concentration (c₁) at one boundary (x=0) and c₂ = 0 at x = 1. Application of boundary condition gives the following expression for diffusion coefficient:

$$D=\frac{1}{A(c_1-c_2)}\frac{\partial Q}{\partial t}$$ (25)

where A = membrane surface area, and Q is the solute mass flux, with $\frac{\partial Q}{\partial t}$ a constant at steady state (Figure 3.2). Using this setup, the authors reported a higher diffusion coefficient of low MW solutes, which correlates well to the theory of size exclusion diffusion in mucus. In addition, ionic interactions and binding proved a significant barrier to diffusion of charged molecules such as NAD, RNA and lysozyme. Table 3.2 contains the diffusion coefficient reported for these solutes[76].

Figure 3.2.

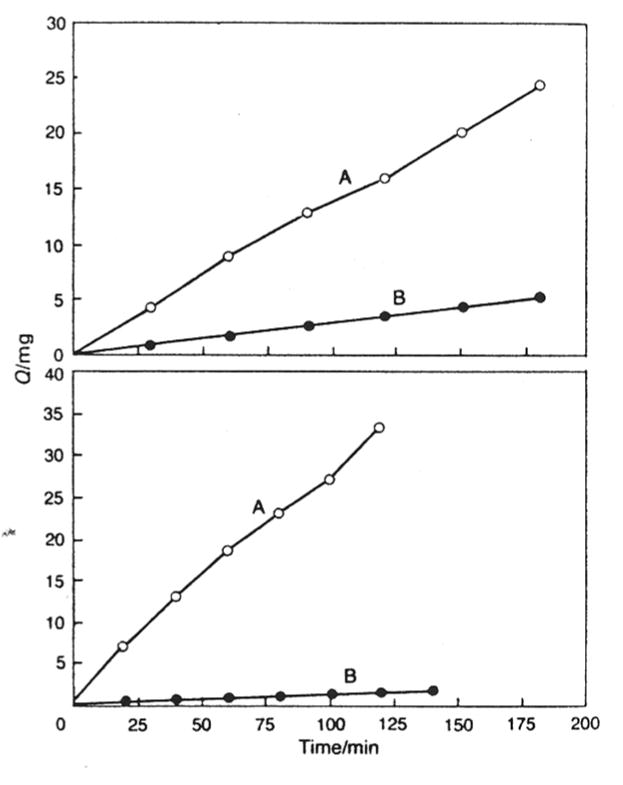
Sample data from reservoir diffusion setup shows two molecular species (A, B) of distinct diffusion properties. Data is recorded as mass vs time [76] - Reproduced by permission of the Royal Society of Chemistry.

Table 3.2.

Diffusion coefficients of solutes as measured by the reservoir setup[76].

Solute	Mw	DA,∞ (10-7 cm2/s)	DA,p (10-7 cm2/s)	DA,∞/DA,p
Phloroglucinol	126	78	24	3.3
5-Hydroxy-L-tryptophan	220	68	14	4.9
Phenolphthalein	318	83	18	4.6
5-Hydroxytryptamine	387	63	14	4.5
Phenolphthalein diphosphate	566	49	33	1.5
NAD	663	11	1.7	6.5
Glycyrrhizic acid	840	67	27	2.5
Cyanocobalamine	1355	26	10	2.6
RNA	4000-8000	160	9	17.8
Lysozyme	14400	120	4.5	26.7

Although these methods consist of a relatively simple setup and straightforward data acquisition and analysis, they suffer from significant drawbacks: 1) any heterogeneity or defects (tear, break, or uneven membrane thickness) in the sandwiched membrane caused by sample handling will be ‘averaged’ into some final concentration in the sink compartment, which may not properly reflect true molecular transport and may be unobserved; 2) the prolonged incubation time and use of a spacer as intermediate between mucus and buffer both alters the mucus/membrane conduction properties and boundary conditions; 3) any specific molecular interaction of solute with matrix cannot be determined during the experiment, since there is no direct observation of the barrier itself; 4) leakage of the gel into solution (such as the case reported by Norris et al.[77]) are possible sources of errors[64].

As an alternative, diffusion of labeled solutes in mucus gel can be observed directly. Due to the size scale differences between the solute and thickness of the mucus layer, the solute is miniscule compared to the diffusion medium. The diffusion process, therefore, is depicted by some as a one dimensional transport in a semi-infinite medium, where the boundary conditions are shown in Figure 3.3[78]. Hence, in addition to the concentration vs time data produced by the reservoir setup, direct observation of diffusion in gels also yields a concentration profile of solute vs distance at a specific time point. There are several experimental systems for visualizing and modeling solute diffusion in this situation.

Figure 3.3.

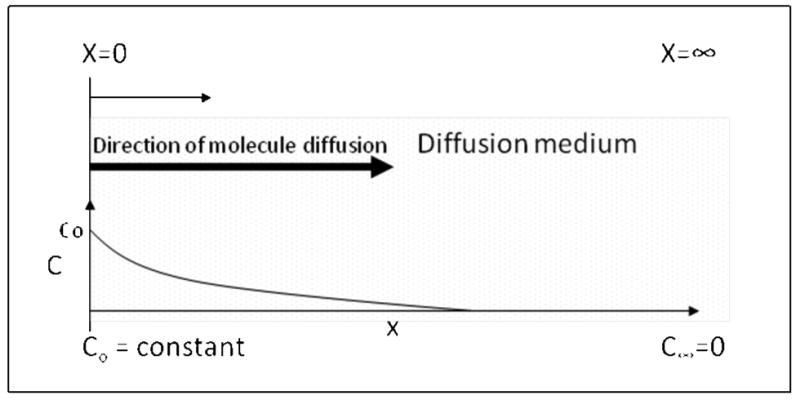
Semi-infinite model of diffusion and boundary conditions.

Radomsky et al. directly measured the diffusion of proteins and antibodies in mucus-filled capillary tubes[79]. The capillary tube was filled at one end with mucus and allowed to interface with the solute, which was provided at some concentration in a buffered solution at the other end of the tube. Imaging of solute movement from the interface into the gel was done with the entire apparatus kept immobile during observation period (Figure 3.4). The concentration profile of solute was then plotted as a function of time (C vs t) at some fixed distance from interface (x=0) or as a function of distance (C vs x) at some fixed time t. Figure 3.5. As expected, solute concentration profiles over time indicate higher concentration further away from the source at longer incubation times; this pattern was observed for both diffusion in phosphate buffered saline and mucus gel.

Figure 3.4.

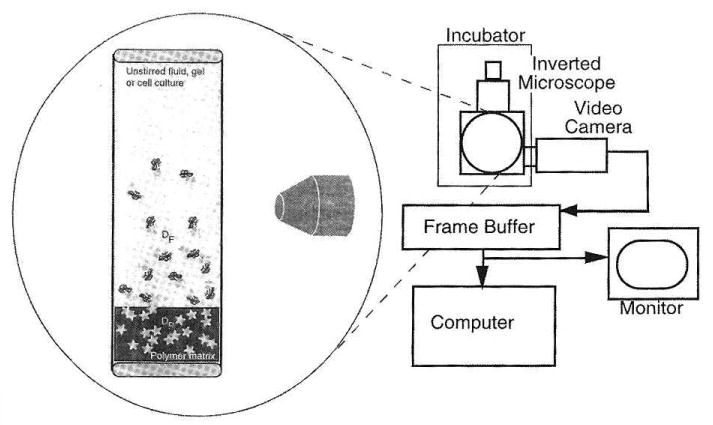
The capillary tube setup for diffusion study, figure from [39] pp. 51, adapted from [79]

Figure 3.5a-b.

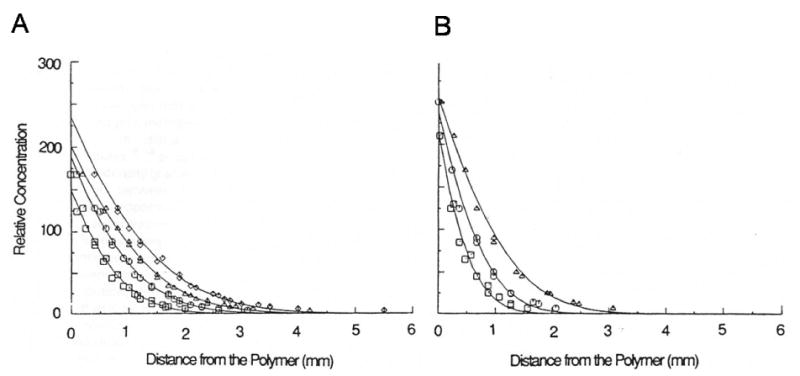
Concentration profile of BSA diffusion in water (A) and cervical mucus (B) at fixed times (1.1hr, 1.9hr, and 3.7hr) from source[79].

Fluorescence recovery after photobleaching (FRAP) can also be used to observe solute diffusion within a smaller volume, though a similar modeling concept is employed[12, 20, 50, 52, 80-82].

These direct measurements offer advantage over the reservoir/chamber model as it allows analysis of a smaller volume, which eliminates issues with membrane average, and also enables measurement over shorter time periods (on order of minutes as opposed to hours in the former)[83]. In addition, observation of solute interactions with the fiber matrix can be done with microscope imaging techniques. Another method to assess mobility of fluorescent solute is by highspeed particle tracking. The average displacement of solutes in the gel over time can be fitted to a random walk model (equation (5), section 2) to determine the effective diffusion coefficient[30, 31, 73]. Rapid acquisition of images at different focal planes in a gel volume makes possible volumetric tracking of single or multiple solutes. However, this technique can suffer from artifacts: invasive methods of introducing particles into fiber matrix could alter the structure and viscosity of the native polymer structure and compromise the accuracy of measurements[64].

3.3 Solute tracking methods

Empirical data for the diffusion of macromolecules through polymer gel can be achieved by several methods. A straightforward approach to obtain concentration profile in a gel slab is to extract solute from sectioned the gel and quantify solute presence by weight[84]. Other non-invasive methods like light or magnetic resonance spectroscopy takes advantage of the existing physical and chemical properties of the molecule, such as size, absorbance, and reactivity to magnetic fields. Techniques with higher sensitivity such as radioactive labeling and fluorescence microscopy require some modifications to the structure of the molecule itself. While providing better signal, covalent modifications may change the molecule's native diffusion rate.

3.3.1 Spectroscopy and light scattering

Spectroscopy (absorbance, interference, and dynamic light scattering) techniques that takes advantage of the natural characteristics of the molecule can also be used to measure diffusion coefficient. Molecules such as proteins have been tracked by holographic interferometry[40, 85], and light scattering[41, 86]. Similarly, this method can be used to measure DNA diffusion in solution[87]. While able to observe diffusion at a smaller length and time-scale, these techniques are subject to high interference and scattering of signals by the thick irregular fibers in the gel.

NMR spectroscopy has also been used for measuring solute movement in gel solutions. Using pulse-field NMR, Gibbs et al. was able to confirm concentration-dependent diffusion of 19F-Ovalbumin through both solution and porous media[88]. Lafitte et al. recently showed diffusion of ethanol and glucose through mucin gel, in a setup similar to top-down capillary tube one dimensional diffusion model[89, 90] This technology is limited, however, to solute or tracers with strong paramagnetic groups.

3.3.2 Radioactive labeling

The use of radioactive tracers to track molecule movement through porous media have been reported[91-93]. This method has inherent advantages in preservation of the chemical and physical properties of the molecule, and high sensitivity. However, it is difficult to resolve changes in diffusion rates at small time intervals. Thus, the process is not desirable due to the time-consuming experiment setup, image/data acquisition and image development[39].

3.3.3 Fluorescence labeling

Fluorescence-labeled probes have been used extensively, primarily because of the availability and wide selection of substrates, and the sensitivity of detection. Multiplexed analysis of differentially-labeled solutes can also reveal their interactions in the diffusion medium under fluorescence imaging. The application of fluorescence imaging is illustrated in a number of studies including: confocal microscopy to visualize uptake through mucus within membranes and cell layers [94], in vivo [95] and with epi-fluorescent microscope for tracking diffusion in gels [12, 30, 72, 73, 79, 83]

The development of multi-photon imaging has helped increase the sensitivity and resolution for fluorescent imaging techniques[96, 97]. Multi-photon imaging permits the focusing of excitation in a smaller volume, and reduces photo-damage on the sample. It has also enabled rapid and sensitive diffusion tracking with methods such as photo-bleaching recovery (FRAP), where diffusion coefficients can be quantified by the time for molecules to fill in a volume that has been bleached out (does not fluoresce)[98, 99].

Fluorescence correlation spectroscopy (FCS)[82, 100] and fluorescence recovery after photobleaching (FRAP)[12, 20, 31, 50, 52, 80, 101, 102] have been employed to visualize proteins and peptides, viruses, nano and micro polymeric particles, and flexible polymers such as Ficoll, Dextran and DNA. Saltzman et al. reported a study of antibody diffusion in human cervical mucus using epi-fluorescent imaging and FRAP. The diffusion coefficients for the solutes (fluorescein, antibodies, and albumin) acquired using both methods from a capillary tube setup were found to be similar, validating the reliability of both techniques in estimating particle diffusion coefficient[12].

Similarly, Olmsted et al. observed diffusion of FITC-labeled antibodies, virus-like particles, viruses (HSV), and polystyrene microspheres through cervical mucus using both FRAP and multiple particle tracking (MIP). MIP was used specifically for HSV samples due to low and non-uniform signals that could not be analyzed by FRAP. HSV was mounted on glass slides for particle tracking, and other samples were loaded in capillary tubes and subjected to FRAP analysis. The authors reported fast diffusion (fluorescence recovery) of antibodies and virus-like particles (38-55 nm), which was comparable to their diffusion coefficient in water, and significantly hindered diffusion of HSV (180 nm) and polystyrene microspheres (59-1000 nm), which adhered strongly to mucin fibers in mucus. An obstruction model was found to fit the empirical data[31]. This study illustrates the necessity in developing versatile imaging techniques and their ability to compensate for one another, where MIP was implemented on HSV samples that could not be analyzed by FRAP.

Labeling of molecules with fluorescent dye is an invasive technique that could affect solubility. However, titrated labeling or use of fewer dye molecules of high quantum yield can be explored to minimize this effect. Other limitations to light-dependent methods (spectrometry or laser excitation) are high interference from medium and scattering of light, and photo-damage of solute or diffusion medium caused by the high laser excitation energy. The issue of signal/noise can be remedied/alleviated, as reported by Berk et al., where a combination of FRAP and post-processing resulted in a better image for estimation of diffusion coefficient[81]. Also, the volume of laser bleaching is in actuality not a cylinder but oblong/oval shaped. This discrepancy with FRAP, which in theory relies on one dimensional diffusion model of a perfect cylinder diffusion volume, is a source of experiment-induced error for measurement of diffusion coefficient[50].

3.4 Some considerations in mucus and gel diffusion studies

Even with the progress reviewed above, we still do not understand the relationship between each component of the mucus gel and rates of diffusion. Theoretical models, when validated by comparison with empirical data, do provide correlations between structure and transport rates that can be exploited to enhance drug delivery. But there are many things that we do not understand well. The presence of some polymers will change the three dimensional structure of mucus[103, 104]. The mucin mesh/filtering effect on particles of various size and surface coating has continued to produce interesting findings, which are not easily explainable with current models [12, 30, 31]. Hence, the need for experimental setups and data acquisition techniques that are highly controlled and least invasive is imperative to correlate theoretical data, to develop models that more accurately reflect the biological reality.

A more controlled system can be realized with the use of purified or synthesized mucin fibers and realistic in vitro experiments by development of mucus-secreting cell-lines[65, 67, 93, 105]. Efforts to model an entire mucosa layer have been proposed, which open an exciting venue in mucosal diffusion studies[106, 107]. The degree of control over the system and isolation parameters provided by artificial models can provide a better understanding of in vivo diffusion. In an early study, Szenkuti et al. showed uptake of dyes, sugars, and polymer particles by in vivo deposition in the rat distal colon[95]. A single model and experimental system cannot provide a comprehensive picture of all the relevant driving forces in diffusion through mucus. This endeavor, however, can be realized by the combination of various models. Hopefully, the techniques will ultimately provide better predictive values for permeability of the solute of interest.

Spectroscopy, radioactive and fluorescent tracking methods have been used to detect solute diffusion through gel. Each technique has advantages and disadvantages, where the limitations are due to the availability of detectable substrate, requirement in setup or apparatus, and/or limit of detection (in both time and sensitivity). The ideal imaging technique to observe solute diffusion within gel is sensitive, allows high resolution of detection, and fast data acquisition. In addition, minimal damage to the diffusion medium or solute must be sought to ensure accuracy of results.

4. Conclusion

The mucus membrane has long been identified as a critical barrier in drug delivery through the respiratory, gastrointestinal, and reproductive tracts. Numerous studies on the properties of mucus have been carried out to identify the major constituents as well as relevant factors that influence solute movement within this barrier. Its structural and chemical components have been well characterized by a several early studies[5, 7, 14, 15, 108-111]. Building upon this understanding, several working models of solute/particle diffusion in fibrous gel mediums such as mucus have been proposed for globular and chain-like solutes. Mathematical models of solute diffusion through mucus gel are based on several competing theories: hindered diffusion governed by geometry or by hydrodynamic effects[16, 17, 24, 25, 112].

Advances in imaging technologies such as spectroscopy, fluorescent imaging, NMR, FRAP, particle tracking and methods in fluorescent imaging analysis enable better empirical observation of diffusion. This empirical data is used for the development, refinement and validation of mathematical models. Progress in mathematical models and empirical data acquisition techniques occurs in synergy. In essence, one drives another: A more comprehensive mathematical model is needed to explain observed data; at the same time, a good experimental technique is needed to accurately produce empirical data for validation of the model.

Further study is needed to arrive at more detailed mathematical expressions for the influence of solute-medium specific properties, such as ligand-specific binding, ionic interactions, or response to environment pH. In addition to enhanced mucus permeability, properties for better solute uptake by epithelial cells may be explored. Often, the properties that make a solute more adherent to cell membranes would also cause it to be entrapped in the mucus layer, thus preventing it from reaching the underlying epithelial cell layer as the mucus gel sloughs off. The development of mucus-producing cell lines, and experimental methods for ex vivo and in vivo diffusion studies, are valuable tools to help address this issue.

A comprehensive and accurate mathematical description of molecular diffusion through mucus is an important tool in evaluation and development of mucosally-administered drugs. A better understanding of the biological system, appropriate mathematical representation of relevant properties and validation of mathematical models using accurate empirical methods are all necessary to attain this goal. Better modeling of diffusion in mucus can lead to more convenient and cost-effective methods to evaluate the barriers that obstruct transport of existing drugs, to predict effectiveness for new drugs, and to design drugs with predictable diffusion properties in mucus.