Automated 5-D Analysis of Cell Migration and Interaction in the Thymic Cortex from Time-Lapse Sequences of 3-D Multi-channel Multi-photon Images

Abstract

This paper presents automated methods to quantify dynamic phenomena such as cell-cell interactions and cell migration patterns from time-lapse series of multi-channel three-dimensional image stacks of living specimens. Various 5-dimensional (x, y, z, t, λ) images containing dendritic cells (DC), and T-cells or thymocytes in the developing mouse thymic cortex and lymph node were acquired by two-photon laser scanning microscopy (TPLSM). The cells were delineated automatically using a mean-shift clustering algorithm. This enables morphological measurements to be computed. A robust multiple-hypothesis tracking algorithm was used to track thymocytes (the DC were stationary). The tracking data enables dynamic measurements to be computed, including migratory patterns of thymocytes, and duration of thymocyte-DC contacts. Software was developed for efficient inspection, corrective editing, and validation of the automated analysis results. Our software-generated results agreed with manually generated measurements to within 8%.

Introduction

Advances in multi-photon time-lapse microscopy and fluorescent protein (FP) technology have ushered in a new era of biological research in which dynamic processes in living specimens can be imaged over extended durations in their three-dimensional (3-D) spatial and temporal context (Cahalan et al., 2002, Robey & Boussso 2003, Miller et al., 2003, Lichtman & Conchello, 2005, Shaner et al., 2005). Using multi-spectral imaging and multiple labeling, it is possible to image multiple structures and cell types in a manner that preserves their relative spatial and temporal relationships. The resulting images are 5-dimensional (5–D), spanning 3-D space (x, y, z), time(t), and spectrum (λ). These image datasets have obvious potential to provide qualitative and quantitative insights, if only they can be analyzed with sufficient accuracy and automation.

For example, quantitative studies of cell motility and interaction patterns is one of the essential foundations for understanding cell behaviors under specific stimuli, either in vitro or in vivo (Bousso & Robey, 2003&2004). Recent studies have provided evidence that the migration patterns of T cells and their interactions with DCs are regulated by T-cell repertoire (TCR) selection events (Bousso & Robey, 2003, Miller et al., 2004, Witt et al, 2005b, Ladi et al., 2008). In these prior studies, cell-cell associations were quantified by tedious and time-consuming manual analysis aided by commercial software for cell tracking. Manual measurements are limited by subjective variability, and human limitations on visualizing multi-dimensional data, especially when image quality is suboptimal. Currently available commercial tools allow excellent visualization, interactive annotation and measurement capabilities, but are lacking in terms of automated analysis. There is a compelling need for objective and automated software tools that are sufficiently robust and adaptive to cope with morphological diversity of cells, dynamic changes in their morphologies, and complex movement/interaction patterns.

From an automated image analysis standpoint, the advent of 5-D imaging and systems biology has created the need for novel types of image-based measurements. Beyond traditional morphological measurements, there is now a need to quantify static/dynamic relationships among two or more structural or functional entities (Roysam et al., 2006). To address this need, we propose associative image analysis methods to quantify spatial associations, temporal associations, and spatio-temporal associations (interaction dynamics), building upon our prior work in tracking and lineage analysis (Al-Kofahi et al., 2006a&b, Roussel et al., 2007).

Recognizing that even the best-available automated image analysis systems have a non-zero (albeit modest) error rate. With this in mind, there is a need for efficient and scalable methods to ensure that the automated measurements are valid and sufficiently accurate for a given study. For this, we developed pattern analysis algorithms to enable efficient visual inspection, and corrective editing of automated image analysis errors, resulting in a set of trustworthy measurements. In addition, records (logs) of corrective editing operations can be used to assess the performance of the automated algorithms, and to plan improvements. These methods extend our prior development of edit-based protocols for fixed specimens (Lin et al., 2007, Tyrrell et al., 2007).

Specimen Preparation and Imaging

To examine the correlation of T-cell receptor (TCR) repertoire selection with increased thymocyte-DC contacts, donor bone marrow from GFP transgenic mice was injected into CD11c-YFP neonatal hosts (Ladi et al., 2008). Using this system to generate hematopoietic chimeras, we evaluated three experimental conditions: positive selection of P14 expressing thymocytes on the B6 background (P14 → B6), negative selection on the DBA background P14 → (DBA × B6), and wild-type thymocytes bearing a diverse TCR repertoire (wt → B6).

Intact thymic lobes from these chimeric mice at 4 – 6 weeks of age were imaged by two-photon two-channel laser-scanning microscopy (TPLSM) while being perfused with warmed, oxygenated media as described previously (Witt et al., 2005a&b). Two-photon excitation was achieved using a Spectra-Physics MaiTai laser tuned to 920nm, and GFP and YFP emission light was separated using a 515nm dichroic mirror and collected using two non-descanned detectors. A Zeiss LSM 510 META/NLO Axioplan Microscope with a Spectra Physics MaiTai Laser was used for these experiments. GFP-labeled donor thymocytes are dominant in the green channel, and YFP-tagged thymic DCs appear in the red channel. Three-dimensional image stacks (164 × 164 × 40 μm) were scanned at the thymic cortex every 37 seconds, generating time series that last 20 – 40 minutes. Figure 1 (A–C) shows sample images of wild type cells, and those undergoing (P14 → B6) selection and P14 → (DBA × B6) selection. The 3-D images at each time point have dimensions 256×256×21 with a dynamic range of 8 bits/voxel. These 3-D datasets are displayed as 2-D axial maximum-intensity projections.

Figure 1.

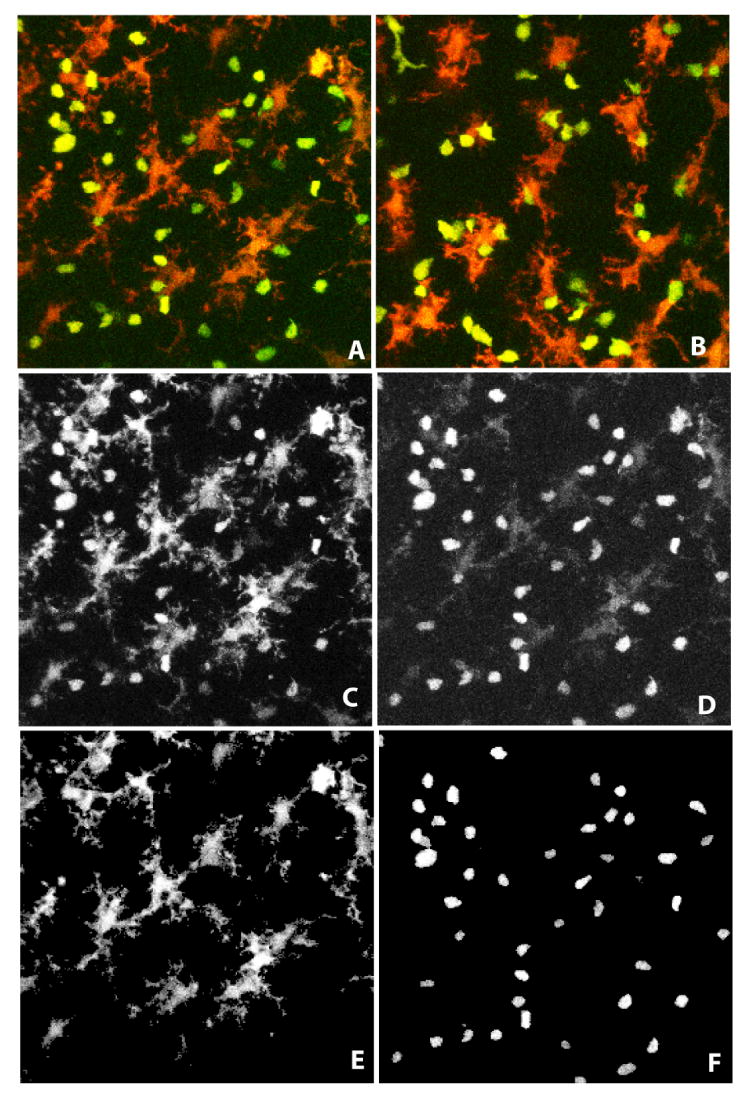
(A, B) Maximum intensity projections of sample 3-D image frames showing GFP-labeled thymocytes (green) and YFP-labeled dendritic cells (red) in thymic lobes for wild-type cells (A), and thymocytes expressing P14 TCR transgene (B), respectively. (C, D) Illustrating the spectral overlap for a sample optical slice from the 3-D image in panel A. The YFP-tagged DCs are dominant in the red channel, while GFP-tagged thymocytes are prominent in the green channel. (E,F) Results of computational unmixing that eliminates the spectral overlap.

Image Analysis Methods

The fluorescence emission spectra of GFP and YFP overlap. One approach to overcoming spectral overlap is spectral fingerprint based unmixing (e.g., Dickinson et al., 2001; Zimmerman 2005; Walter 2004). This method assumes that the overall emission spectrum recorded at each voxel is a linear mixture of the emission spectra (spectral fingerprints) contributed by each fluorophore. The linear unmixing software computes the relative proportions of the mixture components. This approach was not matched to our instrumentation since it requires the emission spectra to be sampled much more finely (typ. 20-50 spectral bands). With these limitations in mind, we adopted a processing strategy based on two observations: (i) thymocytes express higher signal in GFP (green) than in YFP (red) channel; (ii) DC bodies have higher intensity in YFP than the GFP channel.

For describing our unmixing procedure, we denote a voxel in the 5-D image data as I(r,t) where r = (x, y, z) is the vector of spatial coordinates, and t is the temporal sampling index (an integer indicating the frame number, so (t+1) refers to the next frame). We use a subscript to indicate the spectral channel, so voxels in the GFP and YFP channels are denoted I_GFP(r,t), and I_YFP(r,t), respectively. To achieve some robustness to imaging noise (mainly dark noise in the PMTs), we average voxel intensities over a rectangular neighborhood of each voxel denoted N_GFP(r,t), or N_YFP(r,t), as appropriate. The size of the neighborhood is unequal along the axes to compensate for the image anisotropy. In our experiments, it is typically 5 × 5 × 3 voxels, covering a region of 3.2μm×3.2μm×4μm. Larger neighborhood sizes provide greater robustness to noise at the expense of blurring. Our method is not overly sensitive to the size of the neighborhood that is chosen. We computed the average fluorescence intensity values, denoted N̅_GFP(r,t), and N̅_YFP(r,t), respectively, over each neighborhood. We next computed threshold values (intensity cutoffs) denoted (θ_GFP(t),θ_YFP(t)) individually for the GFP and YFP channels, using the widely-used Otsu's automatic threshold selection algorithm (Otsu, 1979). This method has the advantage of compensating for temporal variations in fluorescence intensity.

A direct application of these thresholds to each channel will result in false classifications due to spectral overlap (Figure 1 (C, D)). With this in mind, we use the following alternative strategy. The user specifies an empirical weighting factor α that depends upon the experimental setup, and adjusted α until a satisfactory delineation of thymocytes and dendritic cells is attained. For our work, we used a value of 1.3 for all data sets. Major changes to the imaging system or protocols require an empirical re-estimation of this value. Fully automated methods to select this parameter remain a subject for future research. We first consider voxels for which N̅_GFP(r,t)×α > N̅_YFP(r,t). For these voxels, we examine if N̅_GFP(r,t) > θ_GFP(t). These voxels are labeled as thymocyte voxels, and the rest are considered background voxels. For the remaining unlabeled voxels after the first step, we next examine voxels for which N̅_YFP(r,t) > θ_YFP(t). These are labeled as DC voxels, and the rest are considered background voxels. The above sequential procedure implies that the second segmentation step depends on the results from the first step. This procedure precludes the possibility of two labels per voxel. The results of the above sequence of steps are illustrated in Figure 2.

Figure 2.

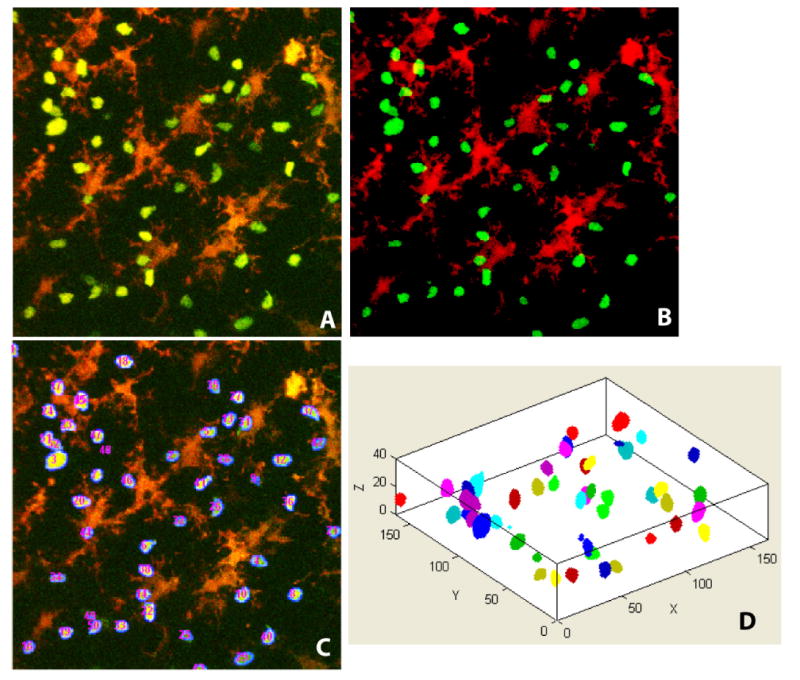
(A) Sample image shown as a 2-D maximum-intensity projection of a full 3-D stack at a randomly chosen sampling time; (B) Results of detecting thymocytes and dendritic cell voxels – thymocyte voxels are displayed in green and DC voxels are displayed in red. Partially imaged cells appear as fragments. (C) Numbered voxel clusters corresponding to thymocytes. (D) An oblique 3-D view of the segmented thymocytes for the same image stack.

Cell Identification

The next step in the processing is to recognize groups of thymocyte voxels representing individual cells in the thymocyte image channel T(t). For this, we treat each cell as a cluster of densely located voxels associated with an individual cell. To delineate these clusters, we used the mean-shift clustering algorithm (Comaniciu et al., 2001 & 2002). This non-parametric method does not require prior knowledge of the number of clusters, and does not constrain the shape of the clusters. Importantly, it requires the fewest adjustable parameters – just the choice of a kernel function. For this work, we adopted a radially symmetric Gaussian kernel function with a width parameter h, and a window Ω. Our mean-shift cell identification algorithm is iterative. First, (at iteration j = 1) the center of each kernel window Ω is initialized to individual thymocyte voxels, i.e., $X_i^1={\text{r}}_i$. At subsequent iterations (j = 2,3,…), the kernel window centers are updated by the following gradient based formula (Fukunaga & Hostetler, 1975):

$$X_i^{j+1}=\frac{\text{∑}_{k\in \Omega }{\text{r}}_{k}exp\left({\Vert \frac{{\text{r}}_i-{\text{r}}_k}{h}\Vert }^2\right)}{\text{∑}_{k\in \Omega }exp\left({\Vert \frac{{\text{r}}_i-{\text{r}}_k}{h}\Vert }^2\right)}.$$

This is repeated until the mean-shift vector defined as m_i,j+1 = X_i,j+1 − X_i,j, converges to zero (to within a chosen tolerance) at a stationary point denoted X̂_i. Then, voxels whose convergence points X̂_i are closer than the spatial bandwidth parameter h are combined into clusters denoted {C₁,C₂,…C_m}. Each voxel is assigned a label corresponding to the cluster number to which it belongs (Cheng, 1995).

In our experiments, the morphological attributes of most thymocytes, such as size and shape, change negligibly over time. This observation allows us to use a fixed bandwidth parameter h for each image frame throughout the time-lapse series. The value of h is selected empirically keeping in mind the amount of variation in cell morphologies among different image sequences. This fixed bandwidth selection method is easily applied, but can yield two types of segmentation errors: (i) over-segmentation caused by an overly tight kernel bandwidth, decomposing a cell body into many fragments; or (ii) under-segmentation caused by a large value of h, grouping closely-localized cells together. To achieve a tradeoff, we consider the following facts: (i) the majority of cells are well separated in 3-D space; (ii) a narrow gap or bottleneck exists between adjacent or touching cells in most cases. Furthermore, we note that it is computationally cheaper to split under-segmented clusters compared to merging fragments to constitute a whole cell. With these issues in mind, we simply selected a relatively loose bandwidth value that was sufficient to eliminate most over-segmentation errors, rather than exhaustively varying the kernel bandwidth. This relaxation of kernel bandwidth produced a number of falsely merged clusters, that are easily refined by a post-processing step. Automated methods to select adaptive bandwidth value remain a subject for our future study. The final segmented images are saved as files, and displayed using a color code (one for each cell), as illustrated in Figure 2.

For each segmented thymocyte, we compute a vector of geometric features that can be used to discriminate cells for the purpose of modeling cellular migration patterns and tracking cells across successive image frames. Specifically, we compute the centroid location (x̅_c(t),y̅_c(t),z̅_c(t)), volume v_c(t), and the radius r_c(t) of each cluster c (each cluster corresponds to a cell). For a cell of volume v_c(t) voxels, the radius is approximated by the formula $r_c(t)={\left(\frac{3}{4\pi }{v}_c(t)\right)}^{\frac{1}{3}}$. These attributes are collected into a feature vector for cell c at frame t, denoted ${\text{f}}_c^t=[{\overline{x}}_c(t),{\overline{y}}_c(t),{\overline{z}}_c(t),v_c(t),r_c(t)]$.

Cell Tracking Algorithm

Common nearest-neighbor tracking algorithms are adequate for tracking multiple targets that are sparsely distributed (Bao et al., 2006; Hamzic et al., 2008). However, their performance degrades greatly when the targets are crowded, and when there are ambiguities (Han et al., 2004; Polat et al., 2002; Meijering et al., 2006). In addition, such methods lack the ability to naturally handle cells that are entering or exiting the field of view. Active contour model based methods (Zimmer et al., 2002; Ray et al., 2002; Dormann et al., 2002, Dufour et al., 2005) provide efficient segmentation and tracking by using outputs resulted from frame t to initialize the process at frame (t+1), and are capable of coping with topology changes (e.g. split or merge). But they still present drawbacks in handling densely-spaced objects with strong interactions due to tracking many single objects independently (Zimmer et al., 2002). Mean-shift based algorithms (Comaniciu et al., 2003; Collins 2003; Debeir et al., 2005) are problematic for similar reasons, and usually fail to explicitly give precise object contours. Commercial software, such as Imaris (Bitplane), identify and track touching cells in 3-D space by placing synthetic spots at voxels of maximum intensity (Witt et al., 2005a). But the diameter of the spot is manually tuned by the user, and the ambiguity of object boundaries still remains. The following paragraphs describe a robust multiple hypothesis tracking algorithm for cell tracking that was used for this study.

Successful tracking requires good modeling of cell behaviors (Al-Kofahi et al., 2007a&b; Roussel et al., 2007). From visual inspection, the vast majority (> 95%) of dendritic cells observed in this study are host-derived, non-motile DCs. The bulky bodies of host-derived DCs are consistently observed to remain in their original positions throughout the time series, and occasionally exhibit minor movements of dendrites (Ladi et al., 2008). Generally, they are a more stationary population compared with thymocytes that engage in rapid movements, frequent changes of trajectory direction, and/or long-term migrations. With this in mind, a cell motility model is developed only for motile thymocytes.

A thymocyte labeled i in image I(r,t), with feature vector f_i(t) that moves to become the thymocyte labeled j in the subsequent image I(r,t+1) with feature vector f_j(t+1) is modeled by a multivariate Gaussian distribution, as follows (Al-Kofahi et al., 2006a):

$$P_{\text{motility}}({\text{f}}_i^t,f_j^{t+1})=\frac{1}{\sqrt{{(2\pi )}^N|\sum |}}exp\left\{-\frac{1}{2}{(d_{i,j}^{t,t+1}-\mu )}^T{\sum }^{-1}(d_{i,j}^{t,t+1}-\mu )\right\},$$ (1)

where N is the dimension of the feature vector, and $d_{i,j}^{t,t+1}=\left|{\text{f}}_i^t-f_j^{t+1}\right|$. The sample mean μ and covariance matrix Σ of the difference vector $d_{i,j}^{t,t+1}$ are learned from training examples. For the training set, we collect the first K (typically 10% of the sequence) image frames from the sequence, and inspect them to make sure they exhibit the typical motion patterns in this time series. Cells in the training sequence were first segmented by the automated methods described above, and tracked using a nearest-neighbor criterion under two assumptions: (i) cells move smoothly, and their motion (speed, direction) does not change abruptly; and (ii) cell appearance (volume, intensity, shape) does not change abruptly. After visually inspecting and editing the few false matches, we computed the mean and covariance (μ,Σ) for the statistical model of cell motion expressed by equation (1).

In designing the tracking algorithm, we also consider three possible behaviors of thymocytes. A cell can either: (1) move from frame t to frame (t+1) (migration); (2) leave the field of view (disappearance); or (3) enter the field of view (appearance). The three events correspond to distinct kinds of matches in the tracking procedure: one to one, one to none, or none to one. To accommodate these situations, we consider multiple potential correspondences for a cell i in image I(r,t) in image I(r,t+1) with comparably high values of $P_{\text{motility}}({\text{f}}_i^t,f_j^{t+1})$, rather than a single hypothesis with the maximum likelihood. To prevent excessive inclusion of hypotheses, we collected k matching candidates with highest scores for each cell i^t and filtered them via an empirical threshold. We also relaxed the constraint that every cell in I(r,t) must have a correspondence in I(r,t+1), and vice versa, accounting for valid appearance/disappearance events as well as segmentation errors, such as false detection of non-existing cells, or failure to detect existing cells.

Our multiple hypothesis tracking algorithm starts by hypothesizing a set of matches denoted $h_{i,j}^{t,t+1}$ between cells i and j identified in images I(r,t) and I(r,t+1), respectively. Each hypothesis is weighted by the likelihood score $P_{\text{motility}}({\text{f}}_i^t,f_j^{t+1})$. For each cell j, we select a subset of k matches with the highest likelihood scores (typ. k = 5). At this point, we simply identify the cell-cell matches for which the sum of the likelihood scores is maximum, subject to the following biologically rooted constraints: (i) a cell in image I(r,t) has at most one correspondence in I(r,t+1); (ii) a cell in image I(r,t+1) has no more than one correspondence in I(r,t). The optimal set of hypotheses is identified by the tracking algorithm described in (Al-Kofahi et al., 2006a&b, Roussel et al., 2007). Any remaining segmentation and tracking failures are corrected via an edit-based post-processing phase described next. Figure 3 shows a sample tracking results for wild-type thymocytes prior to any corrective editing. Tracked thymocytes are displayed with the same color and number. Panel D shows the cell migration paths as a set of red lines, with the cell's initial position displayed in green.

Figure 3.

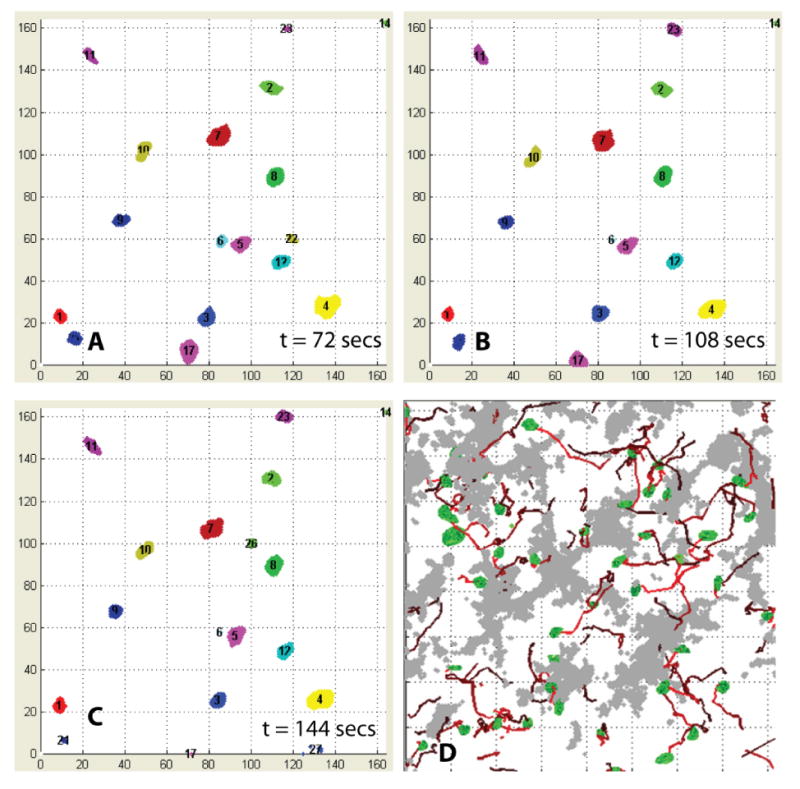
(A – C) Sample cell tracking results for wild-type thymocytes at three successive time points: each tracked thymocyte is numbered, and displayed in consistent colors. (D) Sample display of cell migration paths (red lines) for wild-type thymocytes over 40 time points. Thymocytes segmented in the first frame are displayed in green. The colored paths represent trajectories of migrating thymocytes, coded to depict their temporal ordering (initial points are shown in bright red and later points in dark red).

Edit-based Validation and Performance Assessment

The task of ensuring the validity of automated segmentation and tracking results, and assessing their performance is potentially cumbersome, given the sheer volume and complexity of the 5-D image data. Exhaustive comparison of automatically generated measurements against manual analysis is not only impractical, but also unnecessary, since the automated methods usually have a high success rate with only occasional failures. With this in mind, we developed computer-assisted method (Figure 4) for efficiently inspecting the automated results, and making corrective edits where necessary. Briefly, we use statistical tools to highlight potential errors to the human operator, and identify the nature of the error to aid the user.

Figure 4.

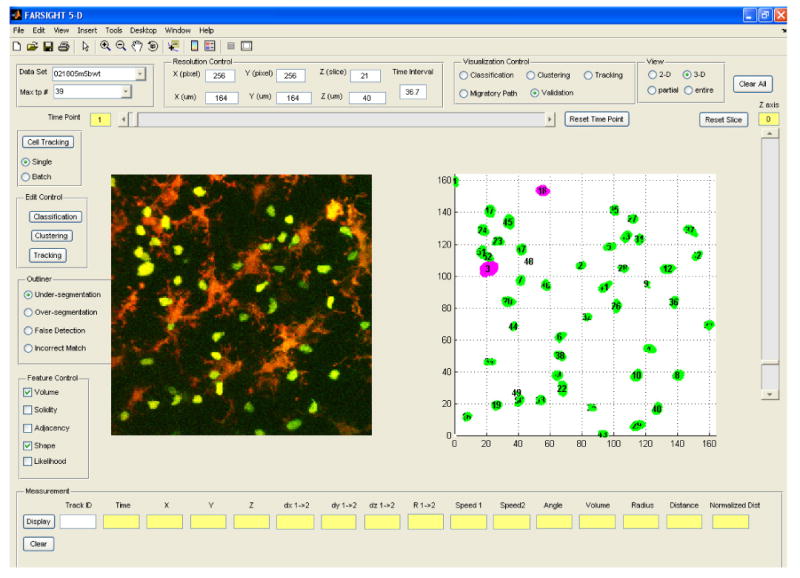
Screen view of the graphical tool for computer-assisted inspection and editing of automated analysis results. The operator can choose features for detecting each type of outliers, and the outliers are displayed in pink, while normal cells are displayed in green. The cells highlighted in pink are statistical outliers that are proposed by the software as candidates for closer inspection and editing.

Segmentation Errors

Four types of segmentation errors are possible: under-segmentation, over-segmentation, false negatives, and false positives. Efficient detection of segmentation errors requires a method to highlight potential errors automatically. For this, we build a multivariate statistical model describing correctly segmented cells from a training set specified by the operator. This model is built using morphological features of the cells. Cells whose features deviate significantly from this model, i.e., statistical outliers, are highlighted for the user to inspect.

The volume of cells is an important indicator of under segmentation and false detection. In the under-segmentation case, multiple cells are falsely grouped as one cluster, so the measured volume v_i deviates far from the distribution mean toward the high end. Most falsely detected cells have very small volumes. With these considerations in mind, we model the volumes of cells as follows:

$$f(v_i)=\frac{1}{\sqrt{2\pi \cdot {\sigma }_v^2}}exp\left\{-\frac{1}{2}{\left(\frac{v_i-{\mu }_v}{{\sigma }_v}\right)}^2\right\}.$$ (2)

Under this model, under-segmented clusters and falsely detected cells are outliers, since they have low f(v_i) values (Figure 5, row A). Comparing the cell volume to the population mean provides an indication of the type of error. Specifically, v_i < μ_v indicates a false detection, and v_i < μ_v indicates under-segmentation.

Figure 5.

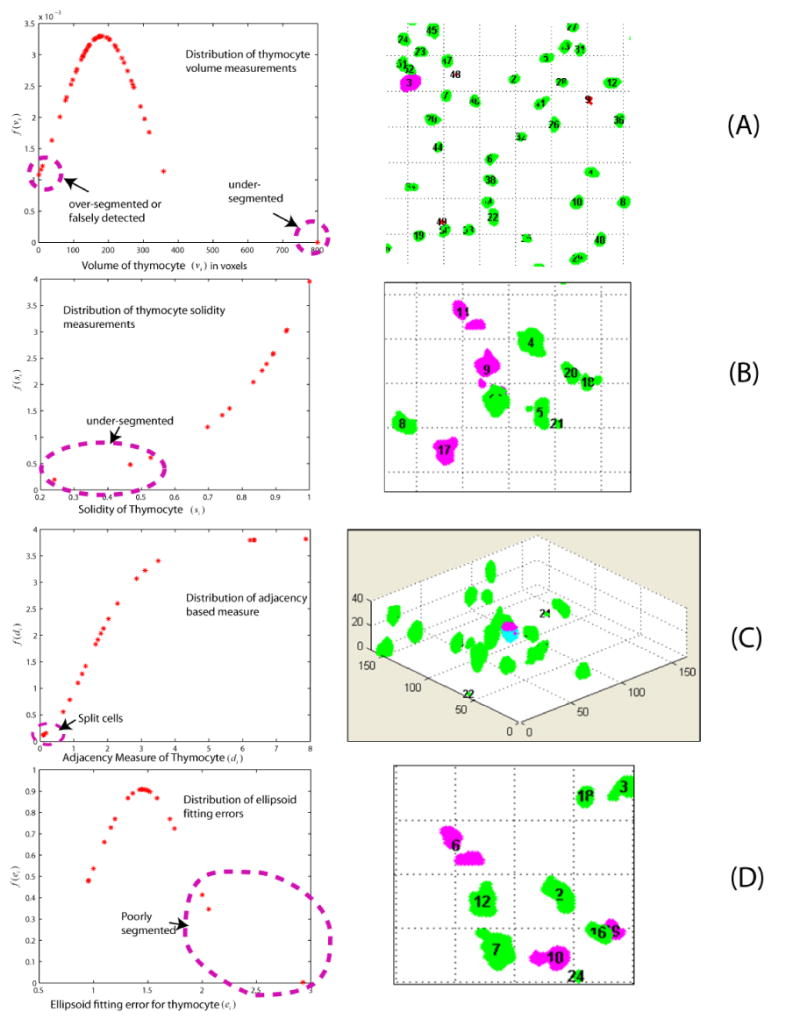
Illustrating the outlier based method to highlight potential errors for closer inspection and editing. The detected outliers marked by the pink ellipse in the left column correspond to the objects highlighted in pink in the right column. (A) Thymocytes with low f(v_i) values are under-segmented, over-segmented, or falsely detected. (B) Thymocytes with low f(s_i) values are under-segmented. (C) Thymocytes with low f(d_i) values are fragmented. The fragments displayed in dark pink and bright blue should be merged into a complete cell. (D) Low f(e_i) values usually indicate poorly segmented thymocytes.

The solidity of a cell, denoted s_i, and defined as the ratio of its volume to the volume of its convex hull is another valuable indicator. It is an effective indicator of under-segmentation, especially when adjacent thymocytes are poorly separated by a narrow spatial gap (Figure 5, row B). Solidity values are modeled by the following exponential distribution:

$$f(s_i)=\frac{1}{1-{\mu }_s}exp\left(-\frac{1-s_i}{1-{\mu }_s}\right).$$ (4)

Another interesting feature results from the observation that fragments of an over-split cell share boundaries (Figure 5, row C). The extent of this shared boundary can be quantified in terms of the distance (d_i) between the boundary voxels of one fragment to the closest voxels in the other fragment. We use the exponential distribution to model these distance values statistically, as follows:

$$f(d_i)=\frac{1}{{\lambda }_d}exp\left(-\frac{exp(-d_i)}{{\lambda }_d}\right).$$ (5)

Outliers relative to this distribution indicate over-segmented objects. Next, we computed the extent to which a segmented cell is ellipsoidal. For this, we computed a feature based on actual fitting of an ellipsoid model, and measuring the fitting error e_i. Assuming that these errors are normally distributed yields the following distribution:

$$f(e_i)=\frac{1}{\sqrt{2\pi {\sigma }_e^2}}exp\left\{-\frac{1}{2}{\left(\frac{e_i-{\mu }_e}{{\sigma }_e}\right)}^2\right\}.$$ (6)

High error values indicate poorly segmented cells (Figure 5, row D). This approach is similar to the method described by Lin et al., (2007).

The outlier detection methods described above represent the simplest choices. They were developed based on visualizing the data using box plots, histograms, and scatter plots (not shown here). In principle, far more sophisticated methods can be employed.

We compute the above confidence scores for every voxel cluster. Clusters with low confidence values are highlighted by color coding for manual inspection using a graphical interface program written in MATLAB (Figure 4). This program also provides tools to make corrective edits such as splitting a cluster, merging multiple fragments, adding a missed cell, and rejecting an invalid object. Table 1 is a summary of automated segmentation performance as measured from the number of corrective edits made by the operator. Note that the entries in Table 1 (and also Table 2 below) are the result of thorough manual inspection, and not just the outlier based identification. In other words, the role of the outliers is to assist the user by highlighting potential errors, but not to replace manual inspection. We did not attempt to quantify the specificity and sensitivity of the outlier detection in this study. The corrected segmentations are processed by the multiple-hypothesis tracking algorithm.

Table 1.

Error rates of automated segmentation outputs compiled from 13 datasets estimated from the corrective edits made by the operator. Three types of segmentation errors are recorded: under-segmentation, over-segmentation, and false detection. The total number of thymocytes and the numbers of individual error types are accumulated throughout all time frames of each dataset. The overall error rate is the total number of errors divided by the number of thymocytes.

Data Set	Total # of Cells	# of Under-segmented Cells	# of Over-segmented Cells	# of Falsely Detected Cells	Error Rate (%)
1	1984	131	50	101	14.21
2	1009	31	18	22	7.04
3	1315	80	41	59	13.69
4	1962	190	38	161	19.83
5	244	0	15	1	6.56
6	476	23	40	16	16.60
7	657	26	23	39	13.39
8	1494	101	47	95	16.27
9	1465	96	50	81	15.49
10	1018	52	23	40	11.30
11	507	12	5	11	5.52
12	1645	141	48	115	18.48
13	885	56	25	47	14.46
Subtotal	14661	939	423	788	14.66

Table 2.

Error rates of automated tracking compiled from 5 datasets. Three types of tracking errors are measured from the operator edits: failure to find a successor (one-to-none match), no match with a predecessor (none-to-one match), and incorrect match. The total number of matches and the numbers of individual error types are accumulated over all time frames of each dataset. The overall error rate is computed as the total number of errors divided by the number of matches.

Data Set	Total # of matches	# of one-to-none matches	# of none-to-one matches	# of incorrect matches	Error Rate (%)
1	1932	34	56	5	4.92
2	472	10	20	1	6.57
3	840	18	23	0	4.88
4	235	7	9	1	7.23
5	643	14	19	1	5.29
Subtotal	4122	83	127	8	5.29

Tracking Errors

The detection of tracking errors is also driven by outlier analysis. We first group possible tracking outliers into three classes: (i) failure to find a successor; (ii) no match with a predecessor; and (iii) an incorrect tracking match. Each of these situations is handled as described below.

1. Failure to find a successor: This can happen for two reasons – a cell exits the field of view of the microscope during the imaging interval [t,t+1], or there is a false-negative error in the cell segmentation. Should a tracked cell exit the field of view, we consider it a valid one-to-none match. Since there is no reliable clue indicating a cell that leaves the field and then re-enters later, we simply terminate its migration path. A failure to find successors due to false negative segmentation errors is diagnosed using a flicker animation display (alternately displaying I(r,t) and I(r,t+1) as a movie animation), and adding the missed cell manually.

2. No match with a predecessor: Since a number of new thymocytes are observed entering the field of view, we allow new trajectories of cells to start at frame (t+1). In a few cases of invalid none-to-one matches, the graphical tool enables the operator to locate and delete falsely detected cells in image I(r,t+1).

3. Incorrect match: To accelerate detection of incorrect cell-cell correspondences, we sort the migration likelihood scores $P_{\text{motility}}({\text{f}}_i^t,f_j^{t+1})$ of matched T cells (i, j) in ascending order, and pick out cells with the lowest scores for further inspection.

Table 2 summarizes the performance of the automated tracking, as estimated from the corrective edits made by the user.

Quantifying Cell-Cell Interactions

To quantify the association between thymocytes and dendritic cells, we center a search window Г at the centroid of each thymocyte. Then, we collect the nearest 5% DC voxels $\Psi =\left\{{\text{d}}_j^t\in \Gamma \right\}$ to each thymocyte (instead of just the single nearest DC voxel), and compute the average of Euclidean distances ${\text{D}}_i^t=\frac{1}{n}\text{∑}_{\Psi }\Vert {\text{c}}_i^t-{\text{d}}_j^t\Vert$ from the thymocyte center ${\text{c}}_i^t$ to each neighboring DC voxel ${\text{d}}_j^t$. This measure is robust to imaging noise, but may not always capture the notion of cell-cell contact. As illustrated in Figure 6, thymocytes with different radii may have similar distance measures ${\text{D}}_i^t$ ^‡. For this reason, we normalize the center-to-edge distances by the thymocyte radii, i.e., ${\widehat{D}}_i^t=\frac{{\text{D}}_i^t}{{\text{r}}_i^t}$, to yield a more effective measure for quantifying the association between thymocytes and adjacent DCs. The frequency of thymocyte-DC contacts is quantified as $P_{\text{contact}}\approx \frac{C_a}{C_T}$, where C_a is the number of time points at which the normalized distance ${\widehat{D}}_i^t$ drops below a user-defined threshold θ_d, and C_T is the total number of thymocytes. Our reason for choosing the center-to-edge criterion rather than a straightforward edge-to-edge criterion is to enable manual validation. The center-to-edge distance is easy to measure manually, but an edge-to-edge distance is much harder and less reliable to generate manually in our study.

Figure 6.

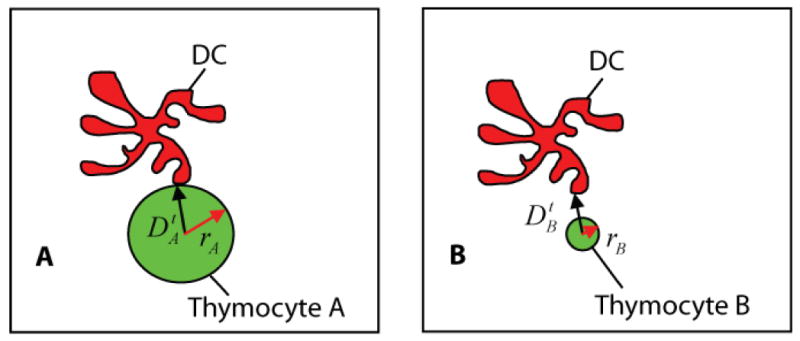
Illustrating the fact that with an un-normalized center-to-edge distance measure, thymocytes of different sizes may have the same center-to-edge distance to a DC. Panel A illustrates a true positive: the case when Thymocyte A (green) with a distance ${\text{D}}_A^t$ indeed touches its neighboring DC body (red). Panel B illustrates a false positive, the case when Thymocyte B having the same distance measure ${\text{D}}_B^t={\text{D}}_A^t$ is incorrectly classified as contacting with the DC. Normalizing the distances by the radii of the thymocytes yields a distance measure that avoids the above problem and compensates for variations in thymocyte volumes between and within populations of various types of cells.

Quantifying the Dynamics of Thymocytes

In addition to geometric features, we computed 9 dynamic features of thymocytes to provide insight into movement behaviors of thymocytes regulated by signal selection events. Quantitation of these parameters is a commonly used approach that allows for the characterization of cell motility and migration (Cahalan & Parker, 2008).

Given a tracked thymocyte i^t located at $({\text{x}}_i^t,{\text{y}}_i^t,{\text{z}}_i^t)$, t = t₁, …, t_n, the instantaneous displacement, denoted ${\text{T}}_i^t$ is the 3-D difference between $({\text{x}}_i^t,{\text{y}}_i^t,{\text{z}}_i^t)$ and $(x_i^{t+1},y_i^{t+1},z_i^{t+1})$. In addition, we measure the overall displacement, denoted T_i from the initial time point t₁ to the last time point t_n of the cell lifetime. The magnitude of the instantaneous translation is measured as ${\text{R}}_i^t=\Vert {\text{T}}_i^t\Vert$. The migration path length, denoted L_i, is the total distance traveled through the cell lifetime T, i.e., $L_i=\text{∑}_{t=1}^{t_n-1}{\text{R}}_i^t$. The average speed is measured as ${\overline{s}}_i=\frac{L_i}{T}$. The instantaneous speed is quantified in two different ways. The Type-I instantaneous speed over a time interval Δt is computed as $s_{i,1}=\frac{{\text{R}}_i^t}{\Delta t}$. The Type-II instantaneous speed is computed as $s_{i,2}=\frac{R_i^{t-1}+{\text{R}}_i^t}{2\cdot \Delta t}$. The turning angle, denoted ${\theta }_i^t$, is the angle between displacement vectors $T_i^{t-1}$ and ${\text{T}}_i^t$. Finally, the directionality index, denoted δ_i : the ratio of displacement over migratory path, ${\delta }_i=\frac{\Vert T_i\Vert }{L_i}$.

In summary, the overall sequence of processing steps is: (i) spectral unmixing; (ii) automated segmentation of each channel; (iii) computer-assisted inspection and editing of segmentation; (iv) automatic tracking of corrected segmentation results; and (v) inspection/editing of tracking results. The resulting segmentation and tracking data form the basis for measuring geometric features and the dynamics of thymocytes.

Experiments and Discussion

One purpose of the experiments described here is to show that the automated system successfully generates data on cell migration and cell-cell interactions that agree with previously reported results. Here we use the interactions between T cells and DCs as an example of robust cell-cell associations, and the interactions between thymocyte and DCs as an example of subtle cell-cell associations. In both cases, our automated results recapitulate observations that were previously recorded manually. Another purpose is to illustrate the ability of the automated system to uncover new observations (e.g., size differences between wild-type and P14 thymocytes) that are difficult to notice manually.

Table 3 summarizes the extent of of T cell-DC contacts computed on published lymph node datasets (Bousso & Robey, 2004), and thymocyte-DC contacts computed on 4 sequences for wild type (wt → B6), 6 series undergoing (P14 → B6) selection, and 3 sets for P14 → (DBA × B6) selection. To explore type-to-type difference, various datasets from the same kind are combined together and analyzed as a group. A threshold of θ_d = 1.7, determined empirically by the biological user based on visual inspection, was used for distance thresholding. A fully automated method to select this threshold value remains a topic for future research. The resulting cellular interaction frequency computed by the automated method was found to concord with un-published manual analysis data (Ladi et al., 2008) to within 8%. The discordance rate is computed by the absolute difference between automated result and manual measurement.

Table 3.

Summary of T cell-DC contact measurements of published lymph node datasets (Bousso & Robey, 2004), and thymocyte-DC contacts. For the percent of time points in contact with DC, the discordance rate with manual analysis is computed by the absolute difference between automated result and manual measurement Automated results were found to agree with unpublished manual measurements (Ladi et al., 2008).

Dataset Type	# of Datasets	# of Thymocytes	Time points with DC contact	Total Time Points examined	Percent of time points in contact with DC	Discordance with manual analysis	# of DC contacts	Total time of tracks examined (hours)	Frequency of contacts per hour	Avg. duration of contact (min)
T-cell without antigen	1	51	124	548	22.63%	N/A	28	4.57	6.13	2.36
T-cell with antigen	1	31	314	437	71.85%	N/A	28	3.64	10.44	5.70
Wild Type	4	402	844	6270	13.46%	1.46%	184	63.9	2.88	2.79
(P14 → B6)	6	456	1808	5354	33.77%	7.73%	328	54.6	6.01	3.47
P14 → (DBA × B6)	3	219	753	3037	24.79%	0.49%	140	31.0	4.52	3.51

We compiled all thymocyte or T Cell data for all time points to yield a sample set of distance measures $\{{\widehat{D}}_i^t\}$. The empirical cumulative distribution function (CDF) of $\{{\widehat{D}}_i^t\}$ provides insight on dataset-to-dataset differences in DC association for T cell populations (Figure 7A) or thymocyte populations (Figure 7(B-C), where both the intra- (e.g. among (P14 → B6) runs) and variations between P14 selections are presented simultaneously.

Figure 7.

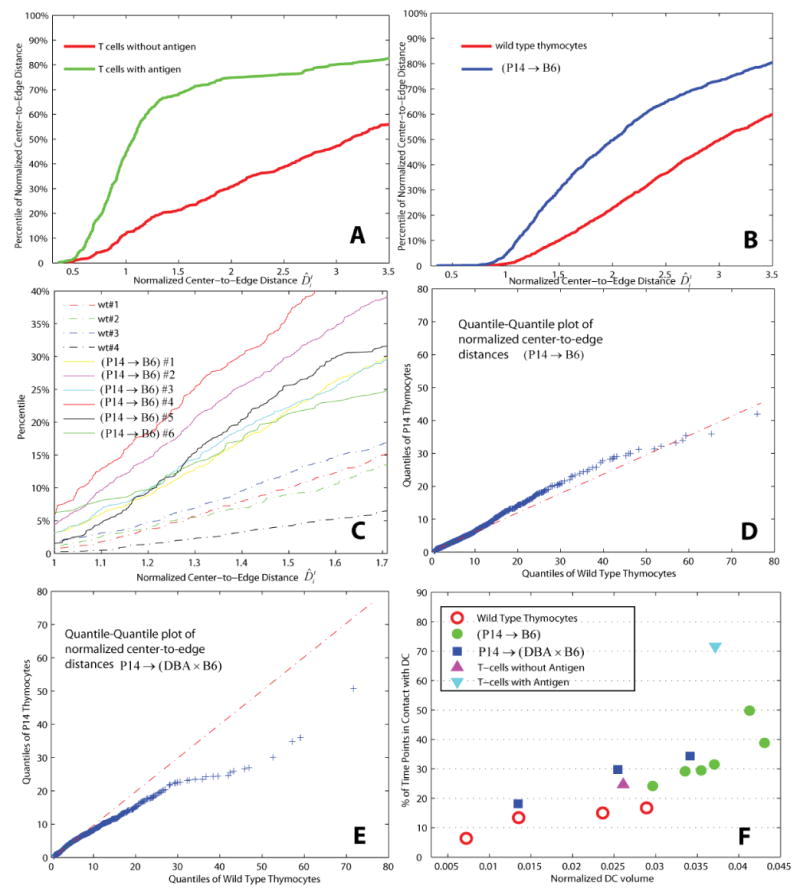
Quantifying thymocyte or T cell-DC associations using the normalized distance measure: (A) Sample empirical CDF of normalized center-to-edge distances for lymph node T cells with and without antigen (Bousso & Robey, 2004); (B) Sample empirical CDFs of distances for wild-type and (P14 → B6) thymocytes computed from 2 image sequences; (C) Percentile plots for individual image sequences; (D) Quantile-quantile plot comparing wild-type and thymocytes in P14 → B6 hosts; (E) Quantile-quantile plot comparing wild-type and P14 → (DBA × B6) thymocytes; (F) Percentage of time points when thymocytes were in contact with DCs as a function of cell type and DC volumes normalized by the volume of the respective image stacks.

To show differences in the distribution of two cell populations, it is valuable to use the quantile-quantile plot (Q-Q plot) which displays the quantiles of one population versus those of the other; here, we use wild type and P14 selections as examples (Figure 7(D, E)). Should the distance measures of wild type and P14 selections come from the same underlying distribution, the points in the Q-Q plot were expected to approximately fit a straight line (Martinez, et al., 2002). On the contrary, a noticeable deviation from a straight line occurs in both cases (i.e. wild type against (P14 → B6), and wild type versus P14 → (DBA × B6)), indicating a significant shift in the distributions.

To summarize run-to-run variations in thymocyte-DC associations, for an individual run of specific sample type (i.e. wild type, (P14 → B6), or P14 → (DBA × B6)), the quantitative measure of thymocyte-DC contacts is plotted against the normalized DC volume (Figure 7F).

We also used the tracking data to quantify the dynamics of cell migration. Our purpose in presenting these data is to show that the automated system (i) successfully recapitulates observations that were made in previous studies using manual analysis, and (ii) is capable of uncovering new patterns. Here, each thymocyte track is processed as a unit, which covers the complete lifetime of that thymocyte within the imaging period. Using these parameters to quantitate the results of our automated analysis, we generated histograms in Figures 8(A–C) that show the frequency distributions of some dynamic attributes. In agreement with the results of the manual scoring (Ladi et al submitted), the percentage of time points thymocytes are in contact with DCs is greater for P14 thymocytes as compared to wt thymocytes (Figures 8A). Also, the average instantaneous speed and the directionality index are also greater for P14 thymocytes than wt thymocytes (Figures 8(B, C)), as has previously been reported (Witt, et al 2005b).

Figure 8.

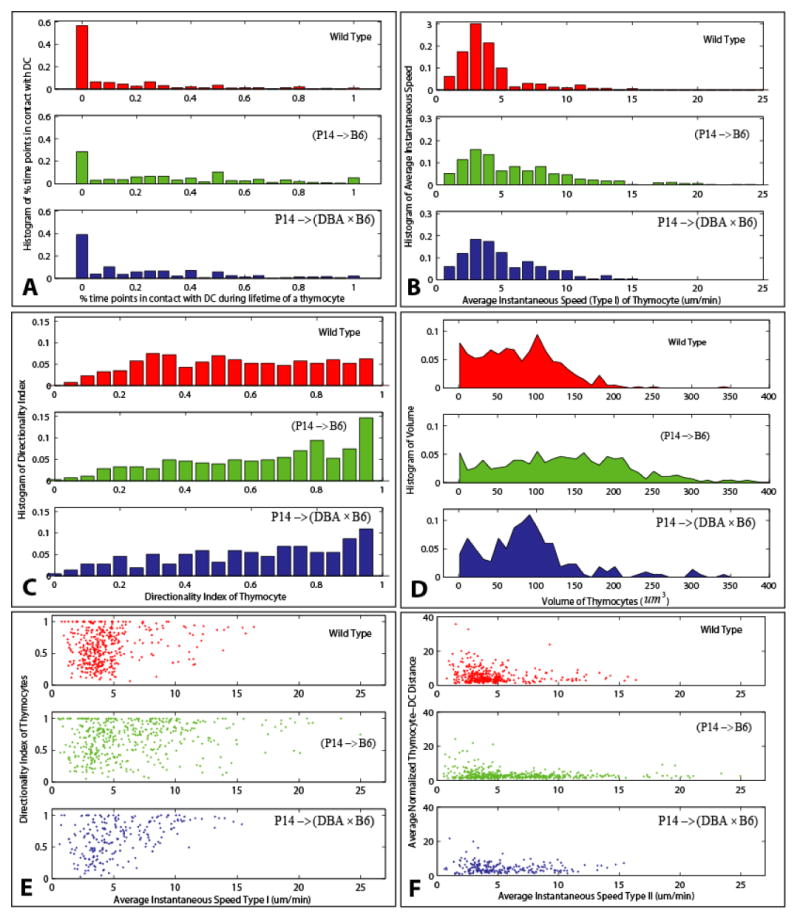
Exploring the dynamics of thymocytes using the automatically generated measurements: (A) Histogram of percentage of time points over its observed lifetime that a thymocyte is in contact with DCs. (B) Histogram of average instantaneous speed (Type I) over the lifetime of a thymocyte. (C) Histograms of the directionality index of thymocytes. (D) Histograms of thymocyte volumes. (E) Scatter plots of average speed against directionality index. (F) Scatter plots of average speed against average normalized thymocyte-DC distance.

In addition to these standard approaches to quantitate 4-D data, our method allows for the comparison of the cell size of these two populations. In the histogram shown in Figure 8D, we show that P14 thymocytes are larger in volume than wt thymocytes, which we have confirmed using flow cytometry measurement of forward scatter (data not shown).

The 2-D scatter-plots reveal additional information about the migration of thymocytes. Figure 8(E, F) shows normalized thymocyte-DC distance or the directionality index as it relates to the average speed of the thymocyte. P14 thymocytes with a faster average speed are closer to DCs (Figure 8E and Ladi et al submitted), and also migrate straighter (Figure 8F and Witt, et al 2005b) when compared to wt thymocytes, or the total population of P14 thymocytes. Importantly, differences in statistical characteristics among various cell types are observable in these graphs and measurements such as the spreads and peaks of the distributions. Table 4 also reveals a visible shift of mean values between wild type and P14 selections, which concords with results of manual analysis (Ladi et al., 2008).

Table 4.

Measurements of dynamic behaviors of thymocytes.

Dataset Type	# of Datasets	# of Thymocytes	Avg. normalized distance	Avg. speed (μm / min)	Avg. directionality Index
Wild Type	4	402	5.36	4.65	0.59
(P14 → B6)	6	456	3.33	6.55	0.68
P14 → (DBA × B6)	3	219	4.57	5.52	0.64

Hypothesis Testing

It is straightforward to utilize our automatically generated measurements to test hypotheses. As a concrete example, we investigate the observation that thymocytes expressing (P14 → B6) selection have higher percentage of time points in contact with DCs, compared with wild-type thymocytes.

We computed the normalized center-to-edge distances $\{{\widehat{D}}_i^t\}$ as described above for all detected thymocytes for three image sequences corresponding to wild-type, (P14 → B6) selection, and P14 → (DBA × B6) selection, respectively. We then computed the empirical cumulative distribution function (CDF) of these distances, given by F(d) = P_contact(D̂ ≤ d). For example, the distribution F_P14+(d) plotted as a blue line in Figure 9(A) is higher than the corresponding distribution for wild-type thymocytes, denoted F_WT(d), and plotted as a dotted red line, suggesting that the normalized center-to-edge distances for (P14 → B6) selection are smaller than for wild-type cells. Figure 9(B) similarly compares wild-type with P14 → (DBA × B6) selection. These plots correspond to a single run.

Figure 9.

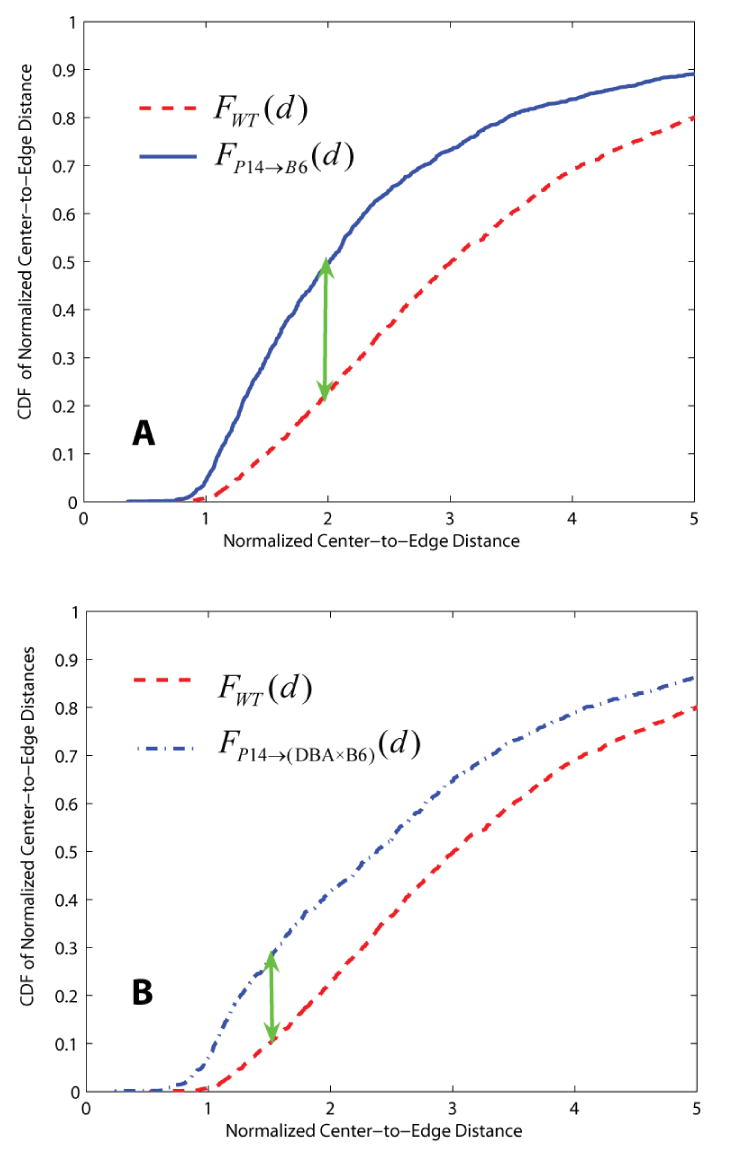
Examples illustrating dissimilarity between the distributions of wild type and P14 selections characterizing the thymocyte-DC center-to-edge distances. The cumulative distribution functions (CDFs) in both Panel A and B indicate that normalized center-to-edge distances for P14 selections have many more smaller values compared to wild-type thymocytes. The green arrows indicate the location of highest dissimilarity between CDFs of wild type and P14 selections for a single run. The Kolmogorov-Smirnov test and Mann-Whitney U-test confirm that the distributions are statistically different (shown as entries in bolded and underlined font in Table 5 and Table 6).

We compared these distributions using the Kolmogorov-Smirnoff test (Martinez et al., 2002). This test for determining if two datasets differ significantly has the advantage of making no assumption about the distribution of the data, unlike the t-test that assumes normality. This test is also robust to outliers. The null hypothesis corresponds to the situation that the two distributions are not different. The alternate hypothesis corresponds to the situation that the two distributions are significantly different. For this, the test requires identification of the distance value (d) corresponding to the maximum absolute value of differences between the cumulative distribution functions, i.e., $\underset{d}{max}\left\{F_{P14\pm }(d)-F_{wt}(d)\right\}$. This value is indicated by green arrows in Figure 9. Table 5 shows p-values of hypothesis testing on wild-type versus P14 selections. The null hypothesis is rejected if the p-value is less than or equal to a significant level α. Those entries depicted in grey color indicate a failure to reject the null hypothesis. The test results of datasets illustrated in Figure 9 are shown in bolded and underlined font, which confirm our visual observations.

Table 5.

Illustrating the Kolmogorov-Smirnov test on distribution of computed measurements: The test analyzes the null hypothesis that two datasets are generated from the same distribution. Each entry in the table corresponds to the p value of the test performed on a pair of datasets. Entries depicted in grey indicate a failure to reject the null hypothesis at a significance level of 5%. The test results of datasets illustrated in Figure 9 are shown in bolded and underlined font, which agree with our visual observations. For convenience, P14+ and P14- refer to P14→B6 and P14→(DBA × B6), respectively.

	P14+	P14+	P14+	P14+	P14+	P14+	P14-	P14-	P14-
wt	0.02	< 10-4	8.76×10-4	1.40×10-3	0.39	0.60	0.22	1.17×10-4	0.05
wt	< 10-4	< 10-4	< 10-4	< 10-4	0.09	0.20	0.11	0.21	1.74×10-4
wt	0.06	< 10-4	2.30×10-3	0.01	0.16	0.77	0.05	< 10-4	0.31
wt	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4

In addition, the non-parametric Mann-Whitney test was also performed to evaluate a possible shift of the median values of two distributions. The null hypothesis suggests that two sample sets are generated from identical distributions with equal medians, while the alternative hypothesis indicates that they do not have equal medians. Table 6 illustrates p-values from testing performed on wild-type vs. P14 selections. This test rejects the null hypothesis if p ≤ α. In terms of rejecting/accepting the null hypothesis, most of the testing results in Table 6 are found to agree with those shown in Table 5.

Table 6.

Illustrating the Mann-Whitney U-test on computed measurements: The test analyzes the null hypothesis that two datasets are generated from identical distributions with equal medians. Each entry in the table corresponds to the p value of the test performed on a pair of datasets. Those entries depicted in grey color indicate a failure to reject the null hypothesis at a significance level of 5%. The test results of datasets illustrated in Figure 9 are shown in bolded and underlined font, which concord with our visual observations. For convenience, P14+ and P14- refer to P14→B6 and P14→(DBA × B6), respectively.

	P14+	P14+	P14+	P14+	P14+	P14+	P14-	P14-	P14-
wt	2.60×10-3	< 10-4	2.46×10-4	9.24×10-4	0.59	0.96	0.79	< 10-4	0.03
wt	< 10-4	< 10-4	< 10-4	< 10-4	0.06	0.06	0.01	0.50	< 10-4
wt	0.02	< 10-4	2.70×10-3	3.50×10-3	0.27	0.77	0.43	< 10-4	0.11
wt	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4	< 10-4

Conclusions & Discussion

This work was motivated by the advent of 5-D microscopy as an investigational tool with unprecedented potential for understanding complex and dynamic immunological processes in their 3-D spatio-temporal microenvironment. This study confirms the power and practicality of building effective associative image analysis systems to quantify cell-cell interactions. Automated systems are unavoidably prone to segmentation and tracking errors. In this context, we have shown the practicality of computer-aided inspection and corrective editing of the automated results with minimal labor. The manual labor roughly scales with the error rate of the automated algorithms rather than the total number of cells in the image data. The use of statistical modeling and outlier analysis to highlighting potential errors made by the automated system, and automatically identifying the nature of these errors is a simple idea that can be extended much further. The editing process also yields data for performance assessment and error analysis that can be used for planning algorithm improvements. One recognized limitation of this method is the potential for the observer to miss some errors. This is not important when the null hypothesis is defeated with adequate confidence. In subtle situations, our protocol can be extended to include additional observers, if needed. Finally, there is plenty of room to develop far more sophisticated and user-friendly visualization & editing tools in the future that further minimize the manual effort and improve the detection of subtle errors.

Although the methods described here were designed for specific questions, our approach to 5-D associative image analysis can be adapted/extended to other problems. The present work mostly involved blob-shaped objects in the image. In general, 5-D image analysis problems could involve more complex object morphologies (e.g., neurites and vasculature). The present work can be extended to include multiple object morphologies, and a corresponding set of associative measurements, by building upon efforts such as the FARSIGHT project (Bjornsson et al., 2008). All of the software tools described here is available freely to interested colleagues on a collaborative basis from the authors.