Motivations and Methods for Analyzing Pulsatile Hormone Secretion

Abstract

Endocrine glands communicate with remote target cells via a mixture of continuous and intermittent signal exchange. Continuous signaling allows slowly varying control, whereas intermittency permits large rapid adjustments. The control systems that mediate such homeostatic corrections operate in a species-, gender-, age-, and context-selective fashion. Significant progress has been made in understanding mechanisms of adaptive interglandular signaling in vivo. Principal goals are to understand the physiological origins, significance, and mechanisms of pulsatile hormone secretion. Key analytical issues are: 1) to quantify the number, size, shape, and uniformity of pulses, nonpulsatile (basal) secretion, and elimination kinetics; 2) to evaluate regulation of the axis as a whole; and 3) to reconstruct dose-response interactions without disrupting hormone connections. This review will focus on the motivations driving and the methodologies used for such analyses.

• I. Overview of Origins of Pulsatile Hormone Secretion

  • A. Definition of pulsatility
  • B. Time scales of pulsatility
  • C. Concept of volleys comprising multiple bursts
  • D. Amplitude- and frequency-dependent control of pulsatility
  • E. Mechanisms of pulse generation
  • F. Damping of secretory bursts in the circulation
  • G. Distinction between bound and free hormone concentrations in pulses
  • H. Sampling at or near the anatomic site of hormone secretion
• II. Physiological Implications of Pulsatile Hormone Signals

  • A. Downstream effects of GHRH and GH pulses
  • B. Target-tissue effects of ACTH and testosterone (Te) pulses
  • C. Other clinical examples (oxytocin, PTH, insulin, glucagon)
  • D. Experimental paradigms to appraise pulse effects in vivo
• III. Altered Pulsatility Control in Pathophysiology

  • A. Neuroendocrine neoplasia
  • B. Type II (noninsulin-dependent) diabetes mellitus
  • C. Fasting-induced hypogonadism
  • D. Hyperprolactinemia secondary to pituitary-stalk disruption
  • E. Primary hyperparathyroidism
  • F. Cortisol-secreting adrenocortical adenomas
  • G. Primary hyperaldosteronism
  • H. Failure of the target organ
• IV. Early Methods of Pulse Analysis

  • A. Empirical threshold approaches
  • B. Semiempirical baseline strategies

• V. Criteria for Optimal Pulse Analysis

• VI. Methodologies for Secretion Estimation (Deconvolution Analyses)

  • A. Motivation
  • B. Definition of deconvolution analysis
  • C. Fixed half-life deconvolution methods
  • D. Challenges in deconvolution analysis
  • E. Simplifying assumptions in deconvolution analysis
  • F. Impact of analytical assumptions on secretion estimates
  • G. Deconvolution analysis of secretory-burst waveform
  • H. Influence of secretory-burst offset
  • I. Regulation of hormone secretory-burst onset
  • J. Deconvolution with pulse detection
  • K. Nature of pulse-timing (pulse-renewal) process
  • L. Stochastic elements in endocrine systems
  • M. Investigational limits of secretion-estimation procedures
  • N. Unresolved issues
• VII. Analyses of Multihormone (Ensemble) Interactions

  • A. Ensemble concept
  • B. Ensemble modeling requirements
  • C. Examples of ensemble-control models in endocrine systems
  • D. Simplifying assumptions
• VIII. Model-Free Evaluation of Endocrine Networks

  • A. Concept of model-free assessment
  • B. Rationale for ensemble statistics
  • C. Approximate entropy (ApEn) as an ensemble measure of regularity
  • D. Artificial neural networks
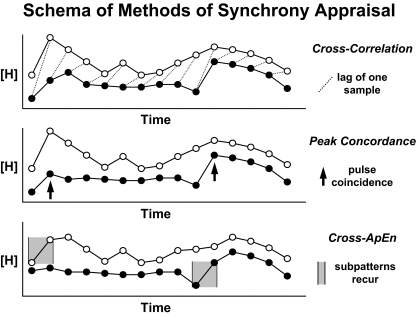
• IX. Methods of Synchrony Appraisal

  • A. Rationale for assessing hormone synchrony
  • B. Cross-correlation analysis
  • C. Exact peak concordance
  • D. Cross-approximate entropy (cross-ApEn)

• X. Summary

I. Overview of Origins of Pulsatile Hormone Secretion

PULSATILITY IS A FUNDAMENTAL property of the majority of hormone secretion patterns. Pulses reflect the mechanistic design of the biological system on the one hand and mediate selective target-tissue effects on the other hand. Early investigators viewed hormone plots over time and marked peaks by eye, concluding that pulses existed. Later work introduced the notion that a peak should exceed random assay variability by some objective amount, such as two or three times the assay coefficient of variation. A subsequent idea was to estimate underlying secretion using information about hormone elimination, thereby gaining insights into the secretion process. The evolution of earlier strategies was reviewed in Refs. 1,2,3,4. Recent developments are highlighted in the present review, along with their advantages, limitations, and complementarity.

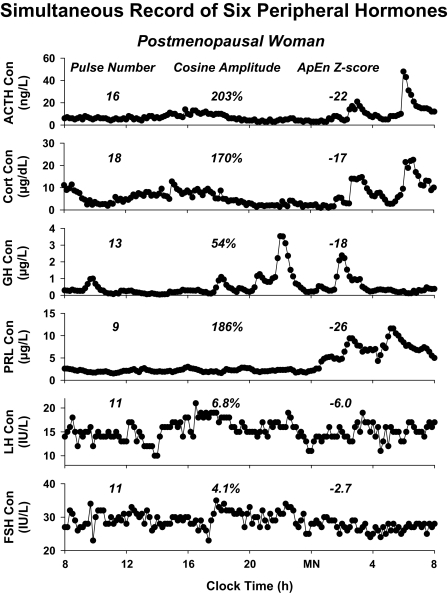
A fundamental perspective is that complementary analytical methods are needed to achieve comprehensive insights into complex regulatory mechanisms in biology (1,2,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18). Figure 1 illustrates this point by highlighting six hormone concentration-time series obtained by frequent sampling over 24 h in the same person. The profiles exhibit diversity in all three of pulsatile (burst-like), nycthemeral (day-night), and entropic (patterned) features. The primary goal of this review is to explicate the biological rationale and review the analytical techniques for quantifying mechanisms that regulate pulsatile hormone secretion. Pulsatility in turn influences 24-h rhythmic and entropic patterns of hormone output (19,20).

Figure 1.

Diversity of pulsatility patterns exemplified by six hormone-concentration profiles obtained simultaneously in the same postmenopausal individual. Numerical values (above columns from left to right) are the number of pulses, the amplitude of the nycthemeral cosine rhythm (% of mean concentration), and relative orderliness defined by the ApEn z score (the absolute value denotes the number of standard deviates that observed ApEn is removed from mean ApEn of 1000 randomly shuffled versions of the same series). Thus, the prolactin pattern is highly regular (absolute z = 26), whereas that of FSH is nearly mean random (absolute z = 2.7). Hormone release was monitored by sampling blood every 10 min for 24 h. Cort, Cortisol; Con, concentration; PRL, prolactin. Data provided by Dr. Ferdinand Roelfsema, University of Leiden (Leiden, The Netherlands).

A. Definition of pulsatility

“Pulsatile” denotes the recurrence of individual punctuated events (bursts, peaks, or pulses) interrupting a more or less constant baseline process. A pulse is identified by an abrupt increase and subsequent decrease in the intensity (size or amplitude) of serially measured output. In principle, the size, shape, and spacing of pulses may be regular or variable, and the underlying baseline process may be fixed or drift gradually (11,12,15,16,21,22,23,24,25,26,27,28).

Reproducibly spaced signals of similar shape and amplitude with minimal associated noise superimposed upon a low stable baseline process are readily quantified by conventional methods developed in the physical sciences, such as fitting the data to the sum of sine and cosine functions (Fourier expansion series) (29,30). However, hormonal secretion patterns are not adequately represented by such rigid formulations (12,16,31,32) (Fig. 1). For example, to capture biological irregularity typically requires a large number of sinusoidal terms, which can result in inappropriate assessments. Such variable pulse patterns are the rule rather than the exception. In particular, random (stochastic) inputs arise from multiple sources, such as: 1) procedural inconsistencies (missing data, outliers) and measurement variability; 2) unexplained trends or epochs related to the host; and 3) biological variability due to memoriless (uncorrelated) pulse times, nonuniformity of successive secretory-burst amplitudes, shapes, and inconsistent pulse-by-pulse stimulus desensitization or facilitation (12,16,33,34,35,36) (Fig. 2). Estimation of neurohormone pulsatility is thus obscured by observational uncertainties, host variables, and stochastic aspects of biological processes. Nonetheless, a fundamentally pulsatile structure underlies peptide, steroid, catecholamine, and neurotransmitter secretion by the hypothalamus, anterior and posterior pituitary gland, adrenal cortex and medulla, testis and ovary, pancreatic islets, and parathyroid glands (21,22,23,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56). Apparent exceptions to pulsatile secretion are total IGF-I, inhibin B, total ghrelin, and total T₄, which exhibit diurnal trends and periprandial epochs of variable hormone release (4,57,58).

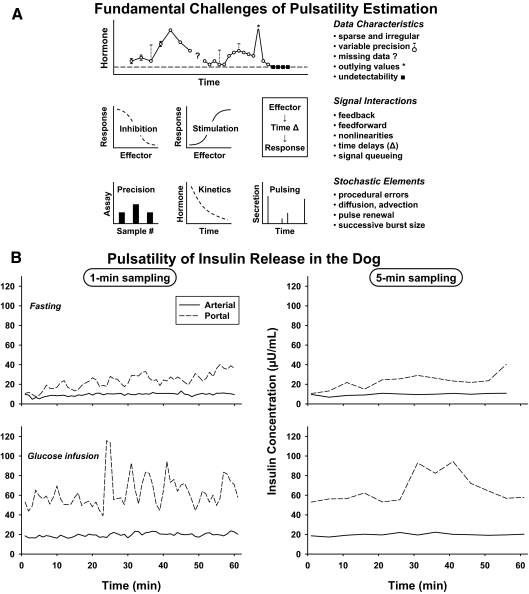
Figure 2.

A, Schema of fundamental analytical hurdles associated with valid estimation of pulsatility. Challenges arise from inherent data limitations, nonlinear signal interactions, and confounding stochastic (random) effects. B, Diptych showing the impact of sampling time interval [1 min vs. 5 min] and sampling site [arterial vs. portal] on the appearance of insulin pulses.

B. Time scales of pulsatility

The time scales of pulsatility extend over at least four orders of magnitude. At one extreme, oscillations of ionized calcium concentrations, [Ca²⁺]_i, exist within single endocrine cells with periodicities of milliseconds to seconds (59). Indirect evidence suggests that unstimulated cycles of [Ca²⁺]_i may prime exocytosis and enhance basal gene transcription in pancreatic β-cells, pituitary gonadotropes, and adrenal chromaffin cells (59). Membrane capacitance measurements indicate that relevant extracellular stimuli evoke rapid transient Ca²⁺ influx, intracellular Ca²⁺ mobilization, and exocytosis of docked and primed secretory granules (60). At the other extreme of the time continuum, large pulses of LH secretion recur every 3 h (1.1 × 10⁴ sec) in the late-luteal phase of the human menstrual cycle (2). The majority of hormones are secreted in an intermediate time frame of pulses every 4–30 min [antidiuretic hormone (ADH), oxytocin, insulin, glucagon, and PTH] or every 45–180 min (anterior pituitary proteins, melatonin, gonadal and adrenal steroids) (23,45,46,54,61,62,63). The latter intervals are termed “circhoral” (approximately hourly), and more generally “ultradian” (two or more pulses per day). In summary, pulses constitute brief episodes of hormone or effector release that are often irregularly spaced in time and of nonuniform size, thus making analysis a special challenge.

C. Concept of volleys comprising multiple bursts

When assessed by sampling blood every 0.5–5 min, the pattern of hormone secretion may be complex (64,65). For example, large secretory episodes often comprise volleys of small pulses (66,67,68,69). The degree to which prominent peaks arise from an array of diminutive pulses is difficult to establish precisely. Patterns of intensively (30-sec) sampled peripheral GH release in the human illustrate this point (64). Selecting 2-, 5-, 10-, and 30-min subsets of the original data progressively censors “pulses within pulses,” spuriously lowers the absolute peak values, displaces peak times, and elevates interpulse nadir concentrations. An investigation that combined 5-min sampling and deconvolution (secretion-based) analysis suggested that the proestrous LH surge in the rat arises from multiple nearly confluent LH pulses of increasing amplitude and frequency (69). Other studies based on 30-sec and 1-min sampling, high-precision peptide assays, and deconvolution analyses have unveiled discrete pulses of 1) insulin every 4–7 min in the human, dog, and rat in vivo and by perifused human islets in vitro (42,70,71); and 2) GH every 35–60 min overnight in healthy young men (64).

Multifold patterns of pulsatility raise the technical question of how analyses should be posed. The challenge is illustrated by the wide range of reported dynamics of insulin secretion monitored during fasting, viz., rapid pulses (every 4–7 min), slower sinusoidal cycles (12–40 min), longer ultradian rhythms (1–3 h per cycle), and nycthemeral (24-h) variations (72,73,74). Some alleged patterns may reflect undersampling of the primary high-frequency process (referred to as aliasing) and others variable epochs of higher-amplitude bursts (75,76,77). An unresolved challenge is finding which blood-sampling schedules and mathematical models are optimal to obtain coherent insights into the unknown true dynamics. Viewing the data as summed wavelets is a possible complementary means to reconstruct underlying patterns across several time scales (78). Wavelets may be viewed approximately as recurring shapes in the data that build up an overall pattern. Further methodological developments will be required to provide analytically sound and biologically useful models to represent volleys and clusters of hormone pulses.

D. Amplitude- and frequency-dependent control of pulsatility

1. Amplitude-selective control.

The size of pituitary-hormone pulses, defined by amplitude (height in concentration units) or mass (amount secreted per burst per unit distribution volume) can vary by as much as 1000-fold in the same individual on the same day. For example, ultrasensitive immunochemiluminescence assays reveal awake daytime food-suppressed plasma GH concentrations of 0.012–0.035 μg/liter and nighttime sleep- and fasting-augmented concentrations of 8–20 μg/liter (79,80). In addition, major variations (3- to 10-fold) in mean GH pulse size unfold in puberty, the menstrual cycle, aging, and obesity and in response to aerobic exercise, stress, sleep, and fasting (4). By current estimation methods, GH secretory-burst frequency does not change concomitantly, except to increase slightly during the hours of sleep.

Less profound amplitude-selective modulation applies to insulin secretion. Pulse-size variations are 2- to 7-fold in diverse pathophysiologies, such as aging, type II diabetes mellitus, renal failure, obesity, and physical deconditioning (81). Two- to 5-fold variations in secretory-burst mass typify ACTH, PTH, aldosterone, and cortisol (45,46,54,82).

The exact physiological implications of such marked absolute excursions in pulse amplitude have not been ascertained. A testable postulate is that different target organs have different absolute pulse-amplitude dose-response dependence. Amplitude-predominant regulation permits rapid and marked increases in mean hormone concentrations. Pulses allow preferential engagement of rate-sensitive cellular signaling pathways, as inferred for certain feedforward actions of GH and feedback actions of cortisol as well as osmotic stimulation of ADH secretion (4,83,84,85,86).

In sum, significant amplitude-varying control of pulsatile secretion is common to nearly all hormones.

2. Preferential frequency control.

Primary frequency control has been reported for oxytocin pulses in parturient and postpartum women (63).

3. Combined amplitude and frequency control.

Nycthemeral (24-h) variations in hormone concentrations are determined primarily by altering both the amplitude and frequency of LH, FSH, TSH, prolactin, and gonadal sex-steroid pulses (15,19,34,45,46,47,62,87,88,89). LH pulsatility is the prototype of dual amplitude and frequency regulation (2). The latter is achieved by way of negative feedback by gonadal sex steroids on the amplitude and frequency of the GnRH pulses and the amplitude of LH secretory bursts (89,90,91,92). The degree to which basal (nonpulsatile) hormone secretion is regulated is not known. Ignorance in part reflects earlier technical uncertainty about the valid estimation of true basal secretion (19,93,94).

4. Triple control of pulse number, size, and shape.

The size (mass), number (frequency), and shape (waveform) of ACTH and TSH secretory bursts are regulated (15,35). Cortisol depletion augments ACTH secretory-burst mass by 9.6-fold, increases ACTH pulse frequency by 1.25-fold, and abbreviates ACTH secretory bursts by 1.5-fold. TSH secretory-burst size and frequency increase by 2.0-fold and 1.2-fold, respectively, overnight, whereas the time to maximal TSH release within a burst decreases by 1.5-fold. These nycthemeral (night-day) changes are selective because the quantifiable regularity of the ACTH and TSH-pulsing mechanism does not vary over 24 h (15,35). The generality of waveform changes over the day and night is not known.

5. Target-tissue effects of pulse size and number.

Quantifying specific facets of regulated secretion is an important step toward elucidating mechanisms of physiological control. A corollary issue is what tissue effects are imparted by pulses. Asked alternatively, what physiological effects are mediated by changes in pulse size or pulse number as distinct from differences in mean hormone concentrations? Documenting amplitude- and frequency-specific hormonal effects in vivo has been difficult. Although most experiments match total hormone doses when comparing pulsatile and continuous stimulation, none has documented that the two stimulus modes confer identical integrated hormone concentrations at the target cell in vivo (95,96,97,98,99,100,101,102,103,104,105,106,107,108,109). A corollary issue for valid comparison is that hormone doses are chosen to include on the one hand the efficacy range and on the other hand the potency range to assess which is/are affected by pulsatile vs. continuous stimulation.

E. Mechanisms of pulse generation

1. In vivo pulsatility of pituitary cells.

Somatic cells of the liver and kidney secrete protein products, such as IGF-I or IGF binding proteins, in a constant nonpulsatile fashion (4). However, neuroectodermally derived cells release exocytotic granules intermittently in response to Ca²⁺ influx and membrane depolarization (60). Pituitary tissue disconnected from the hypothalamus can also generate small, frequent, and irregular pulses (110,111,112). Whether these patterns are physiological or artifactual is not clear. Tight junctions linking the three-dimensional network of somatotrope cells and rhythmic GHRH-inducible Ca²⁺ oscillations in somatotropes are potential physiological bases (59,113). The question then arises whether hypothalamic factors also synchronize or amplify pituitary microbursts, as distinct from inducing large discrete secretory bursts.

Pituitary hormones are secreted in low basal (nonpulsatile) amounts continuously and in prominent pulses of varying amplitude and timing. The precept that large pulses of LH, GH, and ACTH reflect intermittent hypothalamic drive has been verified unequivocally by administering selective releasing-factor antagonists, transgenetically silencing the expression of releasing factors and their receptors, heterotopically transplanting pituitary tissue, directly sampling hypophyseal portal blood, and infusing pulses of synthetic releasing factors (1,2,4,114). Hypothalamic signals such as GnRH, dopamine, and TRH putatively contribute to the genesis of FSH, prolactin, and TSH pulses, respectively.

2. GnRH pulsatility.

The neuronal mechanisms that generate episodic hypothalamic signals are not fully understood. In relation to GnRH neurons, multiple direct and indirect neurotransmitter inputs jointly modulate pulse generation in vivo (115). In addition, GnRH-secreting cells exhibit intermittent depolarization, cyclic GnRH gene expression, and recurrent exocytotic bursts in vitro (48). Although the precise dynamic properties of the in vivo GnRH neuronal network are not known, current models of episodic pulsatility require functional coupling among automata (independently firing units) and/or time-delayed negative feedback (116,117,118,119,120).

Synchrony within an interconnected ensemble can be achieved in theoretical systems by deterministic and stochastic feedback and feedforward controls. Feedback may be enforced via direct cellular contacts, secreted substances (autofeedback), diffusible metabolites, and/or downstream products (45,121,122,123). In relation to GnRH neurons, candidate signals include autofeedback by GnRH itself, inhibitory (γ-aminobutyric acid) and facilitative (glutamate) neurotransmitters, sex steroids, glia-derived peptides, soluble metabolites (adenosine, glucose, lactate, ATP), pituitary LH, and gonadal proteins (124,125,126). Hypothalamic kisspeptin (metastin) is a strong peptidyl activator of GnRH neurons, which could serve as an upstream organizer (115). Multiple collateral factors putatively modulate the unknown primary GnRH-pulsing mechanism depending upon species, gender, developmental age, and pathophysiology (127,128).

The primary objective of developing better models of pulse-generating neurons is to elucidate how time-varying feedback and feedforward by neurotransmitters, sex steroids, and peptides modulate pathophysiology (16,17,129,130,131). Formulations of hormone pulsatility should include dynamic components to explain burst timing and analytical components to quantify regulatory mechanisms. By reductio ad absurdum, comprehensive modeling of any pulse-renewal process would require knowledge of the strength and timing of all proximate feedforward and feedback inputs. Although current models are primitive when judged by this ideal, significant analytical capabilities have been achieved recently via simplified neuroendocrine constructs that allow estimation of pulse-generating dynamics (12,16,17,34,35,131).

3. GH pulsatility.

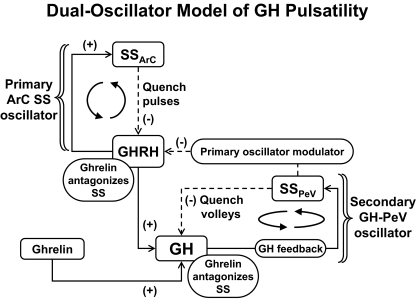
Both isolated and clustered neuroendocrine cells are capable of maintaining pacemaker-like activity. On a larger scale, constructs of time-delayed causal linkages among clusters of somatostatin (SS) neurons in the periventricular nucleus, GHRH neurons in the arcuate nucleus, and somatotrope cells in the pituitary gland are capable of generating recurrent GH pulses (18,132,133,134,135). One such dual-oscillator model is illustrated in Fig. 3. In this formulation, reciprocal interactions between GHRH and SS neurons in the arcuate nucleus mediate rapid GHRH and SS pulses that are out-of-phase, and episodic SS outflow evoked by pulsatile GH feedback onto the periventricular nucleus quenches the arcuate-nucleus oscillator reversibly (135). Ghrelin (GH-releasing peptide) opposes the efforts of periventricular SS on both the arcuate nucleus and pituitary gland (18). However, major questions remain. For example, do separate autonomous SS or GHRH pulse-generating mechanisms exist (4,18,134)? Do reciprocal interactions between hypothalamic GHRH and SS neurons actually mediate rapid GHRH pulsatility (4,133)? Does time-delayed feedback by GH onto SS and/or GHRH neurons set the timing of volleys of GHRH/GH pulses (136)? Do periventricular and arcuate-nucleus SS neurons generate SS pulses via local autonegative feedback (18)? And, do self-regenerating SS pulses generate GH pulses by intermittently repressing arcuate-nucleus GHRH neurons and pituitary somatotrope cells (18,132,135)?

Figure 3.

Interactive model postulated to account for rapid SS, GHRH, and GH pulses within a volley driven by a primary arcuate-nucleus (ArC) oscillator (top). Resultant multipulse volleys of GH are quenched by GH’s autofeedback on the periventricular nucleus (PeV), thus creating a secondary slower oscillator (bottom right). The GH-releasing peptide, ghrelin, amplifies the size of GH pulses by opposing the inhibitory actions of SS on GHRH pulses within ArC and on GH release by somatotropes in the pituitary gland. [Adapted with permission from L. S. Farhy et al.: Am J Physiol Regul Integr Comp Physiol 292:R1577–R1593, 2007 (18).]

4. ACTH pulsatility.

The locus of ACTH pulse generation putatively includes parvocellular CRH and/or arginine-vasopressin (AVP) neurons in the paraventricular nuclei (37,116). However, no definitive neuronal pulse-generator mechanism has been established (137). In addition, the degree to which CRH and AVP secretory bursts are coupled and independent has not been elucidated and may vary among species (37,116). Multidisciplinary efforts that exploit electrophysiological, molecular, cellular, and mathematical models will be needed to elucidate the primary pulse-generating mechanisms in the corticotropic axis.

5. Oxytocin pulsatility.

The magnocellular oxytocinergic system exemplifies pulse generation via positive feedforward by autoreceptors (39,121). Positive-feedback mechanisms elegantly inferred in this system may be instructive to modeling other neuroendocrine systems (117).

6. Other hormonal pulses.

Autonomic innervation of the parathyroid glands and pancreatic islets may contribute to coordinating the in vivo generation of discrete pulses of PTH, insulin, and glucagon (50,138). However, no current models explicate how innervating networks interact with an array of putative autocrine, paracrine, and systemic signals. For example, how does sympathetic innervation of parathyroid tissue modulate feedback by Ca²⁺ and vitamin D onto PTH synthesis and secretion (139,140,141)? How does autonomic innervation alter interactions among insulin, glucagon, and SS within pancreatic islets (50,62,123,142,143)?

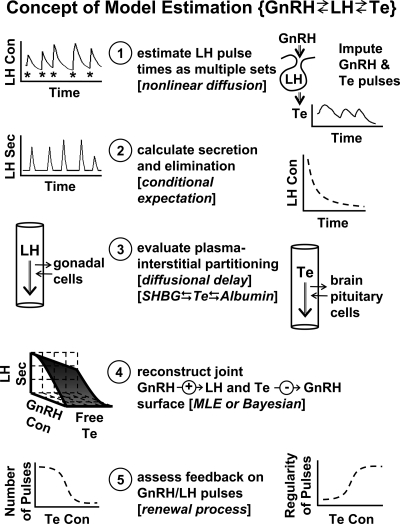
7. Implications.

If multiple feedback and feedforward inputs mediate the generation of coherent pulses, then a critical need in the field is to reconstruct the mechanisms of multipathway regulation in more explicit and tractable terms. To our knowledge, only two analytical models exist that permit noninvasive estimation of unobserved pathways in vivo, viz., for the male GnRH → LH → testosterone (Te) axis and the CRH/AVP → ACTH → cortisol axis (12,16,17).

F. Damping of secretory bursts in the circulation

1. Effect of dilution in sampling volume.

Hormone molecules sampled in the peripheral circulation are proximate in time but substantially removed in space from the secretory gland. The nominal time delay for blood-borne hormones to move from the site of secretion to the point of sampling would be less than the circulation time. This time latency (∼30 sec) is relatively insignificant analytically compared with nominal sampling intervals of 5–20 min and typical hormone half-lives of 5–300 min. More challenging is multifold spatially dependent dilution of secreted molecules within the systemic circulation. For example, the volume of the adult human pituitary gland is approximately 650 mm³ (0.65 ml), whereas the initial plasma distribution volume of GH is about 65 ml/kg or 4550 ml in a 70-kg adult (144,145). Thus, minimal dilution of GH is 7000-fold between interstitial fluid bathing somatotrope cells and recirculated blood in the forearm. The analytical hurdle is that volumetric dispersion of secreted hormone profoundly damps absolute peak concentrations, which are reduced further by irreversible metabolism and elimination. In the case of insulin pulses, the liver removes up to 85% of portal-vein insulin by selectively clearing (extracting) high-amplitude pulses (40,61,71).

2. Influences of basal secretion and half-life.

For any given pulse number, shape, size, and variability, increasing basal (nonpulsatile) secretion or hormone half-life elevates mean and interpeak hormone concentrations linearly. Higher interpulse concentrations in turn attenuate the signal-to-noise ratio, if the pulse-detection methodology depends upon the fractional (percentage) increment of the peak over the interpeak baseline concentration (27,30,146). In contradistinction, this is not a problem for pulse-detection methods that use the absolute increment, defined by the amount of hormone secreted per burst per unit distribution volume per unit time (15,147). The point is illustrated by comparing 10-min sampled 48-h LH and FSH concentration profiles, for which approximate slow-phase half-lives are 1.5 and 10.2 h, respectively (148,149), and percentages of basal secretion are 10 and 50%, respectively. The longer half-life and higher basal secretion rate of FSH than LH together elevate interpulse concentrations. Computer-assisted simulations show that, even if five times more LH than FSH were secreted per burst, fractional peak increments would be 1.8-fold smaller for FSH than LH because of the 6.8-fold longer half-life of FSH. For this reason discriminating pulsatile secretion is more difficult for FSH than for LH using methods that rely on peak/baseline hormone ratios.

The half-life of human chorionic gonadotropin exceeds 36 h, compared with 1.5 h for LH (148,150,151), which explains why quantifying putative pulsatility of the placental glycoprotein remains difficult (152). Disparate elimination kinetics also influence the relative sensitivity of detecting hormone pulses in different species. For example, the half-life of LH is nominally 15 min in the rat, 30 min in the sheep, 90 min in humans, and more than 720 min in the pig and horse (1,148,153,154,155,156). Thus, sampling must be more frequent in the rat to ensure identifying pulses accurately. A plausible suggestion is to obtain a minimum of three to five samples per half-life and per burst duration, whichever is more intensive.

G. Distinction between bound and free hormone concentrations in pulses

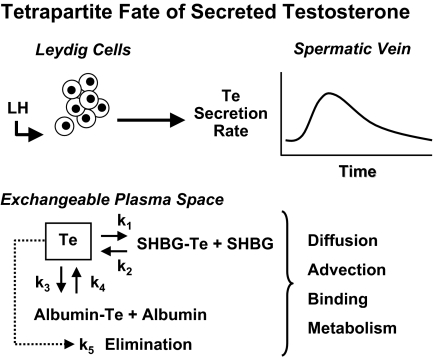
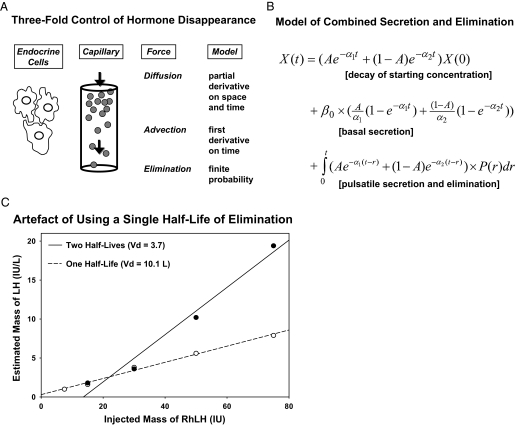
Uncertainty about the physiological role of free hormone concentrations has been heightened by incomplete understanding of the time-varying kinetics of bound and unbound moieties in vivo (1,4). Only a few models embody the nonequilibrium dynamics of unbound hormone concentrations when secretion proceeds in discrete bursts, viz., for GH, Te, and cortisol (16,34,35,144,157). On theoretical grounds, rapid entry of hormone molecules into the bloodstream during a secretory burst could transiently saturate plasma transport proteins, thereby elevating free (unbound) hormone concentrations disproportionately to total values (157,158,159). This is illustrated schematically for an LH-stimulated Te secretory burst in Fig. 4. The multipartite fate of Te includes binding to albumin or SHBG, aqueous diffusion (random molecular dispersion), linear advection (vectorial motion in blood vessels), metabolism, and irreversible elimination (16,34). Recent noninvasive analytical estimates give mean free Te half-lives of 0.77 and 2.5 min (rapid and slow phases) and a total Te half-life of 47 min in young men (34).

Figure 4.

Schema of tetrapartite fate of LH-stimulated Te in plasma. Subscripted “K” values denote rate constants for exchange of Te with binding sites on plasma proteins, solubilization in plasma water, and irreversible elimination.

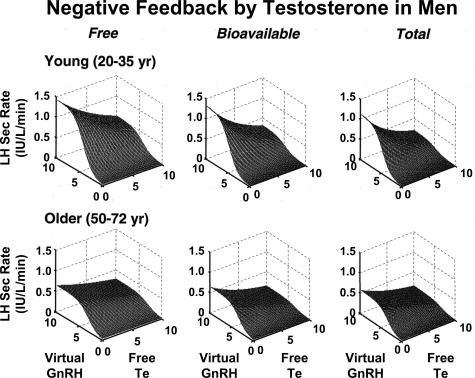
Whether transient marked elevations in free, bound, or total Te concentrations are needed to engage membrane or nuclear Te-signaling mechanisms is not known (128,160). In addition, which target-tissue effects of Te and estradiol (E₂) may be mediated by megalin or other cell-membrane receptors for steroid-bound SHBG is not yet clear (161). However, model-based estimates predict equal feedback repression of LH pulses by free, bioavailable, and total Te concentrations in healthy men (17). In the case of corticosteroid-binding globulin (CBG), rare patients with truncational mutations of CBG who exhibit more than 85% reduction in total cortisol concentrations maintain normal free cortisol and ACTH concentrations (162). This suggests that free cortisol mediates negative feedback. However, the presence of mild hypotension and fatigue in certain kindreds raises the question whether CBG or total cortisol concentrations mediate other tissue effects (162,163). Other effects could be indirect because CBG influences the total cortisol pool size and half-life (164).

Analytical models of nonequilibrium dynamics should be validated experimentally by combining highly frequent blood sampling with precise direct in vivo quantitation of total, bound, and free hormone concentrations. One investigation measured total and bioavailable Te concentrations in blood collected every 10 min for 24 h in two young men (16). However, in view of estimated half-lives of the dissociation of Te from plasma albumin and SHBG at 37 C of 0.2 and 3.8 sec, respectively, and a half-life of free Te’s elimination from plasma of 2.5 min (34), transient elevations in free and bioavailable Te concentrations would not be readily measurable at this sampling rate.

H. Sampling at or near the anatomic site of hormone secretion

Although direct sampling of endocrine glands is not possible in healthy humans for ethical reasons, monitoring hormone pulsatility at or near the secretory source in pathophysiology allows secondary validation of pulsatility models (12,16,17,40,65,165,166). For example, systemic Te pulses are difficult to discern, but direct catheterization of the internal spermatic vein in men with varicoceles revealed Te concentration pulses that are 65-fold larger than those in peripheral blood (51,167). Individual Te pulses so identified coincide with LH pulses generated 40 min earlier. Analogously, sampling the portal vein in patients with transhepatic portasystemic shunts disclosed a 6.6-fold insulin signal-to-noise ratio and a mean interpulse interval of 5 min (40,71). In vitro perifusion of human islets corroborated an interpulse interval of 4–6 min. Peripheral-venous sampling at 1-min intervals combined with high-specificity high-precision ELISA yielded comparable insulin pulse-frequency estimates in healthy individuals with peak-to-nadir insulin concentration ratios of 2.5 (168). The same frequency of insulin pulses has been established in the dog and rat by comparing direct pancreaticoportal vein sampling with peripheral arterial insulin measurements made every 1 min (70). Whether such pulses are perpetuated in interstitial fluid is not known, although oscillations of corticosterone are detectable in the brain (169).

II. Physiological Implications of Pulsatile Hormone Signals

A. Downstream effects of GHRH and GH pulses

Quantifying secretory-burst number, size, and shape confers insights into upstream mechanisms that regulate pulse generation (Section I.E). Extensive studies document that pulse properties differ in relation to species, gender, development, nutrition, and age and vary overtly in stress, illness, and disease (1,2,4). In contradistinction to elegant analyses in laboratory models (170,171), relatively little is known in the human about in vivo tissue-specific effects of hormone pulses. A preeminent exception is GnRH’s drive of LH secretion, in which there is an unambiguous physiological necessity for intermittent stimulation of gonadotrope cells in mammals (172,173,174,175). In animal models, GH pulsatility mediates sexually dimorphic regulation of hepatic and muscle gene expression, somatic growth, and negative feedback on the hypothalamus (4,176). Although fewer studies exist in humans, continuous GH delivery in hypopituitary patients maintains systemic (liver-derived) IGF-I, and lipoprotein(a) concentrations to a greater degree than repeated injections (84,98,177,178). Conversely, bolus injections of GH stimulate visceral lipolysis and elevate HDL concentrations more effectively than constant infusions (84,86,98,179,180). The finding that GH pulses increase insulin requirements more than constant GH infusion in young diabetics further underscores the organ specificity of pulsatility effects.

B. Target-tissue effects of ACTH and testosterone (Te) pulses

Few clinical studies have assessed pulsatile effects of hormones other than GnRH and GH. Continuous infusion of CRH sustains ACTH pulses, and constant infusion of ACTH over 72 h evokes a sustained rise in cortisol production but only a brief increase in aldosterone secretion (106,181,182). In another model, continuous infusion of Te over 48 h suppressed LH pulses more rapidly than bolus Te injections in young men pretreated with ketoconazole to block testicular steroidogenesis (109). The reproducibility and generality of these observations are not yet established.

C. Other clinical examples (oxytocin, PTH, insulin, glucagon)

1. Oxytocin.

Oxytocin is secreted episodically (37,39) and is subject to frequency control in humans (63). Both constant infusion and rapid pulses of oxytocin evoke uterine contractions. Three randomized clinical trials involving a total of 1064 women reported that pulsatile compared with continuous oxytocin infusions reduce the duration of labor and/or the total dose of peptide required (107,183,184). A fourth study in 94 pregnancies described no difference between the two modes of administration (185). Thus, clinical data favor the notion that pulses of oxytocin are physiologically relevant but not obligatory to stimulate human myometrial contraction in parturition. Whether oxytocin pulses convey unique signaling information to enhance milk letdown is not known.

2. PTH.

PTH pulses recur every 8.5 (range, 5–12) min and constitute about 50% of total PTH secretion in the normal human (44,45,49). No clinical studies have examined prolonged tissue effects of such rapid low-amplitude pulses in PTH-deficient subjects. However, once-daily PTH injections are superior to constant 24-h PTH infusions in stimulating osteoblastic activity (100,186). This outcome was foreshadowed by studies in the rat showing that daily infusion of PTH for 1 h, but not for 2, 6, or 24 h, is strongly anabolic to bone (100). Two models have been advanced to account for this temporal selectivity, one based upon receptor kinetics and the other upon bone-cell turnover (187,188). The clinical application of this insight is once-daily administration of biosynthetic N-terminal PTH (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34) for the treatment of osteoporosis (189). The experience with PTH supplementation illustrates that the therapeutic benefit of a particular time mode of hormone delivery (once daily) may derive from factors other than precise mimicry of the primary pulse pattern (a pulse every 8.5 min). Relevant factors determining therapeutic responses putatively include the kinetics of signal transduction, gene transcription, mRNA and protein synthesis, the operation of comodulatory hormones, and systemic and local feedback adaptations (141,187,188). Comparable insights are needed for other pulsatile hormones.

3. Islet-cell hormones.

Insulin and glucagon are released in pulses that recur every 4–7 min and are out of phase (40,50,62,71,168,190). However, whether pulsatile is more effective than continuous insulin infusion in suppressing hepatic glucose output, stimulating muscle glucose uptake, or inhibiting lipolysis in normal volunteers and diabetic patients remains controversial (102,191,192,193). Available outcomes suggest that a sustained (>4 h) train of rapid insulin pulses (periodicity ≤ 10 min) is more effective than continuous stimulation in inhibiting gluconeogenesis in a low-glucagon milieu when submaximally effective concentrations of insulin are achieved. By way of caveats, no clinical paradigm has employed portal-vein pulses every 4–6 min, although tolbutamide stimulation has been proposed as a way to induce portal insulin pulses; statistical power for small negative studies is typically low; no formal metaanalysis exists; and it is unknown whether such rapid pulses persist in tissues.

Several studies have compared the effects of pulsatile and constant glucagon delivery on hepatic glucose output. In the dog, glucagon and insulin pulses may not be critical to hepatic effects (104). In the human, outcomes include attenuated (one analysis) and accentuated (four analyses) hyperglycemic, lipolytic, and/or ketogenic effects of glucagon pulses compared with continuous infusions in healthy young men and NIDDM patients. In the only study available on satiety as the endpoint, pulsatile and continuous glucagon injection had equal effects. The caveats noted for insulin studies apply to glucagon also.

4. Other hormones: role of pulses.

Although data for GH were reviewed recently (4), no comprehensive clinical studies have compared the target-tissue impact of pulsatile vs. continuous stimulation with LH, FSH, TSH, prolactin, ADH, estrogen, cortisol, aldosterone or l-T₄. One investigation in women found that intermittent sc injection mimicked continuous infusion of FSH (194), consistent with the long plasma half-life of human FSH (149). In the male rat and sheep, continuous and pulsatile injections of LH stimulated gonadal Te secretion comparably (95,96). In a limited number of clinical investigations, continuous submaximal stimulation with CRH, TRH, GHRH, and GH-releasing peptide maintained pulsatile secretion of ACTH, TSH, and GH, respectively (41,106,181,195,196). One comparison indicated that GHRH pulses were more effective than continuous GHRH infusion in provoking deep sleep in young men (97). Under in vitro perifusion conditions, pulses of LH stimulated greater progesterone secretion by human granulosa-luteal cells than continuous LH delivery (197). In the monkey, TRH pulses preferentially elevated prolactin, whereas constant TRH infusions especially increased TSH concentrations (103). No similar analyses are available in humans. Accordingly, knowledge of organ-selective and effector-specific actions of hormone pulses remains in its infancy in most cases, except for GH and GnRH.

D. Experimental paradigms to appraise pulse effects in vivo

Excellent studies of frequency-dependent receptor signaling exist in simple in vitro models, such as yeast and single cells (122,124,131,173). Ideal in vivo models to assess tissue effects of pulsatile hormonal stimulation would include: 1) rapid, reversible, and selective suppression of endogenous hormone concentrations to obviate confounding; 2) controlled iv delivery of physiological amounts of biologically active hormone; 3) comparison of physiological and nonphysiological (negative control) secretory-pulse patterns; and 4) concurrent precise, sensitive, valid, and repeated measurements of more than one target-tissue response. Measuring several responses concurrently is valuable because hormone-signaling patterns often convey distinct information to different cells (4). Experiments establish this in relation to GH signaling in brain, skeleton, muscle, and liver. For example, GH pulses are optimal for central nervous-system negative feedback and skeletal and muscle growth, whereas continuous GH stimulation is favored for hepatic expression of IGF-I, GH-binding protein, and low-density lipoprotein receptor (4,198). A relevant molecular explanation is that GH pulses preferentially induce nuclear signaling via STAT5b and HNF4α, which activate anabolic (male-like) patterns of gene transcription (199). Clinical studies of the relevance of pulsatile signals may eventually be facilitated by new drug-delivery systems, such as microchip polymers capable of releasing trains of pulses of a drug or hormone (200).

III. Altered Pulsatility Control in Pathophysiology

A. Neuroendocrine neoplasia

1. Secretory autonomy.

A consistent feature of functioning neuroendocrine tumors is relative secretory autonomy, reflected by a reduction in feedback sensitivity (201,202,203). Secretory autonomy is not absolute, inasmuch as high concentrations of the feedback signal may inhibit secretion partially or substantially. Examples include glucocorticoid-mediated feedback on ACTH secretion by corticotropinomas (Cushing’s disease); saline-induced suppression of aldosterone secretion by aldosteronomas (Conn’s syndrome); IGF-I-enforced inhibition of GH production by somatotropinomas (acromegaly); vitamin D- and Ca²⁺-dependent repression of PTH secretion in hyperparathyroidism; T₄-imposed diminution in TSH release by thyrotropinomas; sex-steroidal feedback on LH or FSH secretion by gonadotropinomas; and insulin-induced suppression of C-peptide secretion by insulinomas (44,202,204,205,206). Toxic thyroid nodules, adrenal and gonadal steroidogenic tumors, gastrinomas, glucagonomas, somatostatinomas, and ectopically secreting benign and malignant neoplasms also exhibit sparing suppressibility by relevant downstream products (201). Thus, relative independence of secretion from negative feedback characterizes the majority of endocrine tumors.

The mechanisms subserving secretory autonomy are not clear. In vitro analyses indicate that expression of feedback-activated receptors may be deficient in some neuroendocrine tumors, such as IGF-I receptors in the case of somatotropinomas and glucocorticoid receptors in corticotropinomas (207,208,209). Postreceptor and nonreceptor-related mechanisms may also contribute to feedback resistance. For example, autonomous tumors may metabolize the feedback hormone more rapidly than normal tissue. This mechanism could apply to corticotropinomas with elevated 11 β-hydroxysteroid dehydrogenase type II, which inactivates cortisol (210).

2. Disruption of orderly secretory patterns.

Disruption of organized secretion characterizes most endocrine tumors. Examples includes somatotropinomas, prolactinomas, corticotropinomas, aldosterone- and cortisol-secreting adrenal adenomas, and parathyroid neoplasms (43,211,212,213,214). Pathophysiological patterns typically comprise three quantifiable abnormalities: 1) decreased serial orderliness, regularity, or reproducibility of hormone-concentration profiles quantified by the approximate entropy (ApEn) statistic (215); 2) frequent but diminutive secretory bursts (reduced mass of hormone release per pulse) estimated by deconvolution analysis to correct mathematically for hormone half-life (213,216); and 3) elevated nonpulsatile hormone secretion inferred by high interpulse hormone concentrations or increased basal secretion rates (211,212,217,218).

GH secretion in patients with acromegaly exemplifies the foregoing alterations by being more irregular in pattern and timing with inconsistently shaped, frequent, small peaks superimposed upon high baseline interpulse GH concentrations (204,211). Imposition of negative feedback by physiological inhibitors (glucose) or pharmacological repressors (a SS analog) usually fails to restore orderly GH secretion patterns (204). In contradistinction, surgical microadenomectomy reinstates physiological secretion patterns, indicating that anomalous GH secretion is due to tumoral effects (218). Successful transphenoidal pituitary surgery in Cushing’s disease also normalizes ACTH secretory patterns in patients with corticotropinomas (212,216,217).

Similar tripartite secretory derangements characterize benign prolactin, cortisol, aldosterone, and PTH-producing tumors (43,213). Whether invasive endocrine neoplasms manifest comparable disruption of normal secretory patterns is uncertain. However, ACTH secretion patterns are paradoxically more orderly in patients with adrenalectomy-associated corticotropinomas (Nelson’s syndrome) than benign corticotropinomas (Cushing’s disease) (219).

In summary, neuroendocrine tumors tend to produce multiple, small, irregular pulses superimposed upon a high basal rate of secretion, which is not fully suppressible by negative feedback.

B. Type II (non-insulin-dependent) diabetes mellitus

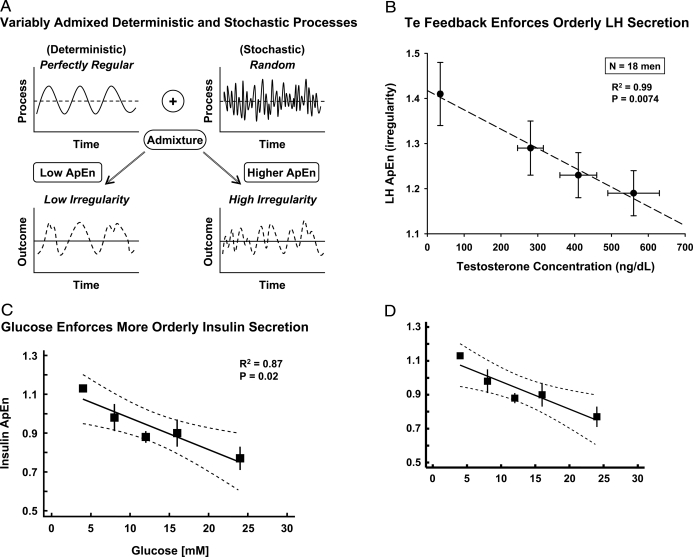
Two prominent anomalies of insulin pulsatility in type II diabetes mellitus [non-insulin-dependent diabetes mellitus (NIDDM)] are diminished secretory-burst mass (as evaluated by deconvolution analysis), and decreased secretory-pattern orderliness (as assessed by ApEn, a regularity measure) (73,220). Smaller pulses are also detected in evolving type I diabetes mellitus (221). Reduced pattern regularity is detected in about 50% of glucose-tolerant first-degree relatives of patients with NIDDM and in patients with diagnosed NIDDM (73). If verified, these data could indicate that attenuation of secretory coordination is a harbinger of metabolic disease or a marker of mild insulin resistance and visceral adiposity. The last two considerations are suggested because small insulin pulses and irregular patterns also occur in obese and healthy older individuals (74,81,222). Conversely, endurance training and weight loss enhance secretory regularity (222). These changes are relatively specific because insulin pulse frequency estimated by sampling blood every 1 or 2 min is normal in NIDDM patients and aging adults (223).

C. Fasting-induced hypogonadism

Extended nutrient deprivation delays or arrests pubertal progression in children (4). Even brief fasting inhibits the secretion of LH and gonadal steroids, and in lesser measure FSH (224,225). In the sheep and rat, undernutrition causes diminutive GnRH and LH pulses. Small LH pulses and low Te concentrations typify fasting-associated hypogonadotropism in young men, which can be ameliorated by exogenous pulses of GnRH (224). Quantifiable regularity of LH secretion patterns increases during fasting, suggesting that negative feedback by Te declines less than feedforward by GnRH. The inference follows because regularity (orderliness) of secretion patterns is maintained by negative feedback (226). Some investigators have reported that LH pulse frequency declines in fasting individuals (reviewed in Ref. 227). This might be due to false-negative errors (pulse censoring) because of insufficiently intensive blood sampling. This flaw became apparent two decades ago in studies of LH, GH, insulin, and PTH secretion (1,2,66,76,228,229).

D. Hyperprolactinemia secondary to pituitary-stalk disruption

Interruption of hypothalamic inhibitory signals to lactotropes results in secondary hyperprolactinemia, the magnitude of which overlaps that of prolactinomas. The question arises whether the dynamics of prolactin secretion in the two pathophysiologies can be distinguished objectively. Recent analyses reveal smaller prolactin pulses and less regular secretion patterns in both primary tumoral and secondary hyperprolactinemia compared with euprolactinemia (214,230). However, tumoral prolactin secretion is marked by more frequent peaks than benign hyperprolactinemia. The basis for apparently increased pulse number is not clear, but might reflect bursts of prolactin released by clusters of autonomous tumor cells (231).

E. Primary hyperparathyroidism

The pulsatility phenotype associated with PTH-secreting adenomas and secondary hyperparathyroidism comprises a normal pulse frequency with irregular patterns superimposed upon high basal concentrations (44,205). Negative feedback imposed by Ca²⁺ infusion fails to repress PTH secretion appropriately or normalize irregular PTH secretion patterns fully (45,232,233).

F. Cortisol-secreting adrenocortical adenomas

Few investigations have applied modern analytical methods to evaluate secretory patterns in primary adrenal hypercortisolism. The only detailed study documented a quadruple phenotype of small, frequent, and irregular secretory bursts superimposed upon high basal secretion (213).

G. Primary hyperaldosteronism

Several frequently sampled analyses of aldosterone pulsatility have been conducted, three in normal subjects and one in patients with primary hyperaldosteronism (43,54,234,235). The study of aldosteronomas identified secretory aberrations typical of other endocrine tumors, viz., frequent irregular pulses with elevated baseline secretion (43). Whether these aberrations are reversed by unilateral adrenalectomy remains unstudied. In healthy men, acute inhibition of angiotensin converting-enzyme activity amplified renin secretory-burst size and enhanced the regularity of renin secretion without influencing aldosterone patterns (234).

H. Failure of the target organ

A fundamental query in pathophysiology is the nature of neuroendocrine adaptations to feedback withdrawal. Patterns of TSH secretion in normal individuals and patients with primary thyroidal failure or pituitary tumors have been evaluated to a limited extent (15,236,237). A consistent observation is that TSH pulses are superimposed upon significant (10–35%) baseline secretion. In addition, patients with primary hypothyroidism exhibit larger TSH secretory bursts with irregular patterns, albeit of normal frequency and still copulsatile with prolactin (52,226). Several months of l-T₄ replacement reinstate near-physiological burst size and regularity (226).

Fasting-associated metabolic changes, which include reduced IGF-I concentrations, unleash large bursts of GH in irregular patterns but at a normal frequency, which are thus distinguishable from acromegaly (211). Irregularity is repressed by IGF-I infusion (226), consistent with expected feedback effects (238).

Another approach to assessing the impact of target-organ failure is experimental interruption of the negative-feedback signal. Pharmacological inhibition of Te synthesis in young men evokes an irregular pattern of small, frequent LH pulses with elevated interpulse concentrations (239). All four features are reversed by iv or transdermal Te repletion (109,240). This is consistent with Te-mediated feedback effects on GnRH/LH secretory-burst number, the regularity of the secretion process, mean LH concentrations, and basal (nonpulsatile) LH release.

Metyrapone-induced cortisol depletion paradoxically enhances the orderliness of ACTH release (35,241). Similar but less pronounced regularity changes are observed in patients with 21-hydroxylase deficiency. Experimental reduction in Ca²⁺ concentrations augments the quantifiable regularity of PTH secretory patterns (45). The exact physiological bases for heightened regularity of ACTH and PTH secretion under low feedback are not known. On theoretical grounds, greater pattern regularity denotes enhanced coordination of the regulatory network (238,242). Thus, possible explanations for greater orderliness include more synchronous feedforward by CRH and AVP on corticotropes and more organized neurogenic (or other) inputs to PTH-secreting cells (44,45).

In summary, disinhibition of negative feedback mimics some features of autonomous neuroendocrine tumors.

IV. Early Methods of Pulse Analysis

A. Empirical threshold approaches

Empirical methods, as defined here, are procedures based upon intuition and reason, which have not been both validated experimentally and verified by mathematical proof. Empirical criteria for detecting discrete peaks in serial hormone concentrations typically specify a threshold increase greater than that explicable by intraassay variability. Assay variability is estimated by the sd or the coefficient of variation (sd/mean × 100%) of replicate measurements in the standard curve and/or experimental samples. Examples are the Santen and Bardin method (for which the threshold is a 20% increment in any single concentration), Cluster analysis (for which the operator specifies a critical two-sample t-statistic for accepting significant upstrokes and downstrokes in a peak), and the regional coefficient of variation (CV) method (which employs local sample variance to test for peaks) (1,243,244). Limitations of these fixed-criterion methods include variable false-positive and false-negative errors introduced by unequal sampling density (e.g., 5-min vs. 10-min intervals) or duration (4 h vs. 24 h), nonuniform pulse shape (abrupt vs. slow rise in concentrations), sample outliers, and variable assay precision.

B. Semiempirical baseline strategies

Semiempirical methods are defined here as those which use nadir and/or baseline estimates to specify superimposed pulsatility but lack the combination of primary in vivo experimental validation and direct mathematical proof. Desade, Ultra, Detect, and Pulsar discriminate baseline or nadir concentrations by numerical filtering, baseline detrending, or line-segmentation criteria (245,246,247). The first three techniques incorporate secretion estimates, thus representing deconvolution approaches. As reviewed earlier (1,2), the performance characteristics and limitations (preceding paragraph) of empirical and semiempirical methods are quite similar. For example, sensitivity and specificity are about 85% for Cluster analysis of 10-min LH data (248,249,250).

V. Criteria for Optimal Pulse Analysis

Several consensus conferences have attempted to formulate minimal requirements for optimal pulse evaluation (146,251). Cardinal but nonexclusive suggestions include the following: 1) high discriminative accuracy (≥90%) of signal detection; 2) direct empirical validation in vivo, in vitro, and by computer simulations; 3) mathematical verification of reproducible parameter estimates; 4) robustness to sampling schedule and assay type; 5) low sensitivity to occasional outliers; 6) automated implementation; 7) quantitation of relevant endpoints like elimination kinetics, basal secretion, pulse signal size (amplitude or mass), duration, shape, and number; and 8) utilization of relevant physiological knowledge of the system.

The challenge inherent in fulfilling the foregoing collective criteria simultaneously has stimulated development of new methods.

VI. Methodologies for Secretion Estimation (Deconvolution Analyses)

A. Motivation

Hormone concentrations are measurements of the amount of hormone contained in a unit of distribution volume (e.g., micrograms/liter for GH, IU/liter for LH, picomoles/liter for glucagon). Any single hormone concentration contains limited information about the endocrine system because the value is determined simultaneously by five distinguishable factors: 1) the amount (mass) of hormone secreted previously and simultaneously, which has not yet been removed; 2) distribution degradation, transformation, or removal (elimination) of measured hormone; 3) unexplained (random) variations in the host or biological system; 4) unknown procedural errors introduced by obtaining the sample; and 5) the precision, validity, reliability, sensitivity, and specificity of the assay.

Recent enhancements in assay performance and sample collection (items 4 and 5 above) include automated blood sampling; greater sensitivity, specificity, precision, and reliability of robotics-assisted double-monoclonal assays; and more rigorous assay-data reduction methods followed by electronic transfer of files (75,79,80). Assay specificity is being addressed by mass spectrometry and ELISA methods, as reported recently in the case of gonadotropin, catecholamine, cortisol, sex steroids, GH, IGF-I, and insulin (252,253,254,255,256,257,258,259,260,261,262). Given optimal sampling and assay conditions, the remaining challenges are to quantify the mass of hormone secreted in pulses and basally (item 1), estimate the amount removed (item 2), and allow for unexplained biological variability (item 3).

B. Definition of deconvolution analysis

Determining underlying secretion or elimination rates (or both) from a hormone-concentration profile is termed deconvolution analysis. According to lexicons, deconvolution is a process by which the result produced by two (or more) interlinked processes is disentangled or disentwined to reveal the underlying components. The etymology is de, from, and convolvere, to roll together. Deconvolution procedures estimate the simultaneous contributions of accumulation (secretion) and dissipation (elimination) to a measured outcome (hormone concentrations). The idea is to decompose a concentration profile into underlying secretion and elimination. Concentrations [C(t)] are described by 1) the elimination of previously secreted hormone; 2) ongoing secretion S(t) into and elimination E(t) from the system; and 3) random experimental variability, as follows:

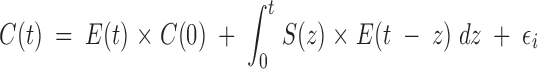1

The first term on the right side of the equation represents the concentration remaining at time t given a starting concentration, C(0), acted upon by an elimination function, E(t). The middle term is a convolution integral, which denotes that secretion and elimination between time zero and t are evaluated by summing the product of their effects over all infinitesimally short intervals, dz. Taking the product of the two functions, S(z) and E(t − z), indicates that the effects of input and output contribute jointly to describing how much of the secretion at time z remains in the concentration at time t. The expression (t − z) in the elimination function denotes that removal only proceeds after secretion has occurred at time t. The rightmost term, ε_i, signifies unexplained variability in the observed concentrations. Random variability may be technical or biological in origin.

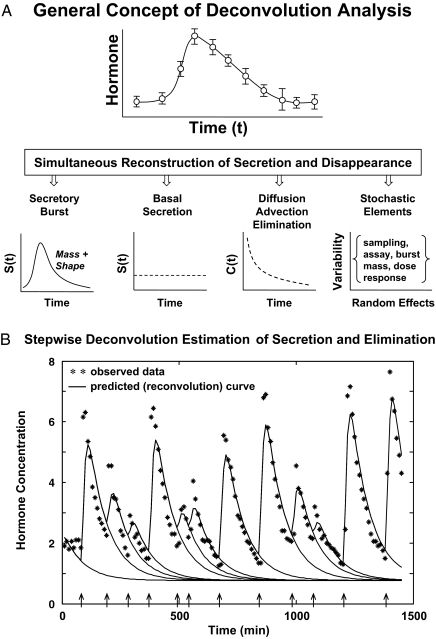
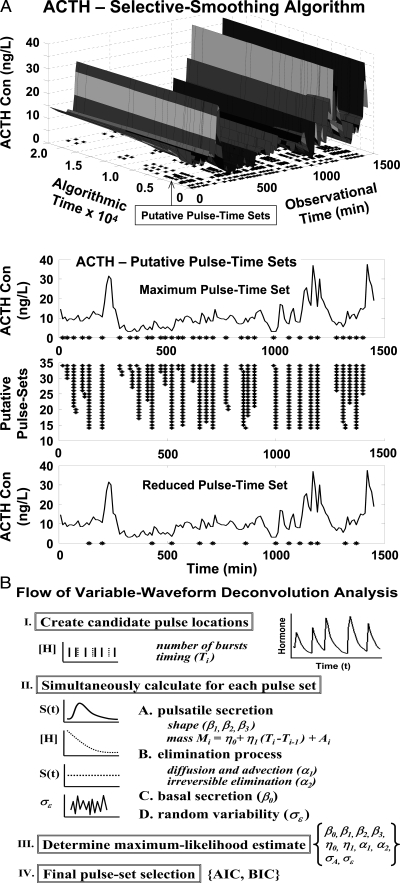
Figure 5A schematizes the fundamental notion of deconvolving (unraveling) a concentration profile into component secretion and elimination rates. Secretion comprises a variably pulsatile (intermittent) and stable basal (nonpulsatile or slowly varying) component, and elimination a biexponential process (26,32). Reconvolution is the inverse operation of calculating C(t), given known or estimated S(t) and E(t). One estimates secretion and elimination parameters iteratively by repeatedly comparing reconvolution curves with measured concentrations. Figure 5B shows one of the steps in this interactive estimation process. Deconvolution methods comprise various analytical algorithms with individual assumptions (Table 1).

Figure 5.

A, Principle of deconvolution analysis to decompose a hormone concentration peak (top) into an underlying secretory burst of finite mass and shape, basal secretion, an exponential elimination process, and random (stochastic) effects (bottom, left to right). B, One step in the interactive process of repeatedly estimating pulse amplitudes (continuous line) and hormone half-life (interrupted line) simultaneously to fit hormone data shown by the asterisks. Arrows depict putative pulse-onset times.

Table 1.

Deconvolution methods: overview

Type	Concept	Examples	First author (Ref.)
Nonparametric component	Smoothed secretion assumed half-life	Insulin	Turner et al. (355)
	Gaussian smoothing	PULSE	Veldhuis et al. (24,30)
	Smoothed secretion	Cortisol	Jusko et al. (22)
	Smoothed secretion	LH	Rebar et al. (21)
	Smoothed baseline	ULTRA	Van Cauter et al. (23)
	Use known kinetics	WENDEC	De Nicolao and De Nicolao (356)
	Maximum-entropy Bayesian method; spline smoothing for basal secretion; pulses superimposed; random effects	Maximum-likelihood and Bayesian estimation	Yan et al. (357)
Discrete	Calculate sample-by-sample secretion rate given half-life	DETECT	Oerter et al. (245)
Parametric	Assumed kinetics: blind method to estimate secretion and kinetics using gaussian bursts	PULSE4, DECONV	Johnson et al. (276), Veldhuis et al. (11,27,93)
Combined nonparametric and parametric	Identify pulses and predict secretion and kinetics; linear or exponential pulse upstroke; poisson pulse timing	Generalized cross-validation, autoregressive with feedback, Bayesian and MLE	O'Sullivan and O'Sullivan (317), Diggle and Zeger (299), Kushler and Brown (246), Guo et al. (358)
	Estimate secretion and kinetics conditional on pulse times	Stochastic components allowable; MLE structure; flexible gamma waveform; Weibull pulse-renewal process; pattern search algorithm with nonnegativity constraint	Keenan et al. (12,16,32), Chattopadhyay (36)
Dual secretory-burst waveforms	Two secretory-burst shapes permitted	Model-selection criteria for 1 vs. 2 burst types	Keenan et al. (15,35)
Bayesian model	Pulsatile and basal secretion jointly estimated	Bayesian and stochastic models nonparametric	Johnson (293), Breda and Cobelli (359)
		Parametric	Keenan et al. (26)
Binding proteins and free hormone included	Pulsatile and basal secretion and unbound-hormone kinetics estimated	Estimate free Te and cortisol kinetics	Keenan et al. (16,17,34,35)
Estimate unobserved hormone signal in tripartite system	Pulsatile and basal secretion; stochastic pulse allowances; feedback and feedforward estimation	GnRH-LH-Te ensemble; reconstruct unobserved GnRH signal; mathematically verified realizability	Keenan et al. (17), Chattopadhyay et al. (36)

Definitions: Bayesian estimation—incorporation of prior knowledge as mathematical conditions, e.g., the measured concentrations, populational distribution of half-lives, to obtain a maximum a posteriori estimate of the parameters. 

Blind deconvolution—estimation of both the input (secretion) and the output (elimination) process, when neither is known. 

Linear system—a model in which a change in an input parameter (secretion rate or half-life) produces a proportionate (linear) change in output (mean concentration). 

MLE—maximum-likelihood estimation wherein the parametric solution is asymptotically unique. 

Model—a theoretical construct used to visualize, predict or estimate the properties of a phenomenon. 

Model-selection criteria—statistical rules for choosing a low-parameter model that is most representative of the data; e.g., AIC or BIC. 

Nonparametric deconvolution—regularized (smoothed) estimation of secretion rates whether or not bursts are present, given elimination rates and a rule for penalizing excessive smoothing. 

Parametric deconvolution—model-defined algebraic construct to estimate secretory-burst shape, size, and number, basal secretion, hormone elimination, and error terms. 

Combined parametric and nonparametric deconvolution—candidate pulse times are proposed independently as discrete values; then, secretion and elimination parameters are estimated as continuous variables conditional on the choice of pulse times. 

C. Fixed half-life deconvolution methods

Deconvolution methods that utilize a priori half-life estimates were developed first historically, as reviewed elsewhere (21,22,263,264). Assuming a known half-life makes the deconvolution problem of calculating secretion (given concentrations) more tractable mathematically (93). A host of nonparametric and some parametric methods are in this category (Table 1). If half-lives are restated as rate constants in the E(t) function (t_½ = ln 2/rate constant), deconvolution permits one to calculate secretion rates, S(t), from serial hormone concentrations, C(t). A caveat is that hormone kinetics (fast and slow half-lives and their relative amplitude contributions) must be estimated validly and precisely in the actual physiological or pathophysiological context under study (e.g., matched for hepatic and renal function, hydrational status, gender, age, and body composition). An issue is whether a mean kinetic estimate obtained in one cohort of subjects is adequately representative in another cohort and among different individuals. In the latter regard, expected biological variability of kinetics among individuals has stimulated the development of so-called blind deconvolution methods to estimate secretion rates and hormone half-lives simultaneously from the hormone-concentration profile (11,15,32). Nonetheless, simultaneous estimation of secretion and elimination rates introduces several fundamental challenges.

D. Challenges in deconvolution analysis

Valid deconvolution analysis requires precisely framing an otherwise ill-posed mathematical problem to allow a computer-assisted solution. The problem is considered ill-posed because several different answers could result from analyses, unless suitable precautions are stipulated. Table 2 illustrates this difficulty, wherein different deconvolution estimates arise for the same method applied to the same data set (LH profiles). Accordingly, a necessary feature of deconvolution analysis is to obtain statistically reliable (reproducible) and valid (true) estimates of basal and pulsatile secretion and hormone elimination simultaneously. Stated technically, the mathematical objective is to guarantee asymptotic parameter uniqueness, defined as model realizability. The point is that many different solutions should not be possible for the same data set. The challenge of ensuring unique estimates of hormone secretion and elimination emerges because of strong statistical interdependence (high cross-correlations) among four classes of parameters (93):

• Half-life of hormone elimination.

• Basal secretion rate.

• Secretory-burst size (amplitude or mass) and shape (waveform).

• Number and locations of secretory bursts.

Table 2.

Example of ill-posed deconvolution problem

	Infused LH profile1			Simulated LH profile2			Sheep LH profile3
A. Starting Estimates
Burst sd (min)a	1	10	30	1	10	30	1	10	30
Half-life (min)	15	50	150	15	50	150	15	50	150
Basal secretionb	0	0.01	0.1	0	0.01	0.1	0	0.01	0.1
Starting concentration	1	1	1	1	1	1	1	1	1
B. Deconvolution results
Frequency (per session)	6	6	zero	16	17	4	zero	zero	zero
Burst sd (min)a	2.6	2.5	−9.9	0.74	1.3	0.5	−0.58	−100	1.2
Half-life (min)	61	49	551	53	50	334	2.2	2.3	391
Basal secretionb	0.03	0.05	0.009	0.02	0.02	0.003	3.0a	2.8	0.02
Mass/burstb	5.9	5.5	zero	3.0	2.9	1.7	zero	zero	zero

Analyses used a web-based automated deconvolution (AutoDecon) program downloaded from http://mljohnson.pharm.virginia.edu/downloads.html on 11/07/07. The three 10-min LH profiles are listed in the Appendix (published as supplemental data on The Endocrine Society’s Journals Online web site at http://mend.endojournals.org) as ″Lhinfused,″ ″Lhsimulated,″ and ″Lhsheep.″ 

^{1, 2, 3} True pulse numbers were 6, 16, and 7, respectively, based upon specified LH injections, explicit simulations, and portal-venous GnRH pulses. 

^asd of Gaussian burst. 

^bConcentration units per minute for basal secretion and concentration units for mass. 

Recent methods to address this impasse exploit specialized model forms and simplifying assumptions.

E. Simplifying assumptions in deconvolution analysis

The particular assumptions underlying any method must be recognized and shown to be noncritical to the study context. Assumptions fall into several broad categories: 1) the half-life and distribution volume (V_d) do not change during the observation interval; 2) basal secretion is arbitrarily time-invariant (a fixed value), zero, slowly varying or some lower bound (e.g., 5%) of all sample secretion rates; 3) pulses are instantaneous secretion events (delta functions) or finite-duration bursts of homogeneous symmetric or asymmetric shape; 4) candidate pulses are identified first, and then secretion and elimination parameters are estimated, conditional on each set of possible pulse times; and 5) stochastic contributions (random effects) enter into the observations and the biological dynamics.

F. Impact of analytical assumptions on secretion estimates

1. Uniformity and reproducibility of half-life and distribution volume.

The assumption that hormone half-life and distribution volume (V_d) are uniform during a sampling session has not been rigorously tested. In one study, the slow component of the biexponential half-life of injected GH in healthy young men was several minutes shorter in the morning than evening, although V_d was not different (265). The exact basis for and reproducibility of the inferred diurnal variation are not known. In another investigation, the metabolic clearance rate (MCR) of infused cortisol [where MCR = (ln 2/half-life) × V_d], was higher after ACTH stimulation than saline infusion (266). This outcome would occur if unbound (free) or albumin-bound cortisol were removed more rapidly than CBG-bound cortisol (35). The same phenomenon could occur briefly in the morning when free cortisol concentrations are higher than in the evening and during stress-induced or pathological cortisol elevations (35,164,267).

A second assumption is that a mean cohort estimate of half-life is appropriate to apply to individual subjects. Data on this point are not extensive. However, analysis of multiple C-peptide decay curves revealed intersubject CVs for the rapid and slow-phase half-lives of 24 and 18.5%, respectively (268). In contrast, intraassay CVs for many hormones are approximately 3–6.5% (75,269). Interindividual CVs for slow-phase half-lives of infused GH in octreotide-treated healthy adults and of LH in GnRH antagonist-treated normal men averaged 20 and 32%, respectively (145,265,270,271,272). Published estimates represent minimal CVs because disease, posture, hydration status, age, gender, and body composition further modify hormone kinetics. For example, in one study visceral adiposity reduced the half-life and increased the MCR of recombinant human GH by 33% in women (273), and in another age augmented the MCR and V_d of recombinant human GH by as much as 65% (274). Thus, investigators must be aware that using fixed cohort-based kinetics may bias secretion estimates in some subjects.

2. Basal hormone secretion.

Basal secretion may be defined as nonpulsatile (constitutive) hormone release, which may or may not be time-invariant over prolonged intervals. The semantically similar term, baseline, refers to noninterventional observations (e.g., baseline measurements). The basal secretion rate is not known in vivo for most hormones. Indeed, few studies have assessed regulation of basal secretion. The difficulty in discriminating between basal and burst-like hormone release arises analytically when 1) pulses overlap or are closely spaced, and 2) blood sampling is too infrequent to demarcate valleys between pulses. These points are exemplified by GH secretion patterns during deep (stages III and IV) sleep and fasting when secretory bursts are partially superimposed, and anytime if blood sampling is too infrequent to capture stretches of interpulse concentrations (64,66,68).

Pragmatic avenues to enhance accurate estimation of basal secretion include: 1) first sample over 24 h to assess when pulses are least frequent and when nonpulsatile release is most apparent; 2) then sample frequently at the best time to obtain three to five consecutive unchanging measurements between pulses; and 3) selectively antagonize the endogenous secretagogue that drives pulsatility. The last point is illustrated by the administration of escalating doses of a selective GnRH-receptor antagonist. The antagonist progressively reduces the size of LH pulses, leaving essentially nonpulsatile LH concentrations (275). At present, this approach is less readily implemented in other axes due to the absence of suitable secretagogue-receptor antagonists. Possible exceptions are GHRH and angiotensin II-receptor antagonists, which in principle could assist in the estimation of basal (or more particularly, non-GHRH dependent and non-angiotensin II dependent) secretion of GH and aldosterone, respectively. However, GHRH is not the sole factor mediating GH pulse generation, inasmuch as normally timed GH pulses persist in patients with inactivating mutations of the GHRH receptor, albeit at 30-fold lower amplitude. The same limitation applies to aldosterone secretion, which is regulated by potassium, ACTH, and other factors distinct from angiotensin II. Accordingly, innovative strategies are needed to determine whether basal secretion of any given hormone is: 1) dependent upon acute vis-à-vis long-term agonist input, and 2) influenced by age, gender, body composition, physiological state, and/or disease.

3. Secretory-burst duration and shape (waveform).

A contemporary tenet is that significant burst-like hormone release reflects intermittent inputs by secretagogues and/or inhibitors. Prototypical examples are GnRH-induced LH and CRH-stimulated ACTH pulses. If this premise is valid, then determining the number and size of secretory bursts should confer insights into the timing of upstream signals, glandular responsiveness to the signals, and concomitant feedback. Accordingly, both the size and shape of secretory events should provide important insights into physiology and pathophysiology. Earlier methods were generally insensitive to subtle or even moderate differences in pulse shape (1,2,3,4).

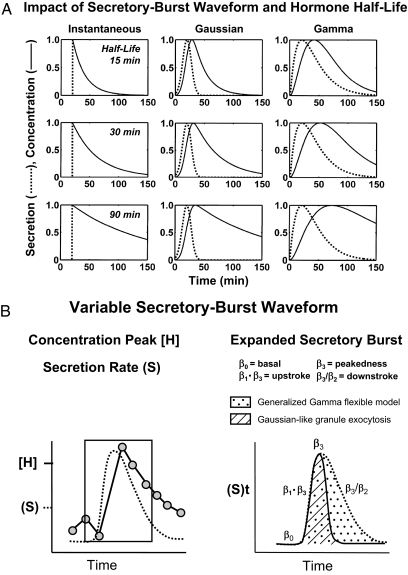
Figure 6A schematizes three principal categories of modeled secretion processes: instantaneous, symmetric and asymmetric burst shapes (waveforms). The waveform of the secretion event at any given elimination half-life controls the shape of the concentration peak. The assumption that in vivo secretory bursts are instantaneous (zero-duration) events is unduly restrictive in many contexts and physiologically invalid in others. This point was demonstrated by directly sampling GnRH, AVP, CRH, GHRH, SS, ACTH, GH, LH, FSH, Te, progesterone, PTH, cortisol, and insulin secretion as often as every 30 sec to 5 min in the horse, sheep, dog, pig, rat, or human (1,4,146). An alternative assumption is that sample-by-sample secretion rates may be smoothed with a fixed Gaussian function would also be arbitrary (24,30,276).

Figure 6.

A, Simulated impact of half-life (top to bottom) and secretory-burst waveform (interrupted curves, left to right) and on the resultant shape of hormone-concentration peaks (continuous curves). Instantaneous secretion (delta function) yields a sharp peak, from which elimination half-lives may be estimated directly by exponential regression (left column). Symmetric Gaussian (middle) and asymmetric gamma (right) secretory bursts widen the peak and slow the descent of the concentration curve. B, Mathematical formulation of a flexible generalized gamma-probability model of secretory bursts. The three-parameter gamma waveform encompasses both rapid initial Gaussian-like (approximately time-symmetric) hormone release and delayed continuing (time-asymmetric) secretion. The three β parameters confer full flexibility of burst shape.

The shape of an underlying secretory burst is defined formally as the time course of instantaneous secretion rates comprising a burst, as distinct from the shape of the measured hormone-concentration peak. Although bursts are difficult to sample directly in the human, insights have been obtained by monitoring venous drainage of endocrine glands in vivo in animals (37,38) and perifused cells in vitro (277,278). Studies of this kind reveal significantly asymmetric secretion events characterized by a rapid increase in secretion toward a maximum, followed by a slow decrease toward basal. This is illustrated when LH secretory bursts are delineated by sampling pituitary blood every 30 sec in the conscious horse. Precisely how hormone type, species, age, sex, stress, and endocrine status modulate secretory-burst shape individually and jointly is not yet known.

Figure 6A illustrates further that when a secretion event is instantaneous (mathematically a delta function), the elimination half-life can be calculated directly by exponential regression of decreasing hormone concentrations on time (left panels). On the other hand, when a secretory burst is asymmetric, but erroneously assumed to be instantaneous, exponential regression of concentrations on time would predict a spuriously long half-life (right panels). An intermediate degree of bias would arise if the secretory event were symmetric, but assumed to be instantaneous (middle panels). Accordingly, a flexible-waveform (gamma) model is important to embody variable waveforms ranging from Gaussian-like to asymmetric bursts (15,16,17,26).

Models of secretory bursts should link time-evolving kinetics of exocytosis to the macroscopic waveform of hormone release (60,279). Figure 6B presents a simplified mathematical construct of a putative in vivo (asymmetric gamma) secretory burst superimposed upon low basal constitutive release. In this model, exocytosis comprises rapid initial Gaussian-like discharge of membrane-localized granules and delayed but sustained exocytosis of newly available secretory granules. The burst is ultimately quenched by feedback factors and dissipation of the agonistic signal (15,32,92).

G. Deconvolution analysis of secretory-burst waveform

Several mathematical approaches exist to evaluate secretory bursts (Table 1). Nonparametric deconvolution methodologies assume a known fixed half-life to obtain estimates of sample-by-sample instantaneous secretion rates (discrete ISR) or locally smoothed secretion profiles (24,30,264,276,280,281), thereby eschewing any model of shape. One parametric deconvolution approach approximates the shape of secretory bursts with a symmetric Gaussian function (two-parameter probability distribution) (11). A Gaussian burst represents rapid initial release but fails to capture delayed secretion. A more recent deconvolution method implements a flexible gamma function (three-parameter probability distribution), which embodies rapid and delayed exocytosis in a continuous asymmetric burst (12,26,32,33,61) (Fig. 6B).

Outcomes of the three constructs (ISR, Gaussian burst, and gamma waveform) are not identical. The discrete ISR technique can yield rapid oscillations in baseline secretion rates referred to as ringing. The Gaussian (symmetric-waveform) model may overestimate pulse frequency and hormone half-life by generating false-positive peaks with slower decay to accommodate de facto burst asymmetry. The gamma (variable-waveform) model should recover burst number and variable secretory-burst shape.

H. Influence of secretory-burst offset

Secretory bursts with finite duration definitionally comprise an onset, a peak rate of secretion, and an offset (trailing edge of diminishing secretion). An important reason to estimate secretory-burst waveform accurately is to decompose (deconvolve) plasma-hormone concentration peaks correctly into underlying secretion and elimination components. An analytical impediment is that secretory-burst shape, size and timing, basal secretion, and elimination half-life are strongly intercorrelated. Interdependence among parameter estimates forces the momentary estimate of any one parameter to alter that of all correlated parameter estimates, rendering unique parameter estimation difficult.

If any given hormone-concentration peak could result from different secretory-burst shapes paired with different half-lives, how could one determine the true shape? A recent approach is to estimate the onset times of secretory bursts independently, and then use maximum-likelihood estimation (MLE) or Bayesian estimation to obtain estimates or probability distributions of the shape parameters and half-life simultaneously (15,17,26,36). The new strategy, which addresses a longstanding quandary (93), was justified by direct mathematical proof of realizability and by primary experimental validation in three species (12,16,17,36).

Burst-like secretion into the bloodstream generates a peak in hormone concentrations. Molecules entering the circulation are subject to rapid initial distribution in the blood due to aqueous diffusion (random molecular dispersion), advection (linear flow due to heart action), and convection (admixture due to fluid turbulence) (282). Molecules are removed more gradually by a finite probability of irreversible elimination (Fig. 7A). Correctly modeling these combined kinetic factors from first principles requires an algebraically biexponential (two half-lives) rather than monoexponential (one half-life) formulation (16,26) (Fig. 7B). The reason is that, although widely used, monoexponential models significantly overestimate basal secretion (by failing to utilize an adequately slow half-life, which is required to find the true basal rate) and underestimate the size of high-amplitude secretory bursts (by failing to use a sufficiently rapid half-life, which is needed to find the true height of the peak) (33). Overestimation of basal secretion accentuates pulse underestimation because a falsely high prediction of the basal contribution to any given concentration reduces the apparent size of each pulse. These points are verifiable empirically by showing that the distribution volume predicted by monoexponential compared with biexponential kinetics is inflated by a factor of as much as 3.3 over that determined independently in LH-depleted men injected with known pulses of synthetic LH (32,148) (Fig. 7C). The distribution volume is the slope of the estimated mass of infused LH (IU per liter of V_d) regressed on the true mass of injected LH (IU).

Figure 7.

A, Fate of hormone molecules secreted into the bloodstream. Mathematical components comprise a partial derivative on space and time to define diffusion (random molecular motion in solution), a first derivative on time to reflect advection (linear blood flow due to cardiac action), and a finite elimination probability to denote irreversible removal or degradation. B, Combined equation system derived from the first principles of panel A. Any momentary concentration, X(t), arises from double-exponential elimination of starting concentrations, X(0), nonpulsatile basal secretion, β₀, and pulsatile hormone secretion, P(r). C, Error in estimating the plasma V_d (slope of deconvolved LH mass regressed on injected LH mass) due to using a single-exponential rather than dual-exponential model of hormone elimination. Independent studies establish that V_d is approximately 3.5 liters for human LH (148).

I. Regulation of hormone secretory-burst onset

Secretory-burst onset (initial rise in or upstroke of secretion rate within a burst) is subject to physiological regulation in each hypothalamo-pituitary axis studied to date, viz., the gonadotropic, corticotropic, thyrotropic, and somatotropic axes. This is exemplified by variable-waveform (gamma rather than Gaussian) deconvolution analyses of 24-h LH-concentration profiles obtained at three stages of the human menstrual cycle and in postmenopausal women (89) (Fig. 8, left). In the gamma model, secretory-burst shape is calibrated by the mode of the secretory burst (time delay from objective burst onset to maximal secretion). For LH, the mode averaged 31 min in the midluteal phase, 19 min in the early follicular phase, and 16 min in estrogen-deficient postmenopausal women. Estimated shapes of ACTH, TSH, and GH secretory bursts are also regulated physiologically. ACTH and TSH secretory bursts are abbreviated by feedback withdrawal and unknown nighttime factors, respectively (15,26,35). Conversely, GH secretory bursts are prolonged by E₂ and shortened by peptidyl secretagogues (283). The collective data indicate that sex steroids, negative feedback, time of day, and secretagogues can control the waveform of pituitary secretory events.

Figure 8.

Left, Analytically estimated LH secretory-burst waveform (shape) in six premenopausal women studied in the early and late follicular and midluteal phases of the menstrual cycle and 16 estrogen-deficient postmenopausal women. The waveform is the time evolution of the secretion rate within a burst, defined independently of mass by using a flexible generalized gamma probability distribution. Open circles and numbers on x-axes give the cohort mean secretory-burst mode (time latency to achieve maximal secretion). LH profiles were obtained by 10-min sampling for 24 h. Right, Interpulse-interval distributions in the same women. Lambda and gamma denote mean probabilistic pulse frequency (per 24 h) and interpulse regularity (unitless), respectively. [Adapted from D. M. Keenan et al.: Am J Physiol 285:E938–E948, 2003 (89).]

J. Deconvolution with pulse detection

1. Critical nature of accurate pulse times.

A significant impediment to valid and reliable parametric deconvolution analysis is that errors made in the assignment of pulse number and/or timing bias estimation of secretion and elimination parameters. Simulations illustrate this issue. Imputing supernumerary pulses (false-positive errors) spuriously decreases estimates of mean secretory-burst mass, basal secretion, and hormone half-life. Omission of true pulses (false-negative errors) has the opposite consequences. Invalid timing of the correct total number of pulses unpredictably corrupts recovery of true burst size, shape, basal secretion, and elimination. Therefore, accurate peak identification is a necessary, but not sufficient, condition for valid parametric deconvolution analysis. Nonparametric deconvolution does not require burst identification and thus has utility when secretion rates but not pulses need to be estimated (21,22,263,264,284).

2. Validation of pulse detection.

Validation of pulse-detection methods requires direct comparison of analytical estimates with known pulse trains using any of several experimental paradigms (Table 2). One needs to identify true-positive, false-positive, true-negative, and false-negative pulses and then construct a receiver operating-characteristic curve (ROC) (285). Validation of a variable-waveform (gamma) deconvolution method recently used several of these approaches, viz.: 1) direct sampling of hypothalamo-pituitary portal-venous blood in the conscious horse or sheep; 2) in vivo suppression/infusion paradigms; and 3) mathematical simulations of pulsatile hormone series (12,16,17,286).

3. Methods of pulse enumeration in deconvolution analysis.

Deconvolution techniques described earlier by Veldhuis and Johnson (11,24,27,30,93,276) did not incorporate automated objective ascertainment of pulse number and locations. Potential pulses were added by the analyst according to empirical criteria such as a run of two or more positive residuals, which suggests underfitting consecutive concentration values (146,287). A putative pulse was ultimately retained if the calculated amplitude (maximal secretion rate) or mass (integral) was significantly nonzero on post hoc testing of individual or joint 95% statistical confidence intervals. Although adding a potential peak is now automated based upon the runs test, autocorrelation, and the reverse-rearrangements test (276), what remains unclear on formal statistical grounds is whether confidence intervals should be calculated for individual pulse amplitudes, for a subset of amplitudes (e.g. smallest one third), for all amplitudes, or for all secretion and elimination parameters simultaneously. Each approach has been used in published analyses (19,68,288,289,290). Empirical simulations suggest that the correct choice for the Gaussian method as framed may depend upon sampling intensity and duration, burst size, number and frequency, data variability, weighting of sample means by the fitting algorithm, percentage basal secretion, and a mono- vs. biexponential half-life model (30,93,146,287). No formal criteria exist to specify these dependencies.

4. Simultaneous pulse detection and deconvolution.

Most earlier deconvolution models do not have mathematically verified unique parameter asymptotes (viz., a maximum-likelihood solution) or Bayesian-estimation capabilities. This limitation opens the possibility that repeated analyses of the same data set could give different answers depending upon initial parameter estimates and/or the order of parameter estimation, as articulated a decade ago (27,93). Simulations readily illustrate this problem when using a web-based automated deconvolution program, wherein three starting guesses are made for basal secretion and burst duration (276). Program results were compared with true-positive pulses created by: 1) infusing known pulses of biosynthetic LH iv after suppressing gonadotropin secretion with a GnRH-receptor antagonist (286); 2) mathematically simulating an LH pulse train from mean secretion and half-life parameters obtained in healthy men (17,34); and 3) monitoring GnRH pulses directly in hypothalamo-pituitary portal blood of the castrate ewe. Limitations of ill-posed techniques have prompted the development of mathematically verified (statistically asymptotic) methods, such as MLE and Bayesian models.

5. MLE.

Several MLE methods exist (Table 1). However, in most cases comprehensive in vivo validation has not been performed. One recent MLE-based deconvolution model was validated experimentally in three mammalian species and verified statistically by direct mathematical proof (15,17,26,32,36). The concept is to first remove any long-term trends in the hormone profile using the classical heat equation, and then normalize concentrations to the unit interval (0, 1) (26,36). The next step is to create a registry of all possible sets of pulse-onset times via repeated incremental smoothing (a nonlinear-diffusion algorithm), motivated by analogy with modern image boundary-detection theory (291). (A pulse onset is analogous to a boundary edge.) To this end, the algorithm initially marks all local minima to define an exhaustive pulse-time set of N pulses, and then very gradually smoothes away (removes) the statistically least significant minimum one at a time to create a succession of reduced pulse-time sets. This is illustrated for a 24-h ACTH profile in Fig. 9A. The outcome comprises multiple successively decremental pulse-time sets containing N, N-1, N-2, N-3 … . 1 pulse(s).

Figure 9.

A, Concept of estimating multiple pulse-onset times by repeated incremental smoothing (nonlinear diffusion) of a hormone-concentration profile (top pictograph). Data are first detrended by the heat equation and normalized to the unit interval (0, 1) (data not shown). The incremental smoothing algorithm then gradually removes individual nadirs (points with least rapid subsequent increases) from the concentration time series (horizontal axis), leaving successive sets with one less pulse time each (asterisks). Thus, algorithmic cycles (oblique axis) create a family of decremental sets of potential pulse times, e.g., 34, 33, 32 … 3, 2, 1 pulse(s) per set. Columns of asterisks (middle section) show the locations of retained pulse onsets as a function of successive algorithmic runs. The maximum (starting) and a reduced candidate pulse set (bottom) are illustrated for a 10-min ACTH concentration profile. B, MLE of 10 simultaneous parameters of secretion and elimination statistically conditioned upon individual candidate pulse sets (step I, top). Pulse-mass random effects are reconstructed as conditional expectations evaluated at the MLE (steps II and III, middle). The final choice among multiple possible pulse-time sets is made by objective model-selection criteria, such as the AIC or BIC (step IV, bottom). Parameter asymptotics were verified by direct mathematical proof, and peak detection was validated by experimental paradigms (15,17,26,36).

To eschew bias, all parameters are estimated simultaneously conditioned on each candidate pulse set (26) (Fig. 9B). The secretion, elimination, and variability (random-effects) parameters (total n = 10) are computed via an MLE procedure. The random effects are reconstructed as their conditional expectations, given the observed data. Then, the most probable (optimal) pulse-time set is chosen from among the registry of N pulse-time candidates via a statistical model-selection criterion, such as the Akaike information criterion (AIC) or Bayesian information criterion (BIC), discussed further in Section VI.N.1 (292).

6. Bayesian estimation.

Bayesian models offer a mathematical strategy that is distinct from and complementary to MLE methods (26,293). A recent Bayesian approach made posterior probability estimates of secretory-burst number, size and shape, hormone half-lives, and basal secretion of multiple anterior pituitary hormones (26). A Bayesian platform allows one to estimate each secretion and elimination parameter as a posterior probability distribution (in this case the distribution is approximated by 100 values). Parameter estimates for any one hormone profile may be viewed as a range of values expected some fraction, such as 50 or 95%, of the time, or as a mean ± sd. The Bayesian structure also permits one to utilize prior independently obtained information, such as the populationally determined half-life, in framing probabilistic estimates of parameters. An experimental limitation is that accurate prior values may not be known for certain study contexts.

7. Future directions.

Formal comparisons are needed between maximum-likelihood and Bayesian models under different conditions of blood sampling, hormone assay, and pathophysiological pulsatility. Innovative analytical approaches should also advance the field further.

K. Nature of pulse-timing (pulse-renewal) process

1. Gaussian and Poisson models.

Accurate pulse enumeration allows one to evaluate pulse-timing (pulse-renewal) mechanisms. This may seem unimportant, inasmuch as hormone pulses recur after apparently random time delays. However, several kinds of random pulse-renewal processes can be distinguished biologically (294,295). The term renewal process implies that successive interpulse-interval lengths (waiting times) are independent (296), and thus the underlying burst-generator mechanism is memoriless (297,298). Any train of N pulses has a set of N-1 interpulse intervals, for which a central tendency (mean, median, mode) and measure of dispersion (range, sd, sem) can be estimated. The question arises what type of stochastic process would best explain interpulse intervals in health and disease. Two common types of random distributions are a truncated-Gaussian (normal) and Poisson (exponential). A Gaussian distribution is defined fully by its mean and sd, and a Poisson process by the probabilistic mean event rate [lambda] (294). Clinical investigations indicate that neither Gaussian nor Poissonian models will adequately explain LH, ACTH, TSH, GH, or insulin pulsatility evaluated by sampling blood every 10 min for 24 h (pituitary hormones) or every 1 min for 2–4 h (insulin) (15,26,34,35,89). Accordingly, earlier pulsatility simulations based upon Gaussian or Poisson models may not be realistic (25,249,299).

2. Weibull pulse-renewal model.

Interpulse-interval variability in human neuroendocrine systems is approximately 20–60% [expressed as a CV (sd/mean × 100%)] (12,15,17,26,34,35,89,91,92,300). Although a two-parameter symmetric Gaussian distribution could have a CV in this range, distributions of physiological interpulse intervals are not symmetric. Albeit asymmetric, the one-parameter Poisson process is unsatisfactory because the interpulse-interval CV is fixed at 100%, given that sd = mean by definition in this case (301). A third model is the Weibull renewal process, which includes the Poisson as a special member (294). The Weibull distribution allows for flexible interpulse-interval variability, wherein CVs can vary from 100 to 0% asymptotically (26,92). Flexibility is achieved by independently defining gamma [a unitless term, proportional to the CV], which describes the regularity of the pulsing and lambda [mean probabilistic pulsing frequency]. For gamma = 1, the Weibull distribution simplifies to the Poisson with an interpulse-interval CV of 100%. For gamma greater than 1.0, the CV of interpulse intervals is less than 100%, thereby emulating inferred physiological variability of 20–30% (15,17,26,89,92). As gamma approaches infinity, the pulse times approach exact regularity, i.e., equal spacing. By way of example, the distribution of 67 LH-interpulse intervals was obtained by analyzing the LH profile of a healthy older man sampled every 10 min for 4 d without interruption. Gamma was 2.51 and lambda 14.9 pulses/24 h, yielding a CV of 22.1%, well below 100% required for a Poisson process. In contrast, when a mechanical infusion pump was used to inject 6-min squarewave iv pulses of recombinant human LH every 120 min, gamma was 164 (denoting marked regularity of interval lengths) and lambda was 12 pulses/24 h. Few data of this kind exist.

3. Physiological insights into pulse-renewal mechanisms.

Application of the flexible Weibull renewal-process model has unveiled physiological regulation and pathological disruption of neuroendocrine mechanisms that control pulsing regularity as well as frequency. For example, gamma (pulsing regularity) and lambda (probabilistic mean pulse frequency) of 24-h LH time series both differ among pre- and postmenopausal women and young and older men (89,92). In particular, the regularity and frequency of LH pulses are lower in the midluteal than the early-follicular phase of young women (89) (Fig. 8, right). Conversely, LH interpulse-interval regularity and pulse frequency are higher in older than young men (300). Reduced cortisol concentrations and sleep increase mean pulse frequencies of ACTH and TSH, respectively, but neither condition alters interpulse-interval regularity (12,15,35). GH pulse frequency and interpulse-interval regularity do not differ in post- and premenopausal individuals (283). Thus, negative feedback, gender, age, and time of day can differentially control pulse frequency and pulsing regularity. The biochemical and cellular bases for such finely tuned regulation of stochastic pulse-renewal processes remain unknown.

4. Weakly coupled pulse automata.

A theoretical rationale for using the Weibull renewal process is to allow for sparse feedforward or feedback coupling among putative pulse automata (294). Automata (independently randomly firing units) are strictly uncorrelated stochastic processes. However, the fact that gamma of Weibull exceeds unity (typical values are 1.8–3.1) in neuroendocrine systems could indicate weak feedforward, partial refractoriness, or delayed feedback among oscillators. Any of these processes would contribute to lesser variability than a classical Poisson process (89). Because gamma (regularity) of LH pulsing is higher in older than young adults, age per se may influence the stochastic behavior of GnRH-neuronal oscillators (89,92).

Beyond comparing the distributions of interpulse intervals, one may ask whether the relative randomness of two sequences of consecutive interpulse intervals is distinguishable. Weak serial correlation was inferable in an autoregressive moving-average model of electrophysiologically defined GnRH interpulse intervals in two ovariectomized monkeys, and by autocorrelation analysis of LH interpulse lengths in women in the late luteal phase of the menstrual cycle (298,302). Autocorrelation was not evident in other stages of the menstrual cycle or in healthy young men (297). A significant degree of (low-order) autocorrelation would suggest that factors associated with the preceding pulse time(s) directly or indirectly influence the next pulse time. The explicit nature of such factors is not known, but it could include autofeedback by secreted or diffusible factors.

A precise discriminator of the relative randomness of serial processes or time series is the ApEn statistic (238,242). ApEn is a sensitive and specific measure of the regularity or reproducibility of subpatterns in numerical sequences (303,304,305,306). ApEn analyses reveal that LH, TSH, ACTH, and GH interpulse-interval sequences in men and women are mean random, viz., statistically indistinguishable from 1000 randomly shuffled versions of the original sequences (15,35,92,307). Analogous studies are needed to assess pulse-renewal processes associated with prolactin, PTH, insulin, sex steroids, cortisol, epinephrine, ADH, and oxytocin secretion. Using data in which LH pulsatility was monitored every 10 min for 4 d in an older man, ApEn of the first differences of the 61 successive interpulse intervals was 1.3910 compared with 1.3636 ± 0.0565 (mean ± sd) of 1000 randomly shuffled versions of the same interpulse-interval sequence (z score = +0.53; P = 0.75; and ApEn ratio = 1.0201 ± 0.0565). The corresponding ApEn ratio was 0.9608 ± 0.0617 (P = 0.18) for the 62 sequential LH burst-mass values. The outcomes are consistent with a memoriless, unpatterned GnRH pulse-generating process in this subject.

L. Stochastic elements in endocrine systems

Dynamic analyses require precise, specific, sensitive, valid (true), and reliable (consistent) measurements of hormone concentrations to accurately reconstruct underlying rates of secretion (system input) and elimination (system output). However, randomness (inexplicable or stochastic variability) enters into experimental observations at multiple levels. Three principal sources of unaccountable variations are: 1) procedural errors (e.g., sampling and assay variations); 2) fluctuations in the status of the sampled host (e.g., sleep-wake cycle, posture, hydration); and 3) variability in the biological system itself (e.g., successive pulse size and timing). Although stochastic processes can enhance deterministic signaling under some conditions, valid estimation procedures must make mathematical allowance for unexplained (model-independent) random components in experimental data (12,15,16,17,35,89,92,308). For example, erroneously assuming a purely deterministic (cause-and-effect) model in which GH secretory bursts are identical in size and timing would markedly bias analyses.

A major advance in the last decade is analytical allowance for possible stochastic variability (12,15,17,26,32,33,36,61,293). Some recent deconvolution models allow for random variability in the size and timing of hormone pulses and/or the elimination process (16,26,32,36,293) (Table 1). Investigations using such models indicate that age accelerates the mean frequency and squelches random variability in the size of LH secretory bursts in healthy men (17,92). Conversely, Te supplementation accentuates random variability in the size of successive GH secretory bursts (307). Additional studies are needed to examine the generality of such inferences and extend insights into stochastic features of other endocrine systems.

M. Investigational limits of secretion-estimation procedures

No current methodology achieves all idealized characteristics of deconvolution analysis. Therefore, the investigator should ask several questions: 1) are a priori kinetic estimates required for the particular deconvolution model chosen? 2) To what degree will the results for the hormone in question depend upon sampling frequency and duration? 3) What analytical assumptions may affect interpretation of outcomes? 4) Has the deconvolution technique been validated in vivo, in vitro, and/or by computer simulations? 5) Has the statistical structure been verified mathematically? 6) Is the hormone time series actually pulsatile? and 7) What are the analytical consequences of baseline trends or short epochs of increased variability in the data?

N. Unresolved issues

Analytical procedures should have primary validity (statistical and empirical verification), reproducibility (reliability), mathematical tractability, physiological relevance, minimal bias, low vulnerability to occasional outliers, flexibility and generality of application. Even when these conditions are met, certain questions remain unresolved.

1. Model-selection criteria.

An important query is how to decide objectively among different potential deconvolution outcomes. This is referred to as a model-selection issue. In economics, statistics, physics, and engineering, common model-selection criteria include the AIC described in 1973, a Bayesian version, the BIC, reported by Schwartz in 1978, generalized cross-validation, and the risk-inflation criterion (309,310,311). Each method defines a particular statistical penalty for imposing greater smoothness or adding more parameters in the analysis. Parameters in deconvolution analysis include the smoothing function in nonparametric methods, the number of pulses, and all the secretion and elimination terms in parametric methods. A reason for penalization is that excessive smoothing degrades the original data structure. Moreover, overparameterization, such as adding a pulse of variable height at every other data point (somewhat akin to Fourier or wavelet analyses with the maximal number of basis functions) or assigning a polynomial function of degree close to N-1 (where N is the number of data points), would represent all time series precisely without yielding any helpful insights into the biological mechanisms.

One earlier deconvolution technique used two parameters for each pulse (viz., its location in time and amplitude), one parameter for basal secretion, a burst half-width term (or Gaussian sd), and three parameters for elimination kinetics, thus necessitating 35 parameters to fit 15 pulses (11,93). This structure is highly parameterized, and therefore difficult to estimate uniquely if few (<50) data points are available. A more recent variable-waveform method specifies 10 secretion/elimination parameters to deconvolve a 15-pulse profile, because the MLE solution is mathematically conditioned on independently identified candidate pulse-time sets. The final parameter set is then selected by probabilistic information criteria (12,15,16,17,26,36). In this case, for a fixed elimination/secretion parameter set, one may identify the optimal pulse-time set by finding the minimum AIC or BIC, defined as follows: AIC = −(log likelihood function) + (2) (# pulses); and BIC = −(log likelihood function) + (ln N) (# pulses).

A question arises in using model-selection criteria as to whether the statistical penalty should be the same for adding one more pulse vis-à-vis one more secretion or elimination parameter. The query arises because for pulsatile time series the number of estimated pulses is implicitly constrained between 1 and (N − 1)/2 for N data points. The probabilistic penalty for adding or removing pulses (given any particular secretion/elimination parameter set and data set) should presumptively grow as the estimated pulse number approaches less likely realizations, such as 1 or the theoretical maximum. According to this reasoning, the penalty term would resemble an inverted “U,” rather than linear, function of pulse number. Because the shape of the postulated U-function is not known, further advances are needed in this area.

2. Empirical validation.

Direct experimental validation of deconvolution methods is complementary to mathematical verification. Table 3 highlights several important validation approaches. One clinical paradigm is to suppress secretion of a hormone and then inject known pulses of the recombinant peptide (such as LH, GH, PTH, insulin) or synthetic molecule (cortisol, Te). This strategy can be applied to the male gonadal axis. Specifically, gonadotropin secretion is first suppressed overnight with a GnRH-receptor antagonist, and then pulses of saline or biosynthetic LH are infused iv the next morning in randomly assigned order (286). True-positive (TP) LH pulses could also be defined reasonably by way of: 1) multiunit electrophysiological activity in the hypothalamus as a surrogate for GnRH release; 2) GnRH pulses sampled in hypothalamo-pituitary portal blood; 3) exogenous GnRH-stimulated LH pulses in hypogonadotropic individuals; 4) in vitro perifusion of pituitary cells stimulated with GnRH; and 5) biomathematical computer-assisted simulation of a train of amplitude-varying LH pulses.

Table 3.

Illustrative methods for primary validation of deconvolution algorithms

1. Direct sampling at the site of secretion to ensure high signal-to-noise ratio

Hypophyseal-portal sampling for oxytocin, CRH, and AVP (37,38)

Pituitary intercavernous-sinus sampling for LH, GnRH, GHRH, somatostatin, and ACTH (65)

Portal- or hepatic-venous sampling for insulin (40,71)

2. Corroboration by independent in situ markers of pulse events

Electrophysiological recordings in hypothalamus to mark oxytocin or GnRH pulses (39,360,361)

Injected GnRH pulses in men with isolated GnRH deficiency (287)

3. In vivo suppression or stimulation paradigms

GnRH-receptor antagonist administered before iv infusion of biosynthetic LH pulses (270,272,286)

Somatostatin, insulin, and glucagon infusions (14)

Insulin-pulse entrainment by oscillatory iv glucose infusion (362)

4. In vitro perifusion models

Ovarian granulosa-luteal cells (41,197)

Human islets (42)

Pituitary cells (363)

5. By computer simulation model-based simulations

Computer-assisted mathematical simulations to designate pulse locations, shape and amplitude, basal secretion, and half-life with superimposed random perturbations (245,249,250,287,313,364)

6. Test-retest reliability analysis

Correlation between estimates made in separate sampling sessions (328,365,366)

Limitations of each approach: 

1. Direct sampling is unethical in healthy humans and may disrupt secretion patterns in animals. 

2. The surrogate marker and pulse might not always correspond 1:1. 

3. Exact experimental mimicry of endogenous pulses is difficult. 

4. Perifusion conditions diverge in complex ways from in vivo physiology. 

5. Mathematical constructs are only estimates of an unknown physiological process. 

6. Reliability coefficients may be reduced by factors unrelated to the algorithm. 

Validation requires comparing experimentally designated (true) and deconvolution-estimated (potential) pulse times to enumerate false-positive (FP), false-negative (FN), true-positive (TP) and true-negative (TN) events. “Sensitivity” is defined as the TP proportion, TP/(TP + FN), and “specificity” as the TN proportion, TN/(TN + FP). From these two outcomes, one may construct a ROC, which relates sensitivity (y-axis) to the difference term, 1-specificity (x-axis) (312). The term “1-specificity” is equivalent to the FP proportion. An ideal methodology with 100% specificity (zero FPs) and 100% sensitivity (zero FNs) would achieve an area of 1.0 under the ROC curve. The ROC area is a measure of overall discriminative accuracy. Specificity and sensitivity of pulse detection can be based on analyses of 5-, 10-, 20-, and 30-min subsets of hormone pulse profiles with known (TP) events. The critical nature of adequate sampling frequency becomes apparent by contrasting pulse-detection sensitivities achieved on 5-min vs. 30-min data. Undersampling typically forces underestimation of pulse frequency and hormone half-life, and overestimation of mean burst size and basal secretion by censoring small events (9,25,249,250,313,314). Moreover, sampling frequency and the deconvolution model influence pulse estimates, thus underscoring the 3-fold importance of adequate sampling intensity, independent validation, and statistical verification (16,17,26,240).

What is unknown is how closely any given in vivo validating paradigm emulates the study context in which the deconvolution method is ultimately applied. The same quandary arises for in vitro perifusion systems and mathematical (in silico) simulations. Inasmuch as estimates of sensitivity and specificity are affected by the validating context, the validation paradigm should be stated when discriminative indices are reported. A minimal performance goal is suggested here as ROC-area estimates of pulse-detection accuracy consistently exceeding 0.90 (90% diagnostic accuracy) in three or more independent realistic validating paradigms, one of which is in vivo and another mathematical.

3. Discordant inferences.

A difficult question in deconvolution analysis is what to do when model-selection criteria, such as the AIC and BIC, are discordant. When samples are collected frequently with respect to burst duration, interpulse interval, and hormone half-life, model-selection differences are uncommon. Accordingly, optimal model-selection criterion require validation as well. Incorporation of independent knowledge of the endocrine system would further enhance the validity of model selection when correctly employed in Bayesian models.

4. Combined approaches.

In principle, selected aspects of nonparametric and parametric likelihood-based and Bayesian formalisms could be combined in composite multistep deconvolution algorithms. An advantage of nonparametric approaches is that structural assumptions (such as secretory-burst shape and basal secretion) are not required, thus extending generality. Well-chosen parametric models reflect specific physiology (such as pulse frequency), thus affording greater insights into underlying biology (9,12,61). Bayesian inference permits one to exploit prior knowledge when well substantiated. Thus, a possible tripartite approach would be, first, estimate a smooth (nonpulsatile) secretion process nonparametrically. Second, estimate all elimination and secretion parameters, conditioned on the putative basal rate. Third, make global estimates of all parameters simultaneously (peak positions, basal and pulsatile secretion, elimination rates) with Bayesian constraints. The latter might include populational probability distributions of hormone kinetics, basal secretion rates, and waveform parameters (26,293). In Bayesian theory, progressive deviation of the parameter estimate from the populational expectation is treated as increasingly improbable. The analytical goal is a valid and reliable algorithm suited to address the particular experimental question in the face of de facto data limitations.

VII. Analyses of Multihormone (Ensemble) Interactions

A. Ensemble concept

Endocrine glands communicate with target cells via intermittent exchange of chemical signals, which vary in frequency, amplitude, duration, and pattern. Interactions are mediated by way of time-delayed feedback (inhibitory) and feedforward (stimulatory) dose-response interfaces. A prototypical signal pair comprises PTH and calcium ions, Ca²⁺, wherein PTH elevates Ca²⁺ concentrations and Ca²⁺ concentrations repress PTH secretion (Fig. 10). Associated regulators include vitamin D, phosphorus, magnesium, phosphotonin, calcitonin, multiple receptors, and second and third messengers. Neuroendocrine ensembles also comprise three or more regulatory loci, viz., the hypothalamus, pituitary gland, and target organ. Because only a subset of signals in the ensemble can be measured directly in vivo, specialized analytical tools are required to evaluate the underlying dynamics accurately. This must be done without disrupting signaling pathways or time delays in the ensemble. Few methods exist to this end.

Figure 10.

Schema of ensemble feedback (−) and feedforward (+) interactions among PTH and calcium ions (top left), vitamin D (top right), phosphorus (bottom left), and other coregulators (bottom right). Unpublished line drawing.

B. Ensemble modeling requirements

Current concepts of ensemble dynamics originate from a long succession of incremental developments. Milestones include the identification of hormone fluctuations, feedback, feedforward, time delays, nonlinearities, and stochastic inputs (6,7,8,10,11,12,16,26,305,315,316,317,318,319). Ensemble models are classifiable as analytical or predictive. An ideal construct embodies both capabilities. Analytical models must account for three features of biological systems: 1) reciprocal interactions, which evolve either concurrently (in parallel) or after time delays (in series); 2) nonlinearities at points of signal convergence (e.g., inhibitory and stimulatory dose-response interfaces); and 3) unknown random (stochastic) variability due to procedural (e.g., assays) and biological factors (e.g., pulsing mechanisms) (Fig. 11). Whatever the resultant formalism, analyses must be robust to relatively short data series, missing observations, occasional outliers, procedural uncertainties, and variable admixtures of deterministic and stochastic effects. The paucity of validated ensemble analytical strategies underscores the inherent difficulty in addressing these needs (12,16,17,36).

Figure 11.

Summary of key elements of ensemble (multipathway) endocrine models. The primary model structure (connections) should reflect known biology (central rectangle). Four main issues emerge, viz., model revision, validation, simplification, and verification. Goals of a valid models are highlighted below the figure.

Suitably rendered analytical and predictive models complement experiments by formalizing objective understanding of the biological processes. The purpose is to buttress intuitive interpretation, facilitate experimental inference, generate new hypotheses, and estimate physiological parameters. Ideal constructs include faithful representation of mechanistic structure, analytical and predictive capabilities, mathematical verification, empirical validation, model revision, and parameter parsimony. A caveat is that no model can overcome inadequate data. For example, equivalent information cannot be extracted from two LH concentration time series with means of 6.2 IU/liter, in which one is corrupted by random sample sd values of 3 IU/liter and the other 0.3 IU/liter, or one is sampled every 30 min and the other every 1 min.

C. Examples of ensemble-control models in endocrine systems

An analytical model was proposed recently to reconstruct endogenous dose-response properties noninvasively without injecting agonists, antagonists, or labeled or unlabeled hormones (12,16,17,34,320). The noninvasive methodology was used to estimate endogenous feedforward dose-response functions linking concentrations of ACTH and LH with secretion rates of cortisol and Te, respectively, in healthy adults (34,320) (Fig. 12, A and B). Analytical estimates of the potencies of endogenous ACTH and LH were 24 ng/liter and 3.4 IU/liter in 32 and 26 adults, respectively. Potency estimates occupied the middle tertile of the normal range of 24-h mean concentrations in the same subjects. Advantages of noninvasive estimation strategies are that physiological pathways are not perturbed experimentally; no investigational compounds are injected; and the reconstructed dose-response function reflects bioactivity of the endogenous agonist acting on the unmanipulated target gland.

Figure 12.

Observed and estimated hormone-concentration and secretion pairs with simultaneously reconstructed dose-response functions encapsulating nonlinear feedforward. The pairs are ACTH concentrations (Con) driving cortisol secretion rates (Sec) (A), and analogously for LH concentrations feeding forward onto Te Sec (B). Each plot depicts data from one healthy adult. Cohort estimates of mean feedforward potencies (±sem) are stated (right lower panels) (N = number of subjects). [Adapted with permission from D. M. Keenan and J. D. Veldhuis: Am J Physiol 286:R381–R389, 2004 (34); and D. M. Keenan and J. D. Veldhuis: Am J Physiol 285:R950–R961, 2003 (35).]

A novel analytical prediction of feedforward estimates is that successive pulses of ACTH and LH in a given subject or animal are associated with nonidentical dose-response properties. The basis for inferable stochastic variability is not known, but may include random fluctuations in blood flow to or from the target gland, intermittent response sensitization and desensitization, or variability in endogenous agonist potency (16,34,320).

The biomathematical formalism for estimating dose-response functions can be extended to three (or more) interlinked signals. Quantitative estimates have been made of dose-response connections implicit among all three of GnRH, LH, and Te (16,17,34). The model includes feedforward and feedback-control equations to embody time delays, nonlinearities of signal interfaces, regulated rates of hormone secretion, distribution and elimination kinetics, and stochastic variability in secretory-burst mass, pulse timing, and dose-response parameters. The ensemble construct allows analytical estimation, hypothesis generation, and outcome simulation using a Matlab framework implemented on desktop computers (12,16,17,34,35,36).

GH secretion has been modeled nonanalytically as the regulated consequence of stimulation by GHRH, potentiation by ghrelin, inhibition by SS, and negative feedback by pulses of GH (18,131,132,133,135). Formulations of the GH system are needed that include necessary and expected stochastic components. Also required are constructs of the GH axis that permit noninvasive dose-response reconstruction without injection of agonists or antagonists.

D. Simplifying assumptions

Estimation of ensemble parameters may require simplifying assumptions and stepwise framing of the solution. Assumptions must be clearly articulated and consonant with known physiological properties of the endocrine system. For example, several plausible assumptions apply in the male gonadal axis. First, discrete bursts of GnRH released by the hypothalamus evoke distinct pulses of LH from the pituitary gland (321). Therefore, although GnRH cannot be measured directly in human hypothalamo-pituitary portal blood, observed LH pulse times could provide a surrogate for unobserved GnRH pulse times (16,17,322) (Fig. 13, top). Second, LH pulses drive Te pulses, as inferred by measurements of LH and Te pulses in the human spermatic vein and by in vitro Leydig-cell perifusion studies (34,51,96). Thus, one may formulate an LH → Te dose-response function linking LH concentrations to calculated Te secretion rates. Third, given that total Te concentrations comprise unbound (free) Te and Te bound to SHBG and albumin, one may create a kinetic model of Te’s binding and distribution in (and elimination from) plasma (Fig. 13, middle). And fourth, experimental data establish that (total, bound, or free) Te noncompetitively represses both the frequency and the size of GnRH pulses and inhibits GnRH’s concentration-dependent stimulation of LH secretion (128) (Fig. 13, bottom). Stating the foregoing points mathematically via coupled time-delayed differential equations permits estimation of the strength of the connecting pathways in individual subjects as well as in a group of subjects analyzed together (17,34,36) (Fig. 14). Thereby, calculated strength of endogenous feedback and feedforward may be related to age, gender, body composition, or other clinical variables. Analyses based upon this model structure suggest that age attenuates all three of hypothalamic GnRH secretion, the efficacy of LH in stimulating Te secretion, and negative feedback by Te onto GnRH outflow in healthy men (17).

Figure 13.

Conceptual steps in analytical reconstruction of unobserved hypothalamic GnRH outflow, given measured serial concentrations of LH and Te and mean values of albumin and SHBG. Top, Identification of multiple potential LH pulse-time sets by incremental smoothing (nonlinear diffusion). Upper, Estimation of all secretion/elimination parameters conditional on a set of putative pulse-onset times. Middle, Nonequilibrium partitioning of Te into plasma diffusion, intravascular advection, protein binding, and irreversible elimination. Lower, Reconstruction of tripartite Te → LH feedback, Te → GnRH feedback, and GnRH → LH feedforward surface. Bottom, Inhibitory feedback by Te on number (Weibull lambda) or regularity (Weibull gamma) of LH pulses. [Derived from Ref. 17.]

Figure 14.

Analytical estimation of age cohort-defined three-dimensional surfaces relating LH secretion (vertical axis) to estimated GnRH outflow (oblique axis) and free Te (left), bioavailable Te (middle), and total Te (right) concentrations (horizontal axes). Data are from 10 young and 8 older men. [Reproduced with permission from D. M. Keenan et al.: Endocrinology 147:2817–2828, 2006 (17).]

Innovative analytical constructs are needed that embody multiple interacting loci. The concept of an ensemble is that all pathways operating together, rather than any single pathway acting in isolation, supervise homeostasis. Conspicuous opportunities exist to formalize ensemble models in endocrine axes.

VIII. Model-Free Evaluation of Endocrine Networks

A. Concept of model-free assessment

Ensemble endocrine systems definitionally comprise three or more neuroanatomic sites, which are: 1) subject to local control mechanisms, and 2) interlinked by secreted signals and the nervous system. For example, the brain-pituitary-adrenal axis is regulated by (at least) AVP, CRH, ACTH, and cortisol; the sympathetic nervous system; and multiple paracrine and autocrine factors. Another biological network is illustrated by the reproductive axis, which has at least 12 (of an unknown total number of) principal connections. Even in this circumscribed network, direct experimental determination of system properties would require monitoring multiple pathways; viz., GnRH → LH, LH → Te, Te → GnRH, Te → LH, GnRH → FSH, FSH → E₂, E₂ → GnRH, E₂ → LH, prolactin → GnRH, E₂ → Prl, and Te → E₂ inter alia. Moreover, measurements would need to be frequent, simultaneous, and nondisruptive of the pathways. The difficulty in fulfilling this experimental demand has motivated complementary noninvasive ways to quantify ensemble behavior indirectly.

B. Rationale for ensemble statistics

Ensemble statistics quantify dynamics of the system as a whole via objective measurements of (at times very) subtle distinctions in the patterns of an observed signal. This perspective is predicated on the thesis that the time patterns of observable signals (e.g., ACTH concentrations) contain significant information about the entire, albeit incompletely observed, network (e.g., brain-pituitary-adrenal axis). The concept is evident intuitively because any interlinked system in some measure reverberates the effects of small changes in the number, direction, delay, and strength of its coupled components. Network-propogated effects would be detectable, in principle, by quantifying subtle alterations in signal patterns observed at any accessible point in the interdigitated system. Ensemble tools include the ApEn statistic (a probabilistic measure of pattern persistence) and artificial neural networks (resembling polynomial-based discrimination). Both approaches are termed model-free because underlying biological pathways are not modeled or necessarily known.

C. Approximate entropy (ApEn) as an ensemble measure of regularity

1. ApEn of concentration or secretion profiles.

The utility of meaningful application of ApEn within clinical and experimental contexts derives from several observations. First, ApEn correlates with subclinical changes often undetected by more classical time-series means, including moment statistics and spectral and correlogram analyses (305). ApEn changes are often predictive of subsequent clinical changes and per-subject longitudinal evolution, such as pubertal development, physiological aging, and postsurgical hormonal recovery (including subsequent relapse) (73,233,323,324). Second, a relatively modest amount of serial data is required for valid application, typically no more than 60 and as few as 10 points (303), which has facilitated the application of ApEn in a wide variety of settings. ApEn evaluates both dominant and subordinate patterns in data and, notably, will detect changes in underlying episodic behavior not reflected in peak occurrences or amplitudes, or even more subtle differences in instances in which no clear waves or pulses are easily identifiable. This fills a critical need because for highly irregular sequences, classical statistics often fail to clearly discriminate such sequences either from one another or from apparent randomness. Furthermore, changes in ApEn have been shown pathophysiologically and mathematically to correspond to mechanistic inferences about relative autonomy vis-à-vis coupling in diverse settings (Table 3).

ApEn is a sensitive and specific statistic for discriminating insidious differences in serial dynamics. ApEn is calculated for any time series as a single nonnegative number, with zero denoting perfect orderliness, as for a sine wave, and larger ApEn values corresponding to more apparently irregular dynamics (238,295). Two input parameters are specified a priori, a threshold for evaluating pattern reproducibility (r) and the number of points over (window) which to test pattern recurrence (m).

ApEn is termed a regularity statistic because it quantifies the relative reproducibility, orderliness, or consistency of subpatterns in sequential measurements (325). The concept is illustrated in Fig. 15A by mixing random (stochastic) input with a perfectly ordered sine wave (deterministic function). Higher ApEn, as the term entropy suggests, denotes greater relative randomness confounding the deterministic process (238,242). Deterministic mechanisms subserve the physiology of dose-response functions; mean secretory-burst size, shape, and frequency; basal secretion; and irreversible elimination. Random elements arise in the measurement technique and the underlying biology (e.g., molecular diffusion and convection, receptor desensitization, and individual pulse timing).

Figure 15.

A, Concept of ApEn statistic, a measure of relative process randomness (irregularity). ApEn distinguishes subtle differences in regularity, orderliness, or reproducibility of subpatterns in sequential measurements. Low ApEn denotes more orderly and less random (irregular) contributions to the signaling pattern. Conversely, high ApEn signifies more irregular or apparently “random” inputs. High ApEn characterizes hormone secretion patterns associated with autonomous endocrine tumors, low feedback states, aging individuals, and fixed exogenous stimulation of hormone output. B and C, Exogenously imposed negative feedback by Te onto LH secretion and by glucose onto insulin secretion. The fall in ApEn with higher feedback-signal concentrations denotes greater regularity of LH and insulin secretion. [Adapted with permission from P. Y. Liu et al.: J Clin Endocrinol Metab 91:4077–4084, 2006 (240).]

In typical biological applications, ApEn calculations are normalized against the sd of the data series by defining a pattern-reproducibility threshold value of r = 0.2 sd validated for data lengths n ≥60 samples (303). This choice of r limits random effects of low measurement variability (typically ≤0.065 sd), thus allowing discrimination between fine gradations in the orderliness of the underlying process. Validation studies have established the suitability of the m = 1 as the pattern-recurrence length for time series comprising 60 <n <300 points, as would be true for many endocrine profiles (211,303). For this (m, r) pair, there is quantifiably greater regularity (lower ApEn) of nocturnal GH secretion in adult male than female rats castrated prepubertally (306). ApEn is translation- and scale-independent mathematically, which means that adding or multiplying each data value by a fixed number does not alter ApEn (10). This feature ensures valid comparisons between different mean concentrations, overall variation, or secretion rates due to age, gender, physiological state, and pathology. For example, more irregular (higher ApEn, less orderly) GH secretion occurs in patients with either hypersomatotropism due to GH-secreting pituitary tumors or hyposomatotropism due to hypopituitarism despite 1000-fold differences in GH production (211,326).

ApEn quantifies marked disruption of the orderliness of secretion patterns in patients with endocrine tumors compared with age-, gender-, and body mass index-matched healthy individuals. Examples are GH and ACTH concentration time series in patients with acromegaly (204,211,218,303) or corticotropinomas (212,216,219) compared with healthy individuals. ApEn may be calculated as an absolute value or as a z score (number of sd values removed from empirically mean random ApEn, estimated by randomly shuffling the order of the time series 1000 times) (20,226). Smaller absolute z scores quantify more irregular (less reproducible) patterns of GH and ACTH secretion by cognate tumors. The sensitivity and specificity of ApEn both exceed 90%, including when as few as 10–17 samples are collected at appropriate times using ApEn thresholds validated for short data series (303,323,327). Test-retest reliability of ApEn analyses of 24-h GH data also exceeds 90% (328).

ApEn quantifies vivid differences in the pattern regularity of LH secretion between young and older men, in women at different stages of the menstrual cycle, and between pre- and postmenopausal individuals (300,304,305,323). In particular, greater randomness (lesser orderliness) characterizes LH secretion in aging men and postmenopausal women than their younger counterparts. In healthy young men, higher Te concentrations impose greater LH regularity (Fig. 15B). Midpuberty is marked by transiently increased regularity of LH and, conversely, decreased regularity of GH release patterns (324,329). Visceral adiposity and female gender are also associated with more disorderly GH secretion compared with a lean phenotype and male gender (306,328,329,330,331,332,333). Although the basis of the adiposity effect is not clear, the gender effect putatively reflects increased estrogen action and greater hypothalamic drive in women than men. Indeed, irregular GH secretion patterns are evoked by E₂ and secretagogues (214,334,335,336).

A common denominator of irregularity is attenuation of negative feedback compared with feedforward (Table 4). Thus, pathophysiologies that impair feedback elevate ApEn (process randomness). Well-established conditions of high ApEn include primary failure of a target gland like the thyroid, testis, and ovary, autonomous endocrine tumors, aging, and PCOS (211,212,218,219,305,327,337,338,339). Additionally, excessive feedforward enforces irregular patterns. PTH secretion is more disorderly in hyperparathyroidism (45,233), and aldosterone secretion in primary and secondary hyperaldosteronism (43,54). In keeping with these inferences, irregularity can be induced experimentally by muting negative feedback by Te, cortisol, and IGF-I, which normally maintain regularity of their upstream hormones (LH, ACTH, GH), as well as by augmenting feedforward by GnRH or GHRH on downstream hormones (LH and GH) (226,239,340).

Table 4.

Illustrative pathophysiologies of putative feedback failure inferred by disorderly secretory patterns^a

	Refs.
I. Autonomous secretion
Somatotropinoma	211,218
Corticotropinoma	212,216,217,219
Prolactinoma	214,230
Parathyroid adenoma	43
Aldosteronoma	213
Cortisol-secreting adrenal adenoma	213
II. Secondary hypersecretory states
Hyperprolactinemia of stalk section	230
Hyperaldosteronism of salt depletion	43
Hyperparathyroidism in renal failure	44
Hypergonadotropism: menopause	304
Fasting-induced GH secretion	211
III. Experimental feedback depletion (signal monitored)
↓ Te (LH secretion)	109,239,340
↓ IGF-I (GH secretion)	226
IV. Puberty
LH, GH: more disorderly despite ↑ Te and ↑ IGF-I	323,324,328,329,334,367
V. Aging
LH, FSH, GH, ACTH	74,81,217,305,327,367,368
IV. Prediabetes or diabetes mellitus type II
Insulin	73
VII. Feedforward enhancement
↑ Orderliness of ACTH with low cortisol	241
↑ Orderliness of PTH with low calcium	226
VIII. Unexplained pathophysiology
PCOS ↓ orderliness of LH and Te	338
Adult GH deficiency ↓ regularity	326
Depression ↓ ACTH/cortisol orderliness	369,370,371
Visceral obesity ↓ GH orderliness	334

↓, Decreasing; ↑, increasing. 

^aDefined quantitatively by elevated ApEn. 

Insulin secretion patterns are more irregular in healthy older and obese individuals and patients with prediabetes or type II diabetes mellitus than in young, nonobese, nondiabetic subjects (73,74,81,223). This may in part reflect failure of negative feedback by glucose, which is otherwise readily inferable by in vitro perifusion studies (Fig. 15C). Inasmuch as disorderly insulin secretion patterns in aging and prediabetes accompany insulin resistance, irregularity may be due to attenuated autofeedback on, or accentuated feedforward onto, insulin secretion.

2. Regularity of pulse-timing mechanisms.

The relative regularity of random pulse-timing (renewal) processes can be discriminated using ApEn. ApEn may be applied to any sequence of consecutive interpulse intervals to quantify reproducibility (regularity) of the burst-generating process. The orderliness of successive interpulse intervals is not the same as the CV of interpulse intervals because the CV is independent of the de facto order of interpulse lengths (89,307). Average ApEn of consecutive GH interpulse intervals determined from 24-h time series in healthy men does not differ from that of 1000 randomly shuffled versions of the same sequences (307). Thus GH pulse timing is irregularly irregular. Specifically, the mean ratio of ApEn of observed-to-random GH interpulse-interval series is 1.000 ± 0.046 (sem). In contrast, ApEn of successive LH interpulse intervals in the luteal phase is less than mean empirically random (89), consistent with weak serial autocorrelation detected earlier (298).

3. Regularity of sequential secretory-burst mass.

ApEn of serial secretory-burst mass values quantifies relative regularity of secretory-burst size. One may thereby estimate individual ratios of ApEn determined on observed and randomly shuffled GH pulse-mass sequences normalized for preceding interpulse-interval length in healthy men. The null hypothesis of mean randomness would predict an average observed/random ApEn ratio of 1.0. The calculated ApEn ratio was 0.462 ± 0.032 in healthy men (307), thus demonstrating substantial serial reproducibility of GH pulse-mass patterns over random expectation (P < 10⁻⁵). The exact basis for significant consistency of successive burst size is not known. Most plausibly, it reflects the feedback-adaptive nature of generating recurrent GH pulses (132,133) (Fig. 3).

D. Artificial neural networks

1. Concept.

The artificial neural-network approach entails creating an array of mathematically interconnected pseudo-neurons, a concept developed initially in artificial intelligence. One does not know a priori exactly how weakly or strongly the virtual neurons should be connected to discriminate among data types. Thus, the first step requires iteratively estimating (training) the set of mathematically defined pathway strengths by repeatedly adjusting coefficients of arbitrarily interlinked algebraic functions. Network training is performed on prototypical time series, such as GH-concentration profiles obtained in healthy men or women (341). Validation requires analyzing a new set of comparable normative data to ensure consistency. The trained neural network is then used to distinguish between putatively abnormal and known normal data series. Discriminative performance can be assessed in terms of diagnostic specificity, sensitivity, and accuracy (285,342).

2. Applications.

Artificial neural networks have been applied successfully in endocrine systems to evaluate risk of thyroid cancer, patterns of GH secretion in acromegaly, PTH release in osteoporosis, and glucose excursions in type I diabetes mellitus (341,343). Limitations include obtaining adequate data for comprehensive primary network training and secondary validation to ensure finely graded distinctions and comparing data collected under different conditions in different laboratories. Advantages are an empirical basis, thus limiting model assumptions, and refinement of discrimination as more data become available.

3. Complementarity with ApEn.

ApEn and artificial neural networks are complementary, given that the former derives from explicit statistical formalism and the latter exploits propitious empiricism (238,242). ApEn has been validated experimentally by manipulating negative feedback in vivo (20,226,303) and verified mathematically by both ensemble neuroendocrine models and reductionistic equation systems (logistic, stochastic, and autoregressive) (12,89,215,300,344).

IX. Methods of Synchrony Appraisal

A. Rationale for assessing hormone synchrony

One way to relate a biological input to a measured output is via a nonlinear dose-response function (5) (Fig. 12). Nonlinearity of the coupling function is predicted on theoretical and empirical grounds (345). However, for some hormone pairs, the question simply arises whether the signals are or are not linked (346). For example, whereas LH concentrations and Te secretion rates are causally connected (16,17,34), it is less evident whether GH and cortisol pulses are temporally concordant. Synchrony analysis rather than dose-response estimation is more appropriate in the latter case (347).

In general, three methodologies have been informative in assessing linkages between hormone time series: 1) linear cross-correlation analysis performed at various lag times (296); 2) discrete peak concordance assessed at various lag times (165,348); and 3) cross-ApEn, a model-free, scale-invariant, and lag-independent joint regularity statistic (242,305) (Fig. 16). Methods in physics also include cross-spectral analysis, which involves a linear combination of sine and cosine functions (349). Cross-spectral methods are useful when the paired signals exhibit consistent periodicity and synchrony. However, uniform periodicity and synchrony are not typical of endocrine systems. In addition, averaging dissimilar cross-spectral results among subjects remains difficult (346).

Figure 16.

Schematic representation of three methods to quantify pairwise synchrony of hormone time series. The techniques give complementary insights into coordinate control. In particular, cross-correlation is linear and lag-specific (top); discrete peak coincidence is probabilistic and lag-specific (middle); and cross-ApEn is a scale-, model-, and lag-free joint synchrony measure (bottom).

B. Cross-correlation analysis

Cross-correlation analysis is analogous to traditional linear correlation, wherein the strength of the relationship between two time series is quantified by a correlation coefficient, rho or r. Cross-correlation is applied to exactly paired (simultaneous) as well as lagged pairs formed when the time series is offset (lagged) in either direction by 1 or any integral number of samples (Fig. 16, top). A range of lag times (relative shifts of the two series) is checked to assess if and when a maximal cross-correlation occurs. The method requires that 1) the series be exactly paired with uniform sample spacing; and 2) a reproducible time lag of maximal correlation exists. The strength of the correlation (percentage of explained variance) is proportionate to r². Limitations arise when lag times are inconsistent and when data series are short. The latter is due to low statistical power, given that the sd of r is (1/[rad]N − k[/rad]), where N is the number of samples and k the lag interval. For example, if only 12 paired data points are obtained, the sd of calculated r at a two-sample lag is 1/[rad]12 − 2[/rad] = 0.316. In a Gaussian (z score) approximation of significance, critical two-tailed z is 1.96 for P = 0.05, and thus absolute r would need to exceed 0.619. On the other hand, cross-correlation based upon 145 paired samples yields a critical absolute r of 0.16. By comparison, typical r values are 0.5 to 0.8 for paired LH-Te and ACTH-cortisol time series and 0.3 to 0.5 for paired LH-prolactin data (53,87,88,348,350).

A conceptual enhancement of the cross-correlation approach is to relate the concentration of a putative input to the secretion rate of the output (e.g., LH → Te or ACTH → cortisol). Analysis is thereby performed using physiologically relevant pairing of concentrations and secretion rates (351,352,353). Another strategy is to perform cross-correlation analysis of paired secretion profiles, which are obtained by deconvolving the concentration data. This allows one to assess more precisely whether hormones with different half-lives are temporally cosecreted (e.g., LH and prolactin). No matter how the data are processed, a pivotal point remains that cross-correlation analysis has good statistical power only when coupled signals are separated by a consistent time lag, the data series are of sufficient length, and the relationship between the amplitudes of the paired signals is linear (305,346).

C. Exact peak concordance

A relevant physiological issue is whether pulses of different hormones coincide (occur concordantly) more often than expected by chance (Fig. 16, middle). One approach is to assume that each sample in a given time series may or may not contain a pulse, as defined by a binomial probability distribution. Then, one binomial distribution would underlie the locations of pulses observed in series A (e.g., LH) and another binomial distribution those in the paired series B (e.g., prolactin). The number of exactly, as well as sample-lagged, concordant pulses can then be compared with the number expected due to chance associations by way of the hypergeometric distribution, which is the conjunction of two binomial processes (346,348). The expected mean and sd of the hypergeometric distribution are determined algebraically from the number of paired observations (samples) and the numbers of pulses in the two series. This simple framework allows one to calculate P values against randomness for any degree of observed concordance between two as well as among three or more pulse trains (348). Nonrandom peak concordance would suggest direct or indirect coupling between the processes that generate the pulse trains. Conversely, suppressed concordance could indicate reciprocally quenched (negatively linked) pulsing processes. Enhanced concordance over randomness was inferred for LH and Te, LH and progesterone, LH and FSH, LH and prolactin, ACTH and cortisol, and insulin and glucagon pulses when assessed at relevant time delays, whereas suppressed concordance has been observed for simultaneous LH and cortisol pulses (53,87,88,348,350). Nonrandom triple concordance has been demonstrated among ACTH, β-endorphin, and cortisol pulses (147).

Disadvantages of binomial peak-concordance statistics are that 1) peak locations are not known perfectly because sampling and detection artifacts yield false-positive and false-negative errors; and 2) the binary view of an equal pulse probability in each sample is oversimplified. More realistic models of the pulse-renewal process, such as the Weibull (or possibly log-normal or Pareto) models, would be preferred to represent an exponential and more general dispersion of interpulse intervals (294).

Other approaches are to simulate randomly reassigned pulse locations or to pair irrelevant pulse trains to obtain empirical estimates of chance pulse concordance (354). However, the first method requires prior knowledge of the true underlying pulse-timing process to ensure valid simulations. The second strategy carries the risk of misrepresenting random coincidence rates if time-of-day influences pulse number.

D. Cross-approximate entropy (cross-ApEn)

Cross-ApEn is a statistic that measures the joint pattern synchrony of two time series (215,242,305). The question asked is: To what extent do subpatterns of successive hormone concentrations in series A recur in series B? Cross-ApEn confers insights into synchrony that are complementary to those of cross-correlation and peak coincidence. This is because cross-ApEn estimates do not depend upon linearity of coupling between the two processes, consistent lag times, prior pulse enumeration, or sampling at fixed intervals (so long as the paired series are matched). Like ApEn, cross-ApEn quantifies relative pattern regularity or reproducibility (Fig. 16, bottom). Cross-ApEn simply uses one series as the template and the paired time series as the mate. To ensure high replicability, data are first normalized by z score transformation.

Important attributes of cross-ApEn like ApEn are model-, lag-, scale-, and translation-independence (344). Model-independence indicates that the underlying biological mechanisms need not be defined a priori (215). Lag independence signifies that joint synchrony encompasses reproducible subpatterns (runs of similar structure) both upstream and downstream in the series matched against the template. This property has considerable utility, given that time lags in biological systems are often inconsistent. Scale-invariance and translation-independence are significant in view of the wide variability in scale encountered in endocrine pathophysiology (3,4,211).

Cross-ApEn, like cross-correlation, may be performed in both a forward direction (wherein series A is the template for series B) and a reverse direction (wherein series B leads series A). Directionality of synchrony for causally paired series may be assessed after deconvolving one of the hormone-concentration time series, so as to relevantly relate concentration (input) to secretion (output) (352,353). When coordinate (synchronous) secretion is evaluated, cross-ApEn could be performed on secretion-secretion rather than concentration-secretion pairs. Application of the concept of forward and reverse cross-ApEn to selected concentration-secretion pairs has revealed that synchrony of cortisol → ACTH feedback is greater than that of ACTH → cortisol feedforward (352,353). In contradistinction, in men Te → LH feedback synchrony exceeds LH → Te feedforward synchrony. Age preferentially degrades feedback synchrony in the ACTH-cortisol axis (353), but erodes feedback and feedback synchrony equally in the LH-Te axis (352). Accordingly, cross-ApEn allows one to identify pathway disruption in a directionally selective fashion.

X. Summary

Pulsatile secretion of endocrine glands was recognized four decades ago and established unequivocally after the development of RIA methods. Quantifying pulsatility provides a window into incompletely understood pulse-generating and feedback-control mechanisms in endocrine systems. In turn, time-delayed exchange of hormonal signals mediates homeostatic adjustments toward species-, gender-, and age-relevant physiology. Specialized quantitative tools are available to assist clinicians and investigators in parsing normal and aberrant mechanisms of secretory control in health and disease. Future developments should help to enlarge insights further into the pathophysiology and physiology of pulsatile hormone secretion.