Abstract
Previous studies have documented two patterns of finger interaction during multi-finger pressing tasks, enslaving and error compensation, which do not agree with each other. Enslaving is characterized by positive correlation between instructed (master) and non-instructed (slave) finger(s) while error compensation can be described as a pattern of negative correlation between master and slave fingers. We hypothesize that pattern of finger interaction, enslaving or compensation, depends on the initial force level and the magnitude of the targeted force change. Subjects were instructed to press with four fingers (I - index, M - middle, R - ring, and L - little) from a specified initial force to a target forces following a ramp target line. Force-force relations between master and each of three slave fingers were analyzed during the ramp phase of trials by calculating correlation coefficients within each master-slave pair and then 2-factor ANOVA was performed to determine effect of initial force and force increase on the correlation coefficients. It was found that, as initial force increased, the value of the correlation coefficient decreased and in some cases became negative, i.e. the enslaving transformed into error compensation. Force increase magnitude had a smaller effect on the correlation coefficients. The observations support the hypothesis that the pattern of inter-finger interaction—enslaving or compensation—depends on the initial force level and, to a smaller degree, on the targeted magnitude of the force increase. They suggest that the controller views tasks with higher steady-state forces and smaller force changes as implying a requirement to avoid large changes in the total force.
Keywords: fingers, force, enslaving, error compensation, synergy
Introduction
When a person produces force at the fingertips, two patterns of force production emerge. One pattern of force interaction, between fingers of a hand, is called enslaving. Enslaving occurs when the fingers not explicitly involved in a pressing task (slave fingers) produce force when a finger from the same hand produces force by instruction (master finger) (Kilbreath and Gandevia 1994; Leijnse 1997; Li at al. 1998; Zatsiorsky et al. 1998; Hager-Ross and Schieber 2000; Kilbreath et al. 2002). With the master force increase, the force generated by an enslaved finger(s) also increases, i.e. the master force and enslaved force are positively correlated. Enslaving can potentially be due to a combination of several factors. They are: 1) peripheral mechanical connections of tissues (Leijnse 1997), 2) multi-digit motor units in the extrinsic flexor and extensor muscles (Kilbreath et al. 2002; Schieber 1991; Schieber 1995) and 3) diverging central commands (Schieber and Santello 2004). In the previous studies on enslaving, the subjects started the trials by pressing with small forces (~0–5% of the maximal voluntary contraction force, MVC) and then significantly increased required force output of master finger(s), typically up to 100% MVC. Enslaved fingers exhibit a linear force increase so that their contribution remains a constant percentage of the total force output. Enslaving effects are strongest in the adjacent finger(s) to the master finger(s) while the index finger is the most independent, or least enslaved, and the ring is the most enslaved (Zatsiorsky et al. 2000). Typically, enslaving effects are observed when a subject initially presses with a very small force against an object (rests the fingers on the sensors) and then increases contact force to a significantly higher level (Zatsiorsky et al. 1998; Zatsiorsky et al. 2000).
Another well documented pattern of force interaction is error compensation. The error compensation is considered to be a fundamental feature of motor synergies (Latash 2008). Error compensation has been observed in finger addition/removal tasks and is characterized by the following: when a finger is added to a pressing task, the forces produced by the original set of master finger(s) drops while when a finger is removed from a pressing task, the remaining master finger(s) significantly increases force production (Latash et al. 2001, Li et al. 2003; Kruger et al. 2007). The error compensation is characterized by a strong negative relation between the force exerted by the manipulated finger and the force produced by other fingers. The phenomenon of the error compensation was explained by the synergic reactions due to the tendency of the central controller to keep the total force generated by all the fingers at the same level (the subjects did not receive any instruction on keeping the total force constant). Often when performing fine manipulations of objects accurate control of total force is desired, this is helped by error compensation. Previous error compensation studies required subjects to add/remove finger(s) from the task permanently for the remainder of trial (Li et al. 2003) or for short intervals in finger tapping movements (Latash et al. 1998). Thus far, all error compensation studies have required subjects to start the task from a relatively high initial force (>10% MVC). Both enslaving and error compensation have shown a history dependent effect (Li et al. 2003).
Enslaving and error compensation strongly disagree with each other in terms of the correlation among finger forces. The enslaving is manifested as positive correlation between the individual finger forces while the error compensation is represented by the negative correlation. The goal of this study is to investigate the conditions that lead to either enslaving or error compensation, and their interaction in multi-finger pressing tasks. We hypothesize that pattern of finger interaction, enslaving or compensation, depends on the initial force level and the magnitude of the targeted force change. To test the hypothesis we manipulated in the experiment the two mentioned variables.
Materials and Methods
Twelve young healthy subjects participated in the experiment (six males and six females). The average age, mass and height of the male subjects were 26.1 ± 4.1 years, 69.4 ± 14.4 kg, and 171.1 ± 10.8 cm, respectively. The average age, mass and height of the female subjects were 25.7 ± 5.1 years, 57.6 ± 6.5 kg, and 162.4 ± 6.4 cm, respectively. Male hand widths for adducted and abducted finger positions were 8.7 ± 0.5 and 9.5 ± 0.5 cm, respectively. Female hand widths were 7.5 ± 0.5 and 8.3 ± 0.4 cm, respectively. Male and female hand lengths were 19.6 ± 0.9 and 17.4 ± 0.9 cm, respectively. All subjects were right-handed. The subjects had no previous history of neuropathies or traumas to the upper limbs. The subjects gave informed consent according to the procedures approved by the Institutional Review Board of the Pennsylvania State University.
Four uni-directional piezoelectric sensors (208C02, PCB Piezotronics) were used for force measurement. The sensors were mounted on a steel frame, which was securely attached to the testing station. Sandpaper pads were attached to the face of the sensors to increase friction and to reduce the temperature effect from the skin. Sensors were spaced 30 mm apart in the direction of finger adduction-abduction. The position of the sensors could be adjusted in the finger longitudinal direction in a range of 40 mm to fit individual subject’s anatomy. A wooden support was made to support the wrist and forearm, as well as to ensure stable contact between the fingers and force sensors. A wooden block was placed under subject’s hand to promote stable hand configuration and avoid pronation/supination during pressing. Analog output signals from the sensors were processed by separate AC/DC conditioners (484B, PCB Piezotronics) connected to a microcomputer (Dimension 2400, Dell) that was utilized for control, acquisition, and processing of the data.
During testing, subjects were seated facing the testing table with the right upper arm at approximately 45° abduction in the frontal plane and 45° flexion in the sagittal plane, and the elbow at approximately 45° flexion. The forearm was fixed to the wooden board with two straps. The left hand rested on the thigh.
The experiment consisted of two parts:
The first part required the subjects to press as hard as possible with each finger individually and all four fingers together. Two trials at each condition were collected, which led to 10 total trials, then the peak force value was used as MVC to provide target forces later in the experiment. For each trial subjects were given a 5-s window to press “as hard as you can” and to relax.
The second part of the experiment was the main part. Subjects were asked to press, so that their finger forces followed a target that featured an initial 4-s constant force followed by a ramp, which varied in length, but had a constant slope of 10% MVC/second, and finally another constant force target following the end of the ramp for 4 s. The instruction was: “Initially press with all fingers to follow target force then, when the ramp begins, press harder with the instructed finger to follow the ramp target and do not pay attention to forces of other fingers. At the end of the ramp, maintain the current force level with all fingers.” Prior to each trial, subjects were told which finger would be pressing harder when the ramp began. The initial constant force level was varied between 0, 5, 10, 15, 20, and 25% MVC and the ramp duration was varied such that the overall force increase was 10, 20, 30, and 40% MVC. These force increases correspond to time lengths of 1, 2, 3, and 4 s, respectively (the rate of force change was held constant at 10% MVC/s). Each combination of initial force level and force increase was performed for each finger, which led to 96 total trials (6 initial force levels × 4 force increases × 4 fingers = 96).
A deception was used in presenting finger force-target force feedback to the subjects. They were told that the sum of the force of all four fingers was presented on the computer screen when in fact it was only the force of the finger instructed to press harder during the ramp. The deception was used so that the transition between a constant force to ramp force would be smooth and the finger pressing harder during the ramp would not have to abruptly increase or decrease force to reach the start of the ramp. When multiple fingers are involved in a pressing task total variances of individual fingers is greater than the variance of the sum of finger forces (Li et al. 1998, Latash et al. 2001, Scholz et al. 2002) thus making it difficult to predict what force a single finger is pressing with.
A LabVIEW program (LabVIEW Version 8.0, National Instruments) was used to collect the force signals and display feedback to subjects. Data was collected at a frequency of 300 Hz. The force data were digitally low-pass filtered using a 4th order low-pass two-way Butterworth filter at 10 Hz using Matlab (Version R2006a, The Mathworks, Inc). A low-pass cutoff frequency of 10 Hz was applied. One and two-way ANOVAs and Student t-tests were performed for statistical analysis at a significance level of 0.05.
Both the finger enslaving and error compensation is manifested as a relation between the force exerted by the master finger and the force of the enslaved finger. With four master fingers and three slave fingers the general format of the studied relations can be represented as a 4×4 matrix in which the elements on the main diagonal are included for notational convenience (notation is Master Finger/Slave Finger). Consequently, 12 finger-finger combinations were addressed. (Note: the abbreviations used are: I – the index finger, M – middle, R – ring, and L – little finger.) Each finger-finger combination was studied at 6 levels of the initial force magnitude (0, 5, 10, 15, 20 and 25 % of MVC) and 4 levels of the prescribed force increase by the master finger (10, 20, 30 and 40% of the MVC). Hence, for each subject performing tasks with 4 fingers there were 4 × 24 = 96 experimental conditions and correspondingly 96 × 3= 288 relations had to be determined. In total, for 12 subjects there were 288 × 12 = 3456 relations. Representing such a huge number of data in a concise form was a real challenge
The data analysis adheres to the following logic. Because the main focus of the interest was on the force-force relations in the master finger-enslaved finger pairs, the 288 relations were determined for each subject. As the measure of the inter-finger relation (IRM), the linear coefficients of correlation were computed, 3456 in total. The coefficients of correlations were then z-transformed to obtain a normal-like distribution (Kutner et al. 2005).
At the second stage of the analysis the two-way repeated measure ANOVAs were performed for each of 12 force-force combinations with the factors: (1) INITIAL FORCE (IF) and (2) FORCE INCREASE (FI) on the z-transformed values of the coefficients of correlation. Significance levels were set to a = 0.05. The data was previously tested for sphericity (Girden 1992); no statistically significant deviation from sphericity was found. Next, the z-transformed coefficients were averaged across conditions with the same master finger (Kutner et al. 2005). For each master finger (M) and each IF-FI combination, three coefficients were averaged: (M-S1 + M-S2 +M-S3)/3, where S is a slaved finger. At this point, we were left with 96 coefficients of correlation.
Then the data was further analyzed in two ways: (1) the data for the same IF level was averaged across the FI’s (10, 20, 30, and 40% MVC) and plotted versus the IF levels (0, 5, 10, 15, 20, and 25 % MVC). (2) Similar as above, but the averaging was performed across the IF levels and the coefficients were compared across the FI levels that were treated as independent variables in this case.
Results
The results are presented in the following sequence: (a) examples of the individual force-force relations, (b) force-force correlation matrices for the group (examples), (c) two-way repeated measure ANOVAs results, (d) regression analysis.
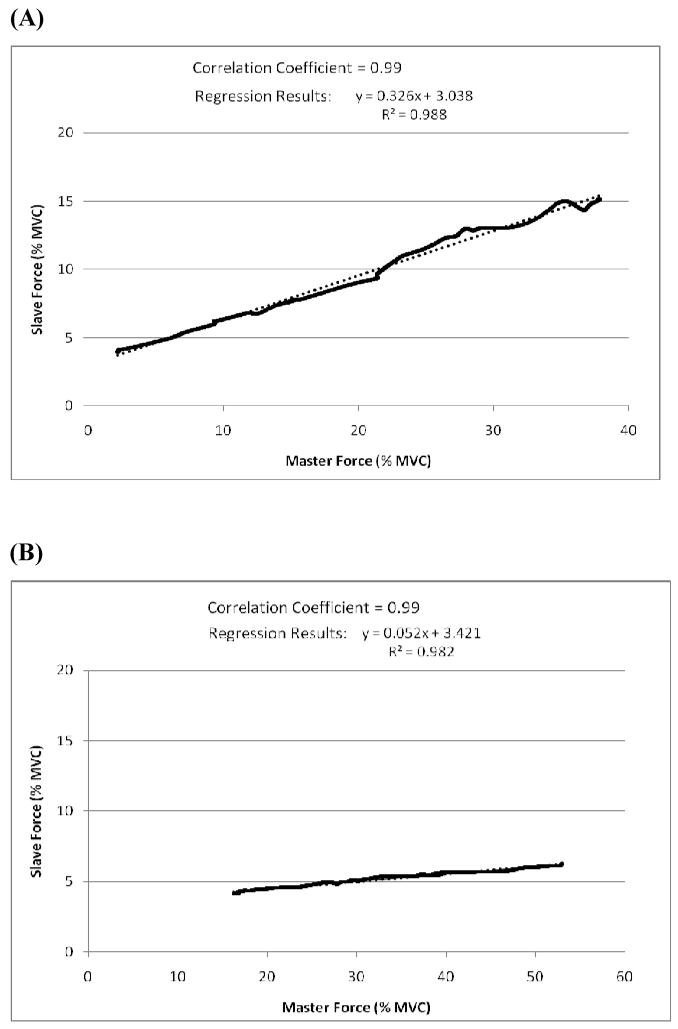
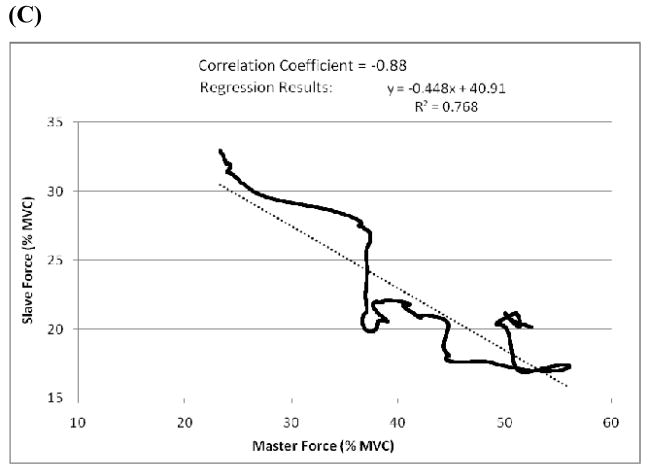
Examples of the force-force relations in individual trials are presented in Fig. 1. It is evident that at different IF-FI combinations the relations are different and can vary from positive to negative. Note that the positive relations indicate finger enslaving while the negative relations are indicative of error compensation, a sign of the tendency to maintain the total force exerted by all the fingers constant.
Fig. 1.
Representative examples of the force-force relations between the M finger (the master finger) and the R finger for a typical subject. (A) The initial force magnitude 0% and the force increase 40%. (B) The initial force magnitude is 10% and the force increase is 40%. (C) The initial force magnitude is 25% and the force increase is 40%. The correlation coefficient and regression equation, with R2 value, for trial shown are included at top of each plot.
Fig. 1. Representative examples of the force-force relations between the M finger (the master finger) and the R finger for a typical subject. (A) The initial force magnitude 0% and the force increase 40%. (B) The initial force magnitude is 10% and the force increase is 40%. (C) The initial force magnitude is 25% and the force increase is 40%. The correlation coefficient and regression equation, with R2 value, for trial shown are included at top of each plot.
The coefficients of correlation were averaged across subjects for each combination of IF and FI. Several examples are shown, in matrix form, of master-slave pairs in Table 1. According to the tested IF-FI combinations there were 24×2=48 such matrices, 24 for the coefficients of correlation and 24 for the regression coefficients. For brevity only 4 such matrices are presented here. A general trend of an increase in the correlation coefficients with an increase in FI as well as a decrease in the coefficients with an increase in IF was observed. These trends are analyzed in detail in subsequent sections.
Table 1.
Exemplary Matrices of Coefficients of a) Correlation Coefficients and b) Regression Coefficients
| a) Correlation Coefficients | |||||
|---|---|---|---|---|---|
| Initial Force = 0% MVC & Force Increase = 40% MVC | |||||
| Slave | Master | ||||
| Finger/Finger | I | M | R | L | |
| I | 1.00 | 0.89 | 0.93 | 0.91 | |
| M | 0.92 | 1.00 | 0.91 | 0.85 | |
| R | 0.81 | 0.83 | 1.00 | 0.97 | |
| L | 0.65 | −0.08 | 0.87 | 1.00 | |
| Initial Force = 25% MVC & Force Increase = 10% MVC | |||||
| Slave | Master | ||||
| Finger/Finger | I | M | R | L | |
| I | 1.00 | −0.56 | −0.35 | −0.03 | |
| M | −0.58 | 1.00 | 0.44 | 0.02 | |
| R | −0.59 | 0.09 | 1.00 | 0.72 | |
| L | −0.62 | −0.87 | 0.00 | 1.00 | |
| b) Regression Coefficients | |||||
|---|---|---|---|---|---|
| Initial Force = 0% MVC & Force Increase = 40% MVC | |||||
| Slave | Master | ||||
| Finger/Finger | I | M | R | L | |
| I | 1.00 | 0.08 | 0.06 | 0.12 | |
| M | 0.08 | 1.00 | 0.06 | 0.40 | |
| R | 0.06 | 0.39 | 1.00 | 0.12 | |
| L | 0.03 | 0.15 | 0.06 | 1.00 | |
| Initial Force = 25% MVC & Force Increase = 10% MVC | |||||
| Slave | Master | ||||
| Finger/Finger | I | M | R | L | |
| I | 1.00 | −0.17 | −0.25 | −0.15 | |
| M | −0.24 | 1.00 | 0.14 | −0.04 | |
| R | −0.09 | 0.01 | 1.00 | 0.02 | |
| L | −0.07 | −0.10 | −0.02 | 1.00 | |
Two-way repeated measure ANOVAs were performed on the z-transformed correlation coefficients with factors IF and FI (significance level: α = 0.05). The effect of the IF factor was significant in all finger-finger pairs and the effect of the FI factor was significant in 10 of 12 pairs. The pairs with non-significant FI factor effects were R–M and L–R. Hence, as a rule, the coefficients of correlation between the master finger and slave finger force changes in the pressing tasks depended both on the IF and FI levels. The calculated p-values can be found in the Table 2.
Table 2.
Two-Way ANOVA Results of the effects of the initial force (IF) and the force increase (IF) levels on the coefficients of correlation between the forces of the master and slave fingers.
| Master-Slave Pair | Initial force p-value | Force increase p-value |
|---|---|---|
| I/M | 0.000 | 0.046 |
| I/R | 0.000 | 0.003 |
| I/L | 0.000 | 0.039 |
| M/I | 0.000 | 0.000 |
| M/R | 0.000 | 0.021 |
| M/L | 0.037 | 0.003 |
| R/I | 0.000 | 0.000 |
| R/M | 0.008 | 0.299 |
| R/L | 0.000 | 0.000 |
| L/I | 0.000 | 0.050 |
| L/M | 0.000 | 0.003 |
| L/R | 0.000 | 0.730 |
Table 2 contains two-way repeated measures ANOVAs p-values results. Two-way ANOVA was computed from the average of each subject’s correlation coefficient for each combination of IF and FI across all master-slave pairs.
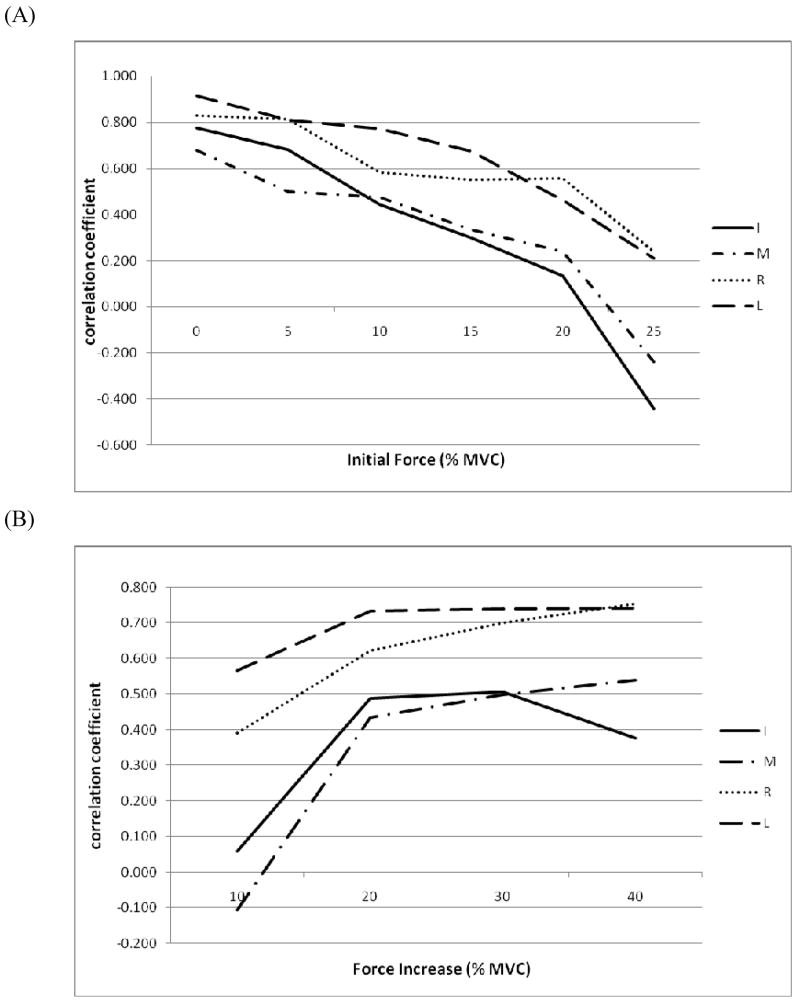
The regression of the coefficients of correlation values averaged across the slave fingers on (a) the IF levels and (b) the FI levels are presented in Figure 2.
Fig. 2.
(A) Averaged correlation coefficients vs. initial force for index master finger. The data was averaged across the FI levels. (B) Averaged correlation coefficients vs. force increase for index master finger. The data was averaged across the IF levels. vs. force increase for index master finger. The data was averaged across the IF levels.
Fig. 2. (A) Averaged correlation coefficients vs. initial force for index master finger. The data was averaged across the FI levels. (B) Averaged correlation coefficients vs. force increase for index master finger. The data was averaged across the IF levels.
It is seen from Fig. 2 that the negative trend occurred: the coefficients of correlation which were large for the zero initial force, gradually decreased with the IF increase and for the I and M fingers became negative at the high levels of the initial force. For the FI, the observed trend was different from the IF with the FI increase to 20% of MVC the coefficients increased and with further FI increase approximately stayed constant. In all cases, the coefficients for the index and middle fingers were below the coefficients for the ring and middle fingers with no point of intersection between lower, I & M, fingers and upper, R & M, fingers. Note that at the small FI values the coefficients for the index finger became negative, i.e. error compensation rather than enslaving occurred.
Discussion
Our observations support the hypothesis formulated at the beginning of the paper that the pattern of inter-finger interaction—enslaving or compensation— during voluntary change of a finger force in multi-finger tasks, depends on the initial force level and on the targeted magnitude of the force increase. These data do not support the opinion (Fahrer 1981; Kilbreath and Gandevia 1994; Leijnse 1997) that the finger interaction is determined mainly by the inter-tendinous connections between the fingers. In the light of the obtained facts (‘switching’ from the force enslaving to the force compensation with the IF rise) the above explanation seems dubious. During the master finger force rise, the passive connections between the fingers either did not change (and hence enslaving effect due to the passive force transmission should not change) or with increased tissue strain the inter-tendon connections could become stiffer and hence the ‘passive’’ enslaving effect should increase. However, our findings are opposite: With the IF increase, the enslaving effects decreased. We may assume that the finger interaction in multi-finger pressing tasks is subjected to two neural mechanisms one of which causes the enslaving and the second is directed at stabilization of the total force output and may be considered a manifestation of the multi-finger synergy. The relative contribution of these mechanisms depends on the initial force levels (mainly) and the targeted magnitude of the force increase. The results show that enslaving exhibits a more complex non-linear behavior than the typical linear behavior that has been reported in previous literature in which enslaving was measured from a 0% MVC initial force level (Zatsiorsky et al. 2000). We admit evident delimitations of this study: 1) only the force increases were studied while the force decreases from initial force levels were not addressed, and 2) the rate of force increase was not varied. A recent study has suggested that the direction of master finger action and the rate could have important effects on the indices of enslaving (Kim et al. 2008). However, the effects of rate of force change on error compensation are unknown and it was decided to be held constant so as to avoid potentially confounding effects of rate of force development on enslaving and error compensation. We hope to address this issue in future experiments.
Enslaving has been shown to be a robust phenomenon across tasks and force ranges (Li at al. 1998; Zatsiorsky et al. 2000). Recent studies of multi-finger synergies in a variety of tasks (Latash et al. 2001, Scholz et al. 2002), reviewed in (Latash et al. 1998), used this fact to perform analysis using a different set of variables, force modes that represent hypothetical control signals to individual fingers that can be modified by the controller one at a time. Indices of co-variation in the space of force modes have been viewed as synergy indices. In the space of finger forces, positive co-variation among the forces is expected as a default due to enslaving. Any deviations from this default reflect synergic relations; hence, synergic relations in the current study may be assumed not only when the correlation coefficients dropped below zero, but when they started to deviate from the highest default values. In our experiments, the subjects were not specifically instructed to keep a value of the total force when the master finger started to increase its force. The following explanation can be offered: at higher forces small enslaving effects can be masked by greater force stabilization effects (we thank an anonymous journal reviewer for suggesting this explanation). In such a case, enslaving might be still due to a passive response rather than to an active neural process. Nevertheless, strong synergic effects were seen across all conditions. These observations suggest that the controller views tasks with higher steady-state forces and smaller force changes as implying a requirement to avoid large changes in the total force (Latash et al. 2001). Possibly, this is conditioned by everyday experience with hand-held objects that could result in failures if large changes in the total finger force occur.
Appendix 1.
| a) Coefficients of Correlation – Averaged Across Subjects and Trials | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IF% MVC) | FI (%MVC) | I/M | I/R | I/L | M/I | M/R | M/L | R/I | RM | R/L | L/I | L/M | L/R |
| 0 | 10 | 0.420 | 0.228 | 0.491 | 0.420 | 0.668 | −0.602 | 0.392 | 0.687 | 0.367 | 0.903 | 0.414 | 0.959 |
| 0 | 20 | 0.904 | 0.871 | 0.609 | 0.899 | 0.908 | 0.287 | 0.813 | 0.930 | 0.836 | 0.944 | 0.819 | 0.967 |
| 0 | 30 | 0.941 | 0.918 | 0.666 | 0.920 | 0.940 | 0.274 | 0.892 | 0.875 | 0.824 | 0.928 | 0.852 | 0.967 |
| 0 | 40 | 0.920 | 0.814 | 0.652 | 0.887 | 0.830 | −0.085 | 0.934 | 0.915 | 0.875 | 0.912 | 0.846 | 0.965 |
| 5 | 10 | 0.923 | 0.592 | −0.002 | −0.150 | 0.711 | −0.702 | 0.195 | 0.863 | 0.551 | 0.770 | 0.201 | 0.838 |
| 5 | 20 | 0.858 | 0.837 | 0.399 | 0.623 | 0.861 | −0.195 | 0.678 | 0.915 | 0.778 | 0.780 | 0.769 | 0.922 |
| 5 | 30 | 0.828 | 0.710 | 0.454 | 0.884 | 0.919 | −0.095 | 0.847 | 0.908 | 0.877 | 0.807 | 0.740 | 0.951 |
| 5 | 40 | 0.919 | 0.591 | −0.043 | 0.861 | 0.840 | −0.426 | 0.838 | 0.852 | 0.908 | 0.850 | 0.731 | 0.861 |
| 10 | 10 | 0.326 | 0.128 | −0.432 | −0.245 | 0.622 | −0.675 | −0.274 | 0.638 | 0.469 | 0.326 | 0.509 | 0.884 |
| 10 | 20 | 0.847 | 0.731 | 0.192 | 0.740 | 0.915 | −0.003 | −0.211 | 0.506 | 0.752 | 0.629 | 0.753 | 0.883 |
| 10 | 30 | 0.782 | 0.696 | 0.044 | 0.742 | 0.853 | −0.033 | 0.395 | 0.882 | 0.827 | 0.605 | 0.743 | 0.927 |
| 10 | 40 | 0.755 | 0.538 | −0.188 | 0.739 | 0.840 | −0.279 | 0.479 | 0.790 | 0.805 | 0.776 | 0.822 | 0.884 |
| 15 | 10 | 0.573 | −0.152 | −0.559 | 0.079 | 0.436 | −0.500 | −0.315 | 0.491 | 0.676 | 0.248 | 0.046 | 0.837 |
| 15 | 20 | 0.457 | 0.195 | −0.225 | 0.333 | 0.547 | −0.344 | 0.314 | 0.772 | 0.631 | 0.521 | 0.491 | 0.923 |
| 15 | 30 | 0.758 | 0.623 | 0.125 | 0.301 | 0.607 | −0.418 | 0.162 | 0.800 | 0.740 | 0.510 | 0.657 | 0.919 |
| 15 | 40 | 0.594 | 0.667 | 0.057 | 0.838 | 0.913 | 0.270 | 0.330 | 0.789 | 0.593 | 0.273 | 0.526 | 0.945 |
| 20 | 10 | 0.374 | −0.145 | −0.462 | −0.300 | 0.797 | −0.711 | 0.155 | 0.842 | 0.171 | −0.097 | −0.229 | 0.706 |
| 20 | 20 | 0.799 | 0.689 | −0.104 | −0.152 | 0.709 | −0.324 | −0.064 | 0.641 | 0.592 | 0.350 | 0.331 | 0.862 |
| 20 | 30 | 0.347 | 0.144 | −0.550 | 0.337 | 0.796 | −0.390 | 0.187 | 0.568 | 0.606 | 0.021 | 0.018 | 0.831 |
| 20 | 40 | 0.387 | 0.105 | −0.352 | 0.621 | 0.666 | 0.107 | 0.567 | 0.881 | 0.797 | 0.422 | 0.482 | 0.844 |
| 25 | 10 | −0.580 | −0.588 | −0.617 | −0.562 | 0.090 | −0.873 | −0.352 | 0.440 | 0.002 | −0.028 | 0.016 | 0.722 |
| 25 | 20 | −0.216 | −0.409 | −0.718 | −0.160 | 0.539 | −0.602 | −0.160 | 0.580 | 0.378 | 0.075 | −0.301 | 0.564 |
| 25 | 30 | 0.031 | −0.167 | −0.203 | −0.290 | 0.343 | −0.478 | 0.085 | 0.349 | 0.316 | 0.193 | 0.032 | 0.518 |
| 25 | 40 | −0.122 | −0.489 | −0.784 | 0.085 | 0.385 | −0.651 | 0.043 | 0.604 | 0.387 | 0.024 | −0.018 | 0.434 |
| b) Regression Coefficients – Averaged Across Subjects and Trials | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Master/Slave Combination | |||||||||||||
| IF (% MVC) | FI (%MVC) | I/M | I/R | I/L | M/I | M/R | M/L | RI | R/M | R/L | L/I | L/M | L/R |
| 0 | 10 | 0.067 | 0.049 | 0.008 | 0.141 | 0.079 | −0.019 | 0.034 | 0.127 | 0.041 | 0.283 | 0.101 | 0.404 |
| 0 | 20 | 0.077 | 0.043 | 0.027 | 0.174 | 0.076 | 0.013 | 0.111 | 0.249 | 0.540 | 0.169 | 0.102 | 0.224 |
| 0 | 30 | 0.063 | 0.036 | 0.012 | 0.146 | 0.083 | 0.005 | 0.123 | 0.222 | 0.102 | 0.207 | 0.167 | 0.257 |
| 0 | 40 | 0.060 | 0.033 | 0.012 | 0.160 | 0.054 | −0.006 | 0.184 | 0.315 | 0.138 | 0.143 | 0.143 | 0.362 |
| 5 | 10 | 0.161 | 0.073 | 0.045 | −0.040 | 0.080 | −0.073 | 0.016 | 0.208 | 0.047 | 0.169 | 0.057 | 0.178 |
| 5 | 20 | 0.071 | 0.028 | 0.006 | 0.056 | 0.074 | −0.006 | 0.083 | 0.235 | 0.097 | 0.118 | 0.164 | 0.409 |
| 5 | 30 | 0.057 | 0.024 | 0.009 | 0.140 | 0.097 | −0.005 | 0.160 | 0.342 | 0.126 | 0.308 | 0.299 | 0.371 |
| 5 | 40 | 0.074 | 0.024 | −0.002 | 0.102 | 0.056 | −0.026 | 0.051 | 0.278 | 0.157 | 0.132 | 0.137 | 0.221 |
| 10 | 10 | 0.036 | 0.003 | −0.038 | −0.103 | 0.045 | −0.056 | −0.082 | 0.218 | 0.062 | 0.071 | 0.108 | 0.214 |
| 10 | 20 | 0.045 | 0.008 | −0.035 | 0.135 | 0.093 | −0.003 | −0.075 | 0.168 | 0.152 | 0.027 | 0.056 | 0.204 |
| 10 | 30 | 0.059 | 0.026 | −0.001 | 0.129 | 0.092 | −0.009 | 0.055 | 0.289 | 0.141 | −0.016 | 0.034 | 0.188 |
| 10 | 40 | 0.045 | 0.017 | −0.008 | 0.127 | 0.102 | −0.018 | 0.064 | 0.328 | 0.205 | 0.181 | 0.214 | 0.370 |
| 15 | 10 | 0.023 | −0.021 | −0.044 | −0.108 | −0.031 | −0.130 | −0.087 | 0.097 | 0.121 | 0.043 | −0.035 | 0.220 |
| 15 | 20 | 0.027 | −0.002 | −0.012 | 0.016 | 0.050 | −0.025 | −0.017 | 0.231 | 0.094 | −0.034 | 0.075 | 0.287 |
| 15 | 30 | 0.061 | 0.026 | −0.003 | −0.016 | 0.059 | −0.044 | −0.017 | 0.304 | 0.106 | 0.016 | 0.122 | 0.232 |
| 15 | 40 | 0.061 | 0.017 | −0.017 | 0.169 | 0.126 | 0.000 | 0.016 | 0.285 | 0.103 | 0.023 | 0.094 | 0.284 |
| 20 | 10 | 0.040 | −0.031 | −0.053 | −0.150 | 0.156 | −0.090 | 0.393 | 0.857 | −0.030 | −0.165 | 0.094 | 0.506 |
| 20 | 20 | 0.051 | 0.024 | −0.053 | −0.186 | 0.024 | −0.085 | −0.151 | 0.124 | 0.116 | 0.012 | 0.049 | 0.246 |
| 20 | 30 | 0.007 | 0.004 | −0.036 | −0.022 | 0.092 | −0.061 | −0.090 | 0.217 | 0.125 | −0.062 | 0.054 | 0.278 |
| 20 | 40 | 0.019 | 0.005 | −0.031 | 0.182 | 0.135 | −0.014 | 0.129 | 0.360 | 0.166 | 0.059 | 0.147 | 0.285 |
| 25 | 10 | −0.142 | −0.083 | −0.072 | −0.196 | −0.032 | −0.154 | −0.172 | 0.177 | −0.020 | −0.129 | −0.038 | 0.273 |
| 25 | 20 | −0.062 | −0.100 | −0.092 | −0.047 | 0.032 | −0.063 | −0.013 | 0.318 | 0.055 | −0.166 | −0.134 | 0.098 |
| 25 | 30 | −0.027 | −0.098 | −0.030 | −0.132 | −0.042 | −0.143 | −0.059 | 0.153 | 0.074 | −0.137 | 0.015 | 0.124 |
| 25 | 40 | −0.027 | −0.053 | −0.076 | −0.106 | −0.028 | −0.117 | −0.005 | 0.238 | 0.141 | −0.097 | 0.022 | 0.262 |
Acknowledgments
The study was in part supported by NIH grants AG-018751, NS-035032, and AR-048563.
References
- Fahrer M. Interdependent and independent actions of the fingers. In: Tubiana R, editor. The Hand. Saunders; Philadelphia: 1981. pp. 339–401. [Google Scholar]
- Girden ER. ANOVA: Repeated Measures. Sage Publications; London: 1992. pp. 15–18. [Google Scholar]
- Hager-Ross C, Schieber MH. Quantifying the independence of human finger movements: comparison of digits, finger movements, and movement frequencies. J Neuroscience. 2000;20:8542–8550. doi: 10.1523/JNEUROSCI.20-22-08542.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilbreath SL, Gandevia SC. Limited independent flexion of the thumb and fingers in human subjects. J Physiol. 1994;479:487–497. doi: 10.1113/jphysiol.1994.sp020312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilbreath SL, Gorman RB, Raymond J, Gandevia SC. Distribution of the forces produced by motor unit activity in the human flexor digitorum profundus. J Physiol. 2002;543:289–296. doi: 10.1113/jphysiol.2002.023861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SW, Shim JK, Zatsiorsky VM, Latash ML. Finger interdependence: Linking the kinetic and kinematic variables. Hum Move Sci. 2008;27:408–422. doi: 10.1016/j.humov.2007.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruger ES, Hoopes JA, Cordial RJ, Li S. Error Compensation during finger force production after one- and four-finger voluntarily fatiguing exercise. Exp Brain Res. 2007;181:461–468. doi: 10.1007/s00221-007-0942-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutner MH, Nachtesheim CJ, Neter J, Li W. Applied Linear Statistical Models. 5. McGraw-Hill Irwin; New York: 2005. [Google Scholar]
- Latash ML, Li ZM, Zatsiorsky VM. A principle of error compensation studied within a task of force production by a redundant set of fingers. Exp Brain Res. 1998;122:131–138. doi: 10.1007/s002210050500. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schoner G. Structure of motor variability in marginally redundant multi-finger force production tasks. Exp Brain Res. 2001;141:153–165. doi: 10.1007/s002210100861. [DOI] [PubMed] [Google Scholar]
- Latash ML. Synergy. Oxford University Press; New York: 2008. [Google Scholar]
- Leijnse JNAL. Measuring force transfers in the deep flexors of the musician’s hand: theoretical analysis, clinical examples. J Biomech. 1997;30:873–882. doi: 10.1016/s0021-9290(97)00045-6. [DOI] [PubMed] [Google Scholar]
- Li S, Latash ML, Zatsiorsky VM. Finger interaction during multi-finger tasks involving finger addition and removal. Exp Brain Res. 2003;150:230–236. doi: 10.1007/s00221-003-1449-x. [DOI] [PubMed] [Google Scholar]
- Li ZM, Latash ML, Zatsiorsky VM. Force sharing among fingers as a model of the redundancy problem. Exp Brain Res. 1998;119:276–286. doi: 10.1007/s002210050343. [DOI] [PubMed] [Google Scholar]
- Schieber MH. Individuated finger movements of rhesus monkeys: a means of quantifying the independence of digits. J Neurophysiology. 1991;65:1381–1391. doi: 10.1152/jn.1991.65.6.1381. [DOI] [PubMed] [Google Scholar]
- Schieber MH. Muscular production of individuated finger movements: the roles of extrinsic finger muscles. J Neuroscience. 1995;15:284–297. doi: 10.1523/JNEUROSCI.15-01-00284.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schieber MH, Santello M. Hand function: peripheral and central constraints on performance. J Appl Physiol. 2004;96:2293–2300. doi: 10.1152/japplphysiol.01063.2003. [DOI] [PubMed] [Google Scholar]
- Scholz JF, Danion F, Latash ML, Schoner G. Understanding finger coordination through analysis of the structure of force variability. Biol Cybern. 2002;86:29–39. doi: 10.1007/s004220100279. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML. Coordinated force production in multi-finger tasks: finger interaction and neural network modeling. Biol Cybern. 1998;79:139–150. doi: 10.1007/s004220050466. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML. Enslaving effects in multi-finger force production. Exp Brain Res. 2000;131:187–195. doi: 10.1007/s002219900261. [DOI] [PubMed] [Google Scholar]