DELAY-AMOUNT TRADEOFFS IN CHOICES BY PIGEONS AND RATS: HYPERBOLIC VERSUS EXPONENTIAL DISCOUNTING

Abstract

An adjusting-delay procedure was used to study the choices of pigeons and rats when both delay and amount of reinforcement were varied. In different conditions, the choice alternatives included one versus two reinforcers, one versus three reinforcers, and three versus two reinforcers. The delay to one alternative (the standard alternative) was kept constant in a condition, and the delay to the other (the adjusting alternative) was increased or decreased many times a session so as to estimate an indifference point—a delay at which the two alternatives were chosen about equally often. Indifference functions were constructed by plotting the adjusting delay as a function of the standard delay for each pair of reinforcer amounts. The experiments were designed to test the prediction of a hyperbolic decay equation that the slopes of the indifference functions should increase as the ratio of the two reinforcer amounts increased. Consistent with the hyperbolic equation, the slopes of the indifference functions depended on the ratios of the two reinforcer amounts for both pigeons and rats. These results were not compatible with an exponential decay equation, which predicts slopes of 1 regardless of the reinforcer amounts. Combined with other data, these findings provide further evidence that delay discounting is well described by a hyperbolic equation for both species, but not by an exponential equation. Quantitative differences in the y-intercepts of the indifference functions from the two species suggested that the rate at which reinforcer strength decreases with increasing delay may be four or five times slower for rats than for pigeons.

Many studies with both human and nonhuman subjects have examined how individuals choose between reinforcers that differ in their delays and amounts. Some of these studies have examined situational factors that can affect such choices (e.g., Dixon, Jacobs, & Sanders, 2006; Grosch & Neuringer, 1981; Mischel, Ebbesen, & Zeiss, 1972; Pitts & Febbo, 2004), others have focused on individual differences (e.g., Green, Fry, & Myerson, 1994; Odum, Madden, & Bickel, 2002; Schweitzer & Sulzer-Azaroff, 1995), and still others have tried to determine the shape of the function that describes the relation between a reinforcer's delay and its strength or value (e.g., Mazur, 1987; Sopher & Sheth, 2006; Woolverton, Myerson, & Green, 2007).

One study designed to study the shape of the delay-of-reinforcement function was conducted by Mazur (1987), who used an adjusting-delay procedure with pigeons. On each choice trial, pigeons chose between a red key (the standard alternative) and a green key (the adjusting alternative). A choice of the red key led to a fixed delay (e.g., 10 s) with red houselights, followed by 2-s access to grain. A choice of the green key led to an adjusting delay with green houselights, followed by 6-s access to grain. The duration of the adjusting delay was increased or decreased many times per session, depending on the pigeon's choices, so as to estimate an indifference point—a delay at which the two alternatives were chosen equally often. For instance, when the standard delay was 10 s, the mean adjusting delay at the indifference point was about 30 s, suggesting that 2 s of grain after a 10-s delay was about equally preferred to 6 s of grain after a 30-s delay. In a series of conditions, Mazur varied the standard delay between 0 s and 20 s, and an indifference point was obtained for each condition. The indifference points were then plotted with the standard delay on the x-axis and the adjusting delay on the y-axis, and Mazur found that the results from each pigeon were well described by linear functions with slopes greater than 1 and y-intercepts greater than 0 (as illustrated in the left panel of Figure 1). He showed that these results were consistent with the predictions of the following hyperbolic equation:

1

where V is the value or strength of a reinforcer, D is the delay between a choice response and the reinforcer, A reflects the amount or size of the reinforcer, and K is a parameter that determines how rapidly V decreases with increases in D.

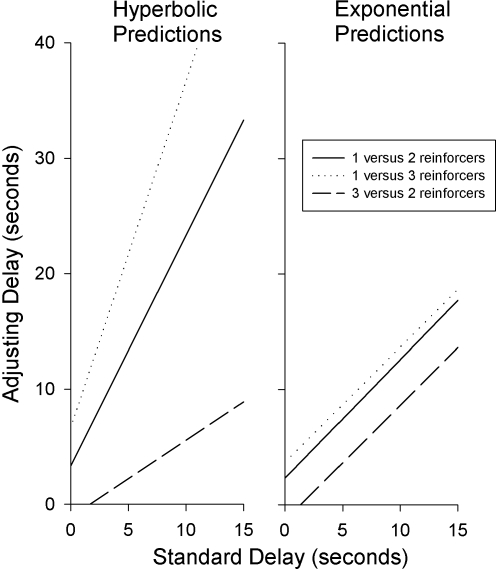
Fig. 1.

Predictions of the hyperbolic equation (left panel) and the exponential equation (right panel) are shown for three different ratios of reinforcer amounts.

Mazur (1987) derived the predictions of Equation 1 for his experiment as follows. He began by assuming that at an indifference point, the values of the two reinforcers are equal:

2

where the subscripts s and a refer to the standard and adjusting alternatives, respectively. It follows from Equations 1 and 2 that:

3

Solving Equation 3 for D_a yields the following equation, which describes how D_a is predicted to increase as a function of D_s:

4

Equation 4 describes a linear function with a slope of A_a/A_s and a y-intercept of (A_a−A_s)/A_sK.

If the reinforcer amount of the adjusting alternative is larger than that of the standard alternative (i.e., if A_a > A_s), then Equation 4 predicts an indifference function with a slope greater than 1 and a y-intercept greater than 0, which is what Mazur (1987) found. Other studies on delay-amount tradeoffs with pigeons (Rodriguez & Logue, 1988) and rats (Mazur, Stellar, & Waraczynski, 1987) have found similar indifference functions.

Mazur (1987) also showed that his results were inconsistent with the predictions of some other possible decay functions, including an exponential function (V  =  Ae^−KD), where e is the base of the natural logarithm, and a simple reciprocal function (V  =  A/KD). Assuming that the value of K is the same for both alternatives, the exponential equation predicts that the indifference functions should have slopes of exactly 1 regardless of what reinforcer amounts are used (i.e., for any positive values of A_s and A_a). (The possibility that K might vary for reinforcers of different amounts will be considered in the General Discussion section.) The simple reciprocal equation is similar to the hyperbolic in that it predicts indifference functions with slopes equal to A_a/A_s, but the reciprocal equation predicts that the y-intercepts will be zero in all cases.

Many studies with both human and nonhuman subjects, using a variety of different choice procedures, have obtained evidence that favors a hyperbolic discounting function over an exponential function (e.g., Bickel, Odum, & Madden, 1999; Grossbard & Mazur, 1986; Rodriguez & Logue, 1988; van der Pol & Cairns, 2002). However, some researchers have argued that an exponential discounting function actually provides a better model of the delay-of-reinforcement function (Schweighofer et al., 2006; Sopher & Sheth, 2006). For instance, Sopher and Sheth had human subjects choose between immediate and delayed amounts of money, and they concluded that their data consistently supported exponential discounting rather than hyperbolic discounting. Because there is still disagreement about which function best describes the effects of reinforcer delay, studies that can clearly differentiate between the predictions of the two equations may help to decide this question.

There is a specific prediction of the hyperbolic equation that has not received much attention. It is not simply that the slopes of the indifference functions should be different than 1: As shown in Equation 4, the slopes should equal the ratio of the two reinforcer amounts. The purpose of the present experiments was to examine the effects of varying reinforcer amounts on the slopes of the indifference functions by presenting both pigeons (Experiment 1) and rats (Experiment 2) with delay-amount tradeoffs, using three different pairs of amounts (one versus two reinforcers per trial, one versus three reinforcers per trial, and three versus two reinforcers per trial). If reinforcer deliveries per trial are interpreted as A_s and A_a, the left panel in Figure 1 shows the predictions of Equation 4: For these three pairs of reinforcer amounts, the slopes of the functions should be 2, 3, and 0.67, respectively. In addition, Equation 4 states that the y-intercepts should also depend on the reinforcer amounts, as shown in Figure 1. (For cases in which the standard reinforcer amount is larger, as in the conditions with three reinforcers for the standard versus two reinforcers for the adjusting alternative, Equation 4 predicts an indifference function with a slope less than 1 and a y-intercept less than 0.) The right panel in Figure 1 shows the corresponding predictions of the exponential equation. The predicted slopes are 1 in all cases, and only the y-intercepts vary with the different reinforcer amounts.

Although the predictions shown in Figure 1 provide a convenient starting point, it is probably unrealistic to assume that A_a and A_s will be exactly proportional to the two reinforcer amounts, because evidence from previous research suggests that the strength of a reinforcer is not strictly proportional to its nominal size. For instance, when reinforcer amounts have been varied in concurrent variable-interval (VI) schedules, substantial undermatching has been found (Schneider, 1973; Todorov, 1973) although overmatching was obtained in at least one study (Dunn, 1982). These results show that there is no simple relation between a reinforcer's nominal size and its effects on choice behavior. In Mazur's (1987) experiment on delay-amount tradeoffs, although the reinforcer durations were 6 s and 2 s, the average slope of the indifference functions for the 4 pigeons was 2.38, not 3. Using the same two reinforcer durations, Rodriguez and Logue (1988) obtained an average slope of 1.9. Based on these findings, a more conservative prediction for the present experiment is that the slopes of the indifference functions will increase as the ratio A_a/A_s increases, but they may not be precisely equal to A_a/A_s.

Two different species were used in this pair of experiments, both to assess the generality of the results and because evidence from prior studies suggest that K, the decay parameter in the hyperbolic equation, may be as much as four or five times smaller for rats than for pigeons (Mazur, 2000, 2007). If this interpretation is correct, it implies that for rats, the value of a delayed reinforcer decreases much more slowly with increasing delay than it does for pigeons. Notice that according to Equation 4, this difference in K should not affect the slopes of the indifference functions, but it should affect the y-intercepts. Specifically, if K is several times smaller for rats than for pigeons, the y-intercepts should be several times further from zero (in a positive direction if A_a > A_s, and in a negative direction if A_a < A_s).

Experiment 1

Method

Subjects

The subjects were 8 male white Carneau pigeons maintained at about 80% of their free-feeding weights. All the subjects had previous experience with a variety of experimental procedures.

Apparatus

The experimental chamber was 30 cm long, 30 cm wide and 31 cm high. The chamber had three response keys, each 2 cm in diameter, mounted on the front wall of the chamber, 24 cm above the floor and 8 cm apart. A force of approximately 0.15 N was required to operate each key. Each key could be transilluminated with lights of different colors. A hopper below the center key provided controlled grain access, and when the grain was available, the hopper was illuminated with a 2-W white light. Eight 2-W houselights (two white, two green, two blue, and two red) were mounted in a row above the Plexiglas ceiling toward the rear of the chamber. The chamber was enclosed in a sound-attenuating box with a ventilation fan. All stimuli were controlled and responses were recorded using an IBM compatible computer using the Medstate programming language.

Procedure

The experiment consisted of 14 conditions using an adjusting-delay procedure. In the different conditions, the standard delay and the number of reinforcers delivered by the two alternatives were varied. Each reinforcer consisted of a 2.5-s presentation of grain. On trials with more than one reinforcer, successive hopper presentations were separated by 0.5-s periods in which the hopper was lowered, the hopper light was turned off, and the white houselights were lit. Throughout the experiment, the left key was the standard alternative and the right key was the adjusting alternative. In different conditions, the standard delay was 1 s, 3 s, 5 s, 10 s, or 15 s. The adjusting alternative was varied according to the subjects' responses and was increased or decreased during the session (as described below). In four conditions, the standard alternative delivered one reinforcer per trial and the adjusting alternative delivered two reinforcers per trial. In four conditions, they delivered one and three reinforcers per trial, respectively. In four conditions, they delivered three and two reinforcers per trial, respectively. Finally, in two conditions, both alternatives delivered one reinforcer per trial. The order of conditions was varied across subjects, as shown in Table 1. The condition names in the table refer to the standard reinforcer amount, the adjusting reinforcer amount, and the standard delay. For example, in Condition 1-3-D10, the standard alternative delivered one reinforcer, the adjusting alternative delivered three reinforcers, and the standard delay was 10 s.

Table 1.

Order of conditions (in bold) and number of sessions needed to meet the stability criteria (in parentheses) for each pigeon in Experiment 1.

Condition	Standard Reinforcer Amount	Adjusting Reinforcer Amount	Standard Delay (s)	Pigeons
				P1	P2	P3	P4	P5	P6	P7	P8
1-2-D1	1	2	1	3 (16)	3 (12)	6 (17)	6 (13)	3 (12)	3 (12)	6 (14)	6 (18)
1-2-D3	1	2	3	4 (14)	4 (19)	5 (16)	5 (16)	4 (12)	4 (19)	5 (15)	5 (22)
1-2-D5	1	2	5	1 (16)	1 (14)	8 (20)	8 (12)	1 (13)	1 (15)	8 (12)	8 (12)
1-3-D10	1	2	10	2 (13)	2 (19)	7 (23)	7 (17)	2 (14)	2 (12)	7 (12)	7 (17)
1-3-D1	1	3	1	6 (12)	6 (12)	3 (12)	3 (12)	6 (14)	6 (20)	3 (16)	3 (13)
1-3-D3	1	3	3	5 (21)	5 (14)	4 (15)	4 (12)	5 (14)	5 (12)	4 (14)	4 (14)
1-3-D5	1	3	5	8 (12)	8 (18)	1 (14)	1 (19)	8 (14)	8 (14)	1 (14)	1 (14)
1-3-D10	1	3	10	7 (13)	7 (16)	2 (12)	2 (13)	7 (17)	7 (19)	2 (12)	2 (16)
3-2-D3	3	2	3	9 (12)	9 (12)	12 (15)	12 (13)	9 (20)	9 (16)	12 (17)	12 (14)
3-2-D5	3	2	5	12 (12)	12 (12)	9 (12)	9 (14)	12 (12)	12 (14)	9 (12)	9 (16)
3-2-D10	3	2	10	10 (19)	10 (13)	11 (19)	11 (12)	10 (14)	10 (15)	11 (12)	11 (19)
3-2-D15	3	2	15	11 (13)	11 (12)	10 (12)	10 (13)	11 (13)	11 (14)	10 (15)	10 (17)
1-1-D5	1	1	5	14 (14)	14 (12)	13 (14)	13 (16)	14 (13)	14 (12)	13 (14)	13 (16)
1-1-D15	1	1	15	13 (23)	13 (15)	14 (17)	14 (13)	13 (13)	13 (13)	14 (13)	14 (14)

Each session lasted 64 trials or 60 min, whichever came first. Each block of four trials consisted of two forced trials followed by two choice trials. At the start of each trial the center key was illuminated with a white light, and the houselights were dark. A single key peck on the center key initiated the start of the trial. On choice trials, after a response on the center key, the light above this key was turned off, and the two side keys were lit. Throughout the experiment, the color of a side key indicated the reinforcers amount for that key—one reinforcer if the key was green, two if the key was blue, and three if the key was red. A single response on the left key constituted a choice of the standard alternative, and a single response on the right key constituted a choice of the adjusting alternative.

If the standard (left) key was pecked during the choice period, both keylights were turned off and the standard delay interval began, during which the houselights were the same color as the standard key had been (green or red, depending on the condition). At the end of the standard delay, the houselights were turned off and, depending on the condition, either one or three reinforcers were delivered. Each reinforcer consisted of a 2.5-s presentation of grain, and if there were three reinforcer deliveries, there was an interval of 0.5 s between deliveries during which the white houselights were lit. After the last reinforcer delivery of the trial, the white houselights were lit and an intertrial interval (ITI) began. For all adjusting and standard trials, the duration of the ITI was set so that the total time from a choice response to the start of the next trial was 50 s.

If the adjusting (right) key was pecked during the choice period, both keylights were turned off and the adjusting delay interval began, during which the houselights were the same color as the adjusting key had been. At the end of the adjusting delay, the houselights were turned off and, depending on the condition, one, two, or three reinforcers were delivered. As with the standard alternative, reinforcer deliveries were 2.5-s presentations of grain, separated by intervals of 0.5 s during which the white houselights were lit. After the last reinforcer delivery of the trial, the white houselights were lit and the ITI began.

The procedure on forced trials was the same as on choice trials, except that only one side key was lit, and a peck on this key was followed by the same sequence of events as on a choice trial. A peck on the opposite key, which was dark, had no effect. Of every two forced trials, there was one for the standard key and one for the adjusting key, and the temporal order of the two types of trials varied randomly.

After every two choice trials, the duration of the adjusting delay might be changed. If the pigeon chose the standard key on both trials, the adjusting delay was decreased by 1 s. If the pigeon chose the adjusting key on both choice trials, the adjusting delay was increased by 1 s (up to a maximum of 45 s). If the pigeon chose each key on one trial, no change was made. In all three cases, this adjusting delay remained in effect for the next block of four trials. At the start of the first session of a condition, the adjusting delay was 0 s. At the start of later sessions of the same condition, the adjusting delay was determined by the above rules as if it were a continuation of the preceding session.

All conditions lasted for a minimum of 12 sessions. After 12 sessions, a condition was terminated for each pigeon individually when several stability criteria were met. To assess stability, each session was divided into two 32-trial blocks, and for each block the mean adjusting delay was calculated. The results from the first two sessions of a condition were not used, and the condition was terminated when the following criteria were met, using the data from all subsequent sessions: (a) Neither the highest nor the lowest single-block mean of a condition could occur in the last six blocks of a condition. (b) The mean adjusting delay across the last six blocks could not be the highest or the lowest six-block mean of the condition. (c) The mean delay of the last six blocks could not differ from the mean of the preceding six blocks by more than 10% or by more than 1 s (whichever was larger). Table 1 shows the number of sessions needed by each pigeon to meet the stability criteria in each condition.

Results and Discussion

All data analyses were based on the results from the six half-session blocks that satisfied the stability criteria in each condition. For each pigeon and each condition, the mean adjusting delay from these six half-session blocks was used as a measure of the indifference point.

Table 2 presents the indifference points from the last two conditions, in which both the standard and adjusting alternatives delivered one reinforcer per trial. These conditions were included to determine whether there was any bias for one of the two alternatives. The standard delays in these two conditions were 5 s and 15 s. Although there was variability among subjects, the mean adjusting delays in these two conditions were 5.37 s and 14.59 s, respectively, which suggests that for the group as a whole, there was no systematic bias for either the standard or the adjusting alternative. It should be noted that these final conditions were the only two in the experiment in which the key colors and houselight colors were the same for both the standard and the adjusting alternatives (both green, to indicate that both alternatives delivered one reinforcer per trial). The use of the same color for both alternatives may have contributed to the variability in the data, particularly with a 15-s delay, because there was no stimulus during the delay to indicate which key had been chosen.

Table 2.

Mean adjusting delays for each pigeon in Experiment 1 from the two conditions with one standard reinforcer and one adjusting reinforcer (Conditions 1-1-D5 and 1-1-D15).

Pigeon	5-s Standard Delay	15-s Standard Delay
P1	7.39	26.40
P2	5.21	15.79
P3	3.76	10.14
P4	5.16	17.71
P5	6.10	9.90
P6	4.10	14.26
P7	6.24	9.54
P8	4.96	13.00
Mean	5.37	14.59
SD	1.18	5.61

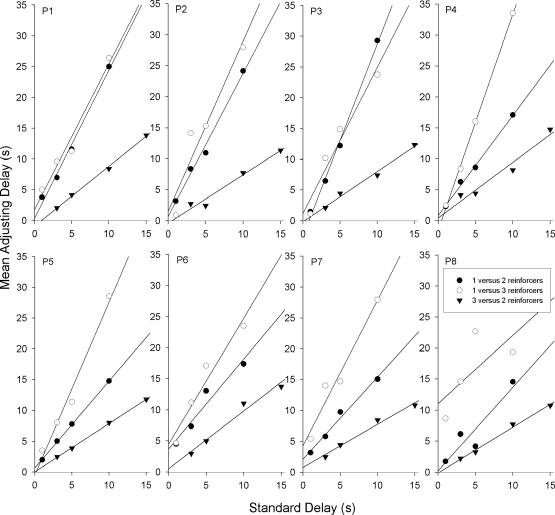
For each of the 8 pigeons, Figure 2 presents the indifference points for the 12 conditions in which the standard and adjusting alternatives delivered a different reinforcer amount. Regression lines are shown for each pair of reinforcer amounts. The slopes, y-intercepts, and percentage of variance accounted for (PVAC) are given in Table 3. The regression lines provided good fits to the data, and the PVAC was greater than 86% in all but one instance (48.7% for Pigeon P8 in the conditions with one versus three reinforcers). The mean PVAC for the 24 regression lines was 95.0%.

Fig. 2.

Mean adjusting delays at each indifference point are shown for each pigeon in Experiment 1. The lines are regression lines fitted to the data points. The slopes and y-intercepts of the lines and percent variance accounted for are given in Table 3.

Table 3.

For each pigeon in Experiment 1, the slopes, y-intercepts, and percentages of variance accounted for (PVAC) are given for the regression lines shown in Figure 2.

Reinforcer Ratio		P1	P2	P3	P4	P5	P6	P7	P8	Mean
1∶3	Slope	2.36	2.74	2.37	3.49	2.81	2.02	2.35	1.10	2.41
	y-int	1.83	1.57	1.23	−1.49	−0.48	4.51	4.33	11.08	2.82
	PVAC	97.0	91.3	94.6	99.8	98.1	94.2	95.9	48.7	89.9
1∶2	Slope	2.40	2.30	3.12	1.61	1.41	1.44	1.33	1.35	1.87
	y-int	0.42	0.72	−2.48	0.91	0.66	3.72	2.13	0.25	0.79
	PVAC	99.0	99.0	99.5	99.6	99.9	94.1	98.4	86.9	97.1
3∶2	Slope	0.97	0.78	0.81	0.89	0.78	0.93	0.69	0.74	0.83
	y-int	−0.85	−0.39	−0.13	0.47	0.05	0.54	0.80	−0.18	0.05
	PVAC	99.7	96.6	98.7	95.2	99.9	97.2	98.2	99.2	98.1

When these results are compared to the predictions of the hyperbolic and exponential equations shown in Figure 1, it is clear that they favor the hyperbolic equation. Recall that the hyperbolic equation predicts that the slopes of these functions should depend on the ratio of A_a/A_s, whereas the exponential equation predicts that the slopes should be 1 in all cases. Consistent with the hyperbolic equation, for the conditions in which A_a/A_s was 3∶1 or 2∶1, the slopes of the regression lines were greater than 1 in 16 of 16 cases. Also consistent with the hyperbolic equation, for the conditions in which A_a/A_s was 2∶3, the slopes of the regression lines were less than 1 in 8 of 8 cases. A repeated-measures analysis of variance (ANOVA) conducted on the slopes of the regression lines found a significant effect of the reinforcer ratio, F(2, 14)  =  19.02, p < .001, and not surprisingly, a significant linear trend indicating steeper slopes with larger reinforcer ratios, F(1, 7)  =  44.84, p < .001.

Table 3 shows considerable variability in the y-intercepts across animals, and as can be seen in Figure 2, the y-intercepts were typically not far from 0. Although both the hyperbolic and exponential equations predict that the y-intercepts should vary as a function of the reinforcer ratio, the amount of variation depends on the value of K. Previous studies with pigeons (Mazur, 1984, 2000) have obtained estimates of K close to 1, and with this value of K, both equations predict small y-intercepts. For example, according to the hyperbolic equation, the y-intercept should equal (A_a−A_s)/A_sK, (see Equation 4). If A_a and A_s are set to 1, 2, or 3 (depending on the reinforcer amounts) and if K is set to 1, the hyperbolic equation predicts y-intercepts of 2, 1, and −0.33 for the conditions with one versus three, one versus two, and three versus two reinforcers, respectively. The mean y-intercepts for these three reinforcer ratios were 2.82, 0.79, and 0.05, respectively—roughly what would be expected if K is close to 1. The predicted y-intercept values were used to generate contrast weights for a planned comparison, which found a significant effect of reinforcer amounts on the y-intercepts, F(1, 14)  =  5.15, p < .05.

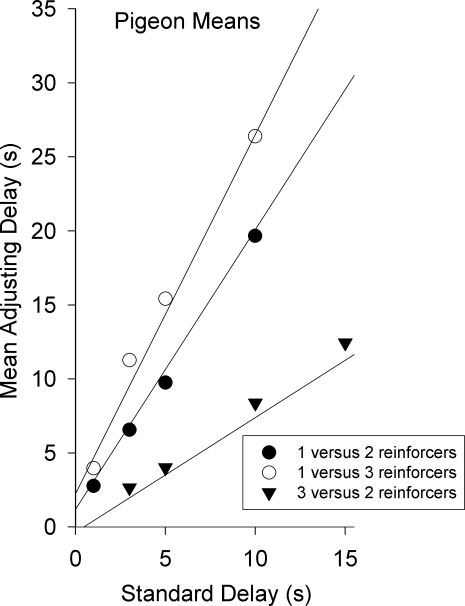
Figure 3 presents the group means from the 8 pigeons. Unlike Figure 2, in which separate regression lines were fitted for each of the three reinforcer ratios, the lines in Figure 3 show the best-fitting predictions of the hyperbolic equation. These predictions were obtained as follows. Let A₁, A₂, and A₃ refer to the effective amounts for trials with one, two, or three reinforcer deliveries, respectively (reflecting the likelihood that two and three reinforcers will not necessarily have two and three times the reinforcing value of one reinforcer). Microsoft Excel Solver was used to find the least-squares fits of Equation 4 when K, A₂, and A₃ were varied as free parameters (with A₁ set equal to 1). The best fits were obtained with K  =  0.64, A₂  =  1.88, and A₃  =  2.43, and the PVAC was 98.4%. Note that the slopes of the lines from the 1∶3 and the 1∶2 conditions were slightly lower than the ratios of the two reinforcer amounts, and this is reflected in the values of A₂, and A₃. The value of K was similar to estimates obtained in other studies with pigeons (e.g., Mazur, 1984, 2000).

Fig. 3.

Group means of the indifference points are shown for the pigeons in Experiment 1. The lines are the best-fitting predictions of Equation 4, which were obtained with the following parameter values: K  =  0.64, A₂  =  1.88, and A₃  =  2.43. See text for details.

Because reinforcer amounts were varied by using one, two, or three 2.5-s hopper presentations (with 0.5 s between presentations), a different approach to this experiment is to view it as one in which multiple delayed reinforcers were delivered. For example, if the adjusting delay was 10 s followed by three hopper presentations, this could be treated as three reinforcers delivered 10 s, 13 s, and 16 s after the choice response. Because of the longer delays to the second and third hopper presentations, their values should be lower than the value of the first hopper presentation. Raineri and Rachlin (1993) used this line of reasoning to explain why there may be diminishing marginal value when reinforcer amounts are increased. As they put it, “For example, an additional apple will be consumed sooner if you already have only one apple than if you already have ten apples. The additional apple has to wait in line, so to speak, to be consumed: the longer the line, the longer the wait. Commodities for which a person (or other animal) has to wait longer are valued less; they are discounted by delay” (p. 78). Therefore, in the present experiment, perhaps the slopes of the indifference functions were less than 2 and 3 (the nominal values of A_a/A_s) because of the extra delays to the second and third hopper presentations.

In previous studies on choice between single and multiple delayed reinforcers (in which the multiple reinforcers were separated by longer delays, not delivered in rapid succession as in the present experiment), Mazur (1986, 2007) used the following version of the hyperbolic decay model to predict the value of an alternative that delivered more than one delayed reinforcer:

5

where A now represents the amount of each individual reinforcer (e.g., a 2.5-s hopper presentation in the present experiment), n is the total number of reinforcers in the series, and D_i is the delay between the choice response and reinforcer i. To determine whether this approach could predict the slopes of the indifference functions, Equation 5 was used to derive predictions for the present experiment. With K  =  1, Equation 5 predicted indifference functions that were approximately linear, with a slope of about 1.96 for the conditions with one versus two reinforcers and a slope of 2.92 for the conditions with one versus three reinforcers. Therefore, taking into account the extra delays to the second and third reinforcers may partially explain why the obtained slopes were lower than the reinforcer ratio, A_a/A_s, but the predictions from Equation 5 were still higher than the best-fitting slopes shown in Figure 3 (1.88 and 2.42, respectively).

In summary, the results of this experiment with pigeons clearly favored the hyperbolic equation over an exponential equation, because the slopes of the indifference functions varied significantly with changes in the ratio of the two reinforcer amounts. The slopes were smaller than the ratios of the two reinforcer amounts, A_a/A_s, however. Experiment 2 used the same adjusting-delay procedure and the same delays and reinforcer ratios with rats as subjects so that the performance of these two species could be compared. As already noted, previous studies (Mazur, 2000, 2007) have suggested that the rate of discounting may be four or five times slower for rats than for pigeons, and this appears in the hyperbolic equation as smaller estimates of K. According to Equation 4, the y-intercept of an indifference function is inversely related to K. Therefore, if there is such a species difference, the y-intercepts for the rats in Experiment 2 should be substantially further from zero than those for the pigeons in Experiment 1.

Experiment 2

Method

Subjects

This experiment used 4 male Long Evans rats approximately 8 months old at the start of the experiment. All were maintained at 80% of their free feeding weight, and all subjects had previous experience with one different experimental procedure.

Apparatus

The experimental chamber was a modular test chamber for rats, 30.5 cm long, 24 cm wide, and 21 cm high. The side walls and top of the chamber were Plexiglas, and the front and back walls were aluminum. The floor consisted of steel rods, 0.48 cm in diameter and 1.6 cm apart, center to center. The front wall had two retractable response levers, 11 cm apart, 6 cm above the floor, 4.8 cm long, and extending 1.9 cm into the chamber. Centered in the front wall was a nonretractable lever with the same dimensions, 11.5 cm above the floor. A force of approximately 0.20 N was required to operate each lever, and when a lever was active, each effective response produced a feedback click. Above each lever was a 2-W white stimulus light, 2.5 cm in diameter. A pellet dispenser delivered 45-mg food pellets into a receptacle through a square 5.1-cm opening in the center of the front wall. A 2-W white houselight was mounted at the top center of the rear wall.

The chamber was enclosed in a sound-attenuating box containing a ventilation fan. All stimuli were controlled and responses recorded by an IBM-compatible personal computer using the Medstate programming language.

Procedure

In most respects, the procedure was similar to the one used with the pigeons in Experiment 1. The experiment consisted of 14 conditions that used the same delays for the standard alternative (1 s, 3 s, 5 s, 10 s, or 15 s), the same reinforcer ratios (one versus two reinforcers, one versus three reinforcers, three versus two reinforcers, and one versus one reinforcers), the same sequencing of forced trials and choice trials (16 blocks of trials per session, each with two forced trials followed by two choice trials) and the same procedure for changing the adjusting delay. The order of conditions was varied across subjects as shown in Table 4.

Table 4.

Order of conditions (in bold) and number of sessions needed to meet the stability criteria (in parentheses) for each rat in Experiment 2.

Condition	Standard Reinforcer Amount	Adjusting Reinforcer Amount	Standard Delay (s)	Rats
				R1	R2	R3	R4
1-2-D1	1	2	1	3 (25)	3 (20)	6 (12)	6 (16)
1-2-D3	1	2	3	4 (34)	4 (17)	5 (13)	5 (14)
1-2-D5	1	2	5	1 (19)	1 (12)	8 (14)	8 (15)
1-2-D10	1	2	10	2 (13)	2 (13)	7 (15)	7 (15)
1-3-D1	1	3	1	6 (14)	6 (14)	3 (14)	3 (16)
1-3-D3	1	3	3	5 (15)	5 (16)	4 (23)	4 (14)
1-3-D5	1	3	5	9 (20)	8 (13)	1 (17)	1 (12)
1-3-D10	1	3	10	7 (14)	7 (17)	2 (12)	2 (12)
3-2-D3	3	2	3	8 (12)	9 (12)	12 (15)	12 (12)
3-2-D5	3	2	5	12 (13)	12 (12)	9 (22)	9 (13)
3-2-D10	3	2	10	10 (12)	10 (12)	11 (13)	11 (15)
3-2-D15	3	2	15	11 (13)	11 (13)	10 (13)	10 (15)
1-1-D5	1	1	5	13 (15)	13 (12)	14 (14)	14 (17)
1-1-D15	1	1	15	14 (15)	14 (12)	13 (15)	13 (12)

At the start of each trial the light above the center lever was illuminated, and the houselight was off. A single lever press on the center lever initiated the start of the trial. On choice trials, after a response on the center lever, the light above this lever was turned off, the two side levers were extended into the chamber, and the lights above the two side levers were turned on. A single response on the left lever constituted a choice of the standard alternative, and a single response on the right lever constituted a choice of the adjusting alternative.

If the standard (left) lever was pressed during the choice period, the two side levers were retracted, the light over the right lever was turned off, and the light over the left lever remained lit for the duration of the standard delay until presentation of the reinforcer. At the end of the standard delay, the light above the left lever was turned off, the chamber was dark, and either one or three pellets were delivered, depending on the condition. For both the standard and adjusting alternatives, if more than one pellet was delivered, there was a 1-s delay between successive pellet deliveries. One second after the last pellet was delivered, the houselight was turned on and the ITI began. As in Experiment 1, for all adjusting and standard trials, the duration of the ITI was set so that the total time from a choice response to the start of the next trial was 50 s.

If the adjusting (right) lever was pressed during the choice period, the two side levers were retracted, only the light above the right lever remained on, and there was a delay of adjusting duration. At the end of the adjusting delay, the light above the right lever was turned off, the chamber was dark, and one, two, or three food pellets were delivered, depending on the condition. One second after the last pellet was delivered, the houselight was turned on, and the ITI began.

The procedure on forced trials was the same as on choice trials, except that only one side lever was extended, the light above it was lit, and a press on this lever was followed by the same sequence of events as on a choice trial. Of every two forced trials, there was one for the standard lever and one for the adjusting lever, and the temporal order of the two types of trials varied randomly.

All conditions for the rats lasted a minimum of 12 sessions, and a condition was terminated for each rat using the same stability criteria as in Experiment 1. Table 4 shows the number of sessions needed by each rat to meet the stability criteria in each condition.

Results and Discussion

All data analyses were based on the results from the six half-session blocks that satisfied the stability criteria in each condition. For each rat and each condition, the mean adjusting delay from these six half-session blocks was used as a measure of the indifference point.

Table 5 presents the indifference points from the last two conditions, in which both the standard and adjusting alternatives delivered one pellet per trial, and the standard delays in these two conditions were 5 s and 15 s. The mean adjusting delays in these two conditions were 5.16 s and 12.64 s, respectively.

Table 5.

Mean adjusting delays for each rat in Experiment 2 from the two conditions with one standard reinforcer and one adjusting reinforcer (Conditions 1-1-D5 and 1-1-D15).

Rat	5-s Standard Delay	15-s Standard Delay
R1	5.56	12.77
R2	5.38	13.23
R3	5.23	14.28
R4	4.48	10.29
Mean	5.16	12.64
SD	0.47	1.69

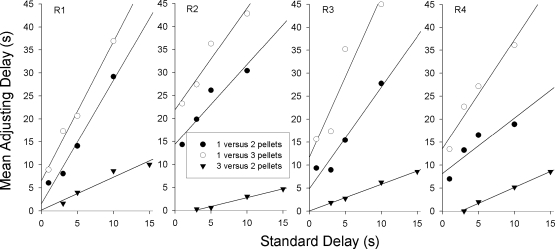
For each of the 4 rats, Figure 4 presents the indifference points for the 12 conditions in which the standard and adjusting alternatives delivered different reinforcer amounts. Regression lines are shown for each pair of reinforcer amounts. The slopes, y-intercepts, and PVAC are given in Table 6. The regression lines provided good fits to the data, and the PVAC was greater than 81% in all cases. The mean PVAC for the 12 regression lines was 94.4%.

Fig. 4.

Mean adjusting delays at each indifference point are shown for each rat in Experiment 2. The lines are regression lines fitted to the data points. The slopes and y-intercepts of the lines and percent variance accounted for are given in Table 5.

Table 6.

For each rat in Experiment 2, the slopes, y-intercepts, and percentages of variance accounted for (PVAC) are given for the regression lines shown in Figure 4.

Reinforcer Ratio		R1	R2	R3	R4	Mean
1∶3	Slope	3.02	2.21	3.48	2.37	2.77
	y-int	6.62	21.92	11.74	13.58	13.47
	PVAC	98.9	93.7	89.6	94.5	94.19
1∶2	Slope	2.67	1.78	2.21	1.21	1.97
	y-int	1.63	14.28	4.85	8.18	7.23
	PVAC	97.8	91.3	94.6	81.3	91.25
3∶2	Slope	0.71	0.38	0.58	0.70	0.59
	y-int	0.19	−1.04	0.08	−1.77	−0.63
	PVAC	93.7	98.8	99.1	99.5	97.80

As with the results from the pigeons in Experiment 1, these results clearly favor the predictions of the hyperbolic equation over the exponential equation (cf. Figure 1). Consistent with the hyperbolic equation, for the conditions in which A_a/A_s was 3∶1 or 2∶1, the slopes of the regression lines were greater than 1 in 8 of 8 cases. Also consistent with the hyperbolic equation, for the conditions in which A_a/A_s was 2∶3, the slopes of the regression lines were less than 1 for all 4 rats. A repeated-measures ANOVA conducted on the slopes of the regression lines found a significant effect of the reinforcer ratio, F(2, 6)  =  31.55, p < .001, and a significant linear trend indicating steeper slopes with larger reinforcer ratios, F(1, 3)  =  61.98, p < .01.

Table 6 shows that the y-intercepts for the rats in the conditions with 1∶3 and 1∶2 reinforcer ratios were further from 0 than those for the pigeons in Table 4. The mean y-intercepts for the rats were 13.5 s and 7.2 s from the 1∶3 and 1∶2 conditions, respectively, compared to 2.8 s and 0.8 s for the pigeons. A repeated-measures ANOVA conducted on the y-intercepts for the rats found a significant effect of reinforcer ratio, F(2, 6)  =  13.81, p < .01 and a significant linear trend indicating larger y-intercepts with larger reinforcer ratios, F(1, 3)  =  16.46, p < .05. As will be discussed below, the differences in y-intercepts between the pigeons and rats may reflect differences in the discounting parameter, K.

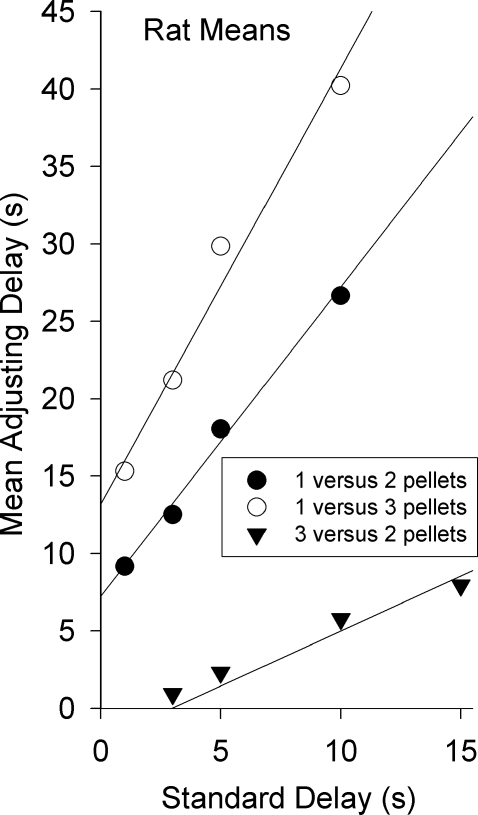
Figure 5 presents the group means from the 4 rats. The lines are the best-fitting predictions of the hyperbolic equation, obtained by varying K, A₂ and A₃ as free parameters, as was done for the pigeon means in Figure 3. The best fits were obtained with K  =  0.14, A₂  =  2.00, and A₃  =  2.82, and the PVAC was 99.2%. These values of A₂, and A₃ were slightly larger than for the pigeons, reflecting slightly steeper slopes of the indifference functions. However, the most obvious difference between the results from the rats and pigeons (as can be seen by comparing Figures 3 and 5) was the difference in y-intercepts. In the conditions with one versus three reinforcers and one versus two reinforcers, the y-intercepts were much larger for the rats than for the pigeons, and with three versus two reinforcers, the y-intercept was smaller (and negative) for the rats. These differences in the y-intercepts resulted in an estimate of K that was about five times smaller for the rats than for the pigeons. Because K is a measure of the rate of temporal discounting, the smaller value of K suggests that as delay increased, the reinforcing value of food decreased about five times more slowly for the rats than for the pigeons.

Fig. 5.

Group means of the indifference points are shown for the rats in Experiment 2. The lines are the best-fitting predictions of Equation 4, which were obtained with the following parameter values: K  =  0.14, A₂  =  2.00, and A₃  =  2.82. See text for details.

The alternate approach suggested by Equation 5 (which takes into account the extra delays to the second and third pellet deliveries) may help to explain why the slopes were, on average, steeper for the rats than for the pigeons. First, whereas the second and third hopper deliveries in Experiment 1 were delayed an extra 3 s and 6 s, the second and third pellets in Experiment 2 were delayed by only 1 s and 2 s. Second, the smaller estimate of K for the rats, which presumably reflects a slower rate of delay discounting, implies that the extra delays to the second and third reinforcer deliveries should have less effect on the rats than the same delays would have on pigeons. Equation 5 was used to make predictions for Experiment 2 with K set at 0.14, the best-fitting estimate for the group data. The predicted slopes from Equation 5 were 1.999 for the conditions with one versus two pellets and 2.998 for the conditions with one versus three pellets—virtually identical to the reinforcer ratios, A_a/A_s. These predictions, when compared to those for Experiment 1, lend some support to the idea that the slightly steeper slopes for the rats could have been due, at least in part, to the faster delivery of the second and third reinforcers and to slower discounting rates for the rats.

General Discussion

The results of these two experiments join many others that have favored a hyperbolic delay discounting equation over an exponential equation (e.g., Bickel, et al., 1999; Grossbard & Mazur, 1986; Mazur, 1987; Mazur, et al., 1987; Rodriguez & Logue, 1988; van der Pol & Cairns, 2002). The novel feature of the present studies was that they specifically tested the prediction of the hyperbolic equation that the slopes of the indifference functions should vary as a function of the ratios of the two reinforcer amounts, A_a/A_s. Consistent with the hyperbolic equation, the slopes of the indifference functions varied systematically with the three different values of A_a/A_s for both pigeons and rats. Note that the slopes were always greater than 1 when the adjusting alternative delivered the larger reinforcer, and they were always less than 1 when the adjusting alternative delivered the smaller reinforcer. It is therefore difficult to argue that the failure to find slopes equal to 1 was the result of some bias or preference for the adjusting alternative.

The exponential equation predicts that the slopes of these indifference functions should equal 1 regardless of the reinforcer amounts as long as K is the same for the two reinforcers. What does the exponential equation predict, however, if K varies for reinforcers of different sizes? Assuming that V_s  =  V_a at an indifference point, it follows from the exponential equation that

6

where K is now subscripted so it can take on two different values for the standard and adjusting alternatives. Solving for D_a yields

7

Equation 7 describes a linear function with a y-intercept of (ln A_a − ln A_s)/K_a and a slope of K_s/K_a. Therefore, if the values of K vary as a function of reinforcer amount, Equation 7 predicts linear indifference functions with slopes that do not equal 1. If the value of K decreases as reinforcer amount increases (i.e., if K_a < K_s whenever A_a > A_s), then the exponential equation, like the hyperbolic, predicts that the indifference functions should be greater than 1 whenever A_a > A_s and less than 1 whenever A_a < A_s (cf. Green & Myerson, 1993). If such variations in K do occur, the predictions of the hyperbolic and exponential equations are similar for the indifference functions in the present experiments, and it would be more difficult to distinguish between them.

Studies with human subjects have found decreases in K with larger reinforcer amounts (e.g., Green et al., 1994; Green, Myerson, & McFadden, 1997; Kirby & Marakovic, 1996). However, experiments with pigeons and rats have found no evidence for an inverse relation between reinforcer amount and the value of K. Richards, Mitchell, de Wit, and Seiden (1997) used an adjusting-amount choice procedure to obtain discounting functions for rats with water as a reinforcer. They varied the reinforcer amounts across conditions, and with 100, 150, and 200 µl of water as the standard alternative, the mean values of K for the rats were 0.11, 0.15, and 0.23, respectively. These differences were not statistically significant, but in any case they were in the opposite direction from what would be needed for the exponential equation to predict the results of the present experiments. Grace (1999) used a concurrent-chains procedure with pigeons, and he found no effect of reinforcer amount on sensitivity to reinforcer delays. More recently, Green, Myerson, Holt, Slevin, and Estle (2004) used an adjusting-amount procedure with both pigeons and rats and food pellets as reinforcers. They varied the reinforcer amounts between 5 and 32 pellets for the pigeons and between 5 and 20 pellets for the rats, and they found no systematic differences in K as a function of reinforcer amount. In summary, the results of these experiments suggest that K does not decrease for rats or pigeons as the amount of food or water increases, and this implies that an exponential equation cannot account for the differences in slopes obtained in the present experiments.

Given the evidence from both human and nonhuman subjects that favors a hyperbolic discounting function over an exponential function, some theorists have proposed variations of the basic exponential equation to try to accommodate the data. For instance, one suggestion is that the value of any delayed reinforcer is first discounted by some constant fraction (when compared to an immediate reinforcer, which is not discounted), and then there is additional, exponential discounting as the delay increases (e.g., Laibson, 1997; O'Donoghue & Rabin, 1999). This produces what is sometimes called a “quasi-hyperbolic” discounting function because its shape can approximate a hyperbola, and its predictions can also be similar to those of a hyperbolic equation in some cases. However, this approach does not seem to apply to the present experiments, because none of the choices were between an immediate reinforcer and a delayed reinforcer. Rather, the choices were always between two reinforcers with different delays, and for choices between two delayed reinforcers, this quasi-hyperbolic model reduces to the simple exponential equation. Perhaps it could be argued that the 1-s delays were so short that these were essentially immediate reinforcers. However, even if the data from the two conditions with 1-s delays are ignored, the remaining data present the same picture—the slopes of the indifference functions still varied as a function of A_a/A_s, which, according to both the simple exponential equation and the quasi-hyperbolic equation, should not happen in choices involving two delayed reinforcers. Therefore, the quasi-hyperbolic equation, which is an exponential equation with an added parameter, does not account for the results of these experiments.

The slopes of the indifference functions varied across subjects, and the slopes of the functions fitted to the group means (Figures 3 and 5) were not exactly equal to the ratios of the reinforcer amounts, A_a/A_s. As already discussed, this may have occurred because the extra delays to the second and third reinforcer deliveries of a trial decreased their values (as expressed in Equation 5). It is interesting to note that for Experiment 2, with extra delays of 1 s and 2 s to the second and third food pellets of a trial, the slopes predicted by Equation 5 are virtually the same as the reinforcer ratios, A_a/A_s. The best-fitting slopes for the group means in Experiment 2 (2.82, 2.00, and 0.71) were close to the corresponding values of A_a/A_s (3, 2, and 0.67, respectively). In contrast, for Experiment 1, where the additional delays to the second and third reinforcers were 3 s and 6 s, Equation 5 predicted slopes that were slightly smaller than A_a/A_s, and this might partially account for the smaller slopes in Experiment 1. However, the best-fitting slopes for the pigeons' group means were even smaller than predicted by Equation 5, which suggests that the additional delay to the second and third reinforcers was not the whole story. There is, of course, no reason why doubling or tripling a reinforcer's amount should precisely double or triple its value, even if the entire reinforcer amount can be delivered simultaneously. The suggestion that a reinforcer's effect on choice behavior is not directly proportional to its amount is reminiscent of the undermatching that has been obtained with concurrent VI schedules when reinforcer amounts were varied (e.g., Schneider, 1973; Todorov, 1973).

Although the results from the rats and pigeons were similar in most respects, the main difference was in the y-intercepts of the indifference functions, which were further from 0 for the rats. Because of this difference in y-intercepts, the best-fitting estimates of K were quite different for the two species (0.64 for the pigeons and 0.14 for the rats). These results are similar to those found in previous experiments by Mazur (2000, 2007), who concluded that delay-discounting rates are four or five times faster for pigeons than for rats. In two experiments with pigeons that used two different procedures to obtain indifference points (Mazur, 2000), the mean estimates of K were 0.67 and 1.05. Using an adjusting-amount procedure with rats, Mazur (2007) obtained a mean estimate of K of 0.10. These estimates are similar to those obtained by other researchers. In two experiments with rats and water reinforcement, Richards et al. (1997) obtained values of K of 0.15 and 0.16. Averaged across subjects and conditions, the estimates of K obtained by Green et al. (2004) with food pellets were 0.47 for pigeons and 0.14 for rats. Although cross-species comparisons should always be interpreted with caution, this collection of studies used a variety of different methods to estimate K, and it seems unlikely that the quantitative differences between pigeons and rats are the result of some procedural differences in testing the two species. Rather, we propose that they reflect a reliable species difference in delay-discounting rates.

Mazur (2004) pointed out that according to the hyperbolic equation, the quantity 1/K can be called a reinforcer's “half-life”—the delay required to reduce the reinforcer's value to 50% of the value it would have if delivered immediately. The estimates of K from these studies therefore suggest that for pigeons, the half-life of a delayed food reinforcer is just 1 or 2 s, whereas the half-life for rats is approximately 5 to 10 s. Pigeons and rats are among the two most commonly used species in research on operant conditioning, and they often exhibit similar behavior patterns when placed on similar tasks (e.g., simple reinforcement schedules, concurrent schedules, signal detection tasks, temporal discrimination procedures). The performance of these two species in the present experiments was qualitatively similar, but the substantial differences in their delay-discounting rates are noteworthy. Considering the broad interest in delay and intertemporal choice by psychologists, behavioral ecologists, and economists, we suggest that it would be quite informative to obtain comparable estimates of delay-discounting rates from a variety of other species.