Water at the Surfaces of Aligned Phospholipid Multi-Bilayer Model Membranes Probed with Ultrafast Vibrational Spectroscopy

Abstract

The dynamics of water at the surface of artificial membranes composed of aligned multibilayers of the phospholipid dilauroyl phosphatidylcholine (DLPC) are probed with ultrafast polarization selective vibrational pump-probe spectroscopy. The experiments are performed at various hydration levels, x = 2 – 16 water molecules per lipid at 37 °C. The water molecules are ~1 nm above or below the membrane surface. The experiments are conducted on the OD stretching mode of dilute HOD in H₂O to eliminate vibrational excitation transfer. The FT-IR absorption spectra of the OD stretch in the DLPC bilayer system at low hydration levels shows a red-shift in frequency relative to bulk water, which is in contrast to the blue shift often observed in systems such as water nanopools in reverse micelles. The spectra for x = 4 – 16 can be reproduced by a superposition of the spectra for x = 2 and bulk water. IR Pump-probe measurements reveal that the vibrational population decays (lifetimes) become longer as the hydration level is decreased. The population decays are fit well by biexponential functions. The population decays, measured as a function of the OD stretch frequency, suggest the existence of two major types of water molecules in the interfacial region of the lipid bilayers. One component may be a clathrate-like water cluster near the hydrophobic choline group and the other may be related to the hydration water molecules mainly associated with the phosphate group. As the hydration level increases, the vibrational lifetimes of these two components decrease, suggesting a continuous evolution of the hydration structures in the two components associated with the swelling of the bilayers. The agreement of the magnitudes of the two components obtained from IR spectra with those from vibrational lifetime measurements further supports the two component model. The vibrational population decay fitting also gives an estimation of the number of phosphate-associated water molecules and choline-associated water molecules from, which range from 1 to 4, and 1 to 12, respectively as x increases from 2 to 16. Time dependent anisotropy measurements yield the rate of orientational relaxation as a function of x. The anisotropy decay is biexponential. The fast component is almost independent of x, and is interpreted as small orientational fluctuations that occur without hydrogen bond rearrangement. The slower component becomes very long as the hydration level decreases. This component is a measure of the rate of complete orientational randomization, which requires hydrogen bond rearrangement and is discussed in terms of a jump reorientation model.

I. Introduction

The boundary between a living cell and its surroundings is the plasma membrane with a thickness ranging from 7-10 nm.¹ This nanoscale structure is primarily composed of phospholipids and embedded proteins. The membrane controls the flow of materials into and out of a cell, and it senses and controls the response of cells to hormones and other external signals. Biological membranes have a basic bilayer structure where the nonpolar chains of the phospholipids form the interior of a molecular bilayer.¹ The organization of phospholipid bilayers and water is important because lipid-water interactions play a key role in native membrane functioning, stability of bilayers, water permeation, and fusion-related repulsive forces between bilayers.²

Numerous studies have been carried out in order to understand the hydration of lipid membranes.^3-6 Experiments and simulations have found that water molecules penetrate the interfacial region (phospholipid head groups) of bilayers, but water has a low probability of being found in the hydrophobic core.^2,7-9 Fully hydrated liquid crystal phase (L_α) phosphatidylcholine lipids such as dipalmitoyl phosphatidylcholine (DPPC) can take up a maximum of ~30 water molecules per lipid, distributed in the interfacial water region and the water layer between the two head group regions of adjacent bilayers.³ However, the amount of water that can hydrate the membrane is dependent on the membrane’s structure. In the more structurally ordered gel phase, only ~13 water molecules per DPPC are absorbed.³ The number of water molecules in the interfacial water region also changes from ~4 per DPPC in gel phase to ~9 per DPPC in the liquid crystalline phase.³ There have been various reports on how the head groups associate with water molecules in bilayers. A variety of techniques including IR, NMR, neutron scattering, and electrical conductivity measurements have been employed in studies on water-head group interactions.^3-6 In spite of this, a clear picture is still lacking for lipid bilayers at various hydration levels. Molecular dynamics simulations on dimyristoyl phosphatidylcholine (DMPC) bilayers suggest that the presence of the hydrophobic choline group in the lipid is responsible for the formation of a “clathrate like” shell at the surface of the lipid bilayer.⁹ Lopez et al. have conducted molecular dynamics simulations on the hydrogen bonding structure of water at the fully hydrated bilayer surface of DMPC.⁷ In addition to the formation of a hydration shell around the choline group where the water molecules are able to form hydrogen bonds with each other by creating a clathrate structure, they also found that the double bonded oxygen atoms of the phosphate group have a 74% probability of forming hydrogen bonds with two water molecules. The importance of the choline group in hydration has also been revealed by electrical conductivity measurements which indicate that the choline group is as important as the phosphate group for absorbing water.¹⁰ Using NMR measurements, Hsieh and Wu studied the structure and dynamics of the hydration shell of DMPC bilayers at temperatures below 0 °C and suggested that the hydration shell of the head group consists of two distinct regions, a clathrate-like water cluster near the hydrophobic choline group and hydration water molecules associated with the phosphate group.¹¹ About one to two water molecules are associated with the phosphate group and are frozen, whereas about five to six waters near the choline group behave as a water cluster and remain unfrozen at temperatures as low as −70 °C.¹¹

Lipid bilayer systems have a unique nanoscale polar interfacial structure where most of the lipid-water interactions occur.^1-6 Water saturated multilamellar arrays of phospholipids in the L_α fluid phase, such as dilauroyl phosphatidylcholine (DLPC, figure 1), have a bilayer repeat spacing, D, of 6.1 nm.¹² The water layer between the two head group regions of adjacent bilayers is 3.8 nm thick, and the interfacial water region is considered to be ~0.9 nm thick.¹²

Figure 1.

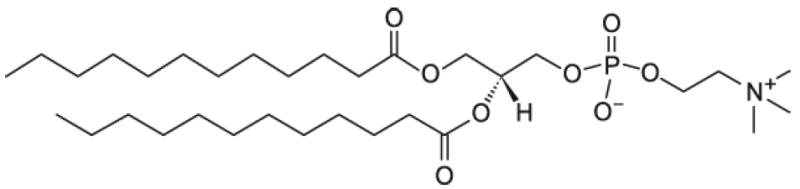
Chemical structure of the phospholipid dilauroyl phosphatidylcholine (DLPC).

Because of the nanoscale confinement, the dynamics of water in the inter-bilayer region are expected to be very different from bulk water in analogy to the substantial deviations from bulk water dynamics observed in other nanoscopic water systems. Ultrafast vibrational spectroscopy has recently emerged as a powerful tool to study the dynamics of water in nanoscopic environments.^13-18 Experiments probing the OD stretching mode of dilute HOD in H₂O in the water nanopool of reverse micelles^13,14,19 or the hydrophilic channels of Nafion membranes^15,16 have shown that the vibrational population relaxation (vibrational lifetime) and the orientational relaxation of water both slow as the amount of water in the system decreases. In AOT reverse micelles, a core-shell model can be used to quantitatively explain the size-dependent infrared (IR) absorption spectra and population relaxation times.¹³ The water dynamics are subdivided into two contributions, a “shell” region consisting of water closely associated with the head groups and a “core” region with bulk-like properties consisting of water molecules away from the head groups. In Nafion membranes,¹⁵ the OD stretch IR absorption spectra can be fit using a two-environment model consisting of bulk water and head group water. The spectrum of the head group waters was obtained from measurements on almost dry Nafion. At a given hydration level, which determines the size of the water channels and the amount of water in the channel, the vibrational population relaxation could be well described in terms of two populations. The population decays were bi-exponential, with the amplitudes of the two components varying systematically with the detection wavelength within the OD absorption band. However, in contrast to AOT reverse micelles, as the hydration level is changed, the lifetimes of the two components change. This result was interpreted as being caused by changes in the interfacial structure and morphology of the channels with changing hydration level. Recent IR pump-probe measurements on dimyristoyl phosphatidylcholine (DMPC) phospholipids that are weakly hydrated with D₂O suggest that water loses most of its bulk properties and has a high degree of structural heterogeneity.^17,18

Here we utilize ultrafast vibrational spectroscopy and IR absorption spectroscopy to probe the nature of water at and near the surface of DLPC phospholipid model membranes. DLPC was chosen based on the stability of its aligned, optically transparent multibilayers for a range of relatively low hydration levels. By using aligned multibilayers, it is possible to examine water molecules at the head group interface without contributions from bulk water and still have a sufficient number of water molecules to perform IR pump-probe experiments. The measurements are made on the OD stretch of dilute HOD in H₂O. The use of dilute HOD as opposed to pure H₂O or D₂O is important to eliminate vibrational excitation transfer.^20-22 Vibrational excitation transfer causes the decay of the transition dipole anisotropy, which interferes with measurements of orientational relaxation. It also changes the location of the excitation, which impedes the use of the vibrational lifetime as a probe of the local environment. shown that dilute HOD in H₂O does not change the behavior of water and that observations of the OD hydroxyl stretch report on the dynamics and local environment of water.

The aligned multibilayers are studied for various hydration levels, x, at 37 °C over the range of 2 to 16 water molecules per lipid (x = moles H₂O per mole DLPC). The alignment of the multibilayers can be maintained at 37 °C for several days, a period of time long enough for the optical measurements to be made. DLPC bilayers can absorb up to about 31 waters per lipid with ~8 water molecules in the head group region in fully hydrated DLPC bilayers.¹² The FT-IR spectra of the OD stretch of HOD in DLPC bilayers at low hydration levels shows that the frequency is red-shifted compared to the spectrum of bulk water. The red-shift in the absorption spectrum is opposite to the blue shift observed in reverse micelles^13,19 and Nafion membranes.¹⁵

Ultrafast IR polarization selective pump-probe experiments on the OD stretch are used to measure vibrational population relaxation as a function of the number of water molecules per lipid, x, and the detection wavelength. In addition, orientational relaxation is measured as a function of x. The population relaxation is best fit with a biexponential decay. The vibrational lifetimes become longer when the hydration level decreases, similar to the results for water confined in reverse micelles and Nafion membranes. The results demonstrate that there are two distinct environments for the water molecules. The changes in the lifetimes with x indicate that the structure of the bilayer surface changes with hydration level. The relatively mild variation of the lifetimes with detection wavelength suggests that each environment has some degree of inhomogeneity. The time dependent anisotropies, which are a measure of water’s orientational dynamics, change dramatically with hydration level. As x decreases, the orientation relaxation becomes increasingly slow. However, the anisotropy decays are not single exponential. A relatively small fast component occurs at all levels of hydration. In other systems, this type of fast decay has been interpreted using a wobbling-in-a-cone model, in which the orientation of the water molecule undergoes fast fluctuations with the original hydrogen bonding network intact. At longer times, hydrogen bond rearrangement results in complete orientational randomization.

II. Experimental Procedures

Synthetic DLPC, 1,2-dilauroyl-sn-glycero-3-phosphocholine, with purity >99%, was purchased from Avanti Polar Lipids, Inc. (Alabaster, AL) and used as received. The sample contained 2.2 wt% residual water (~0.8 H₂O/DLPC) as determined by coulometric Karl Fischer titration. Deuterium oxide (99.9 atom% D) was obtained from Sigma-Aldrich. Deionized ultrafiltered water was obtained from Fisher Scientific.

The aligned multibilayer DLPC lipids DLPC·xH₂O with various hydration levels were prepared for the measurements. Different starting ratio x = 2, 5, 7, 10, and 20 were selected for preparation. The final water to lipid ratio of the samples after the preparation procedure was determined to be x ≈ 2, 4, 6, 8, and 16 by coulometric Karl Fischer titration. For preparation, a series of samples each containing about 65 mg DLPC was weighed in small glass vials. By taking the 2.2 wt% residual water in the DLPC samples into account, calculated volumes of water containing 5.5-8.6 wt% HOD were added to the samples, so that the final HOD concentration was 5 mol% in the water contained in the lipid samples. This concentration is low enough to prevent vibrational excitation transfer. The vials containing the mixtures were tightly sealed to prevent evaporation. The samples were heated in an oven so that the mixture became fluid-like. Periodically the samples were taken out of the oven and shaken to ensure that the lipid was homogeneously hydrated. An oven temperature of ~85 °C was used for x = 2, ~55 °C for x = 4 and 6, and ~45 °C for x = 8 and 16. The samples with x ≥ 8 can also be mixed uniformly at room temperature if they are allowed to equilibrate overnight. When the DLPC lipid samples became homogeneously hydrated after mixing for two to four hours, they were transferred to specially designed heated IR sample cells with two 3 mm thick CaF₂ windows. Teflon spacers with different thicknesses, 45 μm (x = 16), 100 μm (x = 8), 190 μm (x = 4 and 6), and 220 μm (x = 2) were used so that the absorbance of the OD stretch at ~2500 cm^-1 in the samples was in the range of 0.2-0.7.

To make aligned, optically transparent monodomain DLPC multibilayers, a mechanical alignment method, modified from refs. 19-22 was used. The IR cells with the samples of different water concentrations were heated to the temperatures required to obtain homogeneous hydration as discussed above. The cells consisted of two copper plates that compressed the CaF₂ windows and the spacer. The tension on one metal plate was varied by set screws. Flow from one part of the sample to another was observed by gently alternating between compressing and releasing the windows. The alignment was monitored by placing the sample on the stage of a polarizing microscope where the aligned regions appeared uniformly black between crossed polarizers since the optical axis of the homeotropically aligned lipid bilayers is normal to the window surfaces.^24-27 A dark cross pattern was observed using a conoscopic microscope, which demonstrates that the sample is macroscopically aligned. Macroscopic alignment of DLPC for x = 2-8 water molecules was achieved for a variety of temperatures, including 37 °C. However, the sample containing x = 16 water molecules (32 wt% water) could not be macroscopically aligned, in agreement with the literature,^24,25. This sample is still microscopically aligned as the lamellar repeat distance and bilayer thickness change linearly from x = 8 to x = 16 even at 25 °C.²⁸ Once the sample was aligned at elevated temperature, the cell was sealed, and the temperature was gradually lowered to the experimental temperature of 37 °C. After the pump-probe measurements, the each sample was reexamined by FT-IR and with the polarizing conoscopic microscope. No changes were observed in either the alignment or the spectrum. The consistency of the spectrum shows that the samples did not lose water during the measurement.

The pump-probe measurements were conducted using a laser system described previously.^15,16 Briefly, a home-built Ti:Sapphire oscillator and regenerative amplifier operating at 1 kHz were used to pump an OPA and difference frequency stage to produce ~70 fs, ~4 μm IR pulses. The pulses were split into pump and probe pulses with the probe’s polarization set to ~45° relative to the pump. Just prior to the monochromator, the components of the probe with polarization parallel and perpendicular to the pump were selected to avoid depolarization effects due to optics in the beam path. The perpendicular component was then rotated back to parallel by a half wave plate to ensure both components experienced the same diffraction efficiency from the monochromator grating. The spectrally resolved pump-probe signals I_∥ and I_⊥ were detected by an IR array detector. To test the reproducibility, a second set of multibilayer samples was also prepared. The measured data from the two sets of samples agreed.

With accurate measurements of the signal parallel, I_∥(t), and perpendicular, I_⊥(t), to the pump polarization, vibrational excited state population decay, P(t) is obtained using,

$$P(t)=I_{\parallel }(t)+2I_{\perp }(t)$$ (1)

and the orientational relaxation, r(t) (anisotropy decay) is given by,

$$r(t)=\frac{I_{\parallel }(t)-I_{\perp }(t)}{I_{\parallel }(t)+2I_{\perp }(t)}=0.4C_2(t)$$ (2)

where C₂(t) is the second Legendre polynomial orientational correlation function.

III. Results and Discussion

A. Absorption Spectra

In the past decades, many IR studies of lipid hydration have focused on the carbonyl groups and the phosphate group to obtain structural information about the lipid bilayers.^5,6,29,30 There have also been some studies of the hydroxyl stretching modes of water in bilayers containing H₂O or D₂O.^5,29 These studies are more difficult to interpret than an isotopically dilute sample of HOD in H₂O or D₂O because of the spectral overlap of the symmetric and antisymmetric stretching modes as well as the bend overtone in the case of H₂O. The OD stretch of dilute HOD in H₂O in the lipid bilayers studied here provides a simplified spectrum that gives information on the bilayers at various hydration levels. Figure 2 shows the FT-IR absorption spectra of the OD stretch of HOD in H₂O with x = 2, 4, 6, 8, and 16 and bulk water, all at 37 °C. The most interesting feature of the spectra is that the frequency of the OD stretch shifts to the red as the hydration level is reduced. In addition, there is a high frequency shoulder at ~2650 cm^-1 in all samples including the lowest hydration, x = 2. The shoulder is most likely due to water embedded in the hydrophobic core of the lipid bilayer. This same type of feature has been observed in Nafion membranes^14,15 and a similar result was found in H₂O hydrated 1-palmitoyl-2-oleoylphosphatidylcholine (POPC) by Binder who assigned the high frequency shoulder near 3600 cm^-1 to clusters of a few waters with two or less H-bonds each.²⁹ As discussed below, the spectrum of the hydroxyl stretch of a water molecule is dominated the hydrogen bond to the H or in our case D (hydrogen bond donor), rather than hydrogen bonds made to the oxygen (hydrogen bond acceptor).³¹ The large blue shift suggests the water in the hydrophobic region of the bilayer is not a H-bond donor. The observation of this embedded water in the hydrophobic core of the aligned multibilayer sample at x = 2 is an indication that phosphate-associated water is not the only option at low hydration, even though water has a higher binding energy to the phosphate group than it does in bulk water.³²

Figure 2.

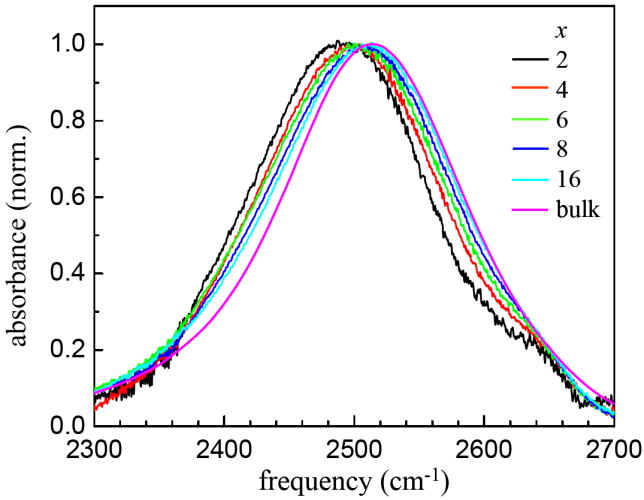
Background-subtracted FT-IR absorption spectra of the OD stretching mode of 5% HOD in H₂O in DLPC multibilayers at 37°C for various water to lipid ratios, x, and bulk water.

In figure 2 for x = 2, the peak is shifted 24 cm^-1 to the red of bulk water. The full width at half maximum (FWHM) of the main peak (the small shoulder on the blue side is excluded) is 160 cm^-1, smaller than that of bulk water, which has a FWHM of 167 cm^-1. As x increases, the peak shifts to the blue, and the FWHM becomes larger, reaching 177 cm^-1 at x = 16. This behavior is very similar to that observed in AOT reverse micelles, except in that system the spectrum shifts to the red as the water content is increased.¹³ AOT has a sulfonate head group and a sodium counter ion. The sodium is almost completely associated with the head groups.^33,34 The reverse micelle with the smallest water nanopool w₀ = 2 (w₀ is the number of water molecules per AOT surfactant molecule) is shifted farthest to the blue and has the narrowest linewidth. As the amount of water is increased, the spectrum broadens and shifts to the red toward the bulk water spectrum. In the AOT study, for very large w₀, e.g. 60, the spectrum narrows again and approaches the bulk water spectrum. In the AOT reverse micelles, it was possible to fit all the spectra with a simple model discussed below that is also successful in describing the spectra shown in figure 2.

First, recent theoretical and experimental work on water in salt solutions can explain why the spectrum shifts to either the blue or the red.³¹ This work is also important in understanding both the spectra presented in figure 2 and the pump-probe population relaxation measurements discussed below. The hydroxyl stretching frequency of aqueous solutions of the potassium salts of F⁻, Cl⁻, Br⁻, and I⁻ were studied. Detailed theory demonstrated that the shift of the spectrum is determined solely by the electric field along the hydroxyl group that donates a hydrogen bond to the negative ion. More distant contributions to the electric field and/or the association of the water oxygen with K⁺ have little effect on the spectrum. I⁻ shows the largest blue shift because the negative charge is spread over the very large ion and produces the smallest electric field at the hydroxyl. Br⁻ has a smaller blue shift, and Cl⁻ and even smaller blue shift. Each of these ions produces a smaller electric field along the hydrogen bond donating hydroxyl than the field generated by hydrogen bonding to a water oxygen. However, hydrogen bonding to F⁻ produces a red shift.³⁵ F⁻ is such a small ion, that the concentrated negative charge produces a field along the associated hydroxyl that is larger than if the hydroxyl formed a hydrogen bond to a water oxygen. These results indicate that the red shift observed for the OD hydroxyl in the phospholipid bilayers arises from ODs associated with the negatively charged phosphate group, and that the phosphate group produces a larger electric field at the associated hydroxyl than if it was hydrogen bonded to a water oxygen.

In AOT reverse micelles¹³ it was determined that the IR spectra at all ω₀ greater than the smallest, ω₀ = 2, could be fit by summing the spectrum of bulk water and the spectrum of the ω₀ = 2 AOT reverse micelle. The only adjustable parameter used to obtain the total normalized spectrum at each ω₀ was the ratio of the ω₀ = 2 and the bulk water spectra. Similarly, the IR spectra of the DLPC samples of x = 4, 6, 8 and 16 can also be fit using the spectrum of the x = 2 sample and that of bulk water from 2250 cm^-1 to 2750 cm^-1. Here, bulk water is used as a model for bulk-like water, which reflects OD hydroxyls that are not associated with the phosphate ion of the DLPC head group. A third small Gaussian peak is included to fit the high frequency shoulder of the water in the hydrophobic regions. Figure 3 shows the results of the fitting procedure for two of the samples, x = 4 (A) and 8 (B). The fits are quite good, capturing both the shift and the change in shape of the spectrum with x. For x = 4, the component of x = 2 contributes 71% and the bulk like component contributes 29%. For x = 6, the components are 59% and 41%, for the x = 2 and bulk-like components, respectively. For x = 8, the components are 41% and 59%, for the x = 2 and bulk-like components, respectively, and for x = 16, the components are 28% and 72%.

Figure 3.

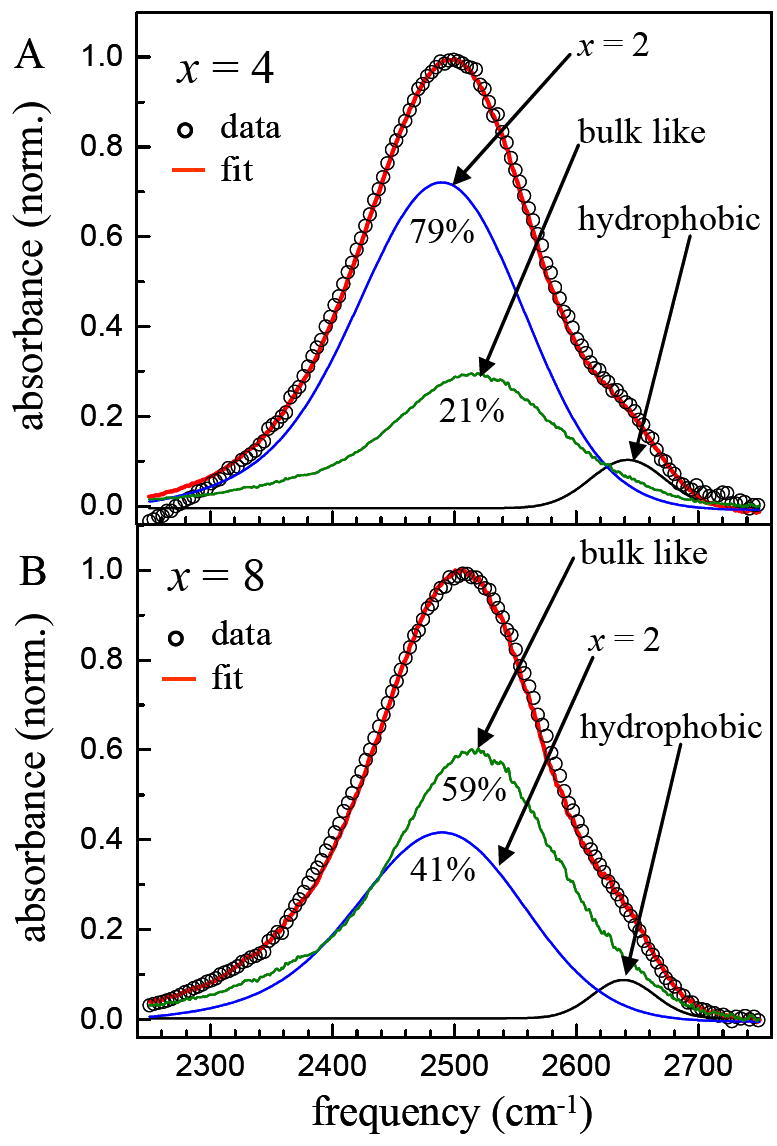
Examples of fitting the absorption spectra for x = 4 (panel A) and x = 8 (panel B). The data (circles) can be fit (red line) by the sum of the spectra of x = 2 and bulk water. Only the relative amplitude of the two spectra is varied. A third small Gaussian peak is included to account for the high frequency shoulder associated with water molecules in hydrophobic regions of the bilayers.

The relative fractions obtained from the fits to the IR spectrum are proportional to μ²C, where μ is the transition dipole moment, and C is the concentration. However, μ depends on the type of hydrogen bond, so the relative fractions are not necessarily directly related to the relative concentrations.¹³ To obtain the concentration ratios, we need to find the ratio of μ² for bulk water and the x = 2 component. The required ratio can be found by measuring the ratios of the spectral areas of 5 mol% HOD in H₂O to 5 mol% HOD in H₂O contained in the x = 2 sample (5.5 wt% H₂O) after correcting for the differences of the water concentrations and sample thicknesses. The ratio of μ² for bulk water to the x = 2 component is 1.07. The determination of the transition dipole ratio enables us to calculate the concentration ratio for the bilayer samples of x = 4, 6, 8 and 16.

Grdadolnik et al. surveyed theoretical calculations of the number of water molecules that can hydrogen bond to the phosphate oxygens.²⁹ They concluded that no more than four water molecules can be accommodated at the phosphate. H-bonding causes the frequency of the PO₂⁻ antisymmetric stretching band to red-shift from 1250 cm⁻¹ for dry to 1230 cm⁻¹ in a hydrated bilayer.^6,29 When x > 3, in addition to the phosphate group-associated water molecules, additional water molecules form bulk-like water clusters near the hydrophobic choline group.¹¹ Thus at the larger values of x it was proposed by Hsieh and Wu that there are two hydration regions.¹¹ As discussed below, the population relaxation experiments combined with the absorption measurements demonstrate that even for x = 2, there are two hydration regions.

The results of the spectroscopic analysis illustrated in figure 3 are summarized in Table 1. The spectral shifts shown in figure 2 can be understood in terms of the recent theoretical and experimental work on aqueous salt solutions.³¹ The aqueous salt solution work indicates that the bulk-like water component arises from waters that are not hydrogen bonded to an anion, and the work of Hsieh and Wu suggests that these waters are associated with the choline group, and are labeled as Ch in Table 1. (By bulk-like, we mean water that has a spectrum similar to that of bulk water, but not necessarily the same dynamics as discussed below. Bulk-like does not mean that there is no association with a head group.) The conclusion that no more than 4 water molecules can be associated with the phosphate group²⁹ is consistent with the results given in Table 1 within experimental error. Even for x = 16, only ~4 water molecules are in the x = 2 component. However, as discussed below, the data in Table 1 will be reconsidered in terms of a more complete analysis that uses the pump-probe data.

Table 1.

Results from fitting the IR spectra (see figure 3). Percent of x = 2 component and bulk-like water (choline associated, Ch) component, where x is the number of waters per DLPC molecule.

x	% x = 2	% Ch (bulk-like)
2	100	0
4	72	28
6	60	40
8	42	58
16	29	71

The shoulder on the blue side of the line at ~2640 cm⁻¹ is more difficult to analyze. The large blue shift suggests that these waters are in a hydrophobic region and will have a much smaller transition dipole than the other components. An analysis of a similar peak in Nafion membranes indicated that μ² for water in a hydrophobic environment is a factor of ~4.8 smaller than that of bulk water.¹⁴ Using this value, the approximate percentages of water in the hydrophobic environment are ~13% in the x = 2 bilayer sample and > 5% in the x = 16 sample. The hydrophobic water component will be neglected in the analysis of the pump-probe data because of its small amplitude and because the pump-probe signal depends on μ⁴C, making the hydrophobic water contribution to the signals negligible.

B. Vibrational Population Relaxation

It has been demonstrated previously that the vibrational population relaxation, P(t), of the OD stretch of dilute HOD in H₂O in nanoscopic water systems is extremely sensitive to local environments.^13-15 Figure 4 shows the vibrational population decays (see equation 1) measured at the peak of the absorption spectrum of each bilayer sample and bulk water for comparison. Vibrational relaxation produces a small heating contribution to the signal at long times. The heating induced signal has been removed using the standard procedure described previously.^13,36 As can be seen in figure 4, the population relaxation becomes slower as x decreases. Even for x = 16, the relaxation is slower than that of bulk water.

Figure 4.

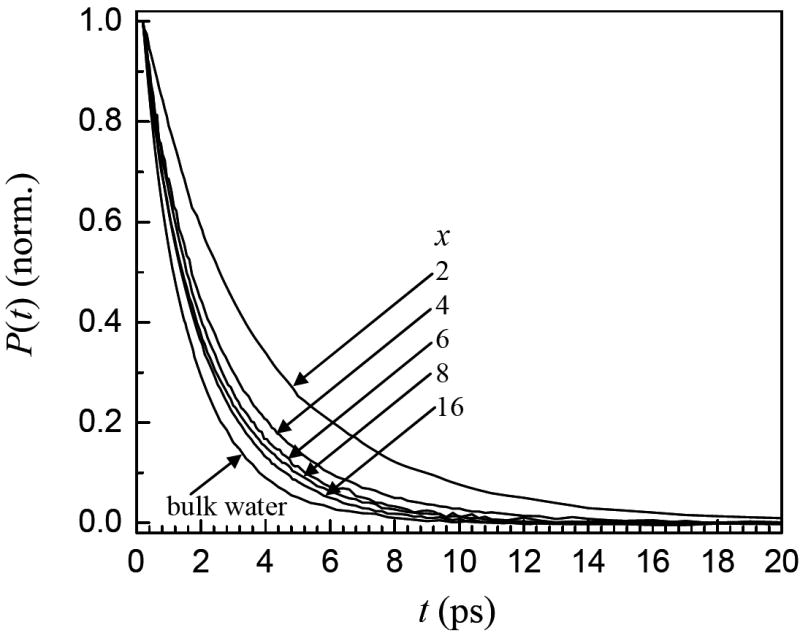
Vibrational population decays of the OD stretch of HOD in H₂O in bilayers for various numbers of waters per lipid, x, and bulk water. As x decreases, the population relaxation slows.

The population relaxation of bulk water is single exponential with a decay time constant of 1.7 ps.¹³ However, a single exponential is not a good description of the vibrational population decay curves for the nanoscopic water in any of the bilayer samples. Instead, they can be fit well with biexponentials. Figure 5 shows the results of a single exponential and biexponential fit to the data for the x = 4 sample. The single exponential systematically misses the data at long times. All of the bilayer data behave in a similar manner. The fit parameters for different samples, each at the peak frequency for that sample are listed in Table 2. The decay time constant of the slow component decreases from 4.5 ps for x = 2 to 2.1 ps at x = 16, approaching the value for bulk water of 1.7 ps.¹³ The lifetime of the fast component decreases from 2.1 ps for x = 2 to 0.62 ps for x = 16. The slow decay is the major component in all cases, accounting for 60 – 80% of the total. The biexponential decays indicate that there are two distinct environments for the water in the interfacial region of the aligned bilayers at all of the hydration levels studied here, including the x = 2 bilayer sample. Note that these fractions do not reflect the concentration ratios because the pump-probe signal is proportional to μ⁴C. To gain insight into the nature of the two components, we examined the wavelength dependence of the vibrational lifetimes.

Figure 5.

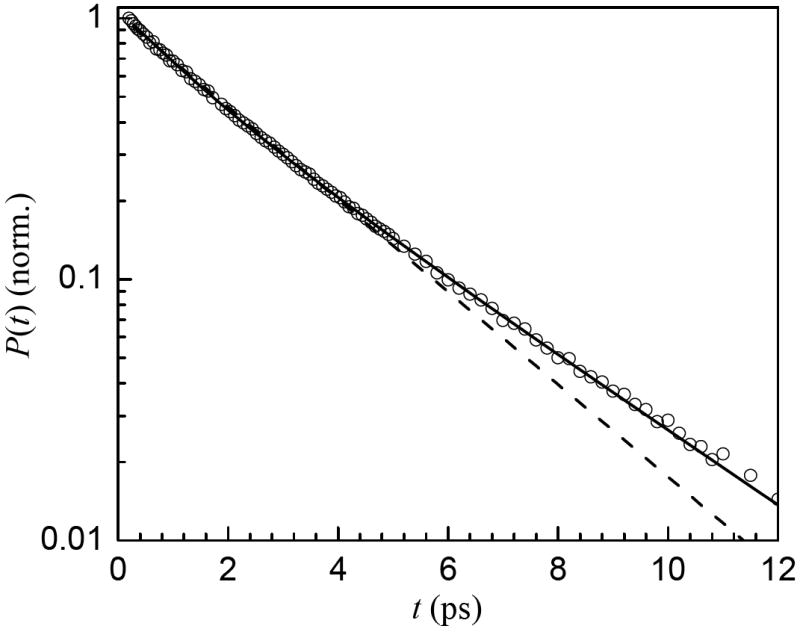
Example of fitting the vibrational population decay data (circles) for x = 4 with a single exponential (dashed) and biexponential (solid) functions. The data for all x are fit well by biexponentials. In contrast, the bulk water population decay is a single exponential.

Table 2.

Biexponential fit parameters for the population decays of nanoscopic water in the bilayers and the decay for bulk water. A₁ and A₂ are the fractions of the total amplitude of the two components in the biexponential fits.

sample	A1	τ1 (ps)	A2	τ2 (ps)
x = 2	0.38	2.1	0.62	4.5
x = 4	0.35	1.3	0.65	3.0
x = 6	0.29	1.0	0.71	2.5
x = 8	0.24	0.74	0.76	2.3
x = 16	0.19	0.62	0.81	2.1
bulk water			1.0	1.7

The spectrally resolved pump-probe experiments on the OD stretch of HOD in H₂O include the 0-1 and 1-2 transitions. The pump-probe spectrum of the x = 4 bilayer sample at 0.24 ps is shown in figure 6A. The positive signal is in the 0-1 region, which has contributions from ground state bleaching and excited state stimulated emission. The negative signal is in the 1-2 spectral region and arises from excited state absorption from the 1 level populated by the pump pulse to the 2 level. Four frequencies in the 0-1 region are indicated by the vertical lines in figure 6A. The population decays at these frequencies are shown in figure 6B. The frequencies were selected such that no contribution from the 1-2 transition is included. It is clear that at different frequencies, the vibrational population decays of the OD stretch are different. As in figure 5, the fits are biexponentials.

Figure 6.

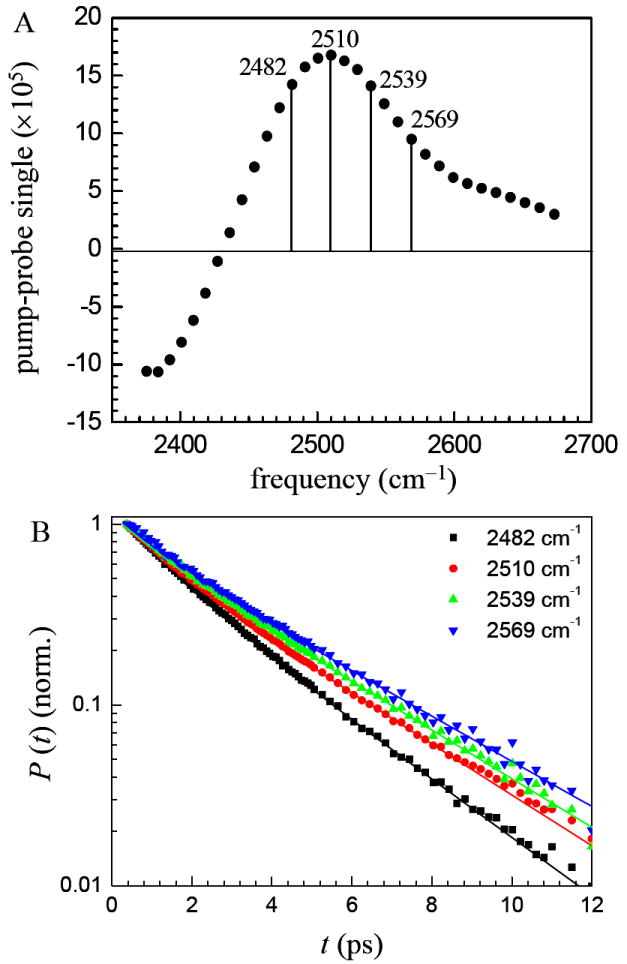
A. Pump-probe spectrum of the OD stretch of HOD in H₂O in bilayers with x = 4 at 0.24 ps. The signal is positive in the 0-1 vibrational transition frequency range and negative in the 1-2 range. B. Vibrational population decays at the four frequencies indicated in A. The decays are wavelength dependent. The solid curves are biexponential fits to the data.

The wavelength dependent biexponential fitting results for all samples are shown in figure 7. The plots display the vibrational lifetimes and the fractions of the total amplitude of the two components in the biexponential fit. Only data in the 0-1 portion of the spectrum are shown. The dashed lines are guides to the eye. The common feature of the vibrational lifetime data for all hydration levels is the existence of two significantly different lifetime components each with substantial amplitude. The vibrational lifetime is very sensitive to the local environment. Two relaxation components and changes in the lifetimes of the two components with hydration level have been observed previously in the nanoscopic water channels of Nafion membranes.^14,15 Figure 7 shows that the population decays display some wavelength dependence. First, consider the population decay time constants, τ₁ and τ₂. For the intermediate values of x, 4, 6, and 8, there is no wavelength dependence for τ₁ within experimental error. Given the lower signal-to-noise ratio because of the low water content for x = 2, it is not clear whether there is a wavelength dependence. For x = 16, there may be a change in τ₁ at lower frequencies. As discussed in detail below, this component is assigned to waters associated with the phosphate groups. The lack of wavelength dependence suggests a relatively uniform environment for waters associated with the phosphates. For τ₂, given the low scatter in the data, it seems clear that there is a wavelength dependence for x = 4, 6, and 8, and most likely for 2, but for x = 16, there is no wavelength dependence. τ₂ reflects the vibrational relaxation of the more bulk like component of the water, which is most likely associated with the choline groups. The fact that the decay constants vary with wavelength indicates that the distribution is inhomogeneous. These waters experience a variety of environments. The wavelength dependence of the decay amplitudes for the x= 2 and 16 bilayers is very pronounced. In both cases, the phosphate associated water fraction becomes large on the red side of the spectrum. In bulk water, molecules that form the shortest, strongest hydrogen bonds have the lowest absorption frequencies.³⁷ As discussed above, recent theoretical work shows that the red shift is caused by an increased local electric field at the OD.³¹ For x = 2, the increased fraction of the phosphate component (the 1 component) on the red side of the spectrum is caused by the hydrogen bonding of the OD to the phosphate group. It is not immediately obvious why the 1 component of the x = 16 sample has such a large presence on the red side of the spectrum. It is possible that it is caused by a combination of ODs bound to the phosphates and water molecules that are becoming increasingly bulk like with stronger hydrogen bonds than waters in the immediate proximity of the choline groups.

Figure 7.

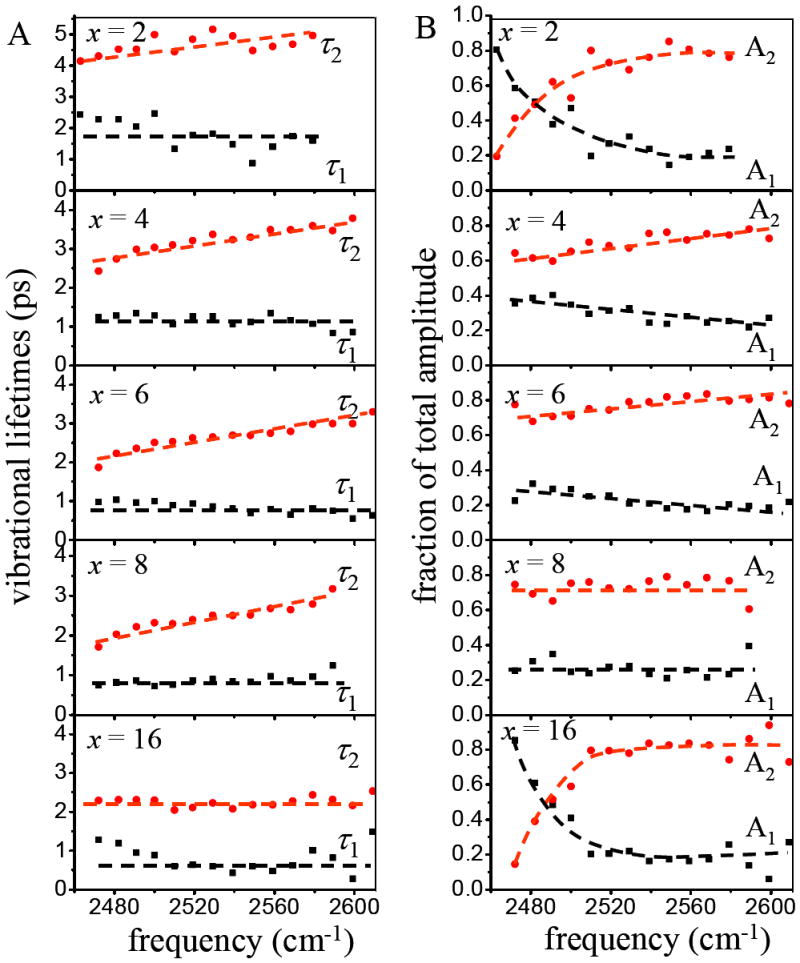
A. Vibrational decay time constants for the two components of the biexponential population decays as a function of wavelength in the 0-1 spectral region for the different values of x. B. Normalized fractions of the total amplitude for the two components of the biexponential population decays as a function of wavelength in the 0-1 spectral region for the different values of x. The dashed lines are guides for the eye. Within experimental uncertainty, some of the data sets are wavelength independent while other data sets display a clear wavelength dependence.

The lifetime data shown in figure 7 demonstrates clearly that there are two distinct types of environments for the water molecules interacting with the head groups of the bilayers. The biexponential decays are consistent with the decomposition of the spectra (figure 3) into two major components. In addition, the lifetime decreases with increased water content, suggesting that an environmental change occurs with hydration consistent with the changes that take place during lipid bilayer swelling.²⁸ It has been reported that the absorbed water molecules are successively accommodated into spaces between head groups and in the inter-bilayer space during stepwise phospholipid hydration.⁵ Table 2 shows that the lifetime of the slower component changes from 4.5 ps at x = 2 to 2.1 ps at x = 16, approaching the lifetime of bulk water (1.7 ps). The approach of the slow component to the bulk water lifetime further suggests that this component is a choline-associated bulk-like water hydration shell, while the faster component is phosphate-associated.

Using the assignment that the fast component in the decays is due to phosphate associated water and the slow component is due to choline associated bulk-like water, we can obtain additional information on the distribution of water in the head group region. In spite of the small number of water molecules and the substantially red shifted absorption spectrum, the vibrational lifetime decay for x = 2 is biexponential indicating that even at the lowest hydration water experiences at least two distinct environments. For x = 2 in Table 2, we take the A₁ value to be determined by the fraction that is from phosphate associate and the A₂ value to be determined by the fraction that is choline associated. However, to get the actual fraction of the concentrations for each type of water in the x = 2 sample, we need to determine the ratio of the two transition dipoles because the pump-probe signal goes as μ⁴C. In Section III A. the ratio of μ² for bulk water to the x = 2 component was found to be 1.07. However, the x = 2 component is itself a mixture of phosphate associated water and choline associated bulk-like water. We use an iterative procedure to determine the correct ratio between the two types of water. Initially, as given in Table 2, we take the x = 2 sample to be 60% choline-associated water and 40% phosphate-associated water, and that the choline-associated water has the same transition dipole moment as that of bulk water. We use the 60/40 ratio and the bulk water x = 2 transition dipole ratio to obtain a first estimate of the μ² ratio for choline-associated water to phosphate-associated water. The 60/40 ratio is used to get μ⁴, which in turn is used to correct the 60/40 initial concentration ratio by multiplying the A₁ value by the μ⁴ value and then renormalizing the total of A₁ and A₂ at x = 2 since C_Ph/C_Ch=μ⁴(A₁/A₂). The procedure is repeated until a constant μ² ratio is reached. The ratio of μ² is found to be 1.17, and the ratio of μ⁴ is 1.37.

With the μ⁴ ratio, the fraction of phosphate associated water and choline associated water for x = 2 is determined to be 46% and 54%, respectively (see Table 3). Clearly these numbers and the other numbers presented in Table 3 are approximate because they depend on an estimated transition dipole ratio. However, other than the x = 2 sample, there are two observables, the spectroscopic data (Table 1) and the pump-probe data (Table 2), for calculating the concentration ratios, which provides a check on the validity of the values. The results are contained in Table 3. The concentration fractions are obtained from the population relaxation data in Table 2 by multiplying the A₁ value by 1.37 (μ⁴) and then renormalizing the total of A₁ and A₂. For the spectroscopic data contained in Table 1, the portion of the x = 2 fraction that is choline associated (54%) must be added to the %Ch (bulk-like) fraction. For example, in Table 1, for the x = 4 sample, the x = 2 component is 0.72, 46% of which is phosphate-associated water. The other 54% is choline-associated. Therefore, 0.72 is multiplied by 0.46 to give 33% phosphate associated, and the other 67% is choline associated water.

Table 3.

Percentages of phosphate-associated water molecules (Ph%) and choline associated bulk -like water molecules (Ch%) determined from the spectroscopic (spec) data in Table 1 and the pump-probe (p-p) population relaxation data in Table 2 for different numbers of water molecules per lipid (x).

x	Ph% (p-p)	Ch% (p-p)	Ph% (spec)	Ch% (spec)
2	46	54
4	42	58	33	67
6	36	64	28	72
8	30	70	19	81
16	24	76	13	87

The fractions of phosphate associated water and choline associated bulk-like water are presented in Table 3. The fractions obtained from the two observables are not identical, but are similar and follow the same trend suggesting that the results are reasonably accurate. The agreement is obtained using only the concentration ratio of the x = 2 sample from the population decay data without adjusting for structural changes that occur at different hydration levels, suggesting that the model based on two types of water molecules is approximately correct. The fractions in Table 3 obtained from the population relaxation data in Table 2 are probably more accurate because the two components of the biexponential decays are relatively straightforward to obtain, and any error in the values given in Table 3 will be predominately caused by the determination of the transition dipole ratio. The fractions determined from the spectroscopic data also require the transition dipole ratio, but in addition, the broad spectra must be fit with two components which are not evident in the spectra, and then the x = 2 component must be reapportioned.

The trend in Table 3 shows that the fraction of phosphate-associated water decreases and that of choline-associated water increases as the hydration level increases. Employing the values obtained from the pump-probe data, the number of water molecules increases from approximately 1 to 4 for the phosphate-associated component and from approximately 1 to12 for the choline-associated component, which is in agreement with the observation that absorbed water molecules are successively accommodated into spaces between head groups and in the inter-bilayer space during stepwise phospholipid hydration.⁵ Although the water molecules can be divided into two types, the wavelength dependence of the two vibrational lifetimes at a fixed hydration level indicates that a given type of water may still experience a range of environments. In figure 7, the slow choline associated water component (τ₂) has a wavelength dependence at all water concentrations except the highest. For τ₁, the x = 4, 6, and 8 do not have a wavelength dependence, which suggests relatively uniform environments for the water molecules associated with the phosphates. As mentioned above, although there are horizontal lines drawn through the x = 2 and 16 data in figure 7, these may have a wavelength dependence, particularly x = 2. The changes in the vibrational lifetimes with hydration level demonstrate that the structures are dependent on the number of water molecules associated with a lipid molecule.

C. Orientational Relaxation

The orientational anisotropy decay is obtained from the pump-probe date using equation 2. Because the experiments are conducted on the OD stretch of HOD using low concentration HOD in H₂O, the measurements determine the orientational relaxation of the HOD molecules directly. The experiment measures the time dependent change in direction of the OD bond vector and avoids problems associated with studying pure H₂O or pure D₂O. In previous studies, measurements were made on water in DMPC “membrane fragments” using either pure H₂O or D₂O.^17,18 Excitation transport from one molecule to another can be a source of anisotropy decay. In addition, because H₂O and D₂O have symmetric and antisymmetric stretching modes, which have transition dipoles that point in different directions relative to the molecular frame, relaxation between these two modes will cause anisotropy decay and may produce fast components in the population relaxation. Nonetheless, these interesting studies reported that water associated with the membrane fragments exists in heterogeneous environments and that orientational relaxation is very slow at very low hydration levels.^17,18

Figure 8 displays the anisotropy decays for the bilayers, x = 2, 4, 6, 8, and 16 and for bulk water taken at the center frequency of the absorption spectrum of each sample. In addition, fits to the data are shown. It is clear from the data that as the number of water molecules per lipid is decreased, the orientational relaxation slows dramatically. Even for x = 16, the orientational relaxation is significantly slower than that of bulk water. Like the lifetime data shown in figure 4, the orientational relaxation shows that 16 water molecules per lipid does not result in the water behaving as water does in the bulk liquid.

Figure 8.

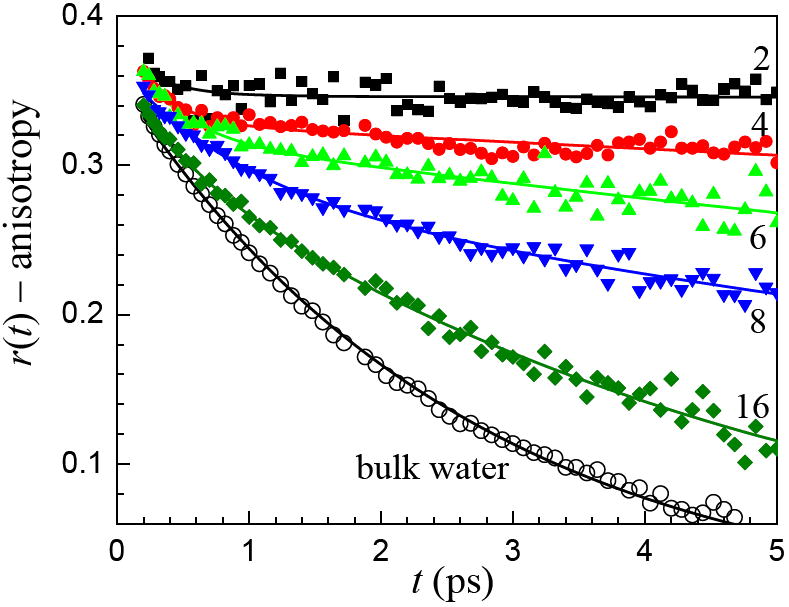
Anisotropy decays (orientational relaxation) of the OD stretch of HOD in H₂O in bilayers for various numbers of waters per lipid, x, and bulk water. As x decreases, the population relaxation slows. The solid curves are biexponential fits to the data except for bulk water, which is a single exponential.

In studies of AOT reverse micelles, dynamical differences between bulk water and water in the reverse micelles are first observed at w₀ = 20, that is 20 waters per head group.¹³ By w₀ = 10, the orientational dynamics are substantially different from those of bulk water. Here the head group is much larger than the AOT head group, and it is a zwitterion. Water molecules that are immediately in contact with an interface or ion are different from bulk water, but so are water molecules for some distance beyond the first contact layer. Given the large surface area of the DLPC head group and what we know about water dynamics in AOT, it is not surprising that at 16 waters per head group, the orientational relaxation of water in the phospholipid multibilayer system is not the same as bulk water.

Fits to the anisotropy data shown in figure 8 yield biexponential decays except for bulk water, which decays as a single exponential. The data in figure 8 follow an ultrafast inertial component that occurs on a sub-hundred femtosecond time scale and is not resolved in these experiments.^13,16,38-40 Table 4 gives the values of the fits. The maximum value of the anisotropy is 0.4 (see equation 2). Because of the ultrafast inertial decay, which causes a portion of the anisotropy to decay on an ultrafast time scale, ^13,16,38-40 the sum of the amplitudes, A₁ (fast component, τ_w) and A₂ (slow component, τ_s), do not add to 0.4. The single exponential decay time constant for bulk water is 2.6 ps. The slow decay component of x = 16 is approximately a factor of two slower than that of bulk water. The fast components for all x are approximately equal and much faster than the slow component at each x. By x = 2, the slow component is so slow, that no slope is apparent in the data. In Table 4, the value is given as ∞, which is to indicate that the data over the time scale of observation shows no decay. For x = 6 and 4, the slow components are so slow that the values are not very reliable, but it is clear that x = 4 is slower than x = 6, and that x = 6 is slower than x = 8.

Table 4.

Biexponential fit parameters for the orientational relaxation r(t).

sample	A1	τw (ps)	A2	τl (ps)
x = 2	0.03	0.3	0.35	∞*
x = 4	0.06	0.3	0.33	70*
x = 6	0.07	0.4	0.32	30*
x = 8	0.07	0.4	0.32	11
x = 16	0.05	0.4	0.32	5
bulk water			0.36	2.6

^*These values are so long compared to the time range over which they are measured that they should be taken to be very approximate. From the data and the fits, it is clear that x = 6 is slower than x = 8, and that x = 4 is slower still. For x = 2, following the initial fast decay, the data are horizontal within experimental error.

Similar biexponential anisotropy decays observed in the nanopools of reverse micelles^13,16,19 and in Nafion membranes¹⁵ have been interpreted using the “wobbling-in-a-cone” model developed by Lipari and Szabo,⁴¹ followed by complete orientational relaxation on a longer time scale. The wobbling-in-a-cone model was originally proposed to describe the restricted sampling of angular space by, for example, the motion of a chromophore that is tethered to a much larger molecule like a relatively immobile macromolecule. The situation for nanoconfined water is different, yet there are parallels that make the model useful. Here the model that can describe the biexponential orientational relaxation of nanoconfined water will be described qualitatively. The mathematical details in a very similar context, orientational relaxation of water in Nafion membranes, have been presented previously.¹⁵

In water, for orientational relaxation to be complete (all directions are sampled by the OD bond vector) the hydrogen bond network must randomize. On short time scales, the hydrogen bond network is intact. Water molecules can still undergo orientational fluctuations, but they cannot sample all orientations.^13,15,16,19 In the wobbling-in-a-cone model, the motion of a molecule on a short time scale is restricted to a cone of semi-angle θ_c⁴¹ which can be determined from the data.¹⁵ It is typically about 30°. On a longer time scale, complete orientational sampling occurs, which gives rise to the long component in the anisotropy decay, τ_l. When the fast decay time constant is much shorter than the long decay constant, the fast decay constant is τ_w, the wobbling-in-a-cone time constant.¹⁵

MD simulations of water in small AOT reverse micelles show biexponential decays following an ultrafast inertial component.^33,34,42 In these MD simulations, water molecules at the interface and water molecules away from the interface were examined separately, and both display biexponential orientational decays. Therefore, the biexponential decays in the simulations are not the sum of two single exponential decays, each corresponding to a distinct environment. The biexponential decays observed in the MD simulations agree semi-quantitatively with the experimental decays of water in AOT reverse micelles, and the simulations have been analyzed with the wobbling-in-the-cone model.¹⁶ In AOT, the OD stretch population relaxation is biexponential.¹³ The AOT experimental data supports the interpretation that one component of the population decay arise from molecules associated with the head groups and one component is more bulk like. Detailed theoretical analysis showed that the orientational biexponential decay could not arise from two environments each giving rise to a single exponential orientational decay.¹³ In the data reported here for water in the DLPC multibilayers, the population decays are also biexponential and are interpreted as arising from two distinct environments. However, given the theoretical analysis that was applied to the AOT orientational relaxation that demonstrated that the biexponential decay could not arise from two environments¹³ and the MD simulation biexponential orientational decays observed for water in both the head group and non-head group regions of the reverse micelles,^33,34,42 it is reasonable to assume that biexponential orientational relaxation observed here arises from wobbling-in-the-cone followed by complete orientational randomization rather than two single exponential decays associated with distinct environments.

For water, recent MD simulations have provided evidence that the long time orientational relaxation does not proceed via small step Gaussian diffusion.⁴³ The MD simulations of Laage and Hynes highlighted the well established tetrahedral nature of the hydrogen bond network of water.⁴³ Based on this physical picture for the microscopic structure of water, Laage and Hynes found that the orientational motions of water molecules are better described by a jump reorientation model based on Ivanov’s approach,⁴⁴ in which the jumps correspond to the rearrangement of hydrogen bonds among water molecules⁴³ or water molecules and ions.⁴⁵ Complete orientational randomization of the hydroxyl transition dipole cannot only involve many infinitesimal random steps but must also involve the breaking and forming of hydrogen bonds. Energetic considerations show that a water molecule will not break a hydrogen bond without virtually immediately forming a new hydrogen bond.⁴⁶ The MD simulations show that the hydrogen bond switching process involves the transient formation of a bifurcated hydrogen bond to reduce the energetic penalty for switching hydrogen bond partners. This bifurcated hydrogen bond is the transition state in the large amplitude orientational jump that leads to the formation of a new local hydrogen bond configuration.⁴³ In the simulation, the average angular amplitude of the jump was determined to be ~60°. This is far from the diffusive limit, yet this model produces a single exponential decay for the orientational correlation function (anisotropy),^43,44 that is, a single exponential decay for the slow component in the orientational relaxation observed here. It is not possible to experimentally determine the jump angles in bulk water and in nanoconfined water systems, but jump angles in the range of 60° to 70°, which should occur in water and water-ion systems,^43,45 lead to values for the jump time that are close to but not identical to the measured long time decay constant, τ_l.¹⁵ In bulk water, the jumps occur between different water hydrogen bond configurations. In DLPC multibilayer system, the hydroxyls can be bound to other water molecules or to ions. Therefore, jumps can occur that involve reformation of the local hydrogen bond structure involving water-water bonds and water-ion bonds.⁴⁵

The wobbling-in-a-cone followed by jump reorientation model is useful for understanding the trends displayed in figure 8 and Table 4. On a short time scale, the fast component of the orientational anisotropy decay reflects the sampling of a range of angular space that occurs without breaking and reforming hydrogen bonds. Thermal energy causes orientational fluctuations within an intact hydrogen bond potential energy well. The long component is caused by jump reorientation. The same model has been applied to the orientational relaxation of water in very concentrated salt solutions.⁴⁷ As mentioned above, the orientational relaxation can involve breaking hydrogen bonds to an ion as well as to other water molecules. ^45,47 Hydrogen bond rearrangement is a concerted process with each jump reorientation event involving a number of water molecules. Each event should not be viewed as consisting of a hydrogen bond breaking and leaving a vacant hydrogen bonding site, but rather a more or less global restructuring of the local network.⁴³ At x = 16, there is a sufficiently large number of water molecules to allow a substantial hydrogen bonding network to form, making concerted jump reorientation relatively fast. Jump reorientation in the hydrated bilayers is still slower than bulk water, however, because interactions with the ions and topological restrictions imposed by the membrane surface limit the extent and flexibility of the hydrogen bonding network.

As the water content is decreased, fast angular sampling of a hydrogen bonding configuration (wobbling-in-a-cone) is still possible, but jump reorientation becomes increasingly difficult. For x = 2, there is approximately one water associated with the phosphate and one with the choline. Jump reorientation becomes highly unfavorable, and the rate of orientational relaxation becomes so long that it is undetectable with the current experiments. For x = 4, there are about 2 water molecules associated with the phosphates and two with the cholines, and the beginning of a hydrogen bonding network becomes possible. Orientational relaxation is still very slow, but detectable. As the number of waters per lipid increases, the hydrogen bonding network grows, and complete orientational relaxation becomes increasingly fast.

IV. Concluding Remarks

In this paper we report polarization and frequency selected ultrafast IR pump-probe experiments and FT-IR absorption measurements on the OD stretching mode of HOD in H₂O in aligned DLPC phospholipid multibilayers. Both the OD stretch vibrational population relaxation and the water orientational relaxation were measured as a function of water content, x, from 2 to 16 water molecules per lipid. The results were compared to the same experiments on bulk water. The aligned bilayers provide a well defined model membrane and at the same time give sufficient water absorption to make the isotopically dilute experiments possible.

The FT-IR spectra of the OD stretch display an increasingly large red shift relative to bulk water as x decreases (figure 2). The peak position and shape of the spectra can be fit using a two component model consisting of the x = 2 spectrum (very low water content) and the bulk water spectrum (figure 3). The vibrational population decays slow substantially as the water content of the bilayers is reduced (figure 4). The pump-probe data display biexponential decays for all x, in contrast to bulk water, where the OD stretch population relaxation is a single exponential (figures 5-7). The biexponential decays combined with the two component fits of the water spectra support the model that water is associated with the bilayers in two distinct environments,^8,11 that is, phosphate associated waters and choline associated waters. Using the pump-probe data and the FT-IR data, it is possible to estimate the number of water molecules in each environment as a function of x (Table 3).

The orientational relaxation (figure 8, Table 4) shows a dramatic slowing as the water content of the bilayers is decreased. The orientational relaxation at all x fit well to a biexponential. It is proposed that the fast component arises from orientational fluctuations that occur with the hydrogen bonding network intact. The slow component, which leads to complete orientational randomization, requires a rearrangement of the hydrogen bond network. The orientational relaxation is discussed in terms of a combined wobbling-in-a-cone⁴¹ and jump reorientation^43,45 model.¹⁵ On a time scale on which the hydrogen bond network is intact, the orientational motion is constrained by the angular potential determined by the local hydrogen bonding network.⁴⁰ On a longer time scale, concerted hydrogen bond rearrangement produces orientational jumps that eventually result in complete orientational randomization. As the water content of the bilayers is decreased, it becomes increasingly difficult for concerted hydrogen bond rearrangement to occur. To reduce the energetic price paid for breaking a hydrogen bond, a new hydrogen bond must be formed. At very low water content, there are no new hydrogen bond acceptors available so hydrogen bond switching is slowed. This is evident in the anisotropy decay for x = 2. Following the fast wobbling, no slow orientational relaxation occurred on the time scale of the experiment indicating a lack of hydrogen bond switching events.

These experiments have implication for the behavior of water in biological systems, particularly water at the surfaces of cell membranes. The biexponential population decays show that there are at least two distinct types of water environments, and the differences in the environments persist even as the hydration level of the membranes increases. At the lowest hydration levels, waters are associated with the ionic portions of the head groups, and, as shown by the orientational relaxation, the structural rearrangement of the water molecules is very slow. However, as the amount of water increases, the ability of the water to restructure increases substantially. By 16 water molecules per head group, the orientational relaxation time is only a factor of two slower than that of bulk water. Membranes of adjacent cells are separated by a few tens of nanometers.^48-50 If the space between cells contained only water, this separation is sufficient that water well removed from the cell membrane surfaces would behave like bulk water. However, the regions between cells are generally crowded with a variety of relatively large biological molecules.^48,49 Therefore, in spite of the relatively large separation between cell membranes, the combination of the interaction of water with the membranes and with the intercellular biomolecules could result in little if any of the water behaving like bulk water.

Future experiments will explore the orientational relaxation in more detail to obtain information on the cone angles and jump times. In addition, analysis of orientational relaxation data can provide information about the angular potential that governs orientational relaxation.⁴⁰ The chemical composition of the bilayers will be changed, by, for example, adding cholesterol.²⁷ Ultrafast 2D-IR vibrational echo spectroscopy will also be employed to study the dynamics of water in the bilayers.^13,47 The 2D-IR vibrational echo experiment measures spectral diffusion, which provides a direct probe of the time dependent structural evolution of water.^46,51-54