Cryocrystallography in capillaries: critical glycerol concentrations and cooling rates

The minimum glycerol concentrations required to obtain vitreous ice during plunge cooling of capillaries in liquid propane and nitrogen are determined as a function of capillary diameter and cooling rate. Capillary-based cryocrystallography will require much larger cryoprotectant concentrations than can be achieved with loop or microfabricated X-ray mount-based methods.

Abstract

Capillary tubes have many advantages over multi-well plates for macromol­ecular crystal growth and handling, including the possibility of in situ structure determination. To obtain complete high-resolution X-ray data sets, cryopreservation protocols must be developed to prevent crystalline ice formation and preserve macromolecular crystal order. The minimum glycerol concentrations required to vitrify aqueous solutions during plunging into liquid nitrogen and liquid propane have been determined for capillary diameters from 3.3 mm to 150 µm. For the smallest diameter, the required glycerol concentrations are 30%(w/v) in nitrogen and 20%(w/v) in propane, corresponding to cooling rates of ∼800 and ∼7000 K s⁻¹, respectively. These concentrations are much larger than are required in current best practice using crystals in loops or on microfabricated mounts. In additon, the relation between the minimum cooling rate for vitrification and glycerol concentration has been estimated; this relation is of fundamental importance in developing rational cryopreservation protocols.

1. Introduction

Capillary tubes have long been used to grow macromolecular crystals (Salemme, 1972 ▶; McPherson, 1999 ▶). They provide a convenient way of controlling crystallization conditions and of handling and storing the resulting crystals. If thin-walled glass or plastic capillaries are used, crystals can be examined in situ by X-ray diffraction.

A variety of growth methods can be implemented in capillaries, including equilibrium dialysis (Zeppezauer et al., 1968 ▶), liquid counterdiffusion (Salemme, 1972 ▶), gel acupuncture (García-Ruiz & Moreno, 1994 ▶), vapor diffusion along the capillary (Sibille et al., 1991 ▶) and vapor diffusion through the capillary walls (Kalinin & Thorne, 2005 ▶). Vapor diffusion rates along the capillary between liquid plugs can be controlled by the choice of separating liquid or gas. When polymer capillaries are used, vapor diffusion rates can be controlled by adjusting the wall thickness and ambient humidity.

Crystal growth in capillaries is attracting renewed interest in the high-throughput era as an alternative to growth on crystallization plates. Using conventional liquid handling devices (Meldrum et al., 2000 ▶) or microfluidics (Li et al., 2006 ▶; Zheng et al., 2003 ▶, 2004 ▶, 2005 ▶), a large number of small-volume crystallization experiments can be conducted in a single capillary. Reagent volumes and the extent of reagent mixing can be precisely controlled. The system described by Meldrum and co-workers accurately dispenses volume increments as small as 0.3 nl in glass capillaries with an inner diameter of 340 µm. The microfluidic system described by Zheng and co-workers dispenses 10–100 nl volumes in glass or Teflon capillaries with diameters near 200 µm. Recent implementations replace free-standing capillary tubes with arrays of capillary lines fabricated in a flat PDMS (polydimethylsiloxane)/Teflon or plastic ‘card’.

An important reason for interest in capillary growth is the possibility of in-situ X-ray examination of individual drops, both as a compliment to optical examination in screening and for full structure determination. Well faceted crystals are often poorly ordered, and any crystals present in a drop may be visually obscured by precipitate or by ‘skins’ covering the drop surface. X-rays directly probe the presence of crystalline order and the extent of this order, the properties of interest in crystallography. For X-ray examination in capillaries, the capillary walls should be thin (typically 10 µm for glass and 25–50 µm for polymers) and of an amorphous, isotropic material to minimize background scatter. Thin-walled polyethylene terephthalate (PET), Kapton and Teflon tubing with good optical and X-ray clarity is commercially available and, unlike glass, does not crack or shatter during handling (Kalinin & Thorne, 2005 ▶).

In situ structure determination at room temperature is complicated by rapid accumulation of radiation damage and by crystal slippage/sedimentation as the capillary is rotated during data collection. Slippage can be reduced by removing excess liquid (which is not practical when multiple drops are dispensed in a single capillary) or by growing the crystals in gels (which increases background scatter). The obvious solution to these difficulties is to cool the crystals in situ to cryogenic temperatures. Solidification of the solvent inside the crystals dramatically reduces radiation damage rates, and solidification of the solvent outside the crystals immobilizes them. In situ capillary cryocrystallography using crystals grown with cryoprotectants and heavy atom compounds has been demonstrated for some model proteins (López-Jaramillo et al., 2001 ▶; Gavira et al., 2002 ▶; Ng et al., 2003 ▶). High-pressure freezing without cryoprotectants has also been demonstrated as a route to structure solution in capillaries (Kim et al., 2007 ▶).

When cooling at ambient pressure, cryoprotectants such as glycerol, polyethylene glycols and 2-methyl-2,4-pentanediol are added to inhibit formation of crystalline ice, both within the crystal and in the surrounding liquid. Ice creates diffraction rings that obscure diffraction from the protein crystal, and growth of ice crystals can disrupt the crystal lattice. Typical cryoprotectant concentrations required to inhibit crystallization of the surrounding liquid are 20–30%(w/v) (Garman & Mitchell, 1996 ▶). In high-throughput capillary growth, these cryoprotectants must be introduced with the original mother liquor and can thus constrain the search for optimal crystallization conditions. Cryoprotectant concentrations required to prevent crystalline ice formation can be reduced by cooling the sample faster (Chinte et al., 2005 ▶; Berejnov et al., 2006 ▶; Warkentin et al., 2006 ▶) or by increasing the pressure (Kim et al., 2007 ▶).

Here we report the cooling rates achieved when thin-walled PET tubing containing a glycerol–water solution is plunged into liquid nitrogen and into liquid propane, and the corresponding minimum glycerol concentrations required to prevent crystalline ice formation. Tubing diameters from 150 µm to 3.3 mm, covering the range of interest for protein crystallography and cryopreservation, are examined. The maximum cooling rates are significantly smaller and the minimum glycerol concentrations are significantly larger than can be achieved when crystals are cooled in standard loop or microfabricated X-ray crystallography mounts (Warkentin et al., 2006 ▶). Combining our results with those of previous studies, we find an approximately exponential relation between minimum cooling rate for vitrification and glycerol concentration, spanning more than five orders of magnitude in cooling rate. This relation provides a basis for designing cryopreservation protocols.

2. Materials and methods

2.1. Critical concentration measurements

One way to determine the efficacy of capillaries for cryopreservation is to measure the minimum amount of cryoprotectant required for vitrification of water–cryoprotectant solutions as a function of tubing diameter. Smaller diameters should give larger cooling rates and require smaller cryoprotectant concentrations.

Optical assays have long been used to quantify phase separation and crystallization in aqueous mixtures and in biological samples, especially during rapid cooling of small volumes for which microcalorimetry measurements are extremely challenging. Density fluctuations associated with the appearance of new phases produce refractive index fluctuations that scatter light, and index variations of as little as 10⁻⁵ on scales of roughly one-tenth of the optical wavelength produce visible contrast and cloudiness. Previous studies have explored the structural state (vitreous/amorphous or crystalline) of rapidly cooled aqueous cryoprotectant solutions. If the sample vitrifies as it cools, it remains transparent; if ice microcrystallites form, they scatter light and the sample becomes cloudy (Luyet, 1957 ▶; Fahy et al., 1984 ▶; Garman & Schneider, 1997 ▶; McFerrin & Snell, 2002 ▶; Chinte et al., 2005 ▶). The transition from transparent to nontransparent occurs over a narrow range of glycerol concentration (less than 2%), if all else is held fixed (Garman & Mitchell, 1996 ▶; Berejnov et al., 2006 ▶). Although earlier X-ray diffraction measurements suggested the presence of crystalline ice in optically transparent samples (McFerrin & Snell, 2002 ▶; Chinte et al., 2005 ▶), more recent measurements with more accurate evaluation of the first visual deviation from complete transparency confirm that this deviation corresponds to a state change from vitreous to microcrystalline, and limit any discrepancy between the optical- and X-ray-deduced transitions to less than 2% in glycerol concentration (Berejnov et al., 2006 ▶).

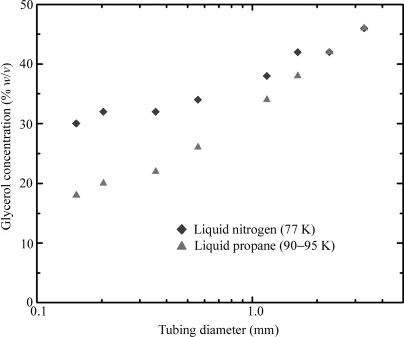
The PET tubing used for all experiments was obtained from Advanced Polymers (Salem, NH, USA) and has excellent X-ray transparency (Kalinin & Thorne, 2005 ▶). Tubing inner diameters ranged from 150 µm to 3.3 mm. Wall thicknesses were either 25 or 50 µm for diameters of 500 µm and larger, and either 12 or 25 µm for smaller diameters. Open-ended pieces of tubing at least ten diameters long were completely filled with water–glycerol solutions of increasing concentration, in increments of 2%(w/v). The solutions were prepared by first weighing out the appropriate amount of glycerol and then thoroughly mixing in water to bring the total solution volume to the desired value. The refractive index of each solution was measured and indicated an error in final concentration of less than 0.2%(w/v), or 10% of our concentration increment. Each sample was then plunged at ∼0.5 m s⁻¹ into liquid propane or liquid nitrogen and held horizontally until all boiling ceased. Sample transparency was determined by holding the sample immediately above the liquid surface and observing it against a black paper background with fiber optic illumination and a boom-mounted stereomicroscope. For each tubing diameter, the smallest glycerol concentration that resulted in a completely transparent sample was recorded, as shown in Fig. 1 ▶.

Figure 1.

The concentration of glycerol in water required to obtain a completely transparent sample upon plunging into either liquid propane or liquid nitrogen. PET tubing wall thicknesses are 12.5 or 25 µm for diameters below 500 µm and 25 or 50 µm for larger diameters.

Liquid nitrogen was held in a glass hemispherical Dewar, 12 cm across and 8 cm deep (Pope Scientific Inc., Saukville, WI, USA), with the liquid level maintained within 2 cm of the brim. Commercial liquid propane (Coleman brand) was transferred from the tank into a 50 ml centrifuge tube held under liquid nitrogen. Commercial propane is safer (owing to additives that give it a putrid smell) and cheaper than pure propane and, because of impurities, freezes at a lower temperature. 10 ml of liquid propane was poured from the tube into a custom aluminium trough roughly 10 cm long, 2 cm deep and with 1 mm-thick walls that was partially submerged in liquid nitrogen. The temperature of the propane was measured using a chrome–constantan thermocouple (CHCO-005, Omega Engineering) and remained in the range 90–95 K provided that the liquid nitrogen level was kept halfway up the side of the trough.

For 150 and 200 µm-diameter capillaries plunged in liquid nitrogen, the fastest cooling was obtained by blowing away the cold gas layer that forms above the liquid using dry room-temperature nitrogen gas (Warkentin et al., 2006 ▶), and only those data are reported. For larger capillaries, the cold gas layer had no effect on the critical concentration. For plunging into liquid propane, the propane was held in a fume hood. The flowing air kept the thickness of the cold gas layer small, and additional blowing was not used so as to minimize warming of the liquid.

2.2. Cooling rate measurements

The temperature inside the capillary during cooling was measured using chrome–constantan thermocouples with lead diameters of either 25 or 75 µm and bead diameters of 80 or 125 µm, respectively (CHCO-001 or CHCO-003, Omega Engineering). Thermocouple response times were measured by directly plunging into propane and into nitrogen and were much shorter than all measured cooling times of liquid-filled capillaries.

For cooling rate measurements in capillaries, a thermocouple was threaded lengthwise through the capillary to place its bead near the center. The capillary was filled with a 60%(w/v) glycerol solution, which vitrifies for all cooling rates and thus does not exhibit temperature anomalies associated with crystallization and release of latent heat. These samples were plunged into the liquid cryogen as in the critical concentration measurements. The bead size and radial position of the thermocouple should affect the measured temperature. In practice, capillary time–temperature profiles for different bead sizes and positions within the capillary were indistinguishable – within the typical 20% trial-to-trial variation in measured cooling rates – down to the smallest capillary sizes. This variation is small compared with the nearly three-orders-of-magnitude variation in cooling rate with tubing diameter. Temperature versus time data were recorded by a 6025e PCI DAQ interface controlled by LabVIEW (http://www.ni.com/labview), both from National Instruments.

3. Results

3.1. Estimation of cooling rates

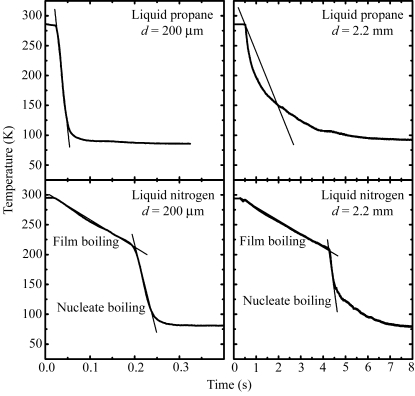
Fig. 2 ▶ shows representative cooling curves for capillaries filled with 60%(w/v) glycerol solution and plunged into liquid nitrogen or liquid propane. Because the slopes of these curves are not constant, it is not immediately clear how to estimate the relevant cooling rate. For propane, the cooling rate is highest immediately after the sample enters the propane. For nitrogen, the cooling rate is largest midway through the cooling process, just after the transition from film to nucleate boiling at ∼200 K (Incropera & DeWitt, 2002 ▶; Gakhar & Wiencek, 2005 ▶). The region of the cooling curves most relevant to successful cryocooling will depend upon the properties of the solution being cooled, as cryoprotectants decrease the homogeneous nucleation temperature and increase the glass transition temperature (Rasmussen & Luyet, 1970 ▶; Mackenzie et al., 1977 ▶).

Figure 2.

Representative cooling curves when capillaries containing 60% glycerol–water solutions are plunged into liquid propane and liquid nitrogen. The slopes of the straight lines give the cooling rates shown in Fig. 3 ▶.

We thus estimated three different cooling rates, as shown in Fig. 2 ▶. For cooling in liquid propane, we evaluated the average cooling rate from the initial temperature down to T = 150 K. The latter temperature was chosen because the glass transition temperatures of most cryoprotectant solutions (Mackenzie et al., 1977 ▶; Harran, 1978 ▶) and of the solvents within protein crystals (Weik et al., 2001 ▶, 2004 ▶, 2005 ▶) are between 140 and 180 K. For cooling in liquid nitrogen, there are two distinct regimes of cooling. In the nucleate boiling regime at lower temperatures, the liquid nitrogen directly contacts the sample and the cooling rate is large. In the film boiling regime at higher temperatures, the cooling rate is roughly an order of magnitude smaller owing to the presence of a layer of vapor insulating the sample from the liquid nitrogen. The transition between these two regimes occurs at the Leidenfrost temperature (Incropera & DeWitt, 2002 ▶). We thus evaluated the average cooling rate in the film boiling regime from room temperature down to the Leidenfrost temperature and the maximum cooling rate just below this temperature in the nucleate boiling regime. A fourth cooling rate (not shown in Fig. 2 ▶) – the average cooling rate in nitrogen from the initial temperature down to T = 150 K – was also evaluated; this is close to the average cooling rate in the film boiling regime.

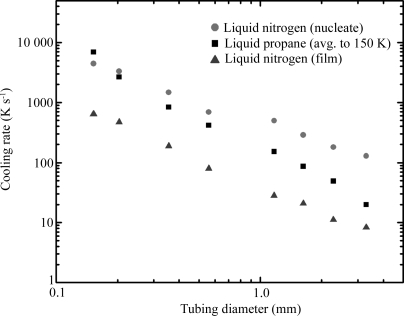
Fig. 3 ▶ shows the resulting cooling rates versus capillary diameter d. All cooling curves show a smooth variation with tubing size. They are well fitted by power laws dT/dt ≃ d ^α with exponents α of −1.75 for cooling in liquid propane, −1.46 for the film boiling regime in liquid nitrogen and −1.14 for the nucleate boiling regime in liquid nitrogen. An exponent of 1 is expected if the cooling rate is dominated by the gas or liquid boundary layer immediately adjacent to the tubing, while a value of 2 is expected if the cooling rate is limited by thermal diffusion (e.g. through the sample or through a coolant in which convection is unimportant) (Zasadzinski, 1988 ▶; Bailey & Zasadzinski, 1991 ▶).

Figure 3.

Cooling rates as a function of tubing diameter, for liquid propane and liquid nitrogen, as estimated in Fig. 2 ▶. Each data point represents an average over 5–10 trials. The trial-to-trial variation is between 10% (for larger diameters) and 20% (for smaller diameters) and is comparable to the height of the symbols used to mark the data.

3.2. Comparison with previous work

Previous studies of cooling using loop-mounted samples found cooling rates similar to those reported here for similar size samples. Teng & Moffat (1998 ▶) examined 125–450 µm-thick films of cryoprotected crystallization buffers suspended on 1.5 mm loops and found cooling rates in gas streams, liquid nitrogen and liquid propane ranging from 130 to 1200 K s⁻¹, depending on the film thickness, the cooling agent and (in the case of liquid nitrogen) the boiling regime. These rates are in rough agreement with the corresponding rates observed in a ∼350 µm capillary shown in Fig. 3 ▶. Walker et al. (1998 ▶) found average cooling rates of 250 and 750 K s⁻¹ in liquid nitrogen and liquid propane, respectively, for a rubber-cement-coated thermocouple forming a spherical sample of diameter 0.7 mm. Interpolating the data of Fig. 3 ▶ to a capillary tube with 0.7 mm diameter gives cooling rates of 67, 338 and 726 K s⁻¹ for film boiling liquid nitrogen, liquid propane and nucleate boiling liquid nitrogen, respectively.

The material at the sample’s surface (aqueous solution in the case of loop-mounted samples, PET or glass for capillary-mounted samples) affects the Leidenfrost temperature and so should modify the observed cooling rates in liquid nitrogen (Gakhar & Wiencek, 2005 ▶). With a higher Leidenfrost temperature, the nitrogen near the sample’s surface will enter the nucleate boiling regime sooner, and the cooling rate to ∼150 K will be larger. For example, the Leidenfrost temperatures for the bare thermocouples (chrome/constantan alloy surfaces) used by Gakhar & Wiencek (2005 ▶) and by Warkentin et al. (2006 ▶) were 130–150 K, compared with nearly 200 K for the PET-covered samples here (see Fig. 3 ▶). In addition, surface roughness can influence the Leidenfrost temperature and the rate of heat transfer in the nucleate boiling regime (Bald & Wang, 1976 ▶; Dhir, 1998 ▶), in both liquid nitrogen and (for larger samples) liquid propane.

In the film boiling regime, the mechanism of heat transfer is comparatively well understood. For a horizontally held cylinder of diameter d, Bromley (1950 ▶) derived a heat transfer coefficient h ≃ d ^−1/4. The cooling rate should then follow dT/dt ≃ d ^−5/4. Subsequent experiments revealed deviations from this power law at small diameters that have been fitted with more sophisticated empirical forms for h (Breen & Westwater, 1962 ▶; Baumeister & Hamill, 1967 ▶). Over the range of diameters examined here, these forms can be approximated by h ≃ d ^−7/12 (Bakhru & Lienhard, 1972 ▶). The cooling rate in the film boiling regime is then dT/dt ≃ d ^−1.58. The exponent is close to the value of −1.46 observed here. A more detailed fit based on the correlation of Baumeister & Hamill (1967 ▶) gives even closer agreement with our experimental results.

4. Discussion

4.1. Implications for cryocrystallography in capillaries

Fig. 1 ▶ indicates that successfully cooling protein crystals in capillaries at ambient pressure will require large cryoprotectant concentrations to prevent crystalline ice formation in the liquid surrounding the crystal. Even with 150 µm-diameter tubing, 30 and 20%(w/v) glycerol will be required for cooling in liquid nitrogen and liquid propane, respectively. Similarly large concentrations of other cryoprotectants can be expected (Berejnov et al., 2006 ▶). For samples in this range of surface-to-volume ratios that are cooled using these cryogens, it has been shown experimentally and theoretically that the thermal conductivity of the sample does not affect the cooling rate (Zasadzinski, 1988 ▶; Bailey & Zasadzinski, 1991 ▶; Kriminski et al., 2003 ▶), and so these results will approximately hold for capillaries made from other materials as well. Fig. 1 ▶ suggests that more manageable cryoprotectant concentrations may be achieved using 10–50 µm-diameter capillaries. For a fixed pressure drop, the speed of capillary flow varies as d ⁴ (Poiseuille’s law), so filling such small capillaries may be problematic. Handling such tiny capillaries and obtaining usable diffraction from the tiny crystals inside would also be difficult. Arrays of capillary tubes can be fabricated in flat plastic sheets, but these have a much larger thermal mass per unit length of capillary and a more unfavorable geometry for heat transfer than isolated capillary tubes.

Compared with crystals in loops (Teng, 1990 ▶) or on microfabricated mounts (Thorne et al., 2003 ▶), performing cryocrystallography on crystals in capillaries presents substantial difficulties. Large cryoprotectant concentrations are required to prevent ice crystallization in the mother liquor surrounding the crystals. Much less cryoprotectant is required to prevent ice formation within the crystal itself, because protein acts as an excellent cryoprotectant at the concentrations found within the crystal (Kriminski et al., 2002 ▶). For crystals in loops or on microfabricated mounts, surrounding mother liquor can be wicked away or replaced with low-viscosity oil. For capillary grown and mounted crystals, removing or replacing this mother liquor without damaging the crystal is not easy and would be less so in high-throughput applications where each small-diameter capillary contains multiple samples. Furthermore, the mother liquor typically has a much larger total mass and thermal mass than the crystals that grow within it; the mother liquor plus crystal have a much larger volume and thus a much smaller surface-to-volume ratio than the crystal itself; and cylindrical capillaries have one-third of the surface-to-volume ratio of equal volume spherical samples. As a result, achievable cooling rates in capillaries are much smaller than those for conventionally mounted crystals, and penetrating cryoprotectants must be included in large concentrations.

The surrounding mother liquor present in capillaries produces background scatter that reduces the signal-to-noise and ultimate resolution of a data set. In batch growth, 1–3%(w/v) of the initial growth solution (10–30 mg ml⁻¹) is protein, so that the maximum protein and solvent mass that ends up within crystals is typically less than 5% of the total mass. A 100 × 50 × 30 µm crystal examined by a 100 µm X-ray beam in a 200 µm capillary will typically have to compete with background scatter from surrounding liquid more than ten times its own volume.

The large amount of surrounding liquid present in capillaries will exert non-uniform stresses on the crystal during cooling, resulting from differences in thermal expansion/contraction of the crystal, of the surrounding liquid and of the capillary itself. Crystals with rod or plate-like shapes are likely to crack under these stresses, broadening their mosaicities.

4.2. Critical cooling rate versus glycerol concentration

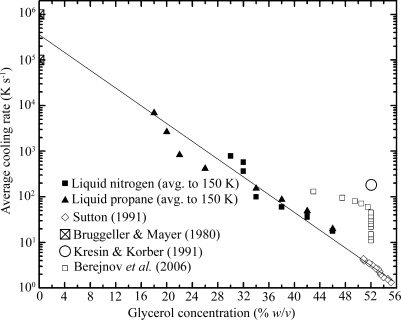
The data in Figs. 1 ▶ and 3 ▶ can be combined to estimate the minimum cooling rate required to vitrify a given glycerol concentration for a wide range of concentrations. The critical cooling rate to achieve vitrification is an intrinsic property of the solution, so it does not depend on details such as sample geometry or coolant type and directly reflects the fundamental physics of glass formation in the water–glycerol system. It can thus be used to design practical cryoprotection protocols in a variety of biological applications. Fig. 4 ▶ is a composite showing our results (taken from Figs. 1 ▶ and 3 ▶), results for high concentrations/slow cooling rates determined by differential scanning calorimetry (DSC) on emulsified samples (Sutton, 1991 ▶), results where cooling rates were estimated from the time between the initial plunge into liquid nitrogen and the Leidenfrost transition to nucleate boiling (Berejnov et al., 2006 ▶), and results for pure water (Bruggeller & Mayer, 1980 ▶). Our data span a large range of glycerol concentrations/cooling rates between those examined in previous studies. A crude fit to the merged data (solid line in Fig. 4 ▶) suggests a simple exponential relation between glycerol concentration and cooling rate. The required cooling rate is halved with each ∼3% glycerol concentration increment.

Figure 4.

Minimum cooling rates required to achieve vitrification of glycerol–water solutions as a function of glycerol concentration. Data inferred from the present study, as well as data for pure water and for glycerol–water solutions obtained in previous studies, are shown. The line corresponds to an exponential relation between cooling rate and glycerol concentration.

In generating Fig. 4 ▶ we have assumed that the cooling rate of a capillary filled with 20–40% glycerol (data from Fig. 1 ▶) is the same as the cooling rate of that same capillary filled with 60% glycerol (data from Fig. 3 ▶). For samples cooled with liquid nitrogen or propane and having surface-to-volume ratios in the range studied here, it has been shown experimentally and theoretically (Zasadzinski, 1988 ▶; Bailey & Zasadzinski, 1991 ▶) that cooling rates depend on the surface-to-volume ratio, the heat transfer coefficient (a property of the coolant) and the volumetric heat capacity of the sample. Similar cooling rates are obtained for samples differing in thermal conductivity by three orders of magnitude. In our experiments, the small difference in heat capacities of 20% glycerol and 60% glycerol solutions modifies cooling rates by less than 10%, and the small difference in thermal conductivity (∼30%) is too small to affect our conclusions.

A potentially important issue in comparing cooling rate results from different measurements is the residual crystalline ice fraction at which a sample is deemed vitrified. Kresin & Korber (1991 ▶) reported measurements similar to those of Sutton (1991 ▶), using DSC on emulsified samples. For Sutton’s 59%(w/v) sample, they estimate an ice fraction of 0.023 and suggest that reducing the ice fraction to 10⁻⁶ would require a cooling rate almost two orders of magnitude larger. The drop size of the emulsion is also important: Kresin and Korber estimate that bulk systems would require a factor of two larger cooling rates than their 2.4 µm-diameter droplets. Measurements of cooling rates to vitrify pure water also have uncertainties associated with the residual crystalline fractions.

In the X-ray diffraction experiments connecting the transparent-to-nontransparent visual transition with the vitreous-ice-to-crystalline-ice transition, crystalline ice becomes clearly noticeable when the ice ring intensity becomes significant compared with the intensity produced by the amorphous ice fraction of the sample (Berejnov et al., 2006 ▶). The minimum detectable crystalline fraction can be estimated from measurements of scattered X-ray intensities from crystalline and amorphous samples versus d spacing. The signal-to-background ratios at the ice ring d spacing for typical amorphous and crystalline samples are ∼1.5 and 10, respectively. If we assume a minimum detectable ice ring intensity of one-tenth of the background intensity from vitreous ice then this implies a minimum detectable crystalline ice fraction of roughly 0.01. This is comparable to the fraction estimated for Sutton’s experiment but much smaller than that in Kresin and Korber’s. Since the visual assay for crystallinity (Luyet, 1957 ▶; Fahy et al., 1984 ▶; Garman & Mitchell, 1996 ▶) corresponds so well with X-ray diffraction measurements (Berejnov et al., 2006 ▶), the values quoted by Sutton are most appropriate for comparison with cooling rates determined here.

5. Conclusion

We have determined the cooling rates of a glycerol–water solution inside thin-walled capillaries when plunged into liquid nitrogen and liquid propane, and the corresponding minimum glycerol concentrations required to prevent formation of crystalline ice. These results can be combined to yield the minimum cooling rate required to achieve a vitreous sample as a function of glycerol concentration, a fundamental property of the water–glycerol solution. For PET capillary tubes of diameters ranging from 150 µm to 3.3 mm, the minimum required glycerol concentration is 20 and 30% for cooling in nitrogen and propane, respectively. These values are comparable to those currently used in cryocrystallography practice, but are much larger than is generally necessary to prevent ice crystallization within the crystal itself. The maximum achievable cooling rates of 300–7000 K s⁻¹ are at least an order of magnitude smaller than can be achieved using crystals on loop or microfabricated mounts. In situ capillary cryocrystallography is thus likely to involve higher cryoprotectant concentrations, more crystal damage during cooling and much larger background scatter from surrounding liquid, and so in most cases is unlikely to yield the highest-resolution structures. Its primary benefit will be in screening diffraction properties and crystallization outcomes in high-throughput capillary crystallization.