Abstract
Understanding the function of complex RNA molecules depends critically on understanding their structure. However, creating three-dimensional (3D) structural models of RNA remains a significant challenge. We present a protocol (the nucleic acid simulation tool [NAST]) for RNA modeling that uses an RNA-specific knowledge-based potential in a coarse-grained molecular dynamics engine to generate plausible 3D structures. We demonstrate NAST's capabilities by using only secondary structure and tertiary contact predictions to generate, cluster, and rank structures. Representative structures in the best ranking clusters averaged 8.0 ± 0.3 Å and 16.3 ± 1.0 Å RMSD for the yeast phenylalanine tRNA and the P4-P6 domain of the Tetrahymena thermophila group I intron, respectively. The coarse-grained resolution allows us to model large molecules such as the 158-residue P4-P6 or the 388-residue T. thermophila group I intron. One advantage of NAST is the ability to rank clusters of structurally similar decoys based on their compatibility with experimental data. We successfully used ideal small-angle X-ray scattering data and both ideal and experimental solvent accessibility data to select the best cluster of structures for both tRNA and P4-P6. Finally, we used NAST to build in missing loops in the crystal structures of the Azoarcus and Twort ribozymes, and to incorporate crystallographic data into the Michel–Westhof model of the T. thermophila group I intron, creating an integrated model of the entire molecule. Our software package is freely available at https://simtk.org/home/nast.
Keywords: RNA structure, 3D RNA structure prediction, knowledge-based energy function, coarse-grained modeling
INTRODUCTION
RNA molecules that play catalytic or structural roles form complex three-dimensional (3D) structures. These diverse molecules include RNA enzymes (ribozymes), which catalyze RNA cleavage (Stark et al. 1978; Kruger et al. 1982; Guerrier-Takada et al. 1983), and riboswitches, which are sequences within some mRNAs that change conformations upon binding small metabolites and subsequently terminate transcription or block translation (Nahvi et al. 2002; Winkler et al. 2002a,b; Rodionov et al. 2003; Vitreschak et al. 2004). Although knowing the structure of these molecules is fundamental to understanding their function, we have only a few high-resolution RNA structures from expensive and lengthy X-ray crystallographic studies. In addition, partially folded states, misfolded states, and flexible regions of a molecule may not be amenable to crystallization. For these reasons, building 3D models of RNA remains an important challenge (Levitt 1969; Michel and Westhof 1990; Westhof and Altman 1994; Fink et al. 1996; Lehnert et al. 1996; Shapiro et al. 2007), one in which the ability to sample diverse conformations is especially important.
The problem of determining RNA structure breaks naturally into two subproblems: predicting the secondary structure, and predicting how the secondary structural elements assemble to form a 3D structure. For the most part, RNA secondary structure forms rapidly, and is substantially complete on a time scale much shorter than the subsequent interaction of the resulting elements. Phylogenetic analysis of aligned RNA homologs is a gold standard for determining secondary structure (Noller et al. 1981; James et al. 1988). Sequence-based prediction of RNA secondary structure is available through tools such as the thermodynamic method, Mfold (Zuker 2003), and the probabilistic method, Contrafold (Do et al. 2006). For 3D modeling, manual structure predictions by RNA structure experts have been successful, including the complete modeling of several group I introns (Michel and Westhof 1990; Lehnert et al. 1996), the RNA component of RNase P (Harris et al. 1994; Westhof and Altman 1994). Despite these successes, manual methods are difficult to generalize and reproduce; they rely extensively on the individual expertise of the modeler.
A number of computational tools have been developed to aid in 3D structural modeling; these can be classified based on whether they are automatic or manual, full atomic or coarse grained, and physics based or knowledge based. Our tool, the nucleic acid simulation tool (NAST), is fully automatic, coarse grained, and uses a statistical potential. Moreover, it is fast enough to generate ensembles of 10,000 or more candidate structures, and thus gives a sense of the degree to which the data constrain the conformational space.
MANIP is an interactive tool that allows users to build RNA structures modularly from fragments frequently found in RNA; however, this is not an automated method (Massire and Westhof 1998). ERNA-3D is a molecular modeling system for generating models of RNA molecules using known fragment structures and has been used to model ribosomal RNA structures (Tanaka et al. 1998). Both MANIP and ERNA-3D are manual tools and generate a handful of models, whereas an automated method would allow the generation of large ensembles of structures.
MC-Fold and MC-Sym build full-atomic models of RNA structures using nucleotide cyclic motifs (Major et al. 1993; Parisien and Major 2008). This tool is powerful for modeling small RNA segments or small RNA molecules, but larger structures remain a challenge because of the computational requirements for full-atomic modeling. FARNA is an automated method that can predict structures of RNA fragments such as base triplets and pseudoknots, but efficient conformational sampling is computationally prohibitive for RNA sequences longer than a few dozen nucleotides (Das and Baker 2007). Both methods are limited in their conformational sampling because of the complexity of full-atomic resolution models. A coarse-grained approach would decrease computational requirements for modeling large structures.
YUP is a very flexible molecular mechanics framework that can incorporate coarse-grained and full-atomic models and associated energy potentials. It has been used to model RNA structures as well as DNA and protein (Tan et al. 2006). In general, the potentials it uses are tailored to the problem at hand, but it is an extensible and useful tool for multiscale modeling. PROTEAN makes probabilistic structure predictions using uncertain data such as cross-linking data and is able to predict both small and large structures, but it only models the relative position of double helical elements and does not include single-stranded regions (Fink et al. 1996). Neither of these methods includes potentials specific to RNA geometry, which would improve the quality of the models. DMD is a coarse-grained molecular dynamics tool that incorporates base-pairing and base-stacking interactions into an energy function to fold small RNA molecules, but has not been applied to molecules larger than 100 nucleotides (nt) (Ding et al. 2008). Of course, full-atomic molecular dynamics simulations of RNA, in principle, can provide useful insight into the folding mechanism, but are expensive and usually not used for initial structural modeling; they are applied most commonly to structures solved by crystallography (Sorin et al. 2002, 2004).
RNA structure has critical differences from protein structure. First, the repertoire of four planar RNA bases is less diverse than the more heterogeneous 20 amino acids. Second, the highly negatively charged RNA creates strong electrostatic interactions within the molecules and with solvent. Third, there is a much clearer separation of time scales of secondary structure formation and tertiary structure formation. Finally, the secondary structure (helical elements) involves the intimate intertwining of two parts of the RNA strand that creates significant topological constraints on the molecule (Fink et al. 1996). In particular, each double helix can have four single-stranded regions that emanate from it, creating a complex network of connections.
There has been great interest in the modeling of 3D protein structures, and methods for proteins may be useful in the context of RNA (Baker and Sali 2001). In particular, some methods for estimating protein structure are knowledge based and rely on collecting the statistics of protein geometry and contact patterns to create objective functions to be minimized in the search for correct conformations (Fischer and Eisenberg 1996; Jaroszewski et al. 1998; Jones 1999; Shi et al. 2001; Rohl et al. 2004). The performance of these methods can match or exceed current physics-based modeling strategies because they learn from the database of observed structures. Until recently, the dearth of solved RNA structures made it difficult to incorporate information from solved structures into new structure models. However, the current availability of RNA crystal structures, especially the ribosome structures (Ban et al. 2000; Yusupov et al. 2001), allows analysis of structural statistics from solved structures and the creation of models that obey these statistics.
In our work, we use a coarse-grained representation (one quasiatom per RNA base) in order to simplify the computations, as described below. This representation provides a starting point for further refinement to atomic models. We note that the strategy we have taken for creating a coarse-grained representation of RNA is similar to the strategy adopted by YUP; however, we have chosen the more central C3 atom, while YUP uses the phosphate along the backbone (Tan et al. 2006). It is possible that the NAST representation and our associated energy function could be incorporated into YUP, as it is very flexible. Our work also differs from YUP because we have created a statistics-based potential to capture RNA geometry at the C3 level of representation, and we specifically have built NAST to allow experimental information to be included as a filtering step.
The statistical potential used by NAST ensures that models will have well-formed secondary structures and plausible single-stranded regions. The topology of an RNA molecule also requires tertiary contacts from experiments or phylogenetic analysis. In addition, other experimental modalities provide useful information about RNA structure. Nuclease footprinting can constrain RNA secondary structure by detecting base pairing (Galas and Schmitz 1978). Hydroxyl radical footprinting can measure solvent accessibility of nucleotides (Tullius 1988; Wang and Padgett 1989; Sclavi et al. 1997). 2′-Hydroxyl acylation analyzed by primer extension (SHAPE) chemistry can constrain both secondary structure and tertiary interactions (Merino et al. 2005; Mortimer and Weeks 2007). Small-angle X-ray scattering (SAXS) provides information about the radius of gyration, distribution of pairwise distances, and the general shape of the molecule (Russell et al. 2000; Doniach 2001). Comparing a model's calculated values for each of these types of data to the experimental values may be a useful filter of structures. We used measurements related to these experimental techniques to evaluate their value in model selection. In particular, solvent accessibility can be estimated based on the exposed surface area of the RNA bases. The radius of gyration can be estimated from the distribution of pairwise distances. The shape of the molecule can be approximated with the three physical principal components.
RESULTS
NAST energy function
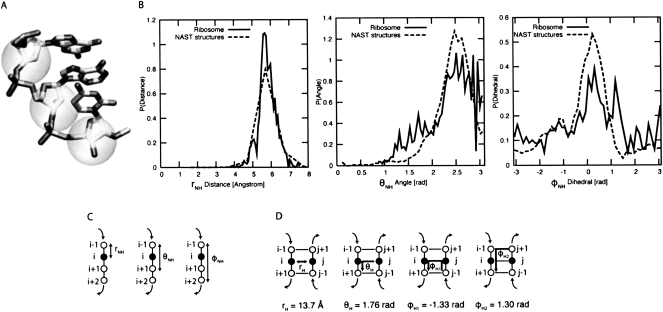
NAST models RNA structure at a coarse-grained level: the position of each base is represented as a single point (Fig. 1A, centered on the C3′ atom), and all constraints are represented with respect to the relative position of these points (Fig. 1C,D). NAST incorporates the statistics of the geometry of these points in RNA crystal structure (Fig. 1B) to constrain the local relationships of bases while generating an ensemble of structures. These structures are considered to be at “nucleotide resolution” because we can distinguish only the positions of nucleotides, and not the individual atoms comprising them.
FIGURE 1.
The NAST energy function. (A) NAST uses a coarse-grained representation of one point per residue centered at the C3′ atom (approximately to scale). (B) Distributions of distances, angles, and dihedrals between consecutive C3′ atoms observed in ribosomal RNA (bold) and generated by the NAST energy function (dashed). (C) Illustration of geometric constraints for nonhelical regions in the NAST energy function. (D) Geometric constraints used in helical regions by the NAST energy function.
We tested NAST by building models of two RNA molecules and by evaluating their agreement to the coarse-grained representation of their respective solved crystal structures. We modeled yeast phenylalanine tRNA and the P4-P6 independently folding domain of the Tetrahymena thermophila group I intron. To validate the NAST energy function, we generated thousands of decoys of each molecule and assessed how close to the crystal structures we were able to sample. We further used NAST to model missing loops in the Azoarcus and Twort ribozyme crystal structures. We then combined information from the incomplete crystal structure of the T. thermophila group I intron with the Michel–Westhof model of the complete structure to build a combined model that agrees with both sets of data.
Structure modeling of the yeast phenylalanine tRNA molecule
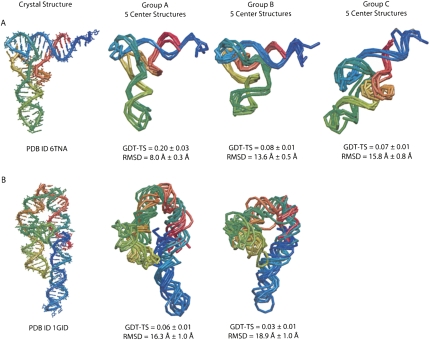
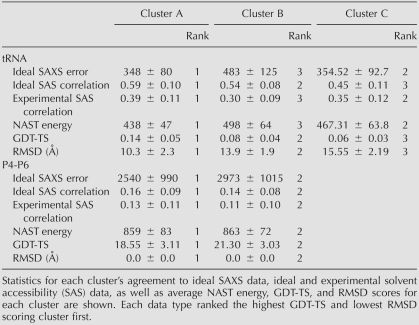
Yeast phenylalanine tRNA is a 76-nt molecule for which the secondary structure and tertiary contacts long have been known (Levitt 1969). Covariance analysis has determined four helical regions and four tertiary contacts, which we show in Supplemental Figure S2 (Klingler and Brutlag 1993). We used only this structural information as input to NAST and did not use any structural data from the tRNA crystal structure as input or in determining the statistical potential. After filtering the ensemble for agreement with tertiary contact constraints and removing structures with extremely large NAST energy values, we clustered the ensemble of decoys into three groups. We show five representative structures for each group in Figure 2A, along with GDT-TS score and RMSD value statistics for those five structures. We ranked each cluster by average agreement with ideal and experimental data, including SAXS, solvent accessibility, and NAST energy (Table 1). All four ranking metrics selected Group A as the best group, in agreement with both the RMSD and GDT-TS rankings.
FIGURE 2.
NAST modeling of tRNA and P4-P6. The tRNA (A) and P4-P6 (B) crystal structures and representative structures from each of the clusters of coarse-grained models generated by NAST.
TABLE 1.
NAST modeling results for tRNA and P4-P6
Structure modeling of the medium-sized RNA molecule P4-P6
The P4-P6 subdomain of the T. thermophila group I intron is a 158-nt structure that folds independently (Murphy and Cech 1993; Cate et al. 1996). We initially modeled this structure using the precrystal secondary structure prediction (Murphy and Cech 1993) and one tertiary contact known from covariance analysis (Michel and Westhof 1990) as input to NAST (shown in Supplemental Fig. S2). Using the same ensemble generation protocol as for tRNA, we clustered the structures into two groups. We show five representative structures from each group in Figure 2B, and the average statistics for each cluster in Table 1. Each metric selected Group A as the best group, in agreement with the RMSD and GDT-TS rankings.
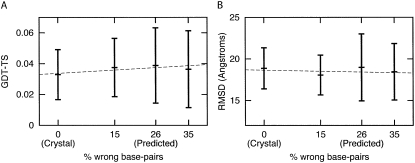
Sensitivity of P4-P6 modeling to secondary structure accuracy
To assess the sensitivity of P4-P6 modeling to secondary structure constraints, we used four constraints with different percentages of wrong base pairs including the predicted structure (26%) and the observed structure (0%). We show the range of GDT-TS scores and RMSD values for each ensemble in Figure 3; we did not observe any significant effect on the quality of structures generated.
FIGURE 3.
Sensitivity of P4-P6 modeling to percentage of wrong base pairs in the specified secondary structure. Mean and standard deviation of RMSD (A) and GDT-TS (B) values for structures generated using 0% (crystal structure), 15%, 26% (predicted secondary structure), and 35% wrong base pairs. We observe no significant effect on the quality of structures generated in this range of wrong base-pair percentages.
Comparison to near-random compact structures
We compared the structures generated by NAST for both tRNA and P4-P6 with near-random compact structures. We generated ensembles of near-random compact structures using the same secondary structure with random tertiary contacts. We selected near-random structures with similar radius of gyration distributions as those observed in the NAST-generated structures. For both tRNA and P4-P6, structures with similar radii of gyration had significantly worse GDT-TS scores (low) and RMSD values (high). We show the distributions of radii of gyration, GDT-TS scores, and RMSD values in Supplemental Figure S3.
Manipulating large RNA structures
Building missing loops
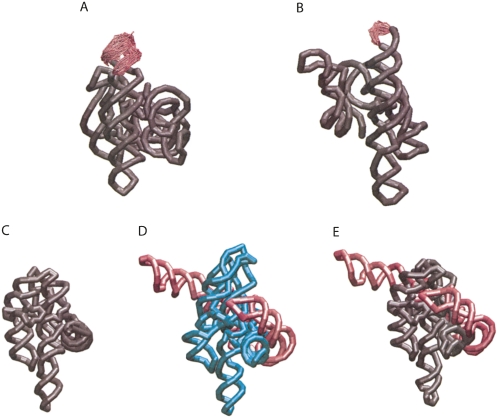
We used geometric constraints from existing loops in the crystal structures of the Azoarcus and Twort ribozymes to build in the loops missing the crystal structures. We show the coarse-grained models we generated in Figure 4, A and B, where the crystal structures are gray and the added loops are pink. We show an ensemble of loop possibilities generated by NAST.
FIGURE 4.
NAST manipulation of large RNA structures. Coarse-grained addition of missing loops (pink) in Twort (A) and Azoarcus (B) ribozymes. (C) Crystal of structure of T. thermophila group I intron with missing helices. (D) Michel–Westhof model of T. thermophila group I intron. (Teal) Residues for which crystallographic information is available. (E) Incorporation of crystallographic information (gray) into the Michel–Westhof model of T. thermophila group I intron.
Combining crystal structure and model
We combined the crystal structure of the T. thermophila group I intron (Fig. 4C), which is missing several peripheral helices as well as one loop, with the precrystal structure Michel–Westhof model (Fig. 4D) to make a combined NAST model (Fig. 4E). We constrained the P4-P6 and core domains of the Michel–Westhof model to their geometries in the crystal structure. The resulting structure is in full agreement with the crystal structure (pink), while using the Michel–Westhof model for the missing peripheral helices (gray).
DISCUSSION
NAST is a coarse-grained knowledge-based software package useful for modeling and manipulating large RNA molecules at one-point-per-residue resolution. NAST samples local geometries observed in ribosomal RNA (Fig. 1B) and uses a simple molecular dynamics engine to sample conformations that satisfy a given set of secondary structure and tertiary contact constraints. There is no term in the energy function for the detection and formation of base pairs, only a pressure to take on an RNA-like geometry. Similarly, there is no consideration of electrostatic attraction or repulsion—we assume that charge is distributed at the atomic level to neutralize the molecule. Using this simple approach we successfully generated tRNA and P4-P6 structures, clustered structures by similarity, and ranked clusters by agreement with several types of ideal and experimental data. Representative structures from the best-ranked clusters had average RMSD values of 8.0 Å and 16.3 Å, and GDT-TS scores of 0.20 and 0.06 for tRNA and P4-P6, respectively. Given the resolution of our coarse-grained model, and the range of RMSD and GDT-TS values observed in near-random compact structures, these models have significant topological similarity to their respective crystal structures. More-sophisticated conformational sampling techniques such as replica exchange (Rhee and Pande 2003) could improve the quality of the structures. However, given the low resolution of the coarse-grained representation, these are likely in the limit of structural information that can be attained from NAST models. In addition to providing information about the likely topology of a molecule, NAST models may provide a good starting point for higher resolution atomic models.
Although the NAST energy function was parameterized using a temperature of 300 K, the temperature and energy values used and reported by NAST have no precise physical interpretation, because we are using a coarse-grained, knowledge-based energy function and because we performed no parameterization simulations at temperatures other than 300 K. However, conformational sampling is still consistent with the Boltzmann distribution, so high-temperature simulations will sample a larger region of configuration space than low-temperature simulations.
To simulate a realistic modeling application, we used only secondary structure and tertiary contact information that was available before the crystal structures of tRNA and P4-P6 were solved. In the case of tRNA, this information was correct and validated by the crystal structure. However, the predicted secondary structure for P4-P6 differs from the native secondary structure (26% wrong base pairs). To assess the sensitivity of P4-P6 modeling to the percentage of wrong base pairs in the secondary structures, we compared the range of GDT-TS scores and RMSD values for structures generated using four different secondary structures. As shown in Figure 3, we did not observe significant differences in the quality of structures generated using this range of percent wrong base pairs. This result suggests that the coarse-grained models generated by NAST are not sensitive to this level of mistakes in predicted secondary structures, making the method useful even in cases where there is uncertainty in the secondary structure. Additionally, these results suggest that NAST could be useful in generating alternative ensembles under “what if” scenarios that could suggest the value of collecting additional experimental data to constrain the modeling, including additional tertiary contacts.
We used four different types of data to rank clusters of structures: (1) ideal SAXS data in the form of distribution of pairwise distances; (2) ideal solvent accessibility (SAS) data; (3) experimental SAS data from hydroxyl radical footprinting experiments; and (4) NAST energy. In most cases, better agreement with data correlated with better quality measures, although some correlations were more significant than others (Table 1). For example, the ensemble of tRNA structures generated by NAST shows a particularly strong correlation between RMSD values and ideal SAS. For P4-P6, we find the strongest correlation between RMSD values and ideal SAXS data, whereas we observe nearly no correlation between both GDT-TS and RMSD, and experimental SAS data (Supplemental Table S3). The comparison between ideal and experimental SAS data gives us additional insight into the information content of noisy experimental data. Additionally, we observe that SAXS data are more useful for P4-P6 modeling than for tRNA modeling, probably because the shape of P4-P6 is less globular and more information is contained in the pairwise distance distributions.
In addition to modeling RNA structures based on secondary structure and tertiary contact information, we used NAST to complete crystal structure models that have missing residues at the coarse-grained level. In this application of NAST, we used crystal structures as data sources, providing pairwise distance constraints that can be constrained more or less strictly. As examples of this capability, we added the missing loops of the Azoarcus and Twort ribozyme structures. We also combined crystallography and model data to build a combined model of the T. thermophila group I intron ribozyme. This functionality can be used to constrain domains such as secondary structure based on crystallographic data, while exploring the conformation space of junctions to study unfolded conformations.
Because of the computational complexity added with each additional nucleotide, modeling large RNA structures is a significant challenge, and most methods do not attempt to model structures larger than the 76-nt tRNA. NAST's coarse-grained resolution allows us to model and manipulate large RNA structures, including modeling the 158-residue P4-P6, solely from sequence, secondary structure, and tertiary contacts. Although the coarse-grained resolution results in models with inherently limited structural information, they can be used as templates for building full-atomic resolution structures, and models for experimental tests.
NAST is limited by its need for secondary structure information. However, these data are available from both experimental and computational methods and are frequently known from natural or artificial phylogenetics for RNA molecules with no solved crystal structure. Additionally, we have shown that the level of error observed in the predicted secondary structure for P4-P6 does not affect significantly the quality of structures generated. NAST is also limited by its need for tertiary contacts. Again, this type of information often is known either through phylogenetic analysis or experimental methods. NAST allows the user to explore the effects of different putative tertiary contacts on the structure of the molecule.
Modeling RNA right-handed helices is a challenge in distance-constraint-based modeling such as nuclear magnetic resonance (NMR), where left-handed helices sometimes result from the ambiguities in chirality. Because distance constraints alone are insufficient to specify chirality, both left- and right-handed helices are equally consistent with distance data. We guarantee right-handed helices by constraining four local geometries (including angles) for each base pair in a helix, as described in the Materials and Methods section. These constraints allow mapping of helices to standard geometries with low variance. It is possible to relax our knowledge-based constraints to allow helices to bend or otherwise match the standard geometry less strictly. Lacking specific information to justify relaxation, we enforced standard helical geometry.
Defining a van der Waals radius for our coarse-grained representation of nucleotides is challenging, as nucleotides are clearly not inherently spherical. We chose to use a small radius (4 Å) to allow close interactions that are occasionally observed in ribosomal RNA. When we examined the ribosome, 99.9% of all contacts were allowed by our empirical van der Waals radius. However, a small spherical radius allows nucleotides to intertwine within helical regions, so we chose to use a slightly larger radius for residues involved in secondary structure. Using a more-complicated geometry that better simulates the shape of nucleotides would reduce the amount of unrealistic packing observed in NAST structures, but would significantly increase computational complexity.
Because of its low computational requirements, flexibility in incorporating data both in modeling and filtering, and ability to model both small and large molecules, NAST is a useful tool for modeling RNA structures. It requires no special RNA modeling expertise, uses available information about the secondary and tertiary structures, and can run on either a single computer or a cluster. Its primary advantages are (1) the use of empirical RNA geometric distributions to create plausible RNA structures; (2) relatively fast modeling using single-point-per-base models; and (3) the ability to incorporate data as both constraints and filters on the models. NAST is available for download with documentation and all the examples presented in this paper at https://simtk.org/home/nast.
MATERIALS AND METHODS
We make the following assumptions in our NAST software package:
Secondary structure is specified, and we constrain these regions to ideal RNA helical geometry.
The geometries of regions not involved in secondary structure follow distributions similar to those observed in solved RNA structures.
We may have knowledge of tertiary interactions within the molecule (from experimental or phylogenetic analysis).
NAST knowledge-based energy function
Coarse-grained representation of RNA
We use a coarse-grained representation of RNA in which each nucleotide is represented by the position of its C3′ atom (Fig. 1A). This representation simplifies the computational complexity of the problem by reducing the number of coordinates to estimate while still allowing use of nucleotide resolution data such as secondary structure, tertiary interactions, and solvent accessibility.
NAST energy function
Four types of statistical information contribute to the NAST energy function:
Geometries from solved ribosome structures (distances, angles, and dihedrals between C3′ atoms of two, three, and four sequential nucleotides, respectively);
Repulsive nonbonded interactions between bases i, j [abs(i − j) > 3];
Ideal helical geometry for nucleotides participating in secondary structure; and
Long-range interactions between nucleotides participating in tertiary contacts.
Geometries of solved RNA structures
The energy function used to sample conformational space is parameterized using statistics collected from three high-resolution RNA crystal structures of large ribosomal RNAs: the 50S and 70S subunits of the Escherichia coli ribosome solved at 3.5 Å resolution (2AW4 chains A and B), and the 30S subunit of the Thermus thermophilus ribosome solved at 3.0 Å resolution (1N32). We collected statistics on distances, angles, and dihedral angles between two, three, and four sequential nucleotides, respectively (Fig. 1C), and assumed these terms to be independent. The normalized probability distributions for these terms are labeled “Ribosome” in Figure 1B for distances, angles, and dihedrals, respectively. We fit the observed distance and angle distribution curves empirically to a normal distribution, and the observed dihedral distribution to a three-term cosine function. We used the Boltzmann relationship (Equation 1, R = 8.31 J/K mol and T = 300 K) to determine the energy function that produces these distributions. We give the equations and coefficients for these functions in Supplemental Table S1. In Figure 1B we also show the distributions of distances, angles, and dihedrals in 100 randomly chosen NAST-generated tRNA structures (labeled “NAST structures”). The match between the thick and dashed lines shows that application of this energy function results in the desired distributions:
Nonbonded interactions
We include a term in our energy function to restrict steric overlap between nonbonded residues separated in sequence by more than three residues. To do this, we use the repulsive term of the Lennard-Jones potential with a well depth of ɛ = 4.184 kJ/mol and hard sphere radii of σ = 5 Å and 4 Å for residues in the secondary structure and not in the secondary structure, respectively (Supplemental Table S1).
Secondary structure geometry
We constrain residues involved in secondary structure helices with an additional set of geometric constraints illustrated in Figure 1D, which ensure an ideal RNA right-handed A′-form helix. These constraints include the distance between paired residues, one angle, and two dihedrals between the two strands involved. We give the equations and parameters for these contributions to the potential in Supplemental Table S1.
Tertiary interactions
NAST also incorporates information about long-range interactions (typically, represented as distances) between residues, both in the case when the distance is known (for example, from a crystal structure) and when it is predicted or measured with noise (for example, from experimental data such as fluorescence resonance energy transfer [FRET]). When crystal distances are known, a term is added to the energy potential that strongly constrains the distance between the two nucleotides by using a tightly constrained spring potential. We do not consider packing effects when using distances from crystal structures. When the distance is not known, we add a weak attractive potential (∼25 times weaker than the potential used for bonds) between the two residues to the energy function. We give the equations and parameters for these energetic contributions in Supplemental Table S1.
Generating decoys
We used two unfolded conformations as starting structures for decoy generation: an unfolded coil and a circle (Supplemental Fig. S1). The unfolded coil conformation uses a distance of 5.78 Å, angle of 2.4 rad, and dihedral of 0.3 rad between each sequential residue. The unfolded circle conformation separates each sequential residue by a distance of 5.78 Å and by an offset of 0.2 Å in the Z-axis so that the residues are not all on the same plane. For each of these starting conformations, we constrained the secondary structure and tertiary contacts for 25, 10, and 5 parallel molecular dynamics runs of 2, 5, and 10 h each. This resulted in 300 CPU hours of molecular dynamics for each molecule. We filtered the resulting decoys by their observance of the tertiary contact constraints, using a cutoff of 15 Å. We also removed structures with unusually high NAST energies (>1500) from the ensemble.
Computational resources
We used the Stanford Bio-X2 cluster resource of 552 Dell CPUs with Intel quad-core 2.33 GHz processors to generate the candidate structures. Although we used a computer cluster to generate ensembles in parallel, our method does not require a sophisticated cluster and can be run on a simple workstation with any number of CPUs. This method also can be modified to run for more or fewer CPU hours depending on available resources.
Clustering structures
We randomly selected 1500 structures from the filtered ensemble and clustered them using k-means clustering with a range of k-values.
Simplified representation
We used a simplified representation of each molecule to reduce the computational cost of calculating pairwise distances between decoys, which facilitated clustering. We segmented each molecule based on secondary structure into helix, loop, and junction regions (Supplemental Fig. S2). We averaged the position of all residues in one fragment, resulting in one point per fragment. We also averaged the positions of all the residues in the molecule to generate another point (representing the center of mass of the molecule). This simplified representation resulted in 11 and 18 points for tRNA and P4-P6, respectively. This representation allowed us to maintain topological information about the positions of segments relative to each other while reducing the number of points in each molecule. We used this representation to calculate all pairwise GDT-TS scores between the 1500 molecules in an ensemble.
k-means clustering
We implemented a k-means clustering algorithm using GDT-TS scores as the distance measure between the simplified representations of molecules in an ensemble. We used k values of 2, 3, 4, and 5, and repeated the clustering 10 times for each value of k. For each clustering round we calculated the ratio of the average within distance to the average without distance. We selected the k-value by plotting the best W in/W out score for each k-value and using the elbow criterion (Supplemental Fig. S4), where W in/W out is defined as the ratio of the average internal distance to the average external distance for the cluster.
Representative structures
We selected the five structures with the lowest average reduced GDT-TS score to all other structures in the cluster as representatives of each cluster (Fig. 2). These “center” structures allow the user to visualize only several structures that represent the ensemble of generated structures.
Ranking clusters
We used three types of data to rank the clusters:
Ideal SAXS data;
Ideal and experimental solvent accessibility data (SAS); and
NAST energy.
For each data type, we averaged the agreement of decoys within each cluster with the data type to rank the clusters relative to each other. For ideal SAXS data, we calculated an error value, while for both ideal and experimental SAS data we calculated a correlation value. We assumed that lower NAST energy should correlate with better structures.
We used two scoring methods to evaluate the quality of structures in each cluster:
GDT-TS; and
RMSD.
The GDT-TS score calculates the percentage of residues that are within 1, 2, 4, and 8 Å of the correct position and averages them. GDT-TS scores range between 0 and 1, with high scores representing better structures. RMSD values are a measurement of error in angstroms, with lower values representing better structures.
Ideal SAXS data
To generate ideal SAXS data, we calculated the distribution of pairwise distance within the coarse-grained crystal structure of the molecule. We evaluated decoys by calculating the same distribution and summing the error over each bin in the distribution of pairwise distances. We used bins with widths of 4 Å and centers ranging from 1 to 121 Å (31 bins total). A lower error corresponds to a better match with the ideal SAXS data.
Ideal and experimental solvent accessibility data
We measured the solvent accessibility profile of each decoy using a published method (Cavallo et al. 2003), using a radius of 4.5 Å for nucleotides and a solvent probe radius of 1.5 Å.
To generate experimental solvent accessibility data for tRNA, we carried out hydroxyl radical footprinting of the yeast phenylalanine tRNA using the protocol described by Das et al. (2005b) and analyzed using SAFA (Das et al. 2005a). The peak intensities of the folded tRNA (50 mM Na-MOPS, pH 7.0, 10 mM MgCl2) at the single-nucleotide level were analyzed using SAFA (Das et al. 2005a) and normalized to the mean protection values for the entire tRNA.
For P4-P6, we used published hydroxyl radical footprinting data for P4-P6 (Takamoto et al. 2004).
For each decoy, we calculated the correlation to both the experimental and ideal solvent accessibility data and averaged the values in each cluster for ranking.
NAST energy
We used the energy function described above to calculate the NAST energy of each decoy with the assumption that a lower NAST energy should correspond to a more RNA-like geometry. Since the NAST energy is knowledge-based and does not have a physical interpretation, it is unitless.
Ranking clusters
For each data type, we calculated the average error or agreement value within a cluster and ranked the clusters based on these values (Table 1). We assigned a rank of 1 to the cluster with the lowest ideal SAXS error, largest ideal, and experimental SAS correlation and lowest NAST energy. We also ranked each cluster by the two quality measurements GDT-TS and RMSD.
Sensitivity to secondary structure prediction
To assess the sensitivity of our method to the accuracy of the secondary structure constraints in modeling P4-P6, we used four sets of constraints with different percentages of wrong base pairs. The secondary structure predicted before the crystal structure contains 26% wrong base pairs relative to the secondary structure observed in the crystal (0% wrong base pairs). We also used two secondary structure definitions with 15% and 35% wrong base pairs. We calculated the range of GDT-TS and RMSD scores for ensembles generated using each secondary structure and show these ranges in Figure 3.
Manipulating large RNA structures
Modeling the missing loops to the Azoarcus and Twort ribozyme crystal structures
We used NAST to model the missing loops in the Azoarcus (PDB ID 1ZZN) and Twort (PDB ID 1Y0Q) ribozymes by adding in the missing residues under the NAST energy function. The Azoarcus crystal structure is missing the loop at the end of the P6a helix (G108–C111), and the Twort ribozyme is missing the end of the P5 helix (A63–U77). We used the NAST energy function to equilibrate the structure, resulting in complete coarse-grained models of the ribozymes. These models are coarse-grained versions of the crystal structures with realistic geometries for the missing loops.
Combining crystallographic and modeling data for the T. thermophila group I intron
Starting with the coarse-grained version of the Michel–Westhof model of the T. thermophila group I intron, we constrained all pairwise distances from the crystal structure to generate a combined model. The resulting model agrees with the crystal structure for those parts of the molecule solved in the crystal structure, and with the Michel–Westhof model for the rest of the molecule.
SUPPLEMENTAL MATERIAL
Supplemental material can be found at http://www.rnajournal.org.
ACKNOWLEDGMENTS
This work was supported through the NIH Roadmap for Medical Research Grant U54 GM072970, by the NIH Grant P01-GM66275, and by the NSF 0443508 for the RNA Ontology Consortium. M.A.J. and S.P. are supported by the National Library of Medicine Training Grant LM-07033. M.A.J. also was supported by the NIH Biotechnology Training Grant 5 T32GM008412-15. A.L. was a Damon Runyon Cancer Foundation Research Fellow and was supported by NIGMS K99-GM079953. We thank Samuel Flores for helpful comments on the manuscript.
Footnotes
Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.1270809.
REFERENCES
- Baker D., Sali A. Protein structure prediction and structural genomics. Science. 2001;294:93–96. doi: 10.1126/science.1065659. [DOI] [PubMed] [Google Scholar]
- Ban N., Nissen P., Hansen J., Moore P.B., Steitz T.A. The complete atomic structure of the large ribosomal subunit at 2.4 Å resolution. Science. 2000;289:905–920. doi: 10.1126/science.289.5481.905. [DOI] [PubMed] [Google Scholar]
- Cate J.H., Gooding A.R., Podell E., Zhou K., Golden B.L., Kundrot C.E., Cech T.R., Doudna J.A. Crystal structure of a group I ribozyme domain: Principles of RNA packing. Science. 1996;273:1678–1685. doi: 10.1126/science.273.5282.1678. [DOI] [PubMed] [Google Scholar]
- Cavallo L., Kleinjung J., Fraternali F. POPS: A fast algorithm for solvent accessible surface areas at atomic and residue level. Nucleic Acids Res. 2003;31:3364–3366. doi: 10.1093/nar/gkg601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das R., Baker D. Automated de novo prediction of native-like RNA tertiary structures. Proc. Natl. Acad. Sci. 2007;104:14664–14669. doi: 10.1073/pnas.0703836104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das R., Laederach A., Pearlman S.M., Herschlag D., Altman R.B. SAFA: Semiautomated footprinting analysis software for high-throughput quantification of nucleic acid footprinting experiments. RNA. 2005a;11:344–354. doi: 10.1261/rna.7214405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das R., Travers K.J., Bai Y., Herschlag D. Determining the Mg2+ stoichiometry for folding an RNA metal ion core. J. Am. Chem. Soc. 2005b;127:8272–8273. doi: 10.1021/ja051422h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding F., Sharma S., Chalasani P., Demidov V.V., Broude N.E., Dokholyan N.V. Ab initio RNA folding by discrete molecular dynamics: From structure prediction to folding mechanisms. RNA. 2008;14:1164–1173. doi: 10.1261/rna.894608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do C.B., Woods D.A., Batzoglou S. CONTRAfold: RNA secondary structure prediction without physics-based models. Bioinformatics. 2006;22:e90–e98. doi: 10.1093/bioinformatics/btl246. [DOI] [PubMed] [Google Scholar]
- Doniach S. Changes in biomolecular conformation seen by small-angle X-ray scattering. Chem. Rev. 2001;101:1763–1778. doi: 10.1021/cr990071k. [DOI] [PubMed] [Google Scholar]
- Fink D.L., Chen R.O., Noller H.F., Altman R.B. Computational methods for defining the allowed conformational space of 16S rRNA based on chemical footprinting data. RNA. 1996;2:851–866. [PMC free article] [PubMed] [Google Scholar]
- Fischer D., Eisenberg D. Protein fold recognition using sequence-derived predictions. Protein Sci. 1996;5:947–955. doi: 10.1002/pro.5560050516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galas D.J., Schmitz A. DNAse footprinting: A simple method for the detection of protein–DNA binding specificity. Nucleic Acids Res. 1978;5:3157–3170. doi: 10.1093/nar/5.9.3157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guerrier-Takada C., Gardiner K., Marsh T., Pace N., Altman S. The RNA moiety of ribonuclease P is the catalytic subunit of the enzyme. Cell. 1983;35:849–857. doi: 10.1016/0092-8674(83)90117-4. [DOI] [PubMed] [Google Scholar]
- Harris M.E., Nolan J.M., Malhotra A., Brown J.W., Harvey S.C., Pace N.R. Use of photoaffinity crosslinking and molecular modeling to analyze the global architecture of ribonuclease P RNA. EMBO J. 1994;13:3953–3963. doi: 10.1002/j.1460-2075.1994.tb06711.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James B.D., Olsen G.J., Liu J.S., Pace N.R. The secondary structure of ribonuclease P RNA, the catalytic element of a ribonucleoprotein enzyme. Cell. 1988;52:19–26. doi: 10.1016/0092-8674(88)90527-2. [DOI] [PubMed] [Google Scholar]
- Jaroszewski L., Rychlewski L., Zhang B., Godzik A. Fold prediction by a hierarchy of sequence, threading, and modeling methods. Protein Sci. 1998;7:1431–1440. doi: 10.1002/pro.5560070620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones D.T. GenTHREADER: An efficient and reliable protein fold recognition method for genomic sequences. J. Mol. Biol. 1999;287:797–815. doi: 10.1006/jmbi.1999.2583. [DOI] [PubMed] [Google Scholar]
- Klingler T.M., Brutlag D.L. Detection of correlations in tRNA sequences with structural implications. Proceedings / International Conference on Intelligent Systems for Molecular Biology; ISMB. 1993;1:225–233. [PubMed] [Google Scholar]
- Kruger K., Grabowski P.J., Zaug A.J., Sands J., Gottschling D.E., Cech T.R. Self-splicing RNA: Autoexcision and autocyclization of the ribosomal RNA intervening sequence of Tetrahymena . Cell. 1982;31:147–157. doi: 10.1016/0092-8674(82)90414-7. [DOI] [PubMed] [Google Scholar]
- Lehnert V., Jaeger L., Michel F., Westhof E. New loop–loop tertiary interactions in self-splicing introns of subgroup IC and ID: A complete 3D model of the Tetrahymena thermophila ribozyme. Chem. Biol. 1996;3:993–1009. doi: 10.1016/s1074-5521(96)90166-0. [DOI] [PubMed] [Google Scholar]
- Levitt M. Detailed molecular model for transfer ribonucleic acid. Nature. 1969;224:759–763. doi: 10.1038/224759a0. [DOI] [PubMed] [Google Scholar]
- Major F., Gautheret D., Cedergren R. Reproducing the three-dimensional structure of a tRNA molecule from structural constraints. Proc. Natl. Acad. Sci. 1993;90:9408–9412. doi: 10.1073/pnas.90.20.9408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massire C., Westhof E. MANIP: An interactive tool for modeling RNA. J. Mol. Graph. Model. 1998;16:197–205. 255–257. doi: 10.1016/s1093-3263(98)80004-1. [DOI] [PubMed] [Google Scholar]
- Merino E.J., Wilkinson K.A., Coughlan J.L., Weeks K.M. RNA structure analysis at single nucleotide resolution by selective 2′-hydroxyl acylation and primer extension (SHAPE) J. Am. Chem. Soc. 2005;127:4223–4231. doi: 10.1021/ja043822v. [DOI] [PubMed] [Google Scholar]
- Michel F., Westhof E. Modeling of the three-dimensional architecture of group I catalytic introns based on comparative sequence analysis. J. Mol. Biol. 1990;216:585–610. doi: 10.1016/0022-2836(90)90386-Z. [DOI] [PubMed] [Google Scholar]
- Mortimer S.A., Weeks K.M. A fast-acting reagent for accurate analysis of RNA secondary and tertiary structure by SHAPE chemistry. J. Am. Chem. Soc. 2007;129:4144–4145. doi: 10.1021/ja0704028. [DOI] [PubMed] [Google Scholar]
- Murphy F.L., Cech T.R. An independently folding domain of RNA tertiary structure within the Tetrahymena ribozyme. Biochemistry. 1993;32:5291–5300. doi: 10.1021/bi00071a003. [DOI] [PubMed] [Google Scholar]
- Nahvi A., Sudarsan N., Ebert M.S., Zou X., Brown K.L., Breaker R.R. Genetic control by a metabolite binding mRNA. Chem. Biol. 2002;9:1043. doi: 10.1016/s1074-5521(02)00224-7. [DOI] [PubMed] [Google Scholar]
- Noller H.F., Kop J., Wheaton V., Brosius J., Gutell R.R., Kopylov A.M., Dohme F., Herr W., Stahl D.A., Gupta R., et al. Secondary structure model for 23S ribosomal RNA. Nucleic Acids Res. 1981;9:6167–6189. doi: 10.1093/nar/9.22.6167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parisien M., Major F. The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data. Nature. 2008;452:51–55. doi: 10.1038/nature06684. [DOI] [PubMed] [Google Scholar]
- Rhee Y.M., Pande V.S. Multiplexed-replica exchange molecular dynamics method for protein folding simulation. Biophys. J. 2003;84:775–786. doi: 10.1016/S0006-3495(03)74897-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodionov D.A., Vitreschak A.G., Mironov A.A., Gelfand M.S. Regulation of lysine biosynthesis and transport genes in bacteria: Yet another RNA riboswitch? Nucleic Acids Res. 2003;31:6748–6757. doi: 10.1093/nar/gkg900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohl C.A., Strauss C.E., Chivian D., Baker D. Modeling structurally variable regions in homologous proteins with rosetta. Proteins. 2004;55:656–677. doi: 10.1002/prot.10629. [DOI] [PubMed] [Google Scholar]
- Russell R., Millett I.S., Doniach S., Herschlag D. Small-angle X-ray scattering reveals a compact intermediate in RNA folding. Nat. Struct. Biol. 2000;7:367–370. doi: 10.1038/75132. [DOI] [PubMed] [Google Scholar]
- Sclavi B., Woodson S., Sullivan M., Chance M.R., Brenowitz M. Time-resolved synchrotron X-ray “footprinting,” a new approach to the study of nucleic acid structure and function: application to protein–DNA interactions and RNA folding. J. Mol. Biol. 1997;266:144–159. doi: 10.1006/jmbi.1996.0775. [DOI] [PubMed] [Google Scholar]
- Shapiro B.A., Yingling Y.G., Kasprzak W., Bindewald E. Bridging the gap in RNA structure prediction. Curr. Opin. Struct. Biol. 2007;17:157–165. doi: 10.1016/j.sbi.2007.03.001. [DOI] [PubMed] [Google Scholar]
- Shi J., Blundell T.L., Mizuguchi K. FUGUE: Sequence-structure homology recognition using environment-specific substitution tables and structure-dependent gap penalties. J. Mol. Biol. 2001;310:243–257. doi: 10.1006/jmbi.2001.4762. [DOI] [PubMed] [Google Scholar]
- Sorin E.J., Engelhardt M.A., Herschlag D., Pande V.S. RNA simulations: Probing hairpin unfolding and the dynamics of a GNRA tetraloop. J. Mol. Biol. 2002;317:493–506. doi: 10.1006/jmbi.2002.5447. [DOI] [PubMed] [Google Scholar]
- Sorin E.J., Nakatani B.J., Rhee Y.M., Jayachandran G., Vishal V., Pande V.S. Does native state topology determine the RNA folding mechanism? J. Mol. Biol. 2004;337:789–797. doi: 10.1016/j.jmb.2004.02.024. [DOI] [PubMed] [Google Scholar]
- Stark B.C., Kole R., Bowman E.J., Altman S. Ribonuclease P: An enzyme with an essential RNA component. Proc. Natl. Acad. Sci. 1978;75:3717–3721. doi: 10.1073/pnas.75.8.3717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takamoto K., Das R., He Q., Doniach S., Brenowitz M., Herschlag D., Chance M.R. Principles of RNA compaction: Insights from the equilibrium folding pathway of the P4-P6 RNA domain in monovalent cations. J. Mol. Biol. 2004;343:1195–1206. doi: 10.1016/j.jmb.2004.08.080. [DOI] [PubMed] [Google Scholar]
- Tan R.K.Z., Petrov A.S., Harvey S.C. YUP: A molecular simulation program for coarse-grained and multiscaled models. J. Chem. Theory Comput. 2006;2:529–540. doi: 10.1021/ct050323r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka I., Nakagawa A., Hosaka H., Wakatsuki S., Mueller F., Brimacombe R. Matching the crystallographic structure of ribosomal protein S7 to a three-dimensional model of the 16S ribosomal RNA. RNA. 1998;4:542–550. doi: 10.1017/s1355838298972004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tullius T.D. DNA footprinting with hydroxyl radical. Nature. 1988;332:663–664. doi: 10.1038/332663a0. [DOI] [PubMed] [Google Scholar]
- Vitreschak A.G., Rodionov D.A., Mironov A.A., Gelfand M.S. Riboswitches: The oldest mechanism for the regulation of gene expression? Trends Genet. 2004;20:44–50. doi: 10.1016/j.tig.2003.11.008. [DOI] [PubMed] [Google Scholar]
- Wang X.D., Padgett R.A. Hydroxyl radical “footprinting” of RNA: Application to pre-mRNA splicing complexes. Proc. Natl. Acad. Sci. 1989;86:7795–7799. doi: 10.1073/pnas.86.20.7795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westhof E., Altman S. Three-dimensional working model of M1 RNA, the catalytic RNA subunit of ribonuclease P from Escherichia coli . Proc. Natl. Acad. Sci. 1994;91:5133–5137. doi: 10.1073/pnas.91.11.5133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler W., Nahvi A., Breaker R.R. Thiamine derivatives bind messenger RNAs directly to regulate bacterial gene expression. Nature. 2002a;419:952–956. doi: 10.1038/nature01145. [DOI] [PubMed] [Google Scholar]
- Winkler W.C., Cohen-Chalamish S., Breaker R.R. An mRNA structure that controls gene expression by binding FMN. Proc. Natl. Acad. Sci. 2002b;99:15908–15913. doi: 10.1073/pnas.212628899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yusupov M.M., Yusupova G.Z., Baucom A., Lieberman K., Earnest T.N., Cate J.H., Noller H.F. Crystal structure of the ribosome at 5.5 Å resolution. Science. 2001;292:883–896. doi: 10.1126/science.1060089. [DOI] [PubMed] [Google Scholar]
- Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]