Bayesian graphical models for regression on multiple data sets with different variables

Abstract

Routinely collected administrative data sets, such as national registers, aim to collect information on a limited number of variables for the whole population. In contrast, survey and cohort studies contain more detailed data from a sample of the population. This paper describes Bayesian graphical models for fitting a common regression model to a combination of data sets with different sets of covariates. The methods are applied to a study of low birth weight and air pollution in England and Wales using a combination of register, survey, and small-area aggregate data. We discuss issues such as multiple imputation of confounding variables missing in one data set, survey selection bias, and appropriate propagation of information between model components. From the register data, there appears to be an association between low birth weight and environmental exposure to NO₂, but after adjusting for confounding by ethnicity and maternal smoking by combining the register and survey data under our models, we find there is no significant association. However, NO₂ was associated with a small but significant reduction in birth weight, modeled as a continuous variable.

1. INTRODUCTION

1.1. Data synthesis in epidemiology

Studies based on synthesis of data sets of different designs are becoming more common in environmental epidemiology. Observational studies in epidemiology are susceptible to a variety of potential biases, as discussed by Greenland (2005), who recommended that the effect of each potential bias on the conclusions should be routinely and jointly assessed. Typically, the biases are not identified by the study data, but information can often be gained by incorporating external data. At the same time, precision can be increased by combining data. We consider studies of the relationship between an exposure and an outcome using a combination of 2 commonly used forms of data:

1. A large administrative data set, such as a census or disease register, which represents the whole population and enables the study of small-scale geographical variations. This may only be published as aggregate data, leading to ecological bias (Greenland and Morgenstern, 1989), and variables of interest may not be recorded.

2. A small individual-level data set containing all key variables but lacking power, in particular, information on geographical variations.

Ecological bias from aggregate administrative data can be alleviated by incorporating surveys of individual exposures (Prentice and Sheppard, 1995, Wakefield and Salway, 2001), exposures and outcomes (Jackson et al., 2006, Jackson et al., 2008) or case–control data (Haneuse and Wakefield, 2007). In this paper, instead of an aggregate data set, we consider the situation where the large administrative data set is an “individual-level” register which includes the exposure of interest but omits important confounders. The register data are complemented by a smaller survey data set which contains all relevant variables. We use multiple imputation methods, within a Bayesian graphical modeling framework, to analyze jointly the combined data.

Gelman et al. (1998) described similar methods for simultaneously analyzing multiple survey data sets in which some questions are not asked in some surveys. That article was focused on producing a set of multiply imputed data sets for later analysis, with multivariate normal observed and missing data. In this paper, we describe a joint model for imputing the data and fitting a regression model to the imputed data. Our application involves a binary outcome and categorical missing data, but the methods can be implemented for general forms of data using general purpose software.

1.2. General model for jointly analyzing data sets with different variables

We are interested in a regression of an outcome y on a set of N covariates x₁,…,x_N when we have 2 or more individual-level data sets. Suppose that observations of y are made in every data set, but only a subset of the covariates is observed in each data set. The idea is to predict the missing covariates in one data set using completely observed variables in the others.

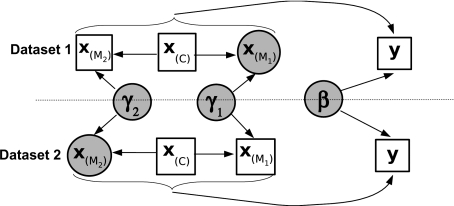
This is illustrated for the simplest case of 2 data sets by a graphical model (Figure 1). To impute the missing covariates x_(M1) in data set 1, we require that there are some covariates x_(C) observed in both data sets and that x_(M1) are observed in data set 2. Firstly, we fit a regression of the x_(M1) on x_(C) using data set 2. Using the x_(C) in data set 1, we predict from this regression to impute the x_(M1) missing in data set 1. Similarly, to predict the x_(M2) missing in data set 2, if x_(M2) are observed in data set 1, we can use data set 1 to estimate a regression model for x_(M2) in terms of x_(C). The regression coefficients of interest β governing the relationship between y and x₁,…,x_N in all data sets, the regression coefficients γ_d governing the imputation model for data set d, and the missing covariates in each data set are estimated simultaneously. In practice, Markov chain Monte Carlo (MCMC) posterior simulation will usually be necessary.

Fig. 1.

General model for regression of y on x using a combination of data sets with different observed covariates. Circles represent unknown quantities and squares represent observed data. Covariates x_(M1) missing in data set 1 are predicted from a regression fitted using the observed values of x_(M1) in data set 2 and variables x_(C) common to both. Covariates x_(M2) missing in data set 2 are predicted in a similar way using information from data set 1.

These principles can immediately be generalized to 3 data sets or more. To predict the missing covariates x_(Md) in data set d, we require that these covariates are observed in at least one other data set, in which there also exist variables observed in data set d to inform a regression model for x_(Md). Indeed, similar principles can be used, if necessary, to impute missing outcomes y. Or, by separating complete from incomplete records, covariates which are missing intermittently within one data set can be imputed.

1.3. Low birth weight and air pollution

This model will be illustrated by a study of the association between low birth weight and exposure to ambient air pollution. Some studies have suggested that exposure to air pollution increases the risk of low birth weight, either as a result of preterm delivery or intrauterine growth retardation. Most of these have been based on births registers covering a single city or region in 1 year, for example, São Paulo (Gouveia et al., 2004), Vancouver (Liu et al., 2003), Sydney (Mannes et al., 2005), and California (Parker et al., 2005). The study in this paper is based on the population of England and Wales, which should enable us to examine a relatively wide range of exposures. In UK, the Office for National Statistics maintains a register of all births, to which we can link modeled pollution exposures by postcode of residence (see Section 2.3). However, many major risk factors for low birth weight, such as ethnicity or maternal age, are either not recorded or not made available in the register. Therefore, we obtain detailed confounder information from a survey of births, the Millennium Cohort Study (MCS).

There are 2 important sources of potential bias. Bias due to confounding by variables absent from the register data can be alleviated by an imputation model for the missing covariates, constructed using the survey data. Inferences from the survey data are also subject to selection bias. This can be alleviated by adjusting models for known factors affecting selection or by weighting observations by the inverse probability of selection, which is known by design. We could consider analyzing the survey data alone, since all relevant variables are observed, and pollution exposure estimates can be linked by postcode. However, inferences from the survey data alone lack power to detect the small risk increases expected for environmental exposures, typically a few percent for a population quartile of a continuous exposure (e.g. Gouveia et al., 2004). We will demonstrate how the graphical modeling framework described in Section 1.2 can incorporate all data sources, controlling biases and improving precision. Bayesian estimation of the joint model ensures that uncertainties are propagated appropriately between different model components.

Section 2 describes our data sources in more detail. Section 3 describes how the model presented in Section 1.2 is specified and implemented to estimate the association between low birth weight and pollution. Section 4 presents the results, including a range of sensitivity analyses to assess the influence of each source of data and each component of the model. Finally, we discuss the advantages and drawbacks of the methods and suggest some ideas for further development.

2. DATA

2.1. National births register

The UK register of births (Office for National Statistics) recorded 579 267 singleton births in England and Wales between September 1, 2000, and August 30, 2001. Information available for every birth includes date of birth, birth weight, sex, and postcode. Social class and employment status of the mother are available for a 10% random sample of every 10th registered birth and we study only this subset of 57 844 births. A total of 1231 individuals who also appeared in the MCS, ascertained by a match on postcode, date of birth, sex, and birth weight, were excluded from the register data. Also, 88 births with missing birth weight were excluded, leaving 56 525 births for analysis.

2.2. Millennium Cohort Study

The MCS (Centre for Longitudinal Studies, 2000–2005) covers 18 819 babies born between September 1, 2000, and August 30, 2001, in the UK. We include only the 14 100 singleton births from England and Wales. Births with postcodes of residence which could not be linked to pollution data, due to incomplete pollution mapping or inaccurate recording of postcodes in the MCS, were excluded, leaving 13 131 births for analysis. The distribution of birth weight was similar between the included and the excluded births.

The MCS was cluster-sampled by electoral wards, areas containing an average of around 5000 individuals. Wards in England were stratified into mutually exclusive categories labeled “advantaged”, “disadvantaged” and “high ethnic minority”, and wards in Wales were stratified into categories labeled advantaged and disadvantaged. A different proportion of wards were sampled from each stratum to achieve adequate representation of each stratum. All families in the sampled wards with children born in the relevant period, resident in the UK at 9 months, were invited to participate. Response rates averaged 70%, but varied by stratum, with the lowest response rate of about 60% in the ethnic minority wards. Variables from the MCS which we consider include birth weight, sex, ethnicity, tobacco smoking during pregnancy, maternal age, parity (number of previous births), height and weight, and socioeconomic characteristics of the mother, including social class, employment status, lone parent, and education over age 16.

2.3. Pollution exposure

Estimated background maps of ambient concentrations of NO₂ and SO₂, for 2001, on a 1-km grid, were obtained from the National Environmental Technology Centre (Stedman et al., 2002). These were modeled from point sources such as power stations, line sources such as road traffic, and monitoring sites, using a dispersion matrix approach. Pollution estimates from 54 517 grid squares in England and Wales were attributed to 566 932 postcodes using area-weighting techniques. The births register and MCS data were linked by postcode to the annual mean pollution concentration for the year (2000 or 2001) in which the nominal date of the middle of pregnancy (140 days prior to birth) falls. Concentrations for the year 2000 were estimated by adjusting the 2001 concentrations by published scaling factors (Department for Environment, Food and Rural Affairs, UK, 2003), calculated from estimated changes in road traffic emissions, which decreased from 2000 to 2001.

2.4. Aggregate data

Some important risk factors for low birth weight are not available from the births register, in particular, ethnic group and tobacco smoking, which are likely to be confounded with air pollution exposure. An imputation model is fitted to individual ethnicity and smoking from the MCS data and subsequently used to predict these variables for the births in the register. To inform this model, geographical aggregate data on these variables were obtained. Neighborhood smoking behavior and ethnicity are expected to be good predictors of their individual-level equivalents. The proportion of the resident population in each of 4 ethnic groups (white, South Asian, black, other) for 46 548 census output areas (areas containing around 200–300 individuals) were obtained from the 2001 UK census. Estimated annual tobacco expenditures, by 2001 census output areas, were obtained from consumer classification data (CACI Information Solutions, Limited). These were linked by postcode to all individuals in the MCS and register.

2.5. Consistency of data sources: selection bias

Table 1 presents a summary of the variables common to the MCS and administrative (either register or aggregate) data. The differences between the administrative and the survey data reflect how the MCS data are not a random sample of the population. However, when the MCS data are summarized using the published survey weights, which are inversely proportional to the proportion of wards sampled in each stratum, the distributions of all variables except social class and employment are consistent with the population summary. The different distribution of social class and employment between the MCS and the register, even after reweighting the MCS, is likely to be caused by inaccurate recording of these variables in the register, rather than selection bias—since the summary of social class and employment from the reweighted MCS was consistent with 1991 UK census data for women between the ages of 12 and 60. The binary smoking status reported by the MCS cannot be directly compared to area-level mean tobacco expenditures.

Table 1.

Summary of register, ecological, MCS data, and MCS data weighted to represent the population. Continuous variables summarized as mean (standard deviation), discrete variables summarized as number and percentage

	Administrative data	Millennum Cohort	Millennium Cohort (weighted)
Register data
Number of births	56 525	13 143	13 143
Birth weight (kg)	3.36 (0.58)	3.33 (0.58)	3.37 (0.57)
Low birth weight (< 2.5 kg†)	3474 (6.1%)	900 (6.8%)	793 (6%)
NO2	29.41 (8.54)	29.19 (8.98)	28.66 (8.25)
SO2	04.2 (1.87)	4.13 (1.7)	4.17 (1.7)
Social class
Professional	1877 (3.3%)	332 (2.5%)	452 (3.4%)
Managerial, technical	12 975 (23%)	2683 (20.4%)	3258 (24.8%)
Skilled nonmanual	12 062 (21.3%)	4104 (31.2%)	4363 (33.2%)
Skilled manual	2875 (5.1%)	1111 (8.5%)	1168 (8.9%)
Partly skilled	4422 (7.8%)	2589 (19.7%)	2329 (17.7%)
Unskilled	539 (1%)	495 (3.8%)	460 (3.5%)
Other	21 775 (38.5%)	1759 (13.4%)	1062 (8.1%)
Aggregate data
Inactive‡	21 573 (38.2%)	7224 (55%)	6480 (49.3%)
Ethnic group
White	88.3%	10 342 (78.7%)	11 484 (87.4%)
South Asian	5.7%	1658 (12.6%)	870 (6.6%)
Black	2.9%	616 (4.7%)	380 (2.9%)
Other	3.1%	489 (3.7%)	372 (2.8%)
Tobacco§	237 (85)
Smoking¶		4036 (30.7%)	3931 (29.9%)

^†The standard definition (United Nations Children's Fund and World Health Organization, 2004).

^‡Unemployed or economically inactive.

^§Annual tobacco expenditure per person (pounds).

^¶Smoking during pregnancy.

We aim to adjust by regression for all factors governing selection (Gelman and Carlin, 2001). The data we study are a combination of a random 10% sample of the register with a selective 2% sample (MCS). The combined data set therefore has a 2-stage selection mechanism. Firstly, the MCS subjects are sampled within 5 strata. Secondly, we assume the remaining subjects (ignoring the 2% of those who also appeared in the MCS) are selected at random from the remaining population, which we consider to be a sixth sampling stratum. This sampling design is accounted for in the model for low birth weight by adjusting for the stratum as a covariate. Other covariates in our model, including ethnicity and social class, are assumed to be sufficient to adjust for nonresponse within the MCS sampling strata.

The sample selection mechanism must also be accounted for in the model we use to impute the missing ethnicity and smoking data in the register. The combination of the MCS and register is considered as a single data set in which the births which came from the register have these covariates missing. These can be modeled using multiple imputation. By adjusting the imputation model for the variables governing selection into the MCS, we can assume a “missing-at-random” mechanism for these variables since missingness is equivalent to inclusion in the portion of the data set which came from the register rather than the MCS.

3. MODELS

Two regression models are estimated in parallel using the combined data: a “model of interest” for the relationship of low birth weight to pollution exposure, and an “imputation model” for 2 potential confounders of this relationship, ethnicity, and smoking, which are missing from the register data but available from the MCS.

3.1. Model of interest for low birth weight

Suppose baby i from ward k in the MCS has low–birth weight indicator y_ik. Let x_ik(C) be a vector of covariates which are observed in both the register and the MCS, and let x_ik(M) be a vector of confounders which are missing in the register but available in the MCS. The model for this individual's risk p_ik of low birth weight is a random-effects logistic regression:

(3.1)

In (3.1), μ_sk represent different baseline risks of low birth weight for the stratum s_k in which ward k is classified, defined by the sampling design of the MCS, and U_k are ward-level random effects, assumed exchangeable within each stratum, with a different variance within each stratum s_k.

Similarly, for baby j, resident in ward l, in the register, where x_jl(M) are unknown,

(3.2)

Ward-level random effects U_l are included, with the same distribution as U_k, to account for any small-area clustering in the risk of low birth weight that is not explained by covariates included in the regression model. The intercept m represents the sixth sampling stratum, discussed in Section 2.5. As in hierarchical related regression (Jackson et al., 2008), the log-odds ratios β_C and β_M are assumed to be the same between the MCS and the register data.

The covariates x_ik(C), available in both data sets and included in the final model for low birth weight, are NO₂ and SO₂, which are continuous, and the mother's social class, which is categorical. Covariates x_ik(M), available in the MCS only, included smoking during pregnancy (binary) and ethnic group (4 categories representing white, South Asian, black and other). Other covariates were either not significant predictors of low birth weight, such as employment status of the mother, or assumed to be not confounded with pollution, such as maternal age, parity, height, and weight. The latter were all found to have negligible correlation with NO₂ and SO₂ in the MCS data. The results of regression models which included pollution exposure as a categorical variable suggested that it was appropriate to treat the effect of pollution as linear. We assume that the covariates we include, in particular the MCS design strata, ethnic group and social class, are sufficient to adjust for all factors governing MCS selection and nonresponse. In Section 4.3, we perform sensitivity analyses to assess this assumption.

3.2. Imputation model for missing smoking and ethnicity

Each x_ik(M) indicates the combined smoking status and ethnic group of individual i in ward k from the MCS. This has 8 categories with probabilities q_ik = (q_ik1,…,q_ik8). A regression model is fitted to x_ik(M) in the MCS data and used to predict the missing x_jl(M) in the register. As recommended by Little (1992), all completely observed variables are used for this prediction. These include the individual-level variables x_ik(C) in the model of interest common to the MCS and register (NO₂, SO₂, social class) and additional variables x_ik(P) specific to the imputation model (individual employment status and aggregate covariates). The aggregate covariates, describing the census output area in which individual i is resident (Section 2.4), include the average annual tobacco expenditure per person for each output area and the log-relative proportions of ethnic minorities, defined as log(ψ_ms/ψ_m1)(s = 2,3,4), where ψ_ms is the proportion of the population of output area m in ethnic group s. A random-effects multinomial logistic regression is fitted for x_ik(M) in terms of x_ik(P) and x_ik(C):

(3.3)

This is fitted to the MCS data and used to predict the missing smoking and ethnicity in the register data. Classical likelihood ratio tests suggested that all covariates, especially individual NO₂ exposure, aggregate ethnicity, aggregate tobacco and individual social class, seem significantly to improve the prediction model. Including further interaction terms did not significantly improve fit. The sampling design of the MCS in model (3.3) is again represented by cluster-level random effects V_k. We assume this model contains all factors governing selection, as discussed in Section 2.5. Different intercepts within each sampling stratum were not used since the strata, based on ward-level child poverty and ethnicity, were highly correlated with the aggregate ethnicity and tobacco data. The low–birth weight outcome also influences this prediction, as described in Section 3.3.

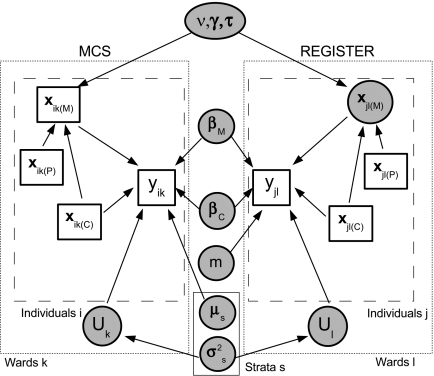
3.3. Graphical model implementation

The model is fully specified by (3.1–3.3). Figure 2 shows the directed acyclic graph for this model, which forms the basis of a MCMC algorithm (Gilks et al., 1996). The joint posterior distribution of the set of all quantities V in the graph is expressible as the product ∏_v∈V p(v|pa[v]) of all conditional posterior distributions, where pa[v] denotes the parent nodes of v. MCMC estimation of the model proceeds by iterative sampling from the full conditional distributions p(v|·) of each node, where · indicates all nodes other than v. Each full conditional distribution is the product of a prior and a likelihood term: p(v|·) = p(v|pa[v])∏_v∈pa[w]p(w|pa[w]).

Fig. 2.

Graphical model (full probability model for imputation and regression). Unknown quantities (parameters or missing data) are represented by circles and observed data by squares.

The right-hand side of the graph illustrates that the prior distribution of the unknown confounders x_jl(M) in the register is defined by the imputation model, parameterized by the ν_r,τ_sk and γ_r = (γ_rP,γ_rC). Information to estimate these parameters comes from their likelihood, which depends on x_ik(M) in the MCS. Also, x_jl(P) denotes variables used in the model for imputing x_jl(M) which do not appear in x_jl(C). In this graph, the low–birth weight outcome y_jl is implicitly involved in the prediction of x_jl(M) since the likelihood term of y_jl, defined by (3.2), involves the unknown x_jl(M).

3.4. Approximation to the full graphical model

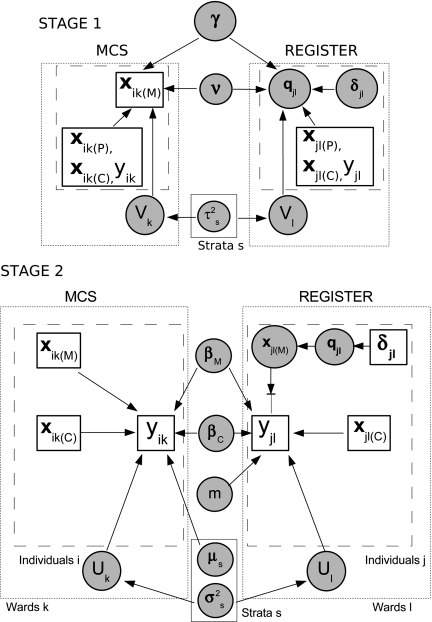
In the full probability model illustrated by Figure 2, we would sample directly from the posterior distribution of the imputation coefficients ν_r,γ_r to calculate the probabilities q_jl governing x_jl(M), thus accounting for the uncertainty about the imputation model while estimating the model for low birth weight. However, we found that the calculation of q_jl on the register data, using the WinBUGS software (Spiegelhalter et al., 2003) for MCMC sampling, was computationally infeasible. Therefore, we proceeded in 2 stages, firstly fitting the imputation model (3.3) to the MCS data to derive a hierarchical prior distribution for x_jl(M), then using this prior distribution to impute missing values of x_jl(M) in Bayesian estimation of the model of interest (3.1) and (3.2).

In the first stage, the posterior distributions of the coefficients of model (3.3) were estimated from the MCS data using MCMC sampling. Variables x_jl(P),x_jl(C),y_jl for each individual j and output area l in the register, and samples of 100 from the posterior distributions of ν_r,γ_r and V_l were used to predict a sample of 100 replicates of the vector of prior probabilities q_jl = (q_jl1,…,q_jl8) for each individual's unknown smoking status and ethnic group x_jl(M). A Dirichlet distribution was then fitted to these replicate vectors, for each j,l, by maximum likelihood (Yee and Wild, 1996,). These Dirichlet distributions were then used as priors for (q_jl1,…,q_jl8) in the second-stage model for low birth weight, thus the uncertainty about ν_r,γ_r is propagated through to the second stage. This is represented by the graphical model illustrated in Figure 3:

(3.4)

Fig. 3.

Graphical model (2-stage imputation and regression). In Stage 1, the imputation model with parameters γ,νis fitted to the ethnicity and smoking data x_ik(M)in the MCS and used to predict probabilities q_jlgoverning the missing data x_jl(M)in the register. In Stage 2, the model of interest is fitted to the low–birth weight outcomes y_ikin the MCS and y_jlin the register, using a Dirichlet prior distribution for q_jlparameterized by δ_jl.

For the Stage 2 model, the prior distributions for the covariate effects comprising β_C and β_M are independent normal with mean 0 and variance 100. Logistic(0, 1) priors were used for the logit baseline risk parameters m,μ₁,…μ₅. Truncated positive N(0, 1) priors were used for σ₁²,…,σ₅² (Gelman, 2006). The data are sufficient to dominate the influence of this choice of priors.

Note that y_jl is included as an explicit predictor of x_jl(M) in the Stage 1 model, through the model for q_jl, instead of implicitly influencing the prediction through its “likelihood” term which depends on x_jl(M). The “valve” on the arrow from x_jl(M) to y_jl in Figure 3, Stage 2, indicates that this likelihood term is omitted from the full conditional distribution of that node. That is, the dependence of y_jl on x_jl(M) is “cut,” so that prior information on y_jl flows in the direction of the arrow, but likelihood information on x_jl(M) does not flow in the reverse direction (Lunn et al., 2008). In the WinBUGS software, this is achieved by “the cut function.” Without this cut, y_jl would effectively have been adjusted for twice.

4. RESULTS

We aim to assess the influence of each source of data on the conclusions and the benefit of each model elaboration. The model defined by (3.1), (3.2) and (3.4) and the various simplifications of it are fitted using all available data and various subsets. In particular, the impact of confounding and selection bias, the benefit gained by combining the MCS and register data, the choice of predictors for the imputation model, the influence of the imputed data, and the benefit of cutting the graphical model are assessed.

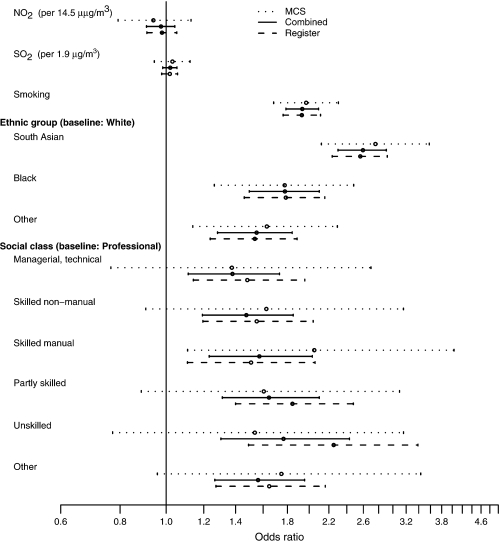
Figure 4 presents the posterior mean odds ratios of low birth weight associated with NO₂ and SO₂ exposure and the odds ratios associated with ethnicity, smoking and the 6 categories of social class in graphical form for 3 important cases. Additional results are given in the supplementary material, available at Biostatistics online (available from http://www.biostatistics.oxfordjournals.org).

Fig. 4.

Odds ratios of low birth weight associated with pollution, smoking, ethnicity, and social class, estimated using 3 different combinations of data. In all cases, the fitted model included pollution, smoking, ethnicity, and social class. Horizontal axis is on the log-scale.

4.1. Impact of confounding

Using the register data alone, a logistic regression for low birth weight on pollution exposures, adjusted for individual social class (available for every mother in the register) but not ethnicity or smoking status, gives an odds ratio of 1.15 for a change in NO₂ equal to its interquartile range across England and Wales (95% credible interval 1.07 to 1.23). Fitting a similar model (model (3.1)) to the MCS data, adjusting for ethnicity and smoking status, suggests that this apparent association is the result of confounding—that there is no association of low birth weight with NO₂ conditionally on ethnicity and smoking. Most studies of low birth weight and pollution have been conducted using birth registers. Our analysis suggests that a misleading result would have arisen given only the UK register, in which we are unable to control for confounding. However, the lack of association with pollution in the MCS may just reflect lack of power, therefore we strengthen our conclusions by combining the MCS and register data under the imputation model.

4.2. Benefit of combining the administrative and survey data

The estimated odds ratio for NO₂ under the full model (3.1), (3.2) and (3.4), combining the MCS and register data, integrating over the missing individual ethnicity and smoking data in the register is 0.98 (0.91, 1.04), demonstrating an increase in precision compared to the MCS alone. Similar increases in precision are shown for all other covariate effects (Figure 4). Note that the increasing risk of low birth weight with decreasing levels of social class now appears significant (Figure 4, “Combined” result compared to “MCS”). A similar odds ratio for the NO₂ effect of 0.97 (0.90, 1.03) is obtained using the outcome data from the register data alone (model 3.2), but controlling for confounding using the imputation model (3.4) (Figure 4). This suggests that the main role of the MCS is to inform the imputation model, while the model of interest is dominated by the register data. For SO₂, the odds ratio from the combined data is 1.02 (0.98, 1.05). Thus, the evidence for lack of an association of either pollutant with low birth weight has been strengthened by combining the register and survey data.

The posterior distribution of the deviance ( − 2× log-likelihood) was calculated for the MCS and register outcomes separately in the model which combined the two, as a measure of model fit. The posterior mean deviances for the MCS and register were 6288 and 25 130, respectively (standard deviations 11 and 57), demonstrating a good fit, comparing with expected deviances for a saturated model of 13 131 and 56 525 respectively (the number of observations in the data).

4.3. Impact of selection bias and data inconsistency

When the differential selection and cluster sampling of the MCS are not accounted for, so that μ_sk is replaced by a constant μ in (3.1) and the random effects U_k and U_l are removed, the combined model yields an odds ratio of 1.00 (0.94, 1.06) for NO₂, implying that the effect of selection bias would not have been great if the sampling design of the MCS had been ignored. An additional model was fitted to the MCS data which ignored confounding by smoking and ethnicity. The estimated odds ratios are similar to those obtained from the same model fitted to the register data alone (first row of Table 3, supplementary material, available at Biostatistics online), but with wider credible intervals. The consistency between the MCS and the population register results suggests that the selection and nonresponse mechanisms in the MCS do not bias the association between pollution and low birth weight. A further model was fitted to the combined data and the MCS alone, excluding social class as a predictor of low birth weight. In both cases, the posterior mean odds ratios and credible limits for NO₂ and SO₂ (not presented) were less than 1% different from those obtained from the model including social class, suggesting that the poor quality of the social class data from the register (discussed in Section 2.5) did not affect the conclusions.

4.4. Influence of the imputation model

The main assumption of this data synthesis is that the imputation model is able to impute the ethnicity and smoking data in the register with sufficient accuracy to control for their confounding effects. We now assess the influence of the imputation model, the choice of predictors in the imputation model, and the amount of power lost by propagating the imputation uncertainty.

Firstly, we assess roughly how many predictors of individual ethnicity and smoking are required from the population data to control for their confounding effects. Our main imputation model uses all available predictors. When the aggregate ethnicity and tobacco data are omitted from this model, so that it depends only on individual-level variables (low birth weight, NO₂ exposure, SO₂ exposure, social class, and unemployment), there is a 5% change in the odds ratio for NO₂ and a greater change in the confounder odds ratios (fifth row of Table 3, supplementary material available at Biostatistics online). With NO₂ also omitted from the imputation model, the biases are greater: the odds ratios in the model of interest are close to those from the register data unadjusted for confounders. Thus, confounding can be controlled to some extent without the auxiliary aggregate data on the confounders, by including a sufficient number of individual predictors of the confounders, provided that the exposures of interest are included in the imputation model.

Secondly, the relative influence of the “observed” and “imputed” confounder data on the model of interest is assessed. The full model was fitted to the combined data, but with the observed confounders in the MCS replaced by multiply imputed values. The odds ratios (ninth row of Table 2, supplementary material available at Biostatistics online) are similar to those with the observed confounders (third row) suggesting that the imputations are consistent with the observed data.

By combining the data, uncertainty is reduced by increasing the sample size, but at the cost of extra uncertainty about the imputed covariate data, which is propagated by the MCMC scheme. The posterior variance of the log-odds ratio for NO₂ is 0.00840 from the MCS only. If the data are combined but imputation uncertainty is ignored, using a single random imputation of the confounders in the register, this variance reduces to 0.00102, about 12% of the variance under the MCS. Propagating the uncertainty only increases this variance to 0.00109, about 13% of the variance under the MCS.

4.5. Benefit of cutting the dependency on birth weight

The full model was also fitted to the combined data with the graph not cut as described in Section 3.4. Here, the low–birth weight outcome is allowed to influence this confounder imputation indirectly through the graph, as well as being implicitly accounted for in the prior parameters δ_jl of x_jl(M). This seems to result in large biases in the odds ratios for NO₂, ethnicity and smoking (Tables 2 and 3, supplementary material available at Biostatistics online). This warns against applying a graphical model naïvely without considering whether its structure implicitly provides information about certain nodes.

4.6. Substantive interpretation

We conclude that in England and Wales there is a large increase in risk of low birth weight associated with maternal smoking (odds ratio [OR] 1.93 [1.79, 2.09]), South Asian ethnic groups (OR 2.6 [2.3, 2.91]), Black ethnic groups (OR 1.78 [1.5, 2.1]), other ethnic minorities (OR 1.55 [1.28, 1.84]), and decreasing social class. Conditionally on these factors, there does not seem to be an effect of exposure to environmental NO₂ or SO₂. These results are not inconsistent with the literature on the effects of pollution exposure on birth weight. While there are several studies suggesting associations between NO₂, PM₁₀, CO, and SO₂ exposure and adverse birth outcomes, these vary in the definition of the exposure and outcome studied and the nature of the association. For example, Mannes et al. (2005) found an association of CO and NO₂ exposure in the first trimester of pregnancy with all birth weight in Sydney and Gouveia et al. (2004) found an association of PM₁₀ and CO exposure (but not NO₂) in the first trimester with low birth weight for gestational age in São Paulo, whereas Hansen et al. (2007) found no association of NO₂ or PM₁₀ exposure with a reduction in birth weight in Brisbane.

Birth outcomes.

The outcome used in our study was low birth weight at all gestational ages. However, the aetiology of preterm birth and intrauterine growth restriction (resulting in low full-term birth weight) is different. The gestational age of each birth is required to distinguish between these 2 outcomes. This is available from the MCS but not from register data. To investigate possible effects on each of these outcomes separately, we fitted standard logistic regression models to the MCS data alone, adjusting for individual ethnicity, smoking, and social class. Around 43% of low–birth weight babies in the MCS were full term ( ≥ 37 weeks gestational age). The associations of NO₂ and SO₂ with low full-term birth weight are similar to those for all low birth weight, and the effects of smoking and ethnicity are stronger (Tables 2 and 3, supplementary material available at Biostatistics online). The only significant predictor of preterm birth was maternal smoking. There does not appear to be an association of preterm birth with pollution exposure. The findings of lack of an association of either outcome with pollution are inconclusive, although there is no strong evidence to suggest important differences in effect according to gestational age. In Molitor et al. (2008), we propose an extension of the current modeling framework to impute missing information on gestational age in the register.

We study low birth weight, defined as less than 2.5 kg, since this is established as an important public health indicator (United Nations Children's Fund and World Health Organization, 2004). As an alternative to a dichotomous outcome, we consider modeling birth weight as a continuous variable. Wilcox and Russell (1983) characterized the population distribution of birth weight as a mixture of a predominant normal distribution and a heavy tail, representing full-term and preterm births, respectively. We fit a mixture of 2 normal distributions to our combined birth weight data, adjusted for the same variables as models (3.1) and (3.2). Uninformative priors were used for the component membership probability and the component-specific means and variances, with an ordering constraint on the component means. The regression coefficients were constrained to be the same between components—allowing them to vary did not improve fit, judging from an increase in the posterior mean deviance. Under this model, there is a change of − 31 g ( − 40 g, − 23 g) associated with a change in NO₂ equal to its interquartile range, similarly 1.1 g ( − 3.6 g, 5.8 g) for SO₂. The significant association of NO₂ with reduction in birth weight contrasts with the results obtained when dichotomizing birth weight. However, the association is small compared to the population mean birth weight of 3374 g and the “low–birth weight” threshold (about the 6.3% percentile) of 2500 g.

Exposure measurement error and variability.

Now, consider the nature of the exposure data in our study. Firstly, the potential impact of measurement error should be considered. The only exposure data we have are modeled annual pollution concentrations in 2000 and 2001 by postcode of residence. These are proxies for the true individual exposures. The true exposures are likely to have higher variance than the observed data (Berkson error), and there is no reason to believe that errors are differential. Thus, while measurement error is likely to reduce power, it is not expected to cause bias in estimated exposure effects Armstrong, 1998, Zeger et al., 2000. To investigate these impacts, we performed a sensitivity analysis. In the model for the combined data, the observed NO₂ exposure x_ik1 was replaced by the unknown true exposure x_ik1^(true) and a Berkson error model was assumed:

The measurement error standard deviation was defined as ω = 0.5λ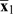, where 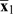is the empirical mean exposure in the combined data, representing the belief that the true value varies within about ±100λ% of the observed value. The observed SO₂ exposure was modeled in the same way. For values of λ up to 1, the estimated odds ratios and their credible limits were within 1% of the estimates with λ = 0, suggesting that measurement error within plausible limits did not affect the power of our analysis.

Secondly, the impact of temporal variations in the exposure should be considered. While our annual mean exposure data only enable us to determine the effect of long-term exposure rather than specific effects in different months of pregnancy, we can investigate seasonal variations. Concentrations of NO₂ and SO₂ were lower in 2001 and are generally higher in winter months (December to February in UK) when the air is cool and stable. Births are approximately uniformly distributed in the data by season. To assess whether there is some seasonal component to the risk of low birth weight after adjusting for annual background concentrations, we fitted the combined model including an extra term for season of birth (categorized as September 2000–November 2000, December 2000–February 2001, March 2001–May 2001, June 2001–August 2001). Small seasonal variations were observed with the lightest births in winter and summer. Relative to a baseline of September–November, the odds ratio for low birth weight for birth in December–February was 1.09 (1.00, 1.18), for March–May 1.04 (0.95, 1.14), and for June–August 1.07 (0.99, 1.17). Lower birth weights in summer may be related to pollution exposure during pregnancy in the winter, although it has been suggested that low temperatures during mid-pregnancy may directly affect foetal growth (Murray et al., 2000).

5. DISCUSSION

Multiple imputation methods, which are more commonly used for intermittent nonresponse within single data sets, can also be used to combine data in situations where some variables are missing by design in particular data sets. In this paper, we presented and applied a model for combining data sets with different sets of variables, generalizing the model presented by Gelman et al. (1998) to include estimation of regression relationships on the imputed data and general forms of observed and missing data, both discrete and continuous. The graphical modeling framework enables a joint probability distribution for the combined data, in which uncertainties from one model component are taken account of in other components. It is easily extensible and can be implemented in general purpose software. For example, the multiple imputation methods could be extended, in the way described by Gelman et al. (1998), to deal with situations in which several individual data sets are modeled, some with certain variables completely absent and others with intermittent nonresponse. Survey-level covariates may be needed to explain systematic biases from each survey, and a hierarchical model may be needed to represent the correlation structure. However, in routine application of graphical models, the structure of the influence relationships must be considered carefully, as we showed by demonstrating the need for “cutting” the dependency of the missing covariates on the observed outcome.

A similar situation of synthesizing data sets with different sets of covariates arises in “2-phase” or 2-stage designs (White, 1982). These are used to improve efficiency, commonly of case–control studies, in situations where covariate collection is expensive. Individuals are classified into strata defined by combinations of an outcome and an exposure of interest, and samples of individuals are selected from each stratum for further covariate collection. By oversampling from the smaller strata and using appropriate methods for inference (Breslow and Holubkov, 1997,), efficiency can be increased. Only the smaller of the 2 data sets, with full covariate information, is analyzed directly, but the information on the exposure-outcome relationship in the larger data set is used indirectly when constructing a model to account for the sampling design. In this paper, we have described how this information can be used directly, in a situation where the design of the smaller data set is not based on the larger data set. The improvement in power comes from constructing an expanded data set on which to estimate the model, rather than from the design of the sample.

By synthesizing data from different sources, inferences can be improved. In our application, we were able to make the most of the strengths of each data set: the large sample size of the administrative data and the more detailed covariate collection of the survey data. However, any analysis of combinations of data, including meta-analysis, is not recommended when the data sets being combined are too heterogeneous. Here, “heterogeneity” is used as a general term encompassing differences in study design, different variables collected, differences in the underlying populations, or systematically different responses to variables which are nominally the same. Ideally, the reasons for heterogeneity should be represented as extra parameters in the model. If these are not identifiable from data, then hierarchical models, as in Gelman et al. (1998), can often help to account for the extra uncertainty incurred by combining the data sets. But if the data sets are too heterogeneous, this extra uncertainty will lose any advantage gained by combining them. For example, if covariates are missing in one data set, then there needs to be sufficient complete data in other data sets to enable their imputation. In our application, if sufficient predictors of individual smoking and ethnicity had not been available from population data, then data synthesis would have been futile. Further work in this area should focus on “calibrating” specific methods of data synthesis to assess the potential benefit of the synthesis before analysis. For example, this may involve determining the amount of covariate information required to inform a multiple imputation before the imputation gives any benefit.

FUNDING

Economic and Social Research Council (RES-576-25-5003); Department of Health (PHI/03/C1/045). Funding to pay the Open Access publication charges for this article was provided by the Medical Research Council (U.1052.00.008, U.1052.00.001).