Statistical monitoring of clinical trials with multivariate response and/or multiple arms: a flexible approach

Abstract

Randomized clinical trials with a multivariate response and/or multiple treatment arms are increasingly common, in part because of their efficiency and a greater concern about balancing risks with benefits. In some trials, the specific types and magnitudes of treatment group differences that would warrant early termination cannot easily be specified prior to the onset of the trial and/or could change as the trial progresses. This underscores the need for more flexible monitoring methods than traditional approaches. This paper extends the repeated confidence bands approach for interim monitoring to more general settings where there can be a multivariate response and/or multiple treatment arms and where the metrics for comparing treatment groups can change during the conduct of the trial. We illustrate the approach using the results of a recent AIDS clinical trial and examine its efficiency and robustness via simulation.

1. INTRODUCTION

Preplanned interim analyses are commonly conducted in clinical trials to monitor subject safety and the evolving efficacy of treatments (see, e.g. Whitehead, 1997; Jennison and Turnbull, 2000; Ellenberg and others, 2002; Proschan and others, 2006). Clinical trials with multiple end points and/or multiple arms are increasingly common, in part because of their efficiency and a greater concern about balancing risks with benefits.

However, in most such trials, formal stopping criteria are based on a single end point, even though 2 or more end points will be major determinants of whether and how the treatment would be used in practice. When formal stopping guidelines are based on a single end point, independent Data and Safety Monitoring Committees (DSMB) can be put in the precarious position of having to impose their own trade-offs between the end point which is formally monitored and other key study end points. For example, the recently completed placebo-controlled Hypertension in the Very Early Trial (HYVET) (Beckett and others, 2008) was stopped “on ethical grounds” because the secondary end point of overall mortality favored the new treatment, even though the primary end point (stroke), while suggestive of a benefit of the treatment, did not achieve the formal stopping boundary. If the stopping guidelines for this study had included both of these end points, it is likely that formal stopping boundaries would have been reached, making the DSMB's job easier and establishing the statistical superiority of the new treatment. This example suggests that interim stopping guidelines based on 2 key end points that would largely determine the ultimate use of a new treatment could lead to improved monitoring of a trial.

Monitoring multiple end points can be critical when there are concerns that a new treatment might be beneficial with respect to one end point but harmful with respect to another. For example, a placebo-controlled clinical trial evaluating the efficacy of testosterone supplements on vitality might also monitor the possible (adverse) effect of testosterone on the risk of prostate cancer (Testosterone and Aging: Clinical Research Directions, 2003). In monitoring such trials, evidence that the treatment may increase prostate cancer risk usually would offset any benefits on vitality. Since the interim results of such a trial would typically not be able to rule out an increased prostate cancer risk, a natural way to monitor the trial would be to a priori determine the range of possible joint effects of the treatment on cancer risk and vitality that would justify continuation of the trial and then base the interim analyses on a comparison of the confidence region for the true value of this bivariate outcome with the a priori range of values.

The timing of treatment effects on study end points can be important. For example, in a trial of severe emphysema comparing medical intervention to surgery (National Emphysema Treatment Trial Research Group, 2003), in which mortality and exercise capacity were primary end points, it was expected in advance that mortality in the surgery group might initially be greater than that in the medical intervention arm but that too large of an initial excess would not be acceptable. Thus, an appropriate interim monitoring plan would recognize that some initial difference in mortality would be acceptable but would allow for termination if this was too large.

As noted by Hughes (1993) and others, difficulties in monitoring trials also arise when there are more than 2 treatment arms, including a control group and several different experimental treatments or a control group and different dosage levels of the same experimental treatment.

Most published approaches on statistical monitoring for studies with multivariate outcomes typically require specifying a parametric underlying probability model and are based on inferences about a small number of the model parameters. Jennison and Turnbull (2000) review approaches for the interim analyses of studies with a multivariate end point and/or multiple arms, including those presented in Hughes (1993), Cook (1994), Proschan and others (1994), Betensky (1996), and Williams (1996). More recent papers include Hellmich (2001) and Kosorok and others (2004). In contrast, Wei and others (1990) present a procedure based on the generalized estimating equations (GEE) (cf., Diggle and others, 1994) for the analysis of repeated measurements by considering a parametric form of the response mean over time that does not require a specified probabilistic model, which can be extended to studies with multivariate outcomes. However, there are practical situations where relatively little may be known at the outset about the nature and magnitude of the expected treatment differences, the clinical significance of certain types of differences in the outcome measures, or the structure of the correlation between the multiple end points. Thus, at the design stage there is uncertainty about the functional form of the likely treatment effects, making it difficult to specify an underlying probability model.

In an attempt to provide an alternative for statistical monitoring of clinical trials with multiple end points/arms, we extend the repeated confidence bands approach (Hu and Lagakos, 1999a, b) to multivariate settings. The proposed approach does not require the use of a prespecified stopping rule but can be used to form stopping boundaries if desired. That is, a decision to stop or continue a trial can be based on the totality of evidence at an interim analysis, without a prespecified stopping rule, and the resulting repeated confidence bands retain their frequentist properties. Such flexibility can be very useful in more complex settings such as the examples described above.

The proposed approach does not rely on a prespecified functional form of the target function. With a repeated measures end point, it reduces to a multivariate version of the procedure proposed in Wei and others (1990) when the average response over time is assumed to have a parametric form. In addition, the approach is well suited for a study where the metric of interest changes as the study proceeds. For example, consider a clinical trial focusing on the mean function of the study outcome variable. The multivariate repeated confidence bands (MRCBs) approach may be applied as follows. Lacking knowledge of the target function, the first interim review can be based on a nonparametric estimator of the mean function to provide a nonparametric confidence band; assuming that there is sufficient information from the first review to specify the mean into a parametric form, say, a linear function, the following reviews can then focus on the slope of the target function and provide confidence intervals of the slope.

We organize the rest of the paper as follows. Section 2 introduces the definition of MRCBs and constructs a class of approximate MRCBs. We show in Section 3 how to implement the MRCBs approach in several applications, through using the data from a recent AIDS clinical trial. Section 4 presents a simulation study to evaluate the efficiency and robustness of the MRCBs approach via comparing them with existing approaches. Section 5 concludes the paper with some remarks.

2. MULTIVARIATE REPEATED CONFIDENCE BANDS

We begin this section with a general definition of MRCBs and then discuss the construction of a particular class of approximate MRCBs.

2.1. Notation and definition

Consider a clinical trial that begins at calendar time 0 and plans to sequentially enroll up to n independent subjects and to follow each for S time units from enrollment. Denote the response of subject i by $\{X_i\left(s\right),s\in [0,S]\}$ and assume that $X_i(·)$ is scheduled to be observed at times in some set  ⊆[0,S]. Here , a predetermined subset of $[0,S]$, contains all the time points of interest; it can be a subinterval, a set of a finite number of times, or a set of subintervals of $[0,S]$.

Suppose the statistical goal of the study is to make inferences on a J-dimensional target function ${\mu }_0\left(s\right)$ for s ∈. For example, in clinical trials with 2 biological marker end points, ${\mu }_0(·)$ might denote the 2-dimensional mean vector function of these markers at some specified time points. In the testosterone example, ${\mu }_0(·)$ might denote the 2-dimensional vector consisting of the treatment effects on the distribution of time to prostate cancer and on mean vitality at specific time points. Or, in a 3-arm clinical trial with a survival end point, ${\mu }_0(·)$ can be 3-dimensional with components representing the pairwise differences between the treatment arms with respect to the outcome. Throughout the paper, we use t for the calendar (or external) time since the study opens for enrollment and s for the study (or internal) time since a subject enters the study.

Suppose that K study analyses, including $(K-1)$ interim reviews and the final analysis, are planned at the prespecified calendar times $T_1,\dots ,T_K$, where $0<T_1\hspace{0.17em}<\hspace{0.17em}\cdots \hspace{0.17em}<\hspace{0.17em}{T}_K$. Let _k denote the available information from the trial up to time $T_k$, where ₁⊆⋯⊆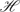_K. For example, if subject i enters the study before T_k, 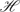_k includes his entry time, say $a_i$, and the response information $X_i\left(s\right)$ for those s ∈  such that $0\le s\le T_k-a_i$.

Consider the functional space of all possible functions ${\mu }_0(·)$ defined over . A sequence of random subsets of this space, denoted by {B_k=B_k(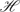_k):k=1,…,K}, is called a set of level $(1-\alpha )$ MRCBs for ${\mu }_0(·)$ if

That is, the probability that ${\mu }_0(·)$ is wholly contained in all the K sets $\{B_k:k=1,\dots ,K\}$ is at least $(1-\alpha )$. This definition is a natural generalization of the repeated confidence intervals of a finite-dimensional parameter given in Jennison and Turnbull (1989) and the repeated confidence bands considered in Hu and Lagakos (1999a, b). Following the notion of Lan and DeMets (1983), we define the spending function corresponding to $\{B_k:k=1,\dots ,K\}$ as $\{{\pi }_1,\dots ,{\pi }_K\}$ with ${\sum }_{k=1}^K{\pi }_k\le \alpha$ and

(2.1)

Here the MRCBs determine the spending function, but as we will see, one can alternatively define a spending function and then determine specific {B_k:k=1,…,K} that form a set of MRCBs.

Depending on the enrollment times $a_i$, $i=1,\dots ,n$, the response for some of the enrolled subjects may not be observed for all s ∈ . In some settings, we may wish to make an inference about ${\mu }_0(·)$ for only a subset of , say, adaptively selected based on the information available at previous interim analyses. We thus let _k ⊆  denote the domain of interest at the kth review. This can be accommodated in the above definition by defining $B_k$ to be noninformative about ${\mu }_0\left(s\right)$ for s ∉ _k and with the following adjustment for the adaptive domains. 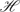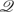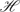Specifically, consider the domain of interest for ${\mu }_0(·)$ at the kth analysis as a random subset of based on _k−1 and the current enrollment information _k, denoted by _k = _k(_k−1,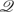_k). The information contained in 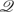_k is independent of the response information collected at time $T_k$ conditional on 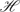_k−1, where  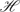0 = ∅, the empty set. To maintain the nominal confidence level, the MRCBs can be chosen sequentially such that, for $k=1,\dots ,K$,

(2.2)

This can be justified with arguments similar to the ones used in Section 3 of Hu and Lagakos (1999b). With adaptive domains, one can utilize the information available at the previous interim reviews to gain flexibility and efficiency in subsequent analyses.

2.2. Construction of MRCBs

Denote an estimator of the target function ${\mu }_0(·)$ based on the information available at calendar time t by 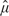n(·;t). Assume that the KJ-dimensional vector process with the kth J-dimensional vector component $(k=1,2,\dots ,K)$ converges weakly for s ∈  to a KJ-dimensional and zero-mean Gaussian process with covariance function

(2.3)

where $\text{cov}(s,u{)}_{kl}$ is the $J\times J$ asymptotic covariance matrix of and , for $k,l=1,\dots ,K$. We provide in the following section and in Section B of the supplementary material, available at Biostatistics online (http://www.biostatistics.oxfordjournals.org), examples of 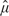n(·;t) in several applications based on estimators discussed in Hu and Lagakos (2007) and the associated consistent estimators of the covariance function in (2.3).

A class of approximate MRCBs can be constructed as follows. For any function $\nu (·)$ in the space of possible ${\mu }_0(·)$ and $k=1,\dots ,K$, define

(2.4)

where $w_n(s;T_k)$ is a weight matrix function which can be deterministic or data dependent with a deterministic limit $w(s;T_k)$ in probability. Let $B_k$ be

(2.5)

where $\Vert ·{\Vert }_k$ is a norm in ${ℛ}^J$ and can be selected adaptively based on 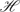_k−1 and 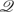_k. Provided that the critical values $c_1,\dots ,c_k$ are determined recursively such that (2.1) is satisfied, $\{B_k:k=1,\dots ,K\}$ defined in (2.5) is then a set of approximate MRCBs with level $(1-\alpha )$. When the domains _k are selected adaptively, we determine the critical values $c_k$ based on (2.2).

Two natural choices of the weight matrix $w_n(s;T_k)$ in (2.4) are S_n(s;T_k) = 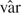(s;T_k)^−1/2 and . Here 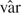(s;T_k) is a consistent estimator of $\text{var}(s;T_k)=\text{cov}(s,s{)}_{kk}$ as defined in (2.3) and $\text{diag}\left[A\right]$ is the diagonal matrix with the diagonal elements of the matrix A. Two choices for the norm in (2.5) are the max-norm $\Vert b{\Vert }_k={max}_j\left\{\right|b_j\left|\right\}$ and $L_2$-norm $\Vert b{\Vert }_k=({\sum }_{j=1}^J{b}_j^2{)}^{1/2}$. Both norms weight different components equally. Norms with different weights for different components may be more suitable in some situations, such as when investigators wish to focus on only some components of the target function at a particular analysis. A special case is a multiarm trial which has one or more of the original arms terminated at the previous analyses.

Different combinations of choices of weight matrix and norm may lead to MRCBs of different features. For instance, a preliminary simulation study suggests that using $S_n(s;T_k)$ with the $L_2$-norm may give more efficient confidence regions when the response components are correlated than using it with the max-norm or than using $A_n(s;T_k)$ in the confidence region construction. On the other hand, an advantage of using the max-norm is that each component of the MRCBs based on the weight matrix $A_n(s;T_k)$ is a set of $(1-\alpha )$ repeated confidence bands for the corresponding component of ${\mu }_0(·)$. As noted in Cook (1994) and Williams (1996), this feature may be desirable for interpretation.

In principle, we could choose the critical values $c_k$ in the construction of MRCBs to approximate (2.1) based on the limiting multivariate Gaussian process of the estimator 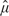_n(·;T_k) with $k=1,\dots ,K$. The computing, however, is generally difficult except in special cases, such as when is finite (i.e. situations with repeated measures or periodic observations), and the limiting distribution is then multivariate normal (Hu and Lagakos, 1999a). Thus, similarly to Hu and Lagakos (1999b), we adapt the resampling method used in Lin and others (1993) to determine $c_k$. The algorithm is presented in the Appendix.

3. ILLUSTRATIVE EXAMPLES

We illustrate the implementation and flexibility of the proposed approach by retrospectively conducting group sequential analyses of results from a study conducted by the AIDS Clinical Trials Group (ACTG); substantive details can be found in Gulick and others (2000). We form MRCBs using nonparametric estimators of ${\mu }_0(·)$, but the same ideas apply when ${\mu }_0(·)$ is assumed to depend on a finite-dimensional parameter θ, say ${\mu }_0(·;\theta )$, and estimated by 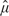n(·;t)=μ₀(·;(t)), where (t) is an estimator of θ based on the information available at calendar time t.

The trial enrolled 277 HIV-infected subjects from 42 units of the ACTG. The subjects were randomized to receive a double antiretroviral (saquinavir and ritonavir/nelfinavir) with either delavirdine and/or adefovir. The key study outcomes were CD4 cell count, HIV viral load as measured by RNA, and toxicities. The immunologic and virologic outcomes were evaluated at weeks 0 (randomization), $4,8,12,16$, and 24, and toxicities were captured in real time. The primary efficacy end points of the study were comparisons of treatment arms with respect to CD4 cell count and viral load at the week 16 study visit.

In the following, we present several applications of the proposed approach to illustrate how it might be applied. In all cases, we assume that there are 2 interim analyses and a final analysis of the trial at $T_1=195$, $T_2=330$, and $T_3=499$ days after the trial was begun, approximately corresponding to the actual times the trial was monitored. We take $\alpha =0.05$ and the conservative O'Brien–Fleming type of spending function, which for these analysis times lead to ${\pi }_1=0.0017$, ${\pi }_2=0.0142$, and ${\pi }_3=0.0341$.

3.1. Assessing individual treatments

For the purpose of this example, we first focus on evaluating the immunologic and virologic outcomes for subjects randomized to receive adefovir, based on CD4 cell count and the indicator of whether or not HIV RNA was undetectable (a value below 500 copies/ml). Thus, the target function ${\mu }_0(·)$ denotes the 2-dimensional vector of mean CD4 cell count and the probability of an undetectable viral load, with domain at the study visit times, that is, {0,4,8,12,16,24}. We estimate ${\mu }_0(·)$ at each study visit by the sample mean of observed values for those subjects who had been on the study long enough to have an observation at that time. After standardization, this estimator converges to a multivariate normal distribution. The algorithm for finding the MRCBs (see Appendix) reduces to sampling directly from the estimated multivariate normal distribution.

We considered 2 ways to construct the MRCBs, one using (2.4) with weight matrix S_n(s;T_k) = 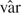(s;T_k)−1/2 and the $L_2$-norm and the other using the weight matrix with the max-norm. A general expression for 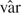(s;T_k) is presented in Section B of the supplementary material, available at Biostatistics online. Because it could be determined that there would be very few subjects with a week 24 visit at the time of the first interim analysis, the MRCBs for this analysis were restricted to the domain ₁={0,4,8,12,16}. The critical values used to form the MRCBs were $(c_1,c_2,c_3)=(3.68,3.13,2.76)$ with weight matrix $S_n$ and $(c_1,c_2,c_3)=(3.92,3.39,3.0)$ with weight matrix $A_n$. By monitoring the resampling algorithm used to compute $(c_1,c_2,c_3)$, we found that values stabilized after 3000 simulated samples, and thus we used this number of simulated samples to evaluate critical values throughout this section.

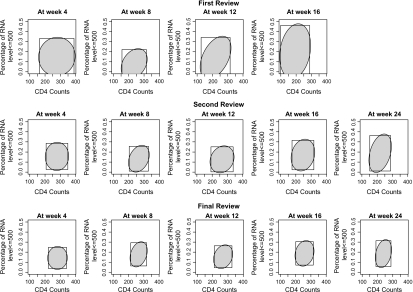
For each of the 3 analyses, the resulting MRCBs for the different visit times are shown in Figure 1. As expected, the confidence regions for each study visit time become more compact with successive analyses. The 2 choices of weights give similar confidence regions. Those based on $A_n(s;T_k)$ can be more readily used to construct separate confidence intervals for mean CD4 cell count and the probability of an undetectable viral load, which can facilitate summarizing the data. Although the oval MRCBs based on $S_n(s;T_k)$ can be rectangularized to achieve the same purpose, this would in general lead to more conservative intervals, especially as these MRCBs become less rectangular in shape.

Fig. 1.

MRCBs with CD4 and RNA outcomes of the pooled adefovir treatment group (shaded ellipses: using $S_n(·;T_k)$ with $L_2$-norm; rectangles: using $A_n(·;T_k)$ with max-norm).

Both components of the target function are nonnegative. However, the obtained confidence regions at the first review include negative values. This could be avoided by first constructing confidence regions for $(\text{log}{\mu }_{01}(·),\text{log}{\mu }_{02}(·){)}^{{}^{\prime }}$ and then transforming them to obtain confidence regions for the target function ${\mu }_0(·)$, analogous to a common practice when estimating a nonnegative parameter. Similar transformations can be applied for other types of constraints to some or all of the components of ${\mu }_0(·)$.

If we had wanted to also include a subject's cumulative number of serious toxicities over time into the interim analysis, we could have augmented the target function ${\mu }_0(·)$ by adding this component and estimated it by

(3.1)

where $X_{3i}\left(s\right)$ denotes the cumulative number of toxicities occurring to subject i by internal time s and ${\delta }_{3i}(s;t)$ indicates whether or not this observation is available at calendar time t. Note that 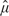_3,n(s;t) in (3.1) is the Nelson–Aalen estimator for the cumulative intensity function based on the information collected up to the external time t (Hu and Lagakos, 1999b). Because toxicity data are collected in real time, the full domain of interest becomes  = [0,24] weeks, with CD4 count and HIV RNA level available only on the subset $\{0,4,8,12,16,24\}$ weeks. This can be accommodated in the construction of the MRCBs by putting all weights in the norm on the toxicity component at study times other than $\{0,4,8,12,16,24\}$.

3.2. Comparing treatment groups

To compare 2 treatment groups in both efficacy and safety, we chose the target function to be the difference between the pooled delaviridine and adefovir groups with respect to mean functions of the 3 end points. To illustrate the flexibility of the MRCBs approach, we used the domain ₁={0,4,8,12,16} and ₂={0,4,8,12,16,24} at the first 2 interim analyses and the single time point week 16 at the final analysis, that is, ₃={16}. This allows us to monitor the difference of the entire mean functions before the final analysis and to concentrate on the difference between the treatment groups at week 16 (the study's primary end point) at the final analysis. Also, in the original study, the second interim analysis focused on toxicity but not on efficacy. To accommodate this we choose the norm at the second interim analysis to place all weight on the toxicity end point.

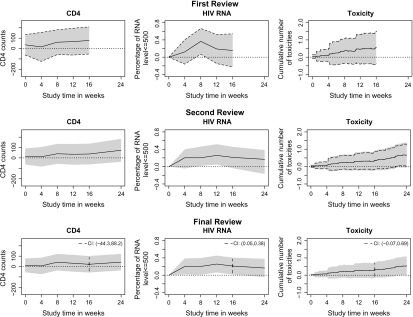
The MRCBs obtained for comparing the pooled delavirdine and adefovir groups, using the $A_n(s;T_k)$ weight matrix, are presented with dashed curves in Figure 2. At the time of the first interim analysis, the delavirdine group had not only somewhat better CD4 and viral load response than the adefovir group but also somewhat higher rates of toxicity. The confidence bands generally included possible differences in the opposite directions. At the time of the second interim analysis, the data suggested a higher cumulative toxicity rate in the delavirdine group at weeks $8,12$, and 16. At the final analysis, where the domain for comparison was study week 16, the confidence intervals indicate a significantly improved rate of undetectable viral load with the delavirdine group than the adefovir group and no significant difference between the groups with respect to CD4 cell count or cumulative toxicities by week 16. The confidence intervals at the final review were close to the corresponding nominal $95\%$ confidence intervals $(-42.9,86.8)$, $(0.05,0.37)$, and $(-0.06,0.68)$, based on which Gulick and others (2000) made their final inferences.

Fig. 2.

MRCBs with difference in CD4, HIV RNA, and toxicity between the pooled delavirdine and the pooled adefovir treatment groups (shaded regions: all 3 end points over the full domain were considered at each review; dashed curves: the 3 end points were considered with the full domain except week 24 at the first review, the second review focused on the toxicity outcome, and the third review considered the 3 end points at time week 16; solid curves: point estimates; dotted lines: line $y=0$).

An alternative monitoring strategy for this study would be to assess all the 3 end points over the full domain at each analysis. The resulting MRCBs are given with the shaded regions in Figure 2. Note that, while the monitoring boundaries at the first review are the same as the ones associated with the analysis described above, those at the second and the third reviews were observably wider, reflecting that better efficiency can be achieved when focusing on a more restricted set of time points or study end points.

The methods presented above can also be used to monitor trials with multiple arms, by taking the target function ${\mu }_0(·)$ to be the vector with the components being the pairwise differences of the treatment groups. We can then apply the MRCBs approach similarly to the above procedure.

4. SIMULATION STUDY

We undertook a simulation study to examine the performance of the MRCBs approach and to compare it with parametric procedures designed for situations with repeated measures. We simulated a randomized trial with $N=300$ subjects and 2 treatment groups (A and B), with interim reviews at $T_1=30$ and $T_2=45$ weeks after the start of the study and a final analysis at $T_3=54$ weeks. Subjects were followed for 24 weeks and evaluated for a bivariate response at $0,4,8,12,16$, and 24 weeks after entry. We generated the subjects’ entry times (in weeks) from the uniform distribution $U(0,30)$. The study response, denoted by $X(·)$, was generated from a Gaussian process with mean $m_{\text{trt}}(·)$, each component of which is a polynomial function, and

The null hypothesis $H_0:m_A(·)=m_B(·)$ was tested with the nominal 5% type I error, using the O'Brien–Fleming type of spending function ${\pi }_1=0.0056$, ${\pi }_2=0.018$, and ${\pi }_3=0.0264$.

We took the target function ${\mu }_0\left(s\right)=m_A\left(s\right)-m_B\left(s\right)$ for $s\in (0,24]$ and implemented the MRCBs approach with weight $A_n(·;T_k)$ and the max-norm. The testing procedure based on the MRCBs is to check whether the confidence band fully contains the zero function at each review time.

For comparison purposes, we also implemented 5 alternative procedures: we conducted group sequential tests based on the Hotelling's $T^2$ testing procedure and using response at study week 16 or 24, denoted in the following by “GST16” or “GST24,” respectively; we considered an extension of the approach proposed by Wei and others (1990) to the bivariate situations and applied it to the current 2-sample problem by specifying the means into linear functions with a common intercept term and assuming a common covariance structure for the 2 groups with (i) the independence working model (as suggested in Wei and others, 1990), (ii) the true covariance matrix, or (iii) the pooled sample covariance matrix, denoted by “WSL1,” “WSL2,” or “WSL3,” respectively. The WSL3 procedure was comparable to the WSL2 when the sample size is relatively large, while the WSL2 is not applicable in practice but was considered to provide an ideal reference.

We varied the values of the coefficients in the mean functions $m_{\text{trt}}(·)$ to give the following different settings for evaluating the different approaches with respect to efficiency and robustness:

Scenario A: $m_A\left(s\right)=m_B\left(s\right)=(0.4s/24,-0.4s/24{)}^{{}^{\prime }}$.

Scenario B: $m_A\left(s\right)=(0.8s/24,-0.8s/24{)}^{{}^{\prime }}$ and $m_B\left(s\right)=(0.4s/24,-0.4s/24{)}^{{}^{\prime }}$.

Scenario C: $m_A\left(s\right)=(3s/24-6(s/24{)}^2+3(s/24{)}^3,-3s/24+6(s/24{)}^2-3(s/24{)}^3{)}^{{}^{\prime }}$ and $m_B\left(s\right)=(0,0{)}^{{}^{\prime }}$.

Each of the 3 experimental settings were simulated 1000 times. We examined the percentages of rejecting $H_0$ at the interim reviews (at times $T_1$ and T₂) and the final analysis (at time T₃) based on the MRCBs and the 5 reference procedures. The 6 monitoring procedures in Scenario A yielded type I error rates very close to the nominal 5% level. Table 1 presents the rejection rates at the 3 analyses in Scenarios B and C. Unlike the other procedures, the overall power of the MRCBs approach remains very high in both scenarios.

Table 1.

Empirical probabilities of rejecting H₀ in simulated trials with 2 interim reviews (at times T₁ and T₂) and the final analysis (at time T₃)

	Scenario B				Scenario C
Procedure	T1	T2	T3	Overall	T1	T2	T3	Overall
MRCB	0.139	0.559	0.222	0.920	0.679	0.259	0.038	0.976
GST16	0.120	0.432	0.131	0.683	0.088	0.311	0.142	0.541
GST24	0.142	0.668	0.160	0.970	0.008	0.018	0.026	0.052
WSL1	0.163	0.498	0.187	0.848	0.340	0.211	0.061	0.612
WSL2	0.699	0.298	0.003	1.00	0.190	0.015	0.053	0.258
WSL3	0.284	0.709	0.007	1.00	0.143	0.082	0.078	0.303

MRCB: multivariate repeated confidence bands approach with weight A_n(·;T_k) and the max-norm. GST16 and GST24: group sequential procedures based on Hotelling's T² test on response at weeks 16 and 24. WSL1, WSL2, and WSL3: extensions of the approach of Wei and others with linear means, using the identity, the true, or the pooled sample covariance matrices.

Scenario B, in which the 2 treatment groups had linear mean functions and the WSL procedures had the correct functional form, was designed to examine the efficiency of the MRCBs approach. In Scenario B, the MRCBs approach is close to the GST24, which tested on the largest difference between the 2 groups and performed similarly to the WSL3 and better than the WSL1 and the GST16.

Table 1 indicates that the performance of MRCBs is better than the WSL and the GST procedures in Scenario C, where the WSL used a misspecified functional form of the means and the GST did not necessarily test the largest difference between the 2 groups. For illustration, Figure 3 presents 2 selected replicates of the simulation with Scenario C. The figure shows the resulting rejection boundaries of the MRCBs approach and the alternative procedures, along with the estimates on which the testing procedures were based. The WSL procedures in the scenario are to check whether the estimates of the slope β of the difference ${\mu }_0(·)$ are contained in the resulting acceptance intervals, equivalent to checking whether the corresponding estimates of ${\mu }_0(·)$, which are in the form of 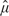₀(s)=s with the GEE estimator of β, are within the resulting acceptance region.

Fig. 3.

Rejection boundaries of MRCBs, GST, and WSL procedures and the associated estimates (solid curves: the true difference function ${\mu }_0(·)$; dotted curves: the upper and lower rejection boundaries of MRCBs; dashed curves: MRCB-based estimates; shaded regions: the acceptance regions of the WSL1 approach; dashed-dotted-dashed curves: WSL-based estimates; solid vertical lines: the acceptance intervals of GST16 or GST24; triangle/circle dots: GST16/GST24-based estimates).

The MRCB approach with the natural nonparametric estimator of ${\mu }_0(·)$ equals the GST16 or GST24 when the domain of interest of ${\mu }_0(·)$ is the single time week 16 or 24. When ${\mu }_0(·)$ is specified into μ₀(·;β), such as in Scenario B, and (t) is the GEE-based estimator of β evaluable at the external time t, the proposed approach with the estimator μ₀(·;(t)) in the construction of MRCBs is close to the corresponding WSL using the pooled sample covariance; the 2 procedures are equivalent when ${\mu }_0(·)$ is linear.

5. DISCUSSION

This paper extends the repeated confidence bands approach (Hu and Lagakos, 1999a, b) to multivariate settings, to monitor clinical trials with multivariate response or more than 2 arms. The associated analysis can provide a comprehensive summary of safety and efficacy outcomes over time. The proposed MRCBs can be used to provide formal stopping guidelines, just as traditional methods, but, as with repeated confidence intervals (see, e.g. Jennison and Turnbull, 2000), need not to be linked to a stopping rule. Rather, monitoring committees can use whatever criteria they wish to decide whether to stop a study, and if they do, the resulting MRCBs would provide valid confidence regions that are adjusted for the multiple analyses that have been undertaken.

The illustrative examples in Section 3 demonstrate advantages of the MRCBs over conventional approaches. One is that different time domains or different sets of end points can be used at different analyses. This allows the DSMB of a trial to assess evolving treatment effects over internal time and have valid intervals for the treatment differences, but then focus on the treatment differences at a particular time point (week 16 in the example) at the final analysis. Using methods analogous to Hu and Lagakos (1999b), the domains for a future analysis can be determined adaptively based on results at the current analysis.

Another advantage is that the provision of a confidence region for 2 end points can allow for monitoring that more closely reflects how a treatment's use in practice will eventually be determined. For example, had the HYVET trial (Beckett and others, 2008) monitored both strokes and mortality as the primary end points, using a predetermined region for hypothetical differences that would correspond to the treatment being preferable, worse, or equivalent to the control, then the trial could have reached a formal stopping boundary because of the suggestive evidence of a benefit of the treatment with respect to both end points.

A major concern about any flexible approach is its efficiency and thus its usefulness in practice. Our simulation study indicates that, compared to 2 approaches on a small number of parameters, the MRCBs approach has acceptable power in the simulated situations, while it does not require a model specification and thus enjoys robustness against possible model misspecification. Moreover, with the target function specified into parametric forms, the MRCBs approach can reduce to the commonly used monitoring procedures.

Several further investigations would be of theoretical and practical interest. One is to explore how to adapt a parametric model as the study proceeds, in order to improve efficiency in the situations where the nature of the outcome measures is unknown at the outset of the trial but may become clearer as the study progresses. Another is to extend the current methods to allow the review times $T_1,\dots ,T_K$ to be adaptively determined. A third is to explore the resulting MRCBs with the critical values $c_k$ in (2.5) depending on the study time s. Finally, the approach can be readily extended to incorporate covariates which, among other things, can be used to assess the dependence of the observation mechanism and the responses.

FUNDING

National Institutes of Health of USA (AI24643 to S.W.L., AI56995 to X.J.H.); Natural Sciences and Engineering Research Council of Canada (RGPIN262823 to X.J.H.).

Appendix: resampling algorithm to determine $c_k$

Suppose that 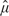n(s;T_k) is consistent and converges weakly as given in Section 2.2 and assume that can be expressed as, or is asymptotically equivalent to,

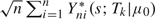where $Y_{ni}(s;T_k|{\mu }_0)$ satisfy the following conditions. The quantity is asymptotically equivalent to , where $Y_{ni}^{*}(s;T_k|{\mu }_0)$ are independent and identically distributed. In addition,

converges to zero in probability for any s, u, and k. It can then be shown that the processes

have the same joint limiting distribution as $W_n(s;T_k|{\mu }_0)$ conditional on the available data, where $Z_i$ are independent standard normal random variables. A proof of this statement is provided in Section A of the supplementary material to this paper, available at Biostatistics online.

Since realizations of (s;T_k) given the observed data can be computer generated, we can use them to obtain approximates of the critical values $c_k$. Provided that $c_1,\dots ,c_{k-1}$ are determined, we choose $c_k$ as follows.

Step A: Generate $M_k$ sets of independent realizations of $Z_i$ for $i=1,\dots ,n$ and compute , for $m=1,\dots ,M_k$.

Step B: Define for $l=1,\dots ,k$ and select c_k such that a proportion ${\pi }_k$ of the $M_k$ realizations satisfy $L_n(T_l{)}_{\left(m\right)}\le c_l$ for $1\le l\le k-1$ and $L_n(T_k{)}_{\left(m\right)}\hspace{0.17em}>\hspace{0.17em}{c}_k$.

The choice of $M_1,\dots ,M_K$ depends in part on the number of interim analyses and the selected spending function. We suggest to monitor the resulting values of $c_k$ periodically as the numbers of simulations increase and to use the corresponding $M_k$ and the associated $c_k$ when the values $c_k$ become stable.