Statistical independence of the colocalized association signals for type 1 diabetes and RPS26 gene expression on chromosome 12q13

Abstract

Following the recent success of genome-wide association studies in uncovering disease-associated genetic variants, the next challenge is to understand how these variants affect downstream pathways. The most proximal trait to a disease-associated variant, most commonly a single nucleotide polymorphism (SNP), is differential gene expression due to the cis effect of SNP alleles on transcription, translation, and/or splicing gene expression quantitative trait loci (eQTL). Several genome-wide SNP–gene expression association studies have already provided convincing evidence of widespread association of eQTLs. As a consequence, some eQTL associations are found in the same genomic region as a disease variant, either as a coincidence or a causal relationship. Cis-regulation of RPS26 gene expression and a type 1 diabetes (T1D) susceptibility locus have been colocalized to the 12q13 genomic region. A recent study has also suggested RPS26 as the most likely susceptibility gene for T1D in this genomic region. However, it is still not clear whether this colocalization is the result of chance alone or if RPS26 expression is directly correlated with T1D susceptibility, and therefore, potentially causal. Here, we derive and apply a statistical test of this hypothesis. We conclude that RPS26 expression is unlikely to be the molecular trait responsible for T1D susceptibility at this locus, at least not in a direct, linear connection.

1. INTRODUCTION

Genome-wide association studies have successfully linked a large number of genetic variants with susceptibility to common diseases (McCarthy and others, 2008). However, these findings need to be followed up in order to understand the functional role of these susceptibility alleles at the molecular level. One way to address this follow-up is to correlate measures of gene expression, or alternative measurements at the protein level, with common susceptibility variants. Owing to the development of affordable genome-wide gene expression analysis and single nucleotide polymorphism (SNP) genotyping technologies, it has recently become feasible to scan the genome for variants that correlate with the expression of nearby genes (eQTLs), affecting either the overall transcription levels or the relative amounts of splice variants. Recent studies have already provided evidence of widespread association of eQTLs with SNPs (Morley and others, 2004; Dixon and others, 2007; Goring and others, 2007; Moffatt and others, 2007; Emilsson and others, 2008). As a consequence, some gene expression quantitative trait loci (eQTL) associations are found in the same genomic region as a disease variant.

An illustration of this example is the colocalization of association signals for type 1 diabetes (T1D) (Todd and others, 2007) and the RPS26 eQTL (Morley and others, 2004; Dixon and others, 2007) in the 12q13 genomic region. A recent study of eQTLs using human liver tissue samples combined with bioinformatic network analyses (Schadt and others, 2008) suggested RPS26 as the most likely T1D susceptibility gene in this chromosome region. Therefore, an obvious question is whether the T1D association signal is a consequence of the RPS26 eQTL. If RPS26 expression is the driving factor for T1D susceptibility, then a genetic variant that affects RPS26 expression should also explain or correlate precisely with the T1D association. In that case, provided that the sample size is sufficient and that the causal variant has been identified, both T1D and eQTL association peaks should coincide. Given the limited fine mapping of both of these traits in this genomic region, the most likely hypothesis is that the actual causal variants, either for T1D or RPS26, remain unknown. Moreover, discrepancies between T1D and RPS26 association maps could result from limited sample sizes. We have designed a statistical test of the presence of a sole, shared causal variant for two overlapping association signals. Using combined data from approximately 4 000 case and 4 000 control British Juvenile Diabetes Research Foundation/Wellcome Trust (JDRF/WT) T1D samples and 387 Epstein Barr virus-transformed lymphoblastoid cell lines (LCLs) measured for RPS26 expression (Dixon and others, 2007), we conclude that the RPS26 eQTL expression is unlikely to be the molecular trait responsible for T1D susceptibility at this locus.

2. METHODS

2.1. Gene expression data

We obtained data from a genome-wide eQTL expression study (Dixon and others, 2007) using RNA from LCLs from unrelated individuals of British descent. RPS26 expression measurements were available for 387 samples. Gene expression measurements were obtained using the Affymetrix HG-U133 Plus 2.0 gene expression chip. Robust multi-array averaging (Irizarry and others, 2003) was applied to the data, providing a log-scale estimate of the gene expression level.

2.2. Case–control samples

Case–control samples were obtained from the UK JDRF/WT T1D case–control collection. Excluding missing data, the full genotype was available for 3 988 healthy controls and 4 141 T1D patients. Patients and healthy controls originated from England, Scotland, and Wales and were matched across 12 subregions of Great Britain.

2.3. SNP selection

For both the RPS26 gene expression study and the T1D case–control collection, genome-wide genotyping data were available. Additional fine-mapping SNP genotyping data were available for the T1D case–control samples. Initially, we restricted our study to SNPs present in both studies with highly significant p-values for T1D and RPS26 eQTL (p < 10⁻¹⁰ in both cases). This resulted in a set of 4 SNPs (rs705704, rs705699, rs1131017, and rs877636) with full genotype data in a case–control set of approximately 4000 cases and 4 000 controls. In addition, full genotype data for these 4 SNPs combined with RPS26 expression were available for the 387 unrelated individuals.

To apply the statistical test presented in this study, we further restricted our analysis to the subset of SNPs with a significant joint contribution to either the T1D status or the RPS26 gene expression measurement (and not simply to SNPs with marginally significant p-values). This was done using a stepwise forward regression approach, adding at each step the most significant SNP and stopping the procedure when the p-value associated with adding a SNP was higher than 0.05. We found that a single SNP could explain the T1D association (rs705704). Similarly, a single SNP (rs1131017) explained the RPS26 eQTL association.

2.4. Statistical test

We assumed a linear relationship between the unobserved causal variant Z, treated as a continuous trait, and the observed genotypes X. This assumption is valid in the context of a region in perfect linkage disequilibrium (Clayton and others, 2004), which is the case in this study: D′ =1 between our best T1D susceptibility (rs705704) and RPS26 gene expression (rs1131017) markers. Hence,

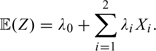This unknown genotype relates to both traits as follows:

where Y denotes the disease status. These equations together imply the following:

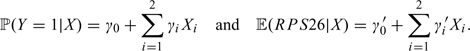Assuming that the link between the observed genotypes X and the unobserved causal variant Z is identical in both studies, the parameters γ_i, i = 1, 2, are a constant multiple of γ_i^′, i = 1, 2. Using the asymptotically Normal distribution of the estimated parameters, we computed the likelihood of the data under the null hypothesis of a sole causal variant and under the alternative and derived a likelihood ratio test statistic. The resulting statistic is distributed as χ² with n − 1 degrees of freedom, where n is the number of SNPs involved in the analysis (n = 2 in the case of this study).

In addition, in the common situation where the genotype effect on disease susceptibility is small, the link between Y and the observed genotypes X can be replaced with a logit function, thus avoiding a complex maximization under the constraint $\mathbb{P}(Y=1|X)=[{\gamma }_0+{\sum }_{i=1}^2{\gamma }_i{X}_i]\in [0,1]$.

2.5. Extension of the test for non linear genotype/phenotype correlations

Our test extends naturally to the nonlinear case by linking both traits to RPS26 using nonlinear relationships:

However, as a result of nonlinearity, both regressions (observed to unobserved genotypes and unobserved genotype to phenotype) could not be combined in a unique regression. Therefore, we used a missing data approach and incorporated the causal genotype Z in our model. Our modified null hypothesis becomes ${\lambda }_i={\lambda }_i^{\prime }$ for $i=0,1,2$.

An additional complexity originated from the fact that when explaining the T1D association, the full model was nearly unidentifiable, owing to the difficulty of differentiating a rare variant with a large effect from a common variant with a small effect. To address this issue, we used an informative Bayesian prior distribution on the minor allele frequency of the causal variant. For each set of values λ₀², we estimated the allele frequency 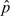in the study and used as prior a beta distribution on 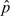centered at a minor allele frequency of 0.43 (a = 150, b = 200, mean 0.43, and standard deviation 0.026). Consequently, we report Bayes’ factors (Kass and Raftery, 1995) rather than p-values when using our extended test. Altering the prior distribution of the minor allele frequency p did not affect our estimates of the Bayes’ factors.

Estimating the Bayes’ factors amounted to estimating three versions of 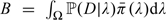(for the eQTL study, the case–control study, and both studies jointly), where 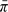denotes the normalized prior on the three-dimensional parameter λ. This estimation used a Monte Carlo Markov chain (MCMC) to sample the parameters λ_i, i = 0, 1, 2, from $\mathbb{P}\left(\lambda \right|D)$. The MCMC algorithm was a random-walk Metropolis–Hastings (Hastings, 1970). Proposal distributions were independent N(0, 0.001²).

2.6. Software

All computations were done using the programming language R (http://www.r-project.org/). We wrote an R package QTLMatch which implements the statistical procedures proposed in this paper (available at http://www-gene.cimr.cam.ac.uk/todd/).

3. RESULTS

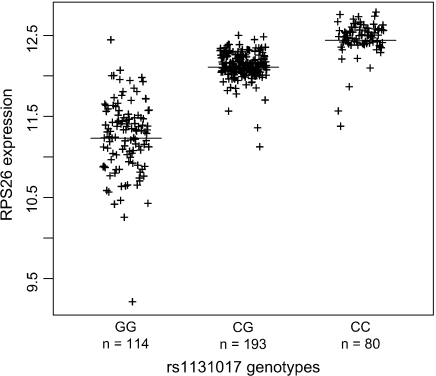
We first used single marker analysis to identify SNPs highly correlated with both T1D status and RPS26 expression. Using p = 10⁻¹⁰ for the T1D association and p = 10⁻⁵⁰ for RPS26 expression as significance thresholds, we selected an initial set of 4 highly correlated SNPs with genotypes available in both studies. A visual illustration of the strong correlations between RPS26 expression and rs1131017 is shown in Figure 1. We also observed clear departure from a linear trend model when comparing a 1-degree-of-freedom trend model with a 2-degree-of-freedom model (p≪0.001).

Fig. 1.

Correlation between RPS26 expression and rs1131017 genotypes. RPS26 expression was measured using the Affymetrix HG-U133 Plus 2.0 gene expression chip.

Subsequent analysis relies on the pattern of linkage disequilibrium to be identical in both data sets. To check this assumption, we computed the pairwise squared correlation coefficients r² and minor allele frequencies for the 4 SNPs in our analysis. We found these measures of linkage disequilibrium to be highly similar (see Table 1), consistent with the fact that all samples are of British ancestry.

Table 1.

Pairwise squared correlation coefficient r² between markers and minor allele frequencies in the T1D case–control samples and the RPS26 gene expression study. The first value relates to the JDRF/WT British T1D case–control collection and the second value to the eQTL study

	rs877636	rs1131017	rs705699	rs705704	MAF (RPS26 study)	MAF (T1D study)
rs877636	—	0.64/0.67	0.56/0.57	0.88/0.88	0.37	0.37
rs1131017	0.64/0.67	—	0.88/0.89	0.69/0.71	0.46	0.45
rs705699	0.56/0.57	0.88/0.89	—	0.61/0.66	0.45	0.44
rs705704	0.88/0.88	0.69/0.71	0.61/0.66	—	0.37	0.37

MAF, minor allele frequency.

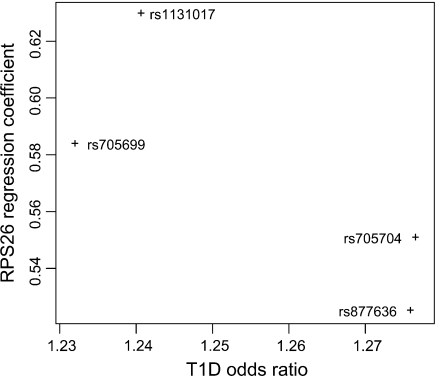
We then compared estimated regression coefficients between the T1D case–control collection and the RPS26 gene expression study. Assuming a sole, shared causal variant for T1D and RPS26, regression coefficients should be proportional between both data sets. However, we found a clear deviation from the proportionality (see Figure 2).

Fig. 2.

Comparison of estimated regression coefficients in the T1D case–control and the eQTL RPS26 expression studies, analyzing 1 SNP at a time. Assuming a sole causal variant for both traits, the estimated regression coefficients should be proportional between both studies.

To further describe these differences, we used a stepwise regression approach. The most significantly associated SNP for RPS26 expression was rs1131017 (p≪ 10⁻⁵⁰)), and the most significantly associated SNP for T1D status was rs705704 (p = 10⁻¹³). When correlating T1D status with rs705704, adding rs1131017 did not improve the model (p = 0.3). Conversely, when correlating RPS26 status with rs1131017, adding rs705704 did not improve the model (p = 0.85). On the other hand, when explaining the T1D variable, the best T1D SNP rs705704 significantly added to the best RPS26 SNP rs1131017 (p < 0.001). And reciprocally, when explaining RPS26 expression, the best RPS26 SNP rs1131017 significantly added to the best T1D SNP rs705704 (p ≪ 10⁻⁵⁰). We estimated from our data that the pairwise r² between rs1131017 and rs705704 is r² = 0.7.

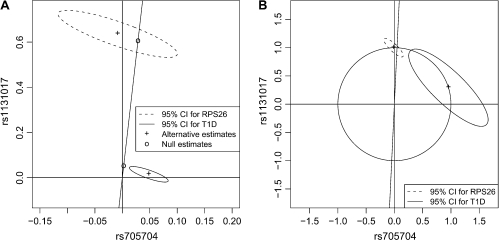
These results indicated discrepancies between the genetics of T1D and RPS26 expression. We therefore devised a formal multilocus statistical test for the existence of a sole, shared causal variant. Because rs1131017 captured all the T1D association and rs705704 captured all the RPS26 expression, we restricted our study to these 2 SNPs. We found that confidence intervals of jointly estimated coefficients are not consistent with the proportionality predicted under the null hypothesis (see Figure 3). As a consequence, our test rejected the null hypothesis of a sole, shared common causal variant (p = 0.001).

Fig. 3.

(A) Jointly estimated regression coefficients and confidence intervals for rs1131017 and rs705704 under the null hypothesis ₀ of a sole common variant and under the alternative ₁. Under the null hypothesis ₀, estimated regression coefficients have to be located on a line passing through the origin. (B) Rescaled version of (A) highlighting the fact that when compared on the same unit scale (i.e. regression estimates located on the unit circle), the variance of the estimated coefficients is higher for the T1D study. Therefore, regression estimates under the null are driven by the RPS26 expression data.

We then extended our analysis to account for the observed nonlinearity between observed genotypes and RPS26 expression. Incorporating a quadratic model to link the causal variant with the RPS26 expression, we also found substantial evidence against the null hypothesis of a shared common variant (Bayes' factor of 10 against the null). These results indicate that it is highly unlikely that both phenotypes share a common causal variant.

4. DISCUSSION

We have derived a statistical procedure to test for the presence of a sole causal variant. Using this test, we could reject the hypothesis of a sole, shared common causal variant for RPS26 expression and T1D status. If the effect of this T1D susceptibility locus was mediated through the expression of RPS26, the RPS26 variant would also be causal for T1D. Therefore, we conclude that the overlap between both associations is probably the result of chance alone and RPS26 expression level is unlikely to be related to T1D susceptibility.

Even if both T1D/RPS26 associations shared a common variant, the expression of RPS26 could still have no etiological effect on T1D susceptibility. This would be the case if the unique variant had an effect on 2 unrelated pathways. On the other hand, T1D susceptibility cannot be the direct consequence of RPS26 expression level if the genetics of both traits do not match, which is the case in our analysis. We note, however, that our analysis relies on RPS26 expression pattern in LCLs. We cannot exclude that the genetics of RPS26 expression and T1D are in fact concordant in a different cell population or under different conditions.

Our statistical analysis relies on the pattern of linkage disequilibrium being identical in both data sets. A better design would consist of sampling individuals from the same population or ideally obtaining gene expression measurements from the same case–control samples. However, the samples in the gene expression study originated from Great Britain and we expect the pattern of linkage disequilibrium to be very similar to the T1D British case–control collection, as indeed we observed (Table 1).

A limitation of our approach is the assumption of a sole causal variant. A more complex scenario, involving several loci and allelic heterogeneity in the 12q13 region, could be evoked in which SNPs do affect T1D susceptibility via RPS26 expression differences. Owing to missing information and complex genetic architecture, we could not confirm this relationship. However, stepwise regression analysis shows that based on currently available data both the T1D association (Todd and others, 2007) and the RPS26 eQTL can be summarized using a single SNP for each trait. Therefore, there is no evidence of allelic heterogeneity either for T1D or for RPS26 eQTL and this more complex scenario appears unlikely.

Nonlinear genotype/phenotype relationships can also affect the outcome of our statistical procedure. The Bayesian extension of our test is designed to address such nonlinear effects. Its main drawback is its reliance on iterative estimation procedures: convergence issues can lead to misestimated Bayes’ factors. On the other hand, we expect our first likelihood ratio test to be robust to limited departure from linearity. Our rationale is the fact that in a generalized regression model where the function linking genotype and phenotype is unknown or misspecified, the intercept parameter is not identifiable but the slope coefficients can nevertheless be robustly estimated up to a proportionality constant (Li and Duan, 1989). Given that proportionality between 2 sets of estimated regression slopes is the focus of our test, the consequence of a nonlinear genotype/phenotype relationship should be limited.

Our approach can be used in future studies to test the existence of causal relationships between eQTLs, or any other phenotype, and disease susceptibility. The same methodology could also be used to compare 2 different disease associations located in the same genomic region. However, our example shows that the most accurately estimated regression parameters come from the gene expression analysis, in spite of a much larger sample size for the case–control study (4 000 controls and 4 000 cases compared to 387 data points for the expression study). This is a consequence of the much stronger genotype/phenotype correlation observed for the eQTL. Therefore, comparing 2 disease associations with small effects will provide large confidence intervals and limited power to separate both signals.

Statistical power to confirm these causal relationships will be increased if the causal variant is tagged effectively, thus motivating ongoing fine-mapping efforts of disease susceptibility loci. Increased case–control sample size will also contribute to greater statistical power to confirm such causal relationships.

FUNDING

Juvenile Diabetes Research Foundation; the National Institute for Health Research, Cambridge Biomedical Research Centre; the Wellcome Trust. Funding to pay the Open Access publication charges for this article was provided by the Wellcome Trust.