Abstract
We describe a behavioral screen for the quantitative study of interval timing and interval memory in mice. Mice learn to switch from a short-latency feeding station to a long-latency station when the short latency has passed without a feeding. The psychometric function is the cumulative distribution of switch latencies. Its median measures timing accuracy and its interquartile interval measures timing precision. Next, using this behavioral paradigm, we have examined mice with a gene knockout of the receptor for gastrin-releasing peptide that show enhanced (i.e. prolonged) freezing in fear conditioning. We have tested the hypothesis that the mutants freeze longer because they are more uncertain than wild types about when to expect the electric shock. The knockouts however show normal accuracy and precision in timing, so we have rejected this alternative hypothesis. Last, we conduct the pharmacological validation of our behavioral screen using D-amphetamine and methamphetamine. We suggest including the analysis of interval timing and temporal memory in tests of genetically modified mice for learning and memory and argue that our paradigm allows this to be done simply and efficiently.
Keywords: D-Amphetamine, genetics, GRPR, interval timing, memory, methamphetamine, space-time memory
In the Pavlovian conditioning tasks commonly used to test for the effects of genetic manipulations on learning and memory, animals learn the intervals in the protocol and time their responding accordingly (for reviews see Gallistel & Gibbon 2000; Killeen & Fetterman 1988; Miller & Barnet 1993; Staddon & Higa 1993). Disruption or degradation of interval timing and memory might account for some or all of the observed behavioral manifestations of the genetic manipulations that affect learning and memory. For example, the measure of fear in fear-conditioning paradigms is the number of seconds of freezing observed during the test trial (or trials) following one or more conditioning trials. Fear responses, like most conditioned responses, are timed relative to the expected time of delivery of the unconditioned stimulus (US). If the subject is less certain about when to expect the fear-inducing US (foot shock), it may begin freezing earlier and stop later relative to the time it expects shock. The degradation of interval timing would thus result in enhanced measures of fear specific to the conditioned stimulus (CS). We report the development of a simple efficient interval timing and memory paradigm suitable for screening genetically manipulated mice and its use to test the hypothesis that the enhanced fear conditioning seen in gastrin-releasing peptide receptor (GRPR) knockout mice is a consequence of degraded interval timing and memory.
The paradigm is a simplification of a time-based switching paradigm first used by Platt and Davis (1983) to study interval timing in the pigeon. There are two types of trials. A trial is either a short- or a long-latency trial. In short-latency trials, a response at the short-delay location after the shorter of two possible temporal intervals has elapsed triggers the delivery of a pellet. In long-latency trials, a response at the short-delay location does not pay off; instead, a response at the long-delay location after the longer temporal interval has elapsed delivers a pellet. Subjects are free to distribute their responses over short-delay and long-delay locations during a trial. However, premature responses in any hopper (i.e. responses prior to the termination of the temporal interval in effect) as well as responses to the ‘incorrect’ location after the end of the interval do not pay off. In the progress of training, when a trial starts, subjects tend to respond first at the short-delay location and to then switch to the long-delay location if and when the short interval elapses without a pellet delivery.
We refined and proved the paradigm using wild-type C57BL/6 mice, the strain from which most knockout strains are derived. We then applied it to the GRPR knockout mice and their wild-type littermate controls. Finally, we conducted the pharmacological validation of this paradigm using methamphetamine and D-amphetamine in two different experimental setups and two different strains of mice. The paradigm was shown to be sensitive enough to detect different effects of these pharmacological agents. Thus, our paradigm provides a sensitive and efficient screen for impaired interval timing, useable in both a genetic and a pharmacological context.
Experiments 1–3
In these initial experiments, we validated the paradigm and assessed its efficiency.
Methods
Subjects
Experimentally naive female C57BL/6N mice (Harlan, Indianapolis, IN, USA) served as subjects. All mice were kept in plastic tubs and maintained on a 12:12 h photoperiod. Other information about the subjects such as their age, weight, and so on is given in Table 1.
Table 1.
Experimental parameters and subject specifications in all experiments and phases
| Session no. and duration (min) | Temporal intervals (seconds) | ITI fixed + variable (seconds) | Self-initiated | Response | No. of subjects | Age (weeks), weight (g), sex | Photoperiod | Counterbalance | |
|---|---|---|---|---|---|---|---|---|---|
| Exp. 1 | 10–12, 20–22, female | Dark cycle | No | ||||||
| Phase 1 | 14/60 | 2 vs. 4 | 30 + 60 | No | NP | 4 | |||
| Phase 2 | 26/60 | 2 vs. 6 | 30 + 60 | No | NP | 4 | |||
| Exp. 2 | 10–12, 20–22, female | Dark cycle | Yes | ||||||
| Phase 1 | 19/60 | 6 vs. 18 | 30 + 60 | Yes | NP | 4 | |||
| Phase 2 | 10/60 | 3 vs. 9, 12 vs. 36 | 30 + 60 | Yes | NP | 2 | |||
| Phase 3 | 21/60 | 3 vs. 9, 12 vs. 36 | 30 + 60 | Yes | NP | 2 | |||
| Exp. 3 | 20/60 | 2 vs. 6, 12 vs. 36, 10 vs. 60 | 30 + 60 | Yes | NP | 6, 3, 3 | 6–8, 16–18, female | Dark cycle | No |
| Exp. 4 | WT + KO | 12–20, 27–33, male | |||||||
| Phase 1 | 24/90 | 3 vs. 9 | 81 + 216 | Yes | NP | 6 + 6 | Dark cycle | Yes | |
| Phase 2 | 6/90 | 3 vs. 9 | 81 + 216 | Yes | NP | 6 + 6 | |||
| Phase 3 | 9/90 | 3 vs. 9 | 54 + 27 | Yes | NP | 6 + 6 | |||
| Phase 4 | 21/90s | 9 vs. 27 | 54 + 27 | Yes | NP | 6 + 3 | |||
| Exp. 5 D-amphetamine | 60 | 3 vs. 9 | 30 + 60 | Yes | NP | 6 | 10–12, 20–22, female | Dark cycle | Yes |
| Exp. 6 methamphetamine | 90 | 3 vs. 9 | 50 + 10 | No | LP | 8 | 4–5, 19, male | Light cycle | Yes |
KO, knockout; LP, lever press; NP, nose poke, WT, wild type. Temporal units are stated in the corresponding columns at the top of the table.
Apparatus
The experiments were run in MED-Associates™ mouse experiment chambers with two opposing metal walls and the other two walls of Plexiglas. The first five experiments were run in the same type of experiment chambers – ENV-307-W: 21.6 (length) × 17.8 (width) × 12.7 cm (height). Two illuminable feeding hoppers (ENV-203-20) mounted at the extreme ends of one metal wall were active. There was an inactive hopper between them and another hopper in the middle of the opposing metal wall, which was used in some experiments to initiate trials. The entrance to each hopper was monitored by an infrared beam. Experimental chambers were enclosed within MED-Associates sound-attenuating boxes – ENV-018-M: 55.9 (width) × 55.9 (height) × 35.6 cm (depth). The experiments were controlled and data logged by programs written in MED-PC™ running on a PC.
Procedure
Familiarization
The mice were food deprived starting 3 days prior to the experiment and were weighed before each session. At the end of each session, they were given additional food to keep them at 85% of their free feeding weight (their weight after 2 days of ad-lib feeding following their arrival). Water was available ad lib in both home cages and experimental chambers. During these initial 3 days, they were familiarized with the experimental chambers, by leaving them in the chambers for 30 min a day. In this period, we left five 20-mg Noyes food pellets (PJAI-0020) a day in their home cages to familiarize them with the reinforcements used during the experiments.
Training and testing
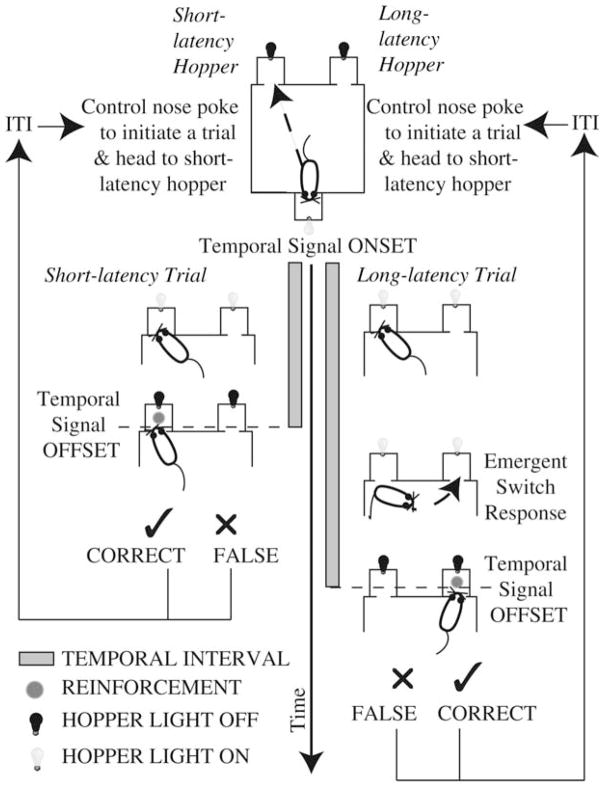
The procedure is schematized in Fig. 1. Trials began with the simultaneous illumination of the two hoppers and the onset of a white noise signal that delimited the to-be-timed interval. The temporal signal terminated after either a short or a long delay, with P(short) = 0.5. If it was a short delay and the short-hole infrared beam was the first to be interrupted at or after this delay, a pellet was delivered in the short hopper. If it was a long delay and the long-hole infrared beam was the first to be interrupted at or after this delay, a pellet was delivered in that hopper. Both hopper lights stayed on until the subject interrupted the infrared beam at one or the other hole, after the temporal interval elapsed. When the wrong beam was the first to be interrupted after the end of the temporal interval in effect, no pellet was delivered, and the trial was repeated until there was a correct response. Each trial was followed by an intertrial interval (ITI), which was composed of a fixed and a variable duration.
Figure 1. Illustration of the general experimental protocol with nose pokes.
In this illustration, the trial-initiating response is included.
In Experiment 1, the new trial was initiated by the program algorithm when the ITI expired. In Experiments 2 and 3, a control hopper on the wall opposite the two feeding hoppers was illuminated when the ITI expired. The mouse self-initiated trials with a poke into the illuminated control hopper. This variation in the procedure fixed the location of the mouse at the beginning of the programmed delays.
Mice received one session a day and they were not run on weekends. In Experiment 1, we initially used delay intervals of 2 and 4 seconds but changed these to 2 and 6 seconds, when the twofold difference in delays proved hard for the mice to learn. In Experiment 2, we trained with delay intervals of 6 and 18 seconds and then tested in a pair of shorter delays (3 and 9 seconds) and a pair of longer delays (12 and 36 seconds), with order counterbalanced across subjects. In Experiment 3, we trained with 2 vs. 6 seconds, then 12 vs. 36 seconds and 10 vs. 60 seconds.
Data analyses
In order for the mouse to judge, solely based on its sense of time, when the short interval has elapsed without a pellet delivery, the ongoing temporal signal needs to exceed the short interval. Thus, meaningful switches occur only on long-latency trials and only these are analyzed and reported in this paper. The cumulative distributions of these departure or arrival times is obtained by first sorting them and then constructing next to the column of sorted times a column in which each row is R/N, where R is the row number in the sort and N the total number of times in the sort. This second column gives the fraction of the total times that were less than or equal to any given time in the ordered list of times. Plotting the second column (the fractions) against the first column (the sorted times) gives the cumulative distribution. The median departure time is the time at which the cumulative distribution attains a value of 0.5. The interquartile interval is the interval between the time at which the distribution attains a value of 0.25 and the time at which it attains a value of 0.75.
Measures gathered from different phases of Experiment 2 were analyzed using repeated-measures analysis of variance (ANOVA). In testing for scalar variability1 in Experiment 2, we applied a relative likelihood analysis (Glover & Dixon 2004; Kass & Raferty 1995) using the Schwarz criterion (Schwarz 1978).
Results
Experiments 1–3
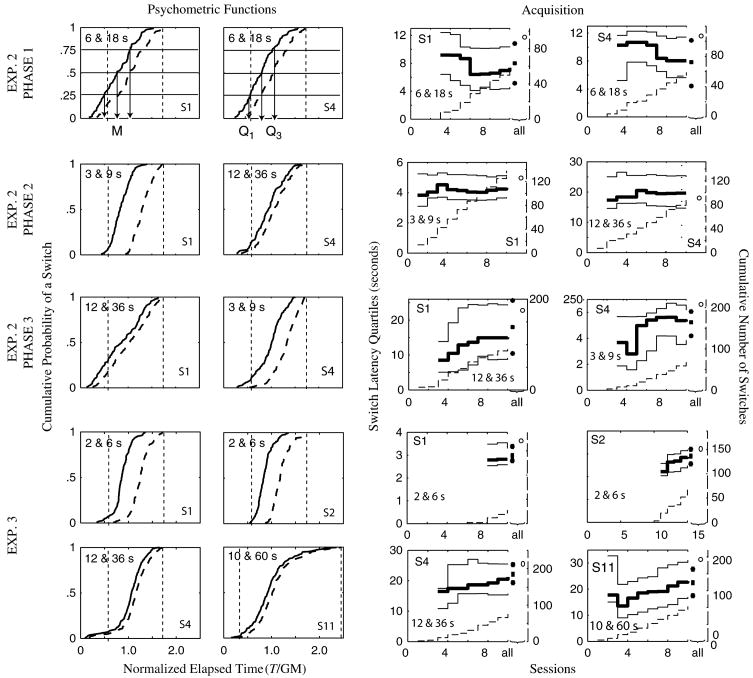
On most of the long-delay trials, each subject poked first into the short-delay station and then switched to the long-delay station before the long temporal interval elapsed, indicating a real-time classification of the elapsing duration, as first reported by Platt and Davis (1983) in the pigeon. Figure 2 (left panel) shows the cumulative distribution of departures from the short-delay station and arrivals at the long-delay station (on long-delay trials only) for some representative subjects from Experiments 2 and 3. The solid lines represent the cumulative distributions of departures (switch latencies), while the dashed lines represent the cumulative distributions of arrivals. The departure was defined as the latency (from trial onset) of the offset of the last poke in the short station prior to the onset of the first poke in the long station. The latency of this latter poke onset was defined as the arrival latency.
Figure 2. Left panel: cumulative distributions of departures (switches, solid curves) and arrivals (dashed curves) from representative subjects plotted against normalized elapsed trial time [trial time, T, divided by the geometric mean (GM) of the short and long intervals].
Intervals are at upper left of each panel; subject ID at lower right. As an illustration, the median is marked on the top left panel with ‘M’, and the first and third quartiles are marked on the top right panel, with ‘Q1’ and ‘Q2’, respectively. Short and long delays are marked by two vertical dashed lines on the normalized scale. Right panel: quartiles of the cumulative switch distributions are plotted against the left ordinates (solid lines), as a function of sessions in Experiments 2 and 3, while the cumulative number of switches is plotted against the right ordinates (dashed lines). In all panels except those for Phase 2 of Experiment 2 (which only lasted for 10 sessions), the solid circles at the extreme right of each panel indicate the quartiles of the final distribution (all switches), while the open circles indicate the total number of switches. These plots correspond to the cumulative distributions presented on the left panel and thus the number indicated by the open circle constitute the number of data points that went into the corresponding cumulative distribution. The durations of the short and long intervals are indicated on each panel, as is the subject ID.
The median switch latency is generally close to the geometric mean of the two delays, as is the so-called point of subjective equality in the bisection procedure when run with non-human animal subjects (Church & Deluty 1977; Fetterman & Killeen 1995; Platt & Davis 1983). The mean normalized median and the mean normalized interquartile intervals of switch latencies are presented in Table 2.
Table 2.
Mean normalized median and IQI from Experiments 1–4
| Mean normalized median ± SE | Mean normalized IQI ± SE | |
|---|---|---|
| Exp. 1: 2 vs. 6 seconds | 1.02 ± 0.02 | 0.44 ± 0.02 |
| Exp. 2 | ||
| 3 vs. 9 seconds | 0.94 ± 0.04 | 0.33 ± 0.03 |
| 6 vs. 18 seconds | 0.78 ± 0.06 | 0.49 ± 0.03 |
| 12 vs. 36 seconds | 0.89 ± 0.02 | 0.58 ± 0.05 |
| Exp. 3 | ||
| 2 vs. 6 seconds | 0.82 ± 0.01 | 0.21 ± 0.01 |
| 12 vs. 36 seconds | 1.04 ± 0.03 | 0.37 ± 0.04 |
| 10 vs. 60 seconds | 0.83 ± 0.05 | 0.46 ± 0.03 |
| Exp. 4 | ||
| 3 vs. 9 seconds | ||
| KO | 1 ± 0.02 | 0.66 ± 0.08 |
| WT | 0.98 ± 0.04 | 0.66 ± 0.15 |
| 9 vs. 27 seconds | ||
| KO | 0.87 ± 0.02 | 0.27 ± 0.03 |
| WT | 0.87 ± 0.06 | 0.5 ± 0.13 |
IQI, interquartile interval; KO, knockout; WT, wild type.
Platt and Davis (1983) tested pigeons with durations ranging between 40 and 200 seconds. This range of durations resulted in a large number of multiple switches. We used much shorter durations (ranging between 2 and 60 seconds, with most of the durations being closer to the lower end). At these durations, multiple switches were less common. In Experiment 2, multiple switches occurred in 13–19% of 36-second trials, only 1% of 12-second trials (in just two subjects) and only 2–4% of 18-second trials (in just two subjects). In Experiment 3, multiple switches occurred in 5%, 7%, 8%, 12% and 23% of 36-second trials, depending on the subject, and in 10%, 15%, 19%, 27%, 40% and 48% of 60-second trials, again depending on the subject. We ran analyses that took into account these multiple switches in the estimation of accuracy and precision. These analyses gave results so similar to the results based simply on the cumulative distributions of first departures and first arrival that we do not report them.
Switch latencies are approximately scale invariant: when the time axis is normalized, the plots look similar over a wide range of delay pairs (given at upper left of each panel). Scale invariance is equivalent to Weber’s law; it implies that where the median lies in relation to the two delays, which is our measure of accuracy, the ratio of the interquartile interval to the median, which is our measure of precision, is independent of the absolute values of the delay pairs. In Experiment 2, each of the four subjects was tested with three different pairs of delays. The delays differed between the pairs by a factor of as much as 6, but the within-pair ratio of the short to the long delay was kept at 1:3. If Weber’s law (the scale invariance of discriminability) holds, then the psychometric functions for different duration pairs should be the same on a normalized scale. It is evident from visual inspection that this property holds, at least to a first approximation.
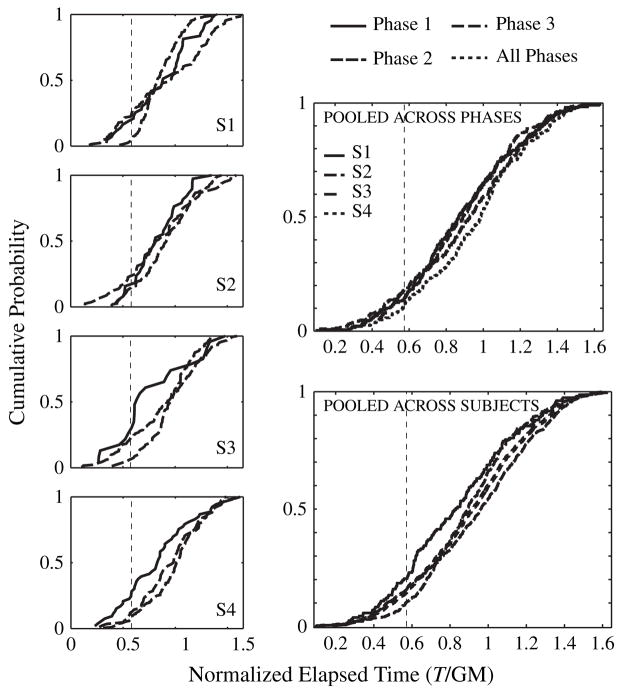
We did a relative likelihood analysis (Glover & Dixon 2004; Kass & Raferty 1995) to test the within-subject scale invariance of the distributions. In this analysis, we fit the normalized switch latencies with Weibull distributions, either separately for each phase (see left four plots in Fig. 3) or after pooling the data from all three phases (see top right plot in Fig. 3). In the former case, we summarize or represent the data with a six-parameter model, a model that assumes that the data from each phase come from a different distribution. In the latter case, we summarize or represent the data with a two-parameter model, assuming that they all come from the same distribution. In computing each fit, we get the maximum log likelihood for the data represented by that fit (how likely those data are, given that model of them). The overall maximum log likelihood for the three-distribution model is the sum of the individual maximum log likelihoods. The maximum likelihood for the three-distribution model may be compared with the maximum likelihood for the one-distribution model, using the Schwarz criterion (Schwarz 1978) to adjust for the difference in the numbers of parameters:
Figure 3. The four figures on the left show the cumulative distributions of switches for the individual subjects in Experiment 2.
In a given plot, each distribution is for a given phase of Experiment 2. The top right plot shows the cumulative distribution of switches for each subject for data collapsed across all phases. The bottom right plot shows the cumulative distribution of switches for each phase for data collapsed across all subjects. It also shows the cumulative distribution of switches for data collapsed across all subjects and phases. On the x-axis, trial time (T) is normalized by the geometric mean (GM). In these plots, data from the later sessions were evaluated. The short delay is marked by the vertical dashed line. Long delay is not marked as it falls out of the range of x-axis in the plots.
Odds ratio (Model1: Model2) = exp[ML1 − ML2 − 1/2 (d1 − d2)log(n)], where ML1 and ML2 are the respective maximum log likelihoods and (d1 − d2) is the difference (=4) in the number of parameters, and n is the number of data points (switches). The Odds ratio is also called the Bayes factor; it is the relative likelihood of the different models vis-a-vis the data. It quantifies how much better one or the other model is at representing the data.
In these analyses we considered data only from sessions 10–19, 2–10 and 6–21 for Phases 1, 2 and 3, respectively. For Subjects 2 and 4, the single distribution (i.e. the scale-invariant model) was more likely than the multidistribution model, whereas for the two other subjects, the reverse was true. Thus, scalar variability holds more or less exactly within some subjects, whereas, with the extreme ranges we tested, there are some modest violations of it in some other subjects.
We compared the medians and interquartile intervals across different phases. The tendency is for the distributions obtained using shorter duration pairs (3 and 9 seconds) to be steeper (have narrower spread) than the distributions with the longer duration pairs (6 and 18 seconds and 12 and 36 seconds). The mean normalized medians (medians divided by the geometric mean of short and long durations) did not differ, but the mean normalized spreads (interquartile intervals divided by the geometric mean of short and long durations) differed across different duration pairs [F(2, 6) = 6.82, P = 0.03, repeated-measures ANOVA]. Similar violations of scalar variability are seen with the peak procedure when subjects are tested over a similarly large range of intervals (Gallistel et al. 2004b; E. A. Ludvig, F. Balci & K. M. Longpre, in review).
In addition to the analysis reported above, we also applied the likelihood analysis for each phase collapsing data across four subjects and the pooled data collapsing data across four subjects and three phases (see the bottom right plot in Fig. 3). For data averaged in this manner, the pooled model was a somewhat better model than the unpooled model; the Bayes factor was 8:1 in favor of the model that assumes no effect of a change in time scale.
Importantly, these measures of timing accuracy and precision are very similar not only across a wide range of intervals but also from one normal (wild-type) subject to the next, as is evident from the just given small standard errors for the mean normalized median and the mean normalized spreads (interquartile intervals) – see Table 2. This is in marked contrast to commonly used measures of strength or latency or rate of performance. Between-subject differences of a factor of 10 or more are common in such measures.
In tasks intended to be used for screening large numbers of genetically manipulated subjects, efficiency is an important consideration: how much training is required? In the right panel of Fig. 2, we plot session by session the cumulative number of switches (dashed stair plots against right ordinates) and, on the same panels, the quartiles (25%, 50% and 75% points) of the cumulative distribution of those switches (solid plots against left ordinates). The plots of the quartiles begin only with the session in which the cumulative number of switches became equal to or greater than 8. For most subjects, these session-by-session plots cover only the first 10 sessions because a clear and stable distribution had developed in that span. The final quartiles (based on all the switches) and the cumulative number of switches across all sessions are given at the extreme right of each plot.
Switching emerged sooner in subjects trained with the longer intervals (12 and 36 seconds or 10 and 60 seconds) rather than the shortest (2 and 6 seconds). In Experiment 3, the six subjects trained with the longer intervals had all made 30 or more switches by the end of the seventh session, while it took between 9 and 15 sessions for the subjects trained with the shortest intervals to reach that point. When naive mice are trained with these longer intervals (and sometimes even when trained with the shorter intervals; see Experiment 2, Subjects 1 and 4), they begin to switch already in the second or third session, and the quartiles of the cumulative switch distribution approximate their final values within six sessions. When subjects were switched to a new pair of intervals, they adjusted within a single session, provided the change was by a factor of no more than 2, in which case the quartiles of the new cumulative switch function approximated their final values after only three sessions (see Phase 2 of Experiment 2, right panels in Fig. 2).
Experiment 4
Shumyatsky et al. (2002) report enhanced fear conditioning in mice in which the gene for the GRPR has been knocked out. After a single pairing of a 30-second tone CS and a 2-second foot shock US, GRPR-deficient mice showed enhanced freezing during testing with the tone alone. The specificity of the anatomical localization of GRPRs in the lateral nucleus of the amygdala, a structure which is a major candidate site for the establishment of fear memories (LeDoux 2000), allowed the authors to infer that the gene deletion might lead to enhanced fear memory. According to this view, when GRP is released by principal neurons, it is taken up by inhibitory interneurons containing GRPRs. Upon activation, these interneurons exert their GABAergic inhibition back to the principal neurons, thereby decreasing those neurons’ excitatory firing. In GRPR-deficient mice, the inhibitory interneurons are insensitive to GRP and therefore cannot inhibit the principal neurons. As a result of the lack of such inhibition, long-term potentiation is enhanced in the cortico-amygdala pathway in these mice (Shumyatsky et al. 2002). Thus, it appears that the disruption of this negative feedback loop results in stronger and more persistent fear memory, as observed with the enhanced conditioned freezing of GRPR knockout mice.
Impaired interval timing offers an alternative interpretation for the observed behavioral phenotype because what is measured is the duration of freezing. When the ‘amount’ – that is, the duration – of freezing is the measure of fear, any manipulation that prolongs the freezing interval surrounding the time of expected shock will be interpreted as an indication of enhanced fear. There are, however, at least two alternative explanations: (i) the precision of subjects’ interval timing is impaired, so their interval of uncertainty surrounding the expected shock delay, the interval during which they are afraid, is increased (Gallistel & Gibbon 2000) and (ii) the uncertainty threshold for freezing behavior is reduced, so that they begin freezing sooner and stop later because they begin and end when the subjective probability of shock is lower than the value at which wild types start and stop freezing.
That an increased interval of uncertainty surrounding the expected time of shock might explain more prolonged freezing in mutant mice is a plausible alternative, given the results gathered from one-trial contextual fear-conditioning paradigms in which animals receive a single shock. These studies showed that animals showed timed freezing response as a function of delay experienced in the single training session. In one of these studies, Fanselow (1986) reported a linear increase in freezing time as a function of delays of shock that ranged from 9 to 81 seconds. Further, Bevins and Ayres (1995) varied the latency of shock for different subjects and showed that peak of freezing later in the session increased as a function of latency of shock experienced in the single training session (also see Bevins et al. 1997). Davis et al. (1989) showed single-trial timing of the startle response. They found that during testing, rats showed maximal fear-potentiated startle after a delay that matched the CS–US interval that they experienced only once during training.
Although these studies showed that conditioned fear responses are timed, the temporal resolution of these protocols is too low to allow reliable estimates of the psychophysical properties of interval timing to be obtained. Moreover, even a careful examination of the time–course of freezing response would not differentiate between the two alternative explanations stated above. A psychophysical paradigm, instead, is more appropriate to test the first explanation. Thus, in Experiment 4, we used our paradigm to test the hypothesis that the precision of interval timing is impaired in GRPR mice.
Method
Subjects
We used male GRPR hemizygous mutant mice (GRPR −/Y), with wild-type mice (GRPR +/Y). They were the littermates produced by crosses between wild-type C57BL/6J males (GRPR +/Y) and heterozygous females (GRPR +/−) that had been backcrossed to C57BL/6J mice for more than 10 generations (N10). During the first Phase of Experiment 4, because of space limitations, most mice were housed in groups of two to five, while later on all but three mice were separated and housed individually. In all other respects, the conditions of housing and deprivation were the same as in Experiments 1–3 (see Table 1).
Apparatus
Same as in Experiments 1–3.
Procedure
We used the self-initiated trials procedure of Experiments 2 and 3. However, the opportunity to initiate a trial was signaled both by the illumination of the control hopper and by the onset of white noise. The temporal interval was bracketed by the offset of the white noise2 and the onset of a brief tone. Thus, time switches were based on the elapsed interval since the offset of the white noise.
We thought that mutant mice might have behavioral disruptions such as less exploratory behavior. To ensure the experience of contingencies by the mutant mice, in Experiment 4 we initially used an autoshaping training protocol in which the pellet was always delivered at the end of the temporal delay, irrespective of whether the mouse poked or not. Subsequently, to see if an operant contingency resulted in substantially more switches and/or a difference in the precision and accuracy measures, we ran a second phase in which autoshaping trials constituted only one quarter of the total trials. The rest were operant trials, in which the mouse had to interrupt the infrared beam in the correct hole after the temporal delay elapsed to receive the pellet.
Data analyses
For the between-subjects comparisons in this experiment, we used independent-samples t-test.
Results
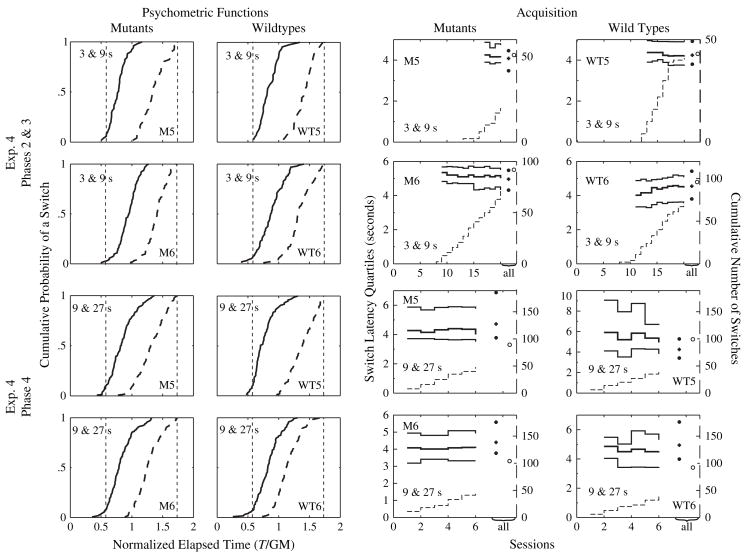
First we checked whether knockouts took longer than wild types to acquire the pattern of switching responses. For this reason, we used the data from Phase 1 (when initial training was given) and compared the number of sessions it took each group to reach eight switches. The knockout group took no longer to acquire switching behavior than did their wild-type littermate controls, t(10) = 0.60, P = 0.56. As may be seen in Fig. 4 (right panel), both wild types and knockouts began to switch around the 10th session. The medians and interquartile intervals approximated their final values within the first few sessions after switching was first observed.
Figure 4. Left panel: cumulative distributions of departures (switches, solid curves) and arrivals (dashed curves) of representative GRPR mutant and wild-type mice plotted against normalized elapsed trial time [trial time, T, divided by the geometric mean (GM) of the short and long intervals].
Intervals are at upper left of each panel; subject ID at lower right. Short and long temporal intervals are marked by two vertical dashed lines on the normalized scale. Right panel: quartiles of the cumulative switch distributions of representative GRPR mutant and wild-type mice are plotted against the left ordinates (solid lines), as a function of sessions in Experiment 4, while the cumulative number of switches is plotted against the right ordinates (dashed lines). In all panels, the solid circles at the extreme right of each panel indicate the quartiles of the final distribution (all switches), while the open circles indicate the total number of switches. These plots correspond to the cumulative distributions presented on the left panel and thus the number indicated by the open circle constitute the number of data points that went into the corresponding cumulative distribution. The durations of the short and long intervals are indicated on each panel, as is the subject ID.
As may be seen in Fig. 4 (left panel), the timing of switching was the same in the knockout mice as in their wild-type littermates. We compared the two genotypes in two different sets of central tendency (median and mean) and variability [interquartile interval and standard deviation (SD)] measures gathered from the psychometric functions of wild-type and mutant mice – see Table 2. We did not find a statistically significant difference between wild types and knockouts in any of these measures in any of the phases.
In short, the interval timing and memory of GRPR knockouts is intact and normal in both accuracy (locus of the median) and precision (interquartile interval). Thus, the alternative timing explanation for enhanced freezing in GRPR knockouts can be rejected, as can any hypothesis that imputes generally improved (or degraded) learning and memory to these mice (as opposed to fear-specific memories). Their learning of and memory for durations is normal.
Experiments 5 and 6: pharmacological validation
In our last two experiments, we conducted the pharmacological validation of the switch procedure by using it with pharmacological agents that have been shown to affect behavioral timing in the peak and bisection procedures. In Experiment 5, we tested the effect of different doses of D-amphetamine on accuracy and precision of interval timing. In Experiment 6, we tested the effect of methamphetamine.
Method
Subjects
In Experiment 5, experimentally naive female C57BL/6N mice (Harlan) served as subjects (see Table 1). In Experiment 6, we used male mice that were derived from wild-type mice from a mixed B6CBAF1 background line maintained at The Jackson Laboratory (Bar Harbor, ME, USA; stock number 006494) repeatedly back-crossed to a B6CBAF1 (JAX Laboratories; stock 100011) in house. These mice had been used as the wild-type control group for an experiment investigating acquisition of lever pressing in mutant R6/2 mice.
Apparatus
In Experiment 5, the apparatus was the same as in the four preceding experiments. In Experiment 6, we adapted the hopper switch protocol to a new experimental environment, in which the mice were asked to lever press rather than nose poke to receive reinforcement. In this experiment, the experiment chamber was ENV-307-A (MED-Associates): 15.9 (length) × 14.0 (width) × 12.7 cm (height). These experimental chambers had two retractable levers, instead of feeding hoppers, at the two extremes of one metal wall. Both levers had a light located above them. There was a feeding hopper between the two levers and a milk dipper was mounted underneath it.
Procedure
In Experiment 5, we used the training protocol of Experiments 2 and 3. Mice were run in this protocol for 29 sessions before the first drug injection.
In Experiment 6, mice first received lever press training under fixed-ratio (FR)-1/fixed-time (FT)-30 schedules for 25 sessions. Lever press training was followed by fixed-interval (FI)-3 and FI-9 training for different levers for six sessions. During this phase only the lever that corresponded to the presented FI was presented on each trial.
During testing, both levers were presented simultaneously on each trial. A trial was either a short-delay or a long-delay trial with equal probability. If it was a short-delay trial, the first lever press to the short-latency lever within 5 seconds following the short FI was reinforced. If it was a long-delay trial, the first lever press to the long-latency lever within 5 seconds following the long FI was reinforced. The reinforcement was 5-second presentation of condensed milk (Carnation™). If the first response was to the long-latency lever after a short FI or to the short-latency lever after a long FI, the trial terminated with no reinforcement. Both levers were retracted after the first lever press following the FI that was in effect in that particular trial or 5 seconds after the FI in effect if no response was made to any lever. Retraction of levers initiated the ITI. To synchronize the video recordings across chambers, the trials started simultaneously across all boxes. During all phases, the extension of levers was accompanied by the illumination of the two lights mounted over them. These lights were turned off with the retraction of the levers. Mice were run with this last protocol for 19 sessions before the first drug injection. Each session consisted of 60 trials (30 short and 30 long) with a variable ITI.
Drug preparation and administration
Methamphetamine was administered at doses of 0.3, 1 and 3 mg/kg in saline. D-Amphetamine was dissolved into phosphate-buffered saline and administered at doses of 0.5 and 1.5 mg/kg. The dosing volume was 10 ml/kg. Drug administration was governed by a Latin square design. On the first injection day, half of the mice received saline and the other half received drug injections. On the second injection day, mice that had received a saline injection on the first day received drug injection and vice versa. The drug was D-amphetamine (Sigma, St Louis, MO, USA) for Experiment 5 and methamphetamine (Sigma) for Experiment 6. Drug and saline were administered intraperitoneally and mice were injected with saline several times prior to the first injection day to habituate them to the injection procedure. The pretreat period was 15 min for Experiment 5 and 30 min for Experiment 6, and the washout period between two injections was 4 and 5 days for Experiments 5 and 6, respectively.
Data analyses
Our drug studies used a within-subjects design to evaluate the effect of the drug on measures of timing. Thus, these data were analyzed using paired-samples t-test.
Results
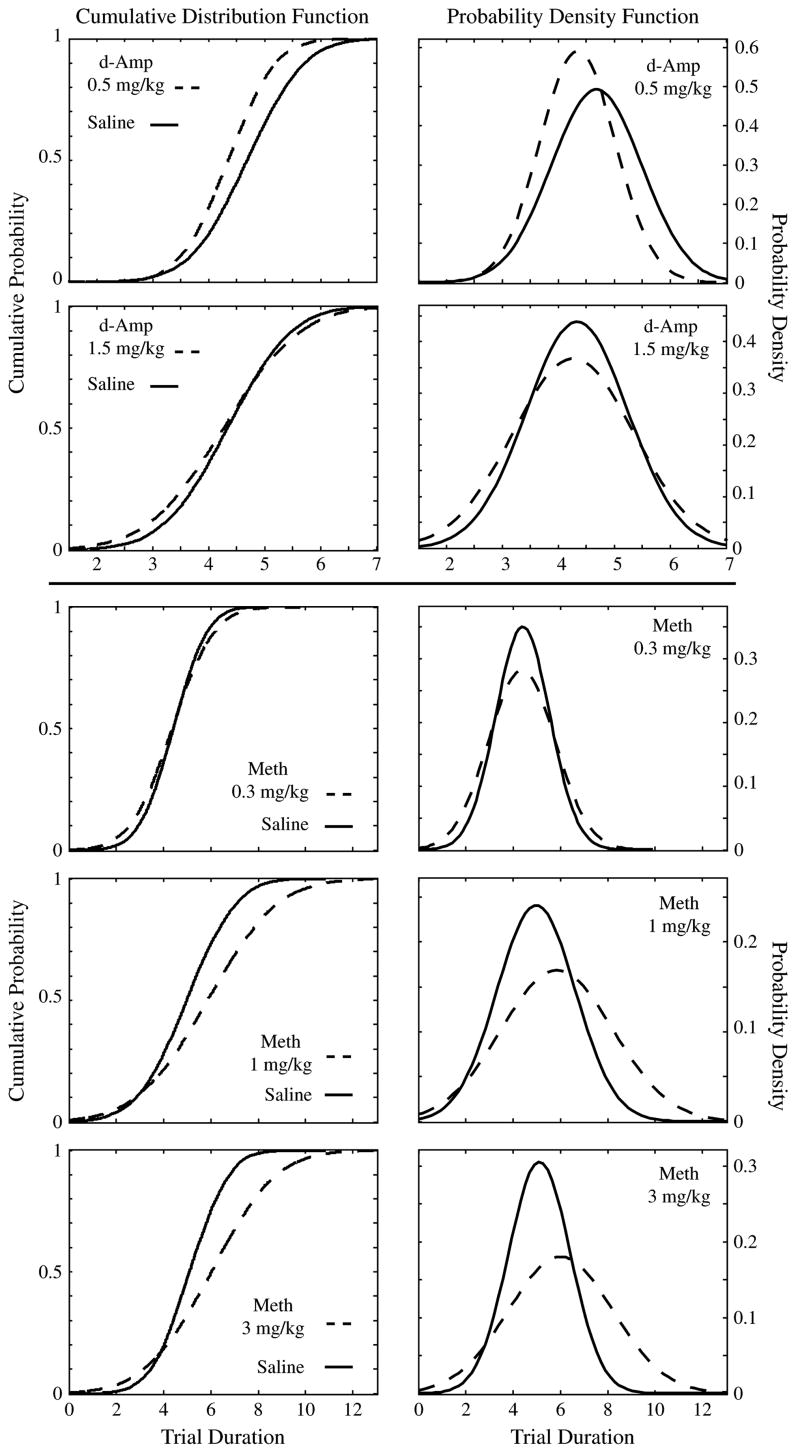
Figure 5 shows the cumulative (left panel) and probability (right panel) density functions (cdf and pdf) of switch points generated from the average mean and SD of the individual switch distributions under drug and vehicle for each dose. A dose of 1.5 mg/kg D-amphetamine increased the variability of the psychometric function as reflected by a significant increase in the interquartile interval [t(4) = 2.82, P = 0.037, two tailed] and SD [t(4) = 3.31, P = 0.03, two tailed]. This effect is reflected on Fig. 5 by a decrease in the steepness of the cdf and an increase in the spread of the pdf. At this dose of D-amphetamine, we excluded data from a mouse that responded in the opposite direction than the rest of the subjects because it also reversed its switch pattern: it almost always started responding at the long-latency hole and then switched to the short-latency one.
Figure 5. cdf (left panel) and pdf (right panel) generated from the average mean and SDs gathered under different drug/dose and saline injections.
Dashed lines represent distribution of switch latencies gathered under drug injections and solid lines represent distribution of switch latencies gathered under vehicle injections.
A dose of 0.5 mg/kg D-amphetamine decreased the central tendency of the switch points as reflected by a significant decrease in the median [t(5) = 3.86, P = 0.01, two tailed] and mean [t(5) = 3.29, P = 0.02, two tailed]. This effect is shown by a leftward shift of the cdf and the peak of the pdf. There was also a marginally significant decrease in the variability measured by the interquartile interval, as would be expected to accompany a decrease in the target point, that is, the decision criterion [t(5) = 2.48, P = 0.056, two tailed]. (The P value for the SD was 0.087, two-tailed t-test.)
Similarly, the analyses of the methamphetamine experiment showed that this dopamine agonist, too, decreased the precision of the temporal discrimination (see Fig. 5). The highest dose of methamphetamine (3 mg/kg) increased the interquartile interval [t(5) = 3.55, P = 0.016, two tailed] and the SD, although the latter effect only approached significance [t(5) = 2.21, P = 0.078, two tailed]. Note that two of the mice did not respond under this dose of methamphetamine and were excluded from the analyses.
The dose of 1 mg/kg methamphetamine increased the SD [t(7) = 2.4, P = 0.048, two tailed]. The increase of the interquartile interval failed to reach significance [t(7) = 2.03, P = 0.08, two tailed), although it did so when a one-tailed test was used. There were no significant effects of a 0.3 mg/kg dose of methamphetamine. The only effect on the central tendency measures that approached significance was an increase in the mean of the switch latencies under a dose of 1 mg/kg methamphetamine [t(7) = 2.07, P = 0.077, two tailed).
We also compared the magnitude of the effect on variability across different doses. The magnitude of an effect was determined by subtracting the value of the measure under saline from the value of the same measure under drug. We did that for each dose and compared the magnitudes across each dose combination. We expected an increase in the variability measures as a function of drug concentration. Therefore, for the comparisons that involved variability measures, we used one-tailed paired samples t-test. Consistent with our prediction, we found that a higher dose (1.5 mg/kg) of D-amphetamine produced an increase in both interquartile interval and SD compared with a lower dose (0.5 mg/kg) of D-amphetamine [t(4) = 3.14, P = 0.017 and t(4) = 2.6, P = 0.03, respectively]. We also found that compared with a low dose of 0.3 mg/kg of methamphetamine, doses of 1 and 3 mg/kg resulted in a larger increase in interquartile intervals (t7 = 2.26, P = 0.029 and t5 = 3.83, P = 0.006, respectively) and in SD (t7 = 2.18, P = 0.033 and t5 = 2.75, P = 0.02, respectively).
Cross-experiment results
Spatial specificity
There is a strong spatial component in the switch task. The mice must remember which station delivers pellets after a short vs. long latency. We observed that occasionally mice visited first the long-latency feeder and then switched to the short-latency feeder. These wrong-way switches could have been as a result of confusion of the memory for the relation between the temporal intervals and spatial locations. As an index of spatial performance, we calculated the proportion of correct first switches in all trials that contained a switch. Table 3 contains the values of these proportions for each condition of Experiments 2–6. These values showed that the spatial performance of all mice (including the GRPR knockouts and the mice injected with D-amphetamine and methamphetamine) is near perfect.
Table 3.
Proportion of correct first switches for different conditions of Experiments 2–5
| Experiment | Condition | Proportion of correct first switches ± SEM |
|---|---|---|
| 2 | Phase 1: 6 vs. 18 seconds | 0.86 ± 0.02 |
| Phase 2: 3 vs. 9 seconds and 12 vs. 36 seconds | 0.93 ± 0.03 | |
| Phase 3: 3 vs. 9 seconds and 12 vs. 36 seconds | 0.95 ± 0.02 | |
| 3 | 2 vs. 6 seconds | 0.96 ± 0.04 |
| 12 vs. 36 seconds | 0.86 ± 0.04 | |
| 10 vs. 60 seconds | 0.88 ± 0.02 | |
| 4 | Phase 1: 3 vs. 9 seconds | Wild types: 0.97 ± 0.01; knockouts: 0.96 ± 0.01 |
| Phase 2: 3 vs. 9 seconds | Wild types: 0.98 ± 0.01; knockouts: 0.99 ± 0.01 | |
| 5 | 0.5 mg/kg: 3 vs. 9 seconds | D-Amphetamine: 0.94 ± 0.03; saline: 0.94 ± 0.04 |
| 1.5 mg/kg: 3 vs. 9 seconds | D-Amphetamine: 0.90 ± 0.07; saline: 0.87 ± 0.08 | |
| 6 | 0.3 mg/kg: 3 vs. 9 seconds | Methamphetamine: 0.95 ± 0.02; saline: 0.96 ± 0.02 |
| 1 mg/kg: 3 vs. 9 seconds | Methamphetamine: 0.94 ± 0.04; saline: 0.92 ± 0.05 | |
| 3 mg/kg 3 vs. 9 seconds | Methamphetamine: 0.98 ± 0.02; saline: 0.97 ± 0.02 |
Effects of conditioning protocols
To estimate the effect of using an operant contingency rather than a Pavlovian (autoshaping) contingency, we compared the number of switches from the last five sessions of autoshaping training to the numbers in sessions two to six of the operant phase in Experiment 4. There were more switches in the operant phase (mean = 27.42, SD = 11.69 and mean = 36.83, SD = 7.27 for autoshaping and operant trials, respectively). However, the difference was small, and it may well be explained by the fact that the operant phase followed the autoshaping phase (so that the subjects by then were better trained). There were no effects of conditioning protocol on accuracy or precision.
Effects of ITI
Finally we compared the cumulative distribution of switches from the first six sessions of Phase 2 (when the ITI was long) with the cumulative distribution of switches from the remaining sessions of that phase (when the ITI was short) to see whether this manipulation affected accuracy and precision. With the exception of a decrease in the spread of the knockouts’ distribution [‘long-ITI’ spread = 0.51 vs. ‘short-ITI’ spread = 0.37, t(5) = 2.27, P = 0.04], the paired-sample t-tests did not show any significant changes in any of the above measures when the ITI was shortened.
Performance in short- vs. long-delay trials
The switch times in our analyses were gathered only from the long-delay trials. One may wonder how performance on short-delay trials compared. We looked at the proportion of reinforced trials for both short- and long-latency trials in Experiment 3. We averaged these proportions across blocks of five sessions and compared them. Our analyses showed that for 12 vs. 36 seconds and 10 vs. 60 seconds pairs, the proportion of reinforced trials was the same for both trial types from the start. For the 2 vs. 6 seconds pair, the performance of subjects was better on long-delay trials during the first five sessions, while it did not differ beyond that point. The proportions of reinforced trials during the last five sessions for 2 vs. 6 seconds, 12 vs. 36 seconds and 10 vs. 60 seconds trials were 0.96 ± SE 0.02 vs. 0.99 ± SE 0.01, 0.93 ± SE 0.02 vs. 0.94 ± SE 0.03, and 0.9 ± SE 0.06 vs. 0.93 ± SE 0.02, respectively.
General discussion
The behavioral tests most commonly used with genetically manipulated mice measure some aspect of the probability or vigor of the conditioned response – the latency to make a response or to reach the goal, the frequency of responding, the time spent responding and so on. These measures show large (2- to 100-fold) variation between subjects within groups and between sessions within subjects – in mice and in other commonly used species (Gallistel et al. 2004a; Papachristos & Gallistel 2006). Moreover, they do not measure what the subject has learned, only whether it has learned. The large between-subject variation within wild-type control groups suggests that these measures are strongly affected by many different performance variables, each presumably reflecting a different physiological process under different genetic control. That makes these simple measures of performance ill suited for screens intended to isolate specific cognitive mechanisms.
Timing paradigms, by contrast, measure the accuracy and precision with which the subject measures and remembers a temporal interval. These measures have one or two orders of magnitude less between-subject and between-session within-subject variability. The small variability in the accuracy and precision of switch timing suggests that this measure primarily reflects the operation of a well-regulated interval timing mechanism. The distinction here is analogous to the distinction between the magnitude of the variability in the amplitude of circadian fluctuations of activity in free-running subjects, which is large, and the relatively much smaller variability in the periods of the observed fluctuations. This makes genetic effects on circadian period more easily detectable and more conducive to genetic dissection than are genetic effects on the amplitude of circadian variations in activity levels.
Successful performance in our simple interval-timing task requires the mouse not only to remember the two different experienced intervals but also to associate those intervals with the two different experienced locations. Thus, it is an efficient screen for intact space-time memory. It is an effective means of ruling out general effects on memory and learning. It is an important test to make whenever a genetic manipulation is thought to affect a general-purpose memory or learning mechanism. If a mutation or a knockout impairs or eliminates memory (tout court), then it must impair or eliminate appropriately timed and directed switching in this simple paradigm.
Our experiments show that one can measure the accuracy and precision of interval timing using our switch paradigm in approximately 10 sessions. The paradigm is entirely automated, minimizing the handling of the mice during testing, and the demands on experimenter/technician time. It is robust: it works with both wild-type and mutant strains. Essentially identical results are obtained using either poking into a hopper (which is very rapidly learned) or lever pressing (which is learned more slowly), with either pellets or condensed milk as reward, and with widely differing ITIs. The data analysis is exceptionally simple: the cumulative distribution of the switch times is in essence a plot of the raw data. There is no averaging and no parsing into starts and stops. The median and interquartile intervals may be read directly off the cumulative distributions.
The measures of the accuracy and precision of interval timing are demonstrably sensitive to the pharmacological manipulations to which other measures of interval timing have been shown to be sensitive. Higher doses of D-amphetamine and methamphetamine impaired timing precision, significantly increasing the variability in the distribution of switch points. This is consistent with findings reported by many studies that tested the effect of dopamine agonists on temporal discrimination (Abner et al. 2001; Çevik 2003; Lieving 2002; Odum et al. 2002; Santi et al. 2001; Stanford & Santi 1998; Stubbs & Thomas 1974; and for review see Balci et al. in press).
A low dose (0.5 mg/kg) of D-amphetamine significantly reduced the median and mean of the cumulative switch function. This leftward shift of the psychophysical function is consistent with other findings that suggested that dopamine agonists increase the speed of the hypothetical pacemaker (e.g. Abner et al. 2001; Maricq et al. 1981; Meck 1983). However, a number of studies have failed to replicate this effect of dopamine agonists on temporal discrimination in rats (Lejeune et al. 1995; Santi et al. 1995 with amineptine; Santi et al. 2001 with quinripole – a dopamine D2 receptor agonist) or pigeons (McClure et al. 2005; Stubbs & Thomas 1974). In addition to these reports, methamphetamine did not shift the psychophysical function in our experiment. This discrepancy may have been because of a different effect of these two drugs as well as the difference in the nature of the timed response that was used in the two experiments (nose poking in the D-amphetamine experiment, lever pressing in the methamphetamine experiment). The experimental conditions such as the type of response required, the inclusion of critical response period (e.g. in Experiment 6), the dimensions of the experimental chamber (determining the distance between two response alternatives), the self-initiation of the trials in Experiment 5 but not in Experiment 6 and the strain of the subjects might also explain the differences in the switch distributions under saline injections in Experiments 5 and 6.
Implications for the GRPR phenotype
We have used the paradigm to show that the precision (variability) of interval timing in GRPR knockouts is normal. Thus, the hypothesis that the prolonged freezing shown by this strain in one-trial fear conditioning is not likely to be a consequence of increased uncertainty about the expected time of the shock. Our findings also make it unlikely that there is a general enhancement of learning and memory in these knockouts, which is consistent with previous observations that their spatial memory is normal in the water maze (Shumyatsky et al. 2002). They develop switching no faster than wild types, and the accuracy and precision of their switches is neither better nor worse.
Acknowledgments
This research was supported by NIMH grant 1 R21 MH63866 to C.R.G. and by NARSAD, New Jersey Governor’s Council on Autism and Busch memorial Fund to G.P.S. and James Leathem Scholarship to E.B.P.
Footnotes
Scalar variability means that the uncertainty increases as a constant proportion of the central tendency. Scalar variability is a way of explaining Weber’s law.
White noise in Experiment 4 was used to signal the opportunity for trial initiation and thus its termination marked the start of the temporal interval.
References
- Abner RT, Edwards T, Douglas A, Brunner D. Pharmacology of temporal cognition in two mouse strains. Int J Comp Psychol. 2001;14:189–210. [Google Scholar]
- Balci F, Moore H, Brunner D. Timing deficits in aging and neuropathology. In: Bizon JL, Wood AG, editors. Animal Models of Human Cognitive Aging. Humana Press; Totowa, NJ: in press. [Google Scholar]
- Bevins RA, Ayres JJB. One-trial context fear conditioning as a function of the interstimulus interval. Anim Lear Behav. 1995;23:400–410. [Google Scholar]
- Bevins RA, McPhee JE, Rauhut AS, Ayres JJB. Converging evidence for one-trial context fear conditioning with an immediate shock: importance of shock potency. J Exp Psychol Anim Behav Process. 1997;23:312–324. doi: 10.1037//0097-7403.23.3.312. [DOI] [PubMed] [Google Scholar]
- Çevik MO. Effects of methamphetamine on duration discrimination. Behav Neurosci. 2003;117:774–787. doi: 10.1037/0735-7044.117.4.774. [DOI] [PubMed] [Google Scholar]
- Church RM, Deluty MZ. Bisection of temporal intervals. J Exp Psychol Anim Behav Process. 1977;3:216–228. doi: 10.1037//0097-7403.3.3.216. [DOI] [PubMed] [Google Scholar]
- Davis M, Schlesinger LS, Sorenson CA. Temporal specificity of fear conditioning: effects of different conditioned stimulus–unconditioned stimulus intervals on the fear-potentiated startle effect. J Exp Psychol Anim Behav Process. 1989;15:295–310. [PubMed] [Google Scholar]
- Fanselow MS. Associative vs. topographic accounts of the immediate shock-freezing deficit in rats: implications for the response selection rules governing species-specific defensive reactions. Learn Motiv. 1986;17:16–39. [Google Scholar]
- Fetterman JG, Killeen PR. Categorical scaling of time: implications for clock-counter models. J Exp Psychol Anim Behav Process. 1995;21:43–63. [PubMed] [Google Scholar]
- Gallistel C, Gibbon J. Time, rate, and conditioning. Psychol Rev. 2000;107:289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Balsam PD, Fairhurst S. The learning curve: implications of a quantitative analysis. Proc Natl Acad Sci. 2004a;101:13124–13131. doi: 10.1073/pnas.0404965101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel C, King A, McDonald R. Sources of variability and systematic error in mouse timing behavior. J Exp Psychol Anim Behav Process. 2004b;30:3–16. doi: 10.1037/0097-7403.30.1.3. [DOI] [PubMed] [Google Scholar]
- Glover S, Dixon P. Likelihood ratios: a simple and flexible statistic for empirical psychologists. Psychon Bull Rev. 2004;11:791–807. doi: 10.3758/bf03196706. [DOI] [PubMed] [Google Scholar]
- Kass RE, Raferty AE. Bayes factors. JASA. 1995;90:773–795. [Google Scholar]
- Killeen PR, Fetterman JG. A behavioral theory of timing. Psychol Rev. 1988;95:274–295. doi: 10.1037/0033-295x.95.2.274. [DOI] [PubMed] [Google Scholar]
- LeDoux JE. Emotion circuits in the brain. Annu Rev Neurosci. 2000;23:155–184. doi: 10.1146/annurev.neuro.23.1.155. [DOI] [PubMed] [Google Scholar]
- Lejeune H, Hermans I, Mocaër E, Rettori MC, Poignant JC, Richelle M. Amineptine, response timing, and time discrimination in the Albino rat. Pharmacol Biochem Behav. 1995;51:165–173. doi: 10.1016/0091-3057(94)00371-o. [DOI] [PubMed] [Google Scholar]
- Lieving LM. MA Thesis. West Virginia University; Morgantown, WV: 2002. Effects of intertrial interval and D-amphetamine on temporally organized behavior of pigeons. [Google Scholar]
- Maricq AV, Roberts S, Church RM. Methamphetamine and time estimation. J Exp Psychol Anim Behav Process. 1981;7:18–30. doi: 10.1037//0097-7403.7.1.18. [DOI] [PubMed] [Google Scholar]
- McClure EA, Saulsgiver KA, Wynne CDL. Effects of D-amphetamine on temporal discrimination in pigeons. Behav Pharmacol. 2005;16:193–208. doi: 10.1097/01.fbp.0000171773.69292.bd. [DOI] [PubMed] [Google Scholar]
- Meck WH. Selective adjustment of the speed of internal clock and memory processes. J Exp Psychol Anim Behav Process. 1983;9:171–201. [PubMed] [Google Scholar]
- Miller RR, Barnet RC. The role of time in elementary associations. Curr Dir Psychol Sci. 1993;2:106–111. [Google Scholar]
- Odum AL, Lieving LM, Schaal DW. Effects of D-amphetamine in a temporal discrimination procedure: selective changes in timing or rate dependency? J Exp Anal Behav. 2002;78:195–214. doi: 10.1901/jeab.2002.78-195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papachristos EB, Gallistel CR. Autoshaped head poking in the mouse: a quantitative analysis of the learning curve. J Exp Anal Behav. 2006;85:293–308. doi: 10.1901/jeab.2006.71-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Platt JR, Davis ER. Bisection of temporal intervals by pigeons. J Exp Psychol Anim Behav Process. 1983;9:160–170. [PubMed] [Google Scholar]
- Santi A, Weise L, Kuiper D. Amphetamine and memory for event duration in rats and pigeons: disruption of attention to temporal samples rather than changes in the speed of the internal clock. Psychobiology. 1995;23:224–232. [Google Scholar]
- Santi A, Coppa R, Ross L. Effects of the dopamine D2 agonist quinpirole on time and number processing in rats. Pharmacol Biochem Behav. 2001;68:147–155. doi: 10.1016/s0091-3057(00)00452-4. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- Shumyatsky GP, Tsvetkov E, Malleret G, Vronskaya S, Hatton M, Hampton L, Battey JF, Dulac C, Kandel ER, Bolshakov VY. Identification of a signaling network in lateral nucleus of amygdala important for inhibiting memory specifically related to learned fear. Cell. 2002;111:905–918. doi: 10.1016/s0092-8674(02)01116-9. [DOI] [PubMed] [Google Scholar]
- Staddon JER, Higa JJ. Temporal learning. In: Medin D, editor. The Psychology of Learning and Motivation. Vol. 27. Academic; New York: 1993. pp. 265–294. [Google Scholar]
- Stanford L, Santi A. The dopamine D2 agonist, quinpirole, disrupts attention to temporal signals without selectively altering the speed of the internal clock. Psychobiology. 1998;26:258–66. [Google Scholar]
- Stubbs DA, Thomas JR. Discrimination of stimulus duration and D-amphetamine in pigeons: a psychophysical analysis. Psychopharmacologia. 1974;36:313–22. doi: 10.1007/BF00422563. [DOI] [PubMed] [Google Scholar]