Joint independent component analysis for simultaneous EEG-fMRI: Principle and Simulation

Abstract

An optimized scheme for the fusion of electroencephalography and event related potentials with functional magnetic resonance imaging (BOLD-fMRI) data should simultaneously assess all available electrophysiologic and hemodynamic information in a common data space. In doing so, it should be possible to identify features of latent neural sources whose trial-to-trial dynamics are jointly reflected in both modalities. We present a joint independent component analysis (jICA) model for analysis of simultaneous single trial EEG-fMRI measurements from multiple subjects. We outline the general idea underlying the jICA approach and present results from simulated data under realistic noise conditions. Our results indicate that this approach is a feasible and physiologically plausible data-driven way to achieve spatiotemporal mapping of event related responses in the human brain.

Introduction

The integration of multiple neuroimaging modalities is motivated by the aim to develop better images of ‘where’ and ‘when’ information processing is taking place in the brain, and to eventually develop a better understanding of ‘how’ the brain works. When used separately, the major neuroimaging methodologies that are currently used for addressing these questions have limitations, and allow only for either spatially or temporally restricted inferences regarding brain function, in other words, inferences based on either method alone are based on partial and not necessarily comprehensive representations of brain activity. This motivates development of recording and analysis approaches which draw upon the strengths of each method to afford a spatiotemporally and functionally more complete characterization of regional brain responses (Dale, et al., 2001; Debener, et al., 2006; Hopfinger, et al., 2005; Horwitz, et al., 2002; Makeig, 2002).

Functional magnetic resonance imaging (fMRI) of the blood oxygenation level dependent (BOLD) response (Bandettini, et al., 1992; Kwong, et al., 1992; Ogawa, et al., 1990) measures local changes in brain hemodynamics with excellent spatial resolution. However, the BOLD contrast is an indirect and delayed metabolic correlate of neuronal processes after a complex set of reactions constituting neurovascular coupling (Lauritzen, et al., 2003; Logothetis, 2003; Villringer, et al., 1995). With some notable exceptions that achieve a temporal resolution on the order of hundreds of milliseconds (Formisano, et al., 2003; Menon, et al., 1998; Ogawa, et al., 2000), measures of the BOLD response in typical experimental designs do not allow for assessment of the chronometry of processing with any relevant precision.

In contradistinction to BOLD-fMRI, electroencephalography (EEG) and event related potentials (ERP) measure the electrical potentials induced by synchronized synaptic activity directly. Typical EEG/ERP measures afford an effective temporal resolution of mental processes on the order of tens of milliseconds, but provide only inferior spatial precision in scalp recordings. This is because the scalp EEG picks up a blurred spatial mixture of the underlying (mainly cortical) activity. Additionally, inferring the spatial locations of electric sources requires a solution to the ill-posed inverse problem of recovering the true 3-dimensional source locations from 2-dimensional sensor data.

Multimodal integration may thus reveal novel information not observed in either technique alone. The neuronal sources underlying the generation of EEG/ERP and fMRI features should ideally be detected by a common fusion model that simultaneously assesses all available data. Currently, the different concepts for EEG-fMRI integration that have been reported in the literature have only partially accomplished this.

One approach is to model the fMRI signal as a function of the EEG convolved with a hemodynamic response function. Assuming a linear neurovascular coupling relationship between the hemodynamic response, local field potentials and the scalp EEG phenomena (Heeger, et al., 2002; Lauritzen, et al., 2003; Logothetis, et al., 2001; Logothetis, 2003; Mukamel, et al., 2005; Shmuel, et al., 2006), this integration by prediction quantifies the covariation in the EEG-fMRI relationship and ensures some specificity with respect to the spatiotemporal inferences. In this fashion, the hemodynamic correlates of EEG rhythms (Feige, et al., 2005; Goldman, et al., 2002; Laufs, et al., 2003; Moosmann, et al., 2003), and interictal EEG phenomena in epilepsy (Gotman, et al., 2004; Salek-Haddadi, et al., 2003) were first studied.

Expanding this approach to single trial (time-domain) data affords the assessment of induced or spontaneous, adaptive modulations of event related responses in the brain (Debener, et al., 2006). The growing number of studies that implement single-trial EEG-fMRI methodology have so far described regional BOLD correlates for a number of components: Contingent Negative Variation (CNV, Hinterberger, et al., 2005; Nagai, et al., 2004), P2 and N2 (Eichele, et al., 2005), P3 (Benar, et al., 2007; Eichele, et al., 2005) and Error Related Negativity (ERN, Debener, et al., 2005). In all of the above cited work there is room for improvement with respect to the proportion of the EEG data that is used for integration. That is, all these studies employed only a subset of the available data, and disregard potentially relevant temporal and spatial information, respectively. Additionally, the visibility of integration by prediction is obscured in conditions where the modulation representing the process of interest is spatially and/or temporally mixed, which applies separately to both EEG as well as fMRI measures (Eichele, et al., 2007). For example, this might lead to false-negative predictions in cases where the EEG-derived predictor is a mixture of two or more sources with different modulations.

In order to overcome these limitations, we propose an analysis scheme for integration of single trial EEG with BOLD-fMRI data that assesses and unmixes all the electrophysiologic and hemodynamic information that is available simultaneously in a common data space.

One possible strategy for fusion of imaging features from different modalities is based on joint independent component analysis (jICA) of ERPs and fMRI together and has been recently implemented (Calhoun, et al., 2006b; Calhoun, et al., 2006c). They established a connection between different components of the ERP waveforms and fMRI spatial maps by entering average ERPs from the vertex electrode and fMRI contrast images for a group of subjects into one joint space, deriving a spatiotemporal solution with jointly estimated maximally independent sources of between-subject effects. It is straightforward to extend jICA (Calhoun, et al., 2006c) to within-subject single trial data (Benar, et al., 2007; Debener, et al., 2005; Eichele, et al., 2005) from both modalities, employing all EEG channels and timepoints in the estimation, thus incorporating all available time-domain and spatial information.

ICA is a blind source separation technique that has been developed to solve a 2D linear mixing problem of spatially, and/or temporally independent sources (Calhoun, et al., 2006a; Hyvarinen, et al., 2000; Stone, 2002). ICA models spatiotemporal data as a linear combination of maps and timecourses while attempting to maximize the independence between either the maps (spatial ICA, sICA) or the time courses (temporal ICA, tICA). ICA has been applied successfully to a variety of problems in auditory signal processing (Bell, et al., 1995), image processing (Bell, et al., 1997), averaged ERPs (Makeig, et al., 1997), single trial EEG (Makeig, et al., 2004; Onton, et al., 2006), fMRI (Biswal, et al., 1999; Calhoun, et al., 2001; McKeown, et al., 1998), and EEG-fMRI integration (Debener, et al., 2005; Eichele, et al., 2007; Feige, et al., 2005).

The key point to consider is that origin, spatial or temporal structure in input data is essentially irrelevant for ICA, such that the data can be organized in any fashion. This also implies that data from different subjects, tasks, and modalities can be used jointly for estimation of components (Calhoun, et al., 2006a; Calhoun, et al., 2006b; Calhoun, et al., 2006c; Eichele, et al., 2006; Kolenda, et al., 2002; Schmithorst, et al., 2004), as long as one can assume a ground truth where each recording faithfully represents features and distributional properties from the same set of sources across repeated measurements, i.e. the covariation across single trials (Benar, et al., 2007; Debener, et al., 2005; Eichele, et al., 2005) and/or subjects (Calhoun, et al., 2006b; Calhoun, et al., 2006c). If one additionally assumes joint independence of the fMRI and EEG portions of the sources, respectively, one can use e.g. extended Infomax ICA which employs a gradient ascent algorithm to maximize the entropy of the output of a single layer neural network (Bell, et al., 1995; Lee, et al., 1999).

In order to focus on correspondences between data modalities, a set of data transformations are necessary to increase the homogeneity of the data within and across subjects and modalities and remove portions of the data that can be assumed not to be mutually represented. For the MRI data, this would typically refer to adequate pre-processing such as transformation of individual anatomies into a standardized space, correction of head motion related image offsets, temporal filtering, and appropriate masking to deal with variability from eyes, ventricles, large vessels, and magnetic susceptibility artefacts. Optionally, this can also be achieved with an individual ICA-step for spatial filtering of artefact components. Matlab-based toolboxes for this purpose such as statistical parametric mapping (SPM, http://www.fil.ion.ucl.ac.uk/) and group spatial ICA (GIFT, http://www.icatb.sourceforge.net) are available as academic freeware.

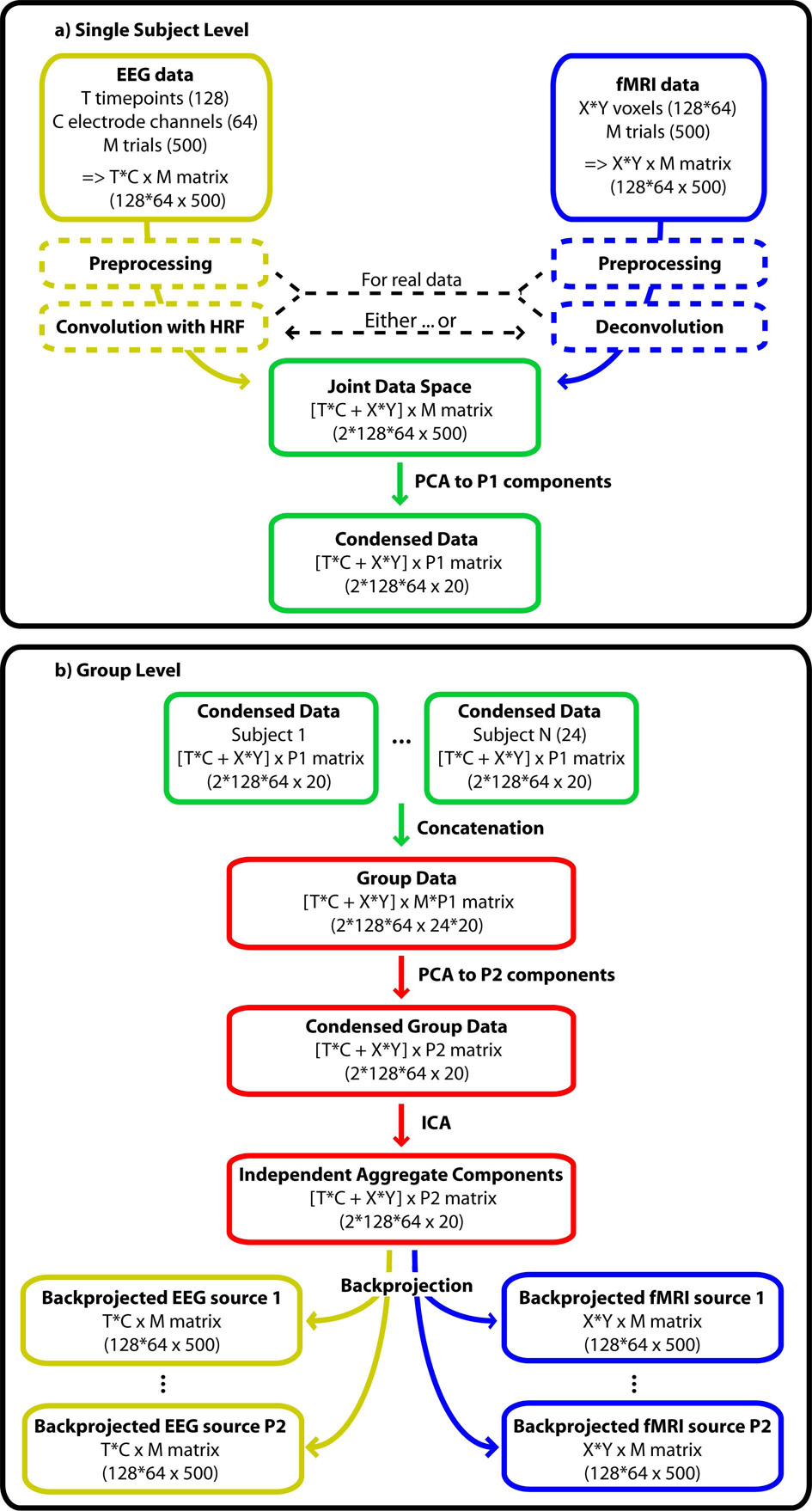
Similarly, for the EEG data, band-pass filtering, event-related epoching, re-referencing, exclusion of paroxysmal artifacts, correction for MR-gradient artefacts (Allen, et al., 2000) and ICA-based reduction of pulse-related (Debener, et al., 2007; Niazy, et al., 2005) and ocular (Jung, et al., 2000a; Jung, et al., 2000b) artefacts are appropriate. Tools for these preprocessing steps are available in e.g. EEGLAB (Delorme, et al., 2004). Additionally, one may consider constraining the time-frequency content by means of wavelet denoising (Quian Quiroga, et al., 2003). Real EEG data would then typically be convolved with a canonical or estimated empirical hemodynamic response function to account for the neurovascular delay. Alternatively, fMRI could be deconvolved, although this has so far not been implemented in the context of EEG-fMRI integration. EEG and fMRI data should be brought into the same range for example by normalization of each sample to unit variance across trials. Both modalities should be about the same size in the joint space, such that the decomposition of variability in the data is based on a balanced representation of EEG and fMRI features. Performing a joint decomposition of two (or more) modalities then provides estimates of components that are linked by common mixing parameters (Fig. 1).

Figure 1.

Schematic illustration of the joint ICA approach. EEG and fMRI data should undergo typical preprocessing, including convolution or deconvolution to compensate for the hemodynamic lag before entering the joint data space. A PCA compresses the data on single subject level. Single subject data are then concatenated in an aggregate set. A second PCA condenses redundant information on group level before the data are decomposed into independent components. Backprojection to EEG and fMRI data space allows the visualization of the separated processes. The numbers in brackets specify the matrix dimension chosen in this simulation. The symbol ‘x’ denotes ‘by’ as in a 10 by 20 matrix whereas the symbol ‘*’ denotes multiplication.

Method

In the generative model for joint ICA we assume a set of latent non-gaussian neuronal sources

$$\mathrm{s}={({\mathrm{S}}_1,{\mathrm{S}}_2,\dots ,{\mathrm{S}}_{\mathrm{n}})}^{\mathrm{T}}$$

whose response properties such as local field potentials are transformed by an unknown mixing matrix A to the observed normally distributed signal x

$$\mathrm{x}=\mathrm{A}\mathrm{s}$$

In single trials of a simultaneous recording, features of the sources and their mixture are observed as volume conducted electrophysiological effects in the scalp EEG E at timepoints t and channels c as A^Es

$${\mathrm{x}}^{\mathrm{E}}={[{{\mathrm{x}}^{\mathrm{E}}}_1(\text{tc}),{{\mathrm{x}}^{\mathrm{E}}}_2(\text{tc}),\dots ,{{\mathrm{x}}^{\mathrm{E}}}_{\mathrm{n}}(\text{tc})]}^{\mathrm{T}}$$

Likewise, the hemodynamic correlates of the neuroelectric/electro-chemical activation are detected in fMRI volumes F at the respective locations v as A^Fs

$${\mathrm{x}}^{\mathrm{F}}={[{{\mathrm{x}}^{\mathrm{F}}}_1(\mathrm{v}),{{\mathrm{x}}^{\mathrm{F}}}_2(\mathrm{v}),\dots ,{{\mathrm{x}}^{\mathrm{F}}}_{\mathrm{n}}(\mathrm{v})]}^{\mathrm{T}}$$

After appropriate transformations (see introduction), the mixture is entered into a common 2D space from which fused signals

$${\mathrm{y}}^{\text{EF}}={[{{\mathrm{x}}^{\text{EF}}}_1(\text{tcv}),{{\mathrm{y}}^{\text{EF}}}_2(\text{tcv}),\dots ,{{\mathrm{y}}^{\text{EF}}}_{\mathrm{n}}(\text{tcv})]}^{\mathrm{T}}$$

are extracted by adjusting the unmixing matrix W (the inverse of A), such that y = Wx optimally represents s. The update equation for the algorithm to compute the common unmixing matrix W and the fused single trial EEG and fMRI sources, u^EF is ΔW = η{I-2 y^EF (u^EF) ^T } W, where y^EF = g(u^EF), and g(x) = 1/(1+e^−x) is the nonlinearity in the neural network.

In this simulation, sources were created whose activities across the observation time are reflected in the trial-by-trial modulation of two-dimensional fMRI spatial maps of 128 by 64 voxels. Simultaneously, the electrophysiological source activities are captured with multi-channel scalp EEG, i.e. spatio-temporal maps containing 128 timepoints and 64 channels. The temporal sampling rate after MR-gradient artefact removal may typically range from 100–1000Hz, so that the current simulation may correspond to e.g. 512 ms epochs with 4 ms samples. In this fashion, 24 data-sets were simulated, corresponding to subjects of a medium sized group study.

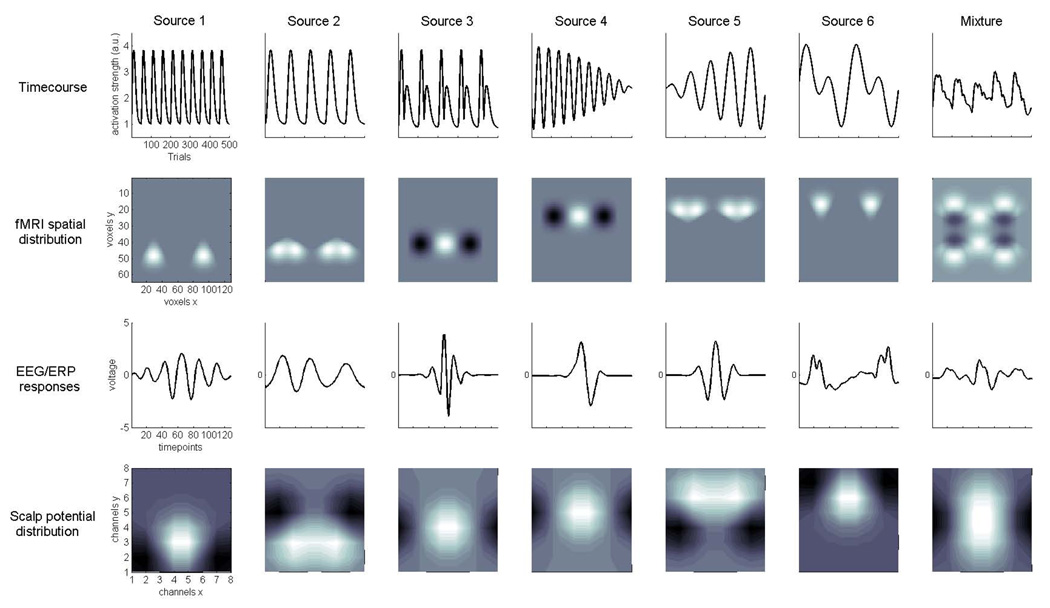
Six hypergaussian sources (S1–S6) were created with activities across 500 observed trials, yielding the source timecourses. These activities were repetitive functions with fast and slow dynamics as might be induced by a stimulation paradigm (Fig. 2, first row): S1 generates a 10-fold repetition of a 50-trial wide gamma distribution function with shape k = 4 and scale θ = 4; S2 a 5-fold repetition of a 100-trial wide gamma function with shape k = 6 and scale θ =6; S3 the approximate derivative of S2; S4 yields the product of two sine waves with f₁=0.00315 Hz and f₂=0.125 Hz; S5 the product of two sine waves with f₁=0.00315 Hz and f₂=0.0625 Hz; S6 the sum of two sine waves with f₁=0.025 Hz and f₂=0.05 Hz. Amplitude variability was incorporated by scaling each point in a timecourse by a random factor ranging from 0.5 to 1.5 around the respective value.

Figure 2.

Joint source model for ERP-fMRI data. The figure shows example of the simulated sources of neuronal activity detected in simultaneous single trial fMRI and EEG/ERP recordings. Columns from left to right contain the Sources 1–6 and their linear mixture: rows contain the key features, i.e. experimental timecourses, fMRI spatial distribution and ERP transient responses and scalp potential distribution. Axes are the same for all columns and are shown on the leftmost plots. For the six 500-point timecourses (1^st row), trains gamma functions of different widths (S1, S2), and combinations of sine waves at different frequencies (S4, S5, S6) were used. fMRI spatial distributions (2^nd row) of hemodynamic responses were simulated as partially overlapping gaussian-smooth regional increases (lighter shading) or decreases (darker shading) of activation in a 128×64 matrix. 128-point ERP transient responses (3^rd row) were taken from filtered real-data averages and selected such that they covered a range of ERP shapes, and more continuous event related oscillations. Symmetric dipolar potential distribution maps (4^th row) were additionally generated for an 8×8 grid of channels on the scalp.

For the fMRI spatial maps (Fig. 2, second row) we assume that at each trial n a number of localized regional brain responses from sources S1–S6 are generated in spatially independent areas that are associated with the dedicated function reflected in the respective timecourse at trial n. The intensities of these largely separated, non-systematically overlapping source activations may be positive and/or negative (corresponding to activations and deactivations, respectively), and approximate medium-sized regional responses with a gaussian shape. This may be due to the spatial properties of the hemodynamic response function per se, and/or as a result of smoothing during pre-processing. The total extent was set to between 10–20% of the volume with overlap of some sources at the outer borders of the active region. Across datasets, separately for each source map but fixed across trials, the locations were varied around the idealized location by randomly drawing the x and y offset-coordinates from a 5-sample gaussian distribution ranging from −2 (11%), −1 (24%), 0 (30%), +1 (24%), +2 (11%). This was done in order to account for a proportion of the commonly observed spatial activation differences between individual brains after spatial normalization and smoothing.

The event related EEG waveforms (Fig. 2, third row) were taken from a group grand average of an unrelated study. These were wavelet filtered to generate 128 point event related time-series with different time-frequency features of the same data. Thus, the shape of the waveforms ranges from continuous oscillations at faster (S1) and slower (S2) scales, more localized activity with faster (S3) and slower transients (S4, S5) to a more complex mixture (S6) with both fast and slow features. Latency jitter is a relevant source of variability in single trials, long-latency components such as the N1 and P3 jitter 10–30 ms in our experience (for comparison, see e.g. Spencer, 2005). For each trial and source separately, latency jitter was generated by randomly shifting the waveform onset by a value drawn from a 7-sample gaussian distribution with the probabilities −3 (3%), −2 (10%), −1 (22%), 0 (29%), +1(22%), +2 (10%), +3 (3%).

Scalp distributions (Fig. 2, fourth row) were generated as a spatial array of 64 channels an 8 × 8 grid as smooth dipolar maps, i.e. with polarity inversions, and with considerable overlap between the sources.

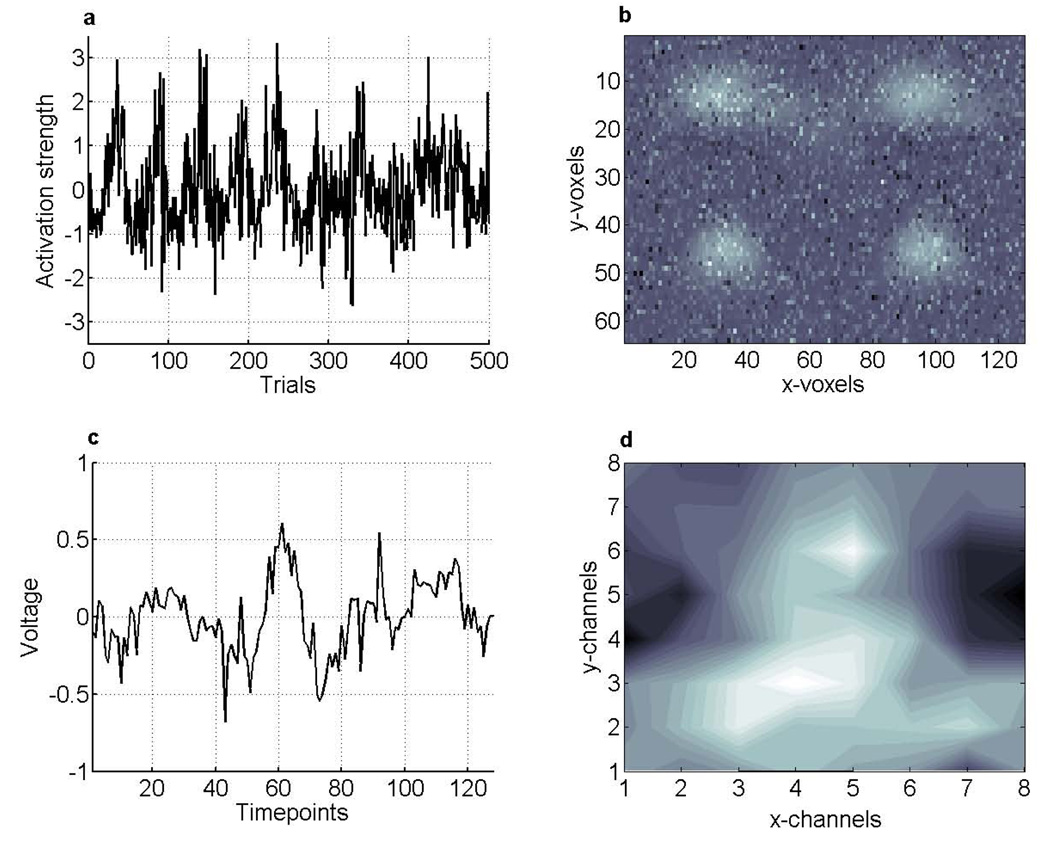
Noise was added to the data by entering random permutations of all sources into the respective portions of the matrix (Fig. 3). In order to demonstrate the feasibility of group ICA for the case of between-subject differences of present sources, only four out of the six possible sources were randomly selected to be present in each data set.

Figure 3.

Simulated data. A 500 trial experimental timecourse from an arbitrary volume element is shown in plot a. Plots b–d depict data from data-set #1 at trial #250, that is, the 128 × 64 voxel fMRI image. Light areas indicate areas of higher activation, and dark areas correspond to lesser activation. Plot c shows the 128 samples ERP voltage timecourse. Plot d shows the 8 × 8 channels 2D scalp potential map for timepoint #64. Lighter areas indicate positive voltage and darker areas negativity, reflecting the dipolar structure of these maps. Multiplication of c with d yields the 128 timepoints × 64 channels spatiotemporal ERP image.

For each of the 500 trials, fMRI spatial maps form one slice of an image volume with 128 × 64 simulated voxels, EEG timecourses and scalp distributions are factored together to form another slice containing 128 time points × 64 channels, containing all the electrophysiological information for one trial.

In the analysis stage, each of the 24 datasets consisting of 500 two-slice volumes were first pre-whitened and reduced using principal component analysis (Calhoun, et al., 2001; Hyvarinen, et al., 2000). PCA whitening preconditions the data and simplifies ICA estimation due to the orthogonal projection, reduction of complexity, and de-noising. This means that for each subject, the matrix of trials-by-EEG*fMRI was reduced to 20 PCs-by-EEG*fMRI, thus condensing the ‘trials’ dimension from 500 to 20 (4% of the raw size) while retaining the major proportion of the variability. These matrices were then concatenated across subjects to form a matrix of size 24*20 PCs-by-EEG*fMRI, that was reduced to 20 PCs, thus condensing the ‘subjects’ dimension. This aggregate matrix is then decomposed to 20 independent components. In this conformation, individual subject maps can be back-reconstructed by partitioning the second PCA decomposition matrix into submatrices corresponding to each subject, and trial-by-trial timecourses are generated by multiplication of the respective portion in the unmixing matrix with the individual raw data (Fig. 1). This way, the joint ICA recovers fMRI/EEG templates of activity that can be traced back to single trials in single subjects through the grand mixing matrix (Calhoun, et al., 2006a; Calhoun, et al., 2001; Schmithorst, et al., 2004).

We deliberately chose the number of components to be estimated to exceed the true number of sources five-fold to demonstrate the stability of the algorithm against misallocation/’splitting’ of components.

Matlab code for data generation and visualization, and the simulated data used here are available in GIFT/SPM and EEGLAB compatible formats from the authors upon request.

Results

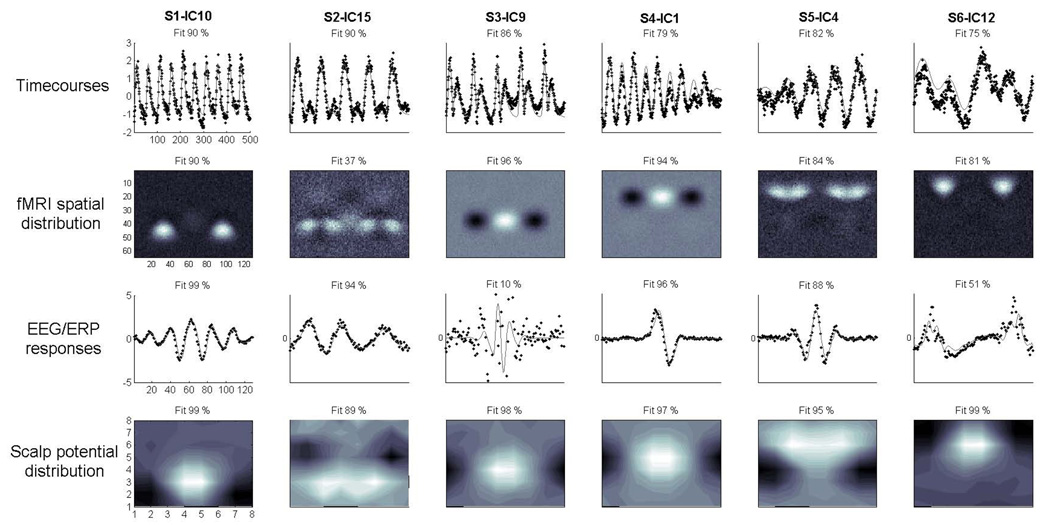
Independent components were estimated, back-reconstructed (for details, see Calhoun, et al., 2001), averaged across data-sets and compared to the original sources with linear regression using least squares. For each of the four features, i.e. the across-trial timecourses, fMRI spatial maps, waveforms and scalp maps the goodness-of-fit was determined. This was done by regressing each of these aspects of the 20 estimated components onto the respective features of the six sources. Table 1 displays all results for one representative jICA decomposition. For each source, the component with best correspondence to the source was determined using the R² sum of the fits over all four features, resulting in the pairings S1 - IC10, S2 - IC15, S3 - IC9, S4 - IC1, S5 - IC4 and S6 - IC12.

Table 1.

Correspondence between simulated sources and independent components. The four features, i.e. timecourse, fMRI spatial, ERP temporal and scalp distribution of the six sources (S1–S6) were projected onto the activation patterns of the twenty estimated independent components (IC 1–20) with multiple linear regression using least squares separately for each of the features. As a goodness-of-fit measure, the R²-value was used.

Component #
IC	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Timecourse
S1	.35	.23	.33	.01	.00	.00	.09	.08	.18	.90	.02	.01	.11	.21	.14	.00	.09	.27	.34	.09
S2	.37	.32	.20	.27	.26	.00	.05	.11	.11	.00	.04	.00	.04	.00	.90	.19	.04	.24	.09	.14
S3	.01	.36	.83	.32	.00	.16	.09	.02	.86	.26	.04	.00	.03	.01	.17	.02	.02	.22	.14	.05
S4	.79	.25	.29	.00	.00	.00	.06	.03	.20	.47	.01	.00	.08	.20	.25	.06	.04	.19	.26	.05
S5	.10	.31	.31	.82	.15	.01	.06	.14	.27	.01	.02	.00	.08	.01	.42	.03	.01	.29	.14	.11
S6	.00	.03	.01	.01	.22	.19	.19	.15	.03	.03	.12	.75	.59	.19	.00	.21	.46	.09	.12	.32
fMRI spatial
S1	.00	.02	.00	.01	.00	.00	.00	.05	.09	.90	.00	.01	.00	.00	.00	.36	.00	.00	.00	.00
S2	.01	.00	.00	.02	.00	.00	.00	.01	.19	.31	.02	.02	.00	.00	.37	.13	.00	.00	.00	.00
S3	.00	.00	.01	.00	.00	.00	.00	.00	.96	.07	.01	.00	.00	.01	.00	.02	.00	.00	.00	.00
S4	.94	.02	.00	.14	.00	.00	.02	.02	.00	.00	.00	.04	.02	.01	.01	.01	.00	.00	.00	.00
S5	.19	.00	.00	.84	.00	.00	.00	.01	.00	.02	.00	.13	.00	.01	.00	.01	.01	.01	.00	.01
S6	.11	.00	.00	.26	.00	.00	.00	.00	.00	.01	.00	.81	.04	.01	.00	.00	.09	.00	.00	.00
ERP temporal
S1	.30	.19	.00	.68	.03	.05	.00	.01	.03	.99	.00	.01	.00	.05	.00	.05	.00	.03	.00	.00
S2	.22	.01	.00	.00	.01	.01	.03	.00	.00	.00	.03	.16	.01	.00	.94	.02	.04	.00	.01	.00
S3	.00	.09	.79	.06	.04	.01	.06	.08	.10	.00	.00	.00	.00	.00	.00	.01	.00	.00	.03	.01
S4	.96	.19	.01	.42	.00	.00	.04	.03	.03	.30	.03	.03	.00	.01	.18	.01	.00	.00	.01	.00
S5	.41	.31	.02	.88	.04	.05	.00	.08	.12	.71	.00	.00	.00	.07	.00	.01	.00	.03	.00	.01
S6	.02	.00	.00	.00	.00	.00	.00	.00	.00	.02	.00	.51	.28	.03	.20	.00	.04	.01	.00	.00
Scalp distribution
S1	.14	.12	.33	.04	.37	.11	.00	.35	.37	.99	.98	.01	.01	.05	.06	.52	.01	.00	.00	.01
S2	.21	.12	.24	.00	.21	.18	.07	.20	.23	.06	.09	.01	.01	.97	.89	.03	.01	.00	.02	.01
S3	.77	.60	.99	.35	.94	.71	.11	.99	.98	.38	.48	.08	.07	.21	.15	.13	.09	.00	.01	.02
S4	.97	.87	.71	.37	.63	.99	.17	.70	.61	.10	.14	.35	.33	.17	.12	.02	.35	.02	.01	.00
S5	.25	.23	.19	.95	.19	.25	.98	.23	.15	.01	.02	.06	.05	.05	.04	.00	.06	.01	.00	.00
S6	.29	.33	.10	.07	.09	.33	.05	.10	.09	.01	.02	.99	.99	.02	.01	.01	1.0	.08	.01	.00
Fit	S4			S5					S3	S1		S6			S2

In summary, all six sources are recovered with sufficient fits on at least three out of four features. Best fits range from R²=0.75 – 0.90 for the six simulated source timecourses, R²=0.37 – 0.96 for the fMRI spatial maps, R²= 0.10 – 0.99 for the waveforms, and R²=0.89 – 0.99 for the scalp distributions. Across all features of the six best-fit components this averaged to R²=0.82, indicating a good overall performance. A number of remaining components do show good fits for one or two features but poor fits with the rest (except for IC3, see below). Poorest performance within the best-fit components (i.e. R² < 0.5) was seen in the fMRI map for S2 (R²=0.37, IC15) which yielded the correct source locations but captured a substantial amount of randomly distributed noise. Also, the ERP waveform associated with S3 (R²=0.10, IC9) is not well represented in this component, but is found in IC3, which in turn does not fit with the fMRI map. The same effect is seen to a weaker extent in S6 (0.51, IC12) where portions of the estimated waveform departs from the source during the fast transients early and late in the waveform. All relevant results are detailed in table 1, and figure 3 displays the best-fit components.

Discussion

This work presents an approach to fuse single-trial electrophysiologic and hemodynamic data from single or multiple subjects on single trial level. The approach uses a combination of principal component analysis for data reduction and independent component analysis that is computed in a common space containing the spatiotemporal data from all subjects and trials. The motivation for the development of this method is to improve the detection and visualization of neuronal mass responses and their conjointly recorded EEG and fMRI correlates.

In order to validate this method we employed a simulation of the data types acquired in simultaneous recordings. A simulation affords to create a situation of known sources and noise parameters and is furthermore useful to illustrate the concept of the joint ICA approach. We implemented within-subject spatial, temporal and amplitude variability as well as between-subject differences in the number and quality of sources. The fit of the jICA solution with the ideal sources demonstrates that this approach offers a feasible solution to factor two separate higher-dimensional data sets into one common data space on single-trial level and achieve plausible results.

Since the decomposition is computed for all data-sets/subjects simultaneously it is straightforward to test the fMRI spatial and EEG spatiotemporal weights of the components to generate random-effects inferences for the time courses as well as the voxel activation maps. This can also be done in the statistical parametric mapping framework where testing within the gaussian random field theory with adjustments for multiple comparisons (e.g. SPM, Friston, et al., 1995; Kilner, et al., 2005).

The advantage of the joint ICA approach is that associations among the EEG/ERP and fMRI data are established during the unmixing process in a fused space, which inherently captures relationships among both data in a more comprehensive fashion and allows for intuitive visualization of sources, as well as inference testing. Apart from being used as a primary tool for inference, we believe that there is a utility for jICA in the mining stage of prediction-based multimodal analysis: for example, in cases where a-priori models can only be poorly specified, e.g. where the selection criteria for appropriate electrodes and time-windows from the EEG data to form the predictors for regression are unclear, jICA results can be used for model specification. Also, jICA can be helpful for ‘data diagnostics’ when prediction-based inferences fail despite strong priors. Here, jICA (or ICA on both modalities separately) can be used to assess the degree to which mixing of latent sources contributed.

An additional advantage is that the spatiotemporal solution is derived selectively from information content and distributional properties, thus bypassing the electromagnetic inverse problem.

One potential limitation of the current method is that jICA does not capture the time-domain of event related oscillations that are not tightly time/phase-locked oscillations in one component. This is a consequence of the mixed trial-to-trial spatio-temporal organization of the data, which inherently limits the visibility of this method to evoked activity, both within and across subjects. Sources that have a loose or stochastic relation to stimulus/response onset (here: sampling in x-direction of the ERP slice), might be represented in more than one component, although being spatially fixed (here: sampling in the fMRI slice and y-direction in the ERP slice). In the simulated data, the occurrence of this split-up phenomenon was moderated by the 5-sample gaussian latency jitter that impacted stronger on the fast transients in S3 and S6 in comparison to the sources with a slower response profile. This is in contradistinction to the performance of temporal ICA on concatenated EEG epochs from single subjects, which is insensitive to trial-to-trial phase/latency variability of sources. However, temporal ICA on EEG single trials in a joint space with the fMRI data appears difficult to implement. As a remedy, one might consider supplementing/replacing EEG/ERP time-domain data with frequency or time-frequency transformed data, or incorporate correction for latency jitter during preprocessing where appropriate (Quian Quiroga, et al., 2003; Spencer, 2005). An alternative to joint estimation is to compute a group ICA on fMRI and EEG data separately (Eichele, et al., 2007), and link the two modalities via correlation methods, clustering, or PCA/ICA on the derived component across-trial timecourses.

We assume from tests in simulated, hybrid, and real data that joint ICA (Calhoun, et al., 2006b; Calhoun, et al., 2005) is a useful addition to the EEG-fMRI integration toolbelt which can successfully decompose a gaussian mixture of non-gaussian sources. In this situation it will perform better than point-to-point correlation analysis with respect to the degree of data reduction/number of tests in the case where the model is spatially or temporally incomplete or ill-specified.

However, one should be careful to keep in mind that it is to date not determined for any of the analysis frameworks, i.e. integration by constraints, integration by prediction and common generative models such as the one presented here, on which conditions they are fully appropriate and ultimately reveal the ‘true’ spatiotemporal maps. This type of validation for EEG-fMRI analysis methods will require a study design that has fMRI, scalp and intracranial EEG available in order to establish a ground truth about the coupling between the modalities.

Figure 4.

Results. The figure displays the averaged estimated independent components with the overall best fit with the respective sources across the four features. Black dotted lines in the timecourse and EEG/ERP response plots indicate IC activation. Original sources were superimposed in grey for comparison in the first and third row. Percentage of variance accounted for is indicated above each plot.