Abstract
Concurrent event-related EEG-fMRI recordings pick up volume-conducted and hemodynamically convoluted signals from latent neural sources that are spatially and temporally mixed across the brain, i.e. the observed data in both modalities represent multiple, simultaneously active, regionally overlapping neuronal mass responses. This mixing process decreases the sensitivity of voxel-by-voxel prediction of hemodynamic activation by the EEG when multiple sources contribute to either the predictor and/or the response variables. In order to address this problem, we used independent component analysis (ICA) to recover maps from the fMRI and timecourses from the EEG, and matched these components across the modalities by correlating their trial-to-trial modulation. The analysis was implemented as a group-level ICA that extracts a single set of components from the data and directly allows for population inferences about consistently expressed function-relevant spatiotemporal responses. We illustrate the utility of this method by extracting a previously undetected but relevant EEG-fMRI component from a concurrent auditory target detection experiment.
Keywords: EEG-fMRI, ICA, ERP, auditory, change detection
Introduction
Processing of simple stimuli and tasks produces spatially and temporally extensive event-related neuronal responses in the brain. For example, auditory target detection induces hemodynamic activation in about fourty cortical, subcortical and cerebellar regions (Kiehl, et al., 2005), complementing the results from intracranial recordings (Baudena, et al., 1995; Halgren, et al., 1995a; Halgren, et al., 1995b). These neuronal mass responses can be observed across scales and modalities from single unit recordings, intracranial and scalp electrophysiology, as well as metabolic and hemodynamic signals, but no single technique provides a sufficient view of the full temporal, spatial and functional extent of these responses. Visibility can be improved with techniques that integrate data across different neuroimaging modalities (Debener, et al., 2006; Hopfinger, et al., 2005; Horwitz, et al., 2002; Makeig, 2002). In the case of concurrent EEG-fMRI recordings, one can complement the temporal resolution provided by scalp potentials with the spatial precision of fMRI. This can be done for example by finding correlations between single-trial modulation at a selected time latency in the event-related EEG and activation in the fMRI volume employing mass univariate voxel-by-voxel analysis (Benar, et al., 2007; Debener, et al., 2005b; Eichele, et al., 2005). Implicit in this approach is the critical assumption that the scalp EEG data from a selected channel and latency can predict the fMRI activation in single voxels (Friston, et al., 1995; Friston, 2005b). This is imposed by the sampling properties of the recordings, and the way fMRI time-series data are commonly analyzed. While this assumption provides a workable solution to ‘integration-by-prediction’, it is not necessarily physiologically plausible for many of the samples from both modalities. The reason for this is that a salient event can induce multiple, simultaneously active, regionally overlapping, and functionally separable responses which add to existing neuronal background activity, in other words, event-related processes are spatially and temporally mixed across the brain. The scalp EEG samples a volume-conducted, spatially degraded version of the responses, where the potential at any location and latency can be considered a mixture of multiple independent timecourses that stem from large-scale synchronous field potentials (Makeig, et al., 2004a; Onton, et al., 2006). Similarly, the neurovascular transformation of the distributed neuronal activity into hemodynamic signals (Lauritzen, et al., 2003; Logothetis, 2003) affords detection of blood oxygenation level dependent responses (BOLD, Ogawa, et al., 1990) that are temporally degraded and spatially mixed across the fMRI volume (Calhoun, et al., 2006a; McKeown, et al., 2003).
This physiological spatiotemporal mixing process creates situations in which prediction of fMRI activity by EEG features has to contend with the fact that neither the predictor, nor the response variables are any likely to represent a single source of variability. For example, the point-to-point correlation between the two data mixtures fails when the trial-to-trial modulation in the EEG receives different contributions from several function-relevant spatially separate sources such that no single regional fMRI response represents the predicted signal. Also, this applies to the case where the EEG feature captures a single source, but the fMRI activity at corresponding locations is buried in the spread of other, unrelated sources, leading to underestimation of the spatial extent of the response. Although denoising and inclusion of parametric modulations into the stimulus paradigm (Eichele, et al., 2005), and temporal unmixing of the EEG (Debener, et al., 2005b) solve parts of the problem and make way for refined spatiotemporal mapping, there is still need for improvement of the analysis tools for integration of concurrent recordings (cf. Debener, et al., 2006). One such improvement is to unmix both modalities in parallel at the single-trial level, which follows naturally from the recent work (Calhoun, et al., 2006c; Debener, et al., 2005b; Eichele, et al., 2005) and the reasoning laid out above.
Following the above arguments, we develop an analysis framework for group data that employs Infomax independent component analysis (ICA, Bell, et al., 1995; Lee, et al., 1999; for an overview see Stone, 2002) to recover a set of statistically independent maps from the fMRI (sICA), and independent time-courses from the EEG (tICA) separately, and match these components across modalities by correlating their trial-to-trial modulation. ICA was developed to address linear mixing problems similar to the ‘cocktail party problem’ in which many people are speaking at once and multiple microphones pick up different mixtures of the speakers’ voices (Bell, et al., 1995). The algorithm used here attempts to separate mixed signals into maximally independent sources by maximization of information transfer between them. ICA has general applicability to normally distributed two-dimensional mixtures, and regarding psychophysiological data it has been used for decomposition of averaged ERPs (Makeig, et al., 1997), single trial EEG (Makeig, et al., 2004b; Onton, et al., 2006), fMRI (Calhoun, et al., 2006a) and EEG-fMRI (Calhoun, et al., 2006c; Debener, et al., 2005b; Feige, et al., 2005). ICA can be used for EEG-fMRI integration assuming that the different recording modalities faithfully sample features from the same set of sources, expressed in the covariation between single trials (Debener, et al., 2005b) or subjects (Calhoun, et al., 2006c).
Unlike univariate methods such as the general linear model, ICA is not naturally suited to generalize results from a group of subjects. There are two strategies to allow for matching of independent components across individuals: one is to combine individual ICs across subjects with clustering techniques (Esposito, et al., 2005; Onton, et al., 2006). Another approach is to create aggregate data containing observations from all subjects, estimate a single set of ICs and then back-reconstruct these in the individual data (Calhoun, et al., 2001; Schmithorst, et al., 2004). We adopted the latter strategy for the group EEG temporal ICA analysis, because it directly estimates components that are consistently expressed in the population and involves the least amount of user interaction and is straightforward to combine with the existing framework for group ICA of fMRI data (Calhoun, et al., 2001).
In summary, possible ways for EEG-fMRI integration include predicting both modalities, a mass-univariate framework testing all voxel timeseries in the fMRI, as well as channels and timepoints in the EEG employing a pre-defined model function as is commonly done in fMRI timeseries analysis (however, to the best of our knowledge this has not yet been realized). Another option is to predict the fMRI data with the measured EEG single trial amplitudes, assuming that some EEG timepoints and channels represent functional processes in some voxels without much overlap, representing a point-to-point correlation between mixtures (Benar, et al., 2007; Eichele, et al., 2005). A third solution is to unmix the EEG and predict the fMRI mixture with the modulation of a temporally independent component (Debener, et al., 2005b; Feige, et al., 2005). The method developed here un-mixes both modalities separately, and matches temporal ICs in the EEG with spatial ICs in the fMRI.
The utility of this method is demonstrated in previously published data that were collected in an auditory oddball with varying degrees of target predictability. The parametric modulation induced distinct EEG-correlated fMRI activation patterns at the latencies of the P2, N2, and P3 (Eichele, et al., 2005; see also Jongsma, et al., 2006). We have re-analyzed these data with the open search question whether systematic EEG-fMRI covariation was missed out in our previous analysis and if it could be recovered by parallel ICA. A likely candidate for such a miss is the auditory onset response and the subsequent low-level orienting/change detection processes. Although being expressed in the N1-ERP (Naatanen, et al., 1987; Woods, 1995) and in bilateral temporal fMRI activation (Kiehl, et al., 2005; Liebenthal, et al., 2003; Linden, et al., 1999) this process did not support a significant correlation between the modalities (cf. Eichele, et al., 2005).
Methods
Subjects
Fifteen healthy, right-handed participants (21–28 years, 7f/8m) took part in the experiment after providing informed consent.
Stimuli
Chords of 50 ms duration were presented in an eyes-closed condition via headphones with an onset asynchrony of 2 seconds. Infrequent targets (500Hz) were presented at a probability of 0.25 among frequent standards (250Hz, P 0.75). Alternating sequences of six successive targets were presented either with pseudorandom target-to-target interval (TTI) ranging from 4 to 22 s or with a regular 8 s TTI. Each of these 12-target sequences lasted on the average 96 s, and were repeated 18 times (216 targets total). In order to avoid speeded response times to predictable targets, participants were instructed to respond in the middle of the interval between the target and the next standard stimulus. Participants were not informed about the presence of regular patterns beforehand.
fMRI data acquisition (fig. 1, Bf)
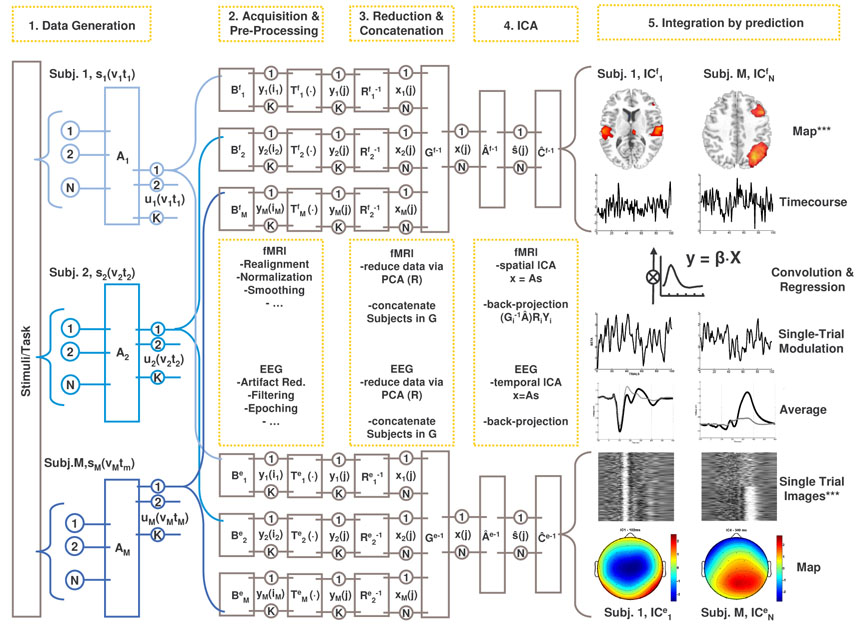
Figure 1. Schematic of parallel group independent component analysis.
We assume that an experimental manipulation induces responses in a set of generic event/function-related neuronal sources (s) in a consistent manner across the sampled population (Subj. 1-M). The sources are expressed spatially (v) and temporally (t) and mixed by the unknown mixing system A. Neurovascular coupling transforms the mixed signals (u) to hemodynamic (BOLD) responses which are sampled from the entire cerebral volume by the MR scanner (Bf), while passive volume conduction enables recording of the signals as scalp EEG (Be). At this step the signals are either temporally (in Bf) or spatially (in Be) degraded, but they sufficiently retain their functional signature, i.e. the trial-to-trial modulation, which affords later matching of components. Modality-specific pre-processing steps (Tf, Te) are then implemented to allow for later group inferences (e.g. spatial normalisation of individual MR volumes), and to reduce noise (e.g. ICA-based artefact removal from the EEG). Hereafter, the individual data are pre-whitened and reduced to N principal component maps (Rf) or timecourses (Re). Individual PCs are then concatenated together in aggregate data-sets (Gf, Ge), containing the N signal mixtures x from all subjects. From the aggregate fMRI data, the mixing matrix Âf and the source maps (s) are estimated using spatial ICA, recovering N spatially independent components in f. From the aggregate EEG data, the mixing matrix Âe and the source timecourses (s) are estimated using temporal ICA, recovering N temporally independent components in e. For each modality, individual component maps and timecourses are back-reconstructed by projecting the aggregate components into the individual, pre-processed data. Components are matched across modalities by correlating the trial-to-trial modulations of the fMRI-sICs with those of the EEG tICs. ***: independent
Imaging was performed on a 1.5T scanner (Siemens, Germany). After scanning of anatomy with a T1-weighted MPRAGE sequence, 300 BOLD sensitive echo planar images (EPI) were collected. EPI volumes were aligned to the anterior-posterior comissura line and consisted of 18 axial slices with 5.5 mm thickness including 0.5 mm interslice gap, flip angle: 90°, excitation time: 60 ms, field of view: 220×220 mm, matrix: 64×64 voxels. A sparse-sampling acquisition protocol (Hall, et al., 1999) with 8 s repetition time and 2 s acquisition time was used. The protocol makes use of the hemodynamic lag between stimulus onset and BOLD peak and allowed for EEG-recording without interfering scanner noise and gradient artefacts during a 6s silent gap between successive volume acquisitions.
EEG data acquisition (fig. 1, Be)
EEGs were recorded continuously at 5 kHz with an amplifier placed inside the MR-scanner (BrainProducts, Germany). Subjects were fitted with an elastic cap containing 30 Ag/AgCl electrodes (FP1, FP2, F7, F3, Fz, F4, F8, T7, C3, Cz, C4, T8, P7, P3, Pz, P4, P8, O1 ,OZ, O2, FC5, FC1, FC2, FC6, CP5, CP1, CP2, CP6, EOG, ECG) referenced to FCz, impedances were kept below 5kΩ.
The analyses reported below were done in Matlab (www.mathworks.com) with the academic freeware toolboxes EEGLAB (http://sccn.ucsd.edu/eeglab), GIFT (http://icatb.sourceforge.org), SPM2 (http://www.fil.ion.ucl.ac.uk/spm), and customized functions. A schematic overview of the analyses is provided in Figure 1.
EEG preprocessing (fig. 1, Te)
Continuous EEGs were downsampled offline to 500 Hz and filtered from 1–45 Hz (24 db/octave). EEG epochs from −312 to 712 ms (512 points) around standard and target sound onsets were recalculated to average reference and subjected to an individual tICA as implemented in EEGLAB (Delorme, et al., 2004). This step was used to identify and remove pulse and eye movement artefacts from the data (cf. Debener, et al., 2007; Jung, et al., 2000), retaining minimally 20 out of 30 components. Single-trials were then wavelet-denoised (Quian Quiroga, et al., 2003), constraining the single trial EEGs to the time-frequency features relevant for the evoked activity.
fMRI preprocessing (fig. 1, Tf)
All images were realigned to the first image in the time-series to correct for head movement and then normalized to the Montreal Neurological Institute (MNI) reference space, and were resliced to a voxel size of 3mm3 and smoothed with a 8mm FWHM gaussian kernel. Voxel timecourses were high-pass filtered at 128 s with a 5th order Butterworth digital filter to remove slow drift, normalized to unit variance, and the image volume for the analysis was constrained to voxels with >50% probability of being grey matter. These pre-processing steps are optional, and empirical choices for this particular data set, but are not principally necessary for sICA of fMRI.
Group spatial ICA of fMRI data (sICA)
An exploratory single-subject spatial ICA was used for inspection of individual components across subjects in our sample, and in order to derive the appropriate number of components to be estimated in the group ICA step using minimum description length criteria (Li, et al., 2006). The estimated dimensionality of the data across subjects averaged to 24, thus the data from each participant was pre-whitened and reduced (in time) to 24 dimensions via principal component analysis (PCA), retaining between 70–90% of the variance (fig. 1, Rf). Individual principal components were then concatenated together in a single set (fig. 1, Gf) in which sICA was performed. In addition to the resulting independent spatial maps, this analysis reconstructs component timecourses by multiplying the dewhitening matrix from the first data reduction by the corresponding partition of the unmixing matrix. These timecourses reflect the trial-to-trial hemodynamic variability of the fMRI experiment and were used for assessment of covariation between components in the two modalities (see tIC-sIC integration). For the fMRI sIC component maps, mean and variance of the voxel weights were calculated, and the variance across subjects was used as an estimate of the population variance. The weights were treated as random variables and entered into voxel-wise one-sample t-tests against the null hypothesis of zero magnitude. Results from these tests were considered significant at 1% false positive discovery rate (FDR, Benjamini, et al., 1995) with a cluster extent threshold of at least 5 voxels.
Group temporal ICA of EEG data (tICA)
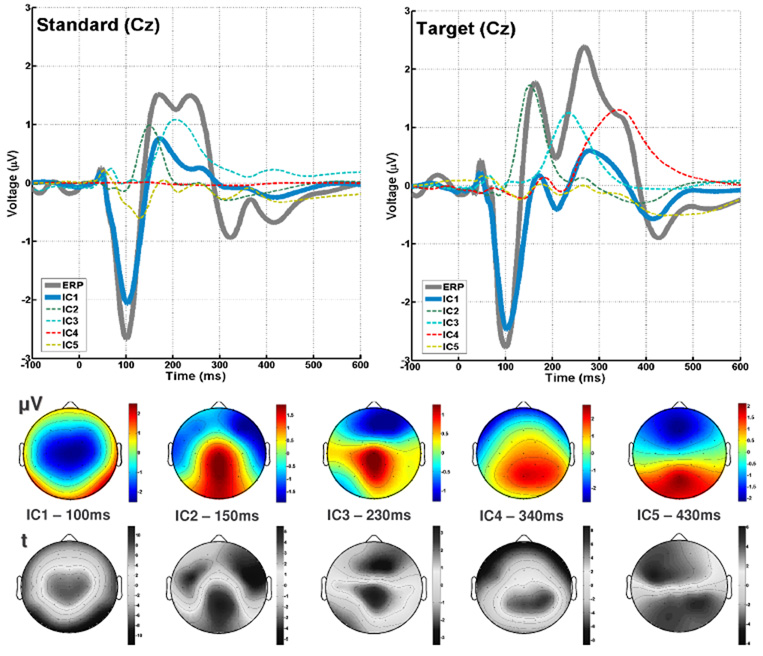
For estimation of the group tICA we adopt the rationale proposed by Calhoun (Calhoun, et al., 2001). The analysis framework is divided into the underlying data generation and mixing process, recording, pre-processing, reduction and component estimation, and is illustrated for both modalities in Figure 1. We assume that the scalp EEG signal is a gaussian mixture containing statistically independent non-gaussian source timeseries s(t) = [s1(t), s2(t), …, si(t)]T indicated by si(t) at time t for the ith source. The sources have weights that specify the contribution to each timepoint. The weights are multiplied by each source’s fixed topography. Secondly, it is assumed that the N sources are linearly mixed so that a given timepoint contains a weighted mixture of the sources. The linear combination of sources is represented by the unknown mixing system A, and yields u(t) = [u1(t), u2(t), …, uN(t)]T, representing N ideal samples of the signals un(t) at time t, for the ith source in the brain. The sampling of the electric activity on the scalp with the EEG amplifier results in y(i) = [y1(i), y2(i), …, yK(i)]T where the EEG is sampled at T timepoints indicated by i = 1, 2,…,T. A set of possible transformations during preprocessing, such as downsampling and filtering determine the effective sampling such that y(j) = [y1(j), y2(j), …, yK(j)]T. For each individual separately, the preprocessed single trial data y(j) are pre-whitened and reduced via principal component analysis (fig. 1, Re1−1 1… ReM−1) containing the major proportion of variance in the N uncorrelated timecourses of x(j) = [x1(j), x2(j), …, xN(j)]T. Then, group data is generated by concatenating individual principal components in the aggregate data set Ge (fig. 1).The choice of twenty PCs was determined by the dimensionality of the data after artefact removal (see above). TICA was performed in this set, estimating the optimal inverse of the mixing matrix (fig.1, Ae-1) that led to the observed scalp data and a single set of source timecourses (s). In order to acquire robust task-related components in the data we ran 50 replications entering random subsamples of 100 standard and 100 target epochs from each subject into the group ICA, estimating 20 components, as determined by the remaining dimensionality of the data after individual ICA. Consistently task-related components were identified by means of two criteria: firstly, replicability of the average component timecourses across analyses (r > 0.90), and secondly, significant differences between standard and target epochs in dependent sample t-tests across timepoints and channels. For the five components (fig. 2) that met these criteria, the aggregate timecourses from all replications were averaged together and used for a two-step back-reconstruction using multiple regression.
Figure 2. tIC timecourses and topographies.
Top: Average ERP and corresponding timecourses of the five independent components or standard (left) and target (right) epochs. Bottom: Component topographies, as scalp potential ( V) and t-statistic (t).
tIC-sIC integration
The computation of an EEG-tICA on the one end, and an fMRI-sICA on the other end replaces prediction of multiple voxel timeseries using multiple channel/timepoint measures by the condensed result from the two separate decompositions: For the timecourses of the 24 spatially independent components in the fMRI separately, data were modelled with a design that was formed by convolving stimulus functions with a canonical hemodynamic response function. The first stimulus function encoded an invariant evoked response to target stimuli. Five additional functions encoded the detrended single trial weights of the EEG tIC’s to find fMRI sIC’s with covarying timeseries. The EEG-tIC weight functions were decorrelated (Schmidt-Gram orthogonalization) from the unspecific hemodynamic response to stimulus onsets per se, ensuring specificity of the inferences from the electrophysiological predictors. The predictors were entered into single-subject fixed-effects regression analyses; on group level, random effects analyses were performed by entering the individual -weights from the regression between each EEG-tIC and fMRI-sIC into one-sample t-tests. The covariation between the trial-to-trial timecourses from the two modalities was considered significant at p < 0.05.
Results
For brevity we focus only on the amplitude effects and fMRI correlates of the first extracted component, which was not detected previously.
Component Backprojection
The first step was to estimate the individual topographies for the components by fitting the tIC timecourses to the individual ERPs from all channels. The goodness-of-fit of this model to the data is expressed in the F-statistic and the percentage-variance-explained (r2) for each channel. Across subjects, weights from each component and each channel were entered into zero-mean t-tests, providing random-effects statistics of the topographies (fig.2). The backprojection for single subject averages attained fit statistics with r2 ranging from 0.10 (F1,506 = 11.28) to 0.99 (F > 103), averaging to 0.75 ± 0.15 (F1,506 = 541±623) across subjects and channels, indicating an overall good prediction of the model with five tICs, considering that low r2-values were found mainly in channels with polarity reversal. The t-tests of the component-weights for each channel across subjects ranged from tdf14 = −7.55 to 7.04 for tIC1, IC2: tdf14 −4.22 to 5.41, tIC3: tdf14−2.43 to 2.78, tIC4: tdf14 −5.70 to 6.25, tIC5: tdf14 −4.26 to 5.97 (all p < 0.05) replicating the component amplitude topographies (fig. 2).
In the second step, tIC amplitudes in all single trials were estimated by forming a design matrix containing predictors from all tIC timecourses concatenated across channels which was fitted to the raw spatiotemporal data of each trial, thus estimating five -weights with the corresponding F-statistic and r2. Separately for the tICs, one-sample t-tests were conducted on the -weights within-subject-across-trials and between-subjects-within-trials. Both types of tests yield information regarding the goodness of the aggregate components in predicting individual trials as opposed to representing average phenomena that are essentially not well represented in single trials. Another purpose of this particular back-reconstruction was to condense topography and timecourse of a component to a single value for each trial, to be used later as a predictor for fMRI activity. This is an appropriate data reduction since the underlying sources are assumed to be spatially fixed, which means that testing of electrodes separately can be omitted. Additonally, we can constrain sources to be uniformly amplitude modulated in each trial, thus omitting testing of multiple latencies. The statistics for the available 3240 single trials resulted in a range of r2 from 0.003 to 0.60, with a mean of 0.15 ± 0.10 (F = 588±519). As a more informative test of the components contributions to the single trials, the t-statistic of the -weights within-subjects (across trials) indicated consistent scaling in the majority of components and subjects. tIC1 was found significant in 15/15 participants (pp) at t(df215) > 2.35 (p < 0.01) with an average (tavg) at t(df215) = 14.49 ± 8.39 (± SD), minimum (min): 3.66, maximum (max): 38.55; tIC2: 14/15 pp, tavg 8.62 ± 6.64, min −2.17 max 24.61; tIC3: 9/15 pp, tavg 6.72 ± 7.42, min −2.16 max 20.90; tIC4: 14/15 pp, tavg 13.91 ± 7.08, min −0.67 max 30.08, tIC5: 14/15 pp, tavg 11.10 ± 6.99, min 0.81 max 28.42. Similarly, at a threshold of t(df14) 2.63 (p < 0.01), the majority of the weight estimates were robust across subjects for the target epochs across the observation time. Here, tIC1 was present in 172 out of 216 epochs (79.6 %) with an averaged t(df14) 3.63±1.29, tIC2 amplitudes were more variable with only 76 (35.2 %) trials, tavg 2.30 ± 1.05; similarly tIC3 with 45 trials (20.8 %) tavg 1.76 ± 1.01; tIC4: 165 trials (76.4 %) tavg 3.48 ± 1.44; tIC5: 123 trials (57.0 %) tavg 2.81 ± 1.17.
tIC1 amplitude effects (fig. 3)
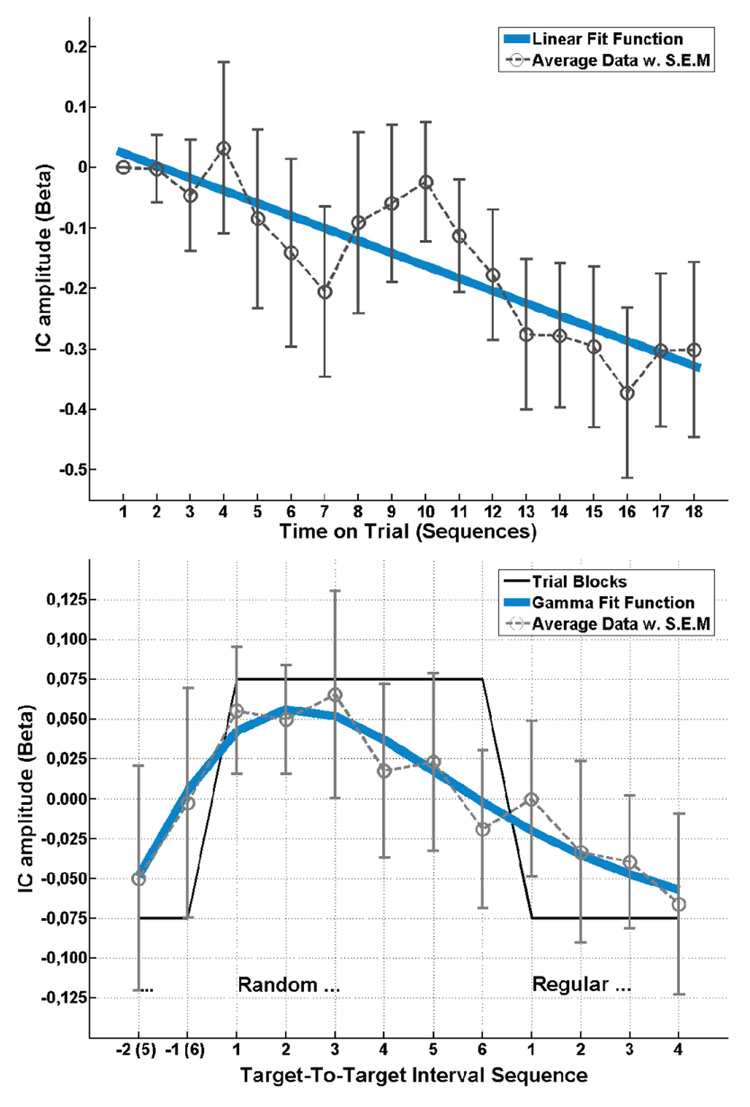
Figure 3. tIC 1 amplitude effects.
Top: Slow linear decrement of component activity with time on trial. Bottom: Within a sequence indicated by the box-car function (black line) the trial-to-trial dynamics yield a gamma-shaped modulation following the transition between regular and random targets.
In order to assess slow drifts evolving with the total time-on-trial regardless of the local manipulation of predictability, the twelve targets within one sequence were blocked and averaged together, yielding one observation for each of the 18 sequence repetitions in each participant, with the first point serving as baseline. The group averaged measure was used to derive a best-fit function (with as little parameters as possible). In this case, a simple linear trend f(x) = s·x + c across repetitions, with a slope (s) of −0.021 and offset c 0.045 provided a reasonable fit (r2 = 0.76). This function was then used as a predictor of the single subject data, yielding sufficient individual statistics in 6/15 participants (r2 0.2, F1,16 4, p 0.06), and the weights being significantly larger than zero (tdf14 = 4.10, p<0.001). Amplitude modulation of tIC1 in response to switching between random and regular TTI was assessed by averaging the 18 repetitions from each of the six random and six regular sequence positions across the observation time together, after removing the mean from each sequence repetition to account for the trend (see above). Inspection of the group averaged response suggested a transient amplitude increment induced by the shift from predictable to unpredictable intervals with a subsequent decline across the remainder of the sequence, while there was no discernible response to the shift from unpredictable to predictable context. This shape was best modelled (r2 = 0.91) as a function following a gamma distribution function , with the parameters shape a = 2.9 and scale b = 1.7. This function was then used as a predictor of the single subject data, yielding sufficient positive correlation with the average-based model in 5/15 participants (r2 0.27, F1,10 3.68, p 0.08), however, a right-tailed t-test on the -weights failed the significance threshold by a small margin (tdf14 = 1.60, p = 0.07). Assuming that the degree of individual variability regarding shape and scale of the gamma function accounted for the failure of the test at small sample size, we conducted a complementary analysis with individual best-fit estimates (maximum positive correlation) from a range of ±0.5 around the group-estimates for a and b. With these parameters left to vary, statistics improved to 8/15 participants (r2 0.31, F1,10 4.55, p 0.06) reaching significance in the t-test (tdf14 = 3.06, p<0.01).
fMRI correlates (fig. 4, table 1)
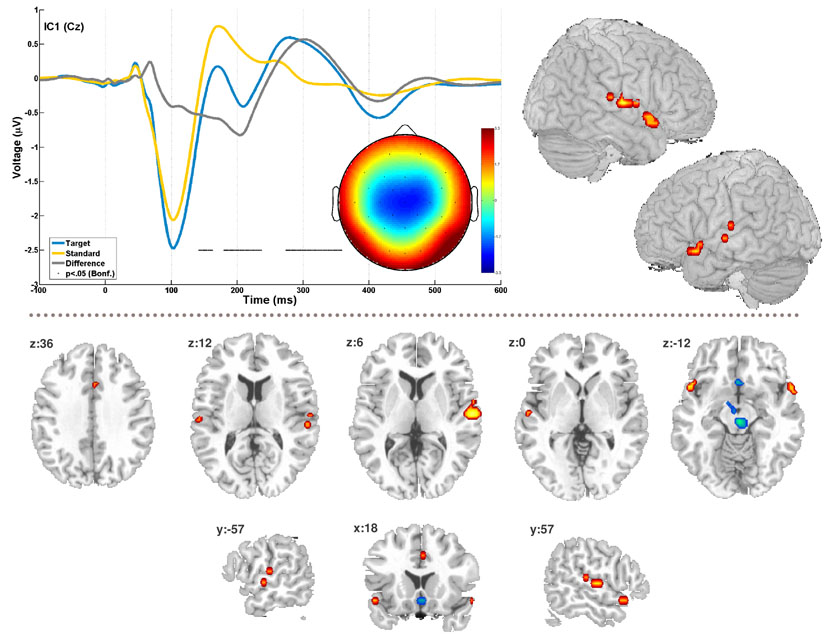
Figure 4. EEG-fMRI component.
The figure shows the timecourse and topography for EEG-tIC1 for standard and target epochs as well as the difference wave between them. The difference wave was subjected to pointwise one-sample t-tests, black dots indicate timeframes with significant difference from zero at p<‥05, Bonferroni corrected for 512 tests (t>6.93). The bilateral temporal activation in the correlated fMRI component is shown as a surface rendering (top right). Additional slices in the lower half illustrate the overall spatial pattern (see also table 1). The fMRI maps are thresholded at 1% false discovery rate, cluster extent 5 voxels. Positive correlation is plotted in red, inverse correlation in blue.
Table 1. fMRI regional activation in the EEG-correlated spatial component.
The table summarizes the Talairach coordinates (x, y, z in mm) and Brodmann area labels for clusters of significant activity (p<0.01, FDR corr.).
| Region | BA | x | y | z | peak voxel (t) |
|---|---|---|---|---|---|
| Subcallosal gyrus, R | 25 | 2 | 18 | −11 | −7.33 |
| Anterior Cingulate Gyrus, R | 32 | 4 | 18 | 32 | 6.52 |
| Transverse Temporal Gyrus, L | 41 | −56 | −19 | 12 | 6.61 |
| Superior Temporal Gyrus, R | 41 | 57 | −24 | 12 | 6.52 |
| Superior Temporal Gyrus, R | 22 | 60 | −13 | 6 | 9.47 |
| Superior Temporal Gyrus, L | 22 | −56 | −13 | 1 | 7.33 |
| STG / Temporal Pole, L | 38 | −58 | 14 | −11 | 8.22 |
| STG / Temporal Pole, R | 38 | 62 | 11 | −6 | 7.87 |
| Brainstem, R | --- | 3 | −22 | −9 | −11.35 |
| Brainstem, L | --- | −3 | −11 | −10 | −6.34 |
The trial-to-trial amplitude dynamic of tIC1 predicted selectively the timecourse of one sIC fMRI map (tdf14 = 2.49, p = 0.02), that is, no other EEG tIC correlated significantly with this sIC, neither did tIC1 covary with any other of the 24 fMRI sICs. The respective maps’ timecourse additionally displayed a strong covariation with the generic evoked response predictor (tdf14 = 11.15, p < 0.001). Local maxima of the FDR corrected t-statistic sIC map (table 1) were located in the posterior superior temporal gyri and temporal poles bilaterally, the anterior cingulate gyrus, the subcallosal gyrus, the global maximum was situated in an area in the right brainstem framed by the landmarks central gray dorsally and red nucleus ventrally. Additionally, a smaller set of voxels was found in the vicinity of the left mamillary body.
Discussion
We have presented a method for parallel spatial and temporal independent component analysis for concurrent multi-subject single-trial EEG-fMRI recordings that addresses the mixing problem in both modalities (fig. 1). The data are integrated via correlation of the trial-to-trial modulation of the recovered fMRI maps with EEG timecourses. The method afforded identification of an additional spatiotemporal process corresponding to the auditory onset response and subsequent low-level orienting/change detection (fig. 4). The discussion details the area of application for this method, and provides an account for the potential functional role of the reported component.
Area of application
The observation that a simple cognitive task such as target detection in an auditory oddball experiment induces spatially and temporally widespread neuronal responses (Baudena, et al., 1995; Calhoun, et al., 2006c; Eichele, et al., 2005; Halgren, et al., 1995a; Halgren, et al., 1995b; Kiehl, et al., 2005) pertains to distributed network responses more than to compartmentalized effects (Fox, et al., 2005; Halgren, et al., 1995c; Nunez, 2000). We see a major utility for parallel ICA in this context as it provides the means to disentangle and visualize these networks both in their spatial and temporal form (Calhoun, et al., 2006a; Debener, et al., 2006; Makeig, et al., 2004a; McKeown, et al., 2003; Onton, et al., 2006).
However, some limitations apply: Infomax assumes sources to have non-normal, either super- or subgaussian distributions (Bell, et al., 1995; Lee, et al., 1999), and this seems to hold for a great variety of physiological signals as well as technical artefacts. However, if sources (or noise) are gaussian, ICA will split these up into spurious non-gaussian components. In practice this occurs mostly for heavily noisy data, and where more sources than present in the data are extracted.
Generally, the utility of blind methods such as ICA lies in data-driven assessment of data where specific hypotheses regarding spatial and temporal relationships are lacking, or are ill-specified. In other words, in situations in which a traditional inference test, and its implementation in the statistical parametric mapping framework (Friston, 2003; Friston, et al., 1995) is not justifiable, or is too insensitive due to ensuing conservative significance thresholds. Concurrent EEG-fMRI data adds another complexity in that one deals with two multivariate spaces, and necessary specifications would not only encompass the regions in which fMRI activation is expected, but also the particular samples from which to derive the predictor from the EEG. Reversely, and somewhat more critically from our perspective, one should also be able to justify which locations and latencies not to test. The two complementary blind decompositions avoid this issue since all available EEG data is used in the estimation and the back-reconstruction to produce maximally condensed predictors, i.e. the trial-to-trial modulation applies uniformly to the entire timecourse and topography of a component, reducing multiple comparisons considerably. Similarly, the separate spatial ICA of the fMRI data involves data reduction since the voxel-wise analysis is replaced by testing of the fMRI component timecourses (here: 24), while the statistical significance of the maps is tested in a separate random-effects analysis, applying appropriate correction using false discovery rate (FDR, Benjamini, et al., 1995). Thus, finding IC-pairs across response modalities identifies coherent neuronal sources that jointly express scalp electrophysiologic and hemodynamic features. However, the current statistic trades in the ‘localizing power’ afforded by the mass-univariate testing (Friston, 2003; Kiebel, et al., 2004), i.e. the possibility of drawing inferences on the effect sizes in particular voxels in the fMRI and timepoints/channels in the EEG. A hybrid approach might be plausible for applications in which one would use parallel ICA for hypothesis generation and employ the components as spatial and temporal filters for region of interest definition prior to mass univariate testing.
Here, we opted for a group ICA implementation because it provides a straight-forward and stringent solution for multi-subject component estimation and directly affords population inferences (Calhoun, et al., 2001; Schmithorst, et al., 2004). Group ICA works well for sources that are spatially and temporally coherent across subjects, and will readily detect such sources when present in about 10% of the sampled population (Schmithorst, et al., 2004). For the sICA on preprocessed fMRI data this means that regional BOLD responses that overlap across subjects can yield group-relevant components, which is the same criterion that applies to group (2nd-level) statistics of fMRI contrast images or simple averaging. Processes that occur in a spatially variable form over time in the recording of a single subject, or that are principally spatially heterogeneous across subjects can not be captured by this implementation. Correspondingly, the group tICA on EEG single trial time domain data is preferentially suited to detect of components that represent or contribute to event-related potentials visible in averaged data. Processes that are not time/phase-locked within and across subjects, such as background rhythms and induced activity are not well visible. However, the choice of input data to parallel ICA is arbitrary such that time domain data can be replaced with e.g. power-spectra or time-frequency data where the fMRI correlates of EEG rhythms or event-related synchronization and desynchronization are subject to study. In this respect, an useful extension of the current framework would be incorporation of multiple EEG and MRI features from single trial data (Calhoun, et al., 2006b).
The prerequisites outlined above do not apply to ICA on individual data, which renders this approach principally a more versatile tool to identify components. Individual ICA results can be combined across subjects by means of subsequent component clustering (Esposito, et al., 2005; Onton, et al., 2006). This allows for group inferences and retains more relevant information about inter-individual variability and its impact on the EEG-fMRI relationship (cf. Goncalves, et al., 2006) than does our analysis, such that one should consider either option in light of the purpose of the experiment at hand. Currently, however, the available techniques are implemented and tested mostly for clustering within a modality, how well clusters can be matched across modalities by their trial-to-trial modulation or other features should be further investigated. Adequate algorithms that jointly cluster the maps and timecourses from both EEG and fMRI will yet have to be evaluated. Another consideration is that clustering techniques impose additional assumptions about between-subject correspondence and do not per se provide a turnkey solution, such that proper handling of these techniques would usually require expert user interaction.
tIC function
tIC1 had a central topography dominated by a large negativity at 100ms (N1), followed by smaller P2 and N2 deflections and a P3 at 270ms. The difference wave between standards and targets yields a biphasic pattern with a sustained negativity from 100–200ms, followed by a P3 (fig. 2, 4). Altogether, this suggests that tIC1 encompasses the N1 onset response per se, N1-enhancement and a subsequent N2b-P3a (Naatanen, et al., 1987; Naatanen, 1992) as one coherent process. Given the current experimental parameters, the 'N1-enhancement' seen here may contain contributions from genuine sources of mismatch negativity (MMN), attentive processing negativity (PN/Nd) and ‘fresh afferents’ of the N1 alike (Naatanen, et al., 1987; Naatanen, 1992). The N2b-P3a portion of the waveform following the N1/MMN is seen with attention-switching at large or task-relevant stimulus contrasts (Naatanen, 1992; Schroger, 1997).
The single trial amplitude estimates of tIC1 selectively covaried with an fMRI map that comprised a set of fronto-temporal and mesencephalic regional responses (figure 4). Activations were present for local maxima in the superior temporal gyri with a rightward dominance, the temporal poles and the anterior cingulate gyrus. This partition of the map encompasses the assumed sources of the scalp N1/MMN (Naatanen, et al., 1987; Picton, et al., 1999; Picton, et al., 2000; Woods, 1995), and correspondingly the brain areas that previous imaging experiments have implicated in automatic auditory deviance detection, stimulus discrimination, sensory memory as well as novelty (surprise) related functions (Liebenthal, et al., 2003; Molholm, et al., 2005; Rinne, et al., 2005; Sabri, et al., 2006). The occurrence of deactivations observed in the subcallosal gyrus and the maps’ global maximum in the vicinity of the midbrain reticular formation was surprising. However, seeing these areas apparently interacting in anti-correlated fashion with auditory function is plausible, since both have been found to be sensitive to novelty/predictability contrasts with more salient stimuli and tasks (Berns, et al., 2001; Bunzeck, et al., 2006).
Two modulatory effects were present in tIC1: one effect was a linear amplitude decrement evolving slowly with time on task, and the other was a local within-sequence gamma-shaped modulation (fig. 3). The slow linear decrement is well in line with reports describing long-term habituation for N1, MMN as well as P3a across the observation time (Debener, et al., 2005a; Friedman, et al., 2001; Loveless, 1983; McGee, et al., 2001; Sambeth, et al., 2004; Woods, et al., 1986). This might correspond to a slow adaptive process related to repetitions of stimulus sequences (Jongsma, et al., 2006) or the overall decline in arousal/vigilance across trials. Although tIC1 responded with amplitude increment at the transition from regular to random intervals, the corresponding transition from random to regular (i.e. the beginning of a pattern) did not elicit a response. Hence, instead of sigmoid learning curves that characterized the behaviour of later components (Eichele, et al., 2005; Jongsma, et al., 2006), a gamma-shaped function provided the best fit. Two explanations for this phenomenon can be offered: Firstly, tIC1 may respond directly only to an increase in surprise. This means that the weight change elicited by the comparison between actual input and the learning history represented in the amplitude of tIC1 would only reflect increments of ‘surprise’ with the appearance of a target at an unpredicted interval at the regular-random transition, but not a constant error or the onset of the regular pattern. The second explanation relates to the time-span for which tIC1 can retain information and incorporate it into the learning history. Assuming a memory trace length at or below 10 seconds (Winkler, et al., 2001), it would be plausible that tIC1 cannot retain enough interval repetitions to recognize the emergence of a pattern‥ For both accounts it is plausible to assume that the modulation is not self-sustaining. It should receive additional backward input from higher levels of processing which would exert an inhibitory influence on tIC1 when intervals are predictable, while the response to the more surprising transition from predictable to unpredictable intervals represents a salient bottom-up signal (Friston, 2005a; Schroger, 1997). Altogether, this indicates that the component is to some extent modulated by target predictability, specifically by increments of surprise/prediction error. This effect needs further examination in ‘attended’ as well as ‘unattended’ settings with variations of stimulus onset asynchrony, rules, and the physical deviant/target features (Baldeweg, 2006; Haenschel, et al., 2005; Sussman, et al., 1998; Ulanovsky, et al., 2004).
In conclusion, we believe that parallel ICA is a useful addition to the selection of analysis methods for concurrent EEG-fMRI, it can serve either as a primary tool for inferences about the unmixed sources, or can be employed for data mining, hypothesis generation and model specification/diagnostics.
Acknowledgment
The present study was financially supported with grants from the Research Council of Norway to Kenneth Hugdahl and by the National Institutes of Health, under grants 1 R01 EB 000840 and 1 R01 EB 005846 to Vince Calhoun.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Baldeweg T. Repetition effects to sounds: evidence for predictive coding in the auditory system. Trends Cogn Sci. 2006;10(3):93–94. doi: 10.1016/j.tics.2006.01.010. [DOI] [PubMed] [Google Scholar]
- Baudena P, Halgren E, Heit G, Clarke JM. Intracerebral potentials to rare target and distractor auditory and visual stimuli. III. Frontal cortex. Electroencephalogr Clin Neurophysiol. 1995;94(4):251–264. doi: 10.1016/0013-4694(95)98476-o. [DOI] [PubMed] [Google Scholar]
- Bell AJ, Sejnowski TJ. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995;7(6):1129–1159. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
- Benar CG, Schon D, Grimault S, Nazarian B, Burle B, Roth M, Badier JM, Marquis P, Liegeois-Chauvel C, Anton JL. Single-trial analysis of oddball event-related potentials in simultaneous EEG-fMRI. Hum Brain Mapp. 2007 doi: 10.1002/hbm.20289. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B. Methodological. 1995;57:286–300. [Google Scholar]
- Berns GS, McClure SM, Pagnoni G, Montague PR. Predictability modulates human brain response to reward. J Neurosci. 2001;21(8):2793–2798. doi: 10.1523/JNEUROSCI.21-08-02793.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunzeck N, Duzel E. Absolute coding of stimulus novelty in the human substantia nigra/VTA. Neuron. 2006;51(3):369–379. doi: 10.1016/j.neuron.2006.06.021. [DOI] [PubMed] [Google Scholar]
- Calhoun V, Adali T. Unmixing fMRI with independent component analysis. IEEE Engineering in Medicine and Biology Magazine. 2006a;25(2):79–90. doi: 10.1109/memb.2006.1607672. [DOI] [PubMed] [Google Scholar]
- Calhoun V, Adali T, Liu J. A Feature-Based Approach to Combine Functional MRI, Structural MRI, and EEG Brain Imaging Data; Paper presented at the EMBS; New York, NY. 2006b. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar JJ. A method for making group inferences from functional MRI data using independent component analysis. Hum Brain Mapp. 2001;14(3):140–151. doi: 10.1002/hbm.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Kiehl KA. Neuronal chronometry of target detection: fusion of hemodynamic and event-related potential data. Neuroimage. 2006c;30(2):544–553. doi: 10.1016/j.neuroimage.2005.08.060. [DOI] [PubMed] [Google Scholar]
- Debener S, Makeig S, Delorme A, Engel AK. What is novel in the novelty oddball paradigm? Functional significance of the novelty P3 event-related potential as revealed by independent component analysis. Brain Res Cogn Brain Res. 2005a;22(3):309–321. doi: 10.1016/j.cogbrainres.2004.09.006. [DOI] [PubMed] [Google Scholar]
- Debener S, Ullsperger M, Siegel M, Fiehler K, von Cramon DY, Engel AK. Trial-by-trial coupling of concurrent electroencephalogram and functional magnetic resonance imaging identifies the dynamics of performance monitoring. J Neurosci. 2005b;25(50):11730–11737. doi: 10.1523/JNEUROSCI.3286-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Debener S, Ullsperger M, Siegel M, Engel AK. Single-trial EEG-fMRI reveals the dynamics of cognitive function. Trends Cogn Sci. 2006;10(12):558–563. doi: 10.1016/j.tics.2006.09.010. [DOI] [PubMed] [Google Scholar]
- Debener S, Strobel A, Sorger B, Peters J, Kranczioch C, Engel AK, Goebel R. Improved quality of auditory event-related potentials recorded simultaneously with 3-T fMRI: removal of the ballistocardiogram artefact. Neuroimage. 2007;34(2):587–597. doi: 10.1016/j.neuroimage.2006.09.031. [DOI] [PubMed] [Google Scholar]
- Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods. 2004;134(1):9–21. doi: 10.1016/j.jneumeth.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Eichele T, Specht K, Moosmann M, Jongsma ML, Quiroga RQ, Nordby H, Hugdahl K. Assessing the spatiotemporal evolution of neuronal activation with single-trial event-related potentials and functional MRI. Proc Natl Acad Sci U S A. 2005;102(49):17798–17803. doi: 10.1073/pnas.0505508102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esposito F, Scarabino T, Hyvarinen A, Himberg J, Formisano E, Comani S, Tedeschi G, Goebel R, Seifritz E, Di Salle F. Independent component analysis of fMRI group studies by self-organizing clustering. Neuroimage. 2005;25(1):193–205. doi: 10.1016/j.neuroimage.2004.10.042. [DOI] [PubMed] [Google Scholar]
- Feige B, Scheffler K, Esposito F, Di Salle F, Hennig J, Seifritz E. Cortical and subcortical correlates of electroencephalographic alpha rhythm modulation. J Neurophysiol. 2005;93(5):2864–2872. doi: 10.1152/jn.00721.2004. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci U S A. 2005;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman D, Cycowicz YM, Gaeta H. The novelty P3: an event-related brain potential (ERP) sign of the brain's evaluation of novelty. Neurosci Biobehav Rev. 2001;25(4):355–373. doi: 10.1016/s0149-7634(01)00019-7. [DOI] [PubMed] [Google Scholar]
- Friston K. Human Brain Function. 2nd ed. Elsevier; 2003. [Google Scholar]
- Friston K. A theory of cortical responses. Philos Trans R Soc Lond B Biol Sci. 2005a;360(1456):815–836. doi: 10.1098/rstb.2005.1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Holmes AP, Poline JB, Grasby PJ, Williams SC, Frackowiak RS, Turner R. Analysis of fMRI time-series revisited. Neuroimage. 1995;2(1):45–53. doi: 10.1006/nimg.1995.1007. [DOI] [PubMed] [Google Scholar]
- Friston KJ. Models of brain function in neuroimaging. Annu Rev Psychol. 2005b;56:57–87. doi: 10.1146/annurev.psych.56.091103.070311. [DOI] [PubMed] [Google Scholar]
- Goncalves SI, de Munck JC, Pouwels PJ, Schoonhoven R, Kuijer JP, Maurits NM, Hoogduin JM, Van Someren EJ, Heethaar RM, Lopes da Silva FH. Correlating the alpha rhythm to BOLD using simultaneous EEG/fMRI: inter-subject variability. Neuroimage. 2006;30(1):203–213. doi: 10.1016/j.neuroimage.2005.09.062. [DOI] [PubMed] [Google Scholar]
- Haenschel C, Vernon DJ, Dwivedi P, Gruzelier JH, Baldeweg T. Event-related brain potential correlates of human auditory sensory memory-trace formation. J Neurosci. 2005;25(45):10494–10501. doi: 10.1523/JNEUROSCI.1227-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halgren E, Baudena P, Clarke JM, Heit G, Liegeois C, Chauvel P, Musolino A. Intracerebral potentials to rare target and distractor auditory and visual stimuli. I. Superior temporal plane and parietal lobe. Electroencephalogr Clin Neurophysiol. 1995a;94(3):191–220. doi: 10.1016/0013-4694(94)00259-n. [DOI] [PubMed] [Google Scholar]
- Halgren E, Baudena P, Clarke JM, Heit G, Marinkovic K, Devaux B, Vignal JP, Biraben A. Intracerebral potentials to rare target and distractor auditory and visual stimuli. II. Medial, lateral and posterior temporal lobe. Electroencephalogr Clin Neurophysiol. 1995b;94(4):229–250. doi: 10.1016/0013-4694(95)98475-n. [DOI] [PubMed] [Google Scholar]
- Halgren E, Marinkovic K. General principles for the physiology of cognition as suggested by intracranial ERPs. In: Ogura C, Koga Y, Shimokochi M, editors. Recent Advances in Event-Related Brain Potential Research. Amsterdam: Elsevier; 1995c. pp. 1072–1084. [Google Scholar]
- Hall DA, Haggard MP, Akeroyd MA, Palmer AR, Summerfield AQ, Elliott MR, Gurney EM, Bowtell RW. "Sparse" temporal sampling in auditory fMRI. Hum Brain Mapp. 1999;7(3):213–223. doi: 10.1002/(SICI)1097-0193(1999)7:3<213::AID-HBM5>3.0.CO;2-N. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopfinger JB, Khoe W, Song AW. Combining Electrophysiology with Structural and Functional Neuroimaging: ERPs, PET, MRI, and fMRI. In: Handy TC, editor. Event Related Potentials. A Methods Handbook. Cambridge: The MIT Press; 2005. pp. 345–380. [Google Scholar]
- Horwitz B, Poeppel D. How can EEG/MEG and fMRI/PET data be combined? Hum Brain Mapp. 2002;17(1):1–3. doi: 10.1002/hbm.10057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jongsma ML, Eichele T, Van Rijn CM, Coenen AM, Hugdahl K, Nordby H, Quiroga RQ. Tracking pattern learning with single-trial event-related potentials. Clin Neurophysiol. 2006;117(9):1957–1973. doi: 10.1016/j.clinph.2006.05.012. [DOI] [PubMed] [Google Scholar]
- Jung TP, Makeig S, Humphries C, Lee TW, McKeown MJ, Iragui V, Sejnowski TJ. Removing electroencephalographic artifacts by blind source separation. Psychophysiology. 2000;37(2):163–178. [PubMed] [Google Scholar]
- Kiebel SJ, Friston KJ. Statistical parametric mapping for event-related potentials: I. Generic considerations. Neuroimage. 2004;22(2):495–502. doi: 10.1016/j.neuroimage.2004.02.012. [DOI] [PubMed] [Google Scholar]
- Kiehl KA, Stevens MC, Laurens KR, Pearlson G, Calhoun VD, Liddle PF. An adaptive reflexive processing model of neurocognitive function: supporting evidence from a large scale (n = 100) fMRI study of an auditory oddball task. Neuroimage. 2005;25(3):899–915. doi: 10.1016/j.neuroimage.2004.12.035. [DOI] [PubMed] [Google Scholar]
- Lauritzen M, Gold L. Brain function and neurophysiological correlates of signals used in functional neuroimaging. J Neurosci. 2003;23(10):3972–3980. doi: 10.1523/JNEUROSCI.23-10-03972.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T, Girolami M, Sejnowski T. Independent Component Analysis Using an Extended Infomax Algorithm for Mixed Subgaussian and Supergaussian Sources. Neural Comput. 1999;11:417–441. doi: 10.1162/089976699300016719. [DOI] [PubMed] [Google Scholar]
- Li Y, Adali T, Calhoun VD. Estimating the Number of Independent Components for FMRI Data. Hum Brain Mapp. 2006 doi: 10.1002/hbm.20359. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liebenthal E, Ellingson ML, Spanaki MV, Prieto TE, Ropella KM, Binder JR. Simultaneous ERP and fMRI of the auditory cortex in a passive oddball paradigm. Neuroimage. 2003;19:1395–1404. doi: 10.1016/s1053-8119(03)00228-3. [DOI] [PubMed] [Google Scholar]
- Linden DE, Prvulovic D, Formisano E, Vollinger M, Zanella FE, Goebel R, Dierks T. The functional neuroanatomy of target detection: an fMRI study of visual and auditory oddball tasks. Cereb Cortex. 1999;9(8):815–823. doi: 10.1093/cercor/9.8.815. [DOI] [PubMed] [Google Scholar]
- Logothetis NK. The underpinnings of the BOLD functional magnetic resonance imaging signal. J Neurosci. 2003;23(10):3963–3971. doi: 10.1523/JNEUROSCI.23-10-03963.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loveless N. The Orienting Response and Evoked Potentials in Man. In: Siddle D, editor. Orienting and Habituation: Perspectives in Human Research. Chichester: Wiley; 1983. pp. 71–108. [Google Scholar]
- Makeig S, Jung TP, Bell AJ, Ghahremani D, Sejnowski TJ. Blind separation of auditory event-related brain responses into independent components. Proc Natl Acad Sci U S A. 1997;94(20):10979–10984. doi: 10.1073/pnas.94.20.10979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makeig S, Debener S, Onton J, Delorme A. Mining event-related brain dynamics. Trends Cogn Sci. 2004a;8(5):204–210. doi: 10.1016/j.tics.2004.03.008. [DOI] [PubMed] [Google Scholar]
- Makeig S, Delorme A, Westerfield M, Jung TP, Townsend J, Courchesne E, Sejnowski TJ. Electroencephalographic brain dynamics following manually responded visual targets. PLoS Biol. 2004b;2(6):e176. doi: 10.1371/journal.pbio.0020176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makeig S, Jung T-P, Sejnowski TJ. Having your voxels and timing them too? In: Sommer F, Wichert A, editors. Exploratory Analysis and Data Modeling in Functional Neuroimaging. Cambridge: The MIT Press; 2002. [Google Scholar]
- McGee TJ, King C, Tremblay K, Nicol TG, Cunningham J, Kraus N. Long-term habituation of the speech-elicited mismatch negativity. Psychophysiology. 2001;38(4):653–658. [PubMed] [Google Scholar]
- McKeown MJ, Hansen LK, Sejnowski TJ. Independent component analysis of functional MRI: what is signal and what is noise? Curr Opin Neurobiol. 2003;13(5):620–629. doi: 10.1016/j.conb.2003.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molholm S, Martinez A, Ritter W, Javitt DC, Foxe JJ. The neural circuitry of pre-attentive auditory change-detection: an fMRI study of pitch and duration mismatch negativity generators. Cereb Cortex. 2005;15(5):545–551. doi: 10.1093/cercor/bhh155. [DOI] [PubMed] [Google Scholar]
- Nunez PL. Toward a quantitative description of large-scale dynamic neocortical dynamic function and EEG. Behavioral and Brain Sciences. 2000;23:371–437. doi: 10.1017/s0140525x00003253. [DOI] [PubMed] [Google Scholar]
- Naatanen R, Picton T. The N1 wave of the human electric and magnetic response to sound: a review and an analysis of the component structure. Psychophysiology. 1987;24(4):375–425. doi: 10.1111/j.1469-8986.1987.tb00311.x. [DOI] [PubMed] [Google Scholar]
- Naatanen R. Attention and Brain Function. Hillsdale: Lawrence Erlbaum Associates; 1992. [Google Scholar]
- Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci U S A. 1990;87(24):9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onton J, Westerfield M, Townsend J, Makeig S. Imaging human EEG dynamics using independent component analysis. Neurosci Biobehav Rev. 2006;30(6):808–822. doi: 10.1016/j.neubiorev.2006.06.007. [DOI] [PubMed] [Google Scholar]
- Picton TW, Alain C, Woods DL, John MS, Scherg M, Valdes-Sosa P, Bosch-Bayard J, Trujillo NJ. Intracerebral sources of human auditory-evoked potentials. Audiol Neurootol. 1999;4(2):64–79. doi: 10.1159/000013823. [DOI] [PubMed] [Google Scholar]
- Picton TW, Alain C, Otten L, Ritter W, Achim A. Mismatch negativity: different water in the same river. Audiol Neurootol. 2000;5(3–4):111–139. doi: 10.1159/000013875. [DOI] [PubMed] [Google Scholar]
- Quian Quiroga R, Garcia H. Single-trial event-related potentials with wavelet denoising. Clin Neurophysiol. 2003;114(2):376–390. doi: 10.1016/s1388-2457(02)00365-6. [DOI] [PubMed] [Google Scholar]
- Rinne T, Degerman A, Alho K. Superior temporal and inferior frontal cortices are activated by infrequent sound duration decrements: an fMRI study. Neuroimage. 2005;26(1):66–72. doi: 10.1016/j.neuroimage.2005.01.017. [DOI] [PubMed] [Google Scholar]
- Sabri M, Liebenthal E, Waldron EJ, Medler DA, Binder JR. Attentional modulation in the detection of irrelevant deviance: a simultaneous ERP/fMRI study. J Cogn Neurosci. 2006;18(5):689–700. doi: 10.1162/jocn.2006.18.5.689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sambeth A, Maes JH, Quian Quiroga R, Van Rijn CM, Coenen AM. Enhanced re-habituation of the orienting response of the human event-related potential. Neurosci Lett. 2004;356(2):103–106. doi: 10.1016/j.neulet.2003.11.025. [DOI] [PubMed] [Google Scholar]
- Schmithorst VJ, Holland SK. Comparison of three methods for generating group statistical inferences from independent component analysis of functional magnetic resonance imaging data. J Magn Reson Imaging. 2004;19(3):365–368. doi: 10.1002/jmri.20009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroger E. On the detection of auditory deviations: a pre-attentive activation model. Psychophysiology. 1997;34(3):245–257. doi: 10.1111/j.1469-8986.1997.tb02395.x. [DOI] [PubMed] [Google Scholar]
- Stone JV. Independent component analysis: an introduction. Trends Cogn Sci. 2002;6(2):59–64. doi: 10.1016/s1364-6613(00)01813-1. [DOI] [PubMed] [Google Scholar]
- Sussman E, Ritter W, Vaughan HG., Jr Predictability of stimulus deviance and the mismatch negativity. Neuroreport. 1998;9(18):4167–4170. doi: 10.1097/00001756-199812210-00031. [DOI] [PubMed] [Google Scholar]
- Ulanovsky N, Las L, Farkas D, Nelken I. Multiple time scales of adaptation in auditory cortex neurons. J Neurosci. 2004;24(46):10440–10453. doi: 10.1523/JNEUROSCI.1905-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler I, Schroger E, Cowan N. The role of large-scale memory organization in the mismatch negativity event-related brain potential. J Cogn Neurosci. 2001;13(1):59–71. doi: 10.1162/089892901564171. [DOI] [PubMed] [Google Scholar]
- Woods DL, Elmasian R. The habituation of event-related potentials to speech sounds and tones. Electroencephalogr Clin Neurophysiol. 1986;65(6):447–459. doi: 10.1016/0168-5597(86)90024-9. [DOI] [PubMed] [Google Scholar]
- Woods DL. The component structure of the N1 wave of the human auditory evoked potential. Electroencephalogr Clin Neurophysiol Suppl. 1995;44:102–109. [PubMed] [Google Scholar]