Substrate Induced Structural and Dynamics Changes in Human Phosphomevalonate Kinase and Implications for Mechanism

Abstract

Phosphomevalonate kinase (PMK) catalyzes an essential step in the mevalonate pathway, which is the only pathway for synthesis of isoprenoids and steroids in humans. PMK catalyzes transfer of the γ-phosphate of ATP to mevalonate 5-phosphate (M5P) to form mevalonate 5-diphosphate. Bringing these phosphate groups in proximity to react is especially challenging, given the high negative charge density on the four phosphate groups in the active site. As such, conformational and dynamics changes needed to form the Michaelis complex are of mechanistic interest. Herein, we report the characterization of substrate induced changes (Mg-ADP, M5P, and the ternary complex) in PMK, using NMR-based dynamics and chemical shift perturbation measurements. Mg-ADP and M5P K_d's were 6-60 μM in all complexes, consistent with there being little binding synergy. Binding of M5P causes the PMK structure to compress (τ_c= 13.5 nsec), while subsequent binding of Mg-ADP opens the structure up (τ_c= 17.6 nsec). The overall complex seems to stay very rigid on the psec-nsec timescale with an average NMR order parameter of S²∼0.88. Data are consistent with addition of M5P causing movement around a hinge region to permit domain closure, which would bring the M5P domain close to ATP to permit catalysis. Dynamics data identify potential hinge residues as H55 and R93, based on their low order parameters and their location in extended regions that connect the M5P and ATP domains in the PMK homology model. Likewise, D163 may be a hinge residue for the lid region that is homologous to the adenylate kinase lid, covering the “Walker-A” catalytic loop. Binding of ATP or ADP appears to cause similar conformational changes; but, these observations do not indicate an obvious role for γ-phosphate binding interactions. Indeed, the role of γ-phosphate interactions may be more subtle than suggested by ATP/ADP comparisons, since the conservative O to NH substitution in the β-γ bridge of ATP causes a dramatic decrease in affinity and induces few chemical shift perturbations. In terms of positioning of catalytic residues, binding of M5P induces a rigidification of Gly21 (adjacent to the catalytically important Lys22), although exchange broadening in the ternary complex suggests some motion on a slower timescale does still occur. Finally, the first 9 residues of the N-terminus are highly disordered, suggesting they may be part of a cleavable signal or regulatory peptide sequence.

INTRODUCTION

Protein motions are critical for various biological functions and occur over a wide range of timescales. There is a strong correlation between structural dynamics and molecular function, and studying these dynamic processes can give site-specific information on motions that span timescales from psec to msec¹. One class of enzymes that undergoes large structural and associated motional changes are the kinases. These changes occur due to the binding of their two ligands, and the need for reactive groups to move into close proximity for catalysis. A model kinase in this regard is adenylate kinase, which consists of two domains that adjust to bring their phosphate donor and acceptor ligands into proximity for reaction to occur ^{2, 3}.

Phosphomevalonate kinase (PMK), the topic of this study, catalyzes a reaction analogous to that of adenylate kinase in that the phosphate acceptor is itself a phosphate group. Human PMK catalyzes the transfer of the γ-phosphoryl group of ATP to mevalonate 5-phosphate (M5P), resulting in formation of mevalonate 5-diphosphate. This is the sole pathway for biosynthesis of steroids and other isoprenoids in mammals^4-7. Despite the importance of this pathway in human heart disease and the fact that it is the biosynthetic source of a diverse class of metabolites, the mechanism of PMK is not completely characterized⁸, although recent studies have identified important catalytic residues^9,10. To better understand the molecular mechanism of catalysis, structural characterizations of protein-ligand complexes are required. Of particular interest are conformational and dynamic changes that are needed to bring the two highly charged substrates in proximity to react. To facilitate this, a homology model for human PMK had been generated using the PHYRE homology model method (≈24% overall sequence identity), since there is no experimental structure yet available for this protein⁹. Our recent NMR chemical shift assignments and subsequent secondary structure analysis has largely validated this model¹¹, based on chemical shift index values that match helical and sheet regions in the model. But, the presence of disordered regions and loops has made it impossible to pursue a complete structure determination. Currently, 77% of the backbone atoms have been assigned, excluding two unassigned gaps that may be disordered regions (residues 56-72 and 99-111). As such, studies herein refer to the homology model. This model consists of two domains. The larger ATP-binding domain is comprised of a 5 stranded parallel β-sheet interweaved with 3 α-helices. The smaller M5P domain is comprised of loop regions and two α-helices. In the model, the ATP and M5P domains are tethered by two hinge regions, analogous to adenylate kinase. These may be involved in opening and closing motions, to permit binding and release of substrates³. Also, recent side-directed mutagenesis studies have identified a “Walker A” ATP binding motif (K17, R18, K19, K22)^12,13. Mutagenesis of some of these residues can decrease catalysis up to 10,000-fold, suggesting this as the active site location for phosphoryl transfer^9,10. “Walker-A” loop residues most important for catalysis include K22 and R18. Outside the “Walker-A” catalytic loop, R110 is also important ^9,10.

To characterize the effects of substrate addition on protein dynamics, we have used NMR relaxation experiments in conjunction with a Modelfree analysis¹⁴ to quantify any changes to the fast timescale motion (psec-nsec) of the protein backbone, especially for catalytically relevant regions. We also report on the conformational effects of substrate addition, by comparing chemical shift changes and backbone ¹⁵N relaxation data for various complexes of PMK: (a) Apo-PMK, (b) the binary complex with Mg-ADP, (c) the binary complex with M5P, and (d) the ternary complex with Mg-ADP and M5P.

MATERIALS AND METHODS

Docking of M5P and ATP into Human PMK Homology Model

The homology model used in our studies was that which was previously prepared and reported by Herdendorf and Miziorko⁹. The binding orientation of ligands in this PMK (human) homology model was determined using Autodock4¹⁵. Gasteiger charges and hydrogens were added using AutoDock Tools (ADT). The docking grids were also prepared using ADT, with a grid size of 60 × 60 × 60 Å and a spacing of 0.375 Å. These grids were centered on the ligands (AMP and GMP) of the homology model template, bacteriophage T4 deoxynucleotide kinase¹⁶. The homology model⁹ and template were superimposed on each other, in order to obtain coordinates for the grid box used to dock the ligands. The overlay was done using Sybyl 6.8 (Tripos Inc., St Louis, MO, USA). Default docking parameters were used, except that 50 genetic algorithm runs were used with 2,500,000 as the maximum number of evaluations. The docking of both ligands was done separately, due to inter-ligand repulsion from the negative charges on M5P and the ATP triphosphate, even after neutralization of two charges (as would be the case with bound Mg²⁺). This repulsive interaction was recognized based on earlier docking attempts to form the ternary complex, which produced erroneously distorted structures with the phosphate groups on the two ligands as far apart as possible in the docking box. This led us to do independent docking of ATP and M5P to produce the separate binary complexes, and these pdb files were then merged to create the ternary complex. This approach positioned the phosphate groups on ATP and M5P in close proximity, as required for the phosphate transfer reaction, and therefore provides strong validation for the docking poses that were generated (Fig. 1).

Figure 1.

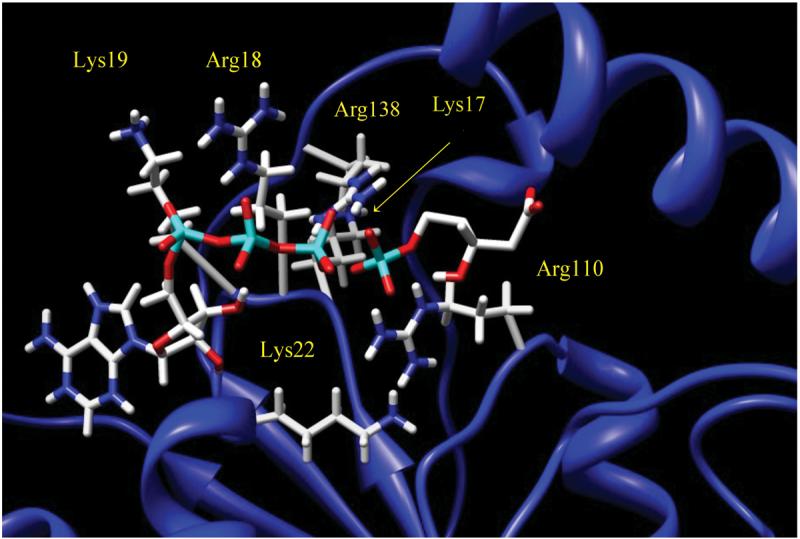
Ternary structure of docked ligands ADP and M5P in the active site, near the “Walker A” loop, of PMK. Catalytically important amino acids are labeled, including Lys's 17, 19, and 22, as well as Arg's 18 and 110.

Protein Expression and Purification

PMK is normally a 192 residue 22.0 kDa protein, although it was expressed with an N-terminal histidine tag and additional linker residues, giving a total molecular weight of 24.2 kDa. Uniformly ¹⁵N labeled PMK samples were prepared using ¹⁵NH₄Cl as the sole source of nitrogen in minimal media and protein was expressed and purified as described previously^9,10. Briefly, E. coli BL21-(DE3) Rosetta cells were transformed with a pET15b(+) expression construct which encoded human PMK with an N-terminal His₆ affinity tag. The transformed cells were plated onto LB (Luria Bertani) agar containing ampicillin (amp) and chloramphenicol (chl). Plates were incubated overnight at 37 °C, and a single colony was picked to inoculate 2 mL of media, and grown to A₆₀₀ ∼ 0.3. This culture was then used to inoculate 20 LB-amp-chl plates. The plates were incubated overnight at 37 °C, and resulting lawns were used to inoculate 500 mL of LB-amp-chl to give A₆₀₀ ∼ 1.0. The liquid culture was then incubated at 30°C for 1 h prior to induction with 1 mM IPTG. The culture was harvested 4 h post induction at A₆₀₀ ∼2.0. Bacterial pellets were resuspended in 100 mL of a 50 mM KP_i (potassium phosphate) buffer containing 100 mM KCl, 5 mM imidazole, and 0.5 mM DTT at pH 7.8. Lysis was accomplished by passage through a microfluidizer at ∼17 kpsi. The lysate was clarified by centrifugation at ∼100,000 g and the supernatant was loaded onto ∼0.5-1.0 mL of Ni-Sepharose Fast Flow resin. The column was washed with lysis buffer until A₂₈₀ < 0.005, and the protein was eluted with lysis buffer supplemented with 300 mM imidazole. The fractions containing PMK were pooled and the concentration was determined spectrophotometrically using an extinction coefficient of ε₂₈₀ = 32,290 M⁻¹ cm⁻¹.

NMR Sample Preparation

All protein samples were buffer exchanged, using ultrafiltration with an Amicon (YM10) membrane, into 5 mM DTT, 20 mM KH₂PO₄, 10% D₂O, and 0.02% NaN₃, and concentrated to 400-600 μM. ADP was complexed with Mg²⁺ by adding a 1:1 ratio of MgCl_2. Mg-ADP and M5P were both concentrated to 50 mM prior to titration, with pH's of 5.0 for ADP and 7.0 for M5P. All experiments were performed at pH 6.5.

NMR Spectroscopy

All NMR experiments were performed on a 600 MHz Varian NMR System at 599.515 MHz using a triple resonance cryoprobe with z-axis gradients at 25 °C. Titrations were performed using 100 μM increments for both ligands, until saturation was achieved based on ¹H-¹⁵N HSQC chemical shift changes (1 mM for M5P and 2 mM for MgADP). There were two sets of titrations performed, first starting with M5P then adding Mg-ADP. To assess binding order and synergy, the second titration started with Mg-ADP followed by M5P. ¹⁵N relaxation experiments were performed on free PMK, PMK saturated M5P (2 mM), PMK saturated Mg-ADP (20 mM; higher concentration was needed due to slow hydrolysis of ADP), and then the ternary complex (using the same saturation concentrations). ¹⁵N-T₁, ¹⁵N-T₂, and {¹H}-¹⁵N NOE experiments were all performed using the BioPack pulse sequences from Varian, Inc (Palo Alto, CA). Delay times for the T₁ experiment were 10.8, 108.3, 216.8, 379.2, 541.7, 758.4, 1083.4, 1516.8, and 2166.8 ms and 4.31, 8.62, 12.9, 17.2, 21.6, 30.2, 38.8, 47.4, 56.1 ms for T₂. T₁ experiments employed the standard inversion-recovery pulse sequence¹⁷, while T₂ experiments employed the CPMG sequence, as implemented previously^18,19. NOE's were obtained by measuring HSQC spectra with and without ¹H saturation for a time of 3 s (same for both), and using an interscan delay of 1 sec. An interleaved approach was used for the T₁ and T₂ experiments, to average out any potential instability over time^{20, 21}.

NMR Spectroscopy Data Analysis

NMR data were processed using NMRPipe/NMRDraw²², and analyzed using NMRView²³. For all experiments, ¹H-¹⁵N spectra were processed using a 90° shifted sine function in the ¹H and ¹⁵N dimensions. For ¹⁵N-T₁ and ¹⁵N-T₂ experiments, the spectra with the shortest relaxation delay were peak picked using NMRView. For {1H}-¹⁵N NOE measurements only one spectrum was peak picked, and for each subsequent spectrum the peak ellipses were manually adjusted to fit each peak.

The R₁ and R₂ relaxation rates were determined by fitting the T₁ and T₂ curves to Equation 1:

$${\mathrm{I}}_{\mathrm{t}}={{\mathrm{I}}_{\mathrm{o}}}^{\ast }{\mathrm{e}}^{(-\mathrm{Rt})}$$ (1)

where I_t is the intensity after time t, I_o is the intensity at time t=0, and R is either R₁ or R₂. Fitting was done using the Rate Analysis package included in NMRView. NOE values were obtained by taking the ratio of the intensity versus the control. This was done with two sets of experiments in order to obtain an error for the analysis. T₁ and T₂ values were measured for PMK at various concentrations and used to calculate τ_c values, to demonstrate that PMK remains monomeric under the conditions of our NMR studies (previous analytical gel filtration studies also established that PMK is monomeric⁹).

Dissociation constants were obtained by measuring the chemical shift changes in going from free to various bound states, monitoring peaks in fast exchange in both ¹H and ¹⁵N dimensions. These changes were then combined using Equation 2:

$$\Delta {\text{shift}}_{\mathrm{obs}}={[{{(}^1\mathrm{H}\text{shift})}^2+{{(}^{15}\mathrm{N}\text{shift}∕6.51)}^2]}^{(1∕2)}$$ (2)

The chemical shift change (Δshift_obs) along with the concentration of the ligand and protein were fitted to a quadratic equation, to determine the dissociation constant K_d:

$$\begin{array}{cc}\hfill & \Delta {\text{shift}}_{\mathrm{obs}}={(\Delta {\text{shift}}_{\max }∕\left(2\left[{\mathrm{P}}_{\mathrm{o}}\right]\right))}^{\ast }\{(\left[{\mathrm{L}}_{\mathrm{o}}\right]+\left[{\mathrm{P}}_{\mathrm{o}}\right]+K_d)\hfill \\ \hfill & -{\{{(\left[{\mathrm{L}}_{\mathrm{o}}\right]+\left[{\mathrm{P}}_{\mathrm{o}}\right]+{\mathrm{K}}_{\mathrm{d}})}^2-4\left[{\mathrm{L}}_{\mathrm{o}}\right]\left[{\mathrm{P}}_{\mathrm{o}}\right]\}}^{1∕2}\}\hfill \end{array}$$ (3)

using Sigmaplot8, where L_o is the total ligand concentration at a particular titration point, P_o is the total protein concentration, and Δshift_max is the maximum chemical shift change observed for the particular peak in question. Fitting to the quadratic equation was required because [P_o] > K_d. Standard deviations resulted from the non-linear least squares fitting process (note: as K_d gets very small relative to [P_o], errors will become larger because K_d become less well-defined in the fitting process).

Modelfree Analysis

The parameters of internal motion were determined from the NMR relaxation data according to the model-free formalism established by Lipari and Szabo^24-26 using Modelfree4 software (version 4.20, A. G. Palmer, Columbia University). The residues were optimized with an isotropic diffusion model using an initial estimate derived from the R2R1_diffusion program (A. G. Palmer, Columbia University). Backbone dynamics calculations were performed with 300 Monte Carlo simulations per run using an internuclear distance r_NH of 1.02 Å and a chemical shift anisotropy (CSA) for the ¹⁵N nucleus of −172 ppm. Five models were used to fit our experimental data and were iteratively tested in order of increasing complexity (M1= S²; M2= S², τ_e; M3= S², R_ex; M4= S², R_ex, τ_e; M5= S²_f, S²_s, τ_e) until an acceptable fit was achieved. S² is the generalized order parameter, τ_e is the internal correlation time, R_ex is the exchange contribution term, and S²_f and S²_s are for sub-nanosecond and nanosecond motions respectively. These models were tested until they could reproduce the experimental relaxation data within 90% confidence limits using appropriate χ² and F-tests¹⁴.

RESULTS

Docking of M5P and ATP to Human PMK

The docking of M5P and ATP (Fig. 1) seems reasonable based on the proximity of the reactive phosphate groups to each other, and also their location within 4.0 Å of the “Walker A” catalytic loop, which includes Lys17, Arg18, Lys19, and Lys22 as well as other basic residues, especially Arg110. It is striking that the independent docking of M5P into PMK positioned its phosphate group within 2.7 Å of the ATP γ-phosphate and 2.8 Å from Arg110 and Arg138.

Chemical Shift Perturbation Studies to Make the Binary and Ternary Complexes

For chemical shift perturbation studies, a dead-end complex was created to ensure that there would be no catalytic turnover during the NMR measurements. AMP-PNP (Fig. 2) is often used to create such dead-end complexes in kinases, but it binds only weakly to PMK and causes few structural changes in PMK compared to ATP (Fig. 3a and supplementary materials) or ADP (Fig. 3c and supplementary materials). As a result, ADP was used to make the dead end complex (Fig. 3c) in our studies. To justify the use of ADP as a suitable replacement for ATP, an ATP titration experiment was carried out and is shown in Fig. 3a. Comparing these spectra, it is clear that they show the same chemical shift changes for the same residues, which infers that the two protein-ligand complexes undergo very similar structural changes. From the HSQC spectra for the Mg-ADP titration (Fig. 3c), a pronounced conformational change is observed upon substrate addition, due to multiple residues that are affected when the complex is formed. Fig. 4a shows the chemical shift perturbations due to Mg-ADP binding mapped onto the PMK model, and is consistent with Mg-ADP causing the protein to undergo a gross conformational change; that is, the whole protein appears to adjust structurally in order to accommodate the addition of Mg-ADP. Notable changes are observed in the loops near the substrate phosphate groups, as well as the region where the two ATP-domain helices contact each other. The Mg-ADP addition was then followed by further titration with M5P to form the ternary complex (Fig. 4b). To determine if there is a preferred sequence for binding, due to synergy, M5P was then titrated first to Apo-PMK (Fig. 4c).

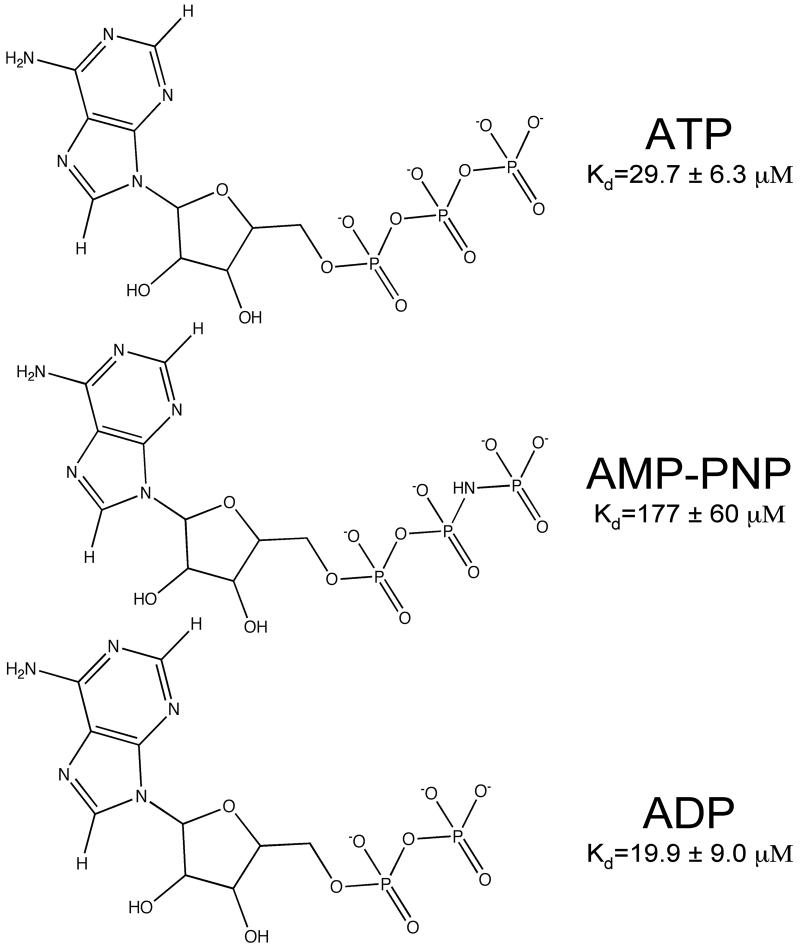
Figure 2.

Structures of adenine nucleotides ATP, AMP-PNP, and ADP with corresponding K_d values.

Figure 3.

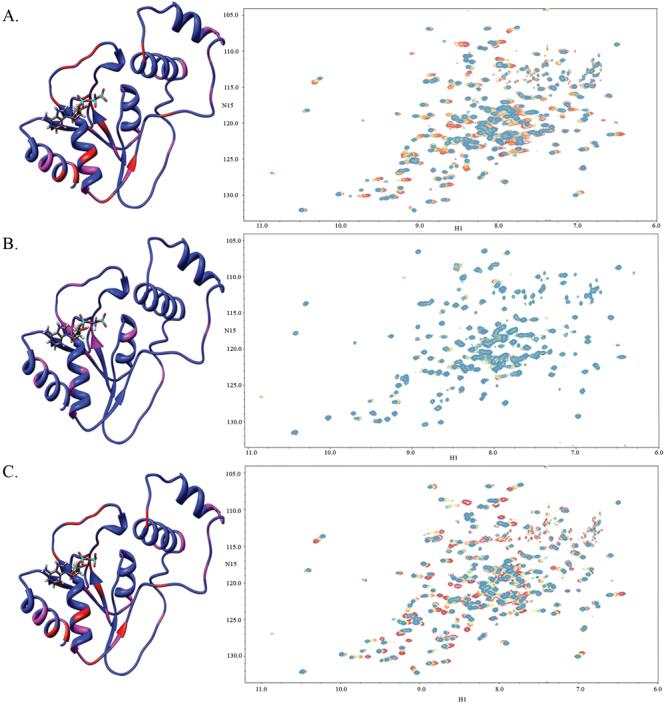
Chemical shift perturbations due to binding of nucleotides a) Mg-ATP titrated to saturation onto Apo-PMK, b) Mg-AMP-PNP titrated to saturation onto Apo-PMK, and c) Mg-ADP titrated to saturation onto Apo-PMK. All experiments begin at the red cross-peaks, with additions in 100 μM increments to saturation, which is indicated by the transition to the blue cross-peaks. The corresponding chemical shifts are mapped on to the human PMK homology model, where the red indicates a large chemical shift change (>0.09 ppm) and pink indicates a medium chemical shift change (0.05-0.09 ppm), while blue indicates a small or no chemical shift change (or no data).

Figure 4.

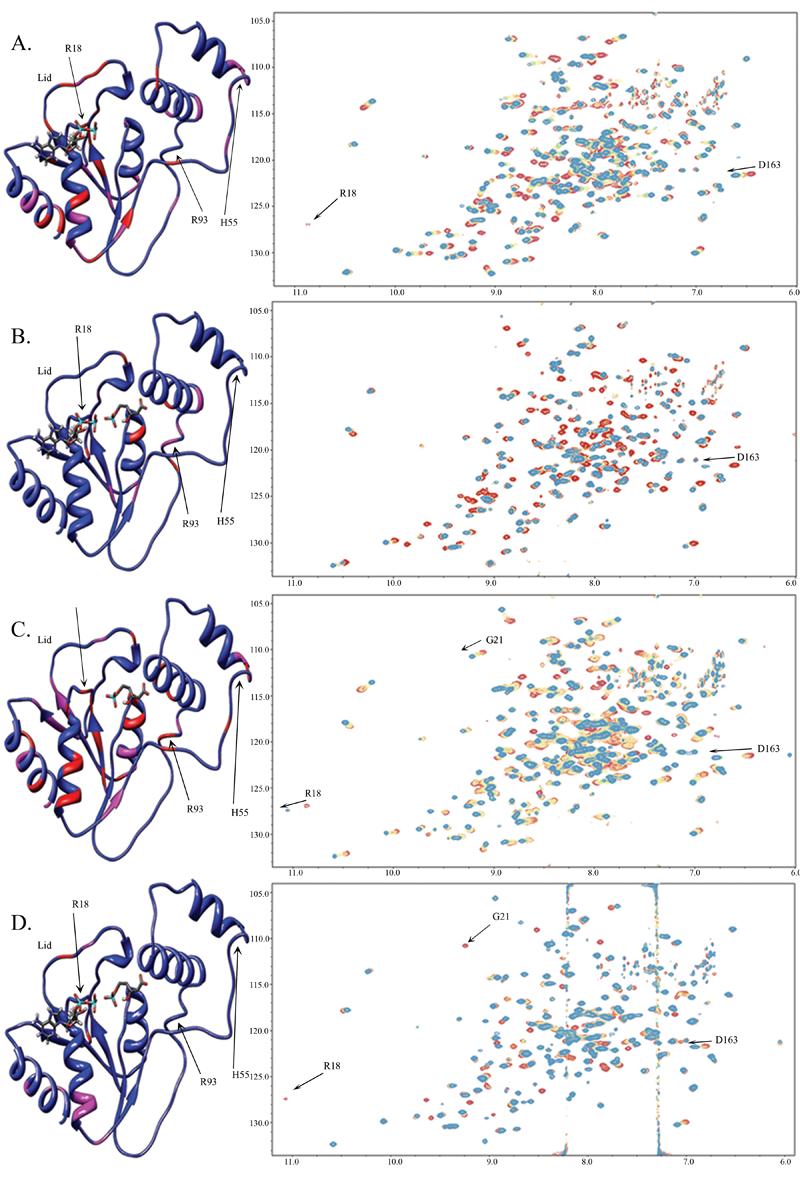
Chemical shift perturbations of: a) Mg-ADP added to saturation to Apo-PMK b) M5P added to saturation to Mg-ADP/PMK c) M5P added to saturation to Apo-PMK and d) Mg-ADP added to saturation to PMK/M5P. All experiments begin with the red cross-peaks and titrations occur at 100 μM increments to saturation, which is indicated by transition to the blue cross-peaks. The corresponding chemical shift changes are mapped on to the human PMK homology model, where the red indicates a large chemical shift change (>0.09 ppm) and pink indicates a medium chemical shift change (0.05-0.09 ppm) while blue indicates small or no chemical shift change (or no data). Note: Gly21 is visible in panel (a) at a lower threshold.

Binding Affinity and Synergy

To quantitatively assess binding affinity and binding synergy, if any, cross-peak perturbations (Figs. 3 and 4) were fitted to obtain K_d values for each binding event. Monitoring chemical shift changes and fitting to the quadratic equation (Eq. 3) permitted determination of dissociation constants (K_d) for the various nucleotides (Fig. 2) and for all four complexes (Fig. 5). The K_d for the Mg-ADP titration to Apo-PMK is 19 ± 9 μM and <20 μM for subsequent M5P binding to form the ternary complex. For the titration of M5P to Apo-PMK the K_d is 6 ± 3 μM and 56 ± 16 μM for the subsequent Mg-ADP addition to form the ternary complex. These values are consistent with the previously reported K_m values of 47 ± 5 μM for ADP and 34 ± 3 μM for M5P ⁹, keeping in mind that K_m values can often deviate from K_d values due to kinetic effects.

Figure 5.

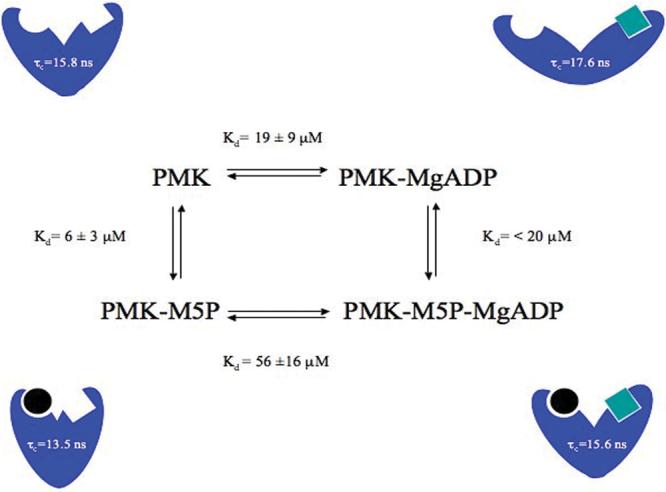
Thermodynamic box for the formation of the dead-end ternary complex of human PMK with corresponding K_d and τ_c values for each complex. Cartoon representations of each complex are shown, with the circles representing M5P and the squares representing ADP.

Relaxation Dynamics

To obtain dynamic information on the psec-nsec time scale, longitudinal (R₁) and transverse (R₂) relaxation rates as well as {¹H}-¹⁵N NOE values were obtained, and are summarized in Fig. 6 for Apo-PMK, Mg-ADP bound PMK, M5P bound PMK, and the ternary (Mg-ADP/M5P) complex. All of the complexes have relatively rigid structures (high S²), indicative of a well-ordered protein backbone on the psec-nsec timescale. Trends in R₁ and R₂ values in Table 1 can best be explained based on changes in the overall correlation time of the protein in the different complexes. It should again be noted that PMK remains in a monomeric state in our NMR studies (Supplementary material), so changes in correlation time are not associated with aggregation effects. The changes in PMK correlation time were verified and quantified in the Modelfree analysis, where it was found that relaxation data could not be properly fitted for the different PMK complexes using the same correlation time. The correlation times obtained from the Modelfree analysis of each complex are summarized in Fig. 5. These correlation time changes are consistent with there being ligand-induced change in overall shape of PMK in the different complexes, as had been previously observed in analogous NMR studies of adenylate kinase.

Figure 6.

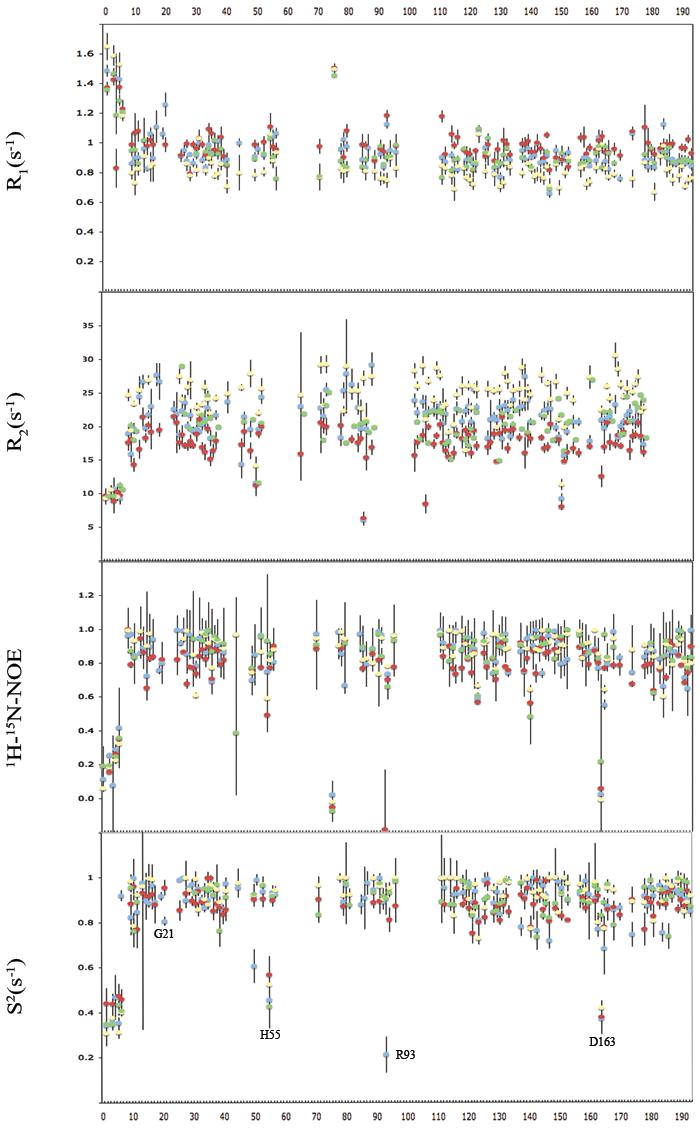
NMR dynamics data including R₁, R₂, NOE, and S² values, where blue is the Apo-PMK complex, red is the M5P saturated complex, yellow is the Mg-ADP saturated complex, and green is the ternary complex.

Table 1.

Average Values of Relaxation Parameters for PMK Complexes

	Apo-PMK	PMK-M5P	PMK-ADP	PMK-ADP-M5P
R1(s−1)	0.945 ± 0.034	0.994 ± 0.046	0.856 ± 0.051	0.933 ± 0.036
R2(s−1)	20.7 ± 1.9	17.3 ± 1.9	24.0 ± 2.0	20.0 ± 1.7
NOE	0.820 ± 0.080	0.766 ± 0.028	0.834 ± 0.065	0.818 ± 0.112
S2	0.881 ± 0.035	0.859 ± 0.046	0.891 ± 0.036	0.873 ± 0.036

DISCUSSION

The studies reported herein are directed to defining the structural and dynamics changes in human PMK, induced by ligand binding events. Studies were based on human PMK that was titrated with MgADP and M5P, and interpreted in light of a previously reported homology model. Results can be interpreted in the context of extensive studies of related proteins, such as adenylate kinase which binds ATP and the substrate to be phosphorylated in two separate domains, and which also contains a “Walker A” catalytic loop capped by a flexible “lid” region.

The docked complex – a structural hypothesis

In our docked complex of human PMK with M5P and ATP (Fig. 1), the key catalytic residues identified by Herdendorf and Miziorko^9,10 (Arg18, Lys22, and Arg110) are all reasonably well positioned for catalysis. The only possible exception is Lys22, which is in the active site but is pointed away from the phosphate; while this may reflect an inaccuracy of the homology model, it is noteworthy that a simple side chain rearrangement could easily position its ε-amino group near the ATP γ-phosphate. Arg18, Lys22, and Arg110, along with the other basic residues in Fig. 1, may be important for forming the ternary complex by neutralizing the negative charges on the two substrates, so that their phosphate groups can move into proximity for phosphoryl transfer. Additional charge stabilization (from Lys22?) may also be needed to stabilize the transition state if it goes by an associative-type mechanism, which would place added charge density on the γ-phosphate. An important feature of the model in Fig. 1 is that the γ-phosphate of ATP is ideally positioned for nucleophilic attack by the M5P phosphate (separated by only 2.7 Å). This provides further validation that this structural model of the ternary complex is reasonably accurate.

Binding synergy … or lack thereof

Based on chemical shift perturbations, it appears that binding of either M5P or ADP to apo PMK can induce a large conformational change. To quantitatively assess binding synergy, if any, cross-peak perturbations were fitted to obtain K_d values for each binding event (Fig. 5). These K_d values are consistent with their being no preferred binding sequence or synergy for the ligands. This is in contrast to the report of an ordered sequential mechanism (M5P binding first and ADP released last) for the pig liver PMK enzyme²⁷, but is consistent with recently reported steady state kinetics on human PMK, where competitive inhibition was observed using mevalonate 5-diphosphate as a product inhibitor versus M5P¹⁰. If anything, our data suggest there is a modest (∼3-fold) anti-synergy, such that affinity for the second ligand is weakened due to presence of the first, which could be due to the charge/charge repulsion by the phosphate groups on both ligands. But, this anti-synergy could be unique to our dead-end complex (MgADP/M5P), and does not necessarily reflect the situation for the catalytically competent Michaelis complex (MgATP/M5P) ²⁸.

Ligand-induced structural changes

Based on the chemical shift perturbations that occurred during titration to form binary and ternary complexes, it can be seen that the largest changes occur in forming the binary complex, whether it is ADP or M5P that binds first (Fig. 4). The chemical shift changes include residues outside the binding site, such as hinge regions between domains, so suggest a conformational change has occurred. In terms of adenine nucleotide binding, it is interesting that while the γ-phosphate of ATP seems to not be important for binding or inducing structural changes, based on comparisons of ATP and ADP (Figs. 2 and 3), the situation is actually more complicated - because simple O=>NH substitution of the bridging heteroatom between the β and γ phosphates has a dramatic effect on binding. In fact, independent kinetic measurements performed at 34 μM ATP (< 1/3^rd K_m for ATP) indicates no inhibition of PMK by AMPNP at levels ranging from 269-1074 μM (Miziorko and Herdendorf, unpublished results). This suggests there may be important interactions with the β-γ bridging heteroatom, which might be important for stabilizing this leaving group during phosphate transfer. It is also noteworthy that ADP (and ATP) binding causes chemical shift perturbations in the Walker A loop (ex. Arg18) as well as the lid that covers the Walker A loop, and a hinge residue for the lid (D163). Opening of this lid motion should only produce a modest change in size of the protein, and so would not be expected to produce a change in correlation time. In contrast, domain movement between ATP and M5P binding domains would be expected to produce a much larger change in size and correlation time, as had been observed in adenylate kinase, and appears to also occur in human PMK (vide infra).

Ligand-induced changes to psec-nsec timescale dynamics … or lack thereof

Based on Modelfree analysis of NMR dynamics parameters (Fig. 6), generalized order parameters were obtained. These clearly indicate that PMK adopts a fairly rigid structure (S² values >0.8) for all the binary and ternary complexes. Furthermore, the average S² values remain largely unchanged upon formation of the binary complex with either ADP or M5P, indicating that the local dynamics for all the complexes are virtually the same (Table 1) on the psec-nsec timescale. The large S² values, which are consistent with a rigid, highly ordered backbone, are not unexpected given the well-structured core of the protein, which includes a 5 stranded parallel β-sheet. One might have expected some ordering in the M5P domain upon ligand binding, given the high content of extended and loop regions, but this does not appear to be occurring.

Inter-domain and loop motion: ligand binding domains, lid and “Walker A” catalytic loop

While the protein core may be largely rigid, it is possible that there is some motion of domains relative to each other, and of other defined regions. Indeed, chemical shift perturbation studies suggested there was a large substrate-induced conformational change (Fig. 4). In fact, there were a small number of residues with small or negative NOE's that gave rise to small S² values (H55, R93, and D163), and these are located in loop and potential hinge regions in the homology model (vide infra). Interestingly, the “Walker A” ATP binding loop shows the same S² values as the rest of the protein (i.e. it is rigid), indicating that if there is any catalytically relevant change in dynamics, it might only occur during turnover with the actual Michaelis complex²⁸, rather than with the “dead end” complex used in our studies. One important exception is Gly21, which is adjacent to Lys22, the catalytically most important residue in PMK⁹. Gly21 undergoes an increase in S² in going from the apo (blue) to the M5P (red) complex, indicating it becomes less mobile in the binary complex (Fig. 6), perhaps as Lys22 moves into position for catalysis (note: Lys22 was not assigned, so changes to its dynamic state are not known). Interestingly, Gly21 exchange broadens in the ternary complex, suggesting it undergoes msec timescale motion. But, in the conversion of apo PMK to the PMK-M5P binary complex, one can see a slow exchange process for Arg18, and a fast exchange process for Gly21 (Fig. 4c, and expansions in supplementary materials). Assuming the same motion occurs for these two “Walker A” loop residues, this timescale flanking permits an estimation of the rate constant for the “Walker A” catalytic loop exchanging between the two states associated with M5P binding as k_ex = 100-600 sec⁻¹ (see supplementary materials). This is likely to be due to a lid opening/closing motion, which would be coupled to “Walker A” loop motion, based on analogy to adenylate kinase where a flexible lid caps the catalytic “Walker A” loop^31-36.

It should be noted that while there doesn't appear to be significant motion of “Walker A” catalytic loop residues on the psec-nsec timescale (besides Gly21), there does appear to be motion on slower (ex. msec) timescales. For example, in the ADP binary and ternary complexes, most crosspeaks for residues in the loop were no longer visible, due to exchange broadening (Fig. 4). For this reason, S² for ADP complexes could not be measured. Accordingly, it is simply not known in these complexes what motion might be occurring on the psec-nsec timescale.

Overall, the psec-nsec timescale dynamics data indicate that M5P binding drives the immobilization of catalytic residues (with Gly21 as our “Walker A” reporter), but there still appears to be msec timescale motion, especially when ADP is bound. This motion might be important for catalysis, but could also be unique to the particular dead-end inhibitory complex used in our study. There is certainly literature precedent for kinase active site loop dynamics being very sensitive to the nature of the inhibitory complex. For example, residual dipolar coupling and ¹⁵N relaxation measurements of various ABL kinase complexes indicated that inhibitors differed significantly in their ability to immobilize the catalytic/activation loop³⁰.

Ligand-induced changes to protein size: inter-domain conformational change?

The chemical shift perturbation studies indicated that binding of either ADP or M5P may cause a large conformational change (Fig. 4), but the above analysis of S² values indicated this did not correspond to any significant changes in dynamics within the two ligand binding domains, other than some changes to the “Walker A” catalytic loop, and the lid that covers it. What about inter-domain motion? The Modelfree analysis provided some insights in this regard. As mentioned in the Methods section, relaxation data fitting was optimized for each complex to find the rotational correlation time τ_c for that complex, since it was not possible to fit all complexes using a single τ_c. Changes to fitted τ_c values for all the complexes (Fig. 5) reveal that the ADP binary complex has the largest τ_c of 17.6 nsec while the M5P binary complex has the smallest, with a τ_c of 13.5 nsec. The Apo-PMK and the ternary complex fall in between these two extremes, with similar τ_c values of ∼15.7 nsec (Fig. 5). This suggests that both ADP and M5P binding induce conformational changes, but in opposite directions. That is, M5P causes a compression of the structure (so PMK tumbles faster), while ADP causes an opening up of the structure (so PMK tumbles slower). Such changes would be consistent with a movement of the two ligand binding domains relative to each other, as occurs in the nucleoside monophosphate kinases^{29, 31-35}.

Why ADP binding causes the structure to open up is not clear. Since the product of the PMK reaction is ADP, it could be that the open conformation reflects the protein trying to release ADP. However, the chemical shift perturbation study with ATP (Fig. 3a) shows the same chemical shift perturbations as with ADP (see supplementary materials), arguing against there being a dramatically different conformation in the ATP vs. ADP binary complexes. The changes in τ_c for the various complexes indicates that protein closure occurs upon binding to M5P, with or without ADP present. This tightening/closure of the structure induced by M5P binding might be associated with domain movement around a His55/Arg93 hinge (Figs. 4 and 6). The chemical shift perturbation studies of PMK bound to M5P, with subsequent addition of Mg-ADP, demonstrate that the protein may open back up to bind ADP/ATP for catalysis.

Hinge regions for lid and domain movement

The previous discussion presented data in support of ligand-induced structural changes, which may be related to inter-domain (ATP/M5P) motion as well as to motion of the “Walker A” catalytic loop and the lid that covers it. Regarding movement of the lid, it is noteworthy that data on adenylate kinase indicates lid movement occurs on the same timescale as catalysis. This is consistent with the lid controlling access to the active site, as well as its packing up against the catalytic “Walker A” loop. In adenylate kinase, a key catalytic residue in the ATP binding site is Lys21²⁹, which twists into an unfavorable double gauche rotamer in order to interact with the ATP phosphate, just as Lys22 would in the human PMK homology model (Fig. 1) if its sidechain were adjusted to permit interaction with the ATP phosphate. This lysine may cycle into a catalytically useful orientation in the transition state to stabilize the increasing negative charge on the γ-phosphate, which would be created in the associative mechanism that is thought to be operative for nucleoside monophosphate kinases²⁹. Such a mechanism would permit selective stabilization of the transition state, and would require motion of the “Walker A” loop as the transition state is approached. So, lid motion is potentially relevant to catalysis. How does lid motion occur in PMK?

As noted earlier, a number of potential hinge residues had unusually small S² values (H55, R93, and D163), which indicates they are mobile on the psec-nsec timescale (note: often, fast timescale motion occurs along with msec timescale motion, which would be more relevant for a hinge region). Specifically, residues H55 and R93 are positioned (Fig. 4) such that they could operate as hinge residues that allow movement between the core ATP domain and the M5P domain, possibly for enabling an opening and closing motion upon substrate binding³. Likewise, Asp163 is located in a potential hinge region for the “lid” loop region that is analogous to the “lid” that is present in the nucleoside monophosphate kinases^{29, 31-36}. This lid caps the catalytic “Walker A” loop in the PMK model. The potential hinge residue, Asp163, also underwent dramatic chemical shift changes upon ligand binding (Fig. 4), as would be expected if there were motion around this hinge region induced by ligand binding. Motion around this hinge region would permit movement of the “Walker A” catalytic loop, which could be coupled to lid motion, as in adenylate kinase. The full extent to which catalytic loop and lid motions are coupled, and what role this motion might have in catalysis in human PMK, is not known, and will be the topic of future studies. But, extensive NMR studies on nucleoside monophosphate kinases²⁹, and especially adenylate kinase as a prototype^31-36, provide a rich literature that describes coupled motions between these loops, and their role in catalysis. These studies have also identified ligand-induced changes in protein correlation times (due to inter-domain movement; opening/closing), as we have now observed in human PMK. It will be interesting to see if human PMK follows the example of the adenylate kinase prototype, or whether it will provide unique and new insights into the role of such loop and domain motions in kinase-mediated phosphate transfer reactions. The studies reported herein provide a foundation for such future studies.

An N-Terminal Region of Unknown Function

The most noticeable feature of the order parameter profile (Fig. 6) is in the N-terminal region, which has no homology to adenylate kinase or to the T4 deoxynucleotide kinase template, upon which the homology model was based. But, there is a dramatic and sharp change in S² from a disordered state (S² ≈ 0.4) to an ordered state (S² > 0.8), occurring immediately after Arg9, where the homology model starts. The fact that these nine residues are completely disordered in apo PMK, and all binary and ternary complexes, combined with the fact that organisms such as C. elegans lack this N-terminal segment entirely, suggests it is not an integral part of the PMK structure. Indeed, inspection of the homology model reveals no potential structural role for these nine N-terminal residues. This led us to speculate that these residues may be part of a signal or regulatory peptide, which might be cleaved off by an as-yet unidentified protease (note: this region shows no homology to membrane-binding peptides, and there are no data suggesting PMK is membrane bound). To begin exploring this hypothesis, and to identify which protease might cleave this N-terminal peptide, an exhaustive search of signal sequence databases was performed, searching only against the peptide sequence in question (i.e. Met1 to just past Arg9). While none of these searches yielded a strongly scoring motif hit, one did give a modest scoring prediction of cleavage immediately after Arg9 This site was identified using the ProP 1.0 server, using a neural network model trained using literature sequence data³⁷. While the score for the cleavage site was relatively low (0.112; scores in the 0.5-1.0 range are considered high probability), it is the best scoring motif hit obtained thus far, and should be interpreted in the context of NMR data that indicate cleavage, if it occurs, would be expected at exactly this site (after Arg9). The enzyme predicted to cleave here is a furin-like protease, which belongs to a family of proteases broadly classified as “proprotein convertases”³⁸. It should also be noted that other functions for this N-terminal region are also possible, such as binding to modular interacting domains of regulatory proteins (note: this sequence has no homology to existing SH3 motifs). This region also scored reasonably well for being a nuclear export signal peptide, using the NetNES 1.1 server. Clearly, the biological function of this N-terminal region remains to be elucidated, and is the topic of ongoing studies.