Hierarchical control of static prehension: I. Biomechanics

Abstract

We explored the action of digits during static prehension tasks involving one hand or two hands of one or two persons. Three hypotheses were tested: To prevent slippage of the object, grip force and safety margin would be largest in bimanual conditions, particularly involving two persons; The distribution of tangential forces would not differ among tested conditions, thus preserving the vertical orientation of the object in a stereotypical way; and The mechanical advantage of fingers would be used to maintain rotational equilibrium. The multi-digit synergies are discussed in the companion paper (Gorniak et al. 2009). The subjects held vertical one of the two handles, a narrow one and a wide one. They used the four fingers of the right hand opposed by either the right hand thumb, the left hand thumb, the left hand index finger, the thumb of an experimenter, the index finger of an experimenter, or an inanimate object. Forces and moments of force produced by each digit were recorded. The first two hypotheses were falsified. Both grip force and safety margin were the largest in the one-hand task, and they were the lowest for the tasks involving two persons. The distribution of tangential forces among fingers was significantly different in the one-hand task. The mechanical advantage hypothesis was supported across all the tested conditions. The results suggest that the neural controller uses a different strategy in the one-hand task as compared to other tasks, while the bimanual prehension involving two persons differs from one-person two-hand tasks. The findings do not support a hypothesis that normal (grip) forces are adjusted to ensure a particular value of the safety margin. Maintaining rotational equilibrium was achieved differently in different tasks. In particular, the one-hand task was characterized by large intercompensated adjustments in different contributors to the total moment of force, which could be described as chain effects; such adjustments were all but absent in the other conditions. The findings may be interpreted within the framework of the reference configuration hypothesis, in which digit forces emerge due to the discrepancies between the actual and the centrally defined (reference) hand aperture.

Introduction

While interacting with the environment, we use both hands to complete tasks everyday. In particular, the two hands can be used together to statically hold an object such as a large box or vase full of water. Coordination of grip force between the two hands is necessary in order to prevent either slippage or crushing of the object, while coordination of the vertical forces and moments of force is necessary to counterbalance the weight of the object and to prevent it from rotating. The coordination of both grip forces (forces applied normal to the object’s surface) and load bearing forces (forces applied at a tangent to the object’s surface) forces has been studied extensively for static (Jenmalm et al. 1998; Westling and Johansson 1984; Shim et al. 2003, 2004a, 2005; Zatsiorsky et al. 2003a,b) as well as dynamic unimanual and bimanual tasks (Burstedt et al 1997; Gao et al. 2005, 2006; Reinkensmeyer et al 1992; Zatsiorsky et al. 2005, 2006).

The neural control of prehensile actions has been commonly considered as involving a two-level hierarchy. At the upper level of the hierarchy the virtual finger (VF, an imagined digit with the mechanical action equivalent to that of the four fingers together) and thumb generate the required mechanical action on the object, while at the lower level, the individual digits produce the VF output (Arbib et al. 1985, MacKenzie and Iberall 1994). Force and moment of force production has been studied extensively for unimanual prehension using this hierarchical scheme (reviewed in Zatsiorsky and Latash 2008). Such a hierarchy has also been proposed and studied for two-hand tasks for bimanual force production on a fixed object (Gorniak et al. 2007a,b; Smits-Engelsman et al. 2004), but has not yet been studied for bimanual prehension of a hand-held object.

One of the commonly used indices of performance in prehensile tasks is the safety margin (SM). SM is the magnitude of exerted normal force above (in %) its value, at which the object begins to slip (Pataky et al. 2004; Zatsiorsky 2002). Average SM for unimanual grip by young, healthy persons ranges between 0.3 and 0.7 (Burstedt et al. 1999; Pataky et al 2004), while special populations, on average, produce higher SM on similar objects (elderly: Cole et al. 1999, Shim et al. 2004b; stroke: Hermsdörfer et al. 2003; multiple sclerosis: Marwaha et al. 2006). A study by Burstedt and colleagues (1997) investigated how fingertip forces exerted on a free object change when one hand or two hands are used in a two-finger precision grip by one person or shared between two people. They reported that SM did not change across grip configurations, despite reliance on different sources of sensory information associated with the different grip configurations.

Previous studies have commonly viewed the coupling between grip and load bearing forces as an example of predictive control based on neural computation of the requisite grip forces via internal models (Davidson and Wolpert 2005; Flanagan and Wing 1997; Witney and Wolpert 2007). The idea of neural computational processes (internal models) leading to predictions of requisite forces has been criticized based on theoretical and experimental grounds (Ostry and Feldman 2003; Feldman and Latash 2005; Feldman et al. 1998; Yang et al. 2007). An alternative interpretation of the force coupling phenomena has been developed based on the reference configuration hypothesis (RC hypothesis) (Pilon et al. 2007). The RC hypothesis suggests that neural control processes define threshold values of muscle length for muscle activation (thresholds of the tonic stretch reflex, see Feldman 1986), while changes in mechanical variables, including forces, occur as results of an interaction between the neural control process and the external force field (reviewed in Feldman and Levin 1995). For multi-joint systems, this is interpreted as defining a reference body configuration corresponding to centrally defined thresholds for activation of all the involved muscles. Typically, the RC is not reached because of anatomical and external force field constraints. The discrepancy between the RC and actual body configuration leads to non-zero levels of muscle activation and active force production. Thus, according to the RC hypothesis grip forces emerge due to the discrepancies between the actual and the centrally defined reference hand aperture.

The goal of the current study (see also the companion paper, Gorniak et al. 2009) has been to investigate how static prehension of a free object changes as different effectors are used for the task. Here we investigate prehension using the four fingers of the right hand (index, middle, ring, and little fingers forming a VF) in opposition to one of the following effectors: the right thumb, left thumb, left index finger, thumb of another person, index finger of another person, and an immobile object. In this paper, we describe the safety margin, forces, and moments of force exerted by the two hands in the grasp plane, while in the companion paper (Gorniak et al. 2009), we describe indices of force and moment coordination using the concept of synergies (reviewed in Latash et al. 2002, 2007). This study may be seen as a further investigation into finger force and moment of force sharing patterns in five-digit grasps (in contrast to the two-digit grasps, Burstedt et al. 1997).

Based on the findings of Pataky and colleagues (2004), we hypothesized that two-hand conditions would show larger grip forces and safety margins, due to subjects employing a ‘better safe than sorry’ strategy to keep the handle from slipping (referred to as Hypothesis 1). In contrast, we did not expect the distribution of applied tangential (load bearing) forces among the individual digits to change across tasks (Hypothesis 2). We also hypothesized that the mechanical advantage of fingers will be used to stabilize moment of forces produced at the lower hierarchical level across all tested digit configurations (Hypothesis 3). This hypothesis is based on several studies showing that fingers with larger lever arms (mechanical advantages) are used more than fingers with smaller lever arms to ensure a required rotational action on the hand-held object (the mechanical advantage hypothesis; Shim et al. 2004a, 2005; Zatsiorsky et al. 2002).

In addition, we manipulated object width in this experiment with an underlying assumption that two-hand actions are more natural for larger objects. This assumption is based on studies that explored preferred grasping patterns for objects of different size and weight (Cesari and Newell 1999, 2000). This was an exploratory manipulation.

Methods

Participants

Five male and six female students served as subjects in this study. Average data for the males were (mean ± SD): 26 ± 2 years of age, 1.77 ± 0.02 m in height, 77.7 ± 12.5 kg in mass, 20.2 ± 0.9 cm for right hand length, 8.7 ± 0.5 cm for right hand width, 20.2 ± 1.0 cm for left hand length, and 8.9 ± 0.4 cm for left hand width. Average data for the females were: 28 ± 4 years of age, 1.69 ± 0.05 m in height, 62.7 ± 3.5 kg in mass, 18.6 ± 1.5 cm for right hand length, 7.8 ± 0.5 cm for right hand width, 18.6 ± 1.1 cm for left hand length, and 7.9 ± 0.4 cm for left hand width. Hand length was measured as the distance from the tip of the distal phalanx of digit three to the distal crease of the wrist with the hand in a neutral flexion/extension pose. Hand width was measured between the lateral aspects of the index and little finger metacarpophalangeal (MCP) joints. Handedness was assessed by the Edinburgh Inventory (Oldfield 1971), which ranges from a laterality quotient (LQ) of −100 (which indicates strong left-handedness) to +100 (which indicates strong right-handedness). All subjects were strongly right-handed (LQ average = +93.1) and had no previous history of neuropathies or traumas to the upper limbs. None of the subjects had a history of long-term involvement in hand or finger professional activities such as typing or playing musical instruments. All subjects gave informed consent according to the procedures approved by the Office of Regulatory Compliance of the Pennsylvania State University.

Experimental Setup

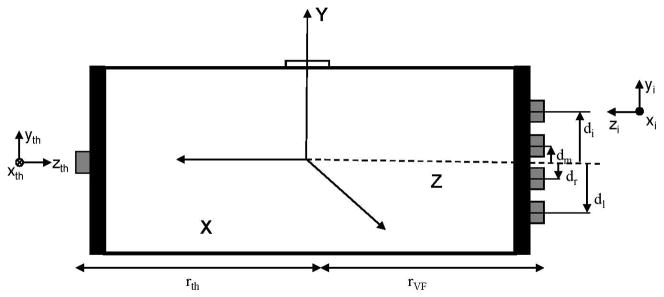
Five six-component force-moment transducers (four Nano-17 and one Nano-25; ATI Industrial Automation, Garner, NC, USA) were mounted on an aluminum handle that could be adjusted with respect to grip width, see Figure 1. The center points of two of the Nano-17 sensors were 0.30 m and 0.10 m above the midpoint of the handle, respectively (X = 0, Y = 0.03 and 0.01 m; capital letters are used for coordinates in the handle-based reference frame, Figure 1). The center points of the remaining two Nano-17 sensors were 0.10 m and 0.30 m below the midpoint (X = 0, Y = −0.01 and −0.03 m) of the handle, respectively. The Nano-25 sensor was located at the midpoint of the handle (with respect to the X- and Y-axes; X, Y = 0). The grip width of the handle (defined as the distance between the contact surface of the Nano-25 sensor and the contact surfaces of the Nano-17 sensors along the Z-axis of the handle) was set to two different values: 0.10 m and 0.32 m, referred to as the narrow and wide configurations, respectively. The point Z = 0 was set as the point halfway between the two sets of sensors. The centers of all the sensors were within one plane referred to as the grasp plane. A circular bullseye level with 2° tolerance was placed on the upper surface of the handle (X, Z = 0). The mass of the handle was 0.323 kg and 0.391 kg for the narrow and wide configurations, respectively. Sandpaper (100-grit) was attached to the contact surfaces of each sensor to increase the friction between the digits and the transducers. The finger pad – sandpaper coefficient of static friction was approximately 1.4 (Pataky et al 2004). Transducer signals were amplified and multiplexed using a customized conditioning box (from ATI Industrial Automation) prior to being routed to a 12-bit analog to digital converter (PCI-6031, National Instruments, Austin, TX, USA). A customized Labview program (National Instruments, Austin, TZ, USA) was used for data acquisition and customized MATLAB (Mathworks Inc., Natick, MA, USA) programs were written for data processing. Signals were sampled at 100 Hz.

Figure 1.

A schematic of the handle in the wide configuration. The Nano-17 and Nano-25 sensors (shown as grey blocks) were attached to vertical aluminum bars. A circular bulls-eye (white block) was placed at the geometric center of the handle. The global reference frame (X,Y,Z) of the handle is shown as well as the local axes of the thumb and index sensors (x_th,y_th,z_th and x_i,y_i,z_i; respectively) Moment arms for the normal (d_j) and tangential (r_i) moments are also denoted.

Procedure

Subjects sat with an erect posture, arms unsupported, in a chair facing the experimenter. Their upper arms were abducted at approximately 45° in the frontal plane, flexed 45° in the sagittal plane, and internally rotated approximately 30°. Each of the hands was in a neutral supination-pronation position. The wrists were extended approximately 10° during each task. At the beginning of each trial, the signals from each of the sensors were set to zero. Subjects were instructed to not touch the handle during the zeroing process.

Subjects were instructed to grasp the handle using one of six different finger combinations (six for the narrow configuration and five for the wide configuration). Finger combinations were: T_R + IMRL_R, T_L + IMRL_R, T_E + IMRL_R, I_L + IMRL_R, I_E + IMRL_R, Object + IMRL_R; where T = thumb, I = index, M = middle, R = ring, L = little fingers, and the subscripts denote the hand to which the fingers belong (R = right, L = left, E = experimenter). In the Object + IMRL_R condition, the handle (in the upright position) was pressed against a large flat inanimate object (with an approximate coefficient of friction of 0.8) which had a level surface normal to the z-axis of the thumb sensor. Throughout the results section and following figures, IMRL_R will be referred to as VF_R for brevity. Note that the T_R + IMRL_R configuration was anatomically impossible for the wide configuration. Subjects were permitted to select comfortable postures of the opposing hand during bimanual tasks (specifically, T_L + IMRL_R and I_L + IMRL_R).

Once the handle was grasped, subjects were instructed to statically hold the handle in the air without deviations from the vertical (Y) axis, using the bulls-eye level as a feedback device. Contact between the hands was not permitted. When subjects reported that they were holding the handle as instructed, data collection began. Subjects were given a practice trial prior to testing each finger combination. During data collection, signals were recorded for 10 s. After data collection stopped, the experimenter retrieved the handle and 10 s of rest was given to the subject. A rest period of three minutes was allowed between finger combinations and a ten-minute rest interval was given between testing blocks. The presentation of tested finger combinations was block randomized, such that handle width (narrow and wide) were the blocking factors. Fifteen trials for each finger combination were collected. A total of 165 trials were performed by each subject.

Data Analysis

The data were processed off-line using customized MATLAB software (Mathworks Inc., Natick, MA, USA). The force and moment data were low-pass filtered at 10 Hz using a 2^nd order, zero-lag Butterworth filter. Data from the interval 5–6 s from each trial were considered during all analyses; all subjects in all conditions held the handle steadily within that time interval.

Local forces and moments of force were computed within sensor-based reference frames for individual sensors referred to as x_j, y_j, and z_j (where j represents: th, i, m, r, and l refer to the thumb, index, middle, ring, and little fingers, respectively). Note that the x_th and z_th axes are in the opposite direction as compared to the axes of the finger sensors (x_i and z_i). Net force and net moment of force data are reported in the handle-based reference frame (X,Y,Z, see Figure 1).

The position of the point of finger force application with respect to the center of the surface of the corresponding sensor is denoted as COP_x and COP_y, and was calculated using the equations for the point of wrench application (Zatsiorsky 2002). The values for COP_y were used in determining the moment arms for individual fingers (d, see Model section). Moments due to the normal forces acting on the handle were calculated with respect to the geometric center of the handle (X,Y,Z = 0). Moments produced by the tangential forces were calculated with respect to an axis corresponding to the balanced static moments of the handle about the X-axis.

Model

For an object in static equilibrium, two equations should be satisfied: ${\sum }_{p=1}^n{\overrightarrow{F}}^p={[0,W,0]}^T$ and ${\sum }_{q=1}^n{\stackrel{\rightharpoonup }{M}}^q={[0,0,0]}^T$, where W is the weight of the object. For this study, we have chosen to focus on the constraints that satisfy these two equations in the grasp (Y–Z) plane.

1. The sum of normal (grip) forces of the individual fingers (along the Z-axis) on the object should be equal and opposite to the normal force of the thumb.

   $$0=F_{VF}^n-F_{TH}^n=F_{VF}^Z-F_{TH}^Z$$ (1)

   $$F_{VF}^Z=F_i^z+F_m^z+F_r^z+F_l^z$$ (2)

2. The sum of the vertical tangential forces of the individual fingers and of the thumb (load bearing forces; along the Y-axis) should be equal to the weight of the object.

   $$W=F_{VF}^t+F_{TH}^t=F_{VF}^Y+F_{TH}^Y$$ (3)

   $$F_{VF}^Y=F_i^y+F_m^y+F_r^y+F_l^y$$ (4)

3. The moment of normal forces (moment due to forces acting along the Z-axis) produced by the individual fingers and the thumb (or another opposing effector) is defined as:

   $$M^n=M_{VF}^n+M_{TH}^n=F_{VF}^n{d}_{VF}+F_{TH}^n{d}_{TH}$$ (5)

   $$M_{VF}^n=F_{VF}^n{d}_{VF}=F_i^z{d}_i+F_m^z{d}_m+F_r^z{d}_r+F_l^z{d}_l$$ (6)

4. The moment of tangential forces (moment due to forces acting along the Y-axis) produced by the individual fingers and the thumb (or another opposing effector) is defined as:

   $$M^t=M_{VF}^t+M_{TH}^t=F_{VF}^t{r}_{VF}+F_{TH}^t{r}_{TH}$$ (7)

   $$M_{VF}^t=F_{VF}^t{r}_{VF}=F_i^y{r}_i+F_m^y{r}_m+F_r^y{r}_r+F_l^y{r}_l$$ (8)

5. The total moment in the grasp plane (about the X-axis) should be equal to zero.

   $$M^{\mathit{TOT}}=M^n+M^t=0,$$ (9)

   where F represents force; M is moment of force; W is the weight of the object; r is the moment arm along the Z-axis; d is the moment arm along the Y-axis; the superscripts n and t refer to moments produced by normal and tangential forces, respectively; the subscripts VF, TH, i, m, r, and l refer to the virtual finger, thumb, index, middle, ring, and little fingers, respectively.

The safety margin (SM) has been defined in literature (Johansson and Westling, 1984; Burstedt et al. 1999; Pataky et al. 2004) as:

$$SM=\frac{(F^z-\mid F^y\mid /{\mu }_s)}{F^z},$$ (10)

where μ_s is the coefficient of static friction between the finger pad and sandpaper interface. Thus, the maximum value for SM is unity if no tangential force (F^y) is exerted on the object and the minimum value for SM is zero if just enough force is exerted on the object to prevent slipping.

Resultant normal force (F_R) was defined as the difference between the grip forces (along the Z-axis) produced by the VF and the corresponding opposing effector (T_R, T_L, T_E, I_L, I_E, or Object; depending on the task conditions), such that positive F_R was always directed towards the opposing effector (+Z, see Figure 1). Total grip force (F_GRIP) was defined as the sum of the grip force magnitudes produced by the VF and the opposing effector. Total vertical tangential force (F_TAN) was defined as the sum of the tangential forces (along the Y-axis) produced by the VF and the opposing effector.

Levels of Analysis

Analysis of the biomechanical variables were performed at two hierarchical levels: the IF level and the VF-TH level. At the IF level, the outputs of fingers within the VF are analyzed (namely IMRL_R). This output includes: normal forces of individual digits ( $F_j^z$;j = i, m, r and l), tangential forces of individual digits ( $F_j^y$), and the moments produced by these forces ( $M_j^n$ and $M_j^t$). At the VF-TH level, the output of the VF and opposing effector are analyzed. This output includes: F_GRIP, F_TAN, Mⁿ, M^t, and M^TOT (see equations 1–9).

Statistics

The data are presented in the text and figures as means and standard errors. Mixed model analyses of variance (ANOVAs) were performed on the force and moment of force data with the factors: Finger Configuration (six levels for the narrow handle width and five levels for the wide handle width; T_R + VF_R, T_L + VF_R, T_E + VF_R, I_L + VF_R, I_E + VF_R, Object + VF_R), Width (two levels; narrow and wide), and Finger (four levels; one for each of the single digits of VF_R involved in the task). A random factor of Subject (10 levels; one for each subject) was also used in the statistical analyses, however significant effects of this factor are not necessarily interpretable and thus not presented in this paper. Post-hoc pair-wise comparisons were performed using Tukey’s tests and Bonferroni statistics to analyze significant effects of ANOVAs. Safety margin data were subjected to Fisher z-transformation to mitigate the ceiling effects inherent to this variable. Non-transformed data are presented in the figures to avoid confusion.

Results

This section is organized in the following way. Results are presented for safety margin (SM), normal forces (Fⁿ), tangential forces (F^t), moments due to the normal forces (Mⁿ), moments due to the tangential forces (M^t), and total moment (M^TOT). Note that positive moment values indicate rotational effort towards the opposing effector in the grasp plane (pronation) while negative moment values indicate rotational effort towards the VF in the grasp plane (supination). In describing the data for each of these variables, we describe the tasks at two levels: the VF-TH level and the IF level. At the VF-TH level, the VF and the opposing effector together are considered as a unit; while at the IF level, the four fingers of the right hand are considered as a unit. For the sake of brevity, here we present the data at the VF-TH level for SM, Fⁿ, and F^t (the results related to Hypothesis #1) and at the IF level for F^t, Mⁿ, M^t, and M^TOT (the results related to Hypotheses #2 and #3). A summary of main results can be found in Table 1 and a summary of the ANOVA findings can be found in Table 2. In the following subsections, a detailed description of the data and statistical analyses related to these effects are presented. The remainder of results at both the VF-TH and IF levels, not specifically related to Hypotheses 1–3, have been included for the sake of completeness and can be found in the Appendix.

Table 1.

Summary of the results

Variable	Level	Result
Fn	VF-TH	--
	IF	I > M, R > L
Ft	VF-TH	--
	IF	I > R > M > L
Mn	VF-TH	--
	IF	|I| > |L| > |R| > |M|
Mt	VF-TH	VF > OE
	IF	|I| > |M|, |R| > |L|
MTOT	VF-TH	VF > OE
	IF	|I| > |M|, |R| > |L|

Inequality relationships among effectors at the two hierarchical levels (VF-TH and IF) are shown. Variables Fⁿ, F^t, Mⁿ, M^t, and M^TOT refer to: normal force, tangential force, moment of normal forces, moment of tangential forces, and total moment of force, respectively. Abbreviations VF, OE, I, M, R, L refer to: virtual finger, opposing effector, index, middle, ring, and little fingers, respectively.

Table 2.

Summary of ANOVA

Variable	Level	Result
SM	VF-TH	TR + VFR > TL, IL, Object + VFR > TE, IE + VFR
	IF	--
Fn	VF-TH	N < W TR + VFR > TL, IL, Object + VFR > TE, IE + VFR
	IF	N < W TR + VFR > TL, IL, Object + VFR > TE, IE + VFR
Ft	VF-TH	N < W TR + VFR > TE, IE, TL, IL + VFR > Object + VFR
	IF	N < W
|Mn|	VF-TH	TR + VFR > TL, IL, Object + VFR > TE, IE + VFR
	IF	N < W TR + VFR > TL, IL, Object + VFR > TE, IE + VFR
|Mt|	VF-TH	N < W TE, IE + VFR > TL, IL + VFR > TR, Object + VFR
	IF	N < W
|MTOT|	VF-TH	N > W TR, Object + VFR > TE, IE TL, IL + VFR
	IF	N < W TR, Object + VFR > TL, IL + VFR > TE, IE + VFR

Significant inequality relationships among levels of factors tested at the two hierarchical levels (VF-TH and IF) are shown. Variables Fⁿ, F^t, Mⁿ, M^t, and M^TOT refer to: normal force, tangential force, moment of normal forces, moment of tangential forces, and total moment of force, respectively. Abbreviations N, W, T_R + VF_R, T_L + VF_R, T_E + VF_R, I_L + VF_R, I_E + VF_R, Object + VF_R refer to: narrow handle width, wide handle width, and the 6 respective finger configurations (as presented in the Methods section).

Since the T_R + VF_R condition was not possible for the wide configuration (see Methods), two sets of mixed effects ANOVAs were performed to analyze the effects of finger configuration. ANOVA-1 refers to analysis of all finger configurations except T_R + VF_R (for both the narrow and wide handle widths) with the factors Width and Finger Configuration. ANOVA-2 refers to analysis of all finger configurations (including T_R + VF_R) possible for the narrow handle width only; hence, ANOVA-2 involves only the Finger Configuration factor, but not the Width factor.

Safety Margin

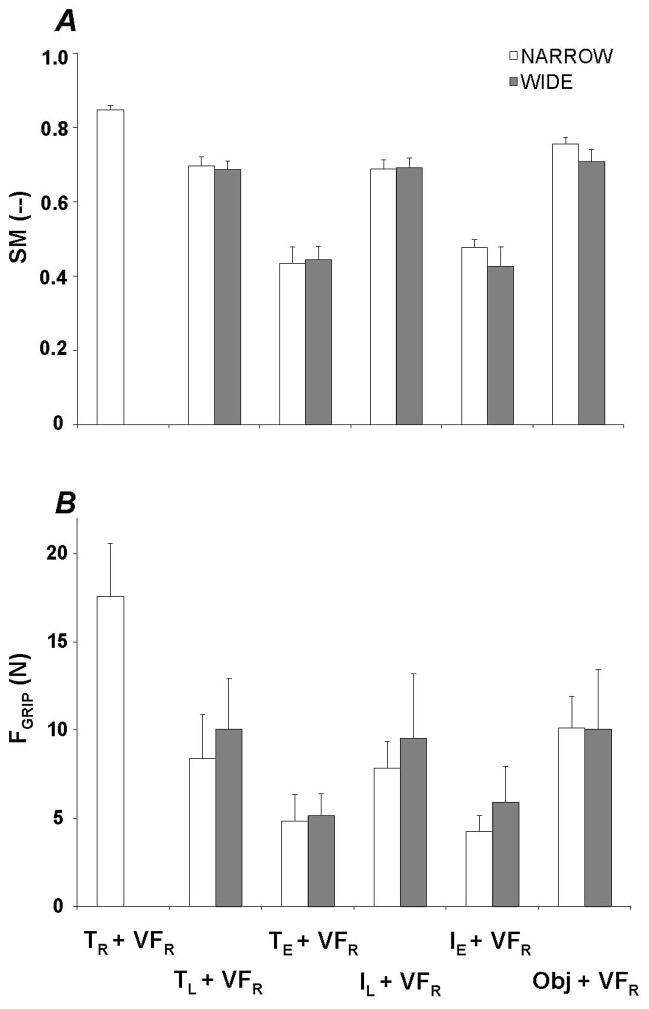
Here we present the results of analysis of the safety margin (SM); specifically, we were interested whether SM changed with the number of persons in a task, consistent with Hypothesis 1. Overall, SM showed the following systematic differences across the conditions (panel A, Figure 2): it was the highest for the five-digit grasp by one hand (T_R+VF_R) and the lowest for the two conditions with the experimenter providing the opposing force to the VF of the subject (I_E+VF_R and T_E+VF_R). Panel A of Figure 2 shows the safety margin (SM) results across all conditions; white bars show the data for conditions tested using the narrow handle while gray bars show the data for the wide handle. There was a nearly two-fold difference in the values of SM between the T_R+VF_R condition and both of the I_E+VF_R and T_E+VF_R conditions. These differences were confirmed using ANOVA-1 and ANOVA-2; main effects of Finger Configuration [F_4,85 = 96.09, p < 0.001 and F_5,45 = 74.34, p < 0.001, respectively] were found without an effect of Width and no interactions. Pair-wise post-hoc Tukey tests revealed that SM for T_R+VF_R was the largest among all finger configurations and that SM for T_E + VF_R and I_E + VF_R was significantly smaller than SM for each of the other finger configurations, while they were not different from each other.

Figure 2.

The safety margin (SM, panel A, dimensionless) and grip force (F_GRIP, panel B) for the narrow (white bars) and wide (gray bars) handle widths. The data averaged across all subjects with standard error bars are shown. The abscissa shows finger configurations; T – thumb, I –index finger, Obj – inanimate object, subscripts R and L refer to the right and left hands, subscript E refers to the experimenter.

Normal Forces (Fⁿ)

Analysis at the VF-TH level

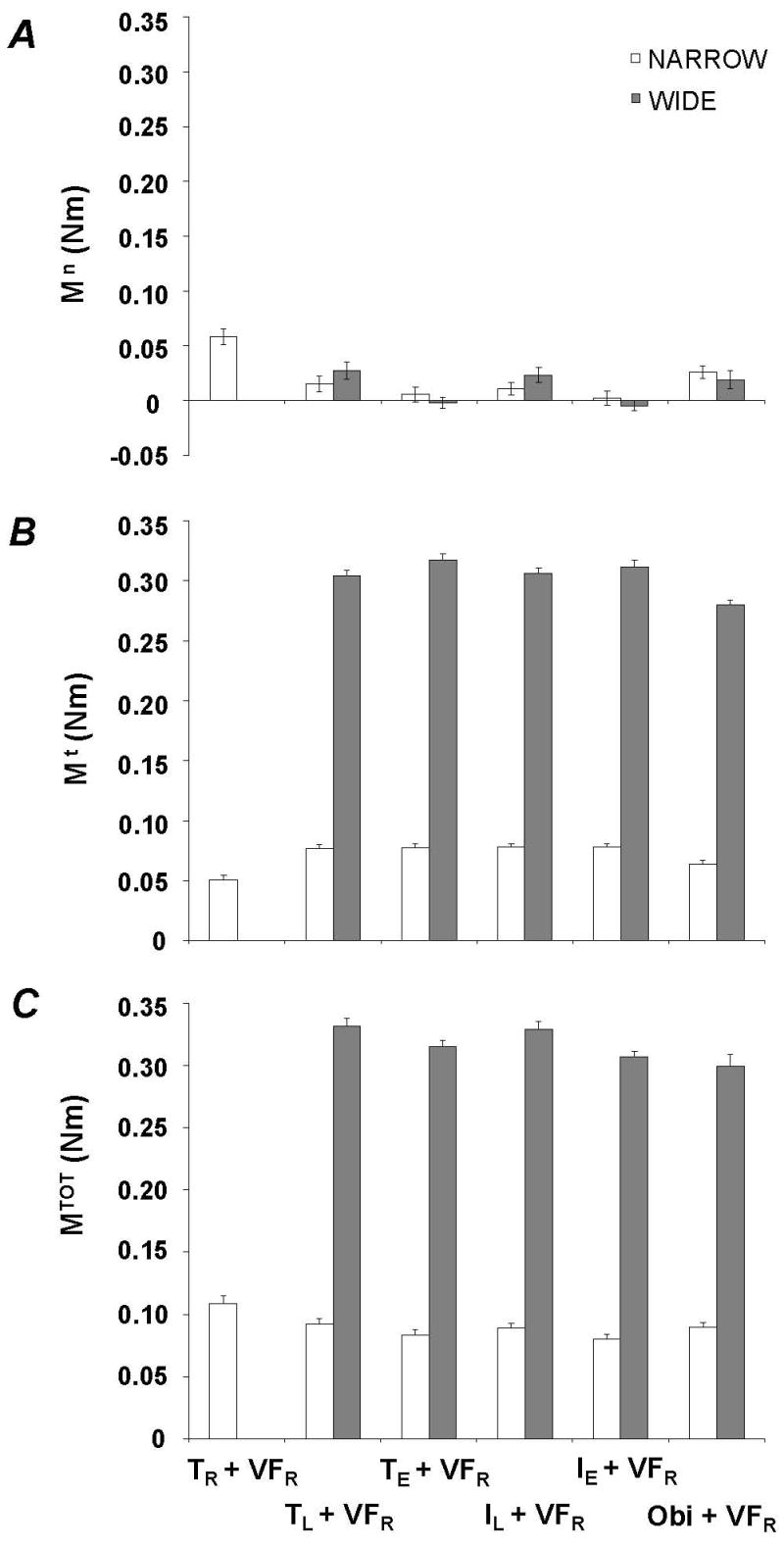
In this section, we analyse how the normal forces of the VF and opposing effector changed across the experimental conditions. In general, the resultant normal force (F_R) was quite small (0.12 ± 0.11N) across all conditions and subjects, as could be expected from the constraints of statics; thus we have chosen to not analyze it further. However, total grip force (F_GRIP, defined as the sum of the grip force magnitudes produced by the VF and the opposing effector) was considered across all tested conditions and subjects. Overall, F_GRIP depended on the number of persons involved in a given task. Configurations in which digits from an experimenter were used resulted in the lowest F_GRIP values as compared to all other finger configurations while it was the highest for the five-digit grasp by one hand, similar to the SM results. Handle width also significantly affected these results; grip forces exerted on the narrow handle were smaller than those for the wide handle over the sets of finger combinations used for both handle width values, i.e. excluding the T_R+VF_R condition. Panel B of Figure 2 shows the F_GRIP results across all tested conditions, for both the narrow (white bars) and wide (gray bars) handle configurations. The results were confirmed using ANOVA-1 and ANOVA-2; main effects of Width [F_1,81 = 14.6, p < 0.005] and Finger Configuration [F_4,81 = 81.83, p < 0.001 and F_5,45 = 108.38, p < 0.001, respectively] were found with no interactions. Pair-wise Tukey tests revealed that F_GRIP was largest for the T_R+VF_R condition and smallest for the T_E + VF_R and I_E + VF_R conditions.

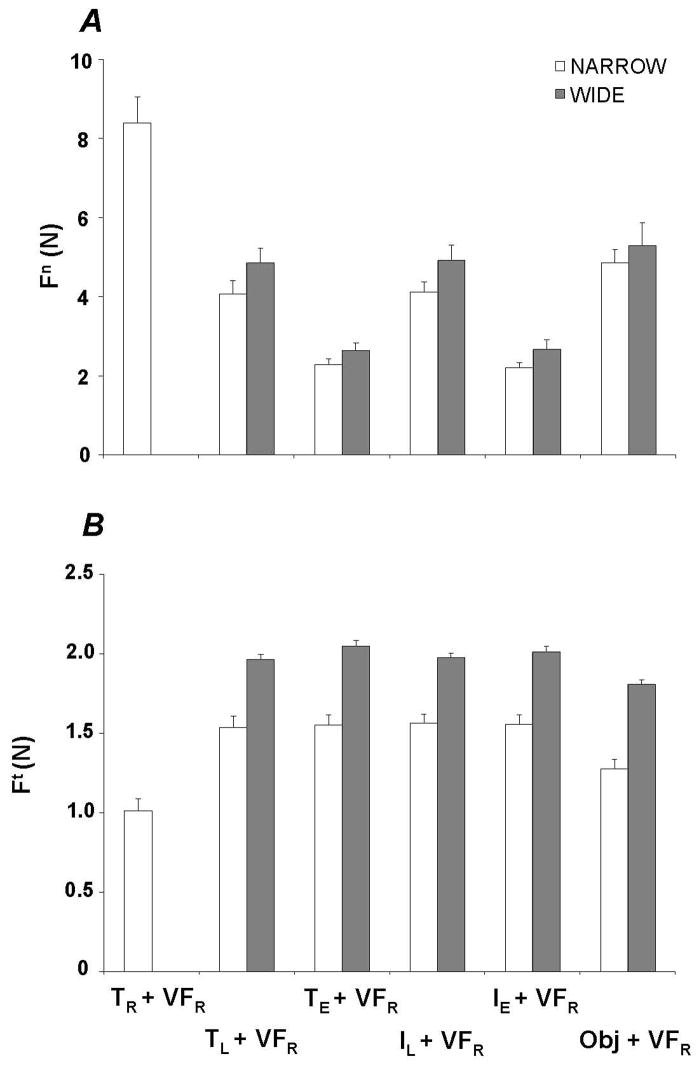
Separate analysis of the VF normal force (Fⁿ) is not presented as it was very close to 50% of F_GRIP since the resultant normal force was close to zero. The data show that the Fⁿ output of VF_R depended on the number of persons in the task, just like the F_GRIP results. This pattern is shown in panel A of Figure 3. Figure 3 illustrates Fⁿ and F^t output of the VF in all finger configurations averaged across all subjects for the narrow (white bars) and wide (gray bars) handle widths.

Figure 3.

The normal force (Fⁿ, panel A) and tangential force (F^t, panel B) of the virtual finger of the right hand (VF_R) for the narrow (white bars) and wide (gray bars) handle widths. The data averaged across all subjects with standard error bars are shown. Abbreviations are the same as in Figure 2.

Analysis at the IF level (see the Appendix).

Tangential Forces (F^t)

Analysis at the VF-TH level

In this section, we examine whether or not the tangential force produced by the VF and opposing effector changed across experimental conditions; in particular, whether the sharing of the load-resisting force remained the same across the tasks as suggested by Hypothesis 2. In general, total load force (F_TAN) was not significantly different from the weight of the handle in either the narrow or wide configurations (mean resultant F_TAN = 0.01 ± 0.05 N). This is consistent with the assumption that the handle was held statically.

Overall, the tangential force output (F^t) of the virtual finger was smallest when the object was supported by an inanimate object and when subjects used the narrow handle. Panel B of Figure 3 illustrates this assertion. These findings were confirmed using ANOVA-1 and ANOVA-2; main effects of Width [F_{1, 81} = 350.05, p < 0.001] and Finger Configuration [F_4,81 = 14.58, p < 0.001 and F_5,45 = 26.49, p < 0.001] were found with no interactions. Pair-wise Tukey tests confirmed that F^t of VF_R was the smallest for Object + VF_R and the narrow handle width conditions while it was the largest for the T_R + VF_R condition.

Analysis at the IF level

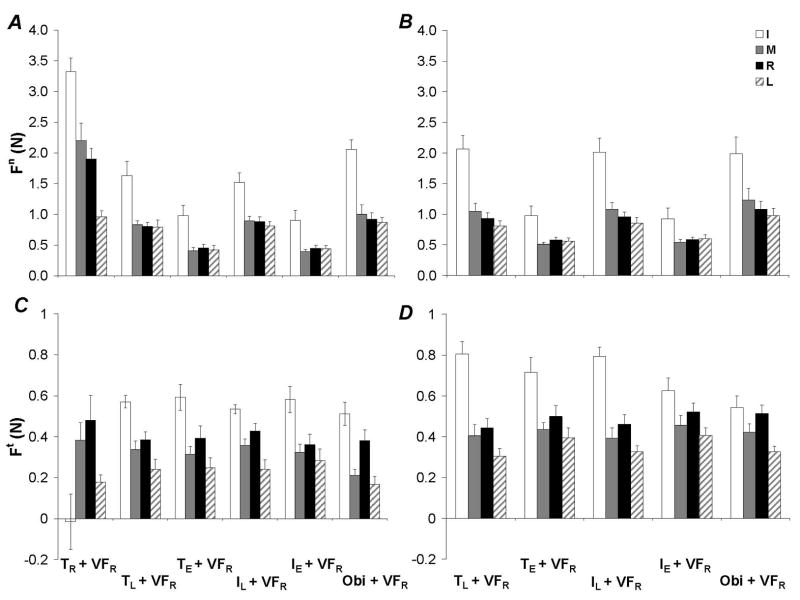
In this subsection, the tangential forces produced by the individual fingers within the VF are analyzed across all tested conditions. Examination of the individual finger forces within VF_R revealed that I_R produced the largest F^t compared to each of the other fingers in VF_R across all tested finger configurations and handle widths, as shown in panels C and D of Figure 4. Panel C shows the contribution of the individual fingers to the F^t output of VF_R for the narrow handle while panel D shows the contribution of the individual fingers for the wide handle conditions. Handle width also had a significant effect, such that Fⁿ(narrow) < Fⁿ(wide). These effects were supported by ANOVA-1 with the additional factor Finger. Statistically significant effects of Width [F_{1, 351} = 60.88, p < 0.001] and Finger [F_3,351 = 92.43, p < 0.001] were found with no interactions. Pair-wise Tukey tests also confirmed that F^t(I_R) > F^t(R_R) > F^t(M_R) > F^t(L_R).

Figure 4.

The normal force (Fⁿ) and tangential force (F^t) for individual fingers within the virtual finger of the right hand (VF_R) are shown across all finger configurations. A: Fⁿ for the narrow handle. B: Fⁿ for the wide handle. C: F^t for the narrow handle. D: F^t for the wide handle. The data averaged across all subjects with standard error bars are shown. Abbreviations are the same as in Figure 2.

When all six finger configurations were considered for the narrow handle, a similar pattern of F^t sharing among the four fingers of VF_R was found except in the case of T_R + VF_R, as shown in panel C of Figure 4. In this panel, it is shown that the F^t output by I_R does not appear to be significantly different from zero. These results were analyzed using ANOVA-2 with the additional factor Finger. Significant effects of Finger Configuration [F_5,207 = 3.62, p < 0.005], Finger [F_3,207 = 18.56, p < 0.001], and the interaction Finger x Finger Configuration [F_12,207 = 4.83, p < 0.001] were found. Pair-wise Tukey tests found that F^t(I_R) > F^t(R_R) > F^t(M_R) > F^t(L_R), consistent with the results of ANOVA-1. Pair-wise analysis did not show statistically significant differences among finger configurations despite a trend towards F^t(T_R + VF_R) < F^t(all other finger configurations), in contrast to expectations based on panel C of Figure 4. The interaction Finger x Finger Configuration showed that the output of I_R in the T_R + VF_R configuration was significantly smaller that I_R output in all other tested finger configurations.

Moment Produced by Normal Forces (Mⁿ)

In general, the moment of grip forces (Mⁿ) was not significantly different from zero (mean Mⁿ = −0.005 ± 0.002 Nm); whereas the moment of tangential forces (M^t), and total moment (M^TOT) were small but significantly less than zero (mean M^t = −0.014 ± 0.003 Nm, mean M^TOT = −0.019 ± 0.002 Nm; the negative sign denotes a supination moment). The rather small non-zero M^TOT was likely related to two factors, possible deviations of the handle from the vertical and errors in the sensor readings. Generally, Mⁿ contributed to 45% and 16% of M^TOT at the VF-TH and IF levels, respectively.

Analysis at the VF-TH level (see the Appendix).

Analysis at the IF level

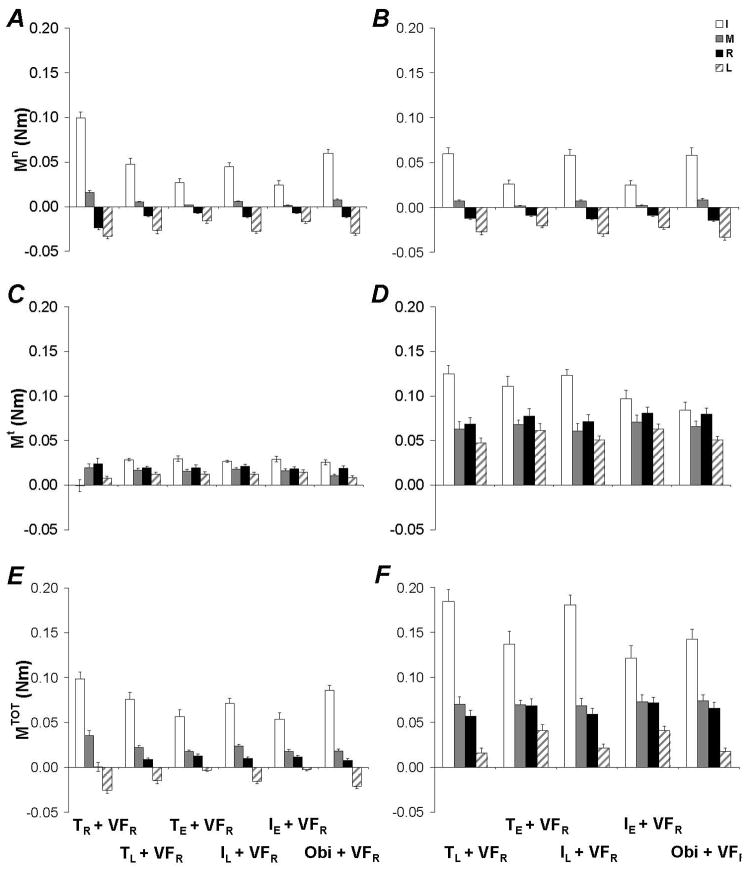
At this level of analysis, the results of |Mⁿ(VF_R)| are analyzed for individual fingers within VF_R. More specifically, we tested whether the sharing of the total moment of normal forces among the four fingers followed the principle of mechanical advantage, consistent with Hypothesis 3. This analysis revealed that I_R contributed to |Mⁿ(VF_R)| more than other fingers. Figure 5 shows the contribution of individual finger moments of force to the total output of VF_R for both Mⁿ and M^t; the data illustrating Mⁿ for the individual finger are shown in panels A and B. It was also found that finger configurations I_E + VF_R and T_E + VF_R showed generally smaller |Mⁿ| across fingers in VF_R as compared to T_R + VF_R. This was tested using ANOVA-1 and ANOVA-2 with the additional factor Finger. Main effects of Width [F_1,346 = 8.73, p < 0.005], Finger Configuration [F_4,346 = 41.84, p < 0.001 and F_5,207 = 55.2, p < 0.001], Finger [F_3,346 = 328.07, p < 0.001 and F_3,207 = 255.55, p < 0.001], and the interaction Finger × Finger Configuration [F_12,346 = 9.63, p < 0.001 and F_15,207 = 13.3, p < 0.001] were found. Pair-wise post-hoc Tukey tests revealed that |Mⁿ(narrow)| < |Mⁿ(wide)| and |Mⁿ(I_R)| > |Mⁿ(L_R)| > |Mⁿ(R_R)| > |Mⁿ(M_R)|. The interaction Finger × Finger Configuration showed that |Mⁿ(I_R)| was smallest for the T_E + VF_R and I_E + VF_R conditions and largest for the T_R + VF_R condition.

Figure 5.

The moment of normal force (Mⁿ), moment of tangential forces (M^t), and total moment of force (M^TOT) for individual fingers within the virtual finger of the right hand. A: Mⁿ for the narrow handle. B: Mⁿ for the wide handle. C: M^t for the narrow handle. D: M^t for the wide handle. E: M^TOT for the narrow handle. F: M^TOT for the wide handle. The data averaged across all subjects with standard error bars are shown. Abbreviations are the same as in Figure 2.

Moment Produced by Tangential Forces (M^t)

Analysis at the VF-TH level (see the Appendix).

Analysis at the IF level

Next, we analyze how moment of tangential force was shared among fingers within VF_R. Examination of M^t produced by the individual fingers within the VF_R revealed that I_R contributed to M^t more so than other fingers whereas L_R contributed the least. Panels C and D of Figure 5 illustrate the contribution of individual finger moments of force to the total output of M^t(VF_R). Panel C shows the contribution of the individual fingers to the M^t output of VF_R for the narrow handle while panel D shows the contribution of the individual fingers for the wide handle conditions. Handle width was confirmed to be significant, such that |M^t(narrow)| < |M^t(wide)|. This was found using ANOVA-1 and ANOVA-2 with the additional factor of Finger. Main effects of Width [F_{1, 346} = 1042.41, p < 0.001], Finger [F_3,346 = 71.8, p < 0.001 and F_3,207 = 35.61, p < 0.001], and the interaction Width x Finger [F_3,346 = 20.76, p < 0.001] were found. Pair-wise Tukey tests confirmed |M^t(I_R)| > |M^t(M_R)|, |M^t(R_R)| > |M^t(L_R)|. The Width × Finger interaction from ANOVA-1 indicated that |M^t(I_R)| > |M^t(R_R)| and |M^t(L_R)| for the narrow conditions while |M^t(I_R)| > |M^t(M_R)| and |M^t(R_R)| > |M^t(L_R)| for the wide conditions.

Total Moment of Force (M^TOT)

Analysis at the VF-TH level (see the Appendix).

Analysis at the IF level

Lastly, we analyzed how total moment of force was shared among fingers within VF_R and whether or not the mechanical advantage of fingers was used, consistent with Hypothesis 3. Examination of the total moments of force produced by individual fingers within the VF_R revealed that I_R contributed the most to M^TOT(VF_R) while L_R contributed the least. Panels E and F of Figure 5 show the contribution of individual finger moments of force to M^TOT(VF_R). Panel E shows the contribution of the individual fingers to the M^t output of VF_R for the narrow handle while panel F shows the contribution of the individual fingers for the wide handle conditions. Handle width was found to be significant, such that |M^TOT(narrow)| < |M^TOT(wide)|. This was confirmed by ANOVA-1 with the additional factor of Finger. Main effects of Width [F_{1, 346} = 618.23, p < 0.001], Finger [F_3,346 = 369.9, p < 0.001], and the interaction Width x Finger [F_3,351 = 45.3, p < 0.001] were found. Pair-wise Tukey tests revealed that |M^TOT(I_R)| > |M^TOT(M_R)|, |M^TOT(R_R)| > |M^TOT(L_R)|. The interaction Width × Finger indicates that |M^TOT(I_R)| > |M^TOT(M_R)|, |M^TOT(R_R)|, |M^TOT(L_R)| for both the narrow and wide handles, while |M^TOT(M_R)| > |M^TOT(L_R)| and |M^TOT(R_R)| > |M^TOT(L_R)| was true only for the wide handle.

Further analysis of narrow handle width conditions, indicated that individual finger contributions to |M^TOT(VF_R)| was largest when one hand was used in the task (T_R + VF_R and Object + VF_R) and lowest when fingers from an experimenter were used (T_E + VF_R and I_E + VF_R). It was also found that IR contributed the most to |M^TOT(VF_R)|. These findings are illustrated in panel E of Figure 5 and were confirmed using ANOVA-2 with the additional factor Finger. Main effects of Finger Configuration [F_5,207 = 15.09, p < 0.001], Finger [F_3,207 = 343.8, p < 0.001], and the interaction Finger x Finger Configuration [F_15,207 = 4.18, p < 0.001] were found. Pair-wise Tukey tests showed that the finger configurations T_R + VF_R and Object + VF_R had the largest |M^TOT(VF_R)|, particularly compared to T_E + VF_R and I_E + VF_R. The interaction Finger x Finger Configuration showed that |M^TOT(I_R)| was smallest for the T_E + VF_R and I_E + VF_R conditions.

Discussion

In the Introduction, we formulated three hypotheses, and two of them have been falsified in this experiment. First, we hypothesized that two-hand conditions would show larger grip forces and safety margins. The results were exactly opposite showing the largest safety margins for the one-hand condition. In contrast to our second hypothesis, there were substantial differences in the distribution of the tangential forces between the VF and the opposing effector across tasks. The third hypothesis on the role of the mechanical advantage of fingers in the production of moments of force have been confirmed: The index and little fingers, on average, produced larger magnitudes of the moment of force than the middle and ring fingers. There were substantial differences across the conditions; in particular, the unimanual prehension condition showed patterns that differed from the other conditions for most of the analyzed mechanical variables. Further, we discuss implications of these findings for the one-hand and two-hand static prehensile tasks.

Safety margin and grip force in one- and two-person tasks

In our experiment, both safety margin and grip force produced by the VF were highest in the unimanual prehension task and lowest in the two-person prehension tasks. This finding was in direct conflict with our initial hypothesis. We had assumed that the uncertainty in force production between the two individuals participating in the given task would result in an increase in the grip force output (and the resulting safety margin) to ensure that the object would not slip. Note that our observations are in an apparent conflict with a report by Burstedt and colleagues (1997) who studied two-digit precision grip and found no changes in the safety margin when the number of hands involved in the task changed.

It is possible that the difference between the results of the two studies reflects the differences in how the hand deals with the main constraints of statics in two-digit precision grip and in five-digit cylindrical grip. In particular, changes in the sharing pattern of the normal force among the four fingers in the five-digit grip allow the point of application of the VF normal force to move within a rather large range. This allows the use of a broad range of solutions for the rotational constraint (Eq. 9 in the Methods). In contrast, in precision grip, the range of lever arm changes of the normal VF force is limited by a few millimeters, an order of magnitude smaller than in the five-digit grip. This limits the range of solutions for the equations of statics and results in more stereotypical solutions that become independent of the number of hands or persons participating in the task.

Changes in the normal VF force across the tasks in our experiments may reflect the tradeoff between ensuring secure grip and close to zero resultant force. When the subject was certain in the amount of force produced by the opposing effector and in variations of this force (for example in the most common one-hand task) he or she applied large normal forces. When the opposing effector was less predictable, applying too much force could be expected to lead to a proportional increase in force variability (reviewed in Newell and Carlton 1993) and cause substantial deviations of the resultant force from zero. Although the inanimate object’s mechanical action in response to changes in the VF force was perfectly predictable (because of the Newton’s Third Law), even better predictable than that of the thumb of the same hand, subjects applied higher normal forces with the four fingers when acting against the inanimate object as compared to acting against the right thumb. The inanimate opposing effector showed similar safety margin and normal force to those shown by the thumb and index finger of the subject’s other hand; these forces were larger than those produced in trials with the experimenter’s thumb. The results suggest that the CNS varies the grip force magnitude based on two factors, ensuring sufficient safety margin and predictability of the opposing effector’s force. With respect to the second factor, the thumb of the same hand was trusted most to produce exactly the required opposing force to the VF force resulting in the highest safety margin, the digits of the other hand were trusted on par with the Third Newton’s Law, and digits of another person were the least trustworthy.

Coordination of normal and tangential digit forces

Many studies have reported parallel changes in the normal and tangential forces during object manipulation tasks. In particular, changes in the normal force are commonly seen prior to an expected change in the tangential (load) force during object lifting (Johansson and Westling 1984), rotation (Gao et al. 2006), and other actions (Flanagan and Wing 1993, 1995; Flanagan and Tresilian 1994; Kinoshita et al. 1996). In the cited studies, the magnitude of the normal force adjustment scaled with the expected magnitude of the load force. These studies have resulted in a hypothesis that normal (grip) forces are adjusted to ensure a particular value of the safety margin (Burstedt et al. 1997; Pataky et al. 2004).

Some of our results do not comply with this hypothesis. In particular, at the VF-TH level, the VF produced the highest normal force in the unimanual (T_R+IMRL_R) condition. In contrast, the VF contribution to the total tangential force was the smallest for the unimanual condition (Figure 3, panels A and B). VF normal force was the smallest for the conditions involving the experimenter, while this was not true for the VF tangential force.

At the single-finger level, individual finger forces showed sharing patterns that differed across conditions such that the index finger produced most of the VF normal force, particularly in the unimanual condition (Figure 4A). The sharing of the tangential force was dramatically different: The index finger produced virtually no tangential force in the one-hand condition, while its contribution to the total tangential force was higher than that of the other fingers in all other conditions (Figure 4C).

Earlier studies of five-digit finger prehension have come up with a conclusion that the middle and ring fingers serve mostly as the load-bearing fingers producing most of the total tangential force, while the index and little fingers with their larger moment arms for the normal forces served to produce a required moment of force (Gao et al. 2006; Shim et al. 2004a, 2005). Our results confirm this conclusion but only for the one-hand conditions (see Figure 4C). In all other conditions, when the four fingers were opposed by an unusual effector, the index and little fingers generated as much tangential force as the middle and ring fingers. Based on these results, one may offer a hypothesis that in the most common, unimanual task the subjects use their fingers in a more versatile way with a broader sharing of the different task components across the fingers. In other tasks, the fingers were used in a more uniform, stereotypical way. We address this hypothesis in more detail in the companion paper (Gorniak et al. 2009).

Keeping rotational equilibrium

Although the magnitudes of the total moment of force were relatively low, they could show significant deviations from zero and significant differences across the conditions Figure 6C, see Appendix). All the subjects showed a tendency to produce a net supination total moment of force, particularly in the trials with the narrow handle. Note that the vertical orientation of the object was part of the task, but the subjects could tilt it slightly given the accuracy (2°) of the level that served as the visual feedback.

Figure 6.

The moment of normal force (Mⁿ, panel A), moment of tangential forces (M^t, panel B), and total moment of force (M^TOT, panel C) are shown for the narrow (white bars) and wide (gray bars) handle widths. The data averaged across all subjects with standard error bars are shown. Abbreviations are the same as in Figure 2.

The one-hand condition was different from other conditions in this task component as well. In particular, the hand produced a non-zero moment of the normal forces into pronation and a non-zero moment of tangential forces into supination in the one-hand condition. In all other conditions with the narrow handle, there was a tendency of producing supination moments by both normal and tangential forces. The presence of the apparent compensation between the two moment components in the one-hand conditions and its absence in the two-hand conditions corroborates our earlier hypothesis on more variable sharing patterns used in the most common one-hand tasks as compared to all other tasks (see also the companion paper Gorniak et al. 2009).

Analysis of the rotational equilibrium presents an example of balanced adjustments of the outputs of different contributors to the moment of force applied to the handle. Such adjustments have been described as chain effects, that is cause-consequence pairs related to constraints of statics (reviewed in Zatsiorsky and Latash 2004, 2008). For example, the fingers of the right hand produced a smaller total tangential force in the one-hand task as compared to all other tasks (Figure 3B). Since the total load-resisting force had to be equal to the weight of the object, this means that the thumb produced higher tangential force in the one-hand tasks leading to a nonzero moment of tangential forces into supination (Figure 6B). To keep the object from rotating, this moment had to be counterbalanced by a non-zero moment of normal forces into pronation (Figure 6A). This was achieved by the disproportionally large normal force produced by the index finger in the one-hand condition (Figure 4A).

The more pronounced balanced adjustments in the one-hand condition may be due to different roles of feed-forward and sensory-based feedback mechanisms of adjustments in mechanical variables. Studies by Johansson and colleagues (Johansson 1996, 1998, 2002; Johansson and Westling 1984, 1987) have emphasized the importance of afferent-based feedback for adjustments of hand action. However, those studies focused mostly on effects of perturbation on the hand produced forces. Several recent studies of unperturbed hand actions have emphasized an important role of feed-forward mechanisms in stabilization of mechanical variables produced by the hand (Goodman and Latash 2006;Gorniak et al. 2008; Shapkova et al. 2008). Such mechanisms may be expected to dominate in well practiced actions such as the one-hand task in our experiments. All other tasks were rather novel and, as such, they could be expected to use feedback sensory loops to stabilize the handle (see Bernstein 1996). This is especially true for two-person tasks when the two opposing effectors were controlled by two central nervous systems.

Possible Physiological Mechanisms and Relation to the Reference Configuration Hypothesis

We would like to use the framework of the equilibrium-point hypothesis (Feldman 1966, 1986) and its more recent development as the reference configuration (RC) hypothesis (Feldman and Levin 1995; Feldman et al. 2007) to illustrate some of our conclusions. To remind, according to the RC hypothesis, digit forces emerge as a result of a discrepancy between a centrally defined RC of the hand and its actual configuration (Pillon et al. 2007). The main physiological mechanism that contributes to the force production is the tonic stretch reflex leading to active muscle force, which is a monotonic function of the difference between the reference (threshold) value of the muscle length and its actual length (Matthews 1959; reviewed in Feldman 1986). In particular, grip force results from a difference between the reference aperture and actual aperture that cannot change because the grasped object prevents the opposing digits from moving towards each other:

$${\text{F}}^{\text{G}}=f({\text{A}}_{\text{REF}}-{\text{A}}_{\text{ACT}}),$$ (11)

where F^G is grip force (equal in magnitude for each effector), A_REF is reference aperture, A_ACT is actual aperture, and f is a function. This scheme works well for a natural one-hand grasp. When an unusual pair of effectors is involved in the action, control with reference aperture may become impossible because the neural circuits controlling each of the opposing effectors are either completely independent (belong to different persons) or belong to different hemispheres of the same brain. In such a situation, reference positions of each of the two effectors have to be specified independently of each other:

$${\text{F}}^{\text{n}1}=f_1({\text{X}}_{\text{REF},1}-{\text{X}}_{\text{ACT},1}),$$ (12)

$${\text{F}}^{\text{n2}}=f_2({\text{X}}_{\text{REF},2}-{\text{X}}_{\text{ACT},2}),$$ (13)

where Fⁿ¹ and Fⁿ² are normal forces of the two effectors, X_REF,1 and X_REF,2 are reference coordinates along the normal force action, X_ACT,1 and X_ACT,2 are actual coordinates along the same axis, and f₁ and f₂ are functions.

Control using eq. (11) has certain advantages such as the equality of the magnitudes of the two opposing forces. Control using eqs. (12) and (13) requires using feedback sensory signals (or additional position stabilizing mechanical properties of the effectors) to adjust the two opposing forces. Equations similar to eqs. (11) - (13) can be written for the tangential force and for the total moment of force. In all cases, using a single controller leads to adjustments of the forces and moments produced by the opposing effectors that does not require using sensory feedback for correction of control signals (RC). These adjustments happen because of the mentioned action of the tonic stretch reflex given a fixed RC value. Using two controllers, as in eqs. (12) and (13), requires using sensory feedback to adjust reference positions of the two end-effectors (X_REF,1 and X_REF,2), for example based on cutaneous, subcutaneous, and/or proprioceptive information on digit tip pressure (the importance of all these information sources for adjustments of grip force has been emphasized by Johansson 1996, 1998; Boudreau and Smith 2001). It is also possible that such adjustments can be made using visual information from the bull’s eye level. There may also be moment-to-moment compensatory adjustments among the digits. Such adjustments may rely on sensory feedback (Todorov and Jordan 2002) or result from a particular feed-forward organization of descending signals (Goodman and Latash 2006). The issue of synergic digit force adjustments is going to be addressed in the companion paper (Gorniak et al. 2009).

Appendix

In the Appendix, we present the results of analyses that were not crucial for addressing the main hypotheses formulated in the Introduction. However, we believe that this information may be useful and present it for the sake of completeness.

Normal Forces (Fⁿ)

Analysis at the IF level

At this level of analysis, normal forces produced by individual fingers of the VF are examined across all tested conditions. Analysis of the individual finger forces within VF_R revealed that I_R produced larger Fⁿ compared to each of the other fingers in VF_R across all tested finger configurations and handle widths, as shown in panels A and B of Figure 4. Panel A shows the contribution of the individual fingers to the Fⁿ output of VF_R for the narrow handle while panel B shows the contribution of the individual fingers for the wide handle conditions. When fingers of an experimenter were used in the tasks, the smallest values of Fⁿ for each of the individual fingers in VF_R were produced. Handle width was found to have a significant effect, such that Fⁿ(narrow) < Fⁿ(wide). These findings were confirmed using ANOVA-1 and ANOVA-2 with the additional factor Finger. Main effects of Width [F_{1, 351} = 17.15, p < 0.001], Finger Configuration [F_4,351 = 66.69, p < 0.001 and F_5,207 = 86.9, p < 0.001], Finger [F_3,351 = 120.22, p < 0.001 and F_3,207 = 82.23, p < 0.001], and the interaction Finger x Finger Configuration [F_12,351 = 3.69, p < 0.001 and F_12,207 = 6.23, p < 0.001] were found. Pair-wise Tukey tests showed that Fⁿ(I_R) > Fⁿ(M_R), Fⁿ(R_R) > Fⁿ(L_R). Post hoc analysis also confirmed the finger configurations T_E +VF_R and I_E + VF_R having the smallest individual finger values of all tested conditions while the finger configuration T_R + VF_R yielded the largest individual finger values. The interaction term from ANOVA-1 highlighted the finding that the output of both I_R and M_R was significantly lower in the T_E +VF_R and I_E + VF_R conditions, compared to their output in the T_L + VF_R, I_L + VF_R, and Object + VF_R conditions. The interaction term from ANOVA-2 revealed that the output for I_R, M_R, and R_R was largest in the configuration T_R + VF_R compared to all other finger configurations

Moment Produced by Normal Forces (Mⁿ)

Analysis at the VF-TH level

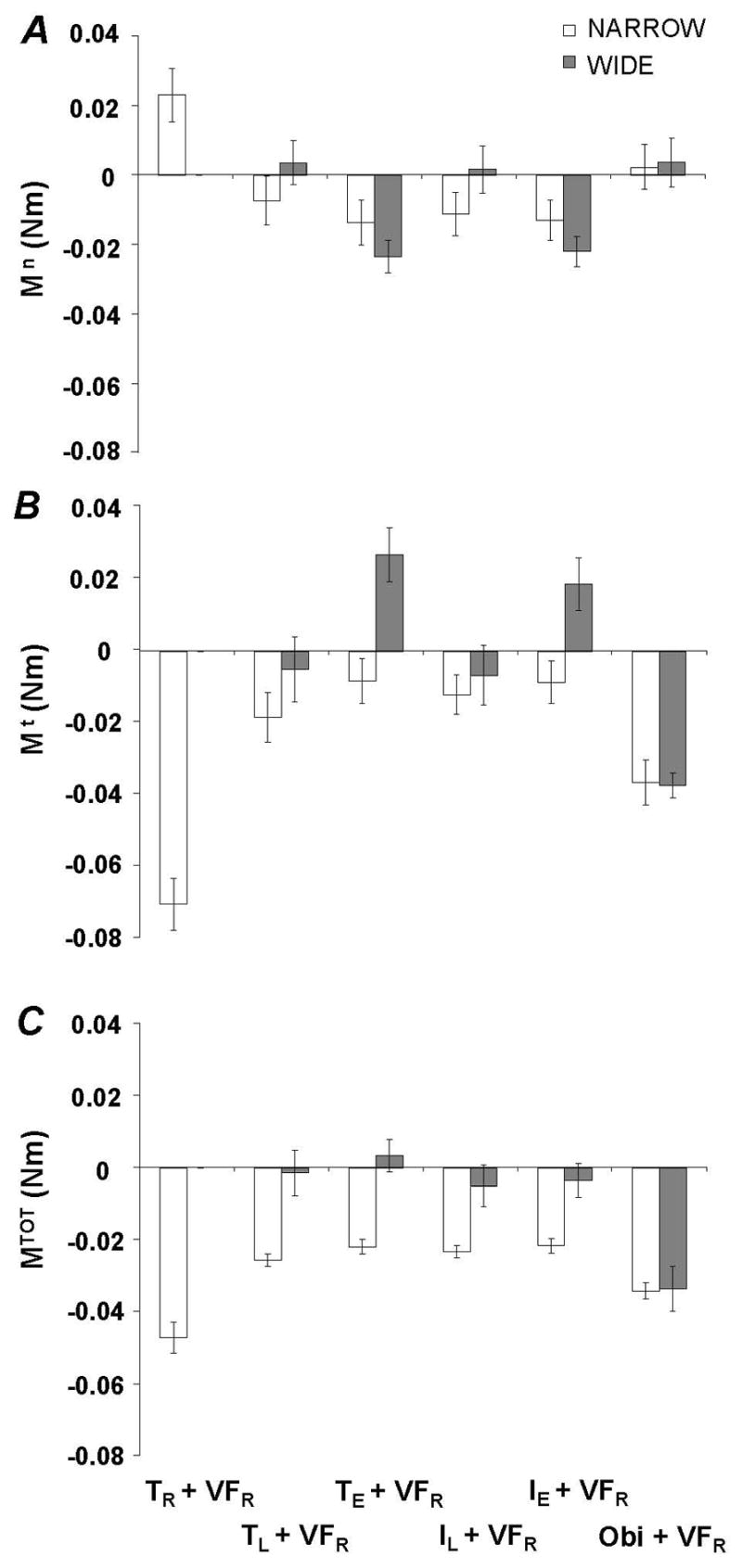
Here we address a question whether the moment of normal forces changed across tested conditions; specifically whether it changed with the number of persons involved in a task. The magnitude of the total moment of normal forces (|Mⁿ|) was not affected by any of the tested factors (Finger Configuration or Width) in either ANOVA-1 or ANOVA-2 at the VF-TH level. The Mⁿ data averaged across subjects can be found in panel A of Figure 6.

Overall, the magnitude of Mⁿ produced by the virtual finger (|Mⁿ(VF_R)|) changed with the number of persons involved in a given task. In conditions in which digits from an experimenter were used, smaller |Mⁿ(VF_R)| was produced as compared to all other finger configurations. Panel A of Figure 7 illustrates that |Mⁿ(VF_R)| is smallest for tasks involving force production involving two persons for both handle widths where white bars represent the narrow handle data and gray bars represent wide handle data. The data were analyzed using ANOVA-1 and ANOVA-2; a main effect of Finger Configuration [F_4,81 = 6.96, p < 0.001 and F_5,45 = 15.22, p < 0.001] were found. Pair-wise Tukey tests revealed that |Mⁿ(VF_R)| was largest for the finger configuration T_R + VF_R and smallest for T_E + VF_R and I_E + VF_R.

Figure 7.

The moment of normal force (Mⁿ, panel A), moment of tangential forces (M^t, panel B), and total moment of force (M^TOT, panel C) produced by the virtual finger of the right hand are shown for the narrow (white bars) and wide (gray bars) handle widths. The data averaged across all subjects with standard error bars are shown. Abbreviations are the same as in Figure 2.

Moment Produced by Tangential Forces (M^t)

Analysis at the VF-TH level

Here, we present the results of analysis of the moment of tangential forces produced by the VF and opposing effector. The magnitude of the total moment of tangential forces (|M^t|) was largest when one hand was involved in the task (Object + VF_R and T_R + VF_R) and smallest when both the right and left hands of one person were used (T_L + VF_R and I_L + VF_R). Handle width was also found to have significant effects, such that |M^t(narrow)| < |M^t(wide)|. Data for both the narrow (white bars) and wide handle widths (gray bars) are illustrated in panel B of Figure 7. Statistical analysis was performed using ANOVA-1 and ANOVA-2; main effects of Width [F_9,81 = 5.22, p < 0.05] and Finger Configuration [F_4,81 = 4.75, p < 0.005 and F_5,45 = 28.23, p < 0.001] were found with no interactions, respectively. Pair-wise post-hoc Tukey tests revealed that the magnitude of M^t was largest for the T_R + VF_R and Object + VF_R finger configurations but smallest for T_L + VF_R and I_L + VF_R.

Further we analyzed how |M^t| was shared between the thumb and VF. Analysis of the magnitude of M^t produced by the virtual finger (|M^t(VF_R)|) showed that this value changed with the number of persons involved in a given task. When digits from an experimenter were used, |M^t(VF_R)| was largest as compared to all other finger configurations. In contrast, when only one hand was involved in the task, |M^t(VF_R)| was smallest. Width was also determined to be significant, such that |M^t(narrow)| < |M^t(wide)|. Panel B of Figure 7 illustrates that |M^t(VF_R)| is highest for tasks involving force production involving two persons, particularly for the wide handle width. This was confirmed by ANOVA-1 and ANOVA-2, which showed main effects of Width [F_1,81 = 11245.33, p < 0.001] and Finger Configuration [F_4,81 = 17.42, p < 0.001 and F_5,45 = 26.38, p < 0.001] with no interactions. Pair-wise Tukey tests revealed that |M^t(VF_R)| was the lowest for the Object + VF_R and T_R + VF_R configurations and largest for the T_E + VF_R and I_E + VF_R configurations.

Total Moment of Force (M^TOT)

Analysis at the VF-TH level

In this section, the total moment of force produced by the VF and opposing effector is examined across all tested conditions. Overall, the magnitude of total moment of force (|M^TOT|) was largest when one hand performed the task (Object + VF_R and T_R + VF_R) compared to all other finger configurations. It was also found that |M^TOT| was largest for tasks performed with the narrow handle. The data supporting these claims can be found in panel C of Figure 6. This was confirmed using ANOVA-1 and ANOVA-2; main effects of Width [F_1,81 = 20.72, p < 0.001] and Finger Configuration [F_4,81 = 14.32, p < 0.001 and F_5,45 = 16.2, p < 0.001] were found with no interactions. Pair-wise Tukey tests revealed that |M^TOT| was larger for the narrow handle and for the Object + VF_R and T_R + VF_R conditions as compared to all other finger configurations. Additional analysis of |M^TOT| produced by the virtual finger (|M^TOT(VF_R)|) was largest when the hands of one person were used in the task (T_R + VF_R, T_L + VF_R, and I_L + VF_R configurations). The data were also affected by handle width, such that |M^TOT(narrow)| < |M^TOT(wide)|. Panel C of Figure 7 illustrates that |M^TOT(VF_R)| was highest for tasks involving hands of the same person, especially for the wide handle width. These findings were confirmed using ANOVA-1; main effects of Width [F_1,81 = 8930.02, p < 0.001], Finger Configuration [F_4,81 = 9.53, p < 0.001 and F_5,45 = 7.24, p < 0.001], and the interaction Width x Finger Configuration [F_4,81 = 5.27, p < 0.005] were found. Pair-wise Tukey tests revealed that |M^TOT(VF_R)| was the highest for the T_R + VF_R, T_L + VF_R, and I_L + VF_R configurations. The Width x Finger Configuration interaction from ANOVA-1 reflected higher |M^TOT(VF_R)| in the conditions T_L + VF_R and I_L + VF_R compared to I_E + VF_R and Object + VF_R, particularly for the wide handle.