Evolutions Equations in Computational Anatomy

Abstract

One of the main purposes in computational anatomy is the measurement and statistical study of anatomical variations in organs, notably in the brain or the heart. Over the last decade, our group has progressively developed several approaches for this problem, all related to the Riemannian geometry of groups of diffeomorphisms and the shape spaces on which these groups act. Several important shape evolution equations that are now used routinely in applications have emerged over time.

Our goal in this paper is to provide an overview of these equations, placing them in their theoretical context, and giving examples of applications in which they can be used. We introduce the required theoretical background before discussing several classes of equations of increasingly complexity. These equations include energy minimizing evolutions deriving from Riemannian gradient descent, geodesics, parallel transport and Jacobi fields.

1. Introduction

One of the main purposes in computational anatomy is the measurement and statistical study of anatomical variations in organs, notably in the brain or the heart. Over the last decade, our group has progressively developed several approaches for this problem, all related to the Riemannian geometry of groups of diffeomorphisms and the shape spaces on which these groups act. Several important shape evolution equations that are now used routinely in applications have emerged over time.

Our goal in this paper is to provide an overview of these equations, placing them in their theoretical context, and giving examples of applications in which they can be used. Because these equations all relate to geometric constructions on the group of diffeomorphisms, some theoretical background is needed. It will be summarized in the next section. We will then discuss equations of increasingly complexity. This will start, in section 3, with energy minimizing equations deriving from gradient descent (using an appropriate definition of the gradient adapted to the Riemannian structure on diffeomorphisms and shapes). We will show applications in area minimization for surfaces, and shape segmentation with ”Diffeomorphic Active Contours”.

The next set of equations are geodesic equations, first on the group of diffeomorphisms, then on the shape spaces on which they project (here, we call “shape” any structure that can be deformed). We will in particular consider “shapes” that are represented by collections of (not necessarily labeled) points, for which the evolution equations reduce to relatively simple ordinary differential equations. Other examples of interest are shapes represented by images and by densities. For computational anatomy, geodesics are of main importance, because they provide what is called normal coordinates, or exponential charts, that can be used to represent anatomical data relatively to a template. We shall also refer to this as the momentum representation, because of the momentum-preservation property of the geodesic equation, as we will describe in section 4.

Geodesic equations correspond to moving in “straight lines” on a curved manifold. The next class of equations we will describe, parallel translation, correspond to keeping track of a given direction while moving on a manifold. This will be discussed in section 5. The final class of equations we will discuss are Jacobi equations (section 6). These equations describe the variation of geodesics with respect to changes in their initial conditions. They are useful when solving variational problems optimizing over geodesics.

Before describing these equations, we need to summarize the theoretical background supporting their construction. This is done in the next section.

2. Mathematical background and notation

There are a few fundamental ingredients in this theory, and our goal is to review them in this section without including the full mathematical machinery. So, even if many of the presented concepts are special cases of a more general (and more abstract) theory, we will only introduce the notions that are needed for the understanding of the rest of this paper.

2.1

We will make our discussion in an arbitrary dimension, denoted d (although d = 3 in the examples and most of the applications in computational anatomy). We will assume that an open subset Ω in ${\mathbb{R}}^d$ is chosen and keep it fixed in the following. For the theory, Ω can be the whole space ${\mathbb{R}}^d$, although numerical implementations would rather have it bounded (with suitable boundary conditions).

2.2

A diffeomorphism of Ω is an invertible transformation from Ω to itself, which is continuously differentiable (C¹) with a differentiable inverse. The identity map, id, is a diffeomorphism, the composition of two diffeomorphisms is a diffeomorphism and the inverse of any of them is a diffeomorphism as well. This implies that the set of diffeomorphisms of Ω, denoted Diff(Ω) has a group structure.

2.3

Diffeomorphisms being transformations of Ω, they alter quantities that are included in, or defined on Ω. We will be particularly interested in collections of points, functions and densities on Ω, and denote these objects with a common notation; most of the time, an object will be denoted m, belonging to some space M. So, depending on the context, M will be the set of all finite configurations of points in Ω, or a set of functions, or densities, defined on Ω. Our construction extends in fact to a wide class of objects, like curves, surfaces, measures, etc.

We will say that diffeomorphisms act on M if, for any diffeomorphism φ and any object m, a deformed object φ · m can be defined. The natural requirements that id · m = m and φ ⋅ (ψ ⋅ m) = (φ ∘ ψ) ⋅ m ensure that (φ, m) ↦ φ is a group action, property that we will always assume. For configurations of points, m = (m₁, …, m_N), we have φ · m = (φ(x₁), …, φ(x_N)). For images, $m:\Omega \to {\mathbb{R}}^k$, we have φ ⋅ m = m ∘ φ^-1. Finally, for densities $m:\Omega \to {\mathbb{R}}^{+}$, we have φ ⋅ m = m ∘ φ^-1 |det D(φ^-1)|, where D is the differential. The interpretation of the action on functions is that (φ · m)(x) is the value of m at the point that has been moved to x by φ. For densities, φ · m is the new repartition of mass after deformation of the space.

2.4

Vector fields are functions $v:\Omega \to {\mathbb{R}}^d$. Given a time-dependent vector field, i.e., a function v: (t,y) ↦ v(t,y) defined on [0, 1] → Ω (arbitrarily choosing the time scale to be 1), one defines the ordinary differential equation (ODE) on Ω by ${\stackrel{.}{y}}_t=v(t,y)$. The flow associated to this equation is the function (t, x) ↦ φ(t, x) such that, for a given x, t ↦ φ(t, x) is the solution of the ODE with initial condition y(0) = x, which is uniquely defined under standard smoothness assumptions on v.

For a fixed t, the function x ↦ φ(t,x) is a diffeomorphism of Ω, provided v has no normal component at the boundary of (if Ω has a boundary). We will also assume that v vanishes at infinity (if Ω is unbounded). This relation between vector fields and diffeomorphisms is a key component of the analysis, as well as an important generative tool for diffeomorphisms [7, 10]. We will use the notation φv(t, .) for the diffeomorphism obtained in this way.

2.5

If v is a C¹ vector field (not time-dependent), the transformation id + tv: x ↦ x + tv (x) is a diffeomorphism for t small enough. For an object m ∈ M, we therefore can define the small deformation (id + tv) · m. The derivative, with respect to t, at time t = 0, of this expression is called the infinitesimal action of v on m and denoted v · m. So,

$$v\cdot m≔\frac{d}{dt}(\mathrm{id}+tv)\cdot m_{{\mid }_{[t=0]}}.$$

Working out this definition with our examples gives

$$v\cdot (x_1,\dots ,x_N)=(v\left(x_1\right),\cdots ,v\left(x_N\right))$$

for configurations of points, v · m = -∇m^T v for images and v · m = -∇ · (mv) for densities (where ∇m is the column vector of derivatives and ∇ · (mv) is the divergence operator).

2.6

We now introduce a dot product norm over vector fields. More precisely, we will consider a space V of vector fields on Ω and a dot product, (v,w) ↦ 〈v, w〉_V on V, denoting ${\parallel v\parallel }_V^2={\langle v,v\rangle }_V$.

The norm on V is associated to an operator L, in the sense

$${\parallel v\parallel }_V^2={\int }_{\Omega }L{v}^{T}vdx.$$ (1)

The previous equation must be understood in a generalized sense. Most of the time (not always) Lv will be a singular object (a generalized function) which can only be computed via its action on smooth functions.

If V is a Hilbert space, which we will be assumed without further comment, this operator is invertible with a very well behaved inverse K = L^-1. For all our models, K is a smooth kernel operator such that there exists a function (x, y) ↦ K (x, y) such that

$$\left(Kv\right)\left(x\right)={\int }_{\Omega }K(x,y)v\left(y\right).$$ (2)

(We make the common abuse of notation of using the same letter for the operator and the kernel.)

In full generality, K(., .) is matrix valued, although all our applications use a scalar kernel.

2.7

This space V and its norm is the final ingredient needed to define Riemannian geometric concepts over diffeomorphisms and shapes.

Again, it is not in our intent to invoke any structured mathematical theory in this paper, especially the one of infinite dimensional Lie groups that suits the present construction. One can understand the Riemannian metric in Riemannian geometry [9] as a way to generalize to curved spaces the concept of kinetic energy. Taking the case of diffeomorphisms, we can consider a trajectory t ↦ φ_t ∈ Diff(Ω). The associated velocity is ρ_t = dφ_t/dt. A Riemannian metric provides the associated energy, in the form

$$E\left({\rho }_t\right)=\frac{1}{2}{\parallel {\rho }_t\parallel }_{{\phi }_t}^2$$

for some norm that may depend on the current position in the group.

Let us write

$${\rho }_{t}dt\simeq {\phi }_{t+dt}-{\phi }_t\simeq ({\phi }_{t+dt}\circ {\phi }_t^{-1}-\mathrm{id})\circ {\phi }_t\simeq dt{v}_t\circ {\phi }_t$$

where

$$v_t=\frac{d}{ds}{({\phi }_{t+s}\circ {\phi }_t^{-1})}_{{\mid }_{[s=0]}}.$$

The interpretation is that v_tdt is the additional infinitesimal displacement required to pass from the deformation φ_t to φ_t+dt. In deformation models inspired by fluid mechanics, the kinetic energy is assumed to only depend on this displacement (This assues that properties of the deformed medium remain invariant). This means that E(ρ_t) only depends on v_t, and we will take

$$E\left({\rho }_t\right)=\frac{1}{2}{\parallel {\rho }_t\parallel }_{{\phi }_t}=\frac{1}{2}{\parallel v_t\parallel }_V^2$$

with $v_t={\rho }_t\circ {\phi }_t^{-1}$.

2.8

One then defines minimizing geodesics as trajectories with minimal energy between their endpoints. Using the ODE representation, minimizing geodesics between the identity map and ψ ∈ Diff (Ω) are given by $t\mapsto {\phi }_t^v$ (with the notation introduced in section 2.4) where v is the time-dependent vector field solution of the variational problem:

$$\text{Minimize}{\int }_0^1{\parallel v_t\parallel }_V^{2}dt\text{subject to the constraint}{\phi }_1^v=\psi .$$

Note that a v with finite energy such that ${\phi }_1^v=\psi$ may not always exist. In fact, the ψ's for which the solution exists form a subgroup of Diff (Ω) which is specified by V and denoted G_V.

The geodesic distance between id and ψ is the square root of the above integral for the optimal v, and will be denoted d_V(id, ψ). So we have

$$d_V{(\mathrm{id},\psi )}^2=\inf \left\{{\int }_0^1{\parallel v_t\parallel }^{2}dt:{\phi }_1^v=\psi \right\}.$$

The geodesic distance between two diffeomorphisms φ and ψ is given by d_V (id, ψ∘φ^-1).

2.9

Since we interpret ${\parallel v\parallel }_V^2∕2$ as a kinetic energy, we will, using (1), interpret Lv as a momentum. As we have remarked, this momentum can be a singular object. Note that this interpretation is not completely physically unsupported. The choice Lv = ρv where ρ is a scalar density is the momentum that leads to the Euler equation in fluid mechanics [2, 3] (when restricting to divergence-free flows). Also, L being a first order operator is related to the $H_1^{\alpha }$ model that supports the Camassa-Holm equation for waves in shallow water [6].

2.10

Before passing to the next section, it remains to describe how this structure on groups of diffeomorphisms “projects” on the object space M via the group action.

The simplest way is to start with the geodesic distance. We define

$$d_V(m,m\prime )=\underset{\phi }{\inf }\{d_V(\mathrm{id},\phi ),\phi \cdot m=m\prime \}$$

(We use the same notation d_V for both distances, which should not cause any confusion since they apply to different variables.)

So the geodesic distance on M coincides with the “Procustean distance” which consists in finding the least-cost deformation that takes m to m′.

The Riemannian structure on M requires, as we have seen, the definition, for all m, of a dot product norm of the form ${\parallel \xi \parallel }_m^2$ where $\xi ={\stackrel{.}{m}}_t$ for some trajectory on M passing at m. This norm is in fact given by the infinitesimal version of the definition of the distance, namely,

$${\parallel \xi \parallel }_m=\inf \{{\parallel v\parallel }_V:v\cdot m=\xi \}.$$

The vector field v that achieves this minimum is called the horizontal lift of ξ and will be denoted vξ (or $v_m^{\xi }$ is the dependency on m is not clear). With this notation, we have

$${\langle \xi ,\eta \rangle }_m={\langle v^{\xi },v^{\eta }\rangle }_V$$ (3)

A vector v is called horizontal at m if it coincides with vξ for ξ = v · m (so if it is the optimal infinitesimal deformation for the variation of m it generates).

We will discuss in section 4 how geodesics in M relate to geodesics in Diff(Ω).

3. Gradient Descent

3.1

We now discuss gradient descent equations in Diff(Ω) and in shape spaces. Let's first consider a function E: φ ↦ E(φ) defined on diffeomorphisms. The gradient of E with respect to the Riemannian metric introduced in section 2.7 is defined by the identity

$$\frac{d}{d\epsilon }E{(\phi +\epsilon \delta \phi )}_{{\mid }_{[\epsilon =0]}}={\langle \nabla E\left(\phi \right),\delta \phi \rangle }_{\phi }$$

for any small variation δ φ of φ (within a suitable class). From the definition of the dot product, this identity can be rewritten

$$\frac{d}{d\epsilon }E{(\phi +\epsilon \delta \phi )}_{{\mid }_{[\epsilon =0]}}={\langle \nabla E\left(\phi \right)\circ {\phi }^{-1},\delta \phi \circ {\phi }^{-1}\rangle }_V,$$

or, letting v = δφ ∘ φ^-1,

$$\frac{d}{d\epsilon }E{((\mathrm{id}+\epsilon v)\circ \phi )}_{{\mid }_{[\epsilon =0]}}={\langle \nabla E\left(\phi \right)\circ {\phi }^{-1},v\rangle }_V.$$ (4)

The left-hand side of (4) is often called the shape derivative of E at φ [8]. If the gradient exists, both sides are continuous linear forms in v (for the V norm).

3.2

To implement gradient descent with respect to this metric, the first step is to identify a function φ ↦ S(φ) ∈ V such that

$$\frac{d}{d\epsilon }E{((\mathrm{id}+\epsilon v)\circ \phi )}_{{\mid }_{[\epsilon =0]}}={\langle S\left(\phi \right),v\rangle }_V.$$

Gradient descent is then simply

$$\frac{d{\phi }_t}{dt}=-\nabla E\left({\phi }_t\right)=-S\left({\phi }_t\right)\circ {\phi }_t.$$ (5)

We will see some simple examples of this construction [25] in the following sections. However, one important property of this equation is that, if v_t = -S(φ_t), this equation becomes dφ_tdt = v_t ∘ φ_t so that φ_t is the flow associated to the time-dependent vector field v_t. As noticed in section 2.4, this implies that φ_t is a diffeomorphism, at least as long as v_t remains “well behaved”.

3.3

One can apply this for image matching and in fact retrieve an algorithm proposed in [7]. Consider two images m and m′ defined on Ω and the matching function

$$E\left(\phi \right)={\int }_{\Omega }{(m\circ {\phi }^{-1}-m\prime )}^{2}dy.$$

Then, the shape derivative is given by

$$\frac{d}{dt}E((\mathrm{id}+\epsilon v)\circ \phi )=-2{\int }_{\Omega }(m\circ {\phi }^{-1}-m\prime )\nabla {(m\circ {\phi }^{-1})}^{T}vdy.$$

From the definition of the dot product in V (see equation (1)), we see that this implies

$$L\left(S\left(\phi \right)\right)=-2(m\circ {\phi }^{-1}-m\prime )\nabla (m\circ {\phi }^{-1})$$

or (since K = L^-1)

$$S\left(\phi \right)\left(x\right)=-2{\int }_{\Omega }K(x,y)(m\circ {\phi }^{-1}\left(y\right)-m\prime \left(u\right))\nabla (m\circ {\phi }^{-1})\left(u\right).$$ (6)

When L = (αID - Δ)^k (where Δ is the Laplacian), the associated gradient descent evolution is the equation proposed in [7]. Note that, because the minimized energy does not include a control of the smoothness of the diffeomorphism, the equation cannot be expected to stabilize and may develop singularity in the long run. If used as such, it must be combined with an appropriate stopping rule [25].

3.4

For the sake of illustration, let's describe what a gradient descent evolution would be for a penalized cost function of the form

$$E\left(\phi \right)={\int }_{\Omega }{(m\circ {\phi }^{-1}-m\prime )}^{2}dy+\lambda {\int }_{\Omega }{\mid D\phi \mid }^{2}dx$$

(with the matrix norm |A|² = trace(AA^T) in the penalty term). This will result in a function S(φ) = S₁(φ) + λS₂(φ), with S₁ given by (6). For S₂, we have

$$\begin{array}{c}\frac{d}{d\epsilon }{\int }_{\Omega }{\mid D((\mathrm{id}+\epsilon )\circ \phi \mid }^{2}dx=\hfill \\ \hfill {\int }_{\Omega }\text{trace}(D\phi D{\phi }^{T}Dv\circ \phi )dx\hfill \\ \hfill ={\int }_{\Omega }\text{trace}(D\phi \circ {\phi }^{-1}{(D\phi \circ {\phi }^{-1})}^{T}Dv){(\det D\phi \circ {\phi }^{-1})}^{-1}dy.\end{array}$$

To compute S₂, a first option is to integrate by parts the above integral and obtain the dot product of some function with v which can be handled as before. Another option, that we now detail, is to use the kernel formulation and make a direct computation. Indeed, if K is smooth enough, one can prove the identity (for a matrix valued function y ↦ A(y))

$${\int }_{\Omega }\text{trace}\left(A^{T}Dv\right)dy={\langle {\int }_{\Omega }A{\nabla }_{1}K,v\rangle }_V$$

where the integral in the right side term represents the function

$$y\mapsto {\int }_{\Omega }A\left(x\right)\frac{\partial K}{\partial x}(x,y)dx.$$

Using this, we can write

$$S_2\left(\phi \right)=2{\int }_{\Omega }{(\det D\phi \circ {\phi }^{-1})}^{-1}D\phi \circ {\phi }^{-1}{(D\phi \circ {\phi }^{-1})}^T{\nabla }_{1}K.$$

3.5

We can also use gradient descent in the group of diffeomorphisms to implement segmentation algorithms. Assuming that the topology of the extracted object is known, we can represent the target object as a deformation φ ·m of a template (or initial guess) m. Let, for example, m be a binary image, representing a 3D volume (so that φ · = m ∘ φ^-1), and define

$$E\left(\phi \right)=-{\int }_{\Omega }m\circ {\phi }^{-1}\left(x\right)f\left(y\right)dy$$

where f is some function, defined on the observed image, quantifying the relative likelihood for a point with coordinate y to belong in the interior of the shape rather than in the exterior. Assuming that f is smooth, and writing

$$E\left(\phi \right)=-{\int }_{\Omega }m\left(x\right)f\circ \phi \left(x\right)\mid \det D\phi \left(x\right)\mid dx$$

we have, with a standard computation [8],

$$\begin{array}{cc}\hfill \frac{d}{d\epsilon }E((\mathrm{id}+\epsilon v)\circ \phi )& =-{\int }_{\Omega }m\nabla \cdot \left(fv\right)\circ \phi \mid \det D\phi \mid dx\hfill \\ \hfill & =-{\int }_{\Omega }m\circ {\phi }^{-1}\nabla \cdot \left(fv\right)dy.\hfill \end{array}$$

This expression can be used to compute the gradient of E for the group metric. If m is the interior of a surface, we can write

$$\frac{d}{d\epsilon }E((\mathrm{id}+\epsilon v)\circ \phi )={\int }_{\phi (\partial m)}{v}^T{N}^{\phi }d{\sigma }^{\phi }\left(y\right)$$

where Nφ is the unit normal to the deformed boundary, φ(∂m), and σφ the volume form on this boundary. This yields ∇E(φ) = S(φ) ∘ φ with

$$S\left(\phi \right)(.)={\int }_{\phi (\partial m)}K(.,y)N^{\phi }d{\sigma }^{\phi }\left(y\right).$$

3.6

Here is an alternative approach, in which we use an additional constraint that discretizes the gradient using some form of finite elements.

Let x₁, …, x_N be control points that have been defined relative to the reference shape m. We want to compute the gradient under the additional restriction to be finitely generated, in the sense that it can be written in the form $\tilde{\nabla }E\left(\phi \right)=\tilde{S}\left(\phi \right)\circ \phi$ with

$$\tilde{S}\left(\phi \right)(.)=\sum _{k=1}^N{K}_0(.,\phi \left(x_k\right)){\alpha }_k.$$

The natural (and optimal) choice is to let $\tilde{S}\left(\phi \right)$ be the orthogonal projection of S(φ) on the vector space

$$W=\left\{\sum _{k=1}^N{K}_0(.,\phi \left(x_k\right)){\alpha }_k:{\alpha }_1,\dots ,{\alpha }_N\in {\mathbb{R}}^d\right\}$$

for the dot product ⟨., .⟩_V (provided, of course, that K₀ is chosen such that W ⊂ V ). Let e₁, …, e_d be the canonical basis of ${\mathbb{R}}^d$. Since the family of vector fields

$$(K_0(.,\phi \left(x_k\right))e_j,k=1,\dots ,N,j=1,\dots ,d)$$

generates W, we need, to compute the orthogonal projection, to solve the linear system of equations

$${\langle S\left(\phi \right),K_0(.,\phi \left(x_k\right))e_j\rangle }_V=\sum _{l=1}^N{\langle K_0(.,\phi \left(x_k\right)e_j,K_0(.,\phi \left(x_l\right)){\alpha }_l\rangle }_V,k=1,\dots ,N,j=1,\dots ,d$$ (7)

This system takes a very simple form when $K_0=K\tilde{K}$, i.e.

$$K_0(x,y)={\int }_{\Omega }K(x,z)\tilde{K}(z,y)dz,$$

where $\tilde{K}$ is another kernel. In this case, (7) gives

$${\int }_{\Omega }\tilde{K}(\phi \left(x_k\right),y)e_j^{T}S\left(\phi \right)\left(y\right)dy=\sum _{l=1}^N\left(\tilde{K}{K}_0\right)(\phi \left(x_k\right),\phi \left(x_l\right))e_j^T{\alpha }_1.$$ (8)

The projected gradient descent can then be implemented as

$$\frac{d{\phi }_t}{dt}\left(y\right)=-\sum _{k=1}^N{K}_0({\phi }_t\left(y\right),{\phi }_t\left(x_k\right)){\alpha }_k\left(t\right)$$

where the α _k's solve System (8) at each time t.

This is particularly simple with Gaussian kernels. Defining

$$g_{{\sigma }^2}\left(u\right)={\left(2\pi {\sigma }^2\right)}^{-d∕2}\exp (-{\mid u\mid }^2∕2{\sigma }^2)$$

for $u\in {\mathbb{R}}^d$, we can take (with σ₀ > σ)

$$\begin{array}{c}\hfill K(x,y)=g_{{\sigma }^2}(x-y)\hfill \\ \hfill \text{and}{K}_0(x,y)=g_{{\sigma }_0^2}(x-y)\hfill \\ \hfill \text{so that}\tilde{K}(x,y)=g_{{\sigma }_0^2-{\sigma }^2}(x-y)\hfill \end{array}$$

(using well known properties of the convolution of Gaussian kernels) and (8) becomes

$${\int }_{\Omega }{g}_{{\sigma }_0^2-{\sigma }^2}(y-\phi \left(x_k\right))e_j^{T}S\left(\phi \right)\left(y\right)dy=\sum _{l=1}^N{g}_{2{\sigma }_0^2-{\sigma }^2}(\phi \left(x_k\right)-\phi \left(x_l\right))e_j^T{\alpha }_1.$$ (9)

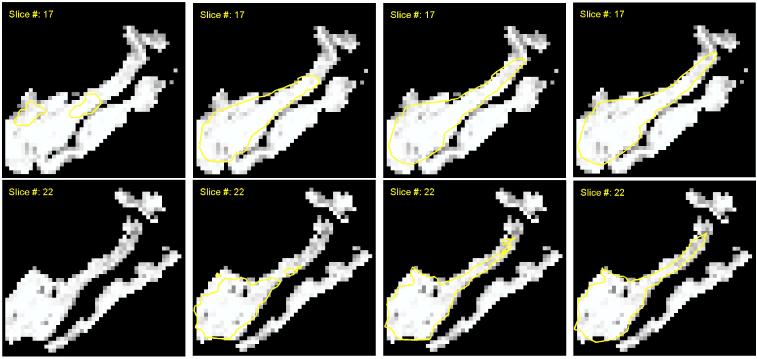
A preliminary experiment using this method is provided in figure 1.

Figure 1.

Evolution of a 3D diffeomorphic active contour in the hippocampal region. Two sections are provided (Rows 1 and 2). The first image shows the position at initial times, and is followed by two images at intermediate times and the final image after convergence. The grey level are proportional to estimated probabilities of grey matter using the AKM method [22]. Fifty control points were used in this experiment.

3.7

We now briefly discuss the relation between the previous gradients in the group of diffeomorphisms and the projected metric on shapes that we have discussed in 2.10.

Given a function defined on shapes, m ↦ F(m), we can always write m = φ · m₀ and proceed as before for the minimization of E(φ) = F(φ ⋅m₀). It is easy to prove that the function U(φ) then only depends on m = φ · m₀, so that we can write the whole computation in terms of F only, solving

$$\frac{d}{d\epsilon }F((id+\epsilon v)\cdot m)={\langle H\left(m\right),v\rangle }_V$$

to obtain H(m) ∈ V and defining the evolution

$$\frac{d{m}_t}{dt}=-H\left(m_t\right)\cdot m_t.$$

This approach is identical to doing gradient descent in the space of shapes with the metric defined in 2.10.

3.8

Gradient descent on the area can also be used to build flows that can smooth surfaces without changing their topology [32]. Letting m be an initial surface, the goal is to build a diffeomorphic evolution φ_t · m minimizing the area functional

$$E\left(\phi \right)=\text{area}(\phi \cdot m).$$

Here, we slightly deviate from the general formulation to make a small change in (3), defining

$$\parallel \xi {\mid }_m^2=\inf \left\{{\langle {\rho }_{m}v,{\rho }_{m}v\rangle }_V,v\cdot m=\xi \right\}.$$

with

$${\rho }_m\left(y\right)=\sqrt{{\int }_{m}K(y,x)d\sigma \left(x\right).}$$

Computing gradient descent with this metric provides, for a closed surface, an area-minimizing flow of the form (for a point p ∈ m)

$$\frac{dp}{dt}={\rho }_m{\left(p\right)}^{-1}{\int }_{m}K(p,y){\rho }_m{\left(y\right)}^{-1}H\left(y\right)N\left(y\right)dy.$$ (10)

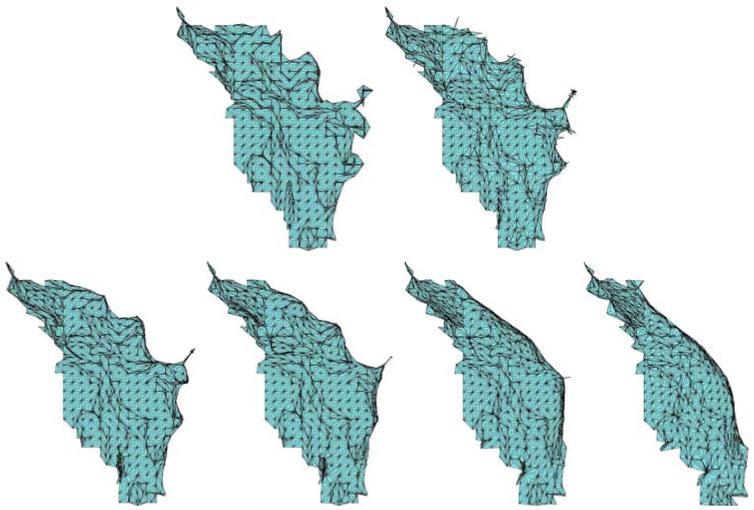
where H is the mean curvature and N the normal to the surface. (A strict application of 3.7 would correspond to taking ρ = 1.) Figure 2 provides an example of applying this algorithm to a surface (which is a piece of cortical surface located within the cingulate gyrus), compared to standard mean curvature flow (dp/dt = HN).

Figure 2.

Diffeomorphic mean curvature flow: a piece of cortical surface (First row, left) is smoothed using area minimizing flows. The right image in the first row shows the result of the classic mean curvature flow after t = 1, with already formed singularities. The second row shows the evolution of diffeomorphic mean curvature flow (10) at times t = 1, 2, 5, 10.

4. Geodesic Equations

4.1

We now switch to the equations that define ‘straight lines’ in our manifolds. These are the Euler-Lagrange equations associated to the construction of paths with minimal kinetic energy between two given points (diffeomorphisms or shapes).

In the group of diffeomorphisms, these equations have been described in [2, 3, 12, 16], and for the particular application to template matching in [19]. They are associated to the following evolution of the momentum

$$\frac{dLv}{dt}+D\left(Lv\right)v+Lv\nabla \cdot v+{\left(Dv\right)}^{T}Lv=0,$$ (11)

combined with dφ_t/dt = v_t ∘ φ_t. Equation (11) must be understood in a generalized sense, and can be rewritten as follows: for all smooth vector field w,

$$\frac{d}{dt}{\int }_{\Omega }L{v}^{T}wdx=-{\int }_{\Omega }L{v}^T(Dvw-Dwv)dx.$$ (12)

We will follow [12] and refer to Equation (11) as the EPDiff equation (it relates to the Euler-Poincaré theory applied to diffeomorphisms [16]).

Geodesics in a Riemannian manifolds are curves that obey the geodesic equations (EPDiff in the case of diffeomorphisms). There is a risk of confusion with what we have defined as minimizing geodesics, which are solutions of the shortest path variational problem. Minimizing geodesics satisfy the geodesic equations, since they are Euler-Lagrange equations for the shortest path. But not all geodesics are minimizing between their endpoints, although they usually are minimizing between points in their trajectory that are sufficiently close to each other.

4.2

For further reference, we note that, letting a_t = Lv_t, the evolution of the diffeomorphism under the EPdiff equation can be written as follows,

$$\{\begin{array}{c}{v}_t=K{a}_t\hfill \\ \frac{d{\phi }_t}{dt}=v_t\circ {\phi }_t\hfill \\ \frac{d{a}_t}{dt}=-D{a}_t{v}_t-a_t\nabla \cdot v_t-{\left(D{v}_t\right)}^T{a}_t\hfill \end{array}\phantom{\}}$$ (13)

4.3

EPDiff provides an important representation of diffeomorphisms via the Riemannian exponential map. This map takes in input an initial velocity v₀ (or the corresponding momentum Lv₀) and solves the EPDiff equation until time t = 1 (one can show that EPDiff has solution over arbitrary time intervals provided K is smooth enough). The output of the map is the final diffeomorphism, φ₁. We therefore have a representation

$$P:L{v}_0\mapsto \phi =P\left(L{v}_0\right)\in G$$

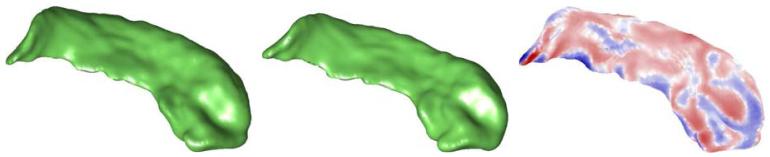
that relates the endpoint of a geodesic to the initial momentum. This is the momentum representation of the deformation. An example of this representation with images is provided in Figure 3.

Figure 3.

Visualizing the momentum on a binary volume. Left: template image; center: target image; right: momentum superimposed on the template image. The momentum can then be used as a deformation signature for shape studies.

4.4

EPDiff is a central equation in computational anatomy. A first reason for this is that it coincides with the Euler-Lagrange equation for the Large Deformation Diffeomorphic Metric Matching algorithm (LDDMM), which minimizes an energy that takes the form

$$E\left(\phi \right)=d_V{(\mathrm{id},\phi )}^2+E_{\text{data}}(\phi \cdot m_0)$$

where the data attachment term is similar to the ones we have discussed above. Since the computation of d_V, (id, φ) is a variational problem itself, any solution of the LDDMM problem must optimize geodesics in some way ([15, 28, 4, 1, 27, 30]), which involves EPDiff.

One of the by-products is that solving the LDDMM problem automatically provides the momentum representation of the optimal diffeomorphism φ. This representation can then be used to analyze anatomical datasets. This approach has been used with hippocampuses [28], in relation to Alzheimer [29], of with the cingulate gyrus, in relation with schizophrenia [24]. Cardiac studies have also been developped in [11] using this method.

4.5

We now discuss the geodesics equation in the object space, M. Because the Riemannian structure on M has been defined as the projection of the one on diffeomorphisms, geodesics on M are directly obtained from geodesics on G_V. More precisely, a geodesic starting from m₀ ∈ M must take the form m_t = φ_t · m₀, such that

1. t ↦ φ_t is a geodesic on G_V (it satisfies EPDiff).

2. The initial velocity at time t = 0 is horizontal at m₀, as defined in section 2.10.

Property (ii) propagates over time: if it is true, then v_t is horizontal at m_t for all t.

Because horizontal vector fields have specific forms for specific types of objects, we will be able to simplify the projection of the EPDiff equation in an object-dependent manner. Note that, in spite of the apparent difference in their form, the equations that follow are all instances of the EPDiff equation with a specific choice for the initial momentum.

4.6

When objects M are point sets, horizontal vector fields at m = (x₁, …, x_N ) must take the form

$$v(.)=\sum _{k=1}^{N}K(.,x_k){\alpha }_k.$$ (14)

Working out the EPDiff equation for such vector fields yields the following geodesic equations on M, which end up forming a system of ordinary differential equations. These equations are written in terms of m_t = (x₁(t), …, x_N (t)) and a_t = (α₁(t), …, α_N (t)), with

$$\{\begin{array}{c}{v}_t(.)=\sum _{l=1}^{N}K(.,x_l){\alpha }_1\hfill \\ \frac{d{x}_k}{dt}-v_t\left(x_k\right)=0\hfill \\ \frac{d{\alpha }_k}{dt}=-\sum _{l=1}^N{\nabla }_{1}K(x_k,x_l){\alpha }_k^T{\alpha }^l\hfill \end{array}\phantom{\}}$$ (15)

Here, ∇₁K represent the gradient of (x, y) ↦ K(x, y) with respect to the first coordinate, x.

The momentum representation for landmarks is captured by the family of d dimensional vectors, a₀. The initial conditions (m₀, a₀) uniquely specify the values of m_t and a_t at all times.

Note that the momentum Lv associated to a vector field given by (14) is singular. In fact, in this case, we have (with some abuse of notation)

$${\int }_{\Omega }L{v}^{T}wdx=\sum _{k=1}^N{\alpha }_K^{T}w\left(x_k\right)$$

for any w ∈ V. The relation between such singular solutions (sometimes called peakons) and soliton waves in fluid mechanics has been described in [13]. A numerical analysis of the stability of these equations is given in [17].

4.7

When objects are images, horizontal vector fields are characterized by the property that Lv is orthogonal to the level lines of the image. (The formal statement to include singular momenta is: Lvv(w) vanishes when applied to a test vector field, w, which is parallel to these level sets).

An interesting example is when Lv₀(x) is given by a₀(x)∇m₀(x). This is a function in the classical sense, parallel to the gradient of m₀. (This is interesting because one can show that solutions of the image matching LDDMM problem take this form [5, 20].) Then the geodesic equations on M are

$$\{\begin{array}{c}{v}_t=-{\int }_{\Omega }K(.,y)a_t\left(y\right)\nabla m_t\left(y\right)dy\hfill \\ \frac{d{m}_t}{dt}+\nabla m_t^T{v}_t=0\hfill \\ \frac{d{a}_t}{dt}+\nabla \cdot \left(a_t{v}_t\right)=0\hfill \end{array}\phantom{\}}$$ (16)

4.8

Equations for densities are very similar. Horizontal momenta at m are also orthogonal to the level sets of m, and when Lv₀ = a₀∇m₀, the evolution equations are

$$\{\begin{array}{c}{v}_t={\int }_{\Omega }K(.,y)\nabla a_t\left(y\right)m_t\left(y\right)dy\hfill \\ \frac{d{m}_t}{dt}+\nabla \cdot \left(m_t{v}_t\right)=0\hfill \\ \frac{d{a}_t}{dt}+\nabla a_t^T{v}_t=0\hfill \end{array}\phantom{\}}$$ (17)

So that the roles of m and a are reversed compared to the image case.

4.9

Note that all the preceding geodesic equations take the form

$$\{\begin{array}{c}{v}_t=F(m_t,a_t)\hfill \\ \frac{d{m}_t}{dt}=v_t\cdot m_t=H(m_t,v_t)\hfill \\ \frac{d{a}_t}{dt}=G(m_t,a_t,v_t)\hfill \end{array}\phantom{\}}$$ (18)

where the functions F, G, H are linear in a and v, but not necessarily in m. (This includes also the case of diffeomorphisms, simply replacing m by φ.) The function t ↦ a_t can be interpreted as a representation for horizontal momenta, via the relation Lv = LF (m, a).

4.10

An interesting variant of the preceding three geodesic equations comes from the theory of metamorphosis. Our models so far only move the objects along trajectories that correspond to diffeomorphic transformations. Taking the case of images, it is impossible, with this approach, to alter topology along geodesics, say to move from a sphere-like object to a torus.

Metamorphosis [21, 26, 14] provides a mechanism that allows the evolution to deviate from pure deformations. The first equation in systems (15), (16), (17) is a conservation (advection) equation of the deformed object, m_t, along the flow. The metamorphosis equations introduce a right-hand side to this equation, in order to provide a slightly inexact advection. The landmark equations, for example, become, introducing a parameter σ²,

$$\{\begin{array}{c}\frac{d{x}_k}{dt}-v_t\left(x_k\right)={\sigma }^2{a}_k\hfill \\ v_t(.)=\sum _{l=1}^{N}K(.,x_l){\alpha }_l\hfill \\ \frac{d{\alpha }_k}{dt}=-\sum _{l=1}^N{\nabla }_{1}K(x_k,x_l){\alpha }_k^T{\alpha }^l\hfill \end{array}\phantom{\}}$$ (19)

For images, they are

$$\{\begin{array}{c}\frac{d{m}_t}{dt}+\nabla m_t^T{v}_t={\sigma }^2{a}_t\hfill \\ \frac{d{a}_t}{dt}+\nabla \cdot \left(a_t{v}_t\right)=0\hfill \\ v_t=-{\int }_{\Omega }K(.,y)a_t\left(y\right)\nabla m_t\left(y\right)dy\hfill \end{array}\phantom{\}}$$ (20)

and for densities

$$\{\begin{array}{c}\frac{d{m}_t}{dt}+\nabla \cdot \left(m_t{v}_t\right)={\sigma }^2{a}_t\hfill \\ \frac{d{a}_t}{dt}+\nabla a_t^T{v}_t=0\hfill \\ v_t={\int }_{\Omega }K(.,y)\nabla a_t\left(y\right)m_t\left(y\right)dy\hfill \end{array}\phantom{\}}$$ (21)

These equations have the fundamental property to remain geodesic equations in the relevant object spaces (for different metrics, obviously). The parameter σ² is a weight defining how close to a pure deformation the evolution will be.

5. Parallel Translation

5.1

We have noticed in paragraph 4.4 that the momentum representation (exponential map) is an important tool that can provide a normalized representation of a family of shapes relative to a fixed template. There are cases, however, in which the registration of all data to a single template may not be the most natural first step in a study. Consider, as an example, the situation in which the data is paired (each subject is associated to two shapes, say left and right), and the issue is to decide whether the two shapes are statistically identical or to exhibit some asymmetry.

One possibility is to register all shapes to a template and design a statistical study of the asymmetry in terms of the momentum representation. A more direct and natural approach, however, would be to register the left shape to the right one and vice versa, and then measure whether the two processes are identical or not.

With LDDMM, the registrations result in momenta sitting on (or horizontal at) the left shape of each subject (for the left to right registrations) and on the right shape (for the right to left). All these momenta are not directly comparable and need to be aligned in order to be horizontal at a single template. The operation that does this with a minimal metric distortion is parallel translation along geodesics, which is the subject of this section. It is important to notice that this operation is done after the within-subject difference has been measured, and not before. This reduces the risk of having this difference mixed in between-subject variation, which is likely to occur if the template registration is performed first.

Finally, let's emphasize that these ideas directly generalize to situations beyond asymmetry. They can be applied to any case in which several shapes are observed for each subject, and the elements of interest are relative differences, within subject, among these shapes. This includes time series and longitudinal data.

This approach using parallel transport has been recently used for several applications. In [31], the left-right asymmetry of the hippocampus for normal subjects has been confirmed as a validation study for the method. In [24], a longitudinal study showed specific evolution patterns for dementia of the Alzheimer's type. Another from of application of parallel transport combined with time series LDDMM is provided in the current issue [23].

5.2

Parallel translation on a manifold is an operation that takes a tangent vector at some point in the manifold and translate it along a given curve. In our discussion, this curve will always be a geodesic from a subject shape to the template. Instead of tangent vectors, however, we will transport momenta. The point of view is equivalent, and more suitable for our discussion. For completeness, let's mention that, for diffeomorphisms, momenta and tangent vectors at φ ∈ G are related via Lv ↔ v ∘ φ.

5.3

We first give the general form of the equation, with the notation used in (18). We assume that a path t ↦ m_t is given, satisfying an equation of the form

$$\frac{d{m}_t}{dt}=F(m_t,a_t)\cdot m_t$$

with the notation of section 4.9. The path t ↦ a_t is what we called the momentum parameter along m_t, with corresponding deformation momentum Lv_t = LF (m_t, a_t). Let b₀ be another momentum parameter at m₀. The following equation translates b₀ along the path t ↦ m_t. We use the same notation as in (18)

$$\{\begin{array}{c}H(m_t,F(m_t,\frac{d{b}_t}{dt}))=\frac{1}{2}\left\{H_m(m_t,v_t){\eta }_t-H_m(m_t,w_t){\xi }_t+H(m_t,F_m(m_t,a_t){\eta }_t-F_m(m_t,b_t){\xi }_t)+H\left(m_t,F(m_t,G(m_t,b_t,v_t)+G(m_t,a_t,w_t))\right)\right\}\hfill \\ {\xi }_t=H(m_t,v_t)=\frac{d{m}_t}{dt}\hfill \\ {\eta }_t=H(m_t,w_t)\hfill \\ v_t=F(m_t,a_t)\hfill \\ w_t=F(m_t,b_t)\hfill \end{array}\phantom{\}}$$ (22)

Here we have denoted F_m and H_m the differentials for F and H with respect to the first variable, m. Note that the first equation defines db/dt implicitly, involving the inversion of the linear operator β ↦ H(m, F(m, β)) = F(m, β) ⋅ m.

If t ↦ a_t satisfies the third equation in (18), namely da_t/dt = G(m_t, a_t, v_t), then m_t is a geodesic, and we have the important property that a_t is its own parallel transport (i.e., b_t = a_t is solution of the equation), since, in this case, the first equation reduces to

$$H(m_t,F(m_t,\frac{d{a}_t}{dt}))=H\left(m_t,F(m_t,G(m_t,a_t,w_t))\right).$$

Another important feature is that the operation conserves the dot product: if w_t and $w_t^{\prime }$ are the results of parallel transports along the same path, then ${\langle w_t,w_t^{\prime }\rangle }_V=\mathrm{cst}$.

5.4

We now discuss this situation in the special cases that we have considered, starting with the full group of diffeomorphisms and equation (13). Here, we have (with m = φ) F(m, a) = Ka (so that F_m = 0), H(m, v) = v ∘ φ and G(m, a, v) given by the right-hand side of the third equation in (13). This implies that

$$H(m,F(m,\beta ))=\left(K\beta \right)\circ \phi$$

which can therefore be easily inverted in β. This provides the following form for parallel translation with diffeomorphisms.

$$\frac{d{b}_t}{dt}=\frac{1}{2}L(D{v}_t.w_t-D{w}_t.v_t)-\frac{1}{2}(D{b}_t{v}_t+b_t\nabla \cdot v_t+D{v}_t^T{b}_t+D{a}_t{w}_t+a_t\nabla \cdot w_t+D{a}_t^T{w}_t)$$ (23)

with a_t = Lv_t and b_t = Lw_t. (This equation, that we have written in classic form, also has a generalized counterpart, since a and b can be singular [18, 30].)

5.5

When considering object spaces, it is important to note that, while the geodesic equations in object spaces were simply special forms of EPDiff adapted to the specific expressions of horizontal vector fields, this is not the case with parallel translation. This is because horizontality is not conserved along (23). More precisely, if A(v_t, w_t) represents the right hand side of (23) (with a_t = Lv_t and b_t = Lw_t), one can check that parallel translation along m_t, as given by (22), is characterized by the two conditions,

1. $(\frac{d{w}_t}{dt}-KA(v_t,w_t))\cdot m_t=0$,

2. w_t is horizontal at m_t.

5.6

For point sets, we have m_t = (x₁(t), …, x_N(t)) and a_t = (α₁(t), …, α_N(t)), with

$$\{\begin{array}{c}F(m,v)=(v\left(x_1\right),\dots ,v\left(x_N\right))\hfill \\ H(m,a)=\sum _{l=1}^{N}K(.,x_l){\alpha }_l\hfill \\ {\left(G(m,a,v)\right)}_k=-D_v{\left(x_k\right)}^T{\alpha }_k\hfill \end{array}\phantom{\}}$$

Using these expressions in (22), the equations for parallel translation are given as follows.

$$\{\begin{array}{c}\sum _{l=1}^{N}K(x_k,x_l)\frac{d{\beta }_l}{dt}=\frac{1}{2}\left(D{v}_t\left(x_k\right){\eta }_k-D{w}_t\left(x_k\right){\xi }_k+\sum _{l=1}^N({\nabla }_{2}K{(x_k,x_l)}^T{\eta }_l{\alpha }_l+{\nabla }_{2}K{(x_k,x_l)}^T{\xi }_l^T{\beta }_l)-\sum _{l=1}^{N}K(x_k,x_l)(D{v}_t{\left(x_l\right)}^T{\beta }_l+D{w}_t^T\left(x_l\right){\alpha }_l)\right)\hfill \\ w_t=\sum _{l=1}^{N}K(.,x_l\left(t\right)){\beta }_l\left(t\right)\hfill \\ {\eta }_k=w_t\left(x_k\right)\hfill \end{array}\phantom{\}}$$ (24)

where ∇₂ is the gradient with respect to the second coordinate. Replacing η_k, ξ_k, Dv(x_k) and Dw(x_k) by their expansions, this system can be rewritten uniquely in terms of m_t, a_t and b_t, yielding a finite dimensional ODE, but with a relatively lengthy expression that we will not detail here (see [31]).

5.7

For images, let m_t be a geodesic for the image metric with v_t = K(a_t∇m_t). Let ${\xi }_t=-\nabla m_t^T{v}_t$, and assume that w₀ = -K(b₀∇m₀) is given with ${\eta }_0=-\nabla m_0^T{w}_0$. Then, the parallel translation of η₀ along m_t for the image metric is

$$\{\begin{array}{c}\nabla m_t^{T}K(\frac{d{b}_t}{dt}\nabla m_t)=\frac{1}{2}\left(\nabla {\eta }_t^T{v}_t-\nabla {\xi }_t^T{w}_t+\nabla m_t^{T}K(a_t\nabla {\eta }_t-b_t\nabla {\xi }_t)-\nabla m_t^{T}K(\nabla \cdot (b_t{v}_t+a_t{w}_t)\nabla m_t)\right)\hfill \\ {\eta }_t=-\nabla m_t^{T}K(b_t\nabla m_t)\hfill \\ w_t=K(b_t\nabla m_t)\hfill \end{array}\phantom{\}}$$ (25)

To explicitly compute db_t/dt, one needs to invert the operator $\zeta \mapsto \nabla m_t^{T}K(\zeta \nabla m_t)$. One can prove that this is invertible with the additional condition that ζ = 0 when ∇m_t = 0. Solving this numerically is however notably harder than the solution of the linear system needed for (24). An algorithm for this has been proposed in [31].

5.8

We now conclude with the case of densities, which, as can be expected, is symmetric to the image case. With the same notation, the equations are

$$\{\begin{array}{c}\nabla \cdot \left(m_{t}K(m_t\nabla \frac{d{b}_t}{dt})\right)=-\frac{1}{2}\left(\nabla \cdot ({\eta }_t{v}_t-{\xi }_t{w}_t)-\nabla \cdot \left(m_{t}K({\eta }_t\nabla a_t-{\xi }_t\nabla b_t)\right)+\nabla \cdot \left(m_{t}K(m_t\nabla \cdot (\nabla a_t^T{w}_t+\nabla b_t^T{v}_t))\right)\right)\hfill \\ {\eta }_t=\nabla \cdot \left(m_{t}K(m_t\nabla b_t)\right)\hfill \\ w_t=-K(m_t\nabla b_t)\hfill \end{array}\phantom{\}}$$ (26)

6. Jacobi Equation

6.1

We conclude this review with the Jacobi equations, which are first order variations of geodesics.

The geodesic evolutions are uniquely specified by the initial position, m₀ (or φ₀ = id for diffeomorphisms), and the initial velocity v₀ (which must be horizontal at m₀ for geodesics in object space). The Jacobi equation measures the variation of the geodesic when these initial conditions are changed.

A formal computation from the general form of the geodesic equation (18) is not too hard. Given initial perturbations m₀ → m₀ + δm₀ and a₀ → a₀ + δa₀, we get m_t → m_t + δm_t, a_t → a_t + δa_t and v_t → v_t + δv_t with

$$\{\begin{array}{c}\delta v_t=F_m(m_t,a_t)\delta m_t+F(m_t,\delta a_t)\hfill \\ \frac{d\delta m_t}{dt}=H_m(m_t,v_t)\delta m_t+H(m_t,\delta v_t)\hfill \\ \frac{d\delta a_t}{dt}=G_m(\delta m_t,a_t,v_t)\delta m_t+G(m_t,\delta a_t,v_t)+G(m_t,a_t,\delta v_t)\hfill \end{array}\phantom{\}}$$ (27)

These equations must be combined with (18) to form a sellf contained dynamical system in (m_t, a_t, δm_t, δa_t). The Jacobi field is, by definition, J(t) = tδm_t with δm_t given by this system.

The equations can now be worked out in each case of interest. Note that they simplify further in the image and density cases, for which all functions are also linear in m, with G independent of m, yielding

$$\{\begin{array}{c}\delta v_t=F(\delta m_t,a_t)+F(m_t,\delta a_t)\hfill \\ \frac{d\delta m_t}{dt}=H(\delta m_t,v_t)+H(m_t,\delta v_t)\hfill \\ \frac{d\delta a_t}{dt}=G(\delta a_t,v_t)+G(a_t,\delta v_t)\hfill \end{array}\phantom{\}}$$ (28)

6.2

This equation is related to a variety of problems. The first one is the optimization of the LDDMM functional, namely

$$E\left(\phi \right)=d_V{(\mathrm{id},\phi )}^2+U(\phi \cdot m_0).$$

The geodesic distance between id and φ is equal to the norm of the initial velocity v₀ along the geodesic. So, denoting by m₁(m₀, a₀) the object obtained by solving equation (18) until time t = 1, the problem is equivalent to the minimization of

$$\tilde{E}\left(a_0\right)={\mid F(m_0,a_0)\mid }_V^2+U\left(m_1(m_0,a_0)\right).$$

(We write $\tilde{E}$ as a function of a₀ only, because m₀ is fixed in the LDDMM problem.)

To compute the effect of a small variation a₀ → a₀ + δa₀, we write (formally applying the chain rule)

$$\delta \tilde{E}=2{\langle F(m_0,a_0),F(m_0,\delta a_0)\rangle }_V+\left(\frac{dU}{dm}\right)\left(\frac{d{m}_1}{d{a}_0}\right)\delta a_0.$$

Now, dm₁/da₀ is precisely the Jacobi field δm₁ when (27) is solved until time t = 1, with initial conditions m₀, a₀, δm₀ = 0 and δa₀. If one is able to write the last term as

$$\left(\frac{dU}{dm}\right)\left(\frac{d{m}_1}{d{a}_0}\right)\delta a_0={\langle F(m_0,b_0),F(m_0,\delta a_0)\rangle }_V,$$ (29)

a gradient descent procedure in the form a₀ → a₀ - ε (2a₀ + b₀)can be used to solve the LDDMM problem. (This is gradient descent for the metric ${\parallel a_0\parallel }^2={\parallel F(m,a_0)\parallel }_V^2$.)

Such gradient descent procedures have been described with landmark matching [28] and image matching [30].

6.3

We now indicate how b₀ can be computed in (29). The first step is to use the dual Jacobi equation. To define this equation, first replace δv by its expression in the last two equations of (27), to obtain a system that takes the form

$$\{\begin{array}{c}\frac{d\delta m}{dt}=A(m,a,\delta m)+B(m,a,\delta a)\hfill \\ \frac{d\delta a}{dt}=C(m,a,\delta m)+D(m,a,\delta a)\hfill \end{array}\phantom{\}}$$ (30)

The functions A and C (resp. B and D) are linear in δm (resp. δa). The dual equation is then given by

$$\{\begin{array}{c}\frac{d\delta m\ast }{dt}=A\ast (m,a,\delta m\ast )+C\ast (m,a,\delta a\ast )\hfill \\ \frac{d\delta a\ast }{dt}=B\ast (m,a,\delta m\ast )+D\ast (m,a,\delta a\ast )\hfill \end{array}\phantom{\}}$$ (31)

where A*,B*,C*,D* are the duals of the operators A, B, C.D (with fixed m and a); they correspond to the usual transposed matrices for finite dimensional evolutions (point sets) and to the L² conjugate for images and densities. Given this system, the computation of b₀ goes as follows:

1. Solve (31) backwards in time (from t = 1 to t = 0) with initial conditions $\delta m_1^{\ast }=0,\delta a_1^{\ast }=(\partial U∕\partial m)\left(m_1\right)$.

2. Let $\delta m_0^{\ast }$ be the value obtained at t = 0 at the previous step; solve the equation

   $$F\ast (m,LF(m,b_0))=\delta m_0^{\ast }.$$

6.4

Another situation in which the Jacobi equation is relevant is based on the remark that the solution of the LDDMM problem must satisfy

$$a_1+\frac{\partial U}{\partial m}\left(m_1\right)=0$$ (32)

where a₁ and m₁ is the final momentum parameter and object for the geodesic starting with (m₀, a₀) (This is an application of the Pontryagin principle.)

The shooting method in optimal control consists in solving this equation directly in terms of the initial parameter, a₀, since m₀ is fixed. Newton's method for this purpose consists in iteratively adapting the current value of a₀ witha₀ → a₀ + δa₀, such that, given the current m₁ and a₁, their variations δm₁ and δa₁ satisfy

$$\delta a_1+\frac{{\partial }^{2}U}{\partial m^2}\left(m_1\right)\delta m_1=-a_1-\frac{\partial U}{\partial m_1}.$$

This requires being able to explicitly compute the transformations δa₀ ↦ (δm₁, δa₁) and inverting the previous equation to obtain δa₀, which is tractable in finite dimension and directly applicable to point sets [1].

6.5

Finally, we can remark that the Jacobi equation is related to parallel translation as follows. If one expresses d² δm_t/dt² as a function of the other variables at t = 0, i.e.,

$${\frac{d^2\delta m_t}{d{t}^2}}_{{\mid }_{[t=0]}}=J(m_0,a_0,\delta a_0),$$

which can be done by differentiating in time the second equation in (27) and replacing the first derivatives by their expressions in the system (and taking advantage of the fact that δm₀ = 0), then the first equation in (24), (25) and (26) is exactly

$$\frac{d\eta }{dt}=\frac{1}{2}J(m,a,b).$$

This can be used to design a numerical implementation of parallel translation based on iterating Jacobi fields, as proposed in [30].

7. Conclusion

We have described, in this paper, a whole range of evolution equations (gradient descent, geodesics, parallel transport, Jacobi fields) that are related to important aspects of computational anatomy. These equations have all taken part in medical imaging applications, for smoothing, segmentation, registration, longitudinal analysis etc.

This provides a complementary angle on computational anatomy, which more often focuses on variational formulations, like LDDMM. While the computation of the solutions of evolution equations has become an important component of the discipline, this also brings new open problems, regarding the extension of their definition to new shape modalities or their numerical implementation, as well as potential new applications in the analysis of medical data. Significant development in these directions can be expected in the future.

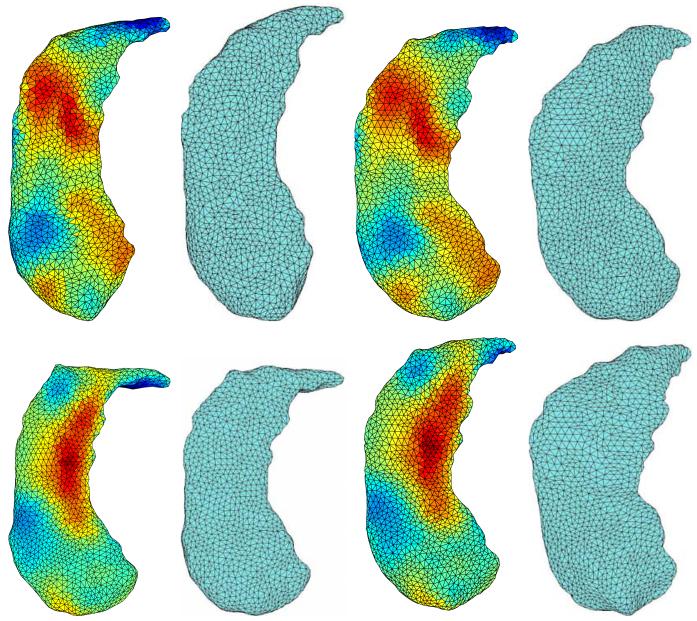
Figure 4.

Parallel tranlation on vertices of triangulated surfaces for pair data. Two examples are provided (one in each row). The first two images in each row represent shapes A and B, shape A being colored according to the Jacobian determinant of the optimal transformation from A to B (blue: atrophy; red: expansion). The last two images are the template, T, and a new synthetic shape S. S is obtained by parallel translating the initial momentum for the A-to-B transformation along the geodesic linking A to T, and then solving EPDiff starting from T with the translated momentum. In each row, T is colored according to the Jacobian determinant of the obtained deformation.