Skip to main content
PMC home page
Clinical Orthopaedics and Related Research logoLink to Clinical Orthopaedics and Related Research
. 2008 Jun 13;467(4):886–893. doi: 10.1007/s11999-008-0336-y

Can the Acetabular Position be Derived from a Pelvic Frame of Reference?

Wael Dandachli 1,✉, Amgad Nakhla 1, Farhad Iranpour 1, Vijayaraj Kannan 1, Justin P Cobb 1
PMCID: PMC2650052  PMID: 18551348

Abstract

Acetabular center positioning has an effect on hip function. However, reported clinical and plain radiographic methods are inaccurate and unreliable for ascertaining acetabular implant location. In an exploratory study we asked whether the normal acetabular position can be derived from simple radiographically measurable pelvic dimensions. We analyzed computed tomographic scans of 37 normal hips using a pelvic frame of reference centered on the ipsilateral anterior-superior iliac spine. We defined the x-, y-, and z-coordinates of the hip center (Cx,Cy,Cz) as a percentage of the corresponding pelvic dimensions (Dx,Dy,Dz). Cx/Dx averaged 9%, Cy/Dy 34%, and Cz/Dz 37%. These ratios had narrow distributions with small confidence intervals. Interobserver agreement tests showed a mean intraclass correlation coefficient of 0.95. We observed gender differences in the ratios of as much as 4%, which correspond to differences of as much as 9 mm in the hip center position. The ratios provide a simple and reliable way of deriving the normal position of the hip center from the pelvic dimensions alone. This gives the surgeon a simple way of planning where the hip center should be and may be particularly helpful in revision hip arthroplasty or in cases involving extensive osteophytes, dysplasia, or protrusio.

Introduction

Positioning of the acetabular center in the pelvis influences function of the hip. The joint contact forces about a reconstructed hip are greater when the hip center is located superiorly, laterally, and posteriorly compared with the original location [18]. Moreover, the force- and moment-generating capacities of the hip muscles are sensitive to the location of the hip center [2, 10–12]. A 2-cm superior displacement, for instance, decreases abduction force by 44% and moment by 49%, whereas a 2-cm medial displacement decreases adduction force by 26% and moment by 40% [10]. Anteroposterior (AP) displacement, which is invisible on AP radiographs, alters the moment-generating capacity of the flexors and extensors considerably [10]. Optimal placement of the acetabulum is also crucial to avoid impingement, accelerated wear, and loosening in a reconstructed hip [9, 22, 28].

One report suggests differences in the width of the true pelvis between males and females account for different joint contact forces in male and female joints [19]. Gender differences also exist in pelvic height, abductor force, and joint contact forces [15]. These difference may be related to the particular position of the acetabulum in the pelvis in males and females.

Unlike acetabular angular orientation, few studies describe accurate methods of defining the acetabular center position in three-dimensional (3-D) space [3, 14, 20]. Predictive methods involve localizing the center in relation to palpable bony landmarks with the position calculated using pelvic dimensions [1, 20, 26]. The pelvic dimensions used in these studies did not take into account the full extent of each dimension. Moreover, errors of as much as 23 mm were observed when applying these methods on dry cadaveric pelves [26]. These noninvasive methods rely on accurate palpation of bony landmarks and the distance between them, which is frequently difficult to measure in the clinical setting.

The alternative functional method involves determination of the center of rotation by fitting a sphere to paths followed by a femur-fixed point as motion occurs about the hip [6, 21, 27]. These methods can be associated with substantial errors. Although functional methods result in hip center location errors less than 26 mm, much larger errors of as much as 70 mm result when data collected during commonly performed hip motions are used [24]. This appears related to inability to move the hip in certain planes, especially the sagittal plane [24].

Radiographic methods of defining the hip center traditionally have relied on 2-D plain radiography [13, 23, 25]. One such method used Koehler’s line and a line joining the two teardrops on plain AP radiographs [13]. In another study, the intersection between Koehler’s line and a line between the upper rims of the two obturator foramina was used as a reference point. The x- and y-coordinates of the hip center then were related to pelvic height [5]. Although these 2-D methods are good at gross positioning the hip center, they lack the accuracy needed for acetabular reconstruction because they are associated with projectional errors.

Given the need for an accurate and reproducible method of determining the optimal position of the hip center during hip reconstruction, we addressed the following questions: (1) Can the normal position of the acetabulum be derived from simple radiographically measured pelvic dimensions?; (2) Will the method relating the acetabular position to these pelvic dimensions be reliable?; and (3) Will there be gender differences in the relationship between the acetabular position and the pelvic dimensions?

Materials and Methods

We analyzed CT scans of 37 pelves (19 female, 18 male). Twenty-nine of these scans were performed before this study to investigate unilateral hip pain in patients who had normal contralateral hips. The other eight scans were performed previously to postoperatively evaluate surgical fixation of unilateral acetabular fractures; the parts of the pelvis used for the analysis, including the studied hips, were normal. Given this was an exploratory study, we did not perform a power analysis for sample size. The patients had a mean age of 59 years (standard deviation, 20 years); and they had varying shapes, sizes, and ethnicity typical of a large cosmopolitan city. A Siemens Sensation 64 scanner (Siemens Medical Solutions, Erlangen, Germany) was used to obtain the 1-mm slices. The protocol used covered an area from the top of the iliac wings proximally to just below the lesser trochanters distally with an average of 250 slices per scan.

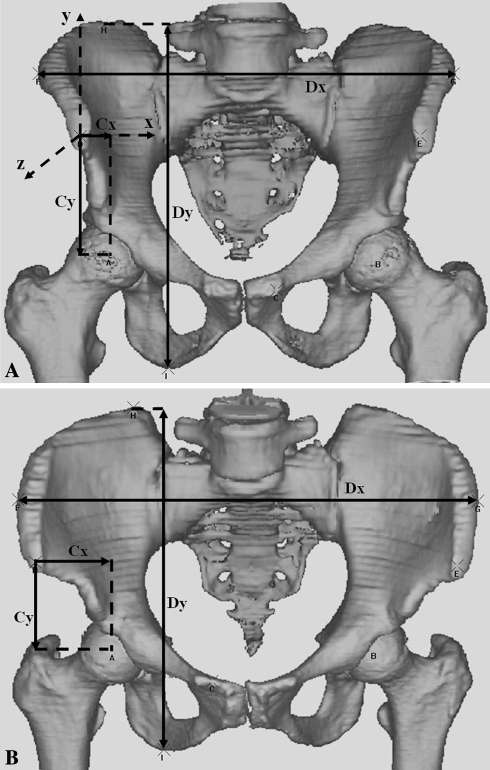
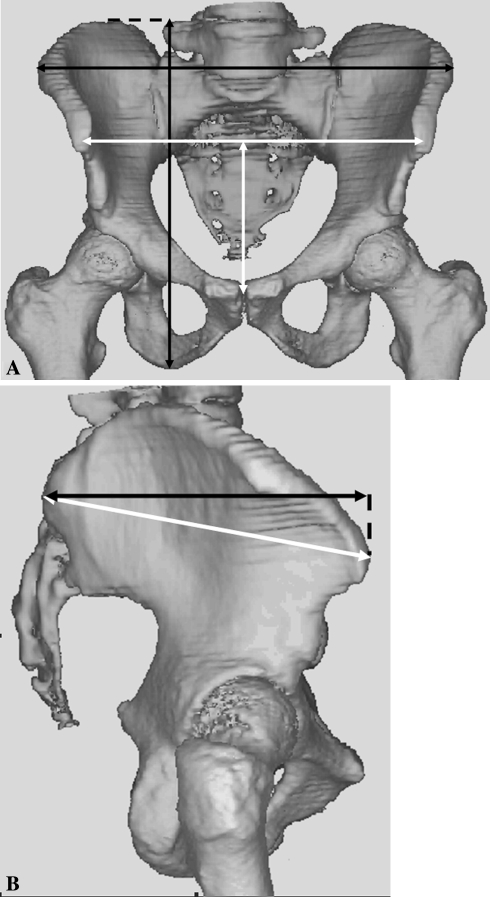
To analyze the CT scans, we used computer software that was validated previously by correlation with dry bone measurements [7, 16]. We chose the anterior pelvic plane, defined by the two anterior-superior iliac spines (ASIS) and the pubic tubercles [8, 17], as the basis of the coordinate system with the origin set at the ipsilateral ASIS. The x-axis pointed horizontally from left to right, the y-axis vertically upward, and the z-axis posterior to anterior. The femoral head center represented the hip center and we measured its coordinates (Cx,Cy,Cz) (Figs. 1, 2).

Fig. 1A–B.

Fig. 1A–B

Open in a new tab

Anteroposterior 3-D views show the x- and y-coordinates of the hip center (Cx, Cy) related to their corresponding horizontal (Dx) and vertical (Dy) dimensions of the pelvis for the right hip in (A) a male and (B) a female pelvis.

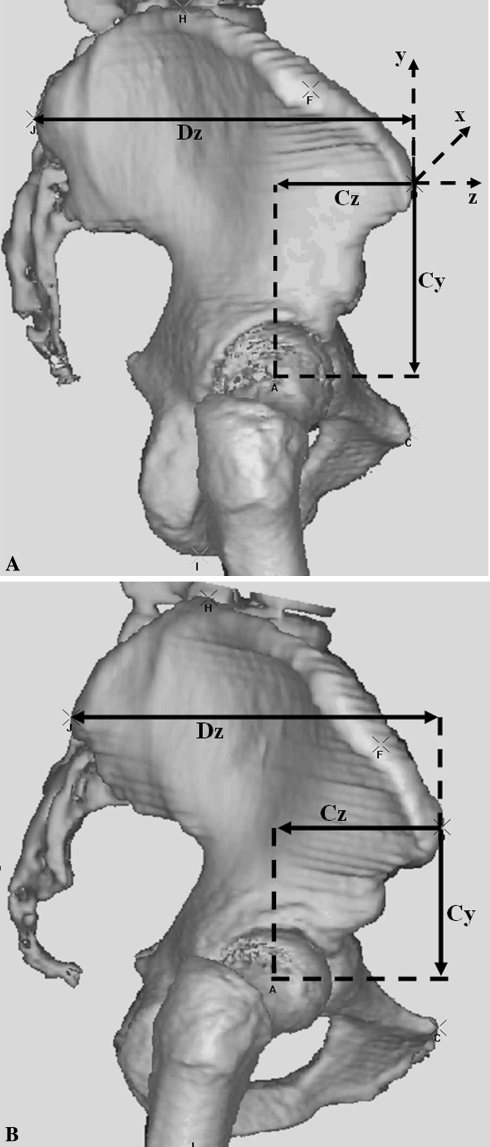
Fig. 2A–B.

Fig. 2A–B

Open in a new tab

Lateral 3-D views show the z-coordinate of the hip center (Cz) related to the AP dimension of the pelvis (Dz) for the right hip in (A) a male and (B) a female pelvis.

After aligning the pelvis with the anterior pelvic plane, we defined the pelvic horizontal dimension (Dx) as the distance between the most lateral points on the iliac crests, and its vertical dimension (Dy) was the distance between the highest point on the iliac wing and the lowest point on the ischial tuberosity. The pelvic depth (Dz) was defined as the horizontal distance between the posterior-superior iliac spine and the ipsilateral ASIS (Figs. 1, 2).

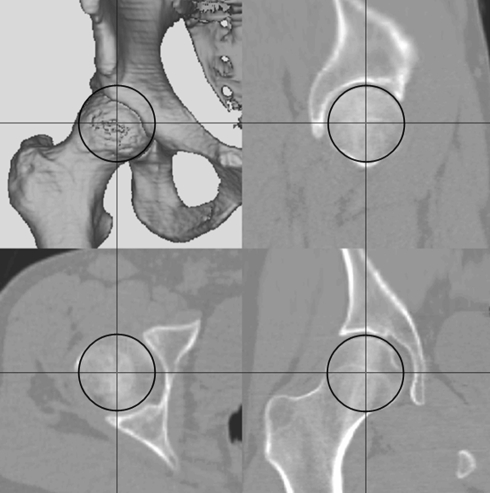
We determined the hip center by using the three orthogonal slices from the CT scan (Fig. 3). Its x-, y-, and z-coordinates were measured in relation to the reference coordinate system described previously. We measured the ratios of these coordinates to their corresponding pelvic dimensions (Cx/Dx, Cy/Dy, Cz/Dz) and expressed them as percentages.

Fig. 3.

Fig. 3

Open in a new tab

The hip center is determined by using the coronal, sagittal, and axial views from the CT scan reconstruction.

In addition to the main investigator (WD), another investigator (AN) independently repeated the landmark acquisition and the measurements for all the scans to test the reliability of the method of determining the ratios. We assessed differences between the two observers using the intraclass correlation coefficients and plotting the Bland-Altman plots [4] for the individual ratios.

Confirmation of accuracy of the method was accomplished by digitizing the relevant landmarks on a rigidly clamped model pelvis using a Faro Titanium Arm (Faro Technologies, Lake Mary, FL). The hip center coordinates and the pelvic dimensions then were compared with those obtained from a CT scan of the model pelvis using the method described above.

To check for gender differences in Cx/Dx, Cy/Dy and Cz/Dz, we grouped the results according to gender. The investigators doing the measurements (WD, AN) had been blinded to the gender of the scans analyzed. Because the tests of normality showed normally distributed results for both genders, and because the variances for the two groups were different, we used the Student’s t-test assuming unequal variances to check for any differences between the genders.

Results

The CT method appeared valid: its accuracy and precision were good. The accuracy on the model pelvis was comparable to that obtained using the Faro digitizing arm, with the differences being within 1 mm. The precision, as tested by differences between measurements made by different observers (interobserver agreement), also was good (see below).

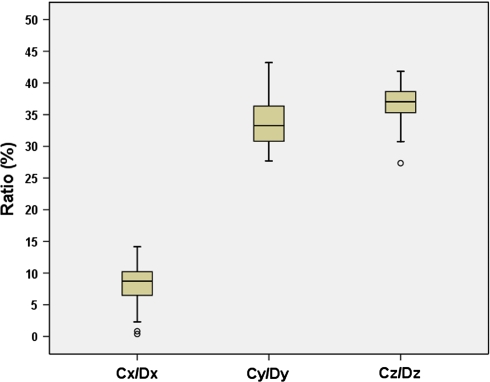
The normal 3-D position of the acetabulum could be derived from simple radiographically measured pelvic dimensions. We found the x-, y- and z-coordinates of the hip center (Cx, Cy, Cz) are related to their corresponding pelvic dimensions (Dx, Dy, Dz). If the pelvic dimensions are known, then the ratios Cx/Dx, Cy/Dy, and Cz/Dz can be used to derive the normal Cx, Cy and Cz. The mean Cx/Dx was 8.8%, the mean Cy/Dy was 33.8%, and the mean Cz/Dz was 37.3%. The distributions of these ratios were narrow and the confidence intervals were small (Table 1; Fig. 4).

Table 1.

Descriptive statistics for ratios of hip center coordinates and pelvic dimensions

Statistic Ratio (%)
Cx/Dx Cy/Dy Cz/Dz
Mean 8.8 33.8 37.3
SD 3.4 3.7 3.3
Minimum 0.4 27.7 27.4
Maximum 14.2 43.2 45.4
Range 13.8 15.5 18.0
95% CI ± 1.1 ± 1.4 ± 1.1
Open in a new tab

Cx, Cy, Cz = x-, y- and z-coordinates of the hip center; Dx, Dy, Dz = x-, y- and z-dimensions of the pelvis; SD = standard deviation; CI = confidence interval.

Fig. 4.

Fig. 4

Open in a new tab

The chart shows the distributions of the ratios Cx/Dx, Cy/Dy, and Cz/Dz.

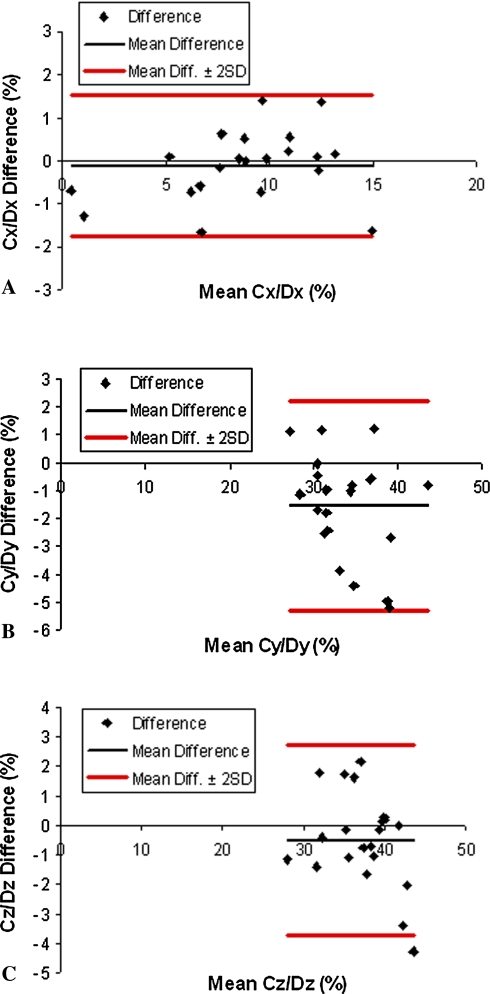
The method by which the ratios were obtained was reliable. This was evident by the high intraclass correlation coefficients (0.98 for Cx/Dx, 0.94 for Cy/Dy and 0.96 for Cz/Dz) and the Bland-Altman plots (Table 2; Fig. 5). The mean differences between the observers’ results were 0.1% (SD = 0.8) for Cx/Dx, 1.5% (SD = 1.9) for Cy/Dy, and 0.5% (SD = 1.6) for Cz/Dz.

Table 2.

Reliability results showing intraclass correlation coefficients for Cx/Dx, Cy/Dy and Cz/Dz

Ratio Intraclass correlation coefficient
Cx/Dx 0.98
Cy/Dy 0.94
Cz/Dz 0.96
Open in a new tab

Cx,Cy,Cz = x-, y- and z-coordinates of the hip center; Dx,Dy,Dz = x-, y- and z-dimensions of the pelvis.

Fig. 5A–C.

Fig. 5A–C

Open in a new tab

Bland-Altman plots for (A) Cx/Dx, (B) Cy/Dy, and (C) Cz/Dz show the interobserver difference in the measurements as a function of the mean. Results within ± 2 standard deviations (SDs) suggest a reproducible method [4].

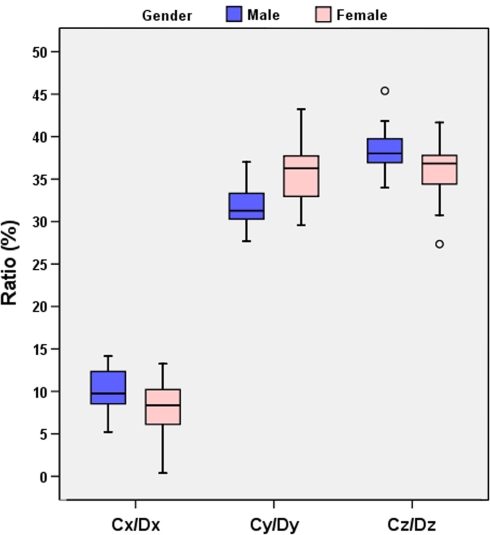
We observed gender differences in the relationship between the acetabular position and the pelvic dimensions for all three ratios Cx/Dx, Cy/Dy, and Cz/Dz (Fig. 6). Cx/Dx was greater (p = 0.04) in males (9.9% versus 7.7%), Cy/Dy was greater (p = 0.002) in females (35.5% versus 31.7%), and Cz/Dz was greater (p = 0.03) in males (38.5% versus 36.1%).

Fig. 6.

Fig. 6

Open in a new tab

The chart shows the gender differences in the ratios Cx/Dx, Cy/Dy, and Cz/Dz.

Discussion

The position of the hip center is crucial for optimal functioning of the hip musculature [2, 10–12], for reducing joint contact forces [18], and for avoiding accelerated wear, impingement, and loosening [9, 22, 28]. Its accurate determination is a major variable over which the surgeon has some control in reconstructive surgery around the hip. We therefore asked three questions: (1) Can the normal position of the acetabulum be derived from simple radiographically measured pelvic dimensions?; (2) Will the method relating the acetabular position to these pelvic dimensions be reliable?; and (3) Will there be gender differences in the relationship between the acetabular position and the pelvic dimensions?

The major limitation of this study was size: we had only 37 hips. This sample was the basis for answering our primary research question. Ideally, a larger sample of normal hips would allow more detailed analysis. Subgroups that are age- and gender-matched then could be compared with greater statistical power. We had hips from only 19 females and 18 males to answer a secondary question regarding gender differences. For an α of 0.05, the power β was 0.50. The error in the measurement software used depended on the scans’ resolution and the presence of artifacts. The scans were 1 mm thick, with an average of 250 slices per scan. Nevertheless, the computer software was confirmed previously on dry bones using similar scanning protocols [7, 16]. We used an indirect measure, namely interobserver agreement, to test the reliability of the method used for measuring the hip center’s coordinates and pelvic dimensions. The data showed good interobserver reliability. This can be seen by the high intraclass correlation coefficients for all the ratios. The Bland-Altman plots suggest almost 100% of the results were within ± 2 standard deviations (Fig. 5). The mean differences between the two observers’ measurements of Cx/Dx, Cy/Dy, and Cz/Dz were small: the mean differences were 0.1% (SD = 0.8) for Cx/Dx, 1.5% (SD = 1.9) for Cy/Dy, and 0.5% (SD = 1.6) for Cz/Dz. Another limitation of the study relates to the CT scans analyzed. The hips contralateral to the studied hips had either early hip disease or operatively fixed acetabular fractures. However, the studied hips and the parts of the pelvis used for measuring their dimensions were normal.

We found a fairly constant relationship among the x- (horizontal), y- (vertical), and z- (AP) coordinates of the hip center and their corresponding pelvic dimensions. The ratios of these parameters give gender-specific values, which provide a way of deriving the normal 3-D position of a patient’s hip center from that individual patient’s pelvic dimensions. The ratios have potential applications for the practicing surgeon. They provide a simple way of deriving the 3-D position of the hip center from the patient’s pelvic anatomy. The surgeon can use standardized plain radiographs, or CT in complex cases, to measure the horizontal (Dx), vertical (Dy), and AP (Dz) dimensions (Figs. 1, 2) of the pelvis. These dimensions, together with the normal ratios reported in this study, then can be used to derive and plan the optimal horizontal (Cx), vertical (Cy), and AP (Cz) position of the hip center in relation to the ASIS. With computer-assisted navigation, the derived values also can be achieved intraoperatively. It also is possible to investigate a malfunctioning hip replacement by exposing and possibly blaming and addressing subtle malpositioning. This may be particularly useful when there are extensive osteophytes or in cases involving complex revision surgery, dysplasia, or protrusio.

There are two main studies in the literature relating the x-, y-, and z-coordinates of the hip center to pelvic dimensions [3, 26]. Both studies involved manual measurements on cadaveric pelves with one relating the three coordinates to pelvic width only [3] and the other also relating them to their three corresponding pelvic dimensions [26]. It is difficult to make direct comparisons between our results and the results obtained in those studies because pelvic dimensions were defined differently (Fig. 7; Table 3). However, the data for the hip center coordinates alone suggest reasonable agreement (Table 4). Differences in the pelvic dimensions then can explain the differences in the ratios or scaled offsets. The difference in the x-coordinate (Cx) may be related to the way the hip center was identified. In the two published studies [3, 26], this was accomplished by manually estimating the center of the bony acetabular rim as opposed to 3-D CT measurement used in our study. Using the acetabular rim center as the hip center makes the assumption that the acetabulum is a hemisphere with a smooth rim.

Fig. 7A–B.

Fig. 7A–B

Open in a new tab

(A) Anteroposterior and (B) lateral 3-D views of the pelvis show the difference in the definition of the horizontal, vertical, and AP dimensions of the pelvis, as defined by Seidel et al. [26] (white arrows) and by us (black arrows).

Table 3.

Literature comparison of definitions of pelvic dimensions

Study Pelvic width Pelvic height Pelvic depth
Seidel et al. [26] Horizontal distance between ASISs Perpendicular distance from pubic center to inter-ASIS line Oblique distance between ASIS and PSIS
Current study Horizontal distance between lateral edges of iliac wings Vertical distance between top of iliac wing and bottom of ischial tuberosity Direct horizontal distance between ASIS and PSIS
Open in a new tab

ASIS = anterior-superior iliac spine; PSIS = posterior-superior iliac spine.

Table 4.

Literature comparison of means of the hip center coordinates, pelvic dimensions, and their ratios

Study Hip center coordinate (mm) Pelvic dimension (mm) Ratio (%)
Cx Cy Cz Dx Dy Dz Cx/Dx Cy/Dy Cz/Dz
Seidel et al. [26] 34 71 57 238 90 164 14 79 34
Current study 24 72 55 275 214 147 9 34 37
Open in a new tab

The gender differences we observed in the ratios Cx/Dx, Cy/Dy, and Cz/Dz are in distinct contrast to the published studies [3, 26]. However, as has been discussed, we used the entire height and width of the pelvis, including the iliac blades and ischial tuberosities. This larger scale may have exposed the proportional differences between the genders.

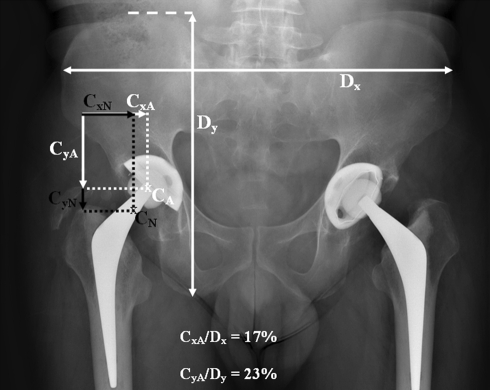
One immediate application of our study relates to revision hip arthroplasty. An acetabular component that has been inserted high or migrated to a high position poses a particular problem for the surgeon. Currently no method exists to help the surgeon predict the correct height for the hip center nor establish whether it has been achieved. The additional help of a position in the x- and z-axes allows the revision to be planned with greater confidence. If height (y) and medial-lateral position (x) are considered important, then sufficient information for most cases will be available from a plain radiograph. An example is a male patient whose right hip replacement has an actual center (CA) which is superior and medialized (Fig. 8). The actual Cx/Dx is high (17%) and the actual Cy/Dy is low (23%) compared with that of a normal male Cx/Dx (9.9%) and Cy/Dy (31.7%). If this patient’s pelvic width is 260 mm and his pelvic height is 220 mm, then the normal position of his hip center (CN) can be planned using the normal male Cx/Dx and Cy/Dy as follows: the hip center’s normal x-position (CxN) is 26 mm ([260*9.9]/100), and its normal y-position (CyN) is 70 mm ([220*31.7]/100) from the ASIS. We believe displacement of the hip center in the AP axis (z) may contribute to poor stability or function. Faced with a difficult revision, using this method to establish a normal hip center may be helpful to the surgeon.

Fig. 8.

Fig. 8

Open in a new tab

An AP radiograph of the pelvis of a male patient shows a hip replacement with a superior and medialized hip center (CA). The positions of the actual (CA) and normal (CN) hip centers are shown. The actual CxA/Dx is high and the CyA/Dy is low compared with the normal male Cx/Dx (9.9%) and Cy/Dy (31.7%). The latter were used to derive the normal position of the hip center (CxN, CyN). Cx,Cy,Cz = x-, y- and z-coordinates of the hip center; Dx,Dy,Dz = x-, y- and z-dimensions of the pelvis.

Acknowledgments

We thank Robin Richards, PhD, for support with the software.

Footnotes

Each author certifies that he has no commercial associations (eg, consultancies, stock ownership, equity interest, patent/licensing arrangements, etc) that might pose a conflict of interest in connection with the submitted article.

Each author certifies that his institution has approved or waived approval for the human protocol for this investigation and that all investigations were conducted in conformity with ethical principles of research.

References

  • 1.Andriacchi TP, Andersson GB, Fermier RW, Stern D, Galante JO. A study of lower-limb mechanics during stair-climbing. J Bone Joint Surg Am. 1980;62:749–757. [PubMed]
  • 2.Asayama I, Chamnongkich S, Simpson KJ, Kinsey TL, Mahoney OM. Reconstructed hip joint position and abductor muscle strength after total hip arthroplasty. J Arthroplasty. 2005;20:414–420. [DOI] [PubMed]
  • 3.Bell AL, Pedersen DR, Brand RA. A comparison of the accuracy of several hip center location prediction methods. J Biomech. 1990;23:617–621. [DOI] [PubMed]
  • 4.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. [PubMed]
  • 5.Boudriot U, Hilgert J, Hinrichs F. Determination of the rotational center of the hip. Arch Orthop Trauma Surg. 2006;126:417–420. [DOI] [PubMed]
  • 6.Cappozzo A. Gait analysis methodology. Hum Mov Sci. 1984;3:27–50. [DOI]
  • 7.Cobb J, Henckel J, Gomes P, Harris S, Jakopec M, Rodriguez F, Barrett A, Davies B. Hands-on robotic unicompartmental knee replacement: a prospective, randomised controlled study of the acrobot system. J Bone Joint Surg Br. 2006;88:188–197. [DOI] [PubMed]
  • 8.Cunningham D. Pelvis. In: Cunningham D, ed. Cunningham’s Textbook of Anatomy. London, England: Hoddr & Stoughton; 1922:255–260.
  • 9.D’Lima DD, Chen PC, Colwell CW Jr. Optimizing acetabular component position to minimize impingement and reduce contact stress. J Bone Joint Surg Am. 2001;83(suppl 2 pt 2):87–91. [DOI] [PubMed]
  • 10.Delp SL, Komattu AV, Wixson RL. Superior displacement of the hip in total joint replacement: effects of prosthetic neck length, neck-stem angle, and anteversion angle on the moment-generating capacity of the muscles. J Orthop Res. 1994;12:860–870. [DOI] [PubMed]
  • 11.Delp SL, Maloney W. Effects of hip center location on the moment-generating capacity of the muscles. J Biomech. 1993;26:485–499. [DOI] [PubMed]
  • 12.Delp SL, Wixson RL, Komattu AV, Kocmond JH. How superior placement of the joint center in hip arthroplasty affects the abductor muscles. Clin Orthop Relat Res. 1996;328:137–146. [DOI] [PubMed]
  • 13.Fessy MH, N’Diaye A, Carret JP, Fischer LP. Locating the center of rotation of the hip. Surg Radiol Anat. 1999;21:247–250. [DOI] [PubMed]
  • 14.Fieser L, Quigley E, Wyatt M, Sutherland D, Chambers H. Comparison of hip joint centers determined from surface anatomy and CT scans: two case studies. Gait Posture. 2000;11:119–120.
  • 15.Genda E, Iwasaki N, Li G, MacWilliams BA, Barrance PJ, Chao EY. Normal hip joint contact pressure distribution in single-leg standing: effect of gender and anatomic parameters. J Biomech. 2001;34:895–905. [DOI] [PubMed]
  • 16.Jakopec M, Harris SJ, Rodriguez y Baena F, Gomes P, Cobb J, Davies BL. The first clinical application of a “hands-on” robotic knee surgery system. Comput Aided Surg. 2001;6:329–339. [DOI] [PubMed]
  • 17.Jaramaz B, DiGioia AM 3rd, Blackwell M, Nikou C. Computer assisted measurement of cup placement in total hip replacement. Clin Orthop Relat Res. 1998;354:70–81. [DOI] [PubMed]
  • 18.Johnston RC, Brand RA, Crowninshield RD. Reconstruction of the hip: a mathematical approach to determine optimum geometric relationships. J Bone Joint Surg Am. 1979;61:639–652. [PubMed]
  • 19.Kersnic B, Iglic A, Kralj-Iglic V, Srakar F, Antolic V. Increased incidence of arthrosis in women could be related to femoral and pelvic shape. Arch Orthop Trauma Surg. 1997;116:345–347. [DOI] [PubMed]
  • 20.Kirkwood RN, Culham EG, Costigan P. Radiographic and non-invasive determination of the hip joint center location: effect on hip joint moments. Clin Biomech (Bristol, Avon). 1999;14:227–235. [DOI] [PubMed]
  • 21.Leardini A, Cappozzo A, Catani F, Toksvig-Larsen S, Petitto A, Sforza V, Cassanelli G, Giannini S. Validation of a functional method for the estimation of hip joint centre location. J Biomech. 1999;32:99–103. [DOI] [PubMed]
  • 22.Malik A, Maheshwari A, Dorr LD. Impingement with total hip replacement. J Bone Joint Surg Am. 2007;89:1832–1842. [DOI] [PubMed]
  • 23.Maruyama M, Feinberg JR, Capello WN, D’Antonio JA. The Frank Stinchfield Award: Morphologic features of the acetabulum and femur: anteversion angle and implant positioning. Clin Orthop Relat Res. 2001;393:52–65. [DOI] [PubMed]
  • 24.Piazza SJ, Erdemir A, Okita N, Cavanagh PR. Assessment of the functional method of hip joint center location subject to reduced range of hip motion. J Biomech. 2004;37:349–356. [DOI] [PubMed]
  • 25.Pierchon F, Migaud H, Duquennoy A, Fontaine C. [Radiologic evaluation of the rotation center of the hip][in French]. Rev Chir Orthop Reparatrice Appar Mot. 1993;79:281–284. [PubMed]
  • 26.Seidel GK, Marchinda DM, Dijkers M, Soutas-Little RW. Hip joint center location from palpable bony landmarks: a cadaver study. J Biomech. 1995;28:995–998. [DOI] [PubMed]
  • 27.Shea KM, Lenhoff MW, Otis JC, Backus SI. Validation of a method for location of the hip joint center. Gait Posture. 1997;5:157–158. [DOI]
  • 28.Yoder SA, Brand RA, Pedersen DR, O’Gorman TW. Total hip acetabular component position affects component loosening rates. Clin Orthop Relat Res. 1988;228:79–87. [PubMed]

Articles from Clinical Orthopaedics and Related Research are provided here courtesy of The Association of Bone and Joint Surgeons

RESOURCES