Inherent flexibility determines the transition mechanisms of the EF-hands of calmodulin

Abstract

We explore how inherent flexibility of a protein molecule influences the mechanism controlling allosteric transitions by using a variational model inspired from work in protein folding. The striking differences in the predicted transition mechanism for the opening of the two domains of calmodulin (CaM) emphasize that inherent flexibility is key to understanding the complex conformational changes that occur in proteins. In particular, the C-terminal domain of CaM (cCaM), which is inherently less flexible than its N-terminal domain (nCaM), reveals “cracking” or local partial unfolding during the open/closed transition. This result is in harmony with the picture that cracking relieves local stresses caused by conformational deformations of a sufficiently rigid protein. We also compare the conformational transition in a recently studied even–odd paired fragment of CaM. Our results rationalize the different relative binding affinities of the EF-hands in the engineered fragment compared with the intact odd–even paired EF-hands (nCaM and cCaM) in terms of changes in flexibility along the transition route. Aside from elucidating general theoretical ideas about the cracking mechanism, these studies also emphasize how the remarkable intrinsic plasticity of CaM underlies conformational dynamics essential for its diverse functions.

To understand protein function, it is often essential to characterize large conformational changes that occur upon ligand binding. Within the population shift mechanism of allosteric conformational change (1), the bound complex is formed when a ligand selects and stabilizes a weakly populated conformational ensemble from the kinetically accessible states of the unbound folded protein. Such conformational dynamics imply an inherent flexibility or “intrinsic plasticity” of the folded state. In this article, we focus on how this inherent flexibility of a protein molecule influences the mechanism controlling the kinetics of allosteric transitions. There are a couple of possible scenarios for the transition mechanism in terms of changes in conformational flexibility. One possibility is that the flexibility adjusts smoothly to conformational deformations connecting two specific metastable states in the free-energy surface. In this case, the inherent flexibility of the protein remains relatively constant if the metastable states have similar flexibilities or else changes smoothly between the flexibilities of the metastable states if the flexibilities are different. An alternative mechanism, called “cracking” (2), has recently been proposed. In terms of conformational flexibility, cracking involves nonmonotonic changes in flexibility along the transitions route. In particular, the flexibility of specific regions of the protein may transiently increase through local unfolding. As explained in ref. 2, local unfolding can relieve specific areas of high stress during conformational deformations that would result in high free-energy barriers if the protein remained uniformly folded throughout the transition.

In the model developed to explore this idea, cracking is introduced directly into the formalism as means to incorporate nonlinear elasticity in an otherwise harmonic description of conformational fluctuations (2, 3). This work clearly shows that local unfolding can dramatically lower predicted free-energy barriers between local free-energy minima and hence facilitates faster kinetics. In contrast, the variational model developed in the present work does not assume cracking from the outset. The evidence of cracking here arises entirely from the analysis of the local changes in flexibility along transition routes predicted by an inherently nonlinear model of conformational transitions. Our results are thus an independent verification of the ideas and formalism developed in the model presented in refs. 2 and 3.

Cracking does not occur in all conformational transitions, but even when it does, the average conformations of the local minima in the free energy may show little signs that local unfolding is involved (2). Instead, cracking is a subtle consequence of the nature of the conformational deformation required to connect the two states. Because cracking is akin to folding of the whole protein, albeit on a constrained and local scale, it is reasonable to ask whether insight appropriated from the energy landscape theory of protein folding (4) can help to anticipate when cracking is likely to be important in conformational transitions between two distinct folded conformations.

One motivation for the work in this article is to investigate whether the cracking mechanism of conformational transitions, like the mechanism for folding of two-state proteins (5), is determined by the structural topology of the two metastable states. To address this question, we study the conformational transitions of the open and closed conformations of the two homologous domains of calmodulin (CaM) and a fragment of CaM involving parts of both domains. Aside from general theoretical implications, the results presented in this article are interesting from the point of view of understanding the well-known and intensely studied thermodynamic differences between the two domains of CaM (6, 7).

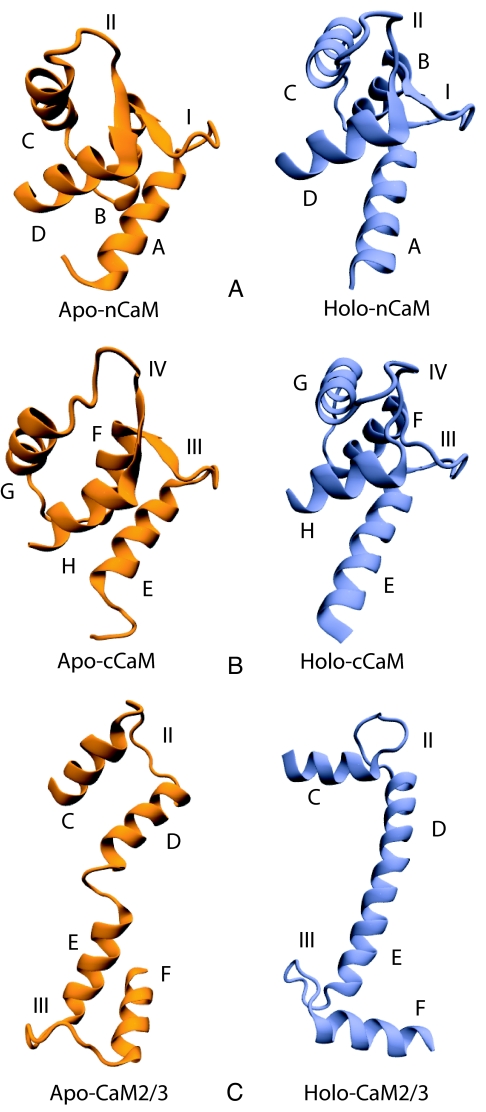
Our approach is based on a coarse-grained variational model developed to characterize protein folding (8). This model is in harmony with several recent coarse-grained simulations based on a folded-state biased interaction potential that interpolates between the contact maps of the metastable states (9–15). Interestingly, some of these recently proposed coarse-grained models can also capture the cracking or local partial unfolding during transition (10, 12, 15). In this article we compare the detailed predicted transition routes for the open/closed conformational change of the C-terminal domain of CaM (cCaM) with that of the N-terminal domain of CaM (nCaM). The open and closed state of each domain is shown in Fig. 1 A and B. Each domain of CaM contains a pair of helix–loop–helix Ca²⁺-binding motifs called EF-hands. In nCaM, EF-hands 1 and 2 consist of helices A/B and C/D (Fig. 1A), respectively, whereas helices E/F and G/H in cCaM (Fig. 1B) form EF-hands 3 and 4, respectively. Hence, the nCaM and cCaM are known as “odd–even” paired EF-hands because of their odd–even sequential numbering of EF-hands.

Fig. 1.

Three-dimensional structures of CaM domains and EF-hands 2 and 3 fragment. The apo-CaM and holo-CaM structures shown here are correspond to human CaM with PDB ID codes 1cfd and 1cll, respectively. (A) The closed, apo and open, holo conformations of nCaM consist of helices A/B and C/D with binding loops I and II, respectively. (B) The closed, apo and open, holo conformations of cCaM consist of helices E/F and G/H with binding loops III and IV, respectively. (C) The apo and holo conformations of CaM2/3 consist of helices C/D and E/F with binding loops II and III, respectively. These three-dimensional illustrations were made by using Visual Molecular Dynamics (VMD) (16).

Although nCaM and cCaM have similar structures, the calculated transition routes predict that the cracking is essential only in cCaM. It is well established that the two domains differ in flexibility and binding affinity for Ca²⁺ (6, 7). These properties are not determined by topology (because they are the same) but ultimately by more subtle structural differences encoded in the sequence of the two domains. Our results suggest that nCaM is flexible enough that cracking is not necessary to relieve stress during the conformational change, whereas the cCaM is relatively rigid so that cracking is involved in essentially the same conformational change. This is the central result of our article.

As an additional illustration of modeling conformation transitions in CaM, we investigate the conflicting Ca²⁺-binding mechanism in the odd–even paired EF-hands (nCaM and cCaM) and “even–odd” paired EF-hands (CaM2/3) of CaM. The fragment CaM2/3 contains EF-hands 2 and 3 with helices C/D and E/F (Fig. 1C), respectively. CaM2/3 is known as even–odd paired EF-hands because of its even–odd sequential numbering of EF-hands. In CaM2/3, an EF-hand from each domain is connected by a flexible helical linker. The extended helical linker separating the two domains shown in the X-ray structure of holo-CaM is known to be flexible in solution (17, 18), making holo-CaM structurally more flexible overall than apo-CaM (19, 20).

In contrast to cCaM and nCaM (20), CaM2/3 has a molten globule-like character in the absence of Ca²⁺ and folds into a structure similar to an intact domain of CaM in the presence of Ca²⁺ (21). Accordingly, a realistic model of Ca²⁺ binding to CaM2/3 would have to treat the ion binding and folding on equal footing as was done for folding azurin in the presence of zinc ions in ref. 22. At the risk overly simplifying the binding mechanism of CaM2/3, we keep the focus of this article on conformational transition routes between two specified conformations instead of binding-induced folding. In particular, we take the two states of CaM2/3 from the X-ray structure of intact CaM as shown Fig. 1C. Although this is a convenient way to define the conformation endpoint structures (and has a certain consistency with our studies of cCaM and nCaM), both the apo-CaM2/3 and the holo-CaM2/3 structures are expected to be low-probability conformations of CaM2/3 in solution: the apo-CaM structure assumed here is unstable to a molten globule state, and the holo-CaM structure inferred from the X-ray structure of CaM is unstable to a structurally compact domain like holo-cCaM or holo-nCaM (21).

Our study of the transition between the conformations of CaM2/3 defined by the structures of the intact CaM suggests that the highly flexible central linker region would locally unfold before gaining helical structure. Even though this model of the binding dynamics of CaM2/3 is based on low-probability conformations in solution (17, 18), our predicted transition route can rationalize the sequential Ca²⁺ binding in CaM2/3 (21) in terms of the differences in conformational flexibility of Ca²⁺-binding loops in CaM2/3. Finally, we address how our comparative study of conformational transitions in odd–even and even–odd paired EF-hands reveals the interplay between intrinsic plasticity, target binding affinity, and function of CaM.

Results

Conformational Flexibility of the CaM Domains.

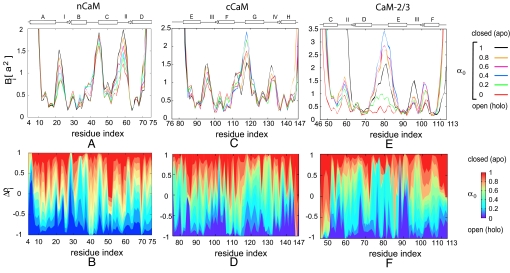
We first compare the inherent flexibility of the two domains of CaM by calculating the mean square fluctuations B_i for each residue in the nCaM and cCaM for the open/closed conformational transitions of each domain. The B_i (related to the temperature factors from X-ray crystallography) contains information about the degree of structural order and conformational flexibility of each residue. Fig. 2A shows B_i along the open/closed conformational transition for each residue of nCaM (23). The magnitude of the fluctuations for each residue of cCaM for the open/closed transition route is shown in Fig. 2C. Comparison of Fig. 2 A and C shows that although the binding loops and helix linker in both domains are very flexible, the apo (closed)-nCaM is inherently more flexible than apo (closed)-cCaM. For nCaM, the flexibility of the binding loops I and II and the B/C helix linker between EF-hands 1 and 2 decreases upon domain opening. Similarly, the flexibility of the Ca²⁺-binding loops III and IV decreases considerably during the opening of cCaM. The fluctuations of the F/G helix linker between EF-hands 3 and 4 has different behavior along the transition route. The flexibility of this region of the protein increases to a relatively high flexibility before reducing to the flexibility of the folded open conformation. (Fig. 2C). We also note that the F/G helix linker in the open structure is more flexible than in the closed structure. The calculated conformational flexibility suggests that unlike the B/C helix linker in the apo (closed)-nCaM the F/G helix linker in the apo (closed)-cCaM is relatively less flexible. In contrast to the B/C helix linker of nCaM, the increase and then decrease in flexibility of the F/G helix linker during the domain opening of cCaM indicates cracking or local partial unfolding in this less flexible F/G helix linker (See the change in fluctuations of the F/G helix linker during domain opening in Fig. 2C.) The model also predicts that binding loop II in nCaM has the highest flexibility compared with other binding loops. This result agrees with a recent molecular dynamics simulation study of CaM D129N mutant, where the binding loop II consistently exhibited higher mobility than the other three Ca²⁺-binding loops (24).

Fig. 2.

Structural characterization of transition routes. (A, C, E) The fluctuations B_i vs. residue index for selected values of the interpolation parameter α₀ of nCaM, cCam, and CaM2/3, respectively. Here, a = 3.8 Å is the distance between successive monomers in our model. The secondary structures for nCaM, cCaM, and CaM2/3 are indicated above each plot. Helices are represented by the rectangular boxes, binding loops and helix linker are indicated by lines, and small β-sheets are shown by arrows. (B, D, and F) Difference between the normalized native density Δρ_i (a measure of structural similarity) vs. residue index for different α₀ of nCaM, cCaM, and CaM2/3, respectively. In each plot the change in color from red to blue indicates the progress along the transitin from the apo to holo conformations. This is normalized to be −1 at the holo state minimum(α₀ = 0; blue) and 1 at the apo state minimum (α₀ = 1; red). (Parts A and B reproduced with permission from S Tripathi and JJ Portman, Journal of Chemical Physics, Vol. 128, page 205104, 2008. Copyright 2008, American Institute of Physics.)

Cracking in the Conformational Transition of cCaM.

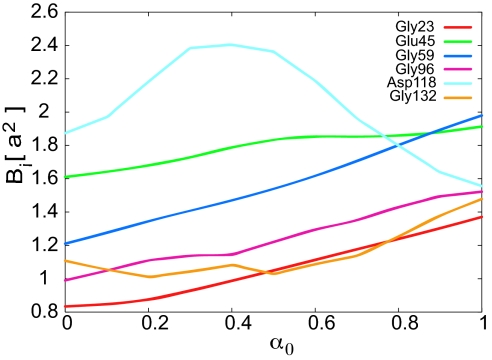
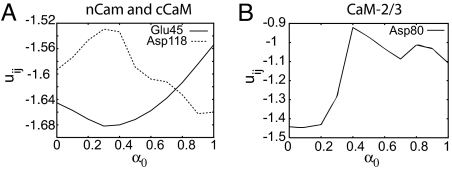
To compare the conformational flexibility of the two CaM domains in more detail we have plotted the change in fluctuations B_i for some specific residues in Fig. 3. Residue Asp-118 of the F/G helix linker from cCaM shows very different behavior relative to the rest of the residues in Fig. 3. Residue Asp-118 shows the highest B_i near the transition state at α₀ = 0.4, whereas B_i of the other residues shown decrease monotonically during closed to open transition. The increase in flexibility of the helix linker region in cCaM near the transition state is caused by local transient unfolding or cracking. For further analysis of cracking in the cCaM we also compare the contact pair potential energy u_ij for residues Glu-45 and Asp-118 from the helix linker of nCaM and cCaM, respectively. Fig. 4A shows that for residue Asp-118, u_ij increases in the transition state region, whereas u_ij for residue Glu-45 from the helix linker of nCaM decreases in the transition state region. This striking difference in u_ij implies that the increase in contact energy of the F/G helix linker during opening of cCaM leads to some transient cracking in this region near the transition state, enhancing the inherent flexibility of this linker during the open/closed conformational change.

Fig. 3.

Change in fluctuations B_i of the residues from binding loops and helix linker of CaM domains along the open/closed conformational transition route for different α₀. Here, a = 3.8 Å is the distance between successive monomers in our model. Residues Gly-23, Gly-59, and Glu-45 are from binding loop I, loop II, and the helix linker of the nCaM, respectively. Residues Gly-96, Gly-132, and Asp-118 are from binding loop III, loop IV, and the helix linker of the cCaM, respectively.

Fig. 4.

Average pair potentials u_ij (in kilocalories per mole) of selected residues along the open/closed conformational transition route for different α₀. (A) Residues Glu-45 and Asp-118 are from the nCaM and cCaM, respectively. (B) Residue Asp-80 is from the central linker of CaM.

Open/Closed Transition Mechanism of the CaM Domains.

To elucidate further the predicted conformational transition mechanisms of domain opening in CaM, we consider a structural order parameter that measures the similarity to the open (holo) or closed (apo) state conformations, Δρ_i, described in Methods. This order parameter is defined such that Δρ_i = 1 corresponds to the closed conformation and Δρ_i = −1 corresponds to the open conformation of nCaM or cCaM. The transition routes illustrated by Δρ_i for each residue of nCaM and cCam are shown in Fig. 2 B and D, respectively. As shown in Fig. 2D, the model predicts that the structural change in binding loop IV occurs earlier than binding loop III during the domain opening of cCaM. (See the sharp change in color near residue number 130 in Fig. 2D.) Also, helix G has an earlier conformational transition than helix F (Fig. 2D). This sequence is quite different from nCaM as shown in Fig. 2B. For nCaM, the structural change in helix B is predicted to be earlier than the structural change in helix C for the closed to open conformational transition. Finally, our results show that the F/G helix linker in the cCaM has abrupt transition near the open state. (See the transition near residue number 115 in Fig. 2D). In contrast, the transition in the B/C helix linker in nCaM is more gradual (see Fig. 2B).

Conformational Flexibility and Cracking of the CaM2/3 Fragment.

The engineered even–odd EF-hands paired CaM2/3 fragment (composed of EF-hands 2 and 3) has been shown recently to have distinct transition characteristics from the odd–even EF-hands paired nCaM and cCaM (21). NMR spectroscopy has shown that Ca²⁺-free (apo) CaM2/3 does not have a stable folded structure but rather shows characteristics of a molten globule state. Ca²⁺ binding induces the folding of this even–odd paired EF-hand motifs CaM2/3, and the Ca²⁺-bound (holo) CaM2/3 adopts a similar structure as holo-nCaM or cCaM [see Protein Data Bank (PDB) ID code 2hf5] (21). In this article, we study the transition between the two metastable conformations, apo-CaM2/3 and holo-CaM2/3 taken directly from the folded apo-CaM (PDB ID code 1cfd) and holo-CaM (PDB ID code 1cll) as another example of flexibility influenced transitions in CaM. Here, we focus primarily on the conformational flexibility and transition of the central linker to an α-helix (even though this conformation has low probability in solution). The central linker of CaM was also studied by molecular dynamics (MD) simulation (18). Although our model does not accommodate the calcium-induced folding of CaM2/3 described in ref. 21, the model does capture certain aspects of the apo/holo conformational transition of this CaM2/3 fragment. In particular, the model predicts the apo-CaM2/3 to holo-CaM2/3 conformational transition mechanism that agrees well with the sequential Ca²⁺-binding mechanism of CaM2/3 suggested by the NMR measurements.

The magnitude of the fluctuations of each residue in CaM2/3 (shown in Fig. 2E) suggests that the changes in conformational flexibility of binding loops II and III of CaM2/3 are very different. In particular, helix C and binding loop II are highly flexible in the apo conformation of CaM2/3. The high intrinsic flexibility of apo-CaM2/3 may account for the molten globule state characteristics described in ref. 21. Fig. 2E also shows that binding loop II is more flexible than loop III. This result is in harmony with the NMR measurements of Ca²⁺ binding in CaM2/3 (21) that show that Ca²⁺ binds to loop III with higher affinity (lower Ca²⁺ concentration) than loop II. Our results also indicate that the flexibility of binding loop III decreases monotonically along the transition route from the apo-CaM2/3 to the holo-CaM2/3 structure. In contrast, the flexibility of helix F increases along the transition route from apo to holo transition of CaM2/3 fragment. In particular, the N-terminal part (close to binding loop III of helix F) partially unfolds when adopting the holo-CaM2/3 conformation. We also notice in Fig. 2E that the domain linker between EF-hands 2 and 3 (residue numbers 74–81) during the apo to holo transition has a relatively large change in conformational flexibility. The fluctuation amplitude B_i of this linker increases in the intermediate states and then decreases abruptly as the helix forms near the holo state. The local unfolding of the domain linker enhances the flexibility of this linker region dramatically, first relaxing in structure and then stabilizing in the holo-CaM2/3 structure. This local unfolding signaled by increase and decrease in flexibility is similar to the cracking exhibited in cCaM.

Local intermediate unfolding (i.e., cracking) of the domain linker during the apo to holo transition of CaM2/3 can also be seen through a change in the pair potential energy u_ij for the Asp residue from the linker at position 80 along the transition route as shown in Fig. 4B. During the apo to holo transition of CaM2/3 the energy of residue Asp-80 increases from the apo-CaM2/3 structure (α₀ = 1) and decreases abruptly at the transition state (α₀ = 0.4) to the minimum at holo-CaM2/3 structure (α₀ = 0) as the helix forms. This increase and then sharp decrease in the contact energy of residue Asp-80 signal cracking (local unfolding and refolding) of the linker in CaM2/3 to a stable α-helix. We note also that the energy relative to the holo-CaM2/3 energy of Asp-80 is higher than that of Asp-118 from the F/G helix linker of cCaM. This emphasizes the importance of cracking in the apo-CaM2/3 to holo-CaM2/3 transition.

Conformational Transition Mechanism of CaM2/3 Fragment.

For CaM2/3, the order parameter Δρ_i = 1 corresponds to the apo state, and Δρ_i = −1 corresponds to the holo state of CaM2/3. Fig. 2F indicates that the structural change in binding loop III is initiated earlier than the structural change in binding loop II. Also, the conformational change in binding loop II is much more gradual than that of binding loop III. Similar to the identification of the Ca²⁺-binding affinity with the changes in inherent flexibility, the early structural change in binding loop III may imply the stepwise binding of Ca²⁺ in CaM2/3 with loop III having a higher binding affinity than loop II.

Discussion

CaM, a small (148-residue) Ca²⁺-binding protein with very high plasticity, may be an ideal system to demonstrate flexibility-influenced conformational transitions. The protein consists of structurally similar N- and C-terminal globular domains connected by a flexible tether also known as central or interdomain linker (17). The Ca²⁺-induced structural rearrangement in CaM results in the solvent exposure of a large hydrophobic surface responsible for molecular recognition of various cellular targets (25).

Although similar in structure and fold, the two CaM domains are quite different in terms of their flexibility, melting temperatures, and Ca²⁺-binding affinities (6, 7). In the two homologous (46% sequence identity) domains of CaM, Ca²⁺ binding occurs sequentially, first, in the binding sites of cCaM and then in the binding sites of nCaM (7). Despite large cooperativity in the Ca²⁺-binding process within each domain, the two domains reflect different Ca²⁺ and target affinities. The N-terminal pair of EF-hands binds to Ca²⁺ ions with much lower affinity than the C-terminal EF-hands pair (7). NMR (26, 27), and MD simulation (28) studies have shown that the Ca²⁺-bound nCaM is considerably less open than the cCaM. This was not observed in the X-ray crystal structure of the protein. Experimentally, it has been shown that the more-conserved cCaM has a greater affinity for Ca²⁺ and some CaM targets, whereas the nCaM is less specific in its choice of target motif (29, 30). Heat denaturation studies have shown that cCaM of Ca²⁺-free (apo) CaM starts to denature slightly above the physiological temperature (6). The denaturation of the apo-cCaM was observed at a lower concentration of denaturant than denaturation of the nCaM, whereas the order was reversed for Ca²⁺-CaM (31). From temperature-jump fluorescence spectroscopy by Rabl et al. (32), the instability of the cCaM was also observed from the study of unfolding of apo-CaM. They suggested that the cCaM was partially unfolded at native conditions. Recent NMR experiments done by Lundstrom and Akke (33) monitoring relaxation rates involving ¹³C^α spins in adjacent residues of E140Q mutant of cCaM revealed transient partial unfolding of helix F. This was interpreted as a global exchange process involves a partially unfolded minor state that was not detected (27, 34). A very recent conformational dynamics simulation of the cCaM by Chen et al. (35) has shown the presence of an unfolded apo state. These observations further suggest that the conformational exchange may be more complex than a simple two-state process.

Differences in inherent flexibility of the two domains can account for their distinct physical characteristics and the complexity in the conformational transition mechanism (26). Our results are consistent with a MD simulation study (36), which has shown that the nCaM is inherently more flexible with lower binding affinity than the cCaM. The more open conformation and lower intrinsic flexibility of the cCaM is also probably the key to understanding initial binding between this domain and CaM target enzymes (36, 37).

The variational model presented in this article predicts that the different inherent flexibilities of the two domains of CaM also lead to distinct transition mechanisms, even though the folded state topology of the two domains is the same. The mechanism controlling the open/closed transition does not involve cracking for the relatively flexible nCaM, whereas the mechanism controlling the conformation transition of the more rigid cCaM exhibits transient partial local unfolding in its helix linker between the binding loops. This partial local unfolding or cracking in the cCaM shows the complexity of the open/closed conformational transition mechanism of cCaM.

A recent NMR experiment studied the EF-hand association effects on the structure, Ca²⁺ affinity, and cooperativity of CaM (21). The EF-hands in CaM domains are odd–even paired with EF-hands 1 and 2 in nCaM and EF-hands 3 and 4 in cCaM. This arrangement of EF-hands in CaM is thought to be a consequence of its evolution from a biologically related ancestor EF-hand by gene duplication (38). The even–odd pairing of EF-hands 2 and 3 (CaM2/3) (Fig. 1C) has been characterized by NMR in ref. 21. In this fragment, EF-hands 2 and 3 are connected by the central linker between nCaM and cCaM. Although from the crystal structure of holo Ca²⁺-CaM the interdomain linker region appears to be a long rigid α-helix (39) several NMR relaxation experiments have demonstrated that this central linker is flexible in solution near its midpoint, and the two domains do not interact (17, 18). In contrast to the high-affinity and positive cooperativity for Ca²⁺ binding in the two odd–even paired EF-hand domains of CaM, the CaM2/3 binds Ca²⁺ in a sequence. First in the high-affinity EF-hand 3 and then in the EF-hand 2 with much lower affinity (21). Although not a direct focus of our article, we also note that a peptide binding to CaM2/3 has also been characterized recently by McIntosh and co-workers (40). It was found that CaM2/3 adopts Ca²⁺-bound structure with peptide binding very much similar to those of nCaM or cCaM. These observations reflect the very high plasticity of the EF-hand association and mediate Ca²⁺-dependent recognition of target proteins.

In this article we study the transition between the two states of the fragment CaM2/3 inferred by the structures of intact CaM. Our results reveal that the central linker in CaM2/3 is highly flexible and dominates the mechanism for this transition. The folding of the linker to an α-helix is preceded by a further increase in its flexibility and local unfolding. This cracking leads to a very sharp transition of the helix linker from apo-CaM2/3 to holo-CaM2/3 conformation. Although our model did not predict partial local unfolding or cracking of helix F from the open/closed conformational transition of cCaM, the apo/holo conformational transition of CaM2/3 reveals cracking in some region of helix F as we have discussed already in comparison with the NMR study (33). The predicted change in conformational flexibility of CaM2/3 reveals the stepwise binding of Ca²⁺ ions with binding loop III having higher affinity than binding loop II. Nevertheless, the relevance of this transition to the binding dynamics of CaM2/3 is somewhat limited because the model is based on low-probability structures in solution.

Methods

Preparation of Structures.

The structures of the two conformations of the transition are rotated to have the same center of mass and minimum root mean square deviation of the C^α positions. The conformational transition in cCaM is modeled from the residues 76–147 of apo-CaM (PDB ID code 1cfd) (19) and holo-CaM (PDB ID code 1cll) (41) structures, whereas the conformational transition in nCaM is modeled from the residues 4–75 of the same PDB structures. The apo to holo conformational transitions of the even–odd paired EF-hand motifs CaM2/3 are modeled from EF-hands 2 and 3, residues 46–113 of apo-CaM (PDB ID code 1cfd) and holo-CaM (PDB ID code 1cll) structures.

Variational Model of Conformational Transitions.

A conformation of a protein in our model (described in more detail in ref. 23) is described by the N position vectors of the α-carbons of the polypeptide backbone, {r_i}. Partially ordered ensembles of polymer configurations are described by a coarse-grained reference Hamiltonian

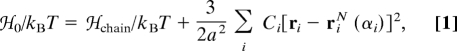where T is the temperature and k_B is the Boltzmann constant. Here, H_chain is a harmonic potential that enforces chain connectivity of a freely rotating polymer with mean bond length a = 3.8 Å (42) and mean valance angle cos θ = 0.8 (43). The second term includes N variational parameters, {C_i}, that control the magnitude of the fluctuations about α-carbon position vectors

Here, we have introduced another set of N variational parameters, {α_i} (ranging between 0 and 1), that specify the backbone positions as an interpolation between the apo-CaM and holo-CaM conformations, {r_i^N_apo} and {r_i^N_holo}, respectively. The probability for a particular configurational ensemble specified by the variational parameters {C_i,α_i} at temperature T is given by the variational free-energy F({C},{α}) = E({C},{α}) − TS({C},{α}). Here, S({C},{α}) is the entropy loss caused by the localization of the residues around the mean positions r_i(α_i)}. The energy is determined by the two-body interactions between distant residues E({C},{α}) = Σ_[i,j] ε_ij u_ij, where u_ij is the average of the pair potential u(r_ij) over H₀ (42) and ε_ij is the strength of a fully formed contact between residues i and j, given by Miyazawa–Jernigan interaction parameters (44). The sum is restricted to a set of contacts [i,j] determined by pairs of residues in the proximity in each of the metastable conformations (23). Each metastable conformation has a distinct but overlapping set of contacts [i,j]_apo, [i,j]_holo, and [i,j] is the union of these sets of contacts. In this model, the interaction energy for contacts that occur exclusively in only one metastable structure is given by exp(−u_ij/k_BT) = 1 + exp(−〈u_ij〉₀/k_BT). This two-state model provides an interpolation at the individual contact level of the interaction energy determined by the two metastable conformations and is similar to some other native state-biased potentials describing conformational transitions. (10–12). Analysis of the free-energy surface parameterized by {C,α} follows the program developed to describe folding (42): the mechanism controlling the kinetics of the transitions is determined by the ensemble of structures characterized by the monomer density at the saddlepoints of the free energy. At this point, we simplify our model and restrict the interpolation parameter α_i to be the same for all residues, α_i = α₀ (45). With this simplification, the numerical problem of finding saddlepoints with respect to {C,α} simplifies to minimizing the free-energy F({C},α₀) with respect to {C} for a fixed α₀.

Conformational Flexibility.

Main-chain conformational flexibility is characterized by the mean square fluctuations {B_i(α₀)} of each α-carbon of the polypeptide chain from its average positions, δr_i along the transition route as α₀ goes from 0 to 1 (23). These natural-order parameters for the reference Hamiltonian H₀, B_i = 〈δr_i²〉₀, contains information about the degree of structural order of each residue (8, 42).

Conformational Transition Mechanism.

The main-chain dynamics responsible for the detailed mechanism of the conformational transition in our analysis is based on the order parameters introduced to describe the folding mechanism ρ_i^apo/holo = 〈exp(−3α^N(r_i − r_i^N_apo/holo)²/2a²〉₀ with α^N = 0.5 defining the width of a Gaussian window about the metastable structure {r_i^N_apo/holo}. In particular, it is convenient to characterize the relative similarity to the apo structure along the transition route through the normalized measure

where ρ_i^apo(α₀) is the monomer density of the ith residue with respect to the apo conformation described by {r_i^N_apo} (23). Similarly, we represent the relative structural similarity to the holo conformation as

where ρ_i^holo(α₀) is the monomer density of the ith residue with respect to the holo conformation described by r_i^N_holo}. In the holo state, ρ_i^apo (0) = 0 and ρ_i^holo (0) = 1, whereas in the apo state ρ_i^apo (1) = 1 and ρ_i^holo (1) = 0. To represent the structural changes more clearly, it is convenient to consider the difference,

for each residue. This difference shifts the relative degree of localization to be between Δρ_i(1) = 1 and Δρ_i(0) = −1 corresponding to the apo and holo conformations, respectively.