Abstract
Complex corticocancellous skeletal sites such as the vertebra or proximal femur are connected networks of bone capable of transferring mechanical loads. Characterizing these structures as networks may allow us to quantify the load transferring behavior of the emergent system as a function of the connected cortical and trabecular components. By defining the relationship between certain physical bone traits and mechanical load transfer pathways, a clearer picture of the genetic determinants of skeletal fragility can be developed. We tested the hypothesis that the measures provided by network percolation theory will reveal that different combinations of cortical, trabecular, and compositional traits lead to significantly different load transfer pathways within the vertebral bodies among inbred mouse strains. Gross morphologic, micro-architectural, and compositional traits of L5 vertebrae from 15 week old A/J (A), C57BL6/J (B6), and C3H/HeJ (C3H) inbred mice (n=10/strain) were determined using micro-computed tomography. Measures included total cross-sectional area, bone volume fraction, trabecular number, thickness, spacing, cortical area, and tissue mineral density. Two-dimensional coronal sections were converted to network graphs with the cortical shell considered as one highly connected node. Percolation parameters including correlation length (average number of connected nodes between superior and inferior surfaces), chemical length (minimum number of connected nodes between surfaces), and backbone mass (strut number) were measured. Analysis of the topology of the connected bone networks showed that A and B6 mice transfer load through trabecular pathways in the middle of the vertebral body in addition to the cortical shell. C3H mice transfer load primarily through the highly mineralized cortical shell. Thus, the measures provided by percolation theory provide a quantitative approach to study how different combinations of cortical and trabecular traits lead to mechanically functional structures. The data further emphasize the interdependent nature of these physical bone traits suggesting similar genetic variants may affect both trabecular and cortical bone. Therefore, developing a network approach to study corticocancellous architecture during growth should further our understanding of the biological basis of skeletal fragility and, thus, provide novel engineering approaches to studying the genetic basis of fracture risk.
Keywords: Percolation theory, Inbred mouse strains, Vertebrae, Corticocancellous architecture, Trabecular network, Biomechanics
Introduction
Growth and development greatly affect peak adult bone properties, which are important determinants of fracture risk early in life and skeletal fragility late in life. Bone mineral density (BMD), which is a measure of the amount of bone, is an important clinical tool used to diagnose fracture risk. However, to study how cancellous architecture arises during growth, multiple measures of bone architecture and tissue quality must be examined rather than simply the amount of bone. Advances in our understanding of genetic variation in growth and development offer insight into the degree of integration among skeletal features that highlights the flaws in analytical approaches that attempt to reduce the skeleton into discrete, supposedly independent traits, each with its own adaptive story [1]. Prior work examining details of trabecular bone architecture revealed that differences in mechanical properties could be explained by regional variation in trabecular architecture [2-4]. However, these studies failed to reveal fully how the entire bone structure is designed (or adapts) to handle the transfer of loads because they focused on a region of interest (ROI) of cancellous bone and did not consider the critical interactions of cortical bone with the flow of stress or were incomplete in that they did not include the variability in material quality. Therefore, a new integrated approach is needed to understand more completely how the underlying biological processes during growth and development determine the load transferring capability of complex corticocancellous structures.
Network science offers an approach that can help shed new light on an old problem [5]. In networks, structure almost always affects function. Researchers are most interested in the relationships between a network’s components because they affect the behavior of the system as a whole. Networks are dynamic, yet robust; maintaining a given function despite adaptive changes in their components with time. The study of a network’s connectivity (its ability to transfer information from point A to point B) is the focus of the percolation theory. The main objectives of the percolation theory are to characterize the distribution of cluster sizes in the network and to determine how the transfer of information depends on network architecture [5]. Although it was originally developed to answer questions in organic chemistry, percolation models have been used successfully to study network related phenomena including forest fires, electrical conductivity, epidemics of disease, and signal transfer in neurons [6].
The corticocancellous architecture of a complex skeletal site such as the vertebra or proximal femur is a connected network of bone capable of transferring mechanical loads, which are the “information” transferred through the network. The adaptive nature of these networks results in bone structures similar in mechanical function, but different in design. Previously, the percolation theory has been used in the description of age-related changes of mechanical competence in an ROI of normal and osteoporotic trabecular bone [4]. A network percolation model can also be used to study how genetic differences in bone growth affect mechanical function. Genetic variation gives rise to variation in the biological activity of each cell population leading to mechanically functional bone networks built with different combinations of trabecular bone, cortical bone, and mineral content. Bone has an inherent adaptive response to modify the apposition, resorption, and mineralization processes that determine bone structure and tissue quality to meet mechanical demands [7]. For example, inbred mice have the capability of modulating compositional and morphological bone traits to meet mechanical demands associated with weight bearing [8,9]. The coupling between bone morphology and tissue quality appears advantageous for ensuring that adequate whole bone stiffness is achieved for day-to-day activity (i.e., create a functional skeleton). However, the disadvantage is that the tissue quality factors that tend to make bone stiff also tend to make bone less ductile, less tough, and more damageable [10]. Thus, understanding the design principles of a functional skeleton and understanding the relationships among skeletal traits are important in determining how genetically varying growth patterns lead to skeletal fragility. Characterizing a complex corticocancellous structure as a connected network allows us to 1) analyze quantitatively the load transferring behavior of the emergent system as a function of the connected components and 2) quantify how the structure evolves over time — specifically, how the biological processes modulate the structure to meet mechanical demands during growth and development.
By defining the relationship between certain morphological traits and mechanical load transfer pathways, a clearer picture of the genetic determinants of skeletal fragility can be developed. To develop the network theory, we made use of the variability in structure-function relationships observed among three inbred mouse strains [11]. Previous work showed that these inbred strains built vertebrae with different combinations of cortical, trabecular, and compositional traits [11]. Here, we tested the hypothesis that the measures provided by the percolation theory will reveal that these different combinations of traits lead to significantly different load transfer pathways within the vertebral bodies among these inbred mouse strains. We used the percolation theory to analyze samples from a prior study [11] and compared indices related to load transfer among inbred mouse strains. Further, we identified which mechanical properties were predicted by percolation parameters.
Materials and methods
Data on vertebrae of inbred mice
In a previous study, female A/J (A, n=10), C57BL/6J (B6, n=10), and C3H/HeJ (C3H, n=10) inbred mice were purchased from Jackson Laboratory (Bar Harbor, ME, USA) at 4 weeks of age [11]. The Committee on Animal Care and Use approved the handling and treatment of mice. Mice were killed at 15 weeks of age and gross morphologic, micro-architectural, and compositional traits of L5 vertebral bodies were determined using a desktop micro-Computed Tomography (micro-CT) system (GE eXplore Locus SP Specimen Scanner; GE Healthcare, London, Ontario, Canada) [11]. Overall measures included the total cross-sectional area (Tt.Ar=cortical bone+trabecular bone+marrow) and the total bone area (B.Ar=cortical bone+trabecular bone). Cortical bone traits included the area of cortical bone (Ct.Ar) and the second area (polar) moment of inertia (Ct.J). Measures of trabecular morphology included trabecular bone volume fraction (Tb BV/TV), trabecular number (Tb.N), trabecular thickness (Tb.Th), and trabecular separation (Tb.Sp). TMD also was calculated from the micro-CT images as described previously [11]. TMD is the average mineral value of the bone voxels alone, expressed in hydroxyapatite equivalents. It should be noted that mice were analyzed at 15 weeks of age so the results reflect genetic differences in the growth and development of mechanically functional vertebrae [11,12].
Whole bone mechanical properties of intact L5 vertebrae (n=10/genotype) were measured previously by compressing the vertebral body with a 3-mm-diameter platen [11]. Mechanical properties, included failure load (Fu), stiffness (S), and total displacement (ΔT) as a measure of ductility. Failure load was defined as the highest load preceding a rapid decrease in the measured load. Total deflection was measured using a custom optical strain measuring system as described previously [11].
The network model and percolation parameters
The network design, or topology, determines the structural stability, dynamic behavior, robustness, and attack tolerance of the structure [13]. Thresholded micro-CT images from the previous study were used to assess the network topology of the vertebral bodies. Using an iterative thinning algorithm (Matlab, The Mathworks Inc., Natick, MA, USA), two-dimensional (2D) coronal sections (two per bone) were skeletonized and nodes and branches were identified (Fig. 1A, B). These 2D sections were taken from each bone at approximately 1/3 and 2/3 of the anteroposterior width of the vertebral body (∼0.35 mm apart). The skeleton graphs were converted into network maps by considering the cortical surface as one highly connected node or hub (Fig. 1C). The degree distribution is a function describing the total number of nodes in a network with a given number of connections to other nodes [13]. The degree distribution of a random network follows a bell curve, in which most nodes have the same number of links, and nodes with a very large number of links do not exist (Fig. 1D). In contrast, the power law degree distribution of a scale-free network predicts that most nodes have only a few links, held together by a few highly connected hubs (Fig. 1D). The distinction between scale-free and random networks is important because it provides context into how to build a functional skeleton and how to assess the deleterious effects of bone loss on mechanical behavior more accurately. Based on the prominence of the cortical shell, the scale-free network topology was applicable for the mouse vertebrae. Further, despite analyzing 2D images where trabecular connections segment the cortex, we chose to view the system as a scale-free network, which is more representative of the 3D vertebral body structure because a continuous cortical shell acts as a network hub connected to many trabecular struts.
Fig. 1.
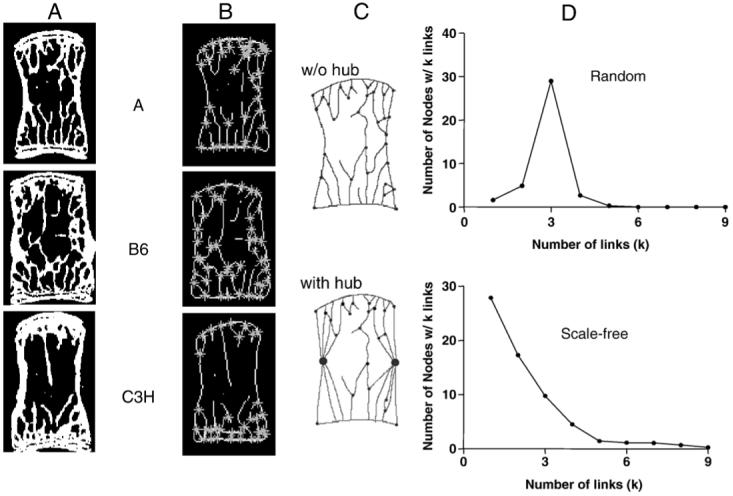
Conversion of 2D vertebral images into network maps. (A) Two-dimensional coronal sections were (B) skeletonized and nodes were identified. (C) The skeleton graphs were converted into network maps by considering the cortical surface as one highly connected node or hub (large circles). (D) Graphical representation of random (no hub) and scale-free (cortical hub) networks.
The percolation model was intended to interpret the relationship between the network structure and mechanical function. Adult, functional bones are assumed to contain percolating clusters or else they would not be able to transfer load. The percolation theory deals with the number and properties of the connected clusters, which are made up of free, or dead ends (non-loaded segments) and a backbone. In terms of vertebral bone architecture, the backbone defines the pathways that transfer load between the superior and inferior surfaces and consists of single connected segments and multi-connected segments.
An algorithm was developed to calculate simple percolation parameters (Matlab, The Mathworks Inc., Natick, MA, USA). The inputs into the algorithm are the set of nodes with their connected neighboring nodes and the starting and end points or surfaces. The only predefined rules for our network are that information can only travel from the superior surface toward the inferior surface (thus load applied to the superior surface can only travel to connected nodes in the network located either horizontal to or below) and the information is self-avoiding (information cannot travel to a node it has been to previously). The correlation and chemical path lengths measure the load sharing capacity of the network, which is expected to vary with genetic background (Fig. 2). The chemical length (ChemL) is the distance of the shortest path in which the percolating network connects opposite boundaries. The correlation length (CorrL) is the average distance between connected opposite boundaries. For bone architecture, path distance is a measure of the number of nodes, or intersections of connected bone struts, between boundaries. Size and geometry also play an important role in a network’s ability to transfer information. The percolation model refers to these characteristics as mass. Backbone mass (BboneMass) was defined as the number of connected struts comprising the dead ends and the cortical and trabecular components of the backbone.
Fig. 2.
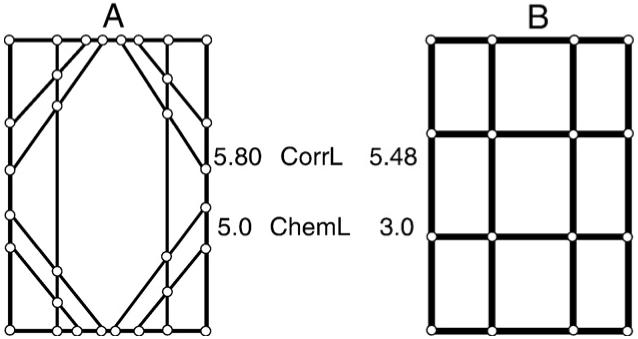
Structures A and B have similar bone volume fractions yet vastly different network topologies for transferring load from top to bottom. Load applied to the top surface can only travel to connected nodes (open circles) in the network located either horizontal to or below and cannot travel to a node it has been to previously. Compared to structure B, structure A has higher correlation length (average number of nodes crossed along paths connecting top and bottom surface; CorrL) and chemical length (fewest number of nodes crossed along paths connecting top and bottom surface; ChemL). Thus, structure A has a higher load sharing capacity.
Previous work showed genetic variation in the combination of trabecular and cortical traits in the construction of mechanically functional vertebrae [11]. To test how these different combinations influence network behavior (mechanical load transfer) the ratio of cortical nodes to trabecular nodes (Ct:Tb Nodes) and the ratio of trabecular struts and cortical struts (Tb:Ct Struts) were calculated. The percentage of existing links connected to the cortex was then calculated (%hub).
Statistical analysis
Differences in percolation parameters among A, B6, and C3H were determined using a one-way analysis of variance (ANOVA) and a Tukey’s posthoc test (GraphPad Prism; San Diego, CA, USA). The relationships between percolation parameters and bone morphology and composition were determined within each genotype and across genotypes by combining individual data from all three strains and calculating correlation coefficients between each percolation parameter (CorrL, ChemL, BboneMass, Tb:Ct Struts, Ct:Tb Nodes, %hub) and each morphological and compositional trait (Tb BV/TV, Tt.Ar, Ct.Ar, TMD, etc.) (Minitab, State College, PA, USA). When a large number of non-independent tests are conducted, the likelihood that at least one will achieve statistical significance on the basis of chance alone increases. To correct this, permutation tests were used to establish a threshold for statistical significance in the correlation analyses [14]. A copy of the analytical program used for this study is available at http://www.jax.org/staff/churchill/labsite under the data sets link [15]. The average threshold values for all 3 strains were r=0.67 for p<0.10 and r=0.61 for p<0.05. After correcting for multiple comparisons, many significant relationships remained. Multiple linear regression analyses were then conducted to 1) determine inter-strain variation in percolation parameters explained by a combination of trabecular, cortical, and compositional traits and 2) identify mechanical properties that are explained by a combination of percolation parameters.
Results
Genetic variation in network structure
The results of the network analysis and the previous structure-function study showed that all three inbred strains constructed mechanically functional vertebrae in different ways (Table 1). Percolation measures revealed that significant differences existed in the way the three inbred mouse strains constructed the bone network of the vertebral body. B6 vertebrae had significantly higher correlation lengths (p<0.001) than A and C3H meaning the B6 connected network was bigger (i.e., more paths shared the load between surfaces). The chemical length (shortest path of load transfer) of B6 mice was also significantly higher than A and C3H (p<0.001). These results were not surprising since B6 had the highest Tb BV/TVand thus, more of the load could be shared through trabeculae in the middle of the vertebral body compared to A and C3H.
Table 1.
Inter-strain differences in morphology, composition, mechanical properties, and network architecture
| A | B6 | C3H | |
|---|---|---|---|
| Physical bone traits | |||
| Tt.Ar (mm2) | 1.4±0.07b,c | 1.6±0.05a,c | 1.7±0.13a,b |
| B.Ar (mm2) | 0.49±0.06b,c | 0.64±0.06a | 0.63±0.08a |
| Ct.Ar (mm2) | 0.28±0.02c | 0.30±0.03c | 0.43±0.03a,b |
| Tb BV/TV (%) | 19.2±2.9b | 26.6±2.6a,c | 16.5±3.8b |
| Tb.Th (mm) | 0.038±0.003c | 0.041±0.004c | 0.047±0.006a,b |
| TbN (1/mm) | 6.2±0.4b,c | 7.8±0.04a,c | 4.0±0.5a,b |
| Tb.Sp (mm) | 0.17±0.03c | 0.10±0.01c | 0.42±0.11a,b |
| TMD (mg/cm3) | 770.4±8.9b,c | 735.1±19.2a,c | 821.7±9.2a,b |
| Mechanical properties | |||
| FU (N) | 19.2±3.1b,c | 28.5±2.5a | 29.7±6.5a |
| Stiffness (N/mm) | 464±166c | 443±158c | 1192±301a,b |
| ΔT (mm) | 0.13±0.05b | 0.19±0.05a,c | 0.07±0.06b |
| Percolation measures | |||
| Correlation length | 5.43±1.36b | 9.06±2.29a,c | 4.27±0.47b |
| Chemical length | 2.47±0.44b | 3.98±1.09a,c | 2.17±0.44b |
| Backbone mass | 35.65±8.27b | 58.25±12.47a,c | 27.35±3.88b |
| Ct:Tb Nodes | 0.82±0.17c | 0.54±0.15c | 1.28±0.67a,b |
| % of links to hub | 26.2±5.6b | 21.6±2.5a,c | 29.8±6.5b |
| Tb:Ct Struts | 16.83±4.13b | 28.13±6.23a,c | 12.43±1.70b |
Significantly different from A, B6, or C3H, respectively (p<0.05). Data shown as mean+standard deviation.
Significantly different from A, B6, or C3H, respectively (p<0.05). Data shown as mean+standard deviation.
Significantly different from A, B6, or C3H, respectively (p<0.05). Data shown as mean+standard deviation.
Differences in the reliance on the cortex were made clearer by comparing cortical and trabecular components of the network. The ratio of cortical to trabecular nodes in the C3H vertebrae was significantly higher than A (p<0.01) and B6 (p<0.001). There was no significant difference between A and B6. Thus, C3H vertebrae relied heavily on the cortex to transfer load from superior to inferior surfaces. B6 had the lowest reliance on the cortical hub with a lower percentage of existing links connected to the cortical hubs compared to A (p<0.05) and C3H (p<0.001). The number and type of struts that were used by each inbred strain to carry load also differed. B6 mice had significantly higher backbone mass than A and C3H (p<0.001). This was mainly due to a higher contribution from trabecular struts in B6 vertebrae, which had a significantly higher ratio of trabecular to cortical struts than A and C3H (p<0.001).
Variation in network structure is dependent on variation in vertebral architecture
All percolation parameters were measured independent of bone size, shape, and mineralization. However, these traits were statistically related to trabecular, cortical, and compositional components of the mouse vertebra. Pearson correlation coefficients determined for each genotype separately revealed that correlations between percolation parameters and physical bone traits were consistent within genotypes (data not shown). The univariate analysis performed across genotypes by combining the datasets revealed that percolation parameters were significantly correlated to physical bone traits specifying trabecular architecture (Tb BV/TV, connectivity, Tb.N, Tb.Sp) and composition (TMD) (Table 2). According to Pearson correlation coefficients, percolation parameters also were significantly related to cortical bone area (Ct.Ar). However, the correlation coefficients were slightly below the threshold determined from permutation tests for p<0.05.
Table 2.
Correlation coefficients for percolation parameters and trabecular, cortical, and compositional traits
| Weight | B.Ar | Tb BV/TV | NNd:NTm | Tb.Th | Tb.Sp | Tb.N | Ct.Ar | Ct.J | Tt.Ar | TMD | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CorrL | -0.27 (0.15) |
0.30 (0.11) |
0.78 (0.00) |
0.74 (0.00) |
-0.05 (0.80) |
-0.63 (0.00) |
0.79 (0.00) |
-0.39 (0.03) |
-0.22 (0.25) |
-0.04 (0.84) |
-0.74 (0.00) |
| ChemL | -0.28 (0.14) |
0.27 (0.16) |
0.71 (0.00) |
0.67 (0.00) |
-0.03 (0.80) |
-0.52 (0.00) |
0.72 (0.00) |
-0.33 (0.03) |
-0.16 (0.39) |
-0.06 (0.75) |
-0.72 (0.00) |
| BboneMass | -0.26 (0.17) |
0.31 (0.10) |
0.85 (0.00) |
0.80 (0.00) |
-0.04 (0.84) |
-0.67 (0.00) |
0.85 (0.00) |
-0.41 (0.03) |
-0.23 (0.22) |
-0.09 (0.63) |
-0.79 (0.00) |
| Ct:Tb Nodes | 0.14 (0.45) |
-0.11 (0.56) |
-0.76 (0.00) |
-0.64 (0.00) |
0.09 (0.64) |
0.75 (0.00) |
-0.80 (0.00) |
0.53 (0.00) |
0.44 (0.02) |
0.31 (0.10) |
0.73 (0.00) |
| % links to hub | 0.25 (0.18) |
-0.12 (0.54) |
-0.59 (0.00) |
-0.55 (0.00) |
0.12 (0.54) |
0.52 (0.00) |
-0.62 (0.00) |
0.36 (0.05) |
0.28 (0.14) |
0.22 (0.24) |
0.54 (0.00) |
| Tb:Ct Struts | -0.25 (0.18) |
0.30 (0.11) |
0.85 (0.00) |
0.79 (0.00) |
-0.05 (0.80) |
-0.68 (0.00) |
0.86 (0.00) |
-0.42 (0.02) |
-0.24 (0.20) |
-0.10 (0.60) |
-0.80 (0.00) |
Pearson correlation coefficients are shown. p-values in parentheses. Bold values significant (p<0.05) above threshold of ±0.61 determined by permutation tests.
Independent of the relationships observed within strains, no relationship observed across the strains was unexpected based on geometry and mathematical dependency. Simple correlation analysis does not convey the nature of these relationships. Therefore, a multivariate analysis was used to investigate how these correlations relate to the mechanical functionality of a structure. Multiple linear regression analyses (Table 3) revealed that a combination of cortical, trabecular, and compositional traits were needed to achieve 60-80% explanatory power for percolation parameters including correlation and chemical length for all three strains simultaneously.
Table 3.
Multivariate analysis comparing percolation parameters with morphological and compositional bone traits
| Equation | R2-adj |
|---|---|
| CorrL=0.2-0.8 Tb BV/TV+1.5 TbN-0.1 TMD+13.4 CtAr+0.1 weight | 0.617 |
| ChemL=13.7-9.8 Tb BV/TV 0.6 TbN-0.02 TMD+11.5 CtAr+0.05 weight | 0.562 |
| BboneMass=-29-50 Tb BV/TV+12.4 TbN-0.06 TMD+120 CtAr+0.7 weight | 0.777 |
| Ct:Tb Nodes=3.9-9.0 Tb BV/TV+0.1 TbN+3.8 CtAr-0.04 weight | 0.681 |
| %hub=1.3-0.14 Tb BV/TV-0.04 TbN-0.001 TMD+0.001 CtAr+0.01 weight | 0.331 |
| Tb:Ct Struts=-16.4-24.4 Tb BV/TV+6.2 TbN-0.03 TMD+58.3 CtAr+0.4 weight | 0.774 |
Multiple linear regression analysis was conducted to determine the amount of inter-strain variation in correlation length (CorrL), chemical length (ChemL), backbone mass (BboneMass), the ratio of cortical to trabecular nodes (Ct:Tb Nodes), and the ratio of trabecular to cortical struts (Tb:Ct Struts). The constants or traits shown in bold depict terms in the regression model showing significant (p<0.05) or borderline significant (p<0.1) contributions. R2 values were adjusted for number of independent variables.
Genetic variation in mechanical properties is dependent on network structure
Multivariate regression analyses (Table 4) examining percolation parameters and whole bone mechanical properties across all three strains revealed that a combination of percolation parameters accounted for >60% of the variation in vertebral stiffness. However, combinations of percolation parameters explained only ∼20% of failure load and ∼40% of total displacement. Thus, the data revealed that combinations of cortical and trabecular morphology and composition contribute to genetic variation in bone network structures and, specifically, to variation in whole bone vertebral stiffness.
Table 4.
Multivariate regression analysis comparing whole mechanical properties with percolation parameters
| Equation | R2 | R2-adj |
|---|---|---|
| Stiff=27+49 CorrL-184 ChemL+78.9 BboneMass+555 Ct:Tb Nodes+883%hub-158 Tb:Ct Struts | 0.633 | 0.504 |
| FU=16.8+0.04 CorrL-1.33 ChemL+1.20 BboneMass+10.1 Ct:Tb Nodes-25.5%hub-2.02 Tb:Ct Struts | 0.210 | 0.000 |
| ΔT=0.22-0.005 CorrL+0.03 ChemL-0.02 BboneMass-0.04 Ct:Tb Nodes-0.32%hub+0.04 Tb:Ct Struts | 0.414 | 0.254 |
Multiple linear regression analysis was conducted to determine the amount of inter-strain variation in stiffness, strength (FU), and total displacement (ΔT) using percolation parameters including correlation length (CorrL), chemical length (ChemL), backbone mass (BboneMass), the ratio of cortical to trabecular nodes (Ct:Tb Nodes), the percentage of links to the cortical hub (%hub), and the ratio of trabecular to cortical struts (Tb:Ct) as predictors. The constants or traits shown in bold depict terms in the regression model showing significant (p<0.05) or borderline significant (p<0.1) contributions. R2 values were adjusted for number of independent variables.
Discussion
Networks reveal functional interactions among sets of traits
The results of this study confirmed the hypothesis that the percolation theory revealed that different combinations of cortical and trabecular morphological and compositional traits contribute to genetic variation in bone network structures and, ultimately, to variation in whole bone mechanical properties. Therefore, load transfer pathways are under genetic control. The data were also consistent with results from previous studies using standard reductionist methods that characterized the quantity of cortical and trabecular traits separately [11,16,17]. The percolation parameters quantified differences in the way load is transferred from superior to inferior surfaces in the inbred mouse vertebral body. B6 vertebrae had higher trabecular BV/TVand thinner cortices, which combined to produce larger networks that shared the load among paths within the trabecular bone of the vertebral body. In contrast, C3H vertebrae had lower trabecular BV/TV, but a higher amount of cortical bone as evidenced by higher reliance on the cortex in load transfer networks. Turner et al. suggested that the lack of trabecular bone in C3H mice could be the result of mechanical adaptation to thicker cortices due to a possible stress shielding effect [16]. We believe these interactions among traits are part of a larger biological paradigm [18]. The network approach presented here was not meant to replace standard reductionist approaches to understanding the structure-function relationships, but to supplement them.
By providing simple quantitative measures of how bone is constructed to transfer load, the current data may provide new insight into skeletal fragility. The correlations among morphological and compositional traits suggest that physical bone traits are coordinated (or are co-adapted) so the sets of traits result in vertebrae that are sufficiently stiff for daily loading demands [11,18]. However, not all sets of traits resulted in equivalent failure mechanisms. In C3H vertebral bodies, decreased BV/TV was compensated by increases in tissue mineral content and the reliance on the cortical shell in its load transfer network. Although the observed co-adaptation of traits had the result of ensuring that C3H vertebrae were sufficiently stiff and strong for daily loading, the combination of thicker cortices and higher mineralization reduced tissue-ductility. Thus, consistent with previous work examining factors that contribute to skeletal fragility [8,9,12,19-22], the co-adaptation of traits may result in the development of sets of traits preferred over others and increase fracture risk under extreme load conditions [18].
Assessment of physical bone traits that determine mechanical strength of corticocancellous bone has largely centered on BMD or trabecular bone volume fraction [2,17,23]. BMD, which is a successful clinical tool for diagnosing fracture risk, is highly heritable [24], making it a good candidate for use as a surrogate measure of fracture risk in many genetic analyses. Recent studies have shown that the contribution of the cortical shell to mechanical function should not be overlooked [11,25-27]. Quantitative trait loci (QTLs) regulating complex properties like bone strength, fragility, and BMD have been identified [28-32]. However, few studies have been conducted with knowledge of the relationships among genes, cellular processes, growth patterns, physical traits, and mechanical functions [30,32-35]. The current data may provide new insight into this problem. Using a single complex trait such as BMD or BV/TV as the sole phenotypic marker in genetic analyses may be insufficient because of the complex relationship between mechanical properties and the underlying bone traits. The cortical, trabecular, and mineral components of the inbred mouse vertebral body are functionally dependent. Based on three distinct inbred mouse strains, the data suggest that individual strains do not inherit a single trait but a set of traits that determines whether bone will be 1) stiff, strong, and tough or 2) stiff, strong, and brittle. These sets of traits reflect the organ-level mechanical functionality of adult bone. Future work will focus on the biological processes that establish this functionality.
Not all load transfer pathways are equal
The results of the multivariate analysis, which showed that percolation parameters accurately explained stiffness but not FU and ΔT, also were consistent with the idea that structures are built to be sufficiently stiff for physiological loading demands. Network topology independent of vertebral size, amount of bone, and composition is sufficient to explain stiffness. However, global failure strength and ductility may depend on local failures in the network’s ability to transfer load, which depends on the morphology and composition of the particular pathway. Additionally, not all pathways are used equally in the transfer of mechanical load. Thus, more information about the structure and how load is shared throughout the network may be needed to explain why the topological measures alone were poor predictors of FU and ΔT.
Fortunately, network science provides the foundation for future analyses studying the “fitness” or significance of certain pathways relative to the global structure [5,13]. Individual trabecular struts and cortices can be assigned fitness values based on their combination of morphological and compositional traits. Different genotypes are expected to use unique combinations of high-fitness load pathways. Based on the data in the present study, C3H vertebrae had fit pathways with a combination of thick, highly mineralized struts (Table 1; Fig. 1A) oriented in the direction of loading whereas B6 and A had fit pathways that were thinner and angled into the cortex compared to the direction of loading (connecting load to cortical boundaries). Knowledge of the failure mechanism of the most used load transfer pathways along with the morphology and composition of the specific paths would be expected to improve the explanatory power for global strength and ductility. Other factors contributing to the lower explanatory power for these regressions include 1) underestimation of FU of C3H vertebral bodies due to brittle failure mode; 2) variation in other matrix components [36,37]; and 3) architectural traits not measured in this study that could contribute to variation in more complex mechanical properties such as FU and ΔT [38,39]. The multivariate analyses performed here lay the groundwork for future analyses aimed at identifying other factors contributing to whole bone mechanical properties and the direction of causality among these traits [40].
Networks are dynamic objects, evolving during growth due to the activities of their components
One of the challenges to a complete understanding of the biological basis of Wolff’s law lies in understanding how architectural changes with growth (and aging) relate to mechanical function. Network science eliminates some of the shortcomings of reductionist techniques (BV/TV, Ct.Th, etc.) by revealing a way to quantify how bone cells establish and maintain a mechanically functional, connected structure throughout life. Fitness, or the probability of a structure to survive, provides a way to test the hypothesis that skeletal architecture changes to meet mechanical demands [41,42]. To satisfy mechanical demands during growth, osteoblasts and osteoclasts are expected to arrange and maintain trabecular struts with the highest fitness relative to load transfer through the whole bone and remove struts that have low fitness or are unloaded. Paths with the highest fitness (i.e., critical to load transfer) would be hypothesized to be the pathways that are retained throughout growth. Thus, this analysis is in line with the idea that mechanical stresses (i.e., fluid flow) on osteocytes are critical for cells to remain viable and for individual bone components to adapt as part of the global structure [43].
The observed relationships among adult bone shape and quality were determined by genetic variation in cellular activity on trabecular and cortical bone surfaces. However, how the cells use available resources to shape the network to share loads is still not fully understood. The functional interaction between cortical and trabecular morphology appears to be an important biological paradigm for vertebrae. Genetic or environmental perturbations that alter these functional interactions during growth would be expected to lead to loss of function and/or suboptimal adult bone quality [18]. The traditional approach of relating individual adult bone traits (BMD, etc.) to QTLs or cellular processes may be improved further by examining how sets of traits develop during growth. Thus, improving our knowledge of the biological control mechanisms coordinating the set of trabecular and cortical traits during growth may provide new targets for genetic analyses as well as new strategies for building more robust bones.
Together with knowledge of mechanical environment, network topology also provides context not only about its transfer capacity in particular directions (normal physical activity versus a fall), but also how to improve the assessment of the deleterious effects of bone loss on mechanical behavior. We found that the vertebrae of three distinct inbred mouse strains could be described as a scale-free network based on the prominence of the cortical shell (Fig. 1D) [11,16,23,44]. If osteoclastic resorption does not discriminate between nodes, but affect small nodes and large hubs with the same probability (i.e., random loss of bone struts due to uniform trabecular thinning), small nodes are far more likely to be dismantled in scale-free networks since there are many more of them [13]. Thus, the critical threshold below which a connected system is virtually unharmed is higher in scale-free networks because the existence of hubs keeps the network together. However, when the largest nodes of a scale-free network are removed (i.e., directed bone loss), there is a critical point beyond which the network breaks apart. Computational models of 3D networks have shown that trabecular perforation leads to the most significant loss of stiffness and strength compared to uniform thinning [45-47]. Therefore, the network topology of adult corticocancellous structures impacts the severity of changes in mechanical integrity due to bone loss. Thus, we expect similar analyses of human bone to be valuable because bone loss appears to be directed and not random [48-50].
This simple 2D analysis shows promise for future 3D analyses, which are used to assess 3D structures such as neural networks. Challenges that make 3D analysis of bone slightly more difficult than neural networks include proper classification of the vertical shell and the complexity of the loads experienced by corticocancellous structures such as the proximal femur. Currently, 3D algorithms are being developed on 3D models and bone volumes.
Summary
The results of this study demonstrate that measures provided by the percolation theory provide additional insight into the contribution of genetically determined bone traits to variation in whole bone mechanical function. The network-based approach developed here introduces a shift in the perspective of bone as a highly organized, aligned, and adapted structure. Specifically, percolation parameters present a new way to attack the challenge of associating the architecture of corticocancellous structures, such as the proximal femur and vertebral body, with mechanical function. Although previous studies were successful in identifying structure-function relationships, the biologically significant aspect of Wolff’s law has not been presented [51]. This study showed that mechanically functional bone networks are built with different genetically determined combinations of trabecular bone, cortical bone, and mineral content. The data suggest that the coordination of the biological activity of each cell population solves the global problem of mechanical functionality by creating and maintaining connected structures throughout life. Therefore, developing a network approach to study corticocancellous architecture during growth should further our understanding of the biological basis of Wolff’s law and, thus, provide novel engineering approaches to studying the genetic basis of fracture risk.
Acknowledgments
The authors thank the National Institutes of Health (NIH AR44927; MH071818; NCRR 1S10RR014801) for their support of this research.
References
- [1].Pearson OM, Lieberman DE. The aging of Wolff’s “law”: ontogeny and responses to mechanical loading in cortical bone. Am J Phys Anthropol. 2004;(Suppl 39):63–99. doi: 10.1002/ajpa.20155. [DOI] [PubMed] [Google Scholar]
- [2].Beamer WG, Donahue LR, Rosen CJ, Baylink DJ. Genetic variability in adult bone density among inbred strains of mice. Bone. 1996;18:397–403. doi: 10.1016/8756-3282(96)00047-6. [DOI] [PubMed] [Google Scholar]
- [3].Ritzel H, Amling M, Posl M, Hahn M, Delling G. The thickness of human vertebral cortical bone and its changes in aging and osteoporosis: a histomorphometric analysis of the complete spinal column from thirty-seven autopsy specimens. J Bone Miner Res. 1997;12:89–95. doi: 10.1359/jbmr.1997.12.1.89. [DOI] [PubMed] [Google Scholar]
- [4].Tabor Z. Simulated aging — a novel method for estimating the risk of fracture of trabecular bone. Bone. 2003;33:229–36. doi: 10.1016/s8756-3282(03)00224-2. [DOI] [PubMed] [Google Scholar]
- [5].Watts DJ. Six degrees: the science of a connected age. W.W. Norton & Company; New York: 2003. [Google Scholar]
- [6].Stauffer D, Aharony A. Introduction to percolation theory. Taylor & Francis Ltd.; London: 1994. [Google Scholar]
- [7].Ferretti JL, Capozza RF, Mondelo N, Zanchetta JR. Interrelationships between densitometric, geometric, and mechanical properties of rat femora: inferences concerning mechanical regulation of bone modeling. J Bone Miner Res. 1993;8:1389–96. doi: 10.1002/jbmr.5650081113. [DOI] [PubMed] [Google Scholar]
- [8].Jepsen KJ, Akkus OJ, Majeska RJ, Nadeau JH. Hierarchical relationship between bone traits and mechanical properties in inbred mice. Mamm Genome. 2003;14:97–104. doi: 10.1007/s00335-002-3045-y. [DOI] [PubMed] [Google Scholar]
- [9].Jepsen KJ, Pennington DE, Lee YL, Warman M, Nadeau J. Bone brittleness varies with genetic background in A/J and C57BL/6J inbred mice. J Bone Miner Res. 2001;16:1854–62. doi: 10.1359/jbmr.2001.16.10.1854. [DOI] [PubMed] [Google Scholar]
- [10].Currey JD. Effects of differences in mineralization on the mechanical properties of bone. Philos Trans R Soc Lond B Biol Sci. 1984;304:509–18. doi: 10.1098/rstb.1984.0042. [DOI] [PubMed] [Google Scholar]
- [11].Tommasini SM, Morgan TG, van der Meulen M, Jepsen KJ. Genetic variation in structure-function relationships for the inbred mouse lumbar vertebral body. J Bone Miner Res. 2005;20:817–27. doi: 10.1359/JBMR.041234. [DOI] [PubMed] [Google Scholar]
- [12].Price C, Herman BC, Lufkin T, Goldman HM, Jepsen KJ. Genetic variation in bone growth patterns defines adult mouse bone fragility. J Bone Miner Res. 2005;20:1983–91. doi: 10.1359/JBMR.050707. [DOI] [PubMed] [Google Scholar]
- [13].Barbasi AL. Linked: the new science of networks. Perseus Publishing; Cambridge: 2002. [Google Scholar]
- [14].Churchill GA, Doerge RW. Empirical threshold values for quantitative trait mapping. Genetics. 1994;138:963–71. doi: 10.1093/genetics/138.3.963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Nadeau JH, Burrage LC, Restivo J, Pao YH, Churchill G, Hoit BD. Pleiotropy, homeostasis, and functional networks based on assays of cardiovascular traits in genetically randomized populations. Genome Res. 2003;13:2082–91. doi: 10.1101/gr.1186603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Turner CH, Hsieh YF, Muller R, Bouxsein ML, Baylink DJ, Rosen CJ, et al. Genetic regulation of cortical and trabecular bone strength and microstructure in inbred strains of mice. J Bone Miner Res. 2000;15:1126–31. doi: 10.1359/jbmr.2000.15.6.1126. [DOI] [PubMed] [Google Scholar]
- [17].Turner CH, Hsieh YF, Muller R, Bouxsein ML, Rosen CJ, McCrann ME, et al. Variation in bone biomechanical properties, microstructure, and density in BXH recombinant inbred mice. J Bone Miner Res. 2001;16:206–13. doi: 10.1359/jbmr.2001.16.2.206. [DOI] [PubMed] [Google Scholar]
- [18].Jepsen KJ, Hu B, Tommasini SM, Courtland HW, Price C, Terranova CJ, et al. Genetic randomization reveals functional relationships among morphologic and tissue-quality traits that contribute to bone strength and fragility. Mamm Genome. 2007;18:492–507. doi: 10.1007/s00335-007-9017-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Duan Y, Seeman E, Turner CH. The biomechanical basis of vertebral body fragility in men and women. J Bone Miner Res. 2001;16:2276–83. doi: 10.1359/jbmr.2001.16.12.2276. [DOI] [PubMed] [Google Scholar]
- [20].Seeman E. Unresolved issues in osteoporosis in men. Rev Endocr Metab Disord. 2001;2:45–64. doi: 10.1023/a:1010054924085. [DOI] [PubMed] [Google Scholar]
- [21].Tommasini SM, Nasser P, Jepsen KJ. Sexual dimorphism affects tibia size and shape but not tissue-level mechanical properties. Bone. 2007;40:498–505. doi: 10.1016/j.bone.2006.08.012. [DOI] [PubMed] [Google Scholar]
- [22].Currey JD. Bone architecture and fracture. Curr Osteoporos Rep. 2005;3:52–6. doi: 10.1007/s11914-005-0004-z. [DOI] [PubMed] [Google Scholar]
- [23].Klein RF, Shea M, Gunness ME, Pelz GB, Belknap JK, Orwoll ES. Phenotypic characterization of mice bred for high and low peak bone mass. J Bone Miner Res. 2001;16:63–71. doi: 10.1359/jbmr.2001.16.1.63. [DOI] [PubMed] [Google Scholar]
- [24].Giguere Y, Rousseau F. The genetics of osteoporosis: ‘complexities and difficulties’. Clin Genet. 2000;57:161–9. doi: 10.1034/j.1399-0004.2000.570301.x. [DOI] [PubMed] [Google Scholar]
- [25].Silva MJ, Keaveny TM, Hayes WC. Load sharing between the shell and centrum in the lumbar vertebral body. Spine. 1997;22:140–50. doi: 10.1097/00007632-199701150-00004. [DOI] [PubMed] [Google Scholar]
- [26].Sornay-Rendu E, Boutroy S, Munoz F, Delmas PD. Alterations of cortical and trabecular architecture are associated with fractures in postmenopausal women, partially independent of decreased BMD measured by DXA: the OFELY study. J Bone Miner Res. 2007;22:425–33. doi: 10.1359/jbmr.061206. [DOI] [PubMed] [Google Scholar]
- [27].Yamauchi M, Sugimoto T, Chihara K. Determinants of vertebral fragility: the participation of cortical bone factors. J Bone Miner Metab. 2004;22:79–85. doi: 10.1007/s00774-003-0480-0. [DOI] [PubMed] [Google Scholar]
- [28].Beamer WG, Shultz KL, Churchill GA, Frankel WN, Baylink DJ, Rosen CJ, Donahue LR. Quantitative trait loci for bone density in C57BL/6J and CAST/EiJ inbred mice. Mamm Genome. 1999;10:1043–9. doi: 10.1007/s003359901159. [DOI] [PubMed] [Google Scholar]
- [29].Klein RF, Mitchell SR, Phillips TJ, Belknap JK, Orwoll ES. Quantitative trait loci affecting peak bone mineral density in mice. J Bone Miner Res. 1998;13:1648–56. doi: 10.1359/jbmr.1998.13.11.1648. [DOI] [PubMed] [Google Scholar]
- [30].Li X, Masinde G, Gu W, Wergedal J, Hamilton-Ulland M, Xu S, et al. Chromosomal regions harboring genes for the work to femur failure in mice. Funct Integr Genomics. 2002;1:367–74. doi: 10.1007/s10142-001-0045-z. [DOI] [PubMed] [Google Scholar]
- [31].Orwoll ES, Belknap JK, Klein RF. Gender specificity in the genetic determinants of peak bone mass. J Bone Miner Res. 2001;16:1962–71. doi: 10.1359/jbmr.2001.16.11.1962. [DOI] [PubMed] [Google Scholar]
- [32].Yershov Y, Baldini TH, Villagomez S, Young T, Martin ML, Bockman RS, et al. Bone strength and related traits in HcB/Dem recombinant congenic mice. J Bone Miner Res. 2001;16:992–1003. doi: 10.1359/jbmr.2001.16.6.992. [DOI] [PubMed] [Google Scholar]
- [33].Leamy LJ, Pomp D, Eisen EJ, Cheverud JM. Pleiotropy of quantitative trait loci for organ weights and limb bone lengths in mice. Physiol Genomics. 2002;10:21–9. doi: 10.1152/physiolgenomics.00018.2002. [DOI] [PubMed] [Google Scholar]
- [34].Li X, Wang H, Touma E, Rousseau E, Quigg RJ, Ryaby JT. Genetic network and pathway analysis of differentially expressed proteins during critical cellular events in fracture repair. J Cell Biochem. 2007;100:527–43. doi: 10.1002/jcb.21017. [DOI] [PubMed] [Google Scholar]
- [35].Mohan S, Masinde G, Li X, Baylink DJ. Mapping quantitative trait loci that influence serum insulin-like growth factor binding protein-5 levels in F2 mice (MRL/MpJ X SJL/J) Endocrinology. 2003;144:3491–6. doi: 10.1210/en.2003-0042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Viguet-Carrin S, Roux JP, Arlot ME, Merabet Z, Leeming DJ, Byrjalsen I, et al. Contribution of the advanced glycation end product pentosidine and of maturation of type I collagen to compressive biomechanical properties of human lumbar vertebrae. Bone. 2006;39:1073–9. doi: 10.1016/j.bone.2006.05.013. [DOI] [PubMed] [Google Scholar]
- [37].Martin RB, Ishida J. The relative effects of collagen fiber orientation, porosity, density, and mineralization on bone strength. J Biomech. 1989;22:419–26. doi: 10.1016/0021-9290(89)90202-9. [DOI] [PubMed] [Google Scholar]
- [38].Fyhrie DP, Schaffler MB. Failure mechanisms in human vertebral cancellous bone. Bone. 1994;15:105–9. doi: 10.1016/8756-3282(94)90900-8. [DOI] [PubMed] [Google Scholar]
- [39].Keaveny TM, Yeh OC. Architecture and trabecular bone — toward an improved understanding of the biomechanical effects of age, sex and osteoporosis. J Musculoskelet Neuronal Interact. 2002;2:205–8. [PubMed] [Google Scholar]
- [40].Li R, Tsaih SW, Shockley K, Stylianou IM, Wergedal J, Paigen B, et al. Structural model analysis of multiple quantitative traits. PLoS Genet. 2006;2:e114. doi: 10.1371/journal.pgen.0020114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Glatt V, Canalis E, Stadmeyer L, Bouxsein ML. Age-related changes in trabecular architecture differ in female and male C57BL/6J mice. J Bone Miner Res. 2007;22:1197–207. doi: 10.1359/jbmr.070507. [DOI] [PubMed] [Google Scholar]
- [42].Ruimerman R, Hilbers P, van Rietbergen B, Huiskes R. A theoretical framework for strain-related trabecular bone maintenance and adaptation. J Biomech. 2005;38:931–41. doi: 10.1016/j.jbiomech.2004.03.037. [DOI] [PubMed] [Google Scholar]
- [43].Wang L, Wang Y, Han Y, Henderson SC, Majeska RJ, Weinbaum S, et al. In situ measurement of solute transport in the bone lacunar-canalicular system. Proc Natl Acad Sci U S A. 2005;102:11911–6. doi: 10.1073/pnas.0505193102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Akhter MP, Iwaniec UT, Covey MA, Cullen DM, Kimmel DB, Recker RR. Genetic variations in bone density, histomorphometry, and strength in mice. Calcif Tissue Int. 2000;67:337–44. doi: 10.1007/s002230001144. [DOI] [PubMed] [Google Scholar]
- [45].Guo XE, Kim CH. Mechanical consequence of trabecular bone loss and its treatment: a three-dimensional model simulation. Bone. 2002;30:404–11. doi: 10.1016/s8756-3282(01)00673-1. [DOI] [PubMed] [Google Scholar]
- [46].Liebschner MA, Muller R, Wimalawansa SJ, Rajapakse CS, Gunaratne GH. Testing two predictions for fracture load using computer models of trabecular bone. Biophys J. 2005;89:759–67. doi: 10.1529/biophysj.104.057539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Silva MJ, Gibson LJ. Modeling the mechanical behavior of vertebral trabecular bone: effects of age-related changes in microstructure. Bone. 1997;21:191–9. doi: 10.1016/s8756-3282(97)00100-2. [DOI] [PubMed] [Google Scholar]
- [48].Ciarelli TE, Fyhrie DP, Schaffler MB, Goldstein SA. Variations in three-dimensional cancellous bone architecture of the proximal femur in female hip fractures and in controls. J Bone Miner Res. 2000;15:32–40. doi: 10.1359/jbmr.2000.15.1.32. [DOI] [PubMed] [Google Scholar]
- [49].Singh M, Nagrath AR, Maini PS. Changes in trabecular pattern of the upper end of the femur as an index of osteoporosis. J Bone Joint Surg Am. 1970;52:457–67. [PubMed] [Google Scholar]
- [50].Mosekilde L, Ebbesen EN, Tornvig L, Thomsen JS. Trabecular bone structure and strength — remodelling and repair. J Musculoskelet Neuronal Interact. 2000;1:25–30. [PubMed] [Google Scholar]
- [51].Cowin SC. The false premise in Wolff’s Law. In: Cowin SC, editor. Bone Mechanics Handbook Boca Raton. CRC Press; 2001. pp. 30.1–30.15. [Google Scholar]


