Contrasting size evolution in marine and freshwater diatoms

Abstract

Diatoms are key players in the global carbon cycle and most aquatic ecosystems. Their cell sizes impact carbon sequestration and energy transfer to higher trophic levels. We report fundamental differences in size distributions of marine and freshwater diatoms, with marine diatoms significantly larger than freshwater species. An evolutionary game theoretical model with empirical allometries of growth and nutrient uptake shows that these differences can be explained by nitrogen versus phosphorus limitation, nutrient fluctuations and mixed layer depth differences. Constant and pulsed phosphorus supply select for small sizes, as does constant nitrogen supply. In contrast, intermediate frequency nitrogen pulses common in the ocean select for large sizes or the evolutionarily stable coexistence of large and small sizes. Size-dependent sinking interacts with mixed layer depth (MLD) to further modulate optimal sizes, with smaller sizes selected for by strong sinking and shallow MLD. In freshwaters, widespread phosphorus limitation, together with strong sinking and shallow MLD produce size distributions with smaller range, means and upper values, compared with the ocean. Shifting patterns of nutrient limitation and mixing may alter diatom size distributions, affecting global carbon cycle and the structure and functioning of aquatic ecosystems.

Body size is one of the most fundamental traits of organisms, affecting almost all aspects of their physiology and ecology (1, 2). Consequently, it is a major component of fitness subject to evolution by natural selection (3, 4). Macroevolutionary and ecological questions about body size include the direction of long-term size evolution, the maintenance of size diversity, and how body size is shaped by environmental factors. Phytoplankton have been used as a model system to explore many fundamental questions in ecology (5). Here, we investigate the role of environmental drivers on size evolution in a major group of phytoplankton, diatoms.

Diatoms are ubiquitous in both marine and freshwater environments, contributing up to 25% of the world's primary productivity and forming the basis of many aquatic food webs (6). Diatom size distributions greatly influence carbon sequestration efficiency: due to their faster sinking and slower dissolution, large cells export disproportionately large amount of carbon to the ocean floor (6, 7). Cell sizes of diatoms and other phytoplankton determine the flow of energy and materials to higher trophic levels and, hence, the structure and functioning of aquatic food webs (6). Consequently, understanding the factors that drive cell size evolution is needed to predict global carbon cycling and the functioning of diverse aquatic ecosystems. Phytoplankton (diatom) cell size is a result of diverse selective forces present in the environment, such as different patterns of nutrient limitation and physical mixing, and grazing pressure (8). Comparing size distributions across ecosystems that differ in their selective pressures should provide new insights on cell size evolution.

Marine and freshwater environments provide an opportunity for such a comparison, because they differ in many physical and chemical characteristics that may exert contrasting selective pressures on phytoplankton cell size. Although both nitrogen (N) and phosphorus (P) can limit different species at different times and locations, overall, N is thought to be more often limiting than P in marine systems, with the reverse in freshwaters (9). The mixed layer depth (MLD) is typically greater in marine systems than in freshwaters (10–12), thus affecting diatom persistence in the water column. Consequently, we anticipate differences in phytoplankton (diatom) size spectra between marine and freshwater systems. No studies to date have compared diatom size distributions from the 2 environments.

Diatom Size Distributions in Marine and Freshwaters.

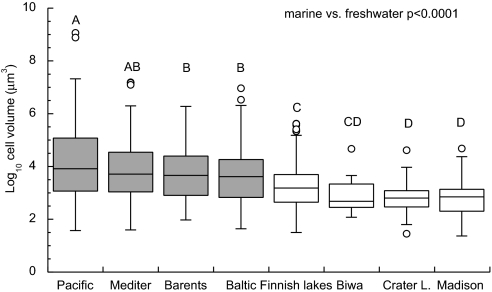
We compiled data on diatom cell sizes from diverse marine and freshwater ecosystems, including temperate and polar oceans and North American, European, and Japanese lakes (see Methods). We find that marine and freshwater diatom size distributions are significantly different (Fig. 1). Marine diatoms span almost 9 orders of magnitude in cell volume, with the largest species reaching >10⁹ μm³, whereas cell volumes of freshwater diatoms vary <6 orders of magnitude, with the largest cells ≈10⁶ μm³. Mean cell volumes of marine diatoms are an order of magnitude greater than in freshwaters (Fig. 1). The differences in size distributions between marine and freshwater diatoms that we report here appear universal, because they are robust across diverse ecosystems (Fig. 1), and thus suggest fundamentally different selective pressures in marine versus freshwater realm. What leads to the contrasting size distributions between marine and freshwater environments?

Fig. 1.

Box-Whisker plot of log₁₀ cell volume distributions of diatoms occurring in diverse marine and freshwater environments. Shaded distributions are from marine and clear distributions are from freshwater environments. Cell volumes are measured in cubic micrometers. The distributions are arranged in order of decreasing means (not medians) and do not account for species abundance. The data on cell volumes were log₁₀-transformed and compared using nonparameteric Wilcoxon test (pooled marine vs. freshwater environments) and Tukey-Kramer HSD test (each ecosystem, square root transformed log₁₀ volumes) using JMP (SAS). See Methods for sources of data and statistical details. Number of species for each ecosystem is given in parentheses: Pacific Ocean (n = 76), Mediterranean Sea (Bay of Marseille) (n = 103), Barents Sea (n = 167), Baltic Sea (n = 220), Finnish lakes (n = 329), Lake Biwa, Japan (n = 31), Crater Lake, OR (n = 56) and Madison, WI area lakes (n = 72). Baltic Sea data include some freshwater species and Finnish lakes data include some marine species (possibly from coastal lakes).

Small cell size makes the acquisition of limiting nutrients more efficient because of high surface area to volume ratio and, should, therefore, be competitively advantageous under nutrient limitation (13). High resource concentrations select species with high maximum growth rates (14), and because maximum growth rates are negatively correlated with cell size (15), small species should again have a competitive advantage. Why then do large sizes ever evolve? One potential mechanism that has been hypothesized to select for large-celled species is nutrient storage ability in a fluctuating nutrient environment (16, 17).

In phytoplankton, key parameters of nutrient-dependent growth and uptake scale allometrically with cell volume (16, 18). Consequently, selective pressures that lead to the evolution of nutrient acquisition traits (e.g., nutrient limitation) will likely alter phytoplankton cell size. Using techniques from evolutionary game theory to integrate these physiological traits into fitness (5, 19), we derive evolutionarily stable cell sizes of marine and freshwater diatoms under different scenarios of nutrient limitation, including fluctuating nutrient conditions.

Model.

We model phytoplankton growth and competition with a periodically forced system of differential equations. Variables are available nutrient R (μmol·L⁻¹), cell density N_i (cells per L) and internal nutrient quota Q_i (μmol nutrient·cell⁻¹) for each species i. Growth depends on nutrient quota following the Droop model (20), with minimum nutrient quota Q_min and theoretical growth rate at infinite quota μ_∞ (day⁻¹). Nutrient uptake follows Michaelis-Menten kinetics with nutrient saturated uptake rate V_max (μmol nutrient cell⁻¹·day⁻¹) and half-saturation constant K (μmol·nutrient·L⁻¹). We further assume negative feedback of internal nutrient quota on nutrient uptake, so V_max declines linearly from V _max^hi at the minimum quota Q_min to V _max^lo at the maximum quota during nutrient-replete exponential growth Q_max (16, 21). We include 2 continuous sources of density-independent mortality: size-independent background mortality at rate m (day⁻¹) and size-dependent sinking losses at rate v/z_m, where v is the sinking rate (m day⁻¹) and z_m(m) is the mixed layer depth (MLD). Taken together, the equations for each species are

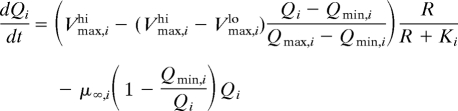Models of this general form have been extensively used to model phytoplankton growth and competition (e.g., refs. 14, 16, and 22).

The following species-specific parameters are assumed to depend allometrically on cell size s: Q_min, Q_max, V _max^hi, μ_∞, K, and v. Other parameters are size- and species-independent, except V _max^lo, which is set to V _max^lo = μ_∞(Q_max − Q_min) so that Q = Q_max when growing at maximum growth rate (16, 21). V _max^hi is constrained to be less than or equal to V_max^lo, but we obtain similar results without this constraint.

Nutrients are continuously taken up by phytoplankton and periodically resupplied with period T (day). Between mixing events,

Mixing events replace a fraction a of the mixed layer with water from the deep, which is assumed to contain no phytoplankton but abundant nutrients R_in. Thus,

for all positive integers j.

We analyze the model using techniques from evolutionary game theory (19, 23). We take log₁₀ cell volume, s, as our trait. A central concept in this approach is invasion fitness, g(s_inv,s⃗_res), which is defined as the invasion rate of a new strategy, s_inv, invading an established community, s⃗_res, when rare. Because our model has both periodic forcing and physiologically structured populations, we numerically calculate invasion fitness as follows: (i) we solve for the resident community dynamics until it reaches a stable limit cycle; (ii) we force the invader's quota equation with the nutrient dynamics determined by the resident community until the invader's quota reaches a stable limit cycle; (iii) we integrate the invader's growth rate over one period based on its stable quota cycle (24). A more formal approach to calculating invasion fitness based on Floquet theory (25) was used by Kooi and Troost (26), which is identical in practice.

We assume that all strategies are accessible, either through mutations of large effect or invasion by a preexisting species. This follows the ESS approach of Brown and Vincent (23, 27) and contrasts with the common assumption of Adaptive Dynamics theory that the only source of new phenotypes is small-effect mutation of an existing species (20). Abrams compares these closely related approaches to evolutionary game theory in (28). We focus on the endpoint of evolution, which is a species or set of species that prevents invasion by any other size species, known as an evolutionarily stable state (ESS) (19). Because we assume that evolutionary change is not restricted to small mutations, we look for globally stable evolutionarily stable states (ESSs) that prevent invasion by all other strategies, rather than locally stable ESSs. An ESS may contain one or more distinct sizes.

Results

In marine environments nitrogen (N) limitation is widespread (9, 29) and thus can be a strong selective force on cell size. Under constant limiting nitrogen supply, selection minimizes R*, a composite measure of nutrient competitive ability, the breakeven resource concentration at which growth equals mortality (14, 30). Given the empirically-derived allometric relationships for nitrogen (nitrate)-related uptake and growth in marine diatoms (Table S1), the minimum R* occurs at extremely small sizes (Evolutionarily Stable Strategy (ESS) size s* = −0.185). Therefore, constant but limiting N supply selects for small sizes. At high nitrogen supply, selection maximizes exponential growth rates (14) resulting in small cell sizes as well (s* = 1.126).

In contrast, pulsed nitrogen supply can lead to larger cells, which dominate because of their enhanced storage capacity (Fig. 2). Nitrogen pulses of different periods and magnitudes produce a wide range of optimal sizes, from <10² (at high and low pulse periods) to 10⁹ μm³ (at intermediate pulse periods) (Fig. 2 and Fig. S1). This predicted range corresponds remarkably well to the observed size distributions of marine diatoms that range from <10² to >10⁹ μm³ (Fig. 1). The dynamics of nutrients, quota, and biomass depend on pulse period (Fig. 3).

Fig. 2.

Evolutionarily stable strategy (ESS) size s* as a function of pulse period T for marine N-limitation. Solid lines represent single species ESSs, dashed lines represent 2-species ESSs. Cell size is expressed as log₁₀ of cell volume (μm³). Sinking rate v = 0. a is the fraction of the mixed layer water replaced each mixing event (a = 0.1, 0.3, 0.5). Deep water nutrient concentration R_in = 40 μmol·L⁻¹. Results for other values of a are given in Fig. S1.

Fig. 3.

Dynamics of the ESS species under different nutrient supply periods for marine N-limitation with a = 0.3. B*Q_min is the size-normalized biomass, Q/Q_minis the size-normalized nutrient quota, and R is the available nutrient. (A) T = 3 days, s* = 6.404. (B) T = 14 days, s* = 8.315. (C) T = 35 days, s* = [2.510 (solid), 8.898 (dashed)]. (D) T = 40 days, s* = 2.297.

Interestingly, at intermediate periods of N supply (≈30–40 days), there is often a 2-species ESS consisting of large and small cell sizes coexisting (Figs. 2 and 3C and Figs. S1 and S2). When they coexist, the small-celled species grows rapidly after a pulse, whereas the large-celled species' greater nutrient-storage ability fuels its growth later in the period (Fig. 3C). The 2-species ESS originates when a single-species ESS loses its global ESS stability (Fig. S2), a generic phenomenon in such models (31). This may contribute to the apparent bimodality of observed size distributions in some marine systems (Fig. S3). With infrequent pulses (T >40 days), conditions approach constant limitation interspersed with high nutrient periods which both select for small sizes (minimization of R* and maximization of exponential growth, respectively).

In the ocean, nutrient pulses result from different physical processes such as internal waves, vertical convective mixing, mesoscale eddies and Rossby waves, among others (32–34). The periods of these pulses range from semidiurnal and several days, common in coastal seas, to biweekly, monthly and up to a year in the open ocean (33–35). Such a wide range of frequencies of nitrogen supply can generate a broad range of optimal sizes, including cell volumes up to 10⁹ μm³ (Fig. 2). Changes in the dominant frequencies of nitrogen pulses may shift the size distributions of diatom communities.

Another selective force on diatom cell size is sinking. Sinking rates are highly variable and depend on the physiological state of cells. In physiologically active diatoms, sinking rates are small and do not depend significantly on cell volume (36). Physiologically compromised cells have higher sinking rates that increase with increasing cell volume (36). We explored the effects of different sinking scenarios on optimal cell size and its dependency on mixed layer depth. Size-independent sinking, as observed in physiologically competent diatoms (36), slightly increases mortality but does not change the optimal sizes significantly, compared with no-sinking scenarios (Fig. 4). The most extreme sinking scenario (inactivated cells) with strong size dependency decreases the maximum possible size, particularly for shallower mixed layer depths (MLD) (Fig. 4). However, extremely large diatoms can have a positive buoyancy and are able to migrate to nutrient-rich depths and upwards (37), thus potentially gaining an additional competitive advantage over small cells.

Fig. 4.

The effect of sinking and MLD on optimal diatom size under pulsed nitrogen supply. Lines represent different sinking and MLD scenarios: Size-independent sinking (v = 0.17 m·day⁻¹) characteristic of healthy diatoms and MLD = 100 m, strong size-dependent sinking (inactivated cells) and MLD = 10, 25, 100, 250 m. Observed size distributions, pooled for marine and freshwater environments from Fig. 1, are shown for comparison.

Phosphorus (P) can sometimes limit phytoplankton, including diatom, growth in the ocean (29, 38). Using the empirically derived P-dependent allometries (Table S1), we found that, in contrast to N limitation, neither constant nor pulsed P supply of any period selected for large sizes; instead smaller sizes are always favored, leading to run-away selection for small size (Fig. S4). The possible mechanism underlying the difference in the effect of N vs. P limitation on cell size is the allometric scaling of the minimum and maximum nutrient quotas (Table S1). For N, the allometric exponent of Q_max is larger than that of Q_min, leading to a disproportionate increase in storage capacity (Q_max/Q_min) with increasing cell size and, thus, to selection for large sizes under pulsed N supply. In contrast, for P, the allometric exponent of Q_max is nearly identical to that of Q_min, limiting relative storage capabilities at large sizes. These differences in N vs. P storage allometries may arise because of different locations of stored N vs. P within a cell: nitrogen (nitrate) is stored primarily in the central vacuole (39); the vacuole volume and, hence, Q_max, increase disproportionately with diatom cell volume, whereas Q_min is determined more by the cytoplasm volume that does not increase with cell volume as rapidly as the vacuole volume (40), possibly leading to the ratio of the allometric exponents of Q_max and Q_min >1. In contrast, P is stored primarily in the cytoplasm (41), therefore, Q_max and Q_min for P are more likely to have similar cell volume exponents. More data on Q_max and Q_min for both N and P for a range of sizes would help test this hypothesis.

In freshwater environments, P is frequently a limiting nutrient (9). We used allometries for P-dependent uptake and growth derived for freshwater diatoms (Table S1) to determine the evolutionarily stable cell size s* under different regimes of P supply. As in marine diatoms, under P limitation, regardless of the temporal regime of supply (constant or pulsed), there is run-away selection for small size. Thus, P-limitation, either at equilibrium or under pulsed supply, cannot explain the large diatoms found in marine and freshwaters. This indicates that other factors such as grazing select for large cells.

Nitrogen limitation also occurs in freshwater environments (29); can it explain diatom size distributions in freshwaters? Insufficient data on N-dependent uptake and growth exist to derive the freshwater diatom-specific allometries, but if we assume freshwater N allometries are identical to those of marine diatoms, large sizes can evolve. However, higher sinking rates in freshwaters, because of a greater volume-specific silicification of cells (42), lower freshwater density and shallower MLD, may decrease optimal cell sizes compared with oceanic environments (Fig. 4).

Discussion

The interplay between N and P limitation may contribute to the evolution of large versus small cell sizes, respectively. Nitrogen limitation and pulsed supply of this nutrient can explain the evolution of extremely large diatom cell sizes found in the ocean. In freshwaters, more frequent P limitation (29) and shallow MLDs drive optimal cell sizes down, resulting in smaller sized diatoms and narrower size distributions in freshwater than in marine environments. If the dominant frequencies of nutrient pulses vary systematically between environments, this could also be reflected in the size spectra of diatoms present.

Using a similar model for generic phytoplankton, Verdy and colleagues (43) independently found that constant environments select for small (10⁻¹ mm³) to medium (10³ mm³) cells, which agrees with our finding that nutrient pulses are required to select for large (>10⁵ mm³) cells.

Our data compilation of size distributions includes only presence/absence of species in a given ecosystem, not their relative abundance, thus reflecting long-term evolution of sizes. Incorporating data on the relative abundances of different sizes in diverse aquatic ecosystems may produce greater variation in distributions, reflecting more immediate, system-specific selective pressures.

Limitation by other nutrients, such as silica and iron, may also exert selective pressure on cell size. Determining the allometric relationships of uptake and growth and the characteristic frequencies of pulses for these nutrients would help derive optimal cell sizes under their respective limitation.

It is widely believed that grazers drive the selection of large phytoplankton cells (44), but here we demonstrate that bottom-up factors can also select for large cells. N vs. P limitation and differences in MLD contribute to the explanation of the observed contrasting diatom size distributions in marine and freshwater environments. In addition to shallow MLD, increased stratification may also exacerbate sinking losses and select for smaller-sized diatoms, as was observed in L. Tahoe (45), thus supporting our predictions. Global change-driven shifts in nutrient limitation patterns and circulation regimes affecting temporal supply of nutrients and mixed layer depth dynamics and stratification (46) may alter the selective pressures on diatom size and thus change biogeochemical cycling, including carbon sequestration, and the functioning of marine and freshwater food webs.

Methods

Size Distribution Data.

The diatom cell volume data were obtained from the following sources: Baltic Sea: ref. 47 and www.helcom.fi/stc/files/Publications/Proceedings/bsep106ANNEX1Biovolumes_web.xls; Barents Sea: ref. 48 and www.nodc.noaa.gov/OC5/BARPLANK/WWW/HTML/bioatlas.html; Mediterranean Sea: ref. 49; Pacific Ocean: cell dimensions were obtained from E. L. Venrick's Ph.D. thesis (50), average dimensions were used to calculate cell volumes using formulas for geometric figures (51); Finnish lakes: www.ymparisto.fi; Crater Lake, Oregon (52); Lake Biwa, Japan (53); and Madison area lakes: North Temperate Lakes Long Term Ecological Research (http://lter.limnology.wisc.edu). Cell volumes were obtained by dividing the biomass values by cell density.

To compare size distributions between marine and freshwater environments, the data were pooled within each environment and tested for normality (Shapiro-Wilk test). Because of the nonnormal distribution and unequal variances, the two environments were compared using nonparametric Wilcoxon test (JMP SAS). Individual ecosystems were compared using Tukey-Kramer HSD test after the square root transformation of the log₁₀ of cell volumes to achieve normality.

Model Analysis.

We find a single-species evolutionarily singular strategy s* by setting a finite differenced approximation to the fitness gradient equal to zero using a numerical root finder. We then check its global evolutionary stability by scanning across all other values of s for positive g. If there are none, s* is a single-species ESS (solid lines in Fig. 2). If there are s that can invade s*, we search for a 2-strategy ESS s⃗ = (s₁*,s₂*) by simultaneously solving

and again checking for global evolutionary stability. In all cases we tested, the 2-species coalitions were evolutionarily stable (dashed lines in Fig. 2).

Pairwise invasibility plots (PIPs) (19) (Figs. S2 and S4) were obtained by evaluating the sign of g for a range of s_res and s_inv values. We include them in for illustration, but note that because we focus on globally stable ESSs, we do not focus on evolutionary branching points.

Our Mathematica code is available upon request.

Allometric Relationships Between Model Parameters and Cell Size.

Allometric relationships between model parameters and cell volume V_cell (Table S1) were determined from the literature as in Litchman et al. (18). Additional data for allometric relationships were taken from Banse (15), Grover (16), Moore and Villareal (37), Montagnes and Franklin (54), Reynolds (55), Rynearson and Armbrust (56) and Villareal et al. (57). We used ordinary least squares (OLS) regression of the log-transformed data to determine allometric coefficients. The reduced major axis (RMA) allometries produced qualitatively similar results (evolution of large size under pulsed N supply). To derive the allometric relationship between μ_∞ and cell volume, for every μ_max and corresponding V_cell, we calculated μ_∞ as follows, based on the relationships derived in Morel (21):

where μ_max were obtained from the literature and Q_max and Q_min were expressed as allometric functions of cell volume (Table S1). The OLS regression was then fitted to the log-transformed data.

Some allometric relationships were not significant at the level of P < 0.05, possibly due to too few data points. If the scaling exponents (b values) were not different from the predicted exponents (see ref. 18), we used the obtained relationships. Where possible, we also ran the model with the theoretically derived allometric exponents (18, 58) or allometries obtained in other studies (16) (see Table S1).

Under N limitation, for larger cell volumes, V _max^hiwas slightly lower than V _max^lo, possibly because of large uncertainty in the estimate of the allometric scaling of V _max^hi due to limited size range of the data available. Because V _max^lo estimates are likely more robust, because they are based on the Q_min and Q_max data from a wide range of cell sizes, we set V _max^hi = V _max^lo when V _max^hi < V _max^lo. Setting V _max^hi = V _max^lo or removing the constraint on V _max^hi instead did not significantly change the results.

Nutrient Limitation Scenarios.

We used deep water nutrient concentration R_in = 40 μmol L⁻¹ for nitrogen limitation and R_in = 40/16 μmol·L⁻¹ for phosphorus limitation scenarios, which are realistic for both marine and freshwater environments (11, 59, 60). Nutrient pulses were modeled as described above, where a, the fraction of the upper mixed layer water replaced by the deep water with nutrient concentration R_in varied from 0.05 to 0.95. Fig. 2 has a = 0.1, 0.3, 0.5, which represent realistic replacement fractions. Data on increases in nitrogen concentration in Sargasso Sea due to eddies (32) suggest that a can be ≈0.2−0.5, given the deep water nitrate concentration in the Sargasso Sea (58). The period of pulses T varied from 0.25 to 60 days, which comprises pulse periods resulting from diverse physical processes supplying nutrients into the upper mixed layer (61).

Sinking Rate.

We used 2 extreme sinking scenarios that bracket most possible sinking rates: (i) sinking rate independent of cell size, often observed in physiologically competent cells (36) and (ii) sinking rate proportional to cell size, observed in physiologically impaired cells (36). The sinking rate independent of cell size was set at 0.17 day⁻¹, as determined from Waite et al. (36). The cell size-dependent sinking was obtained by fitting the OLS regression to the data of Waite et al. (36) on sinking rates of inactivated diatom cells: sinking rate v = 0.43 log₁₀(V_cell) − 0.77. We prevent negative sinking rates by setting minimum sinking rate v = 0.

Mixed Layer Depth Variation.

We used the mixed layer depth z_m of 10, 25, 100 and 250 m, which are representative of many oceanic (25–250 m) and freshwater systems (10 and 25 m), respectively (10, 11, 62).