A High-Resolution Computational Atlas of the Human Hippocampus from Postmortem Magnetic Resonance Imaging at 9.4 Tesla

Abstract

This paper describes the construction of a computational anatomical atlas of the human hippocampus. The atlas is derived from high-resolution 9.4 Tesla MRI of postmortem samples. The main subfields of the hippocampus (cornu Ammonis fields CA1, CA2/3; the dentate gyrus; and the vestigial hippocampal sulcus) are labeled in the images manually using a combination of distinguishable image features and geometrical features. A synthetic average image is derived from the MRI of the samples using shape and intensity averaging in the diffeomorphic non-linear registration framework, and a consensus labeling of the template is generated. The agreement of the consensus labeling with manual labeling of each sample is measured, and the effect of aiding registration with landmarks and manually generated mask images is evaluated. The atlas is provided as an online resource with the aim of supporting subfield segmentation in emerging hippocampus imaging and image analysis techniques. An example application examining subfield-level hippocampal atrophy in temporal lobe epilepsy demonstrates the application of the atlas to in vivo studies.

1 Introduction

The hippocampus is a structure of acute interest in neuroimaging. It is primarily associated with encoding of episodic memory, but is also believed to play an important role in both encoding and retrieval of other types of long term memory (Squire et al., 2004; Moscovitch et al., 2006). Hippocampal neuropathology is of vital interest in the study of dementia, epilepsy, schizophrenia and other neurological and psychiatric disorders. However, the complex anatomy of the hippocampus poses challenges to image-based computational morphometry techniques. The hippocampus is formed by two interlocking folded layers of neurons, the cornu Ammonis (CA) and the dentate gyrus (DG), which are further subdivided into subfields and are believed to subserve different functional roles. Non-uniform neuron loss across the hippocampal subfields has been reported in neurodegenerative disorders (West et al., 2004; Bobinski et al., 1997; Braak and Braak, 1991), as has a non-uniform rate of neuroplasticity (Eriksson et al., 1998; Kuhn et al., 1996; van Praag et al., 2002). However, it is very difficult to distinguish the boundaries between hippocampal layers in clinical MRI modalities, since the voxel resolution of ≈ 1mm³ (isotropic) is larger than the thickness of the DG. The layered structure of the hippocampus can be appreciated in specialized T2-weighted sequences with a limited field of view and highly anisotropic voxels (Zeineh et al., 2003), although partial volume effects are significant in the anterior and posterior of the hippocampus, where the main axis of the structure curves with respect to the imaging plane. Emerging MRI technologies, including multi-coil designs and 7 Tesla human scanners, yield in vivo images with significantly improved resolution, and subfield differentiation is quickly becoming a reality (Van Leemput et al., 2008; Cho et al., 2008; Li et al., 2008; Bernasconi et al., 2008).

Traditionally, morphometry studies have represented the hippocampus as a homogeneous gray matter structure with a blob-like shape (Carmichael et al., 2005; Fischl et al., 2002; Hsu et al., 2002; Jack et al., 1995; Kelemen et al., 1999; Pitiot et al., 2004; Shen et al., 2002; Styner et al., 2004; Shenton et al., 2002). However, some of the more recent studies have focused on detecting disease-related structural and functional differences in the hippocampus at the subfield level (Zeineh et al., 2003; Wang et al., 2006; Apostolova et al., 2006; Kirwan et al., 2007; Mueller et al., 2007). In order to differentiate between subfields, investigators either label the subfields for each of the subjects in a given study or, in the studies that employ large deformation diffeomorphic metric mapping (LDDMM) computational anatomy techniques (Miller et al., 2006), label the template to which subjects’ images are normalized (Csernansky et al., 2005; Wang et al., 2006). In either case, the knowledge of where the subfields lie in image space is based on low-resolution in vivo imagery and the use of references, such as the Duvernoy (2005) atlas. However, emerging imaging modalities are making it possible to delineate hippocampal subfields in vivo with greater reliability. Van Leemput et al. (2008) leverages 3 Tesla multi-coil imaging at 0.4 × 0.4 × 0.8mm resolution to automatically label major hippocampal subfields with excellent accuracy. As 7 Tesla imaging becomes more common, even greater accuracy in subfield resolution will be possible.

The present paper is premised on the belief that a detailed atlas of the hippocampus based on postmortem high-resolution MRI would prove highly complementary to morphological studies that leverage computational anatomy methods. Postmortem imaging allows the hippocampus to be imaged in laboratory conditions, with greater field strength, smaller field of view and longer acquisition time, yielding high-contrast images with voxels about 100 times smaller in volume than in typical in vivo imaging. Indeed, Wieshmann et al. (1999) points out that a twenty-fold increase in resolution over current in vivo modalities is needed to distinguish the layers of the hippocampus reliably. Our approach involves MRI of brain samples containing the intact whole hippocampus at 9.4 Tesla, using overnight scans to achieve good contrast at high resolution. While others have imaged portions of the hippocampus at even higher resolution (Wieshmann et al., 1999; Fatterpekar et al., 2002; Chakeres et al., 2005), to the best of our knowledge, this is the first work to collect images of the entire structure with isotropic or nearly isotropic voxels 8–12nl in volume. We manually label hippocampal subfields relying on a combination of discernable intensity and shape features. To combine data from different samples, we apply an implementation of the unbiased image averaging algorithm by Avants and Gee (2004), which is based on diffeomorphic Lagrangian frame image registration. Registration accuracy is evaluated in terms of subfield label alignment in atlas space.

In addition to describing the postmortem atlas, this paper demonstrates a possible approach for leveraging the atlas in in vivo hippocampal morphometry studies. The atlas is used in combination with conventional geometric and image-based computational anatomy techniques to assess hippocampal atrophy in temporal lobe epilepsy (TLE). Atrophy is evaluated by estimating the asymmetry between the hippocampus contralateral to the side of seizure in TLE and the ipsilateral hippocampus. The postmortem hippocampus atlas allows us to estimate atrophy on a subfield-specific basis, and our experimental results suggest that atrophy across subfields in non-uniform.

2 Methods and Materials

2.1 Specimens and Imaging

Formalin-fixed brain specimens (≥21 days) from three autopsy cases with no abnormal neuropathological findings were studied. Hemispheres were separated from the cerebellum and brain stem, and samples containing the intact hippocampus and not larger than 70mm in diameter were extracted from each hemisphere by making two incisions: the first, orthogonal to the midsagittal plane and parallel to the main axis of the hippocampus, passing through the corpus callosum; the second, parallel to the midsagittal plane, removing the lateral-most third of the sample.

Images of five hippocampus samples (3 right, 2 left) were acquired on a 9.4 Tesla Varian 31cm horizontal bore scanner (Varian Inc, Palo Alto, CA) using a 70mm ID TEM transmit/receive volume coil (Insight Neuroimaging Systems, Worchester, MA). Samples were placed in leak-proof bags and wrapped with plastic to fit snugly inside the coil. ¹ Scanning parameters varied slightly across the samples and are listed in Table 1. All acquisitions used the standard multi-slice spin echo sequence with TR between 4s and 5s, and TE 26ms. An oblique slice plane was chosen to cover the hippocampus with as few slices as possible, requiring around 130 slices with 0.2mm slice thickness for most images. The phase encode direction was from left to right and the readout direction followed the long axis of the hippocampus. Four of the samples were scanned at 0.2mm×0.3mm×0.2mm resolution using 34–45 averages to achieve good contrast; these scans were acquired overnight. One sample was scanned at 0.2mm × 0.2mm × 0.2mm isotropic resolution with 225 averages over 63 hours.

Table 1.

Acquisition parameters for the high-resolution postmortem scans of the hippocampus. Column abbreviations are as follows; ID: scan identifier, TR/TE: relaxation and echo times, respectively, NT: number of averages, NS: number of slices, MAT: matrix size, FOV: field of view, THK: slice thickness, SNR: relative signal-to-noise ratio, where the value of 1000 corresponds to a single-average image with 1mm isotropic voxels, Time: total acquisition time.

ID	TR/TE (ms)	NT	NS	MAT	FOV (mm)	THK (mm)	Voxel Size (mm)	SNR	Time (h:min)
1R	4000/26	34	120	350 × 256	70 × 77	0.20	0.30 × 0.20 × 0.20	70	13:13
2L	5000/26	36	130	280 × 300	56 × 90	0.20	0.30 × 0.20 × 0.20	72	14:00
2R	5000/26	40	130	280 × 300	56 × 90	0.20	0.30 × 0.20 × 0.20	76	15:33
3L	5000/26	225	130	200 × 400	40 × 80	0.20	0.20 × 0.20 × 0.20	120	62:30
3R	5000/26	45	130	240 × 300	48 × 90	0.20	0.30 × 0.20 × 0.20	80	15:00

2.2 Manual Segmentation

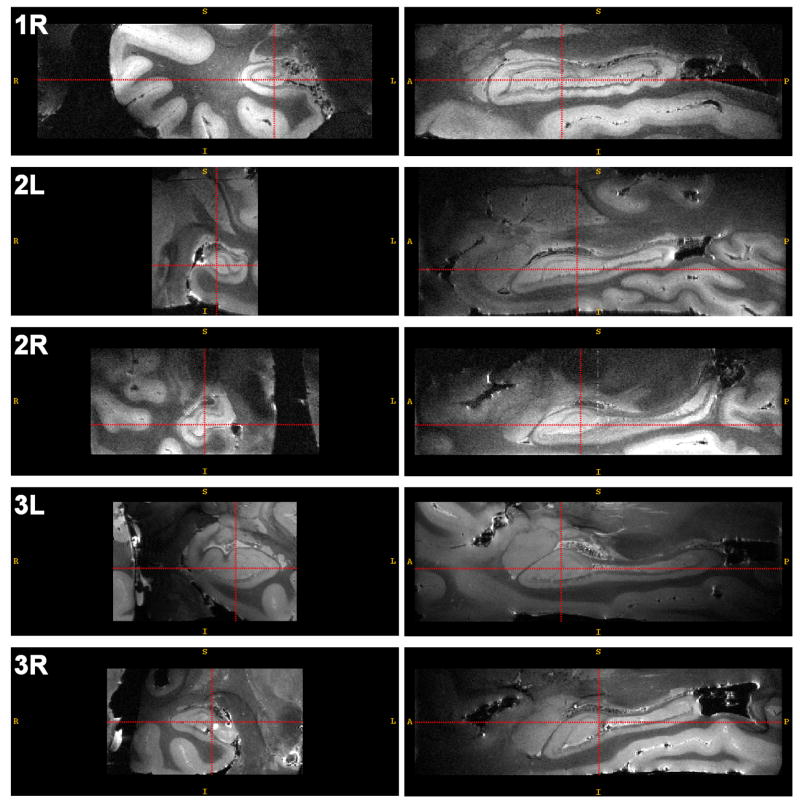
Reconstructed MRI images of each of the samples were segmented by one of the authors (JP) manually. The laminar structure of the hippocampus is clearly observable in these images (Fig. 1). With the help of the Duvernoy (2005) atlas and the labeling of the hippocampus in MRI slices by Fatterpekar et al. (2002), we were able to consistently identify four layers in the hippocampus: the high-intensity layer in the CA formed by the stratum oriens and the pyramidal cell layer; the low-intensity layer in the CA formed by the stratum radiatum, stratum lacunosum-moleculare and the vestigial hippocampal sulcus; the stratum moleculare of the dentate gyrus, and the dentate hilus (referred to as CA4 by some) ² The layers of the dentate gyrus are the most difficult to tell apart, while the contrast between bright layers of the CA, the dark layers of the CA and surrounding structures is very well pronounced. The boundaries between the different subfields in the pyramidal cell layer of the cornu ammonis (CA1, CA2 and CA3), as well as between CA and the subiculum, are not visible, and separation has to be made based on position and shape, rather than intensity. Perhaps the most difficult areas to segment were the transitions between subfields towards the head and the tail of the hippocampus.

Fig. 1.

Coronal and sagittal slices through each of the hippocampus images included in the atlas. The acquisition parameters for these images are listed in Table 1. Image 3L has 0.2mm³ isotropic resolution; other images have resolution 0.3 × 0.2 × 0.3mm³.

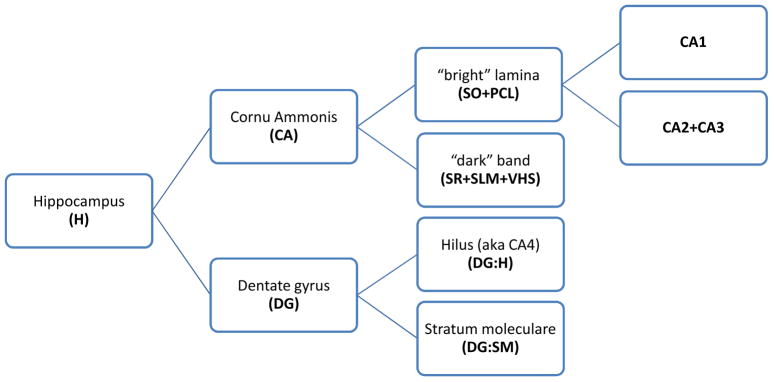
Based on our ability to consistently identify substructures in the hippocampus, we selected five labels for the segmentation: CA1; a label that combines CA2 with CA3; the dentate hilus (i.e., CA4); stratum moleculare of the dentate gyrus; and the label combining stratum radiatum, stratum lacunosum-moleculare and the vestigial hippocampal sulcus (i.e., the prominent ‘dark band’ in the MRI images). A schematic of the labels is shown in Fig. 2.

Fig. 2.

A diagram of the partitioning of the hippocampus into labels used in this paper. The abbreviations used in subsequent figures are in boldface. The leaf nodes in the graphs are the labels that were actually traced in the postmortem MR images. Later in the paper, segmentation repeatability and atlas consistency results are reported for the leaf nodes as well as for the parent-level structures formed by merging the labels corresponding to the leaf nodes. Abbreviations: SO = stratum oriens; PCL = pyramidal cell layer; SR = stratum radiatum; SLM = stratum lacunosum-moleculare; VHS = vestigial hippocampal sulcus.

Labeling was performed using ITK-SNAP (Yushkevich et al., 2006b), an open source image segmentation tool that allows simultaneous tracing in three orthogonal view planes and provides feedback via three-dimensional rendering of the segmentation. Most of the time was spent tracing the subfields in the coronal plane, with verification in the sagittal plane. In most of our images the hippocampus occupies over 200 coronal slices, making segmentation extremely labor-intensive, requiring about 40 hours of tracing and editing per image.

2.3 Reliability Analysis

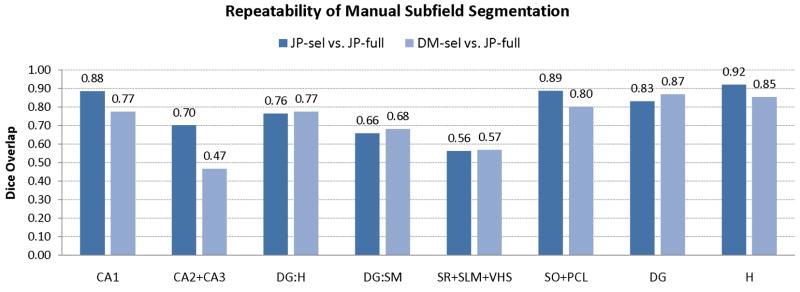
Given the difficulty of segmenting the hippocampus at high resolution, it was deemed impractical to perform reliability analysis, as is commonly done, by having multiple raters make multiple segmentation attempts. Instead, a limited reliability study was performed, in which a subset of five coronal slices was selected in each hippocampus image for repeated labeling. Two slices were selected in the head of the hippocampus, two in the midbody of the structure, and one in the tail. Rater JP segmented each of the slices a month after the completion of the five full hippocampus segmentations. Rater DM segmented the same slices independently after having been trained by JP. Dice overlap between segmentation attempts was used to assess intra-rater and inter-rater reliability.

2.4 Atlas Generation

Combining image data from multiple samples into a common atlas allows us to generate a model of “average” hippocampal anatomy, to boost signal-to-noise ratio, and to study variations in hippocampal structure across subjects. In building an atlas, we follow the work of Guimond and others (Guimond et al., 2000; Davis et al., 2004; Avants and Gee, 2004) by searching for a synthetic image that can be nonlinearly registered to each of the input images with minimal total deformation. Our normalization algorithm belongs to the family of large deformation diffeomorphic registration techniques (Christensen et al., 1997; Joshi and Miller, 2000; Beg et al., 2005; Miller et al., 2006) and is called Symmetric Normalization (SyN) (Avants et al., 2008). It uses a greedy symmetric approach, where, given an image match metricΠ, registration of images I and J seeks a pair of diffeomorphic maps φ₁, φ₂ that minimize

$$\begin{array}{l}E(I,J,{\phi }_1,{\phi }_2)=\mathrm{\Pi }[I({\phi }_1(\mathbf{x},\frac{1}{2})),J({\phi }_2(\mathbf{x},\frac{1}{2}))]+\\ +{\int }_0^{\frac{1}{2}}\parallel {\mathbf{v}}_1(\mathbf{x},t)\mid {\mid }_L\text{d}t+{\int }_0^{\frac{1}{2}}\parallel {\mathbf{v}}_2(\mathbf{x},t)\mid {\mid }_L\text{d}t,\\ \text{subj}.\text{to}\frac{\partial {\phi }_i(\mathbf{x},t)}{\partial t}={\mathbf{v}}_i({\phi }_i(\mathbf{x},t),t),i=1,2.\end{array}$$ (1)

Symmetric diffeomorphic maps from I to J and from J to I are given, respectively, by ${\phi }_2^{-1}\circ {\phi }_1$ and ${\phi }_1^{-1}\circ {\phi }_2$. By implementing a symmetric approach that searches for two coupled diffeomorphisms, SyN simultaneously generates forward and inverse maps between I and J, while the greedy implementation allows for reduced memory use and relatively fast convergence. SyN implements a multi-resolution scheme and our experiments used three levels of resolution, where images were smoothed and subsampled by factors of 4, 2 and 1 in each dimension. The step size is determined by the Courant-Friedrichs-Lewy (CFL) condition which restricts changes to the diffeomorphism to be sub-voxel, in this case, half a voxel in size. To reduce the number of parameters that influence the results and require tuning, optimization at each resolution level continues until there is no reduction in the metric value over several gradient descent iterations. In this way, we find a “best fit” diffeomorphism between the images, given the similarity metric. This philosophy is the natural diffeomorphic extension of basic rigid registration. For speed, linear interpolation of all data is used. Thus, the only parameters that influence outcome are choice of similarity terms, time-step (restricted under the CFL condition) and multi-resolution strategy.

Registration of postmortem MRI is challenging because images have different fields of view and because there are many unique local intensity features in each image (vessels, hyperintensities, imaging artifacts) that make finding one-to-one correspondences difficult. To boost registration accuracy, we introduce two kinds of manually generated aids: landmarks and rough binary masks of the hippocampus. Landmarks are placed at the two ends of each digitation in the head of the hippocampus (digitations are folds that can be seen in the right column of Fig. 1), as well as at the anterior-most point of the head and posterior-most point of the tail. Landmarks are incorporated into SyN by adding an additional term to the optimization criterion, as described in (Avants et al., 2008). SyN thus optimizes the prior (landmark) correspondence term simultaneously with the appearance term, leading to a different solution than an unguided normalization, in particular in the vicinity of the landmarks. Additional details of this approach are given in the Appendix.

Binary masks are generated in a fraction of the time required for the subfield segmentation because they are traced in the axial plane, where the hippocampus occupies the fewest slices, and because they are drawn roughly and made to include a layer of several pixels around the hippocampus. Both the landmarks and the masks require about an hour each to generate for every sample. When building an atlas from a larger postmortem dataset, it would be much more cost-effective to generate these registration aids than full manual segmentations. To incorporate masks into the registration, we apply a dilation operation to the masks with the radius of a few (5) voxels, and multiply the image by the mask. This causes the registration algorithm to line up mask boundaries, while also lining up the image intensity edges associated with the boundary between the hippocampus and surrounding tissues which remain slightly inside the mask. Also, in the presence of a mask, for all similarity metrics, the gradient value is multiplied by the mask value. Thus, information outside of the mask (represented by value zero) has no direct influence on the registration solution.

Initial linear alignment of hippocampus images based on image intensity alone proved difficult in postmortem data. Instead, affine alignment was performed by landmark matching, followed by matching of binary masks. Subsequent atlas building involved the following algorithm (Avants and Gee, 2004): (1) use SyN to register every image to a template; (2) average the intensity of all registered images; (3) average the initial velocity fields υ→(x, 0) of the maps from the template to each of the images and generate a shape distance minimizing diffeomorphic update to the template shape; this step is known as shape averaging (Avants and Gee, 2004); (4) repeat step 1 using the new shape average as the template. To make group-wise registration unbiased, Avants et al. (Avants and Gee, 2004) suggest using the intensity average of affine-registered images as the initial template. However, this requires a substantial number of images, so that the features common to all images are more prominent than the variation across images. Since in our case the number of samples is small, we choose one of the samples as the initial template. We use the normalized cross-correlation image match metric, which is robust to intensity inhomogeneity present in our data.

A consensus segmentation of the atlas is generated by warping the manual segmentations to the atlas and using the STAPLE algorithm (Warfield et al., 2004) to assign a label to each voxel. To examine the quality of alignment, we report the overlap in template space between the STAPLE segmentation and each of the individual segmentations.

3 Results

Fig. 1 shows coronal and sagittal slices through MRI images of each of the five samples used to construct the postmortem atlas. These images have good contrast, and the edges separating the hippocampus from adjacent tissue are well pronounced (e.g., unlike in clinical MRI, the amygdala is clearly separated from the hippocampus). A number of imaging artifacts are also evident: intensity inhomogeneity; hyperintensity and small amounts of distortion at tissue-air boundaries; ringing artifacts are also present in some images.

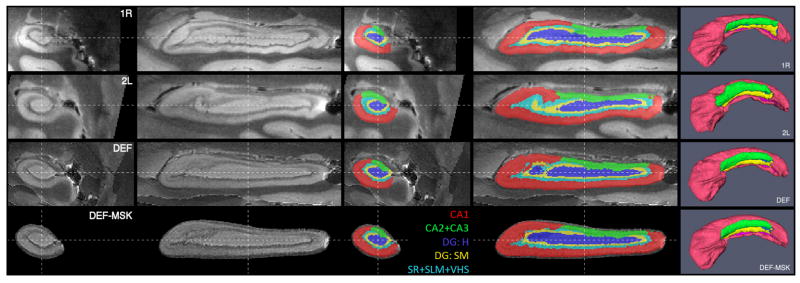
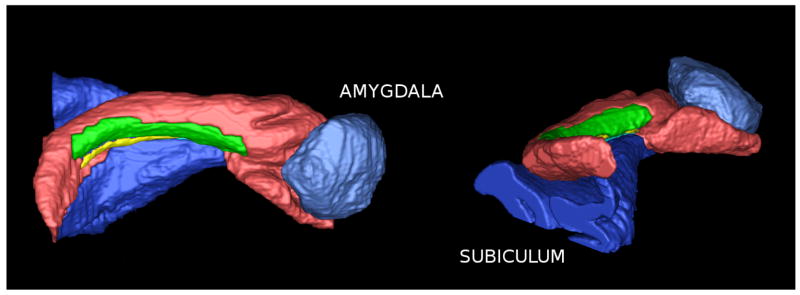
Segmentations of two of the samples are shown in two and three dimensions in Fig. 3. In one of the samples, the amygdala and the subiculum were segmented in addition to hippocampal subfields, shown in Fig. 4.

Fig. 3.

Coronal, sagittal and 3D views of hippocampus images and subfield labels for samples 1R and 2L, following aaffne alignment, and for atlases computed by unsupervised deformable registration (DEF) and mask-aided registration (DEF-MSK). Abbreviations: CA - cornu Ammonis; DG:H - hilus of the dentate gyrus (a.k.a. CA4); DG:SM - stratum moleculare of the dentate gyrus; SR - stratum radiatum; SLM - stratum lacunosum-moleculare; VHS -vestigial hippocampal sulcus.

Fig. 4.

Hippocampus segmentation, along with the adjacent amygdala and subiculum (the subiculum label includes the presubiculum, the parasubiculum and parts of the parahippocampal cortex) Subfield color labels are the same as in Fig. 3.

Overlap-based reliability analysis is given in Fig. 5. The repeatability of the segmentation by rater JP was high, while the inter-rater reliability was significantly lower for CA1 and CA2/3 and approximately the same for the other subfields. Lower reliability for CA2/3 is probably due to the differences in how far into the head of the hippocampus each rater would extend the CA2/3 label: JP did not label CA2/3 in roughly the anterior two fifths of the hippocampus (as seen in Fig. 3), while DM did label CA2/3 in the anterior hippocampus.

Fig. 5.

Analysis of segmentation repeatability, given in terms of Dice overlap between the full 3D segmentations used in constructing the atlas and repeated segmentations of a selected set of slices by two raters. Average Dice overlap for each subfield, as well as various combinations of subfields, is reported. See Fig. 2 for a diagram of the subfield labels appearing on the x-axis.

Atlases generated by diffeomorphic averaging with and without masks and landmarks are shown in Fig. 3. Notice that the atlases have image characteristics and shape similar to those of the input images. This is particularly noticeable in the 3D renderings of automatically generated consensus segmentations, where the folds in the anterior hippocampus are clearly visible.

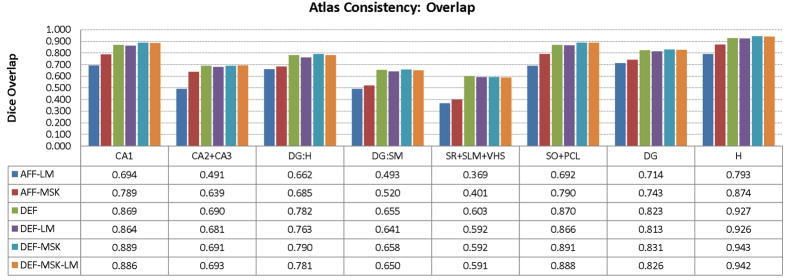
To simultaneously analyze the agreement between subfield labels across segmentations and normalization quality, we measure the overlap between the consensus segmentation of each atlas with the warped segmentations of individual samples. We emphasize that the subfield segmentations are not used during atlas building, although for some of the atlases, we guide registration with binary masks of the whole hippocampus, which are generated in an hour or less, and in the axial plane. For each subfield, Fig. 6 plots the average Dice overlap (Dice, 1945) for each subfield between the segmentation of the subfield in each individual, warped to atlas space, and the consensus segmentation of the subfield in the atlas, obtained using the STAPLE algorithm (Warfield et al., 2004). Based on the overlap, the atlas built using deformable registration with masks but without landmarks has the best consistency. Average overlap is nearly 90% for CA1, which is the largest subfield and nearly 80% for the dentate hilus (DG:H), which is smaller, but also the least hollow of the subfields. When the dentate gyrus is considered as a single structure by combining the dentate hilus with the stratum moleculare, the overlap increases to 83%. For the thinner layers, the dentate’s stratum moleculare and the dark band formed by SR, SLM and VHS, the overlap is below 70%. However, since these layers are very thin, even a small misalignment results in large overlap error.

Fig. 6.

Agreement between the consensus atlas labeling and segmentation of individual samples expressed in terms of average Dice overlap computed in atlas space. Six atlas-building approaches are compared: landmark-based and mask-based affne alignment (AFF-LM/AFF-MSK), image-based deformable normalization (DEF), deformable normalization aided by landmarks (DEF-LM), masks (DEF-MSK) and both masks and landmarks (DEF-LM-MSK). See Fig. 2 for a diagram of the subfield labels appearing on the x-axis.

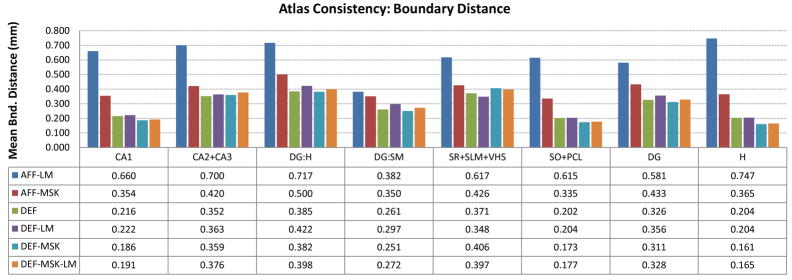
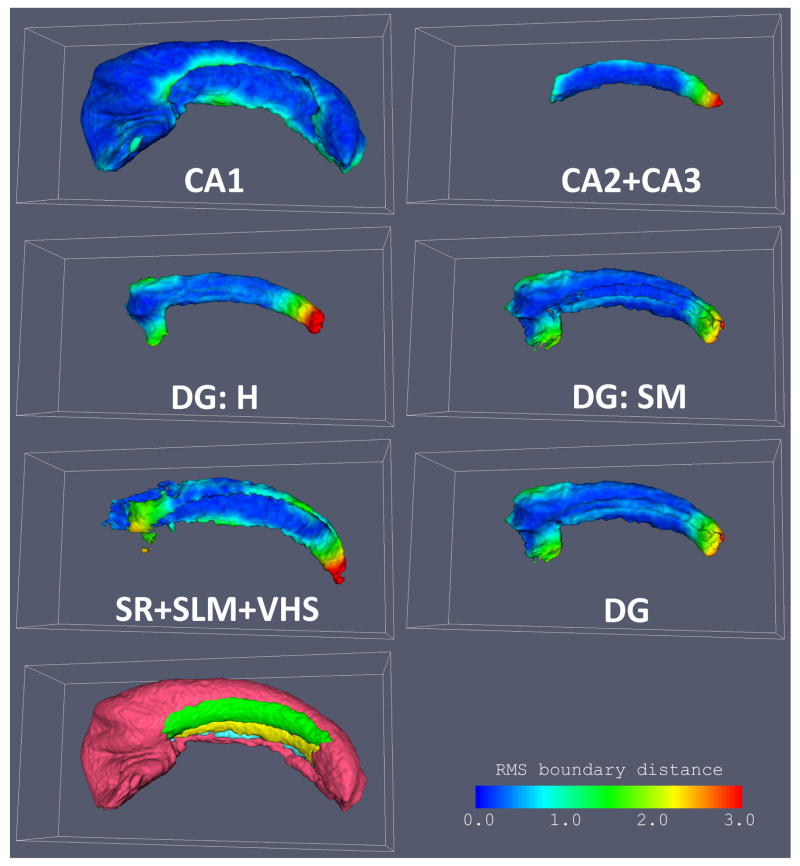
In addition to the overlaps, we plot in Fig. 7 the root mean square distance between the boundary surface of each subfield in the consensus segmentation and the corresponding boundary surface in each of the individual segmentations warped to atlas space. This measure of boundary displacement error is less sensitive to the thickness of structures than Dice overlap, and indeed the difference in this error is much less across all subfields than the overlap differences in Fig. 6. Furthermore, the average boundary displacement error can be evaluated point-wise on the boundary of each subfield in the atlas, resulting in a scalar map that can be helpful to identifying areas where subfield segmentation and normalization are least accurate. Fig 8 shows these maps for each of the subfields in the “DEF-MSK” atlas. It illustrates that the greatest disagreement in subfield labels is at two locations: the point where CA1 and the dentate gyrus merge towards the tail of the hippocampus, and the similar merging point in the head of the hippocampus. These points are very difficult to label consistently due to the lack of intensity features separating CA and the dentate at the anterior and posterior ends of the dentate. However, in the midbody of the hippocampus, the agreement is remarkably good, as is the alignment between the folds in the anterior hippocampus.

Fig. 7.

Agreement between the consensus atlas labeling and segmentation of individual samples expressed in terms of average distance between the boundaries of subfields in the atlas and the boundaries of corresponding subfields in warped individual segmentations. Refer to Fig. 6 for the explanation of different bars in the plot. See Fig. 2 for a diagram of the subfield labels appearing on the x-axis.

Fig. 8.

Surface maps of root mean square distance between each subfield in the atlas and the corresponding subfield segmentation in each of the input images warped to the atlas. The atlas used in this figure was constructed using binary masks and no landmarks (DEF-MSK in Fig. 6). Larger values in the maps (yellow and red) indicate lesser coherence between the atlas and the individual segmentations. At the bottom left, all subfields in the atlas are shown together to provide a visual reference.

Figs 6 and 7 clearly illustrate the improvement given by deformable registration over affine alignment, while the benefit of masks and landmarks used in deformable registration is not immediately apparent. To test if the use of landmarks and masking has a significant effect on Dice overlap, we use a 4-way ANOVA with factors ‘masking’, ‘landmarks’, ‘subfield’ and ‘sample’, allowing subfield-sample and masking-landmarks interactions. When applying ANOVA to Dice overlaps, we first normalize overlaps using the logit transform: logit(α) = log(α) − log(1 − α). As stipulated by Zou et al. (2004), this transform maps the overlaps to the entire real line, making Gaussian-based statistics more appropriate. However, in this particular experiment, this transform does not affect the significance of the ANOVA findings. When using all labels in Fig. 6, the ANOVA reports significant positive effect of masking on overlap (F = 28.3, p < 0.0001) as well as significant negative effect of using landmarks (F = 4.25, p = 0.04). No significant interaction between landmarks and masking is detected. Furthermore, when we exclude CA1 and its parent labels (SO+PCL, H, see Fig. 2), the effect of masking loses significance (F = 2.82, p = 0.10) while the negative effect of using landmarks remains (F = 5.21, p = 0.03). An equivalent ANOVA examination of boundary distances yields similar results: significant positive effect of masking, (F = 6.07, p = 0.02) and negative effect of landmarks (F = 4.61, p = 0.03) when considering all labels in Fig. 6; no significant effect of masking (F < 0.001, p = 1.00) and significant negative effect of landmarks (F = 5.45, p = 0.02) when looking only at internal subfields. These results suggest that the improvement associated with masking is greatest along the outer boundary of the hippocampus (as one would expect, since the mask falls very close to this boundary) while the improvement for the internal subfield alignment is minimal. Surprisingly, the use of landmarks had a counterproductive effect, perhaps because most of the mismatch occurs away from the anterior hippocampus where the majority of the landmarks were placed.

4 Application to In Vivo Studies ³

This section uses a small dataset from a temporal lobe epilepsy (TLE) imaging study to demonstrate how the postmortem hippocampus atlas may be used to analyze “standard” in vivo T1-weighted MRI data with 1mm³ resolution. In this experiment, we test the hypothesis that structural asymmetry between the diseased and healthy hippocampi in unilateral TLE varies across the hippocampal subfields.

Our approach uses standard normalization techniques to estimate volume change between the subfields in the hippocampus contralateral to the seizure focus (the “healthy” hippocampus) and the ipsilateral (“diseased”) hippocampus. The approach combines two normalization schemes: shape-based normalization is used to map subfield labels from the postmortem atlas to binary segmentations of the whole healthy-side hippocampus in T1 data; and deformable image registration is used to estimate asymmetry between the healthy and diseased hippocampus regions. Shape-based normalization yields an approximate labeling of the subfields in the healthy hippocampus and registration produces a field of Jacobian determinant values. By integrating the Jacobian field over the subfield labels, we get an estimate of volume change for each subfield. A drawback of this approach is that it relies on manual or semi-automatic segmentation of the hippocampus in in vivo data and is sensitive to errors in this segmentation, which can be substantial (Carmichael et al., 2005). Sec. 5.2 discusses more advanced potential approaches for postmortem to in vivo mapping.

4.1 Subjects, Imaging and Semi-Automatic Segmentation

Our in vivo experiment uses structural MRI data from an ongoing fMRI study of TLE. The aims and design of the study, which was originally implemented at 1.5 Tesla, are described in (Rabin et al., 2004). An updated protocol that uses 3 Tesla imaging is detailed in (Narayan et al., 2005). Our experiment uses a subset of the structural MRI data collected for the TLE study, according to the following inclusion criteria: (1) diagnosis of medically refractory TLE with a unilateral seizure focus; (2) successful outcome, in terms of seizure control, following epilepsy surgery; (3) absence of other neurological or psychiatric disorders; (4) imaging at 3 Tesla. Of the 12 patients that met these criteria, 5 had seizure focus in the right medial temporal lobe (4 female/1 male; age = 36.6(11.3)) and 7 had a left medial temporal lobe seizure focus (5 female/2 male; age = 40.0(15.4)). For each subject, the imaging data used in our experiment consisted of a high resolution (voxel size 0.9375 × 0.9375 × 1.0mm³) T1-weighted structural MRI scan obtained on a 3 Tesla Siemens Trio MRI scanner using an eight-channel head coil.

The hippocampus was segmented bilaterally by one of the co-authors (JP) using a combination of landmark-driven automatic atlas-based segmentation and manual editing in ITK-SNAP. The details of this semi-automatic segmentation protocol and reliability estimates for the TLE dataset appear in (Pluta et al., 2008). The reported reliability is high, with 85.9% average Dice overlap between manual and semi-automatic segmentation for the hippocampus contralateral to the seizure focus and 83.1% average overlap for the ipsilateral hippocampus.

4.2 Shape-Based Mapping of Hippocampal Subfields from Postmortem Atlas to the Healthy Hippocampus

Shape-based normalization is used to map hippocampal subfield labels from the postmortem hippocampus atlas to the segmentation of the healthy hippocampus in each image. Shape-based normalization is appropriate for mapping anatomical data between structures in situations where image intensity does not provide sufficient cues for establishing a mapping. This is the case for the mapping between the postmortem atlas, where the boundaries between subfields are clearly visible, and the T1 images, where these boundaries are blurred out or invisible because of insufficient resolution and partial volume effects. The assumption of shape-based mapping is that the position of the subfields relative to the overall hippocampus shape is roughly the same in the healthy in vivo hippocampus and the postmortem atlas. We recognize that this is a strong assumption that leads to an inherent level of error in subfield boundary estimation; however, some level of error must be accepted when estimating subfields in clinical resolution in vivo MRI, since the data itself does not provide sufficient clues for determining subfield boundaries.

Shape-based normalization uses the continuous medial representation (cm-rep) method (Yushkevich et al., 2006c, 2007, 2008b). This method represents anatomical structures using deformable models (cm-reps, for short) that describe objects in terms of their geometric skeletons and derive boundary representations of objects as a function of the skeletons. A cm-rep is fitted to the binary segmentation of each healthy hippocampus in the study by maximizing the overlap between the boundary representation and the binary image. During deformable modeling, cm-reps preserve the branching structure of the skeleton, making it possible to fit geometrically congruent skeletons to multiple instances of an anatomical structure, which in turn allows one to leverage geometrical features derived from the skeleton for normalization and shape analysis.

A cm-rep model is defined as follows. The skeleton of a cm-rep model is a surface patch (i.e., a manifold with boundary homeomorphic to the unit disk in ℝ²) that is specified as a triangle mesh. Each node in this mesh consists of a point m ∈ ℝ³ and a positive radius value R. The mesh is constructed by recursive subdivision of a coarse mesh using Loop subdivision rules (Loop and DeRose, 1990). The boundary of the model consists of two surface patches b⁺ and b⁻, one on each side of the skeleton. These boundary patches are derived from the skeleton mesh using the inverse skeletonization formula:

$${\mathbf{b}}^{\pm }=\mathbf{m}+R\left(-{\nabla }_{\mathbf{m}}R\pm \sqrt{1-\parallel {\nabla }_{\mathbf{m}}R\mid {\mid }^2}{\mathcal{N}}_{\mathbf{m}}\right),$$ (2)

where ∇_mR denotes the Riemannian (surface) gradient of R on m and 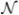_m denotes the unit normal to m. These first-order properties are computed using finite difference approximations (Xu, 2004). Constraints are in place to ensure that the two boundary patches share a common edge and do not self-intersect, thus forming a boundary of a simple region in ℝ³. These constraints are derived in (Yushkevich et al., 2006c) and an approach towards enforcing them on an triangle mesh is given in (Yushkevich et al., 2008b).

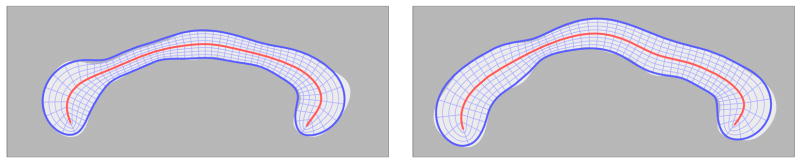
The interior of the cm-rep model is spanned by line segments, called spokes, which extend from points m_i on the skeleton to the corresponding points ${\mathbf{b}}_i^{+}$ and ${\mathbf{b}}_i^{-}$ on the model’s boundary and which are orthogonal to the boundary. As argued in Yushkevich et al. (2006c) and illustrated in Fig. 9, the spokes form a shape-based coordinate system on the interior of the cm-rep model. In this coordinate system, each point x on the interior of a cm-rep model is assigned a tuple (u, υ, ξ), where (u, υ) describes the position of the “tail” of the spoke passing through x on the medial surface m, and ξ describes the relative position of the point on the spoke between the medial surface and the boundary. The values (u, υ) at x depend on the parameterization of m and can be changed using reparameterization. During cm-rep model fitting, the parameterization is constrained to minimize the distortion in the area element of m(u, υ) across the medial surface. This constraint, analogous to uniform arc length parameterization of a curve, ensures that (u, υ) coordinates establish a degree of geometric correspondence between different cm-rep models.

Fig. 9.

A conceptual 2D illustration of shape-based normalization via the cm-rep coordinate system. The central curve is the skeleton m; the radial lines from the skeleton to the boundary are the spokes; the shape-based mapping between the two models is given by the locations of corresponding grid vertices.

Shape-based normalization between the postmortem hippocampus atlas and the hippocampi in in vivo data involves fitting a cm-rep model to the binary segmentation of the hippocampus in each of the images. Then the normalization is simply the set of diffeomorphic maps that take every point with coordinates (u, υ, ξ) in the cm-rep model fitted to the postmortem atlas to the points with the same coordinates in models fitted to the in vivo hippocampi. Using these maps, subfield labels can be assigned to each of the in vivo hippocampi.

4.3 Image-Based Estimation of Healthy-Diseased Asymmetry

Atrophy associated with temporal lobe epilepsy is defined as the localized rate of change in volume estimated using image registration. The rationale for using image registration is that some features revealing subfield boundaries may be present in the in vivo data. While it may be difficult to match these features to the postmortem atlas, which has a different modality, resolution and field of view, matching these features between the left and right hippocampi in the same subject is a less difficult registration problem.

Registration is performed between the healthy and diseased hippocampi for each subject. To initialize the registration, we use cm-rep models. We fit a cm-rep model to both hippocampi, thus establishing a shape-based point correspondence. We then flip the diseased hippocampus model across the MR image left-right axis and use Procrustes analysis to find a six-parameter rigid body transformation of the flipped model that minimizes the sum of squared distances between points in the flipped model and the corresponding points in the model fitted to the healthy hippocampus. This transformation gives a very good initial mapping from the neighborhood of the diseased hippocampus to the neighborhood of the healthy hippocampus (see the left two columns in Fig. 11). The SyN method, described above in Sec. 2.4, is then used to compute a deformable registration between the two hippocampi. SyN generates a deformation vector field in the space of the healthy hippocampus. This field maps each voxel in the neighborhood of the healthy hippocampus to a point in the neighborhood of the rigidly aligned flipped diseased hippocampus. The Jacobian of this vector field estimates the pointwise local rate of atrophy between the healthy and diseased hippocampi. By integrating this Jacobian field over each subfield label (computed for the healthy hippocampus in the previous section), we get an estimate of atrophy for that subfield. We express atrophy using the asymmetry index (AI):

$$\text{AI}=\frac{V_{\text{contralateral}}-V_{\text{ipsilateral}}}{V_{\text{contralateral}}+V_{\text{ipsilateral}}},$$

where V is the estimated volume of a subfield. Positive values of the asymmetry index indicate atrophy in the diseased hippocampus.

Fig. 11.

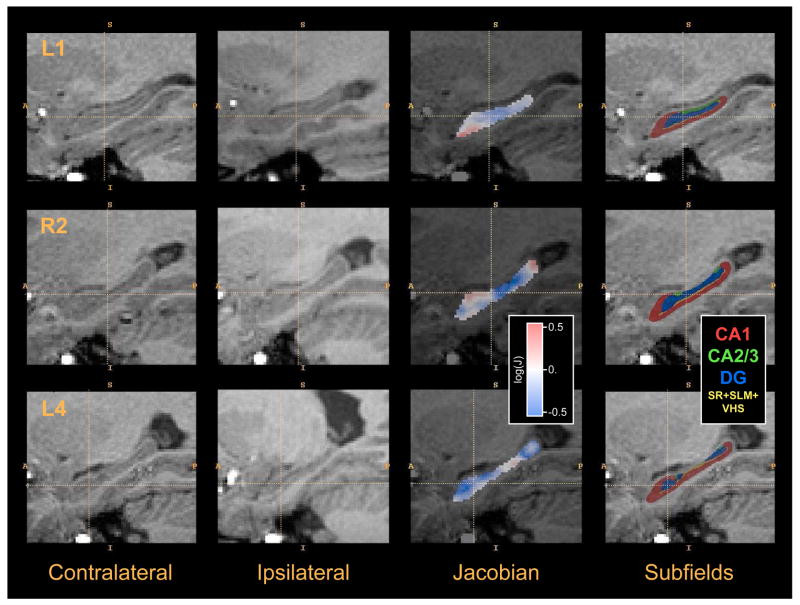
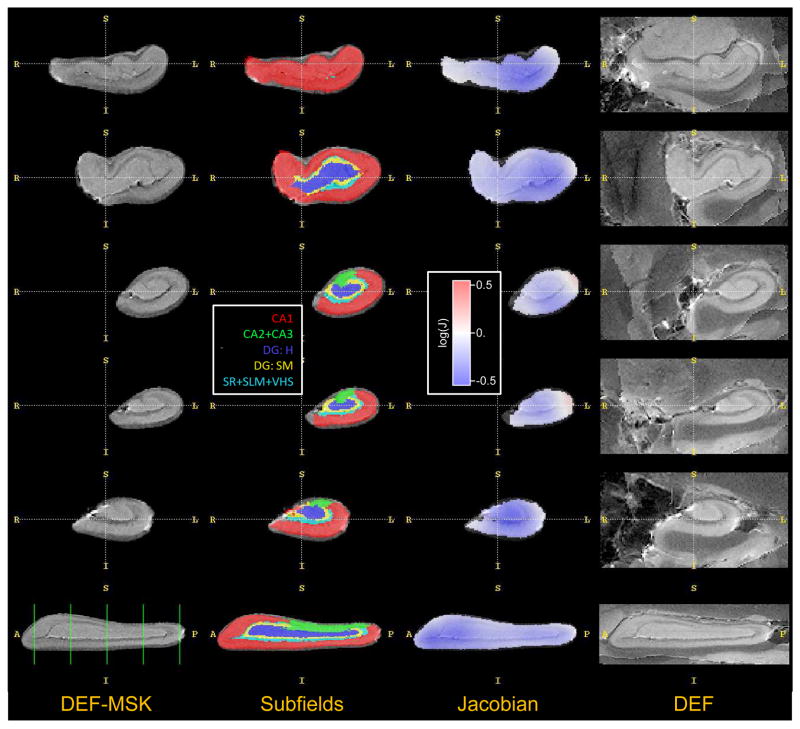
Example images from the in vivo temporal lobe epilepsy hippocampal asymmetry analysis experiment. Each row shows data from one of the subjects in the study. The first column shows a sagittal cross-section of the region surrounding the hippocampus contralateral to the seizure focus (“healthy” side). The second column shows the ipsilateral (“diseased”) hippocampus region after flipping across the midsagittal plane and rigid alignment to the healthy hippocampus. The third column plots the logarithm of the Jacobian of the transformation between the healthy hippocampus and diseased hippocampus computed by deformable image registration. Negative values (blue) indicate that a small region R in the healthy hippocampus maps to a smaller region in the diseased hippocampus; positive values (red) indicate the opposite. The Jacobian map is restricted to the the healthy hippocampus (i.e., to the manual segmentation). The last column shows the estimation of the location of hippocampal subfields in the healthy hippocampus. Subfields are mapped from the postmortem atlas using shape-based normalization.

4.4 Experimental Results

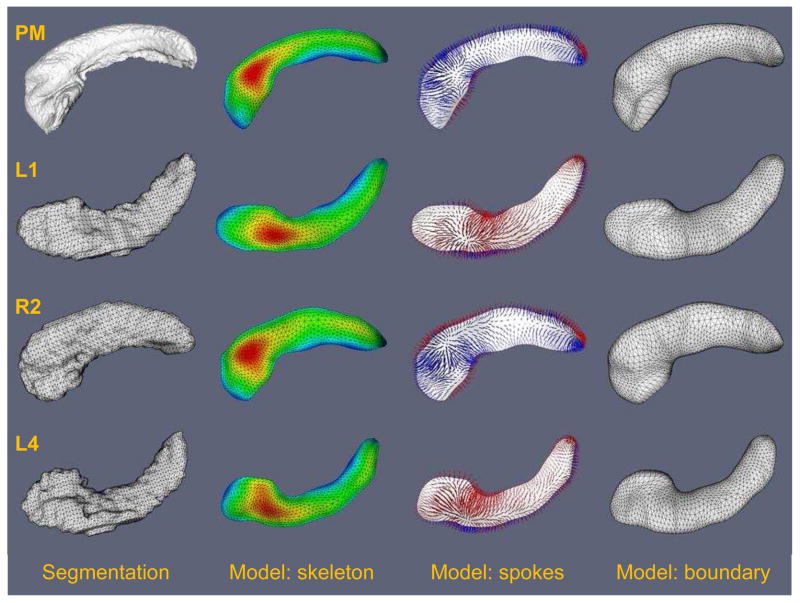
Fig. 10 illustrates the shape-based normalization approach. It shows examples of cm-rep models fitted to the postmortem atlas and to individual hippocampus segmentations from the in vivo data. The average Dice overlap between the segmentations of healthy hippocampi and the cm-rep models fitted to them was 0.921, and the average distance from the cm-rep model boundary to the segmentation boundary was 0.230mm. For the postmortem atlas, the overlap between the segmentation and the model was 0.946 and the average distance from the cm-rep model boundary to the segmentation boundary was 0.126mm. The fitting accuracy is higher for the postmortem hippocampus because its boundary is much smoother (see Fig. 10) and, thus, easier to fit using a deformable geometric model. The subfield mapping obtained using shape-based normalization is illustrated in the last column of Fig. 11. Image-based normalization is illustrated in Fig. 11, which shows examples of healthy hippocampus images, rigidly aligned diseased hippocampus images, and Jacobian determinant fields computed by SyN image registration.

Fig. 10.

Illustration of cm-rep model fitting used for shape-based normalization. The top row shows the cm-rep model fitted to the “DEF-MSK” postmortem hippocampus atlas (see Fig. 3), and the other rows show models fitted to segmentations of the “healthy” hippocampus for three subjects in the TLE study (subjects L1, R2 and L4; selected arbitrarily). The left column shows the target structure, i.e., the segmentation of the hippocampus. The second column shows the skeleton surface m of the fitted cm-rep model, with the color map plotting the radius function R on the skeleton. The third column illustrates the spoke field; spokes are line segments extend from the skeleton to the boundary, are orthogonal to the boundary and “span” the interior of the model (see Fig. 9 for the 2D illustration of spokes). Spokes extending to boundary half b⁻ are shown in blue, and spokes that extend to b⁻ are shown in red. Correspondence on the basis of spoke fields is used to map subfield labels from the postmortem atlas to the in vivo data. The last column shows the boundary surface b = b⁺ ∪ b⁻, which closely approximates the surface of the target hippocampus.

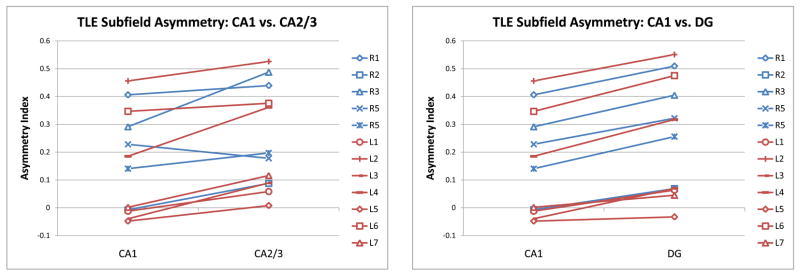
The estimated asymmetry index for subfields CA1, CA2/3 and DG for each subject is plotted in Fig. 13. Asymmetry in CA2/3 tends to be greater than in CA1; likewise, asymmetry is greater for DG than for CA1. These trends are confirmed by paired Student’s t-tests: p = 0.0008 for the AI(CA1) < AI(CA2/3) comparison and p < 0.0001 for the AI(CA1) < AI(DG) comparison. The test does not detect significant differences (p = 0.31) between AI(CA2/3) and AI(DG). To help understand the difference between atrophy across subfields, Fig. 12 projects (using mappings computed by shape-based normalization) the Jacobian maps from all subjects in the study into the space of the postmortem hippocampus atlas. In the coronal slices, the Jacobian appears lower along the middle section of the hippocampus, where DG and CA2/3 are.

Fig. 13.

Plots of volumetric asymmetry between the subfields of the healthy and diseased hippocampi in the in vivo TLE study. Each subject is represented by a line segment, with blue lines representing subjects with the right side of seizure and red lines corresponding to the left side of seizure. The y-axis plots the asymmetry index, i.e., the relative decrease in volume between the subfield in the healthy hippocampus and the same subfield in the diseased hippocampus. The plots illustrate the following trends: asymmetry in CA2/3 greater than asymmetry in CA1 (paired Student t-test p = 0.0008) and asymmetry in DG greater than asymmetry in CA1 (paired Student t-test p < 0.0001).

Fig. 12.

This figure plots the healthy/diseased asymmetry in TLE in a reference space, i.e., in the space of the postmortem hippocampus atlas. The left column shows 5 coronal slices and a sagittal slice through the postmortem atlas “DEF-MSK” (see Fig. 3), which is the atlas used in the TLE experiment. The second column shows the subfield labeling of the “DEF-MSK” atlas. The third column shows the logarithm of the Jacobian determinant of the mapping from the healthy hippocampus to the diseased hippocampus, averaged over all subjects. This average Jacobian map is computed by using shape-based normalization to transform the log-Jacobian maps shown in Fig. 11 back into atlas space, followed by computing the average. Negative values (blue) indicate local volumetric decrease (disease-associated atrophy); positive values (red) indicate local increase in volume. The last column shows corresponding slices from the non-masked postmortem atlas “DEF”, for the purpose of visualizing the adjacent tissues.

5 Discussion

5.1 Contributions

The main contributions of this work are (1) the acquisition and labeling of high-resolution nearly isotropic images of the whole hippocampus; (2) a demonstration of the efficacy of large deformation diffeomorphic mapping techniques normalizing high-resolution postmortem imaging data; (3) a proof-of-concept experiment showing the application of the postmortem atlas to in vivo studies; and (4) open-source public release of a data set and an atlas that have the potential to become valuable resources for investigators studying subfield-level hippocampal morphometry using in vivo imaging.

From the imaging point of view, although a number of authors have imaged the medial temporal lobe at high field and with very high resolution (Wieshmann et al., 1999; Fatterpekar et al., 2002; Chakeres et al., 2005), there has not been an emphasis on imaging the hippocampus as a whole at isotropic or nearly isotropic resolution, as we have done in this paper. Indeed, a common theme in prior postmortem imaging work is the use of MRI as a neuropathology tool, with comparisons between structures visible in MRI slices and corresponding histology slices. This led the authors to select protocols with high in-plane resolution and thick slices. Our principal goal in conducting the postmortem imaging study was to build a three-dimensional model of hippocampal shape and of the spatial distribution of hippocampal subfields. The main benefit of imaging with isotropic voxels, which has been our approach, is the ability to label the structures in the hippocampus in three dimensions.

The computational anatomy aspect of this work, i.e., building an atlas from a set of images, draws on existing methodology. The approach that we use, i.e., normalization via large deformation diffeomorphic registration and atlas generation via minimization of geodesic distance and shape averaging (Avants et al., 2008) is state-of-the-art and builds on some of the most highly acclaimed methodology in the computational anatomy field (Miller et al., 2006; Beg et al., 2005; Joshi and Miller, 2000; Christensen et al., 1997; Guimond et al., 2000; Davis et al., 2004). Probably, the most common application of diffeomorphic registration techniques is to whole-brain normalization, and the images collected in this study pose special challenges for these techniques due to higher resolution, limited and nonuniform field of view, and presence of various artifacts. We demonstrate that with the help of basic aids, such as masks outlining the structure of interest, diffeomorphic techniques can perform reasonably well on challenging data, and that without these aides, the loss in performance is moderate. Our experience may be of benefit to other researchers seeking to apply diffeomorphic techniques to “non-standard” imaging data, in particular ultra high-resolution in vivo imaging of hippocampal subfields that is becoming increasingly relevant with wider availability of 7 Tesla scanners.

The data collected and generated in this study are being made available through the NIH-sponsored Neuroinformatics Tools and Resources Clearinghouse (NITRC) under the name “Penn Hippocampus Atlas”. This resource includes raw imaging data, manual segmentations, affine and deformable transforms from native image space to atlas space, atlases and consensus segmentations. As data acquisition continues, new datasets will be continually released into the public domain. All data thus distributed is fully anonymous. We envision Penn Hippocampus Atlas as a resource that will contribute to the development of image analysis pipelines that allow automatic or semi-automatic estimation of the location, size and shape of hippocampal subfields in in vivo imaging data.

The experiment presented in section 4.4 demonstrates an application of the postmortem atlas on in-vivo data. Hippocampal volumetry has been widely used to study atrophy in TLE patients (Cendes, 1993; Bernasconi et al., 2003). However, as different regions within the hippocampus are known to be affected by the disease process differently, both in terms of their histopathology and seizure onset zones (King et al., 1997), the ability to perform subfield-level morphometry may provide greater insight into the associated atrophy patterns. Neuronal loss in DG, as well as in CA1 and CA3, is a common histological finding in sclerotic hippocampi (Swartz et al., 2006; Bote et al., 2008), which may lead to the volumetric asymmetry in these subfields as observed here (Figure 13). Greater relative atrophy in DG found here is consistent with the fact that the neurons in the hilus of DG are considered to be amongst the most vulnerable in TLE (Robbins et al., 1991), and is sometimes found more consistently than atrophy in CA1/CA3 (Swartz et al., 2006). However, other studies have found greater cellular neuropathology in CA1 (Van Paesschen et al., 1997). The use of subfield-level deformation based morphometry in quantifying atrophy is novel in the study of TLE, and further studies are required to fully evaluate the efficacy of this approach. Nonetheless, subfield-specific morphometric techniques have been shown to be useful in other clinical applications, including Alzheimer’s disease (Mueller et al., 2007), and the proof-of-concept application presented here shows promising preliminary results.

5.2 Potential Future Applications

This section briefly outlines possible approaches for leveraging the hippocampus atlas in in vivo imaging studies. This section is speculative, and its intention is to simply sketch out the range of approaches in which the atlas may be used. One of the main motivations for releasing the atlas publicly is to allow the developers of hippocampus-aimed approaches to leverage it in their algorithms.

We envision essentially three ways to map the postmortem hippocampus atlas to in vivo data: using shape correspondences, using image similarity, and using some combination of the two, as we did in Sec. 4.4. Shape correspondences can be found between manual segmentations of the hippocampus in in vivo data and segmentations in the postmortem atlas. Such correspondences, if interpolated over the interior of each segmentation, could be used to map subfield labels from the atlas to image space. However, the accuracy of shape-based mapping is highly dependent on the quality of the manual segmentation, which in itself is a challenging problem in clinical MRI, especially in the presence of neurodegeneration (Carmichael et al., 2005). Furthermore, the interpolation of correspondences onto the interior of an object means that the mapping of internal subfield boundaries (i.e., boundaries between subfields that are not curves on the hippocampus boundary, such as most of the DG/CA boundary) would be dependent solely on boundary shape cues, making inferences derived from the direct comparison of internal subfields (e.g., DG) across subjects questionable at the least. A more reliable approach, very similar in spirit to the approach taken in Sec. 4.4, is to use shape correspondences to map the postmortem atlas onto the hippocampus segmentation in a in vivo template, to which in vivo data are normalized using deformable image registration. Integration of the Jacobian field associated with this registration over each subfield defined in template space would yield subfield-specific volumetric features. Finally, for some less common imaging modalities, such as T2-weighted in vivo hippocampus-specific imaging at 3 Tesla, as used in (Mueller et al., 2007; Apostolova et al., 2006; Zeineh et al., 2003), or emerging 7 Tesla imaging (Cho et al., 2008; Li et al., 2008; Bernasconi et al., 2008), it may become possible to directly map the subfield information from the postmortem atlas to individual in vivo images on the basis of image similarity, in particular if aids like masks and landmarks are employed. This is the direction of our future work.

Another potential application of a detailed hippocampus atlas is to use it as a prior for deformable model segmentation of the hippocampus in vivo. One of the problems facing model-based segmentation is that the apparent topology of the hippocampus in clinical resolution images can change substantially in the presence of neurodegenerative disease. Some of the topological differences observed in in vivo modalities are due to the boundaries between hippocampal layers not visible in the healthy adult hippocampus appearing in aging and dementia. By inferring the topology and shape of the hippocampal layers from postmortem data and using it as a shape prior during segmentation it may be possible to reduce the number of possible topological configurations and thus enable better normalization of the hippocampus between cohorts.

5.3 Limitations

One of the limitations of this work is that the current atlas is based on a relatively small number of samples. This causes us to combine samples from both hemispheres in a single atlas, whereas it may be more appropriate to have separate atlases of the left and right hippocampus. Even though we believe that in its current state the atlas can be of potential benefit to other researchers, we intend to continue acquiring and labeling images of the postmortem hippocampus in different clinical populations. Specifically, we plan to image the hippocampus region in presence of Alzheimer’s disease and semantic dementia and to build atlases specific to these neurodegenerative disorders. As more samples are added to the atlas, it will become feasible to not only model the average hippocampus shape, but also the variation in the shape and intensity of the hippocampus. Along with collecting more data, we aim to expand the number of structures labeled in each sample to include those shown in Fig. 4. Having a computational model of the relationship between the hippocampal subfields, the amygdala, the fimbria and the subiculum will be of great benefit in in vivo applications where these structures are partially discernable.

Furthermore, the atlas would benefit from an extensive validation of the current postmortem image segmentation protocol. In postmortem data, a direct validation is possible by performing histological staining of the samples. Hippocampal strata and subfields can be differentiated in histological slices, providing a good estimate of ground truth. However, matching 2D histological slices with possible tearing and distortion to the 3D MRI atlas will pose substantial challenges. We have previously developed similar 2D–3D registration techniques for the mouse brain (Yushkevich et al., 2006a), and plan to apply them to the human hippocampus in our future work.

A possible limitation associated with applying the postmortem atlas to in vivo data is that one must be cautious to account for morphological differences between the living brain and formalin-fixed samples. Cutting of the samples may introduce additional deformations, although we take care to leave at least 1cm of tissue around the hippocampus to reduce such distortion. Nevertheless, some form of global shape correction will likely be necessary to account for these differences.

In the current atlas, the consensus segmentation of the hippocampus does not provide guarantees on the topology of the subfields. Indeed, as seen in Fig. 8, some of the thinner subfields have multiple connected components. This can be corrected by deforming a template with correct topology to the consensus segmentation using a label-by-label overlap metric. Incorrect topology may pose difficulty for applications that require geometrical modeling of the subfields, but does not preclude one from performing morphometry, similarly to how many brain tissue class segmentation algorithms can be leveraged without guarantees on the topology of the cortical mantle.

Appendix: Incorporating Landmarks in SyN

Define {Q} as the set of points describing the landmark labels within the template space, I. That is, Q_i ∈ {Q} is the Euclidean position of some labeled point in patient space. Define {q} as the set of points describing the landmark labels within the individual space, J. Note that the cardinality of {Q}, denoted n, and the cardinality of {q}, m, may not be the same. In most cases, however, m ≈ n. Then, given I; J, {q}, {Q}, and some initial estimate for φ₁, φ₂, find the shortest φ ∈ Di f f₀ such that:

1. || I (φ₁(x, 0:5)) − J(φ₂(x, 0:5)) || is minimal,

2. ${\sum }_j{w}_q^j\parallel {\phi }_2({\mathbf{q}}_j,0.5)-CL{({\phi }_1(\{\mathbf{Q}\},0.5))}_{{\phi }_2{q}_j}\parallel$ is minimal and

3. ${\sum }_i{w}_Q^i\parallel {\phi }_1({\mathbf{Q}}_i,0.5)-CL{({\phi }_2(\{\mathbf{q}\},0.5))}_{{\phi }_1{Q}_i}\parallel$ is minimal.

The function, CL({p}_q), represents the “closest point” operation. That is, CL returns the smallest distance between the point set, {p} with respect to the point q. This translates to the following variational problem, with linear operator L,

$$\begin{array}{r}{E}_{\mathit{SyN}}(I,J,\{\mathbf{q}\},\{\mathbf{Q}\})=\underset{{\phi }_1}{inf}\underset{{\phi }_2}{inf}{\int }_{t=0}^{0.5}\{<L{\mathbf{v}}_1,{\mathbf{v}}_1>+<L{\mathbf{v}}_2,{\mathbf{v}}_2>\}dt\\ +{\int }_{\mathrm{\Omega }}[\omega \mid I({\phi }_1(\mathbf{x},0.5))-J({\phi }_2(\mathbf{x},0.5)){\mid }^2\\ +\sum _j{w}_q^j\parallel {\phi }_2({\mathbf{q}}_j,0.5)-CL{({\phi }_1(\{\mathbf{Q}\},0.5))}_{{\phi }_2{q}_j}{\parallel }^2\\ +\sum _i{w}_Q^i\parallel {\phi }_1({\mathbf{Q}}_i,0.5)-CL{({\phi }_2(\{\mathbf{q}\},0.5))}_{{\phi }_1{Q}_i}{\parallel }^2]d\mathrm{\Omega }\end{array}$$

with ω a scalar and w_q and w_Q scalar, spatially varying weights and each φ_i the solution of:

$$d{\phi }_i(\mathbf{x},t)/dt={\mathbf{v}}_i({\phi }_i(x,t),t)\text{with}{\phi }_i(\mathbf{x},0)=\mathbf{x}.$$ (3)

In this work, we set ω = 1 as a constant, $w_q^j$ is a Gaussian smoothed dirac delta function centered at each deformed landmark with value 3 at the peak and $w_Q^i$ starts with the same value as $w_q^j$. We optimize this problem by gradient descent on the total energy, in the same multi-resolution framework as used for non-landmarked SyN.