Markov Chain-based Promoter Structure Modeling for Tissue-specific Expression Pattern Prediction

Abstract

Transcriptional regulation is the first level of regulation of gene expression and is therefore a major topic in computational biology. Genes with similar expression patterns can be assumed to be co-regulated at the transcriptional level by promoter sequences with a similar structure. Current approaches for modeling shared regulatory features tend to focus mainly on clustering of cis-regulatory sites. Here we introduce a Markov chain-based promoter structure model that uses both shared motifs and shared features from an input set of promoter sequences to predict candidate genes with similar expression. The model uses positional preference, order, and orientation of motifs. The trained model is used to score a genomic set of promoter sequences: high-scoring promoters are assumed to have a structure similar to the input sequences and are thus expected to drive similar expression patterns. We applied our model on two datasets in Caenorhabditis elegans and in Ciona intestinalis. Both computational and experimental verifications indicate that this model is capable of predicting candidate promoters driving similar expression patterns as the input-regulatory sequences. This model can be useful for finding promising candidate genes for wet-lab experiments and for increasing our understanding of transcriptional regulation.

1. Introduction

Gene expression in metazoans is regulated at many levels. Regulation of transcription is the first step in the cascade of regulation and is thus of great importance for our understanding of gene expression. Regulation of transcription is determined by the binding of transcription factors (TFs) to their corresponding TF binding sites (TFBSs), and regulatory sequences containing similar sets of TFBSs are expected to be under the control of similar sets of TFs and drive similar expression patterns. Hence, the identification of TFBSs has become a key factor in unraveling the transcriptional regulation mystery. Unfortunately, the identification of these cis-regulatory elements by wet-lab experiments is time-consuming and labor-intensive. Computational methods have come to the rescue, but both their sensitivity and selectivity are severely hampered by the nature of the target motifs: TFBSs tend to be short (typically six to 15 bp) and degenerate, while the sequence in which they are located can be over 10 kb in length. Looking only at the oligonucleotide sequence recognized by a TF, we can expect a number of biologically meaningless occurrences in almost every promoter sequence. The most popular way of modeling TFBSs is by position weight matrices.¹ However, this assumes that the positions within the motifs contribute to the binding affinity in an independent manner. Recent experimental evidence has shown that this assumption is not accurate, and a number of models incorporating position-dependencies have been proposed.^2–6

There is growing evidence that TFs do not work alone, but rather cooperate to confer a specific spatio-temporal expression pattern; for instance, TFs bind to sites located in close proximity to each other, the so-called cis-regulatory modules (CRMs). It is, therefore, not surprising that many approaches to improve the accuracy of tissue expression prediction have focused on clustered groups of predicted binding sites.^7–14 Zhao et al., for example, predicted regulatory modules in Caenorhabditis elegans based on the clustering of a set of motifs correlating with muscle-specific gene expression. Clusters are defined simply as sites of the motifs positioned within a certain distance from each other. Blanchette et al. described a more complex approach where large numbers of PWMs are used to find statistically significant clusters of phylogenetically conserved sites in windows of 100 to 2000 bp. However, focusing only on clustered groups of predicted binding sites might be too simplistic an approach to the problem of TFBS detection and regulatory region architecture modeling. First, most of these approaches do not take into account solitary sites at all, even though some of them are likely to be functional. Secondly, in many CRM-modeling approaches, additional features of TFBSs, such as orientation, positional bias with respect to the transcription or translation start site, and order are ignored, although a number of studies have illustrated the importance of these features for some TFBSs.^15–17 In a genome-wide analysis of TFBSs in the mouse genome, Sharov et al. found that a considerable number of TFBSs showed a significant bias in their orientation. Berendzen et al. studied the importance of position and orientation of cis-regulatory elements and promoter motifs in a number of species. Their results show that several known functional elements appear to be relatively enriched at defined sites in the promoter region. Terai and Takagi showed that it is possible to find motif combinations in yeast that are significantly associated with a certain expression profile if their order is restricted, whereas they are not associated if their order is not taken into account. Methods that have tried to use such features are few in number. The Dragon Promoter Mapper uses a number of motif features such as the orientation, the order, and distances between adjacent motifs.¹⁸ However, the distance to the transcription or translation start site is not taken into account, and the model might have difficulties with motifs that lack a conserved distance between their sites showing a general preference for a certain region within the promoter region. Methods as the one described by Ohler et al. use more diverse physical properties such as DNA bendability, GC content, or stacking energy in addition to predicted TATA-boxes and initiator sites.¹⁹ These methods, however, need hundreds of training sequences and focus only on the core promoter region, where the distances between functional elements are strongly conserved. In addition, the final goal of these programs is fundamentally different from ours. While we predict the promoters with a similar architecture as an input set of promoters, they merely predict the presence or absence of a promoter.

We introduce here a simple Markov chain-based promoter architecture model as an alternative to the existing CRM models. Our model is trained using an input set of promoter sequences and captures information about the orientation, the positional bias, and the order of predicted occurrences of motifs that are over-represented in the input sequences. Subsequently, the trained model is used to predict genes having similar expression patterns.

We applied our model to two promoter sequence datasets: a set of promoter sequences driving expression in pharyngeal muscle cells in C. elegans and a set of muscle-specific promoters in Ciona intestinalis. The muscle system of C. elegans has been extensively studied, and the regulatory regions and expression patterns of a number of genes are relatively well known. C. intestinalis is a chordate model organism that has shown to be very useful for the study of developmental and evolutionary biology, and recently a number of studies have focused on the transcriptional regulation of muscle-specific genes in this organism.^20–23 The availability of relatively well-annotated expression information for C. elegans and the recent interest in the Ciona muscle regulatory system have determined the choice of our datasets. For both sets we trained the model and used it to predict new candidate promoters with similar expression patterns as the input promoter sequences. Finally, our predictions were verified for their accuracy, using both available annotation data and new wet-lab experiments.

2. Methods

2.1. Selection of input sequence datasets

The genomic set of C. elegans promoter sequences was obtained from WormMart (http://www.wormbase.org/, WormBase Release WS170). For each transcript, the 3000 bp upstream of the translation start site were downloaded, and overlapping upstream open reading frames (ORFs) were removed. Finally, repeats were masked using RepeatMasker (version 3.0; http://www.repeatmasker.org).²⁴ A set of 20 promoters, reported on WormBase to drive expression in pharyngeal muscle cells in C. elegans, was selected as input data for the C. elegans pharyngeal muscle model (see Supplementary Material Section 1).

For C. intestinalis, the genomic set of promoters was obtained from BioMart (Release JGI2).²⁵ For each transcript, the 3000 bp upstream of the translation start site were downloaded, overlapping upstream ORFs removed, and repeats masked. The promoter sequences of 19 genes previously shown to be expressed in muscle were used to construct the input promoter data set (see Supplementary Material Section 1).

2.2. Identification of useful over-represented motifs

Over-represented motifs were predicted in each input dataset using the motif-finding programs, MEME,²⁶ Weeder,²⁷ and AlignACE.²⁸ In order not to overlook any significant motifs, different runs on different regions of the input promoter sequences were done, for both strands as well as for single strands (see Supplementary Material Section 2). Finally, only motifs having a length between 6 and 15 bp and having more than five predicted occurrences in their input dataset were considered. Motifs that were obvious repeats (AT-repeats, AT-rich stretches, etc.) were removed. We further removed redundant motifs and selected up to 10 motifs that showed to be the most significantly over-represented in the input promoter sequences. This final set of motifs for each set of input promoter sequences was then used for further analysis and to construct the promoter architecture model.

To model the binding site preferences of each motif, we used a variable-order Bayesian network (VOBN), based on a method described previously.²⁹ Basically, a VOBN model can be regarded as a PWM, with the only difference that a first-order dependency between positions in the motif is allowed. In this study, we have set the conditions for introducing a dependency very strict. Because of this, the majority of positions in the VOBN are of zero-th order, which implies that many motifs are basically modeled as PWMs. Only in cases where a strong dependency was found, a first-order dependency between the positions was introduced (see Supplementary Material Section 3). To model the background nucleotide frequencies of the promoter sequences, both for C. elegans and for C. intestinalis, an interpolated Markov model (IMM) was trained from the genomic set of promoter sequences of each organism. This was done using the procedure described by Salzberg et al.³⁰ The IMM we used here is at most of eighth order. However, in cases where training data is scarce, an interpolation is made with a lower order. Thus the IMM takes advantage of the greater accuracy of higher-order models and, at the same time, avoids the problem of over-fitting caused by insufficient training data.

2.3. Positional bias and promoter sequence partitioning

Using the final set of motifs, for each dataset we scanned the input sequences for occurrences of each motif and represented them visually. As is discussed in the Results and discussion section, in many cases the occurrences of a motif show a certain tendency to appear in a certain region of the promoter sequences. Often, this is the region proximal to the transcription or translational start site; in other cases, it is a region further upstream. Keeping this heterogeneity in mind, it would be unwise to make one single model for the entire promoter structure, not taking into consideration the positional bias of some motifs.

Hughes et al. have introduced a measure for the degree of positional bias P for a motif,²⁸ as calculated by Equation (1).

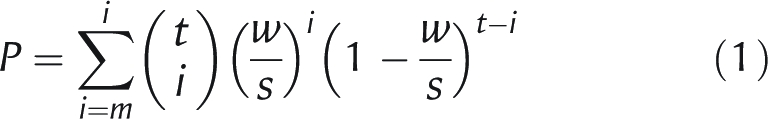1

where t is the total number of predicted sites of a motif in the input promoter sequences, m is the number of sites in a window of size w bp that contains the greatest number of sites, w is set to 300 bp, and s is the average size of the input sequences (typically 2000 < s < 3000). P is a measure of the likelihood of observing by chance more occurrences than the observed number in the densest region of the promoter sequences, given the total number of occurrences of the motif per unit of sequence length. The lower the value, the more significantly the motif is biased in its positional distribution. Given the values of this positional bias score of all motifs for each data set, we can split the promoter structure model into two regions in such a way that more positionally biased motifs will be present mainly in one region, and not in the other. For example, the border between the two regions can be set at 500 bp upstream of the translation start site for all promoter sequences. This could be done a number of times, resulting in an arbitrarily large number of regions, but in this study, we limited the regions to just two: a proximal and a distal one.

2.4. Model training

First-order Markov chains were trained for both the proximal and distal region of the input sequences, and similarly for a set of negative control sequences. Since in practice for many organisms there is little to no information available on tissue-specific expression, the entire set of genomic promoter sequences with their predicted sites was used as negative control set. The conditional probabilities of the Markov chains will be denoted as

2

where set stands either for the input set of promoters and their predicted sites or for the non-input set of promoters and their predicted sites, and region stands for the proximal or distal region of the promoters. A and B represent over-represented motifs or a ‘start’ or ‘stop’ state representing the beginning and the end of the region, and x and y their respective orientation. For the ‘start’ and ‘stop’ states, orientation is not taken into account. The conditional probability of Equation 2 is the chance to observe a site of a certain motif B in a certain orientation y, after a site of a certain motif A in a certain orientation x in the particular region of set. The direction in this process is always from the 3′ end toward the 5′ end; the chance of finding find ‘start’ after ‘end’ is not included as it is not relevant. The conditional probabilities are learned from the predicted sites of the motifs in the respective regions of both the input and background promoter sequences. From the corresponding probabilities of the input and background sequences, we can calculate a log likelihood ratio (LLR) as

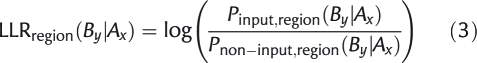3

for each region. Naturally, if the chance of observing a site of motif B in an orientation y after a site of motif A in orientation x is higher in the input than in the non-input promoters, this LLR will have a high positive value, indicating that this transition is more characteristic for the input sequences than for the non-input sequences. Conversely, if the chance of observing a site of motif B in an orientation y after a site of motif A in orientation x is lower in the input than in the non-input, this LLR will have a high negative value, indicating that this transition is less characteristic for the input sequences than for the non-input sequences. If multiple sites of a motif are present in a region, each of them makes a contribution to the score of the region. The addition of pseudocounts was used to avoid over-fitting for motifs with a low number of occurrences.

2.5. Scoring promoter sequences

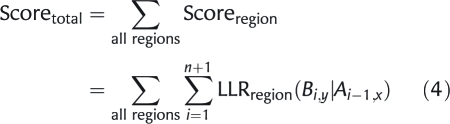
For each promoter sequence to score, we took the regions with their motif sequence (from 3′ to 5′) and the LLR values corresponding to the particular region. The final score Score_total of a promoter sequence is then given by the following equation:

4

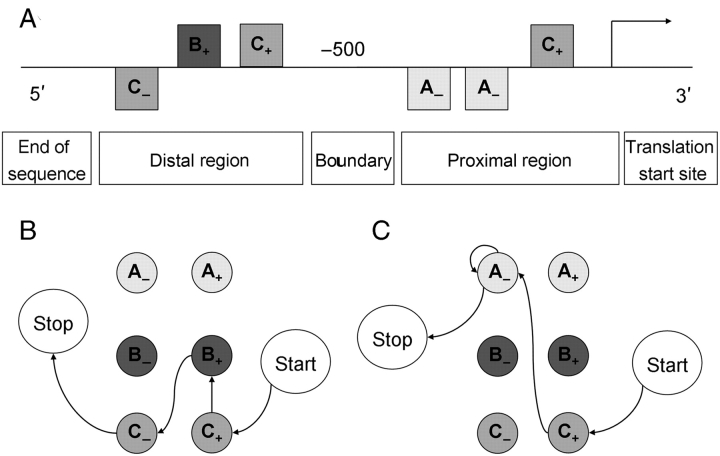
where Score_region represents the score of each region of the promoter sequence, n is the number of predicted cis-regulatory sites in each region, i = 0 represents the start of the region, and i = n + 1 the end of the region. Fig. 1 shows a visual representation of the scoring process.

Figure 1.

A visual representation of the scoring process of the Markov chain-based promoter structure model. (A) A promoter sequence to score. The arrow on the right indicates the translation or transcription start site. The squares represent predicted TFBSs for motifs A, B, and C, with ‘ + ’ and ‘ − ’ indicating their orientation. The promoter sequence is divided into a proximal and a distal region with the boundary between these regions, here set at −500 bp. (B) and (C) A visual representation of the promoter model during the scoring process of the distal region and the proximal region, respectively. The states of the model are shown as circles. Each of the two regions has a ‘start’ and a ‘stop’ state, in addition to states for each motif type in both orientations. To score the sequence shown in (A), in the proximal region of the promoter a transition is made from ‘start’ to ‘C+’, from ‘C+’ to ‘A−’, from ‘A−’ to ‘A−’ and finally from ‘A−’ to ‘stop’, corresponding to the TFBSs predicted in the proximal region of the promoter. The score of the proximal region is the sum of the LLR values associated with each of these transitions (e.g. LLR_proximal(C+ | start) for the transition from ‘start’ to ‘C+’, etc.). This process is repeated for the distal part of the promoter, and the final score of the promoter is the sum of the scores of both regions.

As indicated above, the transitions between motifs that are more characteristic for input promoter sequences will have a high positive score, whereas transitions between motifs that are more characteristic for non-input promoter sequences will have a high negative score. Thus, promoters having similar sets of motifs as the input sequences, with similar orientations and orders as those of the input sequences, in the same region get a high positive score. High-scoring promoters have a structure similar to the input promoters and are, hence, assumed to drive similar expressions. As can be seen from Equation 4, the individual strength of predicted motif sites does not contribute to the score of a sequence.

2.6. In situ hybridization experiments

Mature adults of C. intestinalis were collected from harbors in Murotsu, Hyogo, Japan, and maintained in indoor tanks of artificial seawater at 18°C. Larvae were obtained as described previously²⁰ and fixed overnight in 4% paraformaldehyde in 0.5 M NaCl, 0.1 M, pH 7.5, 3-(N-morpholino) propanesulfonic acid (MOPS) buffer prior to storage in 80% ethanol at −30°C. As the template to synthesize digoxigenin-labeled antisense RNA probes, cDNA clones were obtained from C. intestinalis Gene Collection Release 1.³¹ The RNA probes were synthesized using a DIG RNA labeling kit (Roche Diagnostics, Indianapolis, IN). In situ hybridization of whole-mount specimens was carried out as described previously.³² The larvae were mounted in 50% glycerol containing 2% 1,4-diazabicyclo-2,2,2-octane (DABCO) and observed under a confocal microscope LSM 510 (Zeiss).

3. Results and discussion

3.1. C. elegans pharyngeal muscle promoter architecture model

In a set of 20 promoter sequences reported to drive expression in pharyngeal muscle cells of C. elegans, we predicted over-represented motifs (see Section 2). Table 1 shows the positional bias score of the found motifs, together with the 300 bp window in the input promoter sequences where the occurrences of each motif are the most abundant. None of these motifs showed a significant similarity to motifs in the JASPAR database.³³ Note that some motifs (Cel_PM4, Cel_PM7) show a considerable bias in their orientation. Given that the motifs with the most significant positional bias seem to prefer the region roughly between the translation start site and −1000 bp, we divided the promoter region into a proximal region (from the translation start site to −1000) and a more distal region (from −1000 to the 5′ end of the promoter sequence). Next, for both regions, a first-order Markov chain was trained taking into account the orientation of the motif occurrences as described (see Methods and Supplementary Material Section 4).

Table 1.

The seven motifs used in the C. elegans pharyngeal muscle promoter model, with their consensus sequence

Motif name	Consensus sequence	Positional bias score	Densest 300 bp window	Orientation bias + –(ratio +)
Cel_PM1	TTTSBVRRATTTTMR	7.3e − 9	−862 to −562	25–14 (0.64)
Cel_PM2	ACTCMGAGCA	1.1e − 4	−337 to −37	12–12 (0.50)
Cel_PM3	CGGGATCT	9.1e − 4	−504 to −204	9–16 (0.36)
Cel_PM4	GAATCAGCGC	4.1e − 3	−605 to −305	18–7 (0.72)
Cel_PM5	AAAAATTCAATTTT	0.033	−2240 to −1940	17–17 (0.50)
Cel_PM6	GCARCAWA	0.034	−1742 to −1442	11–12 (0.48)
Cel_PM7	CTCCCTGAGC	0.086	−1307 to −1007	21–7 (0.75)

The third and fourth columns show the positional bias score of each motif and the positions of the densest window relative to the translation start site, respectively. The fifth column shows the number of predicted sites in the input promoters on each strand and the ratio of sites in the ‘plus’ orientation.

In a next step, the genome-wide set of promoters of C. elegans was scored by the trained model (see Methods). Of the 20 input promoters, 11 were in the 100 top-scoring sequences (see Supplementary Material Section 5). To verify the validity of this prediction, we used the expression annotation that can be found in WormBase. For the 100 highest scoring non-input genes having a tissue expression annotation (the first one being ranked 30th, the last one 606th out of 24 446 promoters), we determined which tissues were statistically over-represented. We found that the 100 top-scoring annotated non-input genes are enriched for genes expressed in pharyngeal muscles (10 genes, 4.1 expected by chance, P-value = 0.0025) and muscle tissue in general (42 genes, 30.9 expected by chance, P-value = 0.0072). There was also a slight enrichment for genes expressed in motor neurons (7 genes, 2.4 expected by chance, P-value = 0.0110), which are involved in the regulation of muscle contractions. It is not surprising to find the top-scoring genes to be enriched for not only pharyngeal muscle cells, but also muscle tissues in general, as the input genes’ tissue expression patterns were not restricted to only pharyngeal muscle cells but also included other muscle tissues. Table 2 shows the 10 top-scoring annotated non-input genes and their expression annotation as reported on WormBase. Five of these 10 genes are reported to be expressed in muscle tissue, one of them in pharyngeal muscles. In addition, some genes are reported to be expressed in neurons and motor neurons. It is known that muscle genes and neuronal genes share some regulatory elements, and other studies have reported similar observations.^13,34

Table 2.

The ten highest scoring non-input promoters for the C. elegans pharyngeal muscle promoter model, with their rank, sequence and transcript name and reported expression pattern

Rank	Sequence name	Transcript name	Expression pattern as annotated on WormBase
30	Y24D9A.4	Y24D9A.4a.2	Nervous system, reproductive system, anal depressor muscle, body wall muscle, pharynx
47	F52C9.8	F52C9.8e	Nervous system, intestine
50	T13C5.1	T13C5.1a	Head neurons, hypodermis, vulval muscle, anterior ganglia, spermathecae
72	D1081.2	D1081.2	Stomato-intestinal muscle, anal depressor muscle, body wall muscle
75	F22B7.9	F22B7.9	E lineage, syncytial hypoderm
79	C53C11.3	C53C11.3	Head neurons, ventral nerve cord, tail neurons, nervous system
80	F10E9.6	F10E9.6a.1	Nervous system, reproductive system, body wall muscle, pharyngeal neurons, anal depressor muscle, vulval muscle
83	ZK652.8	ZK652.8	Head neurons, nervous system, intestine, tail neurons
84	C36E6.5	C36E6.5.2	Pharynx, pharyngeal muscle
86	R07B1.1	R07B1.1	Ventral cord motor neurons, seam cells, hypodermal, neuroblasts, head

Of these ten promoters five drive expression in one or more muscle tissues, one specifically in pharyngeal muscles.

3.2. C. intestinalis muscle promoter architecture model

We predicted over-represented motifs in a set of 19 C. intestinalis promoter sequences known to drive expression in C. intestinalis muscle tissue. Table 3 shows the positional bias scores of the detected over-represented motifs. Motif Cin_M1 and motif Cin_M3 have consensus sequences that are highly similar to those of motifs that have been reported before as playing a crucial role in transcriptional regulation of muscle genes in C. intestinalis.²⁰ The binding sites of these motifs show similarity to those of the CREB and Myf (MyoD) TFs, respectively. Note that again in Table 2, some motifs (Cin_M5, Cin_M10) show a considerable bias in their orientation.

Table 3.

The ten motifs used in the C. intestinalis muscle promoter model, with their consensus sequence. See the legend of Table 1 for explanations on the meaning of each column

Motif name	Consensus sequence	Positional bias score	Densest 300 bp window	Orientation bias + –(ratio +)
Cin_1	TKGTGACGTCA	1.2e − 5	−232 to +68	24–14 (0.63)
Cin_2	GCCGGC	1.9e − 3	−1020 to −720	19–10 (0.66)
Cin_3	TGCAGCTGCR	2.5e − 3	−407 to −107	12–14 (0.46)
Cin_4	MACAACARA	4.8e − 3	−328 to −28	15–9 (0.63)
Cin_5	ATAAACGACANA	6.9e − 3	−614 to −314	21–8 (0.72)
Cin_6	ATGCCGAC	0.037	−214 to +86	14–13 (0.52)
Cin_7	CATCGGGGTA	0.040	−398 to −98	14 – 9 (0.61)
Cin_8	NVNNGACAACTG	0.045	−58 to +242	19–18 (0.51)
Cin_9	AMTCAAGCAA	0.094	−150 to +150	17–10 (0.63)
Cin_10	YTTCACTC	0.13	−191 to +109	19–5 (0.79)

Here the positions of the densest window are given relative to the TATA-box.

For this model, predicted TATA-boxes were used as reference points instead of the translational start sites. Sequences in which we could not find a TATA-box within a reasonable distance of the coding region were anchored at the position 100 bp upstream of the translation start site. Given the preference of some motifs for the proximal region, the promoter architecture model was partitioned into a proximal part (from the translation start site to 250 bp upstream of the predicted TATA-box) and a distal part (from 250 bp upstream of the predicted TATA-box until the 5′ end of the promoter sequence). Although our model does not include a direct way to model the clustering of sites, Table 2 illustrates that the proximal part of the promoter model was denser in motif occurrences than the distal part.

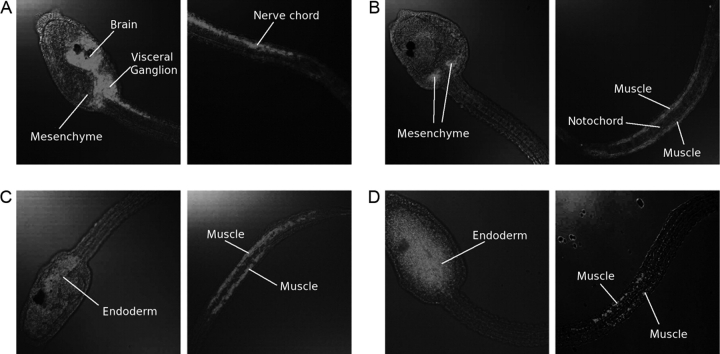
For both regions, a first-order Markov chain was trained (see Methods and Supplementary Material Section 4). The genomic set of promoter sequences of C. intestinalis was then scored using the trained model. The promoters were ranked by their score and the top-scoring genes selected for further analysis. Of the 19 input promoters, 16 are in the top 100 scoring sequences (see Supplementary Material Section 5). As a verification of the predictions, expression patterns of non-input genes from the top 50 scoring sequences were analyzed experimentally by in situ hybridization. Among the 29 non-input sequences in the top 50 list, three sequences, all of which encode muscle actin, were excluded from the analysis because their muscle-specific nature was obvious. Other two genes, whose expression patterns had been already known, were also excluded. Among the 24 sequences remaining, cDNA clones were available for four predicted sequences in C. intestinalis Gene Collection Release 1,³¹ and they were used to synthesize RNA probes for the in situ hybridization analysis. The results of these experiments are shown in Fig. 2. For three of the four tested genes, expression was observed in muscle cells in the tail of the C. intestinalis larva. A fourth gene showed expression in the central nervous system and mesenchyme, but not in muscle tissue.

Figure 2.

Expression signals of four high-scoring genes for the Ciona muscle promoter architecture model, determined by in situ hybridization experiments in C. intestinalis. These are the 20th, 31st, 41st, and 50th highest scoring sequences, respectively. These ranks include the input sequences and possible alternative transcripts. For each gene, the expression in the trunk and in the tail is shown. (A) A gene encoding a protein similar to human ‘vacuolar H+ ATPase E1’. This gene is conspicuously expressed in the central nervous system (brain, visceral ganglion, nerve cord) as well as in mesenchyme, but not in the muscle cells. (B) A gene encoding a protein similar to human ‘deformed epidermal autoregulatory factor 1’. In the trunk, this gene is specifically expressed in mesenchyme cells. In the tail, signals are predominantly found in muscle cells. Note that signals are not found in the notochord and epidermis. (C) A gene encoding a protein similar to human ‘glioma tumor suppressor candidate region gene 1 isoform 4’. It is expressed in endoderm of the trunk and also expressed weakly in muscle cells of the tail. (D) A gene encoding a protein similar to human ‘antigen p97 (melanoma associated) identified by monoclonal antibodies 133.2 and 96.5’. In the trunk, this gene is weakly expressed in endoderm cells. Signals are predominantly found in muscle cells, while signals are not found in the notochord and epidermis. Color versions of these pictures are available upon request.

3.3. Conclusion

We have introduced a simple promoter architecture model that uses the positional bias, the orientation bias, and the order of predicted sites of a set of motifs to predict promoter sequences that drive similar expression patterns as the input promoter sequences. As this model does not directly model the clustering of motifs, it can be considered as an alternative to the existing CRM-based models. During the training of the model, only one parameter needs to be set (i.e. the position of the boundary between the regions). We did not use any tissue-specific or organism-specific information in the construction of the model, so we can expect it to be applicable in other tissues and organisms as well. The fact that we could successfully predict expression profiles in two organisms illustrates the general applicability of our approach. Moreover, the motifs we used in the two datasets and described here were based solely on computational predictions, illustrating that this method does not require prior knowledge of the regulatory factors involved and their binding sites. Apart from a set of promoter sequences of co-regulated genes no other input data are needed. However, the structure of promoters driving expression in other tissues, such as the photoreceptor in C. intestinalis, has shown to be more challenging. Improvements to the model, such as the incorporation of additional information (e.g. the clustering of sites, the distance between pairs of sites, or evolutionary conservation) are likely to improve its prediction performance and are now being studied.

Supplementary Data

Supplementary data are available online at www.dnaresearch.oxfordjournals.org.

Funding

This work was supported by a Grant-in-Aid for Scientific Research from JSPS (17310114) and was supported in part by another grant (18370089) and by BIRD of Japan Science and Technology Agency (JST). A.V. is also supported by the Japanese Government Scholarship (Monbukagakusho; MEXT).