The Structure of F-pili

Abstract

Exchange of DNA between bacteria involve conjugative pili. While the prevailing view has been that F-pili are completely retracted before single-stranded DNA is passed from one cell to another, it has recently been reported that the F-pilus, in addition to establishing the contact between mating cells, serves as a channel for passing DNA between spatially separated cells during conjugation. The structure and function of F-pili are poorly understood. They are built from a single subunit having only 70 residues, and the small size of the subunit has made these filaments difficult to study. Here, we have applied electron cryo-microscopy and single particle methods to solve the long-existing ambiguity in the packing geometry of F-pilin subunits. We show that the F-pilus has an entirely different symmetry from any of the known bacterial pili as well as any of the filamentous bacteriophages, which have been suggested to be structural homologs. Two subunit packing schemes were identified: one has stacked rings of four subunits axially spaced by ∼ 12.8 Å; while the other has a one-start helical symmetry with an axial rise of ∼ 3.5 Å per subunit and a pitch of ∼ 12.2 Å. Both structures have a central lumen of ∼ 30 Å diameter that is more than large enough to allow for the passage of single-stranded DNA. Remarkably, both schemes appear to coexist within the same filaments, in contrast to filamentous phages that have been described as belonging to one of two possible symmetry classes. For the segments composed of rings, the twist between adjacent rings is quite variable, while the segments having a one-start helix are in multiple states of both twist and extension. This coexistence of two very different symmetries is similar to what has recently been reported for an archaeal Methanococcus maripaludis pili filament and an archaeal Sulfolobus shibatae flagellar filament.

Bacterial conjugation has important consequences for human health, as it is one of the means by which antiobiotic resistance can be transferred to a large population of bacteria. Conjugation among gram-negative bacteria is mediated by conjugative pili, F-pili in the case of cells expressing the tra genes of the F plasmid¹. F-pili are also absorption sites for certain bacteriophages. In particular, filamentous bacteriophages absorb to the tip of F-pili, while icosahedral phage absorb to the sides of F-pili². F-pili filaments are up to 20 μm long, with an outside diameter^3,4 of 85 Å to 95 Å and a ∼ 2 nm diameter central lumen⁵. They are assemblies of small (70 amino acid) largely α-helical subunits, F-pilin, though indirect evidence has suggested that quantitatively minor protein components could also exist^6,7.

Whether DNA passes through the hollow lumen of the F-pilus during conjugation has remained controversial, even after many years of study⁸. While it was originally believed that the F-pilus conducted DNA from donor to recipient, the current view in the field is that the F-pilus retracts, bringing donor and recipient into close contact before DNA can be transferred. However, new observations show that DNA can also be transferred over a distance, presumably via F-pili, albeit at relatively low frequency⁹. This has heightened interest in understanding the structure of F-pili.

Although the structure of F-pili has been studied by EM and x-ray fiber diffraction, there remains some ambiguity regarding the packing geometry of F-pilin subunits in the filament. Original mass per unit length measurements obtained by scanning transmission electron microscopy were combined with x-ray fiber diffraction to suggest a helical symmetry of 3.6 subunits per 12.8 Å pitch helical turn¹². However, it was subsequently realized that the prepilin gene product is proteolytically cleaved before assembly, and the pilin incorporated into F-pilus has only 70 residues, and not 120. This led to a reassessment of the symmetry based upon the smaller molecular weight with the suggestion of 5.4 or, more likely, 4.6 subunits per 12.8 Å pitch helical turn¹⁰. However, an alternative model was favored¹⁰ consisting of stacked rings of five subunits spaced by ∼ 12.8 Å and rotated 29° with respect to adjacent rings. In the model with stacked rings, there would be a 5-fold rotational symmetry (C₅) in the filament, as there is in the filamentous phage fd which attach in a tip-to-tip manner to F-pili. The ambiguity in symmetry arose as the result of alternative interpretations of the strong meridional or near-meridional reflection at 1/(12.8 Å) in the x-ray fiber diffraction patterns¹⁰, since stacked rings of subunits would give rise to a true meridional reflection at this spacing, while the one-start helix would give rise to an off-meridional reflection.

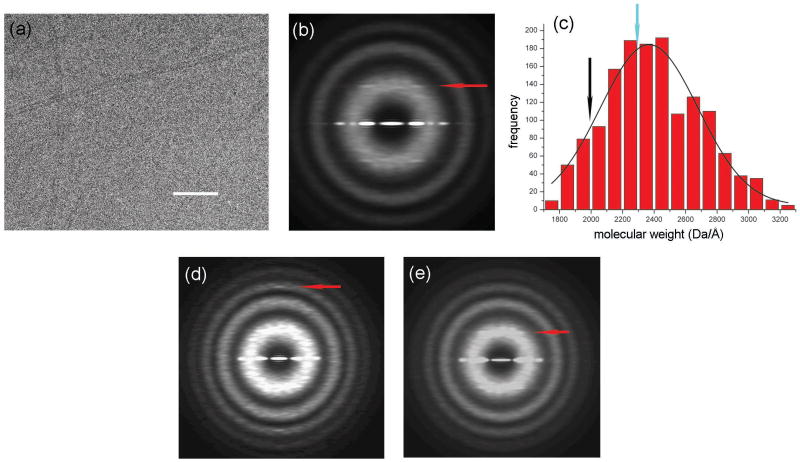
We have used electron cryo-microscopy to re-examine the structure of F-pili. The filaments appeared by cryo-EM (Fig. 1a) as thin, featureless rods. We extracted 10,952 overlapping segments (each 200 pixels or 480 Å in length) from filaments in ice (Fig. 1a), and then added together the power spectrum from each segment (Fig. 1b). This method is independent of any alignment needed to average together images, and is thus unbiased¹¹. The resulting power spectrum shows only one layer line. This layer line at ∼1/(32.2 Å) (red line, Fig. 1b) arises from either a four-start helix or a five-start helix, based upon the diameter of the filaments and the distance of the peak from the meridian. The layer line observed in fiber diffraction patterns¹² at 1/(12.8 Å) is not visible in the averaged power spectrum because of heterogeneity in symmetry (see below).

Figure 1.

Electron micrograph of frozen-hydrated F-pili (a). The space bar is 1000 Å. F-pili were prepared by a method found to minimize aggregation. F⁺ cells lacking type I pili were grown to an optical density of 2.0. Cells were rapidly chilled by addition of crushed ice, harvested by sedimentation, and suspended in 3 mL/L of culture of 60% (w/v) sucrose in 20 mM Tris-HCl, pH 7.6. The suspension was brought to 30% sucrose with Tris buffer and cells were removed by sedimentation. F-pili were purified from the supernatant fraction by two cycles of isopycnic sedimentation in sucrose gradients (density range = 1.16 to 1.29 g/mL). Fractions at ∼1.2 g/mL were examined by fluorescence microscopy for F-pili²⁸ and by SDS gel electrophoresis for purity (where preparations were judged to be >90% F-pilin). Images of frozen-hydrated F-pili were collected on a Tecnai 20 field emission gun microscope at 200 keV. Imaging and analysis were done by similar methods as described previously¹⁶. Negatives were scanned with a Nikon Coolscan 8000 as 16-bit images using a raster of 2.4 Å/pixel. 10 images with defocus values in the range of 1.5–2.7 μm were selected for further processing, since the n=4 layer line has a maximum near the first maximum of the contrast transfer function (CTF) at these defocus values. All cryo-EM images were multiplied by the theoretical CTF to correct for phase reversals and to optimize the signal-to-noise ratio. An averaged power spectrum (b), generated from 10,952 overlapping segments (each 200 pixels or 480 Å in length) of frozen-hydrated pili shows one layer line (red arrow) at ∼ 1/(32.2 Å) which can be interpreted as either n=4 or n=5, based upon the distance of the peak from the meridian and the diameter of the filaments. Mass per unit length measurements from Scanning Transmission Electron Microscopy (STEM) were made by similar methods as described previously²⁹, and yielded an average of 2,368.4 ± 8.0 (SEM) Da/Å (c). Digital STEM dark-field micrographs of freeze-dried specimens were recorded with 512 × 512 pixels at raster steps of 1.0 or 2.0 nm per pixel. The F-pili data were normalized to the known mass-per-unit-length of tobacco mosaic virus (1,314 kDa/nm). Histograms were calculated with 1-kDa/nm bins. A Gaussian was then fit to the distribution using the Origin software package (OriginLab company). The 10,952 segments from the cryo-EM images were sorted into two groups by models with either point group symmetry or one-start helical symmetry. 13% of the segments were sorted to have point group symmetry while the remaining 87% were sorted to have a one-start helix. The mass per unit length from the subset of segments reconstructed with point group symmetry (c, cyan arrow) is larger than that of the subset of segments with one-start helical symmetry (c, black arrow). The averaged power spectrum from the segments sorted as having point group symmetry (d) has a meridional layer line (red arrow) at ∼ 1/(12.6 Å). The averaged power spectrum from the segments sorted to have one-start helical symmetry (e) has a layer line (red arrow) at ∼ 1/(32.2 Å) which can be interpreted as n=4, based upon the distance of the peak from the meridian and the diameter of the filaments.

Since the averaged power spectrum did not provide enough information to establish the helical symmetry, mass/length was measured using scanning transmission electron microscopy (STEM)¹³. The STEM results yield a mass/length of 2,368.4 ± 8.0 (SEM) Da/Å (Fig. 1c). A previous estimate of ∼ 3,000 Da/Å for F-pili from STEM⁹ was due to the use of a calibration standard, filamentous phage fd, whose mass/length was not accurately known. Since F-pilin is 7.2 kDa^14,15 the averaged axial rise per subunit must be ∼ 3.0 Å. The mass/length distribution is broader than that of archaeal Methanococcus maripaludis pili¹⁶, suggesting that F-pili might be more structurally heterogenous due to variable compression and extension. For a one-start helical symmetry, our mass/length measurements suggest ∼ 4.3 subunits per 12.8 Å turn. If there is a point-group symmetry, with rings of subunits at the same axial level, then our mass/length measurements suggest a four-fold symmetry (C₄) and predict a meridional layer line at ∼ 1/(12 Å).

We used the iterative helical real space reconstruction (IHRSR)^17,18 method to reconstruct the pili from cryo-EM images. The IHRSR approach has been shown to be a powerful method for 3D reconstruction of helical filaments, especially when the filaments are flexible¹⁹, heterogeneous²⁰, suffer from Bessel overlap²¹, or are weakly diffracting¹¹. We started the procedure with 10,952 overlapping segments (each 480 Å in length) extracted from cryo-EM images of the pili. The IHRSR approach failed to converge to the same solution from different starting values for the axial rise and the twist using either the C₄ point-group symmetry or the one-start helical symmetry described previously^10,12. Based upon previous experience with applications of the IHRSR method^11,16,22,23, the failure of convergence suggested structural polymorphism. However, we were unable to sort the filaments into more homogeneous subsets using variations of the two proposed symmetries. Analysis of an archaeal pilus¹⁶ suggested to us the possibility of two different subunit packing arrangements existing within the same population of filaments. We therefore sorted the segments into two groups using a stacked disk structure with spacings of 12.8 Å between disks and a continuous one-start helix with a pitch of 12.8 Å as reference structures. Two groups were generated: 13% of the segments were characterized as having point group symmetry (stacked disks) while the remaining 87% were characterized as having one-start helical symmetry. The distribution of the two states showed clustering along the filaments, as might be expected, and was not random. The validity of the sorting was confirmed by the differences between the averaged power spectra from the two groups (Fig. 1d,e). The averaged power spectrum from the group sorted as point group symmetric (Fig. 1d) had a strong, thin meridional layer line (red arrow, Fig. 1d) at ∼ 1/(12.6 Å), suggesting the axial rise is relatively fixed in this group. The averaged power spectrum for the group sorted as one-start helically symmetric (Fig. 1e) had a broad layer line at ∼ 1/(32.2 Å). The distance of the peaks from the meridian and the diameter of the filaments indicate that this layer line arose from a four-start helix. The n=1 layer line is not visible, probably because of additional heterogeneity in structure within this group (see below). The IHRSR iterations from different starting points in each group (C₄ and one-start symmetries) failed to converge, suggesting further heterogeneity. We therefore attempted to sort each of the two groups into more homogeneous subgroups.

Four-fold rotational symmetry

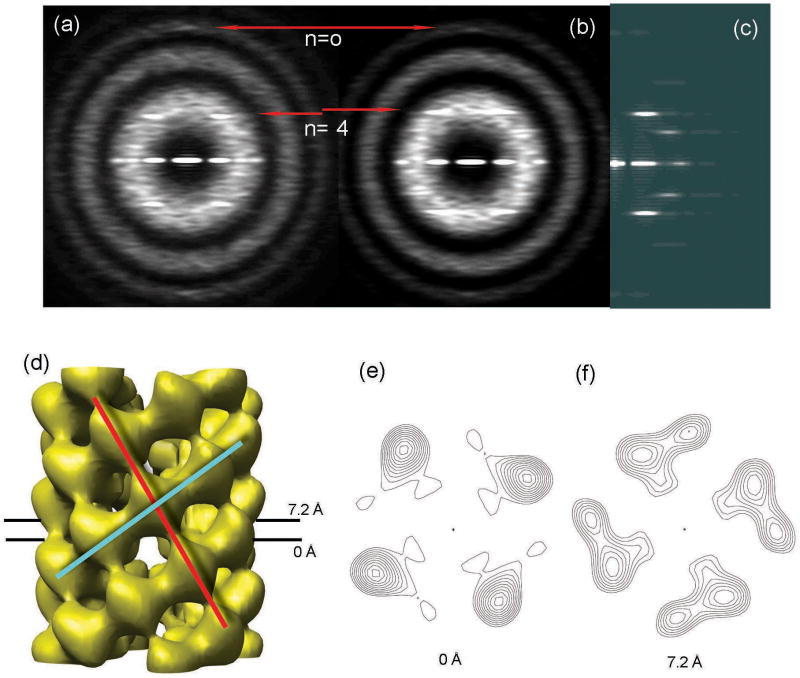
The STEM measurements (Fig. 1c) suggest that the axial rise per ring of four subunits in C₄ symmetry is ∼ 12 Å. A meridional layer line is seen in the averaged power spectrum from this group (Fig. 1d) at 1/(12.6 Å). Variability in the twist between adjacent rings could account for the failure to see other layer lines in this average power spectrum. We therefore sorted this group using a multi-reference alignment against variants of a global reconstruction with different twists imposed. This approach identified subgroups differing in twist within a range of ∼ 22° to 42° (data not shown). Because of the C₄ symmetry, the twist between rings cannot exceed 90°, so the observed 20° range is quite large. We validated the twist variants inferred from IHRSR by comparing power spectra. Given a constant axial rise of 12.6 Å, different twist values should lead to predictable differences in layer line spacing observable in power spectra. The position of the n=4 layer line should be (4*Δϕ)/(Δz*360°), where Δz is the axial rise per subunit and Δϕ is the twist per subunit, both along the four-start helix. For the subgroup with Δϕ = 30°, the expected n=4 layer line should be at 1/(37.8 Å); and when Δϕ = 34°, the n=4 layer line should be at 1/(33.4 Å). Comparison of power spectra from 360 segments initially classified as having twists clustered around 30° (Fig. 2a) with 417 segments having twists clustered around 34° (Fig. 2b) confirmed just such a shift. The shift could not be simply due to differences in magnification because the distances of the peaks from the meridian of the transforms were the same. The n=-4 layer line is not visible at ∼ 1/(19 Å) to 1/(20 Å) because this would be at a spacing that is near a minimum in the averaged CTF. This shift explains why the n=4 layer line was not visible in the global power spectrum of this group (Fig. 1d) and why sorted subsets containing less than 4% of the total population generated better power spectra than the population as a whole.

Figure 2.

The 1,464 segments of the first class were sorted into six subgroups by differences in the angular rotation between adjacent rings of subunits. The averaged power spectra from the two most populated subgroups (a,b) are much improved compared to the averaged power spectrum before sorting (Fig. 1d), suggesting reduced heterogeneity in each subgroup. The meridional layer line is fixed while the n=4 layer lines shift as expected in the two subgroups (a,b, red lines). The first subgroup was sorted to have a twist of ∼ -30°. The averaged power spectrum (a) can be interpreted as having an n=0 layer line at ∼ 1/(12.6 Å) and an n=4 layer line at 1/(37.1 Å). The second subgroup was sorted to have a twist of ∼ 34°. The averaged power spectrum (b) can be interpreted as having an n=0 layer line at ∼ 1/(12.6 Å) and n=4 at 1/(33.1 Å). The n=-4 layer line is not visible because it would be at a spacing that is near a minimum in the averaged CTF. The reconstruction of the most populated subgroup (d) has a C₄ symmetry with an axial rise of 12.8 Å and a twist of 34.2°. The reconstruction has been divided by the weighted sum of the squared CTF functions and filtered to a resolution of ∼ 14 Å as determined by the 0.5 Fourier Shell Correlation criterion. The power spectrum from the projection of this reconstruction (c) matches the corresponding averaged power spectrum (b). The surface thresholds (d-f) have been chosen to enclose 100% of the expected molecular volume. The main connectivity between subunits is along a left-handed eight-start helix (d, red line) and a right-handed four-start helix (d, cyan line). Two cross-sectional contour plots (e,f) that are spaced 7.2 Å away from each other have similar outer diameters (85 Å) and similar size lumens (30 Å).

We used the IHRSR method to reconstruct the most populated subgroup which was classified as having a twist of ∼ 34° (containing 28% of the segments within the class characterized as having a point group symmetry). The reconstruction from this subgroup (Fig. 2d) has C₄ symmetry with an axial rise of 12.8 Å and twist of 34.2° (or -55.8°) per subunit between adjacent rings. The reconstruction does not determine the absolute hand; thus, the 34.2° twist (or -55.8° twist) might actually be -34.2° (or +55.8°). The power spectrum generated from the projection of the reconstruction (Fig. 2c) matches the power spectrum of the corresponding subgroup (Fig. 2b) well, which supports the validity of the reconstruction and the sorting. In the reconstruction the connectivity between subunits is along both a left-handed eight-start helix (Fig. 2d, red line) and a right-handed four-start helix (Fig. 2d, cyan line). Cross-sectional contour plots of the reconstruction (Fig. 2e,f) show a rather constant lumen of ∼30 Å diameter. The outer diameter of the filament is ∼ 85 Å. The large variability in twist does not introduce any variability in the mass/length, which is ∼ 2.3 kDa/Å in this state. This value (Fig. 1c, cyan arrow) is quite close to the mean of the rather broad mass/length histogram obtained by STEM.

Using the 0.5 Fourier Shell Correlation criterion, we find that the resolution of the reconstruction is ∼ 14 Å. We think that the main limitation on resolution is the small number of segments and the continuous variability of the twist in this subgroup.

One-start helical symmetry

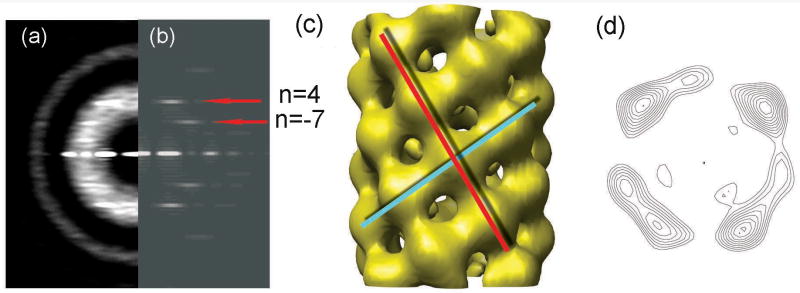
A similar approach was used to further decompose the group that was sorted to have one-start helical symmetry. The poor power spectrum of this group (Fig. 1e) suggested significant structural heterogeneity. Consistent with this, IHRSR generated different solutions from different starting points. A multi-reference sorting against projections of three different initial reconstructions did classify image segments into three subgroups. One subgroup (containing 23% of the total) is relatively homogeneous, as suggested by the convergence to the same structure from different IHRSR starting symmetries. The remaining two subgroups failed to show such convergence. The averaged power spectrum (Fig. 3a) from the relatively homogeneous subgroup showed two layer lines. Based on the distance of the peaks from the meridian and the diameter of the filaments, the layer line at ∼ 1/(32.2 Å) (upper red arrow, Fig. 3b) must arise from a four-start helix, while the layer line at ∼ 1/(51.0 Å) (lower red arrow, Fig. 3b) arises from a seven-start helix. In order to prove that layer line at ∼ 1/(51.0 Å) is not n=8 (which corresponds to C₄ symmetry), we reconstructed this subgroup assuming that they really have C₄ symmetry, and that the putative n=7 is really an n=8. The power spectrum from the projection of the resulting reconstruction with C₄ symmetry (data not shown) does not match the averaged power spectrum of this subgroup (Fig. 3a), suggesting that C₄ symmetry is not correct for this subgroup and the layer line at ∼ 1/(51.0 Å) is indeed n=7. Simple considerations of helical symmetry show that these layer lines must have the opposite sign. We have arbitrarily set the four-start helix to be right-handed (n=4) and the seven start helix to be left-handed (n=-7). The positions of the n=4 and the n=-7 layer lines predict that the n=1 layer line should be at ∼ 1/(12.2 Å). As a result, this power spectrum can only be interpreted as a one-start helical symmetry with ∼ 3.6 subunits per ∼ 12.2 Å turn, and cannot arise from the segments that have point-group symmetry. The expected position of the one-start layer line is near the meridional layer line in the subgroup with C₄ symmetry, which explains the ambiguity regarding the interpretation of x-ray fiber diffraction patterns¹⁰.

Figure 3.

The 9,488 segments of the set classified as having a one-start helical symmetry were further sorted into three subgroups by a multi-reference sorting against projections of three different initial reconstructions. The averaged power spectrum from one relatively homogeneous subgroup (containing 23% of this group) (a) is much improved compared to the averaged power spectrum before sorting (Fig. 1e), suggesting reduced heterogeneity in this subgroup. The averaged power spectrum (a) can be interpreted as having an n=4 layer line at ∼ 1/(32.2 Å) (upper red arrow) and n=-7 at ∼ 1/(51.0 Å) (lower red arrow). The reconstruction of this subgroup (c) has an axial rise of 3.5 Å and a twist of 99.6° per subunit. The reconstruction has been divided by the weighted sum of the squared CTF functions and filtered to a resolution of ∼ 13 Å as determined by the 0.5 Fourier Shell Correlation criterion. The power spectrum from the projection of this reconstruction (b) matches the corresponding averaged power spectrum (a). The surface thresholds have been chosen to enclose 108% of the expected molecular volume, since there is a loss of inner connectivity when a 100% threshold is used. We expect that this is due to limited resolution. The main connectivity between subunits is along a left-handed seven-start helix (c, red line) and a right-handed four-start helix (c, cyan line). A cross-sectional contour plot (d) shows similar outer diameter (85 Å) and lumen (30 Å) to that in the point group symmetry set (Fig. 2e,f).

We used the IHRSR method to reconstruct the relatively homogeneous subgroup. The reconstruction (Fig. 3c) converges to a right-handed one-start helical symmetry with an axial rise of 3.5 Å and a twist of 99.6° per subunit. The absolute hand is unknown and we use the convention that the hand is as shown. There would also be a left-handed one-start helix in this symmetry. The right-handed one-start helix has a pitch of 12.7 Å (3.5 Å*360°/99.6°), whereas the left-handed one-start helix has a pitch of 4.8 Å (3.5 Å*360°/260.4°). Since the molecular weight of each subunit is known to be 7.2 kDa, the axial rise of 3.5 Å corresponds to a mass/length of ∼ 2.1 kDa/Å, which is shifted from the mean of the mass/length histogram obtained by STEM (Fig. 1c, black arrow). This is consistent with the variability in extension of F-pili as suggested by the broad mass/length histogram. Since 77% segments within the group with one-start helical symmetry (67% of all segments) failed to converge, this might account for the larger mass/length portion of the histogram.

The power spectrum generated from the projection of the reconstruction (Fig. 3b) matches the power spectrum of the corresponding subgroup (Fig. 3a) very well, which supports the validity of the reconstructions and the sorting. In the reconstruction the connectivity between asymmetric subunits is along a left-handed seven-start helix (Fig. 3c, red line) and a right-handed four-start helix (Fig. 3c, cyan line). A cross-sectional contour plot of the reconstruction (Fig. 3d) shows a lumen of ∼ 30 Å diameter. The outer diameter is ∼ 85 Å. The lumen diameter and outer diameter are similar to the dimensions from the reconstruction with C₄ symmetry. Using the 0.5 Fourier Shell Correlation criterion, we find that the resolution of the reconstructions is ∼ 13 Å. As with the subgroup having point group symmetry, we think that the main limitation on resolution is the heterogeneity within this subgroup. This heterogeneity also explains why the layer line arising from the right-handed one-start helix is not visible at ∼1/(12.2 Å) in the power spectrum (Fig. 3a).

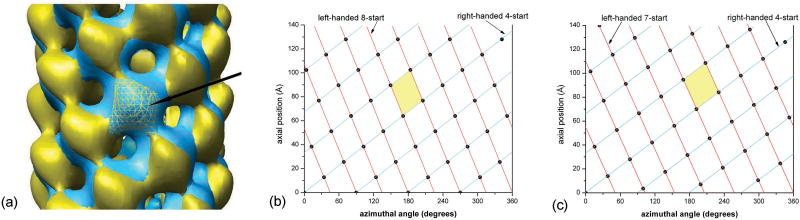
A superposition of the reconstructions with C₄ symmetry and one-start helical symmetry (Fig. 4a) in which one subunit in each has been aligned (black arrow) shows the similarity of the structure in terms of the appearance of subunits at the available resolution. These two reconstructions differ subtly in structural terms. The difference in helical symmetry can be understood by looking at the helical nets (Fig. 4b,c), which are schematic diagrams showing the helical lattice on the surface of a cylinder. For the filaments with C₄ symmetry, the main connectivity between subunits is along a left-handed eight-start helix and a right-handed four-start helix. For the filaments with one-start helical symmetry, the connectivity switches to the right-handed four-start helices and left-handed seven-start helices. However, the “unit cell” (colored in yellow in Fig. 4b,c) is very similar in dimension and orientation in both. We have tried to see whether individual pili are in one symmetry state (either C₄ or one-start helix) and the switching in symmetry is between filaments, or whether this mixture of symmetries occurs within filaments. We looked at the four longest pili in our data, and classified segments from these filaments using multiple references. Each of these filaments suggested that both states are present within individual filaments.

Figure 4.

A superposition (a) of the reconstructions with C₄ symmetry and one-start helical symmetry in which one subunit in each has been aligned (a, black arrow) shows the similarity of structure for subunits and difference in subunit packing. The yellow surface has C₄ symmetry with an axial rise of 12.8 Å and a twist of 34.2° (Fig. 2d), while the cyan surface has a one-start helical symmetry with a twist of 99.6° and an axial rise of 3.5 Å. (Fig. 3c). The aligned subunit in the yellow structure is shown as mesh for clarity. A surface lattice (b,c) shows the arrangement of subunits on the surface of a cylinder, using the convention that the cylindrical surface has been cut open and we are looking at the outside of the surface. Within segments having C₄ symmetry (b), the strongest observed connectivity between subunits is along the left-handed eight-start helices (red) and the right-handed four-start helices (cyan). Two helical families are labeled in the helical net for the one-start helix (c). The strongest observed connectivity between subunits within segments having a one-start symmetry is along the right-handed four-start helices (cyan) and the left-handed seven-start helices (red). A unit cell has been colored yellow (b,c) in each, showing that despite the differences in symmetry, the local packing is very similar between the two states.

The transition between the two states must involve a switch between seven and eight protofilaments, and this would seem to raise questions about how this might occur. While we have no information about what the filament looks like at these interfaces, precedence for the existence of such transitions comes from microtubules. It has been observed by cryo-electron microscopy that the number of protofilaments can change abruptly within an individual microtubule²⁴. The coexistence of two very different symmetries is very similar to what has recently been reported for an archaeal Sulfolobus shibatae flagellar filament²⁵ and an archaeal Methanococcus maripaludis pili filament¹⁶, with two distinct subunit packing arrangements existing within both filaments. The heterogeneity in packing arrangement explains some of the previous ambiguity regarding the helical symmetry. Techniques such as x-ray fiber diffraction tend to average out the variation within filaments. Because techniques to examine such filaments in the electron microscope without obscuring underlying heterogeneity have only recently become available, we think that the structural polymorphism in filaments such as pili and bacteriophages may actually be more prevalent than assumed.

We show that F-pili with either C₄ symmetry or one-start helical symmetry have a central lumen of ∼ 30 Å, which would allow single-stranded DNA transfer during conjugation⁹. The ∼ 85 Å diameter, the existence of a central lumen, and the small largely α-helical subunits are all reminiscent of filamentous bacteriophages. F-pili are absorption sites for class I filamentous bacteriophage, typified by fd. The fd filaments have a 5-fold rotation axis combined with a helical rotation of ∼ 34.6° between adjacent rings of subunits¹¹. The central lumen of fd is slightly smaller (at the available resolution) than what is seen in F-pili, possibly because the DNA densities in the lumen of the fd are averaged in the reconstruction and possibly because DNA does not have to move through the lumen, which can fit more tightly around the DNA. While a fivefold rotation axis was previously suggested for F-pili based on a model of specific tip-to-tip symmetry match between F-pili and fd filamentous bacteriophage¹⁰, here we show that it is not the case and that there must be a symmetry mismatch between any tip-to-tip interaction involving F-pili and fd.

The variability in F-pilus structure that we observe is likely to be functionally important. In addition to any direct role in DNA transfer during the late stages of conjugation, F-pili first sample large volumes around each donor cell for the presence of a recipient, bind to the recipient via the pilus tip, and bring donor and recipient cells into contact, when other components of the F-encoded type IV secretion system then stabilize the contacts to allow DNA transfer²⁶. Each of these F-pilus functions will likely depend on the mechanical properties of the filaments as reflected in their structural variability. For example, we have previously shown that the EspA needle extension of a bacterial Type Three Secretion System has a large variability in the axial rise per subunit but a rather fixed twist. We suggested that this might allow the hollow lumen to remain constant while the filament extended and compressed to resist breakage²³. Similarly, we suggest that the even greater structural variability of F-pili, in twist, extension, and symmetry, will prove to be an adaptive attribute, especially in liquid media, where bacterial motility, turbulence, brownian motion, and other factors all contribute to instability²⁷.