Covariate-Adjusted Linear Mixed Effects Model with an Application to Longitudinal Data

Abstract

Linear mixed effects (LME) models are useful for longitudinal data/repeated measurements. We propose a new class of covariate-adjusted LME models for longitudinal data that nonparametrically adjusts for a normalizing covariate. The proposed approach involves fitting a parametric LME model to the data after adjusting for the nonparametric effects of a baseline confounding covariate. In particular, the effect of the observable covariate on the response and predictors of the LME model is modeled nonparametrically via smooth unknown functions. In addition to covariate-adjusted estimation of fixed/population parameters and random effects, an estimation procedure for the variance components is also developed. Numerical properties of the proposed estimators are investigated with simulation studies. The consistency and convergence rates of the proposed estimators are also established. An application to a longitudinal data set on calcium absorption, accounting for baseline distortion from body mass index, illustrates the proposed methodology.

1 Introduction

Longitudinal data are common in biomedical and health sciences research, where repeated measurements are obtained over time for each individual. Linear (and nonlinear) mixed effects models are useful for analyzing longitudinal data, providing a simple and effective way to incorporate within-subject and between-subject variation and the correlation structure of longitudinal data. Comprehensive overviews of mixed effects models for analyzing longitudinal data include [1, 2, 3], among others.

When the response and predictors are observed under possibly nonparametric effects of a confounding covariate, a direct application of linear mixed effects (LME) models may lead to biased estimates of the regression relationship of interest. As an example, we consider the relationship between calcium intake and calcium absorption. Insufficient calcium intake has an important influence on bone heath and the risk of osteoporosis [4], especially in women, who comprise ~80% of cases. More recently, low intake has also been associated with the risk of colorectal cancer [5], hypertension [6] and obesity [7]. The resulting health benefits of calcium depend on the body’s ability to absorb the ingested calcium, which is partly affected by body composition, e.g., underweight, overweight, obese. Thus, it is of interest to examine the effect of calcium intake levels on absorption, where the response measurements and the effect of the predictor are both potentially modulated by a common observable confounding factor, body mass index (BMI). BMI is a standard measurement that characterizes body composition taking into account both height and weight (BMI = kg/m²; e.g. overweight: 25.0 to 29.9, obese: 30+). The dual confounding effects of BMI on both the response and the predictor coupled with the uncertainty of the exact form of these effects motivate our proposed approach, which involves a LME model combined with nonparametric modeling of the confounder effects.

More specifically, for the true underlying relationship between repeatedly measured calcium intake (X) and absorption (Y), we assume/postulate an (unobserved) latent linear mixed effects model with random intercept and/or slope parameters to accommodate subject-specific variation. The response and predictor modulating factor, namely U = BMI, is referred to as the “distorting” or confounding covariate. The distorting effects of BMI on both the response and predictor are modeled flexibly through the unknown, unspecified smooth distorting functions ψ(U) and φ(U) as

$$\stackrel{\sim }{Y}=\psi (U)Y,\text{and}\stackrel{\sim }{X}=\phi (U)X,$$ (1)

where Ỹ and X̃ denote the observed response and predictor variables, respectively. The above multiplicative distortion modeling framework was previously proposed for covariate-adjusted regression (CAR) in the context of linear regression models for cross-sectional data [8]. Note that the formulation in (1) allows for the flexibility of nonparametric modeling of the distortion due to U = BMI on absorption and effects of intake, using the general unknown smooth functions ψ(·) and φ(·), because one does not have a priori knowledge of these functional dependencies.

The motivation for the multiplicative distortion form (1) was based on studies that involve adjustment for body configuration measures, such as U = BMI, through division of the main variables of interest by U, i.e. ψ(U) = φ(U) = U so that Y = Ỹ/U and X = X̃/U. For many applications, the multiplicative distortion model (1) can be justified, but alternative distortion models, including additive (Ỹ = ψ(U) + Y, X̃ = φ(U)+X) and no distortion (Ỹ = Y, X̃ = X), can be considered. See [8] for a more extended discussion. Although formulated in terms of general multiplicative distortion (1), the CAR estimation method from [8] is actually adaptive to all three distortion cases (multiplicative, additive and no distortion) in that it yields consistent regression coefficient estimates in all these distortion settings. This flexibility to accommodate a variety of distortion models also generalizes to the method proposed in this paper. This is further discussed in Section 3.2.

The latent LME model for the underlying response and predictor coupled with their nonparametric distortion models described above is referred to as the covariate-adjusted linear mixed effects (CA-LME) model. The main objective of this paper is estimation of the underlying latent relationship between the response and predictor based on the observed (distorted) longitudinal data {Ỹ, X̃, U}. This involves estimation of fixed parameters, random effects and variance components of the model. The previous work of [8] involves estimation of fixed parameters in regression models for cross-sectional data. In the current work we account for correlation between repeated measurements in the estimation of fixed parameters and propose estimation methods for variance components and subject-specific effects, adjusted for the distorting effects.

We note that the above framework has similarities with measurement error modeling [9] if one views ψ(U) and φ(U) as unobserved errors affecting the response and predictor. The proposed modeling can then be viewed as a multiplicative measurement error model where the error is in both the response and predictor. There is a large literature on additive measurement error modeling, although work on multiplicative measurement error models is limited to multiplicative errors only in the predictors [10, 11]. Also, a key difference with the errors in variables setting is that a part of the error, namely U, is observed in the CA-LME model. This additional information from U is utilized in our proposed estimation method.

The paper is organized as follows. We describe the main ideas of the CA-LME models with a single predictor in Section 2. Estimation of the fixed effects, subject-specific effects and variance components and the adjustments to eliminate the distortion effects are described in Section 3. In Section 4, we discuss generalizations of the CA-LME model that allow for (1) multiple predictors under general fixed and random effects structures, as in standard LME modeling of directly observed longitudinal data, and (2) combination of predictors with and/or without distortion in the model. The asymptotic results for the proposed CA-LME estimators are also given in Section 4. An illustration of the proposed CA-LME methodology to longitudinal data on the effects of calcium intake on absorption, as introduced above, is summarized in Section 5. Numerical properties are investigated in Section 6 and technical details are deferred to an appendix.

2 Covariate-Adjusted Linear Mixed Effects Models

To present the main ideas of covariate-adjusted linear mixed models, we first consider the case of a single, possibly time-varying, predictor. Suppose that we have repeated measurements from a longitudinal study. Denote the unobserved true response variable of the i^th subject by Y_ij (i = 1, …, n) at the j^th time point (j = 1, …, n_i) and the unobserved true predictor variable by X_ij. A simple LME model for the outcome Y_ij is

$$Y_{ij}=({\gamma }_0+{\gamma }_1{X}_{ij})+({\gamma }_{0i}+{\gamma }_{1i}{X}_{ij})+e_{ij},$$ (2)

where e_ij denotes the mean zero random measurement error term for subject i at occasion j. For convenience we may write model (2) using matrix notation as Y_i = 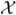_i(γ + γ_i)+ e_i, where the vector of fixed effects or population parameters is γ = (γ₀, γ₁)^T, the vector of subject-specific random effects is γ_i = (γ_0i, γ_1i)^T, the vector of response values for subject i is Y_i = (Y_i1, …, Y_ini)^T, and the corresponding matrix of predictor values is 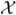_i with the j^th row given by ${\mathbf{X}}_{ij}^{\text{T}}=(1,X_{ij})$. The error term, e_i = (e_i1, …, e_ini)^T, is assumed to be e_i ~ (0, R_i) and the random effects γ_i ~ (0, D), where R_i and D = (D_kl) (k, l = 1, 2) denote the covariance matrices of e_i and γ_i, respectively. For simplicity, we may assume that R_i = σ²I_ni and define the collection of parameters of interest as θ_i = (γ, γ_i, σ², D).

The standard LME model (2) provides a reasonable approximation in many longitudinal data settings, given that the underlying observations {Y_ij, X_ij} are observable. In this case, standard estimation of the model parameters, namely the fixed effects (γ), random effects (γ_i), and variance components (σ² and D), can be based on maximum likelihood (ML) or restricted maximum likelihood (REML) methods (see e.g. [1]). However, these standard estimation approaches are no longer applicable for distortion-prone response and predictors.

We consider estimation in model (2) under the following longitudinal data distortion framework, where only distorted versions of Y_ij and X_ij are available. More precisely, the estimation must be based on the available distorted response and predictor data,

$${\stackrel{\sim }{Y}}_{ij}=\psi (U_i)Y_{ij},\text{and}{\stackrel{\sim }{X}}_{ij}=\phi (U_i)X_{ij}.$$ (3)

The unknown distorting functions {ψ(U_i), φ(U_i)} are assumed to be smooth functions of the observable confounder U. The distorted data available for estimation is the collection ${\{{\stackrel{\sim }{\mathbf{Y}}}_i,{\stackrel{\sim }{\mathcal{X}}}_i,U_i\}}_{i=1}^n$ for n subjects, where the n_i-vector Ỹ_i and matrix of predictors 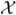˜_i are defined analogously to Y_i and 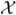_i above. Also, we let T denote the number of distinct observation times, t₁, …, t_T.

There are some important consequences of distortion-prone data on the standard ML or REML estimation methods for the LME model (2). As will be illustrated subsequently, the estimates for γ can be severely biased and variance components estimates will also be off-target. Additionally, efficiency considerations, such as incorporating an estimate of the covariance structure between repeated measurements into the standard estimation procedure, do not reduce the apparent bias resulting from the distortion. Because of the data contamination, common methods for estimating the covariance structure in longitudinal data, including parametric and nonparametric approaches (e.g., [12]), can-not capture the true covariance structure of the response, $\text{Var}({\mathbf{Y}}_i)={\mathbf{R}}_i+{\mathcal{X}}_i\mathbf{D}{\mathcal{X}}_i^{\text{T}}$, due to biases in variance components estimation. We will propose an estimation method to resolve these problems due to the data distortion in Section 3.

Some constraints on the unknown distortion functions are needed for the identifiability of the estimation problem. Similar to the identifiability condition used for covariate-adjusted regression for cross-sectional data, we use the condition that the distortion is mean preserving, i.e., the means of the observed variables E(Ỹ_ij) and E(X̃_rij) are the same as that of the underlying variables, E(Y_ij) and E(X_rij), respectively. This identifiability condition (IC) is equivalent to the following constraint on the distorting functions [8]:

$$E\{\psi (U_i)\}=1\text{and}E\{\phi (U_i)\}=1.$$ (4)

Note that since the mean preserving distortion is an identifiability condition, it is not testable. This is analogous to the zero mean errors for additive distortion in the measurement error literature. That is, the IC for multiplicative distortion on X is E(X̃) = E(Xφ(U)) = E(X) since E(φ(U)) = 1 and for additive distortion, it is E(X̃^*) = E(X + φ^*(U)) = E(X) since E(φ^*(U)) = 0.

3 Estimation Procedure

3.1 Observable Mixed Effects Varying Coefficient Model

To motivate the proposed estimation method, we first note that the conditional mean of the observable response variable Ỹ_ij, given the subject-specific effects γ_i and data 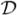≡ { 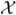˜_i, U_i; i = 1, …, n} is,

$$E({\stackrel{\sim }{Y}}_{ij}\mid \mathcal{D},{\gamma }_{0i},{\gamma }_{1i})={\beta }_0(U_i)+{\beta }_1(U_i){\stackrel{\sim }{X}}_{ij}+b_{0i}(U_i)+b_{1i}(U_i){\stackrel{\sim }{X}}_{ij},$$ (5)

where the fixed and subject-specific coefficient functions in (5) are

$${\beta }_0(U_i)={\gamma }_0\psi (U_i),{\beta }_1(U_i)={\gamma }_1\frac{\psi (U_i)}{\phi (U_i)},\text{and}$$ (6)

$$b_{0i}(U_i)={\gamma }_{0i}\psi (U_i),b_{1i}(U_i)={\gamma }_{1i}\frac{\psi (U_i)}{\phi (U_i)},$$ (7)

respectively. Thus, the above relationship (5) suggests that the regression of the available distorted data {Ỹ_ij, X̃_ij, U_i} leads to the following observable varying coefficient model with both fixed and random coefficient functions,

$${\stackrel{\sim }{Y}}_{ij}={\beta }_0(U_i)+{\beta }_1(U_i){\stackrel{\sim }{X}}_{ij}+b_{0i}(U_i)+b_{1i}(U_i){\stackrel{\sim }{X}}_{ij}+{\epsilon }_{ij},$$ (8)

where ε_ij ≡ e_ijψ(U_i). Model (8), written more succinctly in matrix notation, is

$${\stackrel{\sim }{\mathbf{Y}}}_i={\stackrel{\sim }{\mathcal{X}}}_i\{\mathit{\beta }(U_i)+{\mathbf{b}}_i(U_i)\}+{\mathit{\epsilon }}_i,i=1,\dots ,n,$$ (9)

with the vectors of functions β(U_i) = {β₀(U_i), β₁(U_i)}^T and b_i(U_i) = {b_0i(U_i), b_1i(U_i)}^T, where ε_i = (ε_i1, …, ε_ini)^T. Also note that given U_i = u, b_i(u) = {b_0i(u), b_1i(u)}^T ~ (0, D̃(u)) and ε_i ~ (0, R̃_i(u)), where R̃_i(u) ≡ Var(ε_i) and D̃ (u) ≡ Var{b_i(u)}.

We note that the above observable mixed varying coefficient model shares some common features with the class of “random varying coefficient” models [13], where the index of the fixed and subject-specific coefficient functions is the observation time, t_ij, instead of U_i. The observation that model (8) is a varying coefficient model is useful for developing the estimation technique proposed to target γ and γ_i. More specifically, we will first use a computationally efficient method based on binning to target the varying coefficient functions in (8). Our proposed estimators for γ and γ_i will then be derived using the relations between the varying coefficient functions and the underlying parameters given in (6) and (7).

Note that even though the connection between the CA-LME model in (2) and the varying coefficient model (VCM) in (8) facilitates estimation in the CA-LME model, the proposed CA-LME model is distinct from the VCM in that it is free from or adjusted for the effects of U. The VCM can be viewed as a stratified analysis (with respect to U) and such a model aims to address the question, “What is the relationship between Ỹ and X̃ at varying levels of U?” This is an important question in itself, however this is not the object of inference of interest with respect to the proposed CA-LME model. The object of inference in the CA-LME model is the relationship between X and Y (not directly observed). This relationship corresponds to the relation between Ỹ and X̃ with the effects of U removed, i.e. free of U, which is quite different than the target relationship of interest in the VCM. We discuss in further detail the distinction between CA-LME and VCM as well as their limitations, advantages and disadvantages in the Discussion Section.

Thus, the main contribution of this paper (given in Sections 3.2, 3.3. and 3.4) is the proposal of and the estimation and inference procedures for a latent variable model that explains the regression relation between the variables of primary interest adjusted for U in the context of repeated (correlated) measurements. Previous work in covariate adjusted modelling considers a linear regression model for cross-sectional/uncorrelated data, whereas the CA-LME model is designed for correlated data. The proposed estimation procedure is also new where the specific contributions include developing consistent point estimates for fixed effects, estimation of random effects and (within and between subject) variance components from distorted data.

3.2 CA-LME Parameter Estimation

Estimation of the underlying parameters of interest, namely θ_i = (γ, γ_i, σ², D), requires (a) estimation of the fixed and random varying coefficient functions in the mixed effects varying coefficient model (8), (b) estimation and incorporation of the covariance structure among repeated measurements (distinguishing within- and between-subject variation) and (c) adjustment for the distortion effects. The estimation method has three main steps: (1) binning (or “stratification”) of the data with respect to the confounding variable U, (2) fitting a LME model within each bin to obtain bin-specific estimates and (3) aggregating or averaging bin-specific estimates to obtain the covariate-adjusted LME estimators of θ_i. The basic approach to eliminating the distorting effects of U is to localize the model fitting by using data in each bin only. Details of each step are provided next.

The observable data available for estimation is the collection ${\{{\stackrel{\sim }{\mathbf{Y}}}_i,{\stackrel{\sim }{\mathcal{X}}}_i,U_i\}}_{i=1}^n$. Assuming that the confounding covariate U is bounded, a ≤ U ≤ b where a < b are real numbers, the initial step of the estimation procedure divides the interval [a, b] into H equidistant intervals, denoted B₁, …, B_H and referred to as bins. Let L_v be the number of subjects falling into bin v, for v = 1, …, H. To track the data corresponding to subjects falling into a given bin, observations in any given bin are marked by a prime. More specifically, the data for which U_i ∈ B_v, for i = 1, …, n, is given by the collection { $(U_{vk}^{\prime },{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime },{\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime })$, k = 1, …, L_v,}. Let $n_{vk}^{\prime }$ denote the number of repeated measurements for subject k in bin v, then the data corresponding to the k^th subject falling in bin v is $(U_{vk}^{\prime },{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime },{\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime })$, where ${\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime }={({\stackrel{\sim }{Y}}_{vk1},\dots ,{\stackrel{\sim }{Y}}_{vk{n}_{vk}^{\prime }})}^{\text{T}},{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }$ is the $n_{vk}^{\prime }$ × 2 matrix of predictor values, and $U_{vk}^{\prime }$ is the confounder. For example, if subjects 2 and 3 fall into the bin v = 7, then k = 1, 2, L₇ = 2 and $n_{v1}^{\prime }=n_2$ with ${\stackrel{\sim }{\mathbf{Y}}}_{\text{71}}^{\prime }={\stackrel{\sim }{\mathbf{Y}}}_2,{\stackrel{\sim }{\mathcal{X}}}_{71}^{\prime }={\stackrel{\sim }{\mathcal{X}}}_2$, and $U_{71}^{\prime }=U_2$. Similarly, $n_{v2}^{\prime }=n_3,{\stackrel{\sim }{\mathbf{Y}}}_{72}^{\prime }={\stackrel{\sim }{\mathbf{Y}}}_3,{\stackrel{\sim }{\mathcal{X}}}_{72}^{\prime }={\stackrel{\sim }{\mathcal{X}}}_3$ and $U_{72}^{\prime }=U_3$.

After binning the data, we approximate the mixed effects varying coefficient model (9), specifically Ỹ_i = 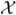˜_i {β(U_i) + b_i(U_i)} + ε_i, for i = 1, …, n, local to bin v (v = 1, …, H). This is achieved by fitting a LME model using the data within each bin. More precisely, for each bin v = 1, …, H, we fit the following LME model,

$${\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime }={\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }\{{\mathit{\beta }}_v+{\mathbf{b}}_{vk}\}+{\mathit{\epsilon }}_{vk}^{\prime },k=1,\dots ,L_v,$$ (10)

where β_v = (β_0v, β_1v)^T, b_vk = (b_0vk, b_1vk)^T and ${\mathit{\epsilon }}_{vk}^{\prime }={({\epsilon }_{vk1},\dots ,{\epsilon }_{vk{n}_{vk}^{\prime }})}^{\text{T}}$ denote bin-specific vectors of fixed effects, subject-specific effects and errors for subject k in bin v. Also, denote the bin-specific covariance matrices by D̃_v ≡ Var(b_vk) and ${\stackrel{\sim }{\mathbf{R}}}_{vk}\equiv \text{Var}({\mathit{\epsilon }}_{vk}^{\prime })$.

Model (10) can be interpreted as an approximation to model (9) “local” to bin v. Note that because model (10) is based on data local/specific to bin v, the resulting fixed effects and variance components estimates in model (10), denoted β̂_v, ${\widehat{\stackrel{\sim }{\mathbf{D}}}}_v$ and ${\widehat{\stackrel{\sim }{\mathbf{R}}}}_{vk}$ target β(·), D̃(·)and R̃_k(·) evaluated in the specific neighborhood associated with bin B_v. It follows from standard LME model theory that the estimator of β_v and b_vk are

$${\widehat{\mathit{\beta }}}_v={\mathbf{M}}_v^{-1}\left\{\sum _{k=1}^{L_v}{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime \mathrm{T}}{\stackrel{\sim }{\mathbf{\Omega }}}_{vk}{\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime }\right\},\text{and}$$ (11)

$${\widehat{\mathbf{b}}}_{vk}={\stackrel{\sim }{\mathbf{D}}}_v{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime \mathrm{T}}{\stackrel{\sim }{\mathbf{\Omega }}}_{vk}({\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime }-{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }{\widehat{\mathit{\beta }}}_v),$$ (12)

where ${\stackrel{\sim }{\mathbf{\Omega }}}_{vk}={\stackrel{\sim }{\mathbf{V}}}_{vk}^{-1},{\stackrel{\sim }{\mathbf{V}}}_{vk}={\stackrel{\sim }{\mathbf{R}}}_{vk}+{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }{\stackrel{\sim }{\mathbf{D}}}_v{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime \mathrm{T}}$ and ${\mathbf{M}}_v={\sum }_{k=1}^{L_v}{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime \mathrm{T}}{\stackrel{\sim }{\mathbf{\Omega }}}_{vk}{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }$. When D̃_v and R̃_vk are unknown, they can be estimated using the REML (or ML) method [3]. The REML estimators of D̃_v and R̃_vk, denoted ${\widehat{\stackrel{\sim }{\mathbf{D}}}}_v$ and ${\widehat{\stackrel{\sim }{\mathbf{R}}}}_{vk}$, are substituted into (11) and (12).

The covariate-adjusted linear mixed effects estimators of the fixed effects, γ₀ and γ₁, involve averaging of the bin-specific estimated fixed varying coefficient functions, namely ${\{{\widehat{\mathit{\beta }}}_v\}}_{v=1}^{\text{H}}$, to eliminate the distortion across U. The CA-LME estimators are given by

$${\widehat{\gamma }}_r=\frac{1}{{\overline{\stackrel{\sim }{X}}}_r}\frac{1}{T}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}\sum _{k\in I_{vj}}{\widehat{\beta }}_{rv}{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime },r=0,1,$$ (13)

where ${\overline{\stackrel{\sim }{X}}}_r=T^{-1}{\sum }_{j=1}^T{m}_j^{-1}{\sum }_{i\in I_j}{\stackrel{\sim }{X}}_{\mathit{rij}}$ is the overall mean of the predictor variable (with X_0ij ≡ 1, X_1ij = X_ij). Here m_j denotes the number of subjects observed at time t_j. Also, I_j denotes the set of indices of subjects that are observed at time t_j. Similarly, I_vj is the set of indices of subjects in bin B_v observed at time t_j. Note that the distortion effects of U cancel in the CA-LME estimators given in (13) and γ̂_r targets the fixed effect parameter γ_r, since E{β_r(U)X̃_rj} = γ_rE{ψ(U)X_rj} = γ_rE(X_rj) = γ_rE(X̃_rj), for all j = 1, …, T and r = 0, 1. The CA-LME estimators, γ̂_r, can be interpreted as method of moments estimators, because ${\overline{\stackrel{\sim }{X}}}_r$ targets E(X̃_r) and ${\widehat{\gamma }}_r{\overline{\stackrel{\sim }{X}}}_r$ targets E{β_r(U)X̃_r}.

We note here that the proposed estimators in (13) are consistent under multiplicative distortion (Theorem 1). Note also that an alternative way to handle multiplicative distortion in practice would be to transform it into additive distortion by taking logarithms where the underlying latent model would then be holding between the logarithm of the underlying variables. However, if the distortion is in fact additive taking logarithms would not deal with the problem. Even though the proposed estimators are formulated for multiplicative distortion, they are also consistent under additive distortion (Ỹ = ψ(U) + Y and X̃_r = φ_r(U) + X_r) as well as the trivial case of no distortion as is shown next. The fact that the proposed estimators are consistent under different types of distortion and no distortion is an advantage of the proposed method over taking logarithms, since it is difficult (and more typically not possible) to justify one type of distortion over another a priori.

The consistency of the estimators given in (13) for the additive distortion and no distortion cases follows from the fact that both of these cases also lead to a mixed varying coefficient model between the observed variables, as described for the multiplicative distortion in Section 3.1 above. More precisely, in the mixed varying coefficient models derived from these two cases, β₁(U) = γ₁ (in both models), β₀(U) = γ₀ for the no distortion case and β₀(U) = γ₀ − γ₁φ(U) + ψ(U) for the additive distortion case. Hence, it is follows that E{β_r(U)X̃_rj} = γ_rE(X̃_rj) holds for all cases, because E{φ(U)} = E{ψ(U)} = 0 under additive effects guaranteeing no distortion on average, i.e. E(X̃) = E(X) and E(Ỹ) = E(Y). Using this information Sentürk and Müller (2005) proposed a diagnostic tool to check whether the underlying distortion is additive by checking whether the slope function of the fitted varying coefficient model is equal to a constant. Similarly, for the case of no-distortion, one can check whether the slope and the y-intercept functions are both constant functions. This diagnostic tool provides information on the type of distortion based on the data and is implemented in Section 5 via the proposed bootstrap hypothesis test of Sentürk and Müller. This is helpful in identifying cases where a simpler estimation approach can be adopted when the model reduces to additive or no distortion.

Next, we consider the estimators (predictors) of the subject-specific effects for the CA-LME model, namely γ_ri for the i^th individual. Recall from (7) that we have

$${\gamma }_{ri}=b_{ri}(U_i)\frac{{\phi }_r(U_i)}{\psi (U_i)}=b_{ri}(U_i)\frac{{\gamma }_r}{{\beta }_r(U_i)},r=0,1,$$

where the last equality above follows directly from equation (6). Assume without loss of generality that the i^th subject is the k^th individual in bin v. Then the estimator of the random effect coefficient function, b_ri(·), is targeted by the subject-specific estimator b̂_rvk from bin v, given by (12). Targeting β_r(U_i) and γ_r by β̂_rv and γ̂_r, we arrive at the following plug-in estimator of γ_ri for individual k in bin v

$${\widehat{\gamma }}_{\mathit{rvk}}={\widehat{b}}_{\mathit{rvk}}\frac{{\widehat{\gamma }}_r}{{\widehat{\beta }}_{rv}},r=0,1.$$ (14)

3.3 Covariate-Adjusted Estimators of Variance Components

Similar to the estimation of the fixed and random effects, adjustments are also needed for the estimation of the variance components. The effects of the data distortion on the variance components estimation can be seen from the mixed effects varying coefficient model (8). Thus, given U_i = u, the within-subject covariance matrix is R̃_i(u) ≡ Var(ε_i) = ψ²(u)σ²I_ni and the between-subject covariance matrix is

$$\stackrel{\sim }{\mathbf{D}}(u)\equiv \text{Var}\{{\mathbf{b}}_i(u)\}=\left[\begin{array}{cc}{\psi }^2(u)D_{11}& \{{\psi }^2(u)/\phi (u)\}{D}_{12}\\ \{{\psi }^2(u)/\phi (u)\}{D}_{12}& \{{\psi }^2(u)/{\phi }^2(u)\}{D}_{22}\end{array}\right].$$

The above calculation shows the direct relationship between the variance components of the true unobserved LME model (i.e. σ² and D) and the corresponding ones in the mixed effects varying coefficient model (8), at U_i = u. Thus, the bin-specific (REML) estimators of the variance components, namely ${\widehat{\stackrel{\sim }{\mathbf{D}}}}_v$ and ${\widehat{\stackrel{\sim }{\mathbf{R}}}}_{vk}$, target D̃(·) and R̃_i(·) evaluated in the specific neighborhood of U, respectively.

Consider the average of the unadjusted bin-specific between-subject variance components estimators, i.e. $\overline{\stackrel{\sim }{\mathbf{D}}}=({\overline{\stackrel{\sim }{D}}}_{l{l}^{\prime }})={\text{H}}^{-1}{\sum }_{v=1}^{\text{H}}{\overline{\stackrel{\sim }{\mathbf{D}}}}_v$ for l, l′ = 1, 2, which target

$$\left(\begin{array}{cc}{\lambda }_{11}{D}_{11}& {\lambda }_{12}{D}_{12}\\ {\lambda }_{12}{D}_{12}& {\lambda }_{22}{D}_{22}\end{array}\right),$$

where λ₁₁ = E{ψ²(U)}, λ₁₂ = E{ψ²(U)/φ(U)} and λ₂₂ = E{ψ²(U)/φ²(U)}. To obtain the underlying between-subject variance components, D_ll′, we estimate the coefficients λ_ll′ and make the required adjustments. The estimated adjustment coefficients are

$${\widehat{\lambda }}_{11}={\widehat{\gamma }}_0^{-2}\sum _{v=1}^{\text{H}}\frac{L_v}{n}{\widehat{\beta }}_{0v}^2,{\widehat{\lambda }}_{22}={\widehat{\gamma }}_1^{-2}\sum _{v=1}^{\text{H}}\frac{L_v}{n}{\widehat{\beta }}_{1v}^2,\text{and}{\widehat{\lambda }}_{12}={\widehat{\gamma }}_1^{-2}{\mu }_{{\stackrel{\sim }{X}}_r}^{-1}\sum _{v=1}^{\text{H}}\frac{L_v}{n}{\widehat{\beta }}_{1v}^2{\mu }_{{\stackrel{\sim }{X}}_{r}v},$$

where ${\mu }_{{\stackrel{\sim }{X}}_r}=n^{-1}{\sum }_{i=1}^n{n}_i^{-1}{\sum }_{j=1}^{n_i}{\stackrel{\sim }{X}}_{\mathit{rij}}$ and ${\mu }_{{\stackrel{\sim }{X}}_{r}v}=L_v^{-1}{\sum }_{k=1}^{L_v}{n}_{vk}^{\prime }{\sum }_{j=1}^{n_{vk}^{\prime }}{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }$. Hence, the covariate-adjusted between-subject variance and covariance estimators are obtained as ${\widehat{D}}_{l{l}^{\prime }}={\widehat{\lambda }}_{l{l}^{\prime }}^{-1}{\overline{\stackrel{\sim }{D}}}_{l{l}^{\prime }}$, for l, l′ = 1, 2. Similarly, for the within-subject variance, averaging the bin-specific within-subject variances, namely ${\overline{\stackrel{\sim }{\sigma }}}^2={\text{H}}^{-1}{\sum }_{v=1}^{\text{H}}{\widehat{\stackrel{\sim }{\sigma }}}_v^2$, will target λ₁₁σ², where ${\widehat{\stackrel{\sim }{\sigma }}}_v^2$ is the bin-specific within-subject variance estimate obtained from bin v. Therefore, the adjusted within-subject variance estimator that targets σ² is ${\widehat{\sigma }}^2={\widehat{\lambda }}_{11}^{-1}{\overline{\stackrel{\sim }{\sigma }}}^2$.

Finally, we note that it is not difficult to see that the estimators of the required adjustment factors, namely {λ̂₁₁, λ̂₂₂, λ̂₁₂} given above, are sample averages/moments corresponding to the expectations {λ₁₁, λ₂₂, λ₁₂}, which follows from (6). That is, we have from (6) that ${\lambda }_{11}={\gamma }_0^{-2}E\{{\beta }_0^2(U)\},{\lambda }_{22}={\gamma }_1^{-2}E\{{\beta }_1^2(U)\}$ and ${\lambda }_{12}={\gamma }_1^{-2}E\{{\beta }_1^2(U){\stackrel{\sim }{X}}_1\}/E({\stackrel{\sim }{X}}_1)$. We note that showing the consistency of λ̂_ll′ for λ_ll′ involves similar arguments as in the proof of Theorem 2 in [14] and, therefore, is omitted in this work.

4 Model Generalization and Consistency

For simplicity of exposition, we have considered a LME model with a random intercept and slope and one predictor variable as the underlying model (2). Generalization to a model containing (a) multiple predictors, (b) a mixture of distorted and undistorted predictors, and/or (c) more complex random effects and covariance structures would broaden the applicability of the proposed method. We now consider a more general CA-LME model that incorporates extensions (a), (b) and (c). Denote p distorted predictors by X̃_rij, for r = 1, …, p, where X̃_rij = φ_r(U_i)X_rij. Note that the distortion on each predictor is modeled flexibly by allowing a different distorting function, φ_r(·), corresponding to the r^th predictor. Furthermore, to accommodate undistorted predictors in the regression model, such as age or time, let W_rij, r = 1, …, q, be a set of q undistorted predictors. For instance, descriptive and graphical analysis may suggest a model with baseline age and a quadratic trend in time, $t_{ij}^2$. In such a case, one may choose to include the terms $W_{1ij}=t_{ij}^2$ and W_2ij = age_i in the model as undistorted predictors.

Without loss of generality, we may assume that random effects are associated with the first p₁ distorted predictors (p₁ ≤ p) and the first q₁ (q₁ ≤ q) undistorted predictors. Then the underlying linear mixed effects model for individual i at time t_j is

$$Y_{ij}=\sum _{r=0}^p{\gamma }_r{X}_{\mathit{rij}}+\sum _{r=1}^q{\delta }_r{W}_{\mathit{rij}}+\sum _{r=0}^{p_1}{\gamma }_{ri}{X}_{\mathit{rij}}+\sum _{r=1}^{q_1}{\delta }_{ri}{W}_{\mathit{rij}}+e_{ij},$$

or equivalently

$${\mathbf{Y}}_i={\mathcal{X}}_i\gamma +{\mathcal{Z}}_i{\gamma }_i+{\mathbf{e}}_i,$$ (15)

where 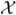_i is a n_i ×(p+q+1) predictor matrix for the fixed effects with the j^th row given by (1, X_1ij, …, X_pij, W_1ij, …, W_qij), 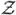_i is and n_i×(p₁+q₁+1) predictor matrix corresponding to the random effects with the j^th row given by (1, X_1ij, …, X_p1ij, W_1ij, …, W_q1ij), γ = (γ₀, γ₁, …, γ_p, δ₁, …, δ_q)^T and γ_i = (γ_0i, γ_1i, …, γ_p1i, δ_1i, …, δ_q1i)^T. The corresponding observable mixed effects varying coefficient model, generalizing (8), is

$${\stackrel{\sim }{Y}}_{ij}=\sum _{r=0}^p{\beta }_r(U_i){\stackrel{\sim }{X}}_{\mathit{rij}}+\sum _{r=1}^q{\eta }_r(U_i)W_{\mathit{rij}}+\sum _{r=0}^{p_1}{b}_{ri}(U_i){\stackrel{\sim }{X}}_{\mathit{rij}}+\sum _{r=1}^{q_1}{g}_{ri}(U_i)W_{\mathit{rij}}+{\epsilon }_{ij},$$ (16)

where X̃_0ij ≡ 1 and the fixed and random varying coefficient functions are

$$\begin{array}{c}{\beta }_r(U_i)={\gamma }_r\frac{\psi (U_i)}{{\phi }_r(U_i)},0\le r,\le p,{\eta }_r(U_i)={\delta }_r\psi (U_i),1\le r\le q,\\ b_{ri}(U_i)={\gamma }_{ri}\frac{\psi (U_i)}{{\phi }_r(U_i)},0\le r\le p_1\text{and}{g}_{ri}(U_i)={\delta }_{ri}\psi (U_i),1\le r\le q_1,\end{array}$$

with φ₀(U_i) ≡ 1. The LME model local to bin v, approximating model (16) is

$${\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime }={\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }{\mathit{\beta }}_v+{\stackrel{\sim }{\mathcal{Z}}}_{vk}^{\prime }{\mathbf{b}}_{vk}+{\mathit{\epsilon }}_{vk}^{\prime },k=1,\dots ,L_v,$$ (17)

where β_v = (β_0v, β_1v, …, β_pv, η_1v, …, η_qv)^T and b_vk = (b_0vk, b_1vk, …, b_p1vk, g_1vk, …, g_q1vk)^T are coefficient vectors, ${\mathit{\epsilon }}_{vk}^{\prime }={({\epsilon }_{vk1},\dots ,{\epsilon }_{vk{n}_{vk}^{\prime }})}^{\text{T}}$ is the vector of bin-specific errors, and ${\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }$ and ${\stackrel{\sim }{\mathcal{Z}}}_{vk}^{\prime }$ are the fixed and random predictor matrix for individual k in bin v analogous to the predictor matrices 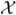_i and 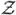_i defined above. The coefficients β’s and η’s correspond to the distorted and undistorted fixed effects and the b’s and g’s correspond to distorted and undistorted random effects.

The solution to (17) is similar to the single-predictor case given by (11)–(12) in Section 3.2. More specifically, the estimator of β_v is as given by (11), except that the matrix ${\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }$ is replaced by the one defined above for the more general fixed and random effects structure (after equation 15). The estimator for the subject-specific effects given by (12) is modified accordingly as ${\widehat{\mathbf{b}}}_{vk}={\stackrel{\sim }{\mathbf{D}}}_v{\stackrel{\sim }{\mathcal{Z}}}_{vk}^{\prime \text{T}}{\stackrel{\sim }{\mathbf{\Omega }}}_{vk}({\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime }-{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }{\widehat{\mathit{\beta }}}_v)$, where ${\stackrel{\sim }{\mathbf{\Omega }}}_{vk}={\stackrel{\sim }{\mathbf{V}}}_{vk}^{-1}$ and ${\stackrel{\sim }{\mathbf{V}}}_{vk}={\stackrel{\sim }{\mathbf{R}}}_{vk}+{\stackrel{\sim }{\mathcal{Z}}}_{vk}^{\prime }{\stackrel{\sim }{\mathbf{D}}}_v{\stackrel{\sim }{\mathcal{Z}}}_{vk}^{\prime \text{T}}$. As before, we replace the unknown D̃_v and with their R̃_vk REML estimators, ${\widehat{\stackrel{\sim }{\mathbf{D}}}}_v$ and ${\widehat{\stackrel{\sim }{\mathbf{R}}}}_{vk}$, based on data within bin v. Note that the implementation requires no new ideas from the simple case because the fitting can be achieved by common software packages (e.g. R, SPLUS, SAS) as in the simple case. One only needs to specify the additional columns of data corresponding to the predictors in ${\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }$ and ${\stackrel{\sim }{\mathcal{Z}}}_{vk}^{\prime }$.

The CA-LME estimators of the fixed and subject-specific effects are computed similar to (13) and (14), respectively, as

$$\begin{array}{c}{\widehat{\gamma }}_r=\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}\sum _{k\in I_{vj}}{\widehat{\beta }}_{rv}{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime },1\le r\le p,{\widehat{\delta }}_r=\frac{1}{T}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}\sum _{k\in I_{vj}}{\widehat{\eta }}_{rv},1\le r\le q,\\ {\widehat{\gamma }}_{\mathit{rvk}}={\widehat{b}}_{\mathit{rvk}}\frac{{\widehat{\gamma }}_r}{{\widehat{\beta }}_{rv}},0\le r\le p_1\text{and}{\widehat{\eta }}_{\mathit{rvk}}={\widehat{g}}_{\mathit{rvk}}\frac{{\widehat{\delta }}_r}{{\widehat{\eta }}_{rv}},1\le r\le q_1.\end{array}$$

The covariate-adjusted estimation of the variance components proceeds similarly as described in Section 3.3 and details for the more general case are in Appendix A.

We state the consistency result of the proposed CA-LME model estimators, γ̂₀, …, γ̂_p, δ̂₁, …, δ̂_q, when the total number of subjects n and the number of subjects observed at time j, m_j (j = 1, …, T) tend to infinity for a fixed number of total time points T. The proof is deferred to Appendix B. Consistency is established for data missing completely at random (unbalanced data). For m₀ = inf_j m_j, assume that m₀ → ∞. As is typical for smoothing, the total number of bins H satisfies H → ∞ and m₀/{H log(m₀)}→ ∞ as m₀ → ∞. The CA-LME model estimators are averages of the bin-specific varying coefficient function estimators: ${\widehat{\mathit{\beta }}}_v={({\widehat{\beta }}_{0v},{\widehat{\beta }}_{1v},\dots ,{\widehat{\beta }}_{pv},{\widehat{\eta }}_{1v},\dots ,{\widehat{\eta }}_{qv})}^{\text{T}}={\mathbf{M}}_v^{-1}{\sum }_{k=1}^{L_v}{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime \text{T}}{\stackrel{\sim }{\mathbf{\Omega }}}_{vk}{\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime }$, v = 1, …, H. These estimators for the varying coefficient functions and therefore ${\stackrel{\sim }{\mathbf{\Omega }}}_{vk}={\stackrel{\sim }{\mathbf{V}}}_{vk}^{-1}$ must exist for each bin in order for the proposed estimators to be well-defined Therefore, it is required that M_v and Ṽ_vk be nonsingular.

Theorem 1

Under the technical conditions given in Appendix B,

$$\begin{array}{l}{\widehat{\gamma }}_r={\gamma }_r+O_p(m_0^{-1/2})+O({\text{H}}^{-1}),0\le r\le p\\ {\widehat{\delta }}_r={\delta }_r+O_p(m_0^{-1/2})+O({\text{H}}^{-1}),1\le r\le q.\end{array}$$

5 CA-LME Model of Calcium Absorption and Intake

The relationship between the effects of calcium intake and absorption is important for a variety of human health issues and disease prevention. For example, adequate calcium intake is important in preventing osteoporosis, a condition characterized by porous and fragile bones associated with increased risks of bone fractures especially in women. More recent studies, although preliminary, have linked increased calcium intake to lowered blood pressure, decreased risk of colon adenomas, and reduced weight gain over time. Although the outcome of complex diseases are typically multifactorial in nature, one relationship of interest is between calcium intake and absorption, which we explore in this section.

In particular, we are interested in examining the relationship between the effect of calcium intake levels on calcium absorption, where the response measurements and the effect of the predictor are both potentially modulated by body mass index (BMI). Because different body compositions (e.g. underweight, overweight, obese) may partly influence individuals’ ability to absorb the ingested calcium, BMI is a suitable marker for body composition that accounts for both height and weight (BMI = kg/m²). Also, because absorption continually declines with age our underlying LME model for calcium absorption for individual i at measurement occasion j is

$$ca.ab{s}_{ij}={\gamma }_0+{\gamma }_{0i}+({\gamma }_1+{\gamma }_{1i}){\mathit{intake}}_{ij}+{\delta }_{1}ag{e}_{ij}+e_{ij},$$

where the parameters of interest include γ = (γ₀, γ₁)^T, γ_i = (γ_0i, γ_1i)^T, δ₁, σ² = Var(e_ij) and D = Cov(γ_i) as previously described in Section 2. Estimation is based on the observed data, denoted { ${\stackrel{\sim }{ca.\mathit{abs}}}_{ij},{\stackrel{\sim }{\mathit{intake}}}_{ij}$, age_ij} and body mass index for each subject (bmi_i). Note that age is incorporated as an undistorted fixed effect. The data is from a longitudinal study on n = 188 female subjects [15], between age 35 and 45 at the beginning of the study and repeated measurements were taken every 5-year intervals for a total of four occasions (1 ≤ n_i ≤ 4, j = 1, …, n_i). The number of subjects with 1, 2, 3 and 4 repeated measurements were 31, 41, 50 and 66, respectively.

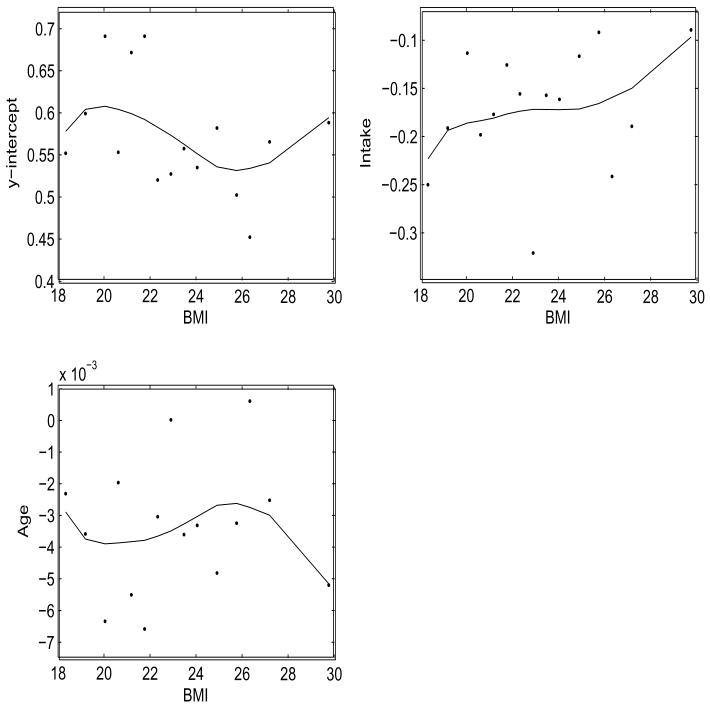
Figure 1 displays the varying coefficient estimates utilized in arriving at the parameter estimates of the CA-LME model. The observed calcium intake and age both have a negative relationship with the observed calcium absorption, while the effect of the observed intake seem to decline with increased body mass index. The y-intercept and slope varying coefficient functions for observed calcium intake are both found to be different than a constant function using the bootstrap test of ªentürk and Müller (2005) (p-values: 0.0239, 0.0153, respectively). This implies that the distortion does not reduce to the additive or the no distortion case from the goodness of fit discussion outlined in Section 3.2.

Figure 1.

Plot of β̂₀(·), β̂₁(·) and η̂(·) for the calciuⁱm absorption data.

Table 1(A) summarizes the parameter estimates for the CA-LME model, γ̂₀, γ̂₁ and δ̂₁. As a baseline comparison, Table 1(A) also displays the estimates of the underlying regression parameters using a standard LME (restricted maximum likelihood; REML estimation) with the same fixed and random effects structure as the the CA-LME model. The only difference is that the effects of BMI are ignored and estimates are obtained from an unadjusted LME model. We first note that given calcium intake, there is a significant natural decline in absorption with age that is consistent between the CA-LME analysis (δ̂₁ = −0.0035) and the unadjusted-LME analysis (age slope estimate also −0.0035), where the ratios of estimates to standard errors (S.E.) are approximately −4.807 and −5.151, respectively. The significant, but small, absolute magnitude in the estimated coefficient for age reflects the age range of the study subjects (between 35 and 64 across all measurement occasions), unlike in young adulthood where there is typically a rapid decline in absorption after reaching peak bone mass and density for skeletal development (e.g., see [16]). Our main parameter of interest is γ₁ for calcium intake and the unadjusted-LME model yields a significant estimate of −0.1489 (S.E., 0.0114). Similarly, the CA-LME model which accounts for the possible distortion effects of body mass index, yields the estimate of γ̂₁ = −0.1705. Although both estimates of the effect of calcium intake on calcium absorption is clearly significant and in the same direction, the estimate from the CA-LME model is approximately 1.89 standard errors lower, relative to the unadjusted estimate. Thus, the CA-LME model analysis suggests a stronger inverse (negative) relationship between calcium intake and absorption after adjusting for body configuration, BMI. We note that this inverse relationship between calcium intake and absorption is consistent with previous studies (e.g., see [17]). Since bin specific estimators given in (11) are heteroskedastic, we use the wild bootstrap method with 400 boostrap replications to obtain the standard errors for the CA-LME estimates (Table 1). Details of the boostrap implementation are provided in Appendix C.) For this data we note that the precision did not improve with increased replication beyond ~100.

Table 1.

Estimation of fixed effects and variance components for the unobserved latent model of calcium absorption as a function of calcium intake and age: E(ca. abs_ij) = γ₀ + γ_0i + (γ₁ + γ_1i)intake_ij + δ₁age_ij, based on observed data ${\{{\stackrel{\sim }{ca.\mathit{abs}}}_{ij},{\stackrel{\sim }{\mathit{intake}}}_{ij},{\mathit{age}}_{ij}\}}_{j=1}^{n_i}$ for n = 188 women and 1 ≤ n_i ≤ 4. Standard errors (S.E.) corresponding to CA-LME model estimates are obtained using 400 bootstrap samples.

	CA-LME		Unadjusted-LME
(A) Fixed effects estimates and standard error (S.E.)
Parameter	Estimate	S.E.	Estimate	S.E.
Intercept (γ0)	0.5698	0.0059	0.5575	0.0262
Intake (γ1)	−0.1705	0.0041	−0.1489	0.0114
Age (δ1)	−0.0035	0.0001	−0.0035	0.0005
(B) Variance components estimates
d11 = Var(γ0i)	0.0067		0.0042
d22 = Var(γ1i)	0.0084		0.0012
d12 = Cov(γ0i,γ1i)	−0.0062		−0.0020
σ2	0.0042		0.0046

The within- and between-subject variance parameter estimates are given in Table 1(B). The estimate of within-subject variance is smaller than the variation in the calcium intake slope parameter among individuals (as well as the intercept) for the CA-LME model. Both CA-LME and the unadjusted-LME models suggest a strong correlation between subject-specific intake slopes and intercepts $(\widehat{\text{Corr}({\gamma }_{0i,}{\gamma }_{1i}})=-0.83$ and −0.92, respectively). The within-subject variance estimates are similar for both models (σ̂² ≈ 0.004), although variation in the calcium intake slope is appreciably lower when not adjusting for BMI. Also, the number of bins used in the analysis of the calcium data was 15 for a sample size of n = 188. The coefficients estimates are similar for different number of bins used and this is further explored in the simulation study given in the next section.

6 Numerical Properties

To evaluate the performance of the proposed method, we consider a model with a mixture of fixed and random effects and distorted and undistorted predictors. The underlying LME model, analogous to the model used for calcium absorption is

$$Y_{ij}={\gamma }_0+{\gamma }_{0i}+({\gamma }_1+{\gamma }_{1i})X_{ij}+{\delta }_1{W}_{ij}+e_{ij},$$ (18)

where (γ₀, γ₁, δ₁) = (1.5, 2.0, 0.75) and the subject-specific effects are obtained as bivariate normal random variates: γ_i ~ Normal(0, D) with D₁₁ = Var(γ_0i) = 0.5625, D₂₂ = Var(γ_1i) = 1.0, and D₁₂ = Cov(γ_0i, γ_1i) = 0.375; thus, Corr(γ_0i, γ_1i) = 0.5. The undistorted predictor, W_ij, is taken to be the time points t_ij. The within-subject covariance matrix is R_i = 0.5²I_ni. The predictor values are obtained as X_ij ~ Normal[1.5(t_ij +1)², 1], where the sequence of time points are t_ij = j/(T + 1), for j = 1, …, T = 6.

To mimic unbalanced data, a common feature in longitudinal data, we randomly removed a proportion, π, of observations from the complete data. We implemented the simulation study for different configurations of sample size and missing rate, (n, π), with n ranging from 100 to 800 and π from 0.1 to 0.4. Each simulation configuration was replicated 1000 times. The distorted data are Ỹ_ij = ψ(U_i)Y_ij and X̃_ij = φ(U_i)X_ij with ψ(u) = u(u/4 + 3)/v₁ and φ(u) = (3u − 1)²/v₂. The constants v₁ and v₂ are normalizing constants so that the distorting functions satisfy the identifiability condition (4). The confounding variable U_i was obtained as U_i ~ Uniform[2, 6].

The main CA-LME estimation results are summarized in Table 2 for the fixed effects (γ) and Table 3 for the variance components. Given are estimates based on the CALME analysis, the unadjusted analysis which is the standard LME model fitted to the observed data, and the benchmark (optimal) analysis which is the latent LME model (18) fitted to the underlying (unobserved) data (Y_ij, X_ij, W_ij). The last approach is clearly the optimal one, but these estimates would not be available in practice since (Y_ij, X_ij) are not directly observable. However, for simulation studies they can be used as the benchmark to compare the proposed CA-LME model analysis and the unadjusted analysis. Generally, as expected, unadjusted LME estimates are biased, whereas the CA-LME estimates target the true parameters. More specifically, the fixed effects estimates in Table 2 suggest that the CA-LME estimates are close to the benchmark LME estimates (LME-benchmark, Table 2) and the bias decreases as sample size increases. Furthermore, the standard unadjusted LME estimates can be severely biased for all sample size configurations.

Table 2.

Simulation study: estimation of fixed effects for unbalanced data with 20% missing. Numbers given are (A) averages and (B) standard deviation across 1000 simulations.

Fixed effects (γ0 = 1.5, γ1 = 2, δ1 = 0.75)
n	CA-LME			Benchmark-LME			Unadjusted-LME
True	1.5	2	0.75	1.5	2	0.75	1.5	2	0.75
(A) Mean
100	1.4956	2.0044	0.7489	1.4948	1.9983	0.7504	1.5337	2.2316	0.8790
200	1.4997	1.9988	0.7523	1.4989	1.9996	0.7508	1.5395	2.2298	0.8830
400	1.4982	2.0003	0.7480	1.4991	2.0006	0.7501	1.5401	2.2334	0.8802
800	1.4997	1.9985	0.7478	1.4996	1.9984	0.7491	1.5395	2.2304	0.8802
(B) Standard deviation
100	0.1156	0.1244	0.1726	0.0972	0.1081	0.1519	0.1165	0.1517	0.1716
200	0.0861	0.0825	0.1217	0.0716	0.0739	0.1105	0.0870	0.1010	0.1209
400	0.0595	0.0575	0.0845	0.0503	0.0490	0.0770	0.0602	0.0712	0.0854
800	0.0434	0.0424	0.0611	0.0363	0.0363	0.0550	0.0438	0.0518	0.0617

Table 3.

Simulation study: estimation of variance components for unbalanced data with 20% missing. Numbers given are (A) averages and (B) standard deviation across 1000 simulations.

Variance components: σ2 = 0.25, D11 = 0.563, D22 = 1, D12 = 0.375
n/10	CA-LME				Benchmark-LME				Unadjusted-LME
	σ2	D11	D22	D12	σ2	D11	D22	D12	σ2	D11	D22	D12
(A) Mean
10	0.236	0.589	1.008	0.359	0.250	0.569	1.010	0.382	0.289	0.920	0.182	1.735
20	0.237	0.584	0.986	0.356	0.250	0.562	1.006	0.376	0.289	0.910	0.175	1.730
40	0.240	0.566	0.981	0.360	0.250	0.563	1.002	0.375	0.289	0.907	0.175	1.729
80	0.242	0.561	0.985	0.367	0.250	0.563	0.998	0.376	0.289	0.912	0.175	1.719
(B) Standard deviation
10	0.033	0.190	0.226	0.112	0.021	0.144	0.145	0.103	0.035	0.226	0.145	0.350
20	0.023	0.125	0.157	0.078	0.015	0.097	0.103	0.071	0.025	0.159	0.096	0.252
40	0.014	0.086	0.108	0.057	0.010	0.069	0.073	0.052	0.018	0.114	0.070	0.181
80	0.010	0.064	0.073	0.039	0.007	0.050	0.049	0.035	0.012	0.085	0.049	0.124

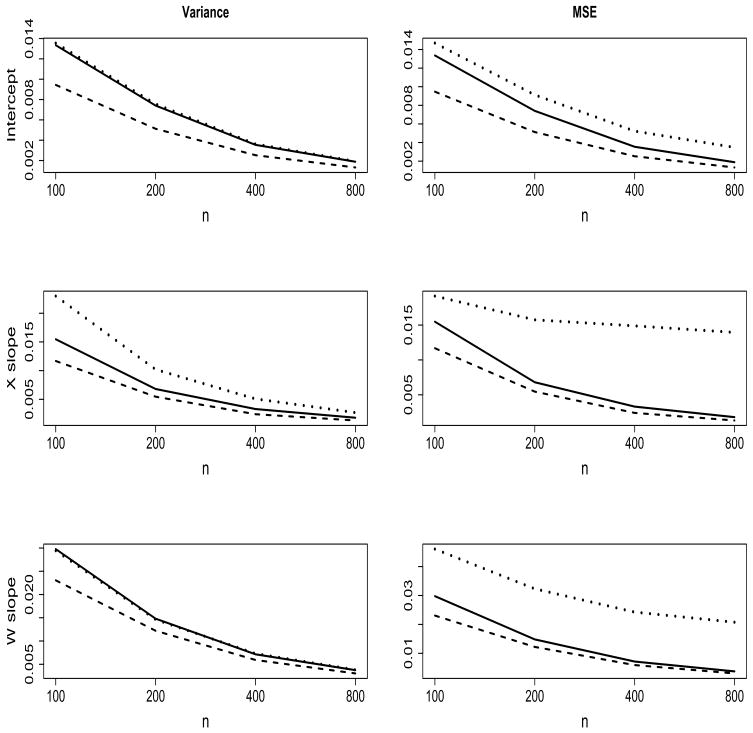
Similarly, the unadjusted LME estimates of the true variance components (σ² and D) are generally off-target and the absolute biases are many folds larger relative to the CA-LME and benchmark estimates (Table 3). Also, similar to the fixed effects parameter estimates, the variance components estimates for CA-LME track closely the benchmark estimates. In evaluating the performance of the proposed estimators, we also examined the variance and mean square error (MSE) in estimating the fixed effects and variance components. From the fixed effects results displayed in Figure 2, we make the following observations regarding this specific simulation study. (1) The variability in the proposed CA-LME estimators is much lower in the estimation of γ₁ (X-slope) and is similar for γ₀ (intercept) and η₁ (W-slope) compared to the unadjusted LME analysis. (2) Lower variance combined with the small bias (Table 2) result in substantially reduced MSE for the CA-LME estimators, where the estimated MSE tracks the optimal MSE closely as n increases. These results also hold for the covariate-adjusted variance components (results not shown).

Figure 2.

Estimated variance and mean square error (MSE) for estimation of fixed effects coefficients, specifically for the intercept (γ₀), X slope (γ₁) and W slope (δ₁), corresponding to the benchmark (dashed line), CA-LME (solid line) and unadjusted LME (dotted line) estimates. Due the large MSE for the unadjusted LME estimates of the X slope, we plotted 1/4× MSE (of the unadjusted estimates) so that it would be on a similar order as the CA-LME and benchmark MSEs (column 2, row 2).

The general pattern of results described above for 20% missing data is similar to the cases with 10%, 30% and 40% missing data. The implementation of the binning algorithm require specification of the number of bins H. There are some practical restrictions on the choice of the number of bins, H. From the practical point of view, H should be chosen such that there are enough points to fit the corresponding mixed effects models in each bin. From a theoretical point of view, H → ∞and m₀/(H log(m₀)) → ∞. This means that the number of bins and the number of points within each bin both increase with sample size. Thus, we performed a sensitivity analysis to analyze the effects of the number of bins on the proposed estimators. For the current longitudinal data setting, our study suggests that given the minimal requirement that there are enough data to fit the LME model within each bin, the CA-LME estimates are fairly robust to the bin choice H. This was also reported in the case of linear regression models for cross-sectional data (ªentürk and Müller 2006). For the simulation results reported, the average number of bins were 10, 19, 29 and 45 corresponding to sample size n = 100, 200, 400 and 800, respectively. For each of these sample sizes, Monte Carlo simulation suggests that the correponding range of bins where the estimates are robust are (8, 14), (10, 21), (20, 33) and (30, 54), respectively. For example, Table 4 illustrates the robustness of the proposed estimators for n = 200 for the number of bins ranging from 10 to 21. Given are the bias and MSE for each parameter of the model.

Table 4.

Effects of the number of bins H on estimation (γ₀ = 1.5, γ₁ = 2.0, δ = 0.75) Results given are averages over simulation runs.

# bin H	Estimates			MSE
10	1.4967	1.9988	0.7497	0.0060	0.0083	0.0110
13	1.4938	1.9879	0.7514	0.0053	0.0073	0.0125
16	1.4992	1.9975	0.7565	0.0075	0.0070	0.0120
19	1.5007	1.9880	0.7481	0.0066	0.0066	0.0137
21	1.5052	2.0048	0.7681	0.0069	0.0059	0.0127

Next, to assess the subject-specific estimators {γ̂_0i, γ̂_1i}, we define the following average residual sum of squares error (ARSSE) quantities of prediction error,

$${\text{ARSSE}}_1=\frac{1}{n}\sum _{i=1}^n\frac{1}{n_i}\sum _{j=1}^{n_i}{\left(Y_{ij}-{\widehat{Y}}_{ij}^{(1)}\right)}^2\text{and}{\text{ARSSE}}_2=\frac{1}{n}\sum _{i=1}^n\frac{1}{n_i}\sum _{j=1}^{n_i}{\left(Y_{ij}-{\widehat{Y}}_{ij}^{(2)}\right)}^2,$$

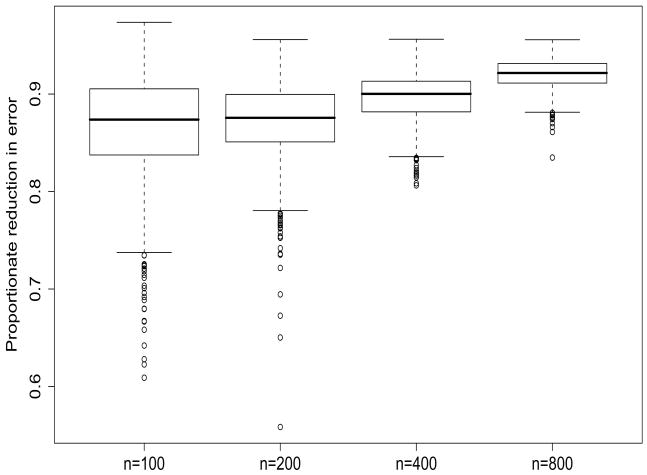
where ${\widehat{Y}}_{ij}^{(1)}={\widehat{\gamma }}_0+{\widehat{\gamma }}_1{X}_{ij}+{\widehat{\delta }}_1{W}_{ij}$ is the population fitted values and ${\widehat{Y}}_{ij}^{(2)}=({\widehat{\gamma }}_0+{\widehat{\gamma }}_{0i})+({\widehat{\gamma }}_1+{\widehat{\gamma }}_{1i})X_{ij}+{\widehat{\delta }}_1{W}_{ij}$ is the fitted values with the addition of subject-specific random effects. We examine the proportionate reduction in error (PRE) due to the addition of the random effects, namely PRE = (ARSSE₁ − ARSSE₂)/ARSSE₁. For example, with n = 200 subjects, the minimum, mean, and maximum PRE among the 1000 simulation replications are 0.56, 0.87, and 0.96 with a standard deviation of 0.04. Thus, the addition of the CA-LME predicted subject-specific effects reduce, on average, about 87% reduction in prediction error. Note that this is a substantial reduction, especially given that we have demonstrated that the bias in the population estimates (γ̂₀, γ̂₁, δ̂₁) is very small (Table 2). The distribution of the PREs, for each sample size (20% missing), are summarized in Figure 3. The results show appreciable reduction in error for all sample sizes and, as expected, this improves with sample size.

Figure 3.

Proportionate reduction in error (PRE) due to the inclusion of estimated subject-specific effects. Displayed are results for 1000 Monte Carlo data sets (20% missing data) for each sample size n.

Finally, we note that proposed method can be implemented in standard statistical software with LME model routines, including SAS, R or Splus since they involve fitting LME models after binning by U. The computational cost is modest as it involves mainly fitting the H LME models.

7 Discussion

As described in Section 3.1, the varying coefficient model can be applied to study the relationship between the observed variables Ỹ and X̃ at varying levels of U, although this is not the objective of inference for CAR (or the CA-LME) model. Thus, the main distinction (difference) between the two approaches of analyzing the data with VCMs and with CAR is that in the latter approach, U is viewed as a “nuisance” parameter. Hence in the CAR analysis, the result is a model that is free from or adjusted for the effects of U (by removing its effect). The object of inference in the CAR/CA-LME model is the relationship between X and Y (not directely observed). Thus, if one were interested in inference for the relationship between Ỹ and X̃ and how this relationship/effect is modified by U, the VCM is the preferred/suitable modelling approach and CAR would not be suitable for this specific aim. Also, we emphasize that in the VCM analysis, U is an important part of the modelling where one of the main goals is to recover (understand) the effects of U via the varying coefficient functions, i.e. the β_r(·)’s.

Although VCMs and CAR models both serve useful, but different, purposes (as described above) the applicability of CAR can seem limited, when viewed from a latent variable modelling perspective. From a latent variable modeling perspective, it is true that not being able to check the linearity of the underlying model is a limitation that it shares with other latent variable models. However, the applicability and advantage of CAR is in (biomedical) applications where the adjustments (for U) is due to general measurement errors induced by U, therefore, U is nuissance (so that the relationship of interest is between X and Y). The most common example of this in literature is the adjustment for U via division (which originally motivated the CAR method). That is, the motivation for the treatment of U as a nuisance variable and, hence, for our covariate adjusted approach comes from studies that involve adjustment via division by body configuration measures (such as body mass index or body surface area). An example is the 2002 study of Kaysen et al. [18] where albumin turnover and protein catabolic rate were among the variables that were adjusted for body surface area via division. After the adjustment, researchers proceed to analyze the linear regression relation between the adjusted variables. Here the assumption is that the effects of U on the variables are removed by the division. Thus, in such cases, CAR has an advantage over the simple adjustment via division, in that the distortion effects of U are in fact unknown (a priori) and CAR provides a way to model this uncertainty.

Also, we point out here that for the particular simulation set-up considered in Section 6, it was observed that the variance of CA-LME estimators are lower than or approximately equal to those of the unadjusted estimators. Even though we know that the unadjusted estimators do not target the underlying regression parameters (bias does not decrease with increasing n), since the variance formulas are not derived for CA-LME estimators, one cannot claim that their variance will always be larger compared to the variance of the CA-LME estimators generally. Also, unlike other typical studies where the bias and variance trade-off of two estimators can be studied via a tuning parameter, like the bandwidth, the current setting does not lend itself to such a simple analysis. With respect to this issue, there are (at least) two key considerations that explains the complicated bias-variance relationship. First, the effect of the distortion functions on the variance of both estimators are different, which makes it difficult to predict which variance will be larger in a given set-up (i.e. generally). Second, since the unadjusted estimators do not target the underlying regression parameters, they are estimating a different quantity. Hence, the estimators can potentially have very different variances. In our study, we have two estimators that have completely different forms due to the distortion and they target two different quantities.

Finally, while estimation of the varying coefficient functions (i.e. the β(·)’s) are a natural by-product of the proposed estimation procedure, estimation of φ(·) and ψ(·) is not. Although this can be viewed as an advantage of the covariate adjusted estimation approach, i.e. that without having to know the form of distortions, or without targeting these distortion functions, the underlying relationship can be targeted directly; these functions can provide information graphically. Formulating an alternative estimation algorithm to also target the distortion functions is a challenge for further research.

Appendix A: Covariate-Adjusted Variance Components

Denote the vector of distorted and undistorted random effects for the underlying LME model (15) by ${\mathit{\gamma }}_i={({\mathit{\gamma }}_i^{(1)\text{T}},{\mathit{\gamma }}_i^{(2)\text{T}})}^{\text{T}}$, where ${\mathit{\gamma }}_i^{(1)}={({\gamma }_{0i},\dots ,{\gamma }_{p_{1}i})}^{\text{T}}$ and ${\mathit{\gamma }}_i^{(2)}={({\delta }_{1i},\dots ,{\delta }_{q_{1}i})}^{\text{T}}$. We express the covariance matrix of these random effects, D ≡ Var(γ_i), as

$$\mathbf{D}=(D_{l{l}^{\prime }})=\left(\begin{array}{cc}{\mathbf{D}}^{(11)}& {\mathbf{D}}^{(12)}\\ {\mathbf{D}}^{(21)}& {\mathbf{D}}^{(22)}\end{array}\right),1\le l,l^{\prime }\le p_1+q_1+1,$$

where ${\mathbf{D}}^{(11)}=\text{Var}({\mathit{\gamma }}_i^{(1)}),{\mathbf{D}}^{(22)}=\text{Var}({\mathit{\gamma }}_i^{(2)}),{\mathbf{D}}^{(12)}=\text{Cov}({\mathit{\gamma }}_i^{(1)},{\mathit{\gamma }}_i^{(2)})$. The observable varying coefficient model is (16) where the random varying coefficients at U_i = u is denoted by ${\mathbf{b}}_i(u)={\{{\mathbf{b}}_i^{(1)\text{T}}(u),{\mathbf{b}}_i^{(2)\text{T}}(u)\}}^{\text{T}}$ with ${\mathbf{b}}_i^{(1)}(u)={\{b_{0i}(u),\dots ,b_{p_{1}i}(u)\}}^{\text{T}}$ and ${\mathbf{b}}_i^{(2)}(u)={\{g_{1i}(u),\dots ,g_{q_{1}i}(u)\}}^{\text{T}}$. Direct calculation yields,

$$\stackrel{\sim }{\mathbf{D}}(u)=\text{Var}\{{\mathbf{b}}_i(u)\}=\left(\begin{array}{cc}{\stackrel{\sim }{\mathbf{D}}}^{(11)}(u)& {\stackrel{\sim }{\mathbf{D}}}^{(12)}(u)\\ {\stackrel{\sim }{\mathbf{D}}}^{(21)}(u)& {\stackrel{\sim }{\mathbf{D}}}^{(22)}(u)\end{array}\right),$$

where

$$\begin{array}{c}{\stackrel{\sim }{\mathbf{D}}}^{(11)}(u)=\text{Var}\{{\mathbf{b}}_i^{(1)}(u)\}=\left[\begin{array}{cccc}{\psi }^2(u)D_{11}& \frac{{\psi }^2(u)}{{\phi }_1(u)}{D}_{12}& \cdots & \frac{{\psi }^2(u)}{{\phi }_{p_1}(u)}{D}_{1,p_1+1}\\ \frac{{\psi }^2(u)}{{\phi }_1(u)}{D}_{12}& \frac{{\psi }^2(u)}{{\phi }_1^2(u)}{D}_{22}& \cdots & \frac{{\psi }^2(u)}{{\phi }_1(u){\phi }_{p_1}(u)}{D}_{2,p_1+1}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\psi }^2(u)}{{\phi }_{p_1}(u)}{D}_{p_1+1,1}& \frac{{\psi }^2(u)}{{\phi }_1(u){\phi }_{p_1}(u)}{D}_{p_1+1,2}& \cdots & \frac{{\psi }^2(u)}{{\phi }_{p_1}^2(u)}{D}_{p_1+1,p_1+1}\end{array}\right],\\ {\stackrel{\sim }{\mathbf{D}}}^{(12)}(u)=\text{Cov}\{{\mathbf{b}}_i^{(1)}(u),{\mathbf{b}}_i^{(2)}(u)\}=\left(\begin{array}{ccc}{\psi }^2(u)D_{1,p_1+2}& \cdots & {\psi }^2(u)D_{1,p_1+q_1+1}\\ \frac{{\psi }^2(u)}{{\phi }_1(u)}{D}_{2,p_1+2}& \cdots & \frac{{\psi }^2(u)}{{\phi }_1(u)}{D}_{2,p_1+q_1+1}\\ ⋮& \ddots & ⋮\\ \frac{{\psi }^2(u)}{{\phi }_{p_1}(u)}{D}_{2,p_1+2}& \cdots & \frac{{\psi }^2(u)}{{\phi }_{p_1}(u)}{D}_{2,p_1+q_1+1}\end{array}\right),\end{array}$$

and ${\stackrel{\sim }{\mathbf{D}}}^{(22)}(u)=\text{Var}\{{\mathbf{b}}_i^{(2)}(u)\}={\psi }^2(u){\mathbf{D}}^{(22)}$. Therefore, the average of the variance components estimates from each bin, namely $\overline{\stackrel{\sim }{\mathbf{D}}}=({\overline{\stackrel{\sim }{D}}}_{l{l}^{\prime }})={\text{H}}^{-1}{\sum }_{v=1}^{\text{H}}{\widehat{\stackrel{\sim }{\mathbf{D}}}}_v(1\le l,l^{\prime }\le p_1+q_1+1)$, can be adjusted to obtain the covariate-adjusted variance components estimators. From the above expression for D̃(u), the required adjustment coefficients involve

$$\begin{array}{c}{\lambda }_0\equiv E\{{\psi }^2(U)\},{\lambda }_{rr}\equiv E\left\{\frac{{\psi }^2(U)}{{\phi }_r^2(U)}\right\},1\le r\le p_1,\\ {\lambda }_r\equiv E\left\{\frac{{\psi }^2(U)}{{\phi }_r(U)}\right\},1\le r\le p_1\text{and}{\lambda }_{rs}\equiv E\left\{\frac{{\psi }^2(U)}{{\phi }_r(U){\phi }_s(U)}\right\},1\le r,s\le p_1,r\ne s.\end{array}$$

Similar to Section 3.3, it can be shown that ${\lambda }_0={\gamma }_0^{-2}E\{{\beta }_0^2(U)\},{\lambda }_{rr}={\gamma }_r^{-2}E\{{\beta }_r^2(U)\},{\lambda }_r={\gamma }_r^{-2}E\{{\beta }_r^2(U){\stackrel{\sim }{X}}_r\}/E({\stackrel{\sim }{X}}_r)$ and λ_rs = (γ_rγ_s)⁻¹E{β_r(U)β_s(U)}. The estimators for the adjustment coefficients are:

$$\begin{array}{c}{\widehat{\lambda }}_0={\widehat{\gamma }}_0^{-2}\sum _{v=1}^{\text{H}}\frac{L_v}{n}{\widehat{\beta }}_{0v}^2,{\widehat{\lambda }}_r={\widehat{\gamma }}_r^{-2}{\mu }_{{\stackrel{\sim }{X}}_r}^{-1}\sum _{v=1}^{\text{H}}\frac{L_v}{n}{\widehat{\beta }}_{rv}^2{\mu }_{{\stackrel{\sim }{X}}_{r}v},1\le r\le p_1,\\ {\widehat{\lambda }}_{rr}={\widehat{\gamma }}_r^{-2}\sum _{v=1}^{\text{H}}\frac{L_v}{n}{\widehat{\beta }}_{rv}^2,1\le r\le p_1\text{and}{\widehat{\lambda }}_{rs}={({\widehat{\gamma }}_r{\widehat{\gamma }}_s)}^{-1}\sum _{v=1}^{\text{H}}\frac{L_v}{n}{\widehat{\beta }}_{rv}{\widehat{\beta }}_{sv},1\le r,s\le p_1,r\ne s.\end{array}$$

They are sample moments corresponding to theoretical moments {λ₀, λ_rr, λ_r, λ_rs}.

Appendix B: Proof

Technical conditions

The following assumptions are made.

• C1. The covariate U is bounded below and above: −∞< a ≤ U ≤ b < ∞, for real numbers a < b. The density f(u) of U satisfies inf_a≤u≤b f(u) > 0, sup_a≤u≤b f(u) < ∞, and is uniformly Lipschitz; that is there exists a real number M such that sup_a≤u≤b|f(u + c) − f(u)|≤M|c| for any real number c.

• C2. The needed dependence/independence structure is that U is independent of e_j, X_rj is independent of e_j and U; and W_sj is independent of e_j for r = 1, …, p, s = 1, …, q, j = 1, …, T.

• C3. For the predictors, sup |X_rij|≤B₁ and sup |W_rij|≤B₂ for some bounds B₁, B₂ ℝ⁺ and where sup is taken over 1 ≤ i ≤ n, 1 ≤ r ≤ p, 1 ≤ j ≤ n_i. In addition $T^{-1}{\sum }_{j=1}^{T}E(X_{rj})\ne 0$ for 1 ≤ r ≤ p.

• C4. The functions ψ(·) and φ_r(·), 1 ≤ r ≤ p, are twice continuously differentiable, satisfying E{ψ(U)} = 1 E{φ_r(U)} = 1 and |φ_r(·)| > c, for some constant c > 0.

• C5. Define ${\mathbf{\Omega }}_i^{\ast }$ to be the normalization of Ω_i, where the $j_1^{\text{th}}$ row and $j_2^{\text{th}}$ column element of ${\mathbf{\Omega }}_i^{\ast }$ is given as ${({\mathbf{\Omega }}_i)}_{j_1{j}_2}^{\ast }={({\mathbf{\Omega }}_i)}_{j_1{j}_2}/m_{j_1{j}_2}$, and m_j1j2denotes the number of subjects observed at both times t_j1 and t_j2. As inf_j1j2 m_j1j2 → ∞, ${\sum }_{i=1}^n{\mathcal{X}}_i^{\text{T}}{\mathbf{\Omega }}_i^{\ast }{\mathcal{X}}_i\to \mathcal{C}$ in probability where the limiting p + q + 1 × p + q + 1 matrix 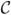is nonsingular.

Proof of Theorem 1

We first introduce some boundedness considerations. Since X_rij and W_rij are assumed to be bounded (C3) and U has compact support (C1), X̃_rij are also bounded. The matrices Ṽ_vk and ${\mathbf{M}}_v={\sum }_{k=1}^{L_v}{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime \text{T}}{\stackrel{\sim }{\mathbf{\Omega }}}_{vk}{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime }$ have been assumed to be invertible previously; more precisely, assume ${\text{sup}}_{1\le v\le \text{H}}{\mathbf{M}}_v^{-1}=O(1){\mathbf{1}}_{(p+q+1)\times (p+q+1)}$, where 1_a×b is an a ×b dimensional matrix of ones. We define ${\mathrm{\Delta }}_{vk}=\psi (U_{vk}^{\prime })-\psi (U_v^{\prime \ast })$ and ${\mathrm{\Delta }}_{\mathit{rvk}}^{\prime }=\psi (U_{vk}^{\prime })/{\phi }_r(U_{vk}^{\prime })-\psi (U_v^{\prime \ast })/{\phi }_r(U_v^{\prime \ast })$ for 1 ≤ k ≤ L_v, 1 ≤ r ≤ p, 1 ≤ v ≤ H, where $U_v^{\prime \ast }=L_v^{-1}{\sum }_{k=1}^{L_v}{U}_{vk}^{\prime }$, is the average of the U’s in B_v. The following boundedness results for 1 ≤ r ≤ p, 1 ≤ k ≤ L_v can be obtained using Taylor expansions: ${sup}_{v,k}\mid U_{vk}^{\prime }-U_v^{\prime \ast }\mid \le (b-a)/\text{H}$; sup_v,k |Δ_vk| = O(H⁻¹); ${sup}_{v,k}\mid {\mathrm{\Delta }}_{\mathit{rvk}}^{\prime }\mid =O({\text{H}}^{-1})$.

The coefficient function estimators β̂_v can be expressed as

$$\begin{array}{l}{\widehat{\mathit{\beta }}}_v={\mathbf{M}}_v^{-1}\left\{\sum _{k=1}^{L_v}{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime \text{T}}{\stackrel{\sim }{\mathbf{\Omega }}}_{vk}{\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime }\right\}={\mathbf{M}}_v^{-1}\times \\ \{\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{({\stackrel{\sim }{\mathbf{\Omega }}}_{vk})}_{j_2{j}_1}\left[\begin{array}{c}{\sum }_{r=0}^p{\beta }_r(U_{vk}^{\prime }){\stackrel{\sim }{X}}_{{\mathit{rvkj}}_1}^{\prime }+{\sum }_{r=0}^{p_1}{b}_{\mathit{rvk}}(U_{vk}^{\prime }){\stackrel{\sim }{X}}_{{\mathit{rvkj}}_1}^{\prime }\\ ⋮\\ {\stackrel{\sim }{X}}_{{\mathit{pvkj}}_2}^{\prime }[\{{\sum }_{r=0}^p{\beta }_r(U_{vk}^{\prime })+{\sum }_{r=0}^{p_1}{b}_{\mathit{rvk}}(U_{vk}^{\prime })\}{\stackrel{\sim }{X}}_{{\mathit{rvkj}}_1}^{\prime }]\\ ⋮\\ W_{{\mathit{qvkj}}_2}^{\prime }[\{{\sum }_{r=0}^p{\beta }_r(U_{vk}^{\prime })+{\sum }_{r=0}^{p_1}{b}_{\mathit{rvk}}(U_{vk}^{\prime })\}{\stackrel{\sim }{X}}_{{\mathit{rvkj}}_1}^{\prime }]\end{array}\right]\\ +\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{({\stackrel{\sim }{\mathbf{\Omega }}}_{vk})}_{j_2{j}_1}\left[\begin{array}{c}{\sum }_{r=1}^q{\eta }_r(U_{vk}^{\prime })W_{{\mathit{rvkj}}_1}^{\prime }+{\sum }_{r=1}^{q_1}{g}_{\mathit{rvk}}(U_{vk}^{\prime })W_{{\mathit{rvkj}}_1}^{\prime }+{\epsilon }_{{\mathit{vkj}}_1}^{\prime }\\ ⋮\\ {\stackrel{\sim }{X}}_{{\mathit{pvkj}}_2}^{\prime }[\{{\sum }_{r=1}^q{\eta }_r(U_{vk}^{\prime })+{\sum }_{r=1}^{q_1}{g}_{\mathit{rvk}}(U_{vk}^{\prime })\}{W}_{{\mathit{rvkj}}_1}^{\prime }]+{\epsilon }_{{\mathit{vkj}}_1}^{\prime }\\ ⋮\\ W_{{\mathit{qvkj}}_2}^{\prime }[\{{\sum }_{r=1}^q{\eta }_r(U_{vk}^{\prime })+{\sum }_{r=1}^{q_1}{g}_{\mathit{rvk}}(U_{vk}^{\prime })\}{W}_{{\mathit{rvkj}}_1}^{\prime }]+{\epsilon }_{{\mathit{vkj}}_1}^{\prime }\end{array}\right]\}.\end{array}$$

Next we expand ${\beta }_r(U_{vk}^{\prime })$ and ${\eta }_r(U_{vk}^{\prime })$ in the above formulation around $U_v^{\prime \ast }$, the average of the U’s in bin B_v. The remainder terms from this expansion, when averaged to form γ̂_r, will be shown to be either $o_p(m_0^{-1/2})$ or o_p(H⁻¹), while the leading term will be shown to be ${\gamma }_r+O_p(m_0^{-1/2})+O({\text{H}}^{-1})$, hence Theorem 1 follows. Details are given below.

Making use of the remainder terms Δ_vk and ${\mathrm{\Delta }}_{\mathit{rvk}}^{\prime }$ defined above, we have

$$\begin{array}{l}{\widehat{\mathit{\beta }}}_v={\mathbf{M}}_v^{-1}{\mathbf{M}}_v{\left\{{\gamma }_0\psi (U_v^{\prime \ast }),{\gamma }_1\frac{\psi (U_v^{\prime \ast })}{{\phi }_1(U_v^{\prime \ast })},\dots ,{\gamma }_p\frac{\psi (U_v^{\prime \ast })}{{\phi }_p(U_v^{\prime \ast })},{\delta }_1\psi (U_v^{\prime \ast }),\dots ,{\delta }_q\psi (U_v^{\prime \ast })\right\}}^{\text{T}}\\ +{\mathbf{M}}_v^{-1}{\mathcal{S}}_{XZ}{\left\{{\gamma }_{0vk}\psi (U_{vk}^{\prime }),{\gamma }_{1vk}\frac{\psi (U_{vk}^{\prime })}{{\phi }_1(U_{vk}^{\prime })},\dots ,{\gamma }_{p_{1}vk}\frac{\psi (U_{vk}^{\prime })}{{\phi }_{p_1}(U_{vk}^{\prime })},{\delta }_{1vk}\psi (U_{vk}^{\prime }),\dots ,{\delta }_{q_{1}vk}\psi (U_{vk}^{\prime })\right\}}^{\text{T}}\\ +{\mathbf{M}}_v^{-1}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{({\stackrel{\sim }{\mathbf{\Omega }}}_{vk})}_{j_2{j}_1}\left[\begin{array}{c}{\gamma }_0{\mathrm{\Delta }}_{vk}+{\sum }_{r=1}^p{\gamma }_r{\mathrm{\Delta }}_{\mathit{rvk}}^{\prime }{\stackrel{\sim }{X}}_{{\mathit{rvkj}}_1}^{\prime }+{\sum }_{r=1}^q{\delta }_r{\mathrm{\Delta }}_{vk}{W}_{{\mathit{rvkj}}_1}^{\prime }\\ ⋮\\ {\stackrel{\sim }{X}}_{{\mathit{pvkj}}_2}^{\prime }({\gamma }_0{\mathrm{\Delta }}_{vk}+{\sum }_{r=1}^p{\gamma }_r{\mathrm{\Delta }}_{\mathit{rvk}}^{\prime }{\stackrel{\sim }{X}}_{{\mathit{rvkj}}_1}^{\prime }+{\sum }_{r=1}^q{\delta }_r{\mathrm{\Delta }}_{vk}{W}_{{\mathit{rvkj}}_1}^{\prime })\\ ⋮\\ W_{{\mathit{qvkj}}_2}^{\prime }({\gamma }_0{\mathrm{\Delta }}_{vk}+{\sum }_{r=1}^p{\gamma }_r{\mathrm{\Delta }}_{\mathit{rvk}}^{\prime }{\stackrel{\sim }{X}}_{{\mathit{rvkj}}_1}^{\prime }+{\sum }_{r=1}^q{\delta }_r{\mathrm{\Delta }}_{vk}{W}_{{\mathit{rvkj}}_1}^{\prime })\end{array}\right]\\ +{\mathbf{M}}_v^{-1}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{({\stackrel{\sim }{\mathbf{\Omega }}}_{vk})}_{j_2{j}_1}\left[\begin{array}{c}\psi (U_{vk}^{\prime })e_{{\mathit{vkj}}_1}^{\prime }\\ ⋮\\ {\stackrel{\sim }{X}}_{{\mathit{pvkj}}_2}^{\prime }\psi (U_{vk}^{\prime })e_{{\mathit{vkj}}_1}^{\prime }\\ ⋮\\ W_{{\mathit{qvkj}}_2}^{\prime }\psi (U_{vk}^{\prime })e_{{\mathit{vkj}}_1}^{\prime }\end{array}\right],\end{array}$$

where ${\mathcal{S}}_{XZ}\equiv {\sum }_{k=1}^{L_v}{\stackrel{\sim }{\mathcal{X}}}_{vk}^{\prime \text{T}}{\stackrel{\sim }{\mathbf{\Omega }}}_{vk}{\stackrel{\sim }{\mathcal{Z}}}_{vk}^{\prime }$. Thus, the CA-LME estimators γ̂_r becomes

$$\begin{array}{l}{\widehat{\gamma }}_r+\frac{{\gamma }_r}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}\sum _{k\in I_{vt}}\frac{\psi (U_v^{\prime \ast })}{{\phi }_r(U_v^{\prime \ast })}{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }\\ +\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}{\{{\mathbf{M}}_v^{-1}\}}_{r+1,1}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{(\stackrel{\sim }{\mathbf{\Omega }})}_{j_2{j}_1}{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }{\stackrel{\sim }{\mathbf{Z}}}_{{\mathit{vkj}}_1}^{\prime }{\mathbf{b}}_{vk}+\cdots \\ +\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}{\{{\mathbf{M}}_v^{-1}\}}_{r+1,p}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{(\stackrel{\sim }{\mathbf{\Omega }})}_{j_2{j}_1}{\stackrel{\sim }{X}}_{{\mathit{pvkj}}_2}^{\prime }{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }{\stackrel{\sim }{\mathbf{Z}}}_{{\mathit{vkj}}_1}^{\prime }{\mathbf{b}}_{vk}+\cdots \\ +\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}{\{{\mathbf{M}}_v^{-1}\}}_{r+1,q}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{(\stackrel{\sim }{\mathbf{\Omega }})}_{j_2{j}_1}{W}_{{\mathit{qvkj}}_2}^{\prime }{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }{\stackrel{\sim }{\mathbf{Z}}}_{{\mathit{vkj}}_1}^{\prime }{\mathbf{b}}_{vk}\\ +\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}{\{{\mathbf{M}}_v^{-1}\}}_{r+1,1}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{(\stackrel{\sim }{\mathbf{\Omega }})}_{j_2{j}_1}{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }{A}_{{\mathit{rvkj}}_1}+\cdots \\ +\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}{\{{\mathbf{M}}_v^{-1}\}}_{r+1,p}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{(\stackrel{\sim }{\mathbf{\Omega }})}_{j_2{j}_1}{\stackrel{\sim }{X}}_{{\mathit{pvkj}}_2}^{\prime }{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }{A}_{{\mathit{rvkj}}_1}+\cdots \\ +\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}{\{{\mathbf{M}}_v^{-1}\}}_{r+1,q}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{(\stackrel{\sim }{\mathbf{\Omega }})}_{j_2{j}_1}{W}_{{\mathit{qvkj}}_2}^{\prime }{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }{A}_{{\mathit{rvkj}}_1}\\ +\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}{\{{\mathbf{M}}_v^{-1}\}}_{r+1,1}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{(\stackrel{\sim }{\mathbf{\Omega }})}_{j_2{j}_1}{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }\psi (U_{vk}^{\prime })e_{{\mathit{vkj}}_1}+\cdots \\ +\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}{\{{\mathbf{M}}_v^{-1}\}}_{r+1,p}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{(\stackrel{\sim }{\mathbf{\Omega }})}_{j_2{j}_1}{\stackrel{\sim }{X}}_{{\mathit{pvkj}}_2}^{\prime }{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }\psi (U_{vk}^{\prime })e_{{\mathit{vkj}}_1}+\cdots \\ +\frac{1}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^T\frac{1}{m_j}\sum _{v=1}^{\text{H}}{\{{\mathbf{M}}_v^{-1}\}}_{r+1,q}\sum _{k=1}^{L_v}\sum _{j_1=1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{(\stackrel{\sim }{\mathbf{\Omega }})}_{j_2{j}_1}{W}_{{\mathit{qvkj}}_2}^{\prime }{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }\psi (U_{vk}^{\prime })e_{{\mathit{vkj}}_1}\\ \equiv P_1+(P_2+\dots P_{p+q+3})+(P_{p+q+4},\dots ,P_{2p+2q+5})+(P_{2p+2q+6}+\dots +P_{3p+3q+7}),\end{array}$$

where $A_{{\mathit{rvkj}}_1}={\gamma }_0{\mathrm{\Delta }}_{vk}+{\sum }_{r=1}^p{\gamma }_r{\mathrm{\Delta }}_{\mathit{rvk}}^{\prime }{\stackrel{\sim }{X}}_{{\mathit{rvkj}}_1}^{\prime }+{\sum }_{r=1}^q{\delta }_r{\mathrm{\Delta }}_{vk}{W}_{{\mathit{rvkj}}_1}^{\prime }$ and ${\stackrel{\sim }{\mathbf{Z}}}_{{\mathit{vkj}}_1}^{\prime }={(1,{\stackrel{\sim }{X}}_{1{\mathit{vkj}}_1}^{\prime },\dots ,{\stackrel{\sim }{X}}_{p_1{\mathit{vkj}}_1}^{\prime },W_{1{\mathit{vkj}}_1}^{\prime },\dots ,W_{q_1{\mathit{vkj}}_1}^{\prime })}^{\text{T}}$. Let us analyze each term separately. Term P₁ becomes

$$\begin{array}{l}{P}_1=\frac{{\gamma }_r}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^{\text{T}}\frac{1}{m_j}\sum _{v=1}^{\text{H}}\sum _{k\in I_{vt}}\frac{\psi (U_{vk}^{\prime })}{{\phi }_r(U_{vk}^{\prime })}{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime }+O({\text{H}}^{-1})\\ =\frac{{\gamma }_r}{T{\overline{\stackrel{\sim }{X}}}_r}\sum _{j=1}^{\text{T}}\frac{1}{m_j}\sum _{i\in I_j}\frac{\psi (U_i)}{{\phi }_r(U_i)}{\stackrel{\sim }{X}}_{\mathit{rij}}^{\prime }+O({\text{H}}^{-1})={\gamma }_r+O_p(m_0^{-1/2})+O({\text{H}}^{-1}).\end{array}$$

Note that E(P₂|U, 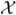˜, L_v, ) = 0 and since ${\{L_v^{-1}{\mathbf{M}}_v\}}^{-1}$ is bounded uniformly in v,

$$\begin{array}{l}var(P_2\mid U,\stackrel{\sim }{\mathcal{X}},L_v,\mathcal{X})=\frac{1}{T^2{\overline{\stackrel{\sim }{X}}}_r^2}\sum _{j=1}^T\frac{1}{m_j^2}\sum _{v=1}^{\text{H}}{(L_v^{-1}{\mathbf{M}}_v^{-1})}_{r+1,1}\\ \times \frac{1}{L_v^2}\sum _{k=1}^{L_v}\sum _{j_1}^{n_{vk}^{\prime }}\sum _{j_2=1}^{n_{vk}^{\prime }}{({\stackrel{\sim }{\mathbf{\Omega }}}_{vk})}_{j_2{j}_1}^2{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime 2}\sum _{s_1=1}^{p_1+q_1+1}\sum _{s_2=1}^{p_1+q_1+1}{({\stackrel{\sim }{\mathbf{D}}}_v)}_{s_1{s}_2}{({\stackrel{\sim }{\mathbf{Z}}}_{{\mathit{vkj}}_1}^{\prime })}_{s_1}{({\stackrel{\sim }{\mathbf{Z}}}_{{\mathit{vkj}}_1}^{\prime })}_{s_2}\\ \approx \sum _{j=1}^T\frac{1}{m_j^2}\sum _{v=1}^{\text{H}}\frac{1}{L_v^2}\sum _{k=1}^{L_v}{\stackrel{\sim }{X}}_{\mathit{rvkj}}^{\prime 2}=o_p(m_0^{-1}).\end{array}$$

Thus, $P_2=o_p(m_0^{-1/2})$ and so is P₃, …, P_p+q+3. With similar expansions and using the fact that Δ_vk, ${\mathrm{\Delta }}_{\mathit{rvk}}^{\prime }$ are O(H⁻¹), $P_{p+q+4},\dots ,T_{2p+2q+5}\approx {\sum }_{j=1}^T{m}_j^{-1}{\sum }_{v=1}^{\text{H}}{L}_v^{-1}{\sum }_{k=1}^{L_v}O({\text{H}}^{-1})=o_p({\text{H}}^{-1})$. Similar considerations of conditional mean and variance can be used to show that $P_{2p+2q+6},\dots ,T_{3p+3q+7}\approx o_p(m_0^{-1/2})$. Thus, it follows that ${\widehat{\gamma }}_r={\gamma }_r+O_p(m_0^{-1/2})+O({\text{H}}^{-1})$ for 0 ≤ r ≤ p. Showing that ${\widehat{\delta }}_r={\delta }_r+O_p(m_0^{-1/2})+O({\text{H}}^{-1})$ follows closely the derivation above and therefore is omitted here.

Appendix C: Bootstrap estimate of standard errors

To obtain standard error estimates for the data analysis of section 5, the wild bootstrap is used as it is more suitable for heteroskedastic cases that commonly arise in nonparametric regression. For the covariate-adjusted regression model, the point estimators for the fixed effects are obtained by averaging heteroskedastic estimators coming from each bin given by equation (11). Bin specific estimators are indeed heteroskedastic since their variance depends on U. The wild bootstrap algorithm implemented is as follows.

1. Within each bin v, bin specific estimates are obtained based on the original data and the resulting residual vectors are ${\widehat{\mathit{\epsilon }}}_k^{\prime }$ for subject k in bin v (k = 1, …, L_v).

2. We multiply each residual belonging to a specific subject and repetition (i.e. each component of ${\widehat{\mathit{\epsilon }}}_k^{\prime }$) by a random variable sampled from the two-point distribution attaching masses $(\sqrt{5}+1)/2\sqrt{5}$ and $(\sqrt{5}-1)/2\sqrt{5}$ to the points $-(\sqrt{5}-1)/2$ and $(\sqrt{5}+1)/2$ to obtain the wild bootstrap residual vectors ${\widehat{\mathit{\epsilon }}}_k^{\prime \ast }$, k = 1, …, L_v. (These wild bootstrap residuals approximate the variance and skewness of the residuals for each subject.)

3. The new responses in bin v, ${\stackrel{\sim }{\mathbf{Y}}}_{vk}^{\prime \ast }$, are obtained from the wild bootstrap residuals; and bootstrap bin-specific estimates (11) are obtained based on the bootstrap data.

We repeat the above procedure to obtain B = 400 bootstrap samples to estimate the standard errors. (Standard error estimates in this case stabalize after B = 100 bootstrap samples.)