Evaluation of a Highly Sensitive Qualitative Human Immunodeficiency Virus Type 1 (HIV-1) RNA Assay for Detection of HIV-1 Suppression

Abstract

By using a mathematical model, the APTIMA human immunodeficiency virus type 1 (HIV-1) RNA qualitative assay was evaluated as a semiquantitative assay to distinguish HIV-1 patient samples needing quantitation from samples in which the virus was suppressed with antiretroviral therapy.

The quantitation of human immunodeficiency virus type 1 (HIV-1) RNA in plasma is a useful tool for prognosis and is recommended to be obtained upon entry into care, before the initiation of highly active antiretroviral therapy (HAART), upon the failure of HAART, and at least every 3 to 6 months while a patient is receiving HAART (12). The plasma RNA level is routinely used to determine when treatment is succeeding or failing (2, 9, 11, 12), and some experts also use the viral load in determining when to initiate therapy in individuals with CD4 cell counts of >350/mm³ (2). For HIV-1, the quantitation of patient plasma viral loads (pVL) can be performed with (among other tests) the COBAS AMPLICOR HIV-1 MONITOR test version 1.5 (Roche Molecular Systems, Inc.), which is an FDA-approved quantitative PCR test that has been extensively validated and compared to other similar licensed technologies (1, 3). The limit of detection of the COBAS HIV-1 test is 50 HIV-1 genome copies/ml (cp/ml), and no clinical data that support the practice of monitoring levels lower than this are available. Intermittent, low-level but detectable HIV-1 viremia near the limit of detection is not highly significant in terms of prognosis, although some reports indicate that it may be associated with the development of drug resistance (5-7, 10, 13, 14).

Between May 2002 and April 2005, 5,076 HIV-1 patient plasma samples, 2,736 (53.9%) of which had <50 cp/ml, were processed by the Veterans Administration San Diego Healthcare System (VASDHS). During the 2005 fiscal year, 1,763 samples, of which 1,054 (59.8%) had <50 cp/ml, were assayed with the current COBAS HIV-1 test (data not shown). These numbers suggest that a screening assay capable of accurately identifying specimens with pVL below 50 cp/ml would eliminate the need to perform a quantitative assay on a large number of specimens received.

The APTIMA HIV-1 qualitative RNA assay (Gen-Probe Incorporated) was licensed by the FDA for use as an aid in the detection of acute HIV-1 infection in plasma specimens and as an additional, more specific test to confirm HIV-1 infection in plasma repeatedly reactive in assays positive for HIV-1 antibodies. This assay uses transcription-mediated amplification and has a 95% limit of detection of 13.1 cp/ml, correlating with approved quantitative HIV-1 RNA tests (8, 15; APTIMA HIV-1 qualitative RNA assay package insert [Gen-Probe, San Diego, CA]). An analyte signal/cutoff (S/CO) value of ≥1 indicates that the sample is reactive, or positive for HIV-1 RNA. We explored whether increasing S/CO values to reduce assay sensitivity would reduce or eliminate the detection of samples with pVL of <50 cp/ml yet retain the detection of clinically relevant samples.

Plasma samples collected during routine clinical monitoring of pVL in HIV-1-seropositive VASDHS patients were obtained and used with exemption from consent under University of California, San Diego-Veterans Affairs Human Research Protection Program protocol no. 060068, “Evaluation of a highly sensitive qualitative HIV-1 RNA assay as a screen for HIV-1 suppression.” Specimens were quantitated with the COBAS HIV-1 test by VASDHS microbiology personnel according to the directions of the manufacturer with standard laboratory operating procedures.

A total of 445 patient samples, including 283 samples with pVL below the limit of detection by the COBAS HIV-1 test, were evaluated with the APTIMA HIV-1 assay by using the package insert instructions. Samples were grouped into four general categories based on pVL (<50, 51 to 400, 401 to 3,000, and >3,000 cp/ml) (12). Within these categories, the results were then grouped by S/CO values into three subcategories: S/CO values greater than or equal to 1 but less than 10, values of 10 or greater but less than 15, and any value of 15 or greater (Table 1). Of the 283 samples with quantitated viral loads of <50 cp/ml, 146 (51.6%) were negative by the APTIMA HIV-1 assay and thus would not have required pVL quantitation. However, a large proportion of samples (48.4%) containing <50 cp/ml were considered positive.

TABLE 1.

Analysis of sample reactivity^a

S/CO value	Result for indicated sample viral load
	<50 cp/ml		51-400 cp/ml		401-3,000 cp/ml		>3,000 cp/ml
	No. reactive/no. tested	% Reactive	No. reactive/no. tested	% Reactive	No. reactive/no. tested	% Reactive	No. reactive/no. tested	% Reactive
>1 and <10	137/283	48.4	45/45	100	27/27	100	90/90	100
≥10 and <15	66/283	23.3	42/45	93.3	27/27	100	90/90	100
≥15	44/283	15.6	36/45	80	26/27	96.3	89/90	98.9

^aA total of 445 patient samples grouped by pVL into four categories were tested with the APTIMA HIV-1 RNA qualitative assay. The percent reactivity in the APTIMA HIV-1 assay for each viral load group was calculated using the standard S/CO value of 1 or an S/CO value of 10 or 15.

To decrease the sensitivity of the APTIMA assay so that it could be used as a reliable predictor of whether samples had viral loads of less than or greater than 50 cp/ml, patient sample results were reanalyzed after the S/CO value was raised to 10 and then to 15. Raising the S/CO value to 10 decreased the proportion of reactive results from 48.4 to 23.3% for samples in the <50-cp/ml category, and raising the S/CO value to 15 further decreased the proportion of reactive results to 15.6% (Table 1). Results from the other three categories (51 to 400, 401 to 3,000, and >3,000 cp/ml) were analyzed in a similar fashion. For the two categories with the highest pVL (401 to 3,000 and >3,000 cp/ml), raising the S/CO value to 10 maintained 100% detection. However, when the S/CO value was raised to 15, one sample in each of the categories was missed. Clearly, an approach other than assigning an arbitrary S/CO value was needed to calculate a value that would predict optimal sensitivity with statistical certainty.

A mathematical algorithm was developed to calculate the optimal S/CO value needed to maximize the differentiation of samples with clinically relevant pVL. While receiver operating characteristic curves were constructed to evaluate test performance and allowed the identification of sensitivity and specificity for arbitrary S/CO values (data not shown), a more sophisticated statistical treatment was required to estimate the error in sensitivity and specificity at each cutoff value for different viral loads and accurately predict the S/CO parameter to use for optimal clinical classification. For the purposes of this study, clinically relevant samples were defined as those with pVL above 1,000 cp/ml. This cutoff was chosen based on the historical use of <400 cp/ml as an indication of clinical suppression and on the geometric nature of error from a PCR-based test, where a ∼2.5-fold difference in values is generally accepted as evidence of significant change. In addition, transient viremia at levels of <1,000 cp/ml is not associated with clinical failure (7), and genotypic resistance testing to guide change in therapy is often not successful when viral loads are in this range. Sensitivity₉₉ was defined as the fraction of poor antiviral responders (pVL > 1,000 cp/ml), including a weighted fraction of moderate responders (pVL between 50 and 1,000 cp/ml), expected to be detected with 99% probability. Specificity₉₉ was defined as the fraction of antiviral responders (pVL < 50 cp/ml), including a weighted fraction of moderate responders (pVL between 50 and 1,000 cp/ml), expected to be detected with 99% probability. The algorithm was executed in SigmaPlot 10.1 (Systat Software, Inc.) and consisted of the following process.

In step A, the sample values were assigned to one of four categories, as follows: (i) true positives, samples with an S/CO value greater than or equal to the predefined S/CO value (the S/CO_test value) and a pVL of >1,000 cp/ml; (ii) false positives, samples with an S/CO value greater than or equal to the S/CO_test value and a pVL of ≤50 cp/ml; (iii) true negatives, samples with an S/CO value less than the S/CO_test value and a pVL of ≤50 cp/ml; and (iv) false negatives, samples with an S/CO value less than the S/CO_test value and a pVL of >1,000 cp/ml.

In step B, step A was repeated 40 times as the S/CO_test value was increased to 41 in increments of 1.

In step C, samples with pVL between 51 and 1,000 cp/ml were fractionally distributed to the <50- and >1,000-cp/ml categories. This linear fractional assignment is the simplest categorization strategy from a mathematical perspective and was based on the ratio of the sample copy level minus 51 to the difference between 1,000 and 51. The relevant fraction of each sample was then assigned to one of the four categories listed above. For example, with an S/CO_test value of 20, a sample with a pVL of 525 cp/ml and an S/CO value of 30 would have 0.5 assigned to the true-positive category and 0.5 assigned to the false-positive category. Similarly, if this sample had an S/CO value of 3, 0.5 would be assigned to the true-negative category and 0.5 would be assigned to the false-negative category.

The results of steps A to C were the numbers of true-positive, true-negative, false-positive, and false-negative samples obtained as a function of the S/CO_test value.

In step D, the sensitivity₉₉ at each S/CO_test value was calculated as the ratio of the number of true-positive samples to the sum of the numbers of true-positive and false-negative samples. The specificity₉₉ at each S/CO_test value was calculated as the ratio of the number of true-negative samples to the sum of the numbers of true-negative and false-positive samples.

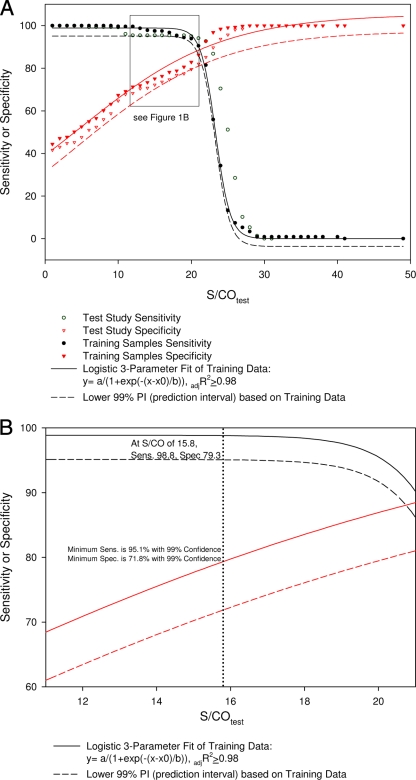
In step E, the following modified logistic function, which provided a better R² value than the standard logistic function, was fit to the sensitivity and specificity values (Fig. 1):

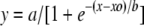where xo, a, and b are calculated coefficients of regression. The adjusted R² value of each regression was greater than 0.98, and all coefficients of regression were significant (P < 0.05).

FIG. 1.

Effect of the S/CO_test value on sensitivity and specificity. Results from the first study were used to generate the regression model and lower 99% PI as described in the text. The graph in panel A was overlaid with results from the masked study with additional specimens to verify the model. Panel B focuses on the area where the S/CO value is set to maximum sensitivity (sens.). _adjR², adjusted R² value; spec., specificity.

In step F, the one-sided lower 99% prediction interval (PI) was also calculated for each regression by a commercially available SigmaPlot algorithm.

By using this model, the S/CO_test value at which maximum sensitivity₉₉ and specificity₉₉ (i.e., minimum miscategorization) were achieved was 21.2, with a sensitivity₉₉ and specificity₉₉ of 88.6% (Fig. 1). For clinical application, the maximum sensitivity₉₉ was of more importance so that patient samples with clinically relevant viral titers would not be missed. In this model, the maximum sensitivity₉₉ plateaued at 98.8% with an S/CO_test value of 15.8. Concomitantly, the specificity₉₉ dropped to 79.3%, meaning that 79.3% of samples with pVL of <50 cp/ml would not have been sent for quantitation because the viral loads were undetectable by the APTIMA HIV-1 assay.

To verify whether this model could effectively discriminate between patient samples with pVL of <50 cp/ml (not requiring quantitation) and clinically relevant samples (pVL ≥ 1,000 cp/ml), a blinded validation study was performed. An additional 359 VASDHS clinical specimens from HIV-1-seropositive patients were tested with the APTIMA qualitative assay. The resulting S/CO values and the corresponding pVL data were recorded as true positive, true negative, false positive, or false negative. Sensitivity₉₉ and specificity₉₉ were calculated as a function of the S/CO_test value, and the sigmoidal model shown in Fig. 1 was overlaid with the resulting values. All of these values were greater than the 99% lower PI (Fig. 1). Since the 99% lower PI represents the worst-case expected sensitivity₉₉ or specificity₉₉ with 99% confidence, assignment steps A to C and the sigmoidal model provide a reasonable predictor of the effect of increasing S/CO values on the sensitivity₉₉ and specificity₉₉ achieved by the APTIMA HIV-1 assay.

These results establish proof of concept for this model. With respect to the quantitation of viral RNA in antiretroviral therapy patient samples, this model would have reduced the amount of samples requiring quantitation by an average of 79.3% while maintaining greater than 98.8% detection of clinical samples with quantifiable levels of HIV RNA with 99% confidence. A formal cost analysis is needed to confirm whether this reduction is significant and would need to address many factors outside the scope of this study, including sample volume, pooling strategies, viral load distribution, and turnaround time differences between platforms, as well as other variables.

In real-world settings, a limitation on the approach described in this study would be that extra time will be necessary to perform an additional quantitative test on samples that are positive when tested with the APTIMA HIV-1 assay. The processing efficiency and turnaround time would need to be evaluated if this model was to be validated for commercial use. In addition, different lots of reagents and repeat testing of the same specimen would be needed in order to determine the impact of day-to-day fluctuations in S/CO values and the impact of using different reagent lots.