High-Resolution Ion Cyclotron Mobility Spectrometry

Abstract

A novel ion mobility spectrometry instrument incorporating a cyclotron geometry drift tube is presented. The drift tube consists of eight regions, four curved drift tubes and four ion funnels. Packets of ions are propagated around the drift tube by changing the drift field at a frequency that is resonant with the ion’s drift time through each region. The approach trims each packet of ions as it leaves and enters each new region. An electrostatic gate allows ions to be kept in the drift tube for numerous cycles, increasing the ability to resolve specified ions. We demonstrate the approach by isolating the [M+2H]²⁺ or [M+3H]³⁺ charge state of substance P as well as individual trisaccharide isomers from a mixture of melezitose and raffinose. Resolving powers in excess of 300 are obtainable with this approach.

Introduction

We describe the development of the first cyclotron geometry drift tube. In this instrument a packet of ions is released into the cyclotron and transmitted through multiple cycles by oscillating the applied drift fields at an appropriate frequency.¹ As the ions cycle, species with different mobilities are pulled apart in time. After a desired number of cycles, only species with mobilities that are in resonance with the drift field application frequency are trapped, and subsequently these ions are released into a mass analysis region and detected. We demonstrate storage of ions for more than 10 cycles (a total drift distance of 20.75 m) and an experimental resolving power, R = t/Δt > 300, where t is the drift time of an ion measured at the center of its peak in a drift time distribution, and Δt is the full width at half-maximum (fwhm) of the peak.

For the last decade, there has been significant interest in developing new ion mobility spectrometry (IMS) technologies that couple with mass spectrometry (MS) analyses.^2–6 The primary motivation for coupling these techniques is that IMS separates ions based on differences in their shapes,^2–7 and MS provides primary structural information.⁵ It is anticipated that combinations of IMS-MS with other condensed-phase separation methods will lead to a more comprehensive understanding of complex molecular systems, such as molecular mixtures that arise in analysis of biological systems.⁸

Although some remarkable separations of isomers^9–13 and different conformers^14–16 have been reported, IMS is generally thought of as a low resolution technique. Several groups have constructed instruments with resolving powers in excess of 100.^3,4,17,18 To date the highest reported resolving power for an IMS separation was obtained for the [M-4H]⁴⁻ ion of CH₃(SO₂NHSO₂(CH₂)₆)₅SO₂NHSO₂CH₃, reported as t/Δt = 240.¹⁹ Jarrold and coworkers developed a high resolution instrument for studying cluster ions and reported R = 172 for carbon clusters and sodium dichloride (NaCl)_nCl⁻ ions.³ Hill,⁴ Smith,¹⁷ and their collaborators have developed high-resolution instruments for separating biomolecular ions and have reported resolving powers ranging from 100–216. In general the resolving power of traditional IMS methods becomes limited because it increases as the square root of the key experimental values E and L (the drift field and length, respectively). Our current efforts to develop cyclotron geometry instruments are aimed at ultimately increasing the resolving power by allowing ions to experience very long drift regions through multiple cycles. As a final note, the term cyclotron is used here to draw parallels with ion cyclotron resonance MS²⁰ with respect to the ability to achieve a high-resolution measurement; no magnetic fields are employed to manipulate ion trajectories.

Experimental

General

Detailed descriptions of IMS theory and instrumentation are provided elsewhere;^{1–10,17,18,21–26} only a short description of the instrument used for these studies is provided. A diagram of the instrument and pulse sequence is shown in Figure 1. Ions generated by electrospray ionization²⁷ accumulate in a Smith-geometry ion funnel (F1).²⁸ Packets of ions are periodically introduced into the cyclotron drift tube via an electrostatic gate (G1) following the pulse sequence shown in Figure 1. This initial pulse is also used to trigger the data acquisition system that is used to record drift times.

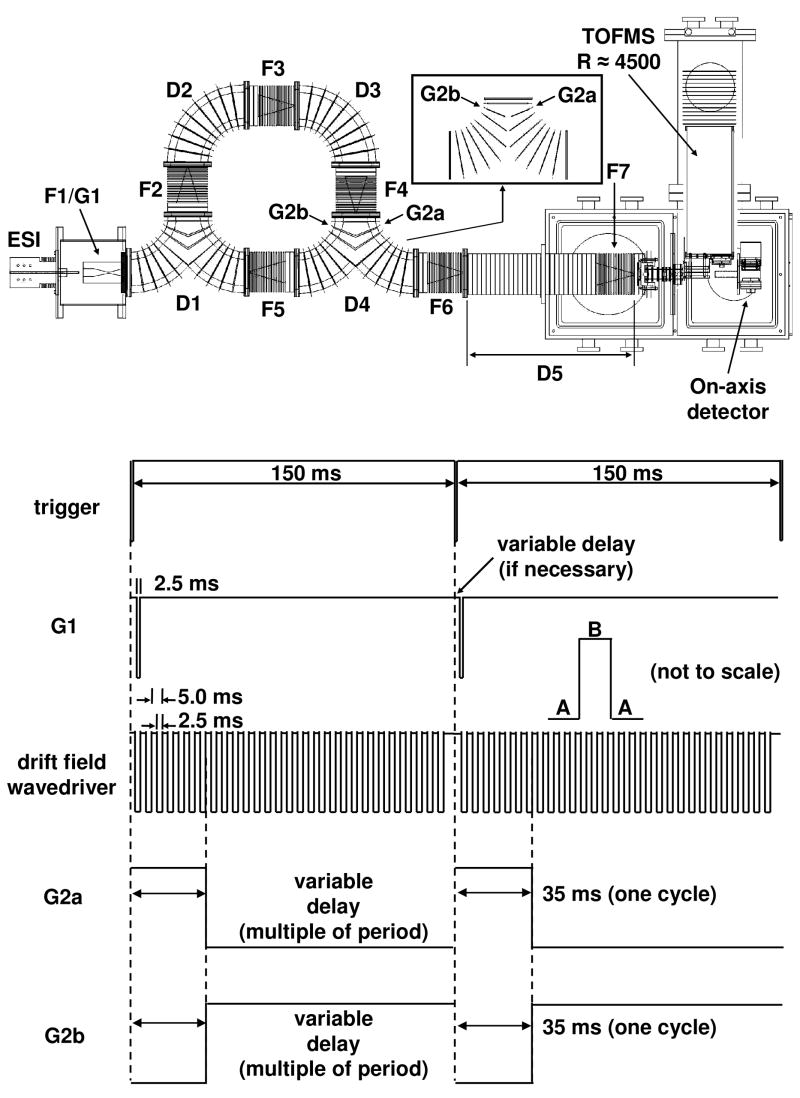
Figure 1.

Schematic of cyclotron geometry IMS-TOF instrument. The inset displays the split-lens geometry employed for the forked regions, D1 and D4. The two lenses G2a and G2b are operated as individual elements in the D4 region only. Below is the sequence of pulses applied to the source funnel (G1), the drift field wavedriver, and the G2a/G2b gate. By switching between two states with the drift field (A and B), it is possible to transmit ions of a particular mobility around the cyclotron. A time-of-flight pulse (not shown) is used to inject ions into the orthogonal TOFMS for mass analysis. Pulse diagram shown for two full injection sequences at one cycle with a drift field wavedriver frequency of 200 Hz, see text for more details.

As the packet of ions leaves the source it drifts around a curve into the main body of the multipass drift tube. The cyclotron region of the drift tube consists of eight separate components: four curved drift regions (D1–D4), each 30.01 cm in length; and four ion funnels (F2–F5), each 15.21 cm in length. Each of these has voltages applied to the first and last lens of the segment by a home built drift field wavedriver.¹ A series of resistors (5 MΩ3 for each curve, 1.5 MΩ for each funnel) is used as voltage dividers and establishes the drift field along the length of each section. Two sections (D1 and D4) have Y-shaped geometries. These regions are used to maintain ions inside the cyclotron, or to move ions into (D1) or out of (D4) the cyclotron. Both ion trajectory simulations with the program SIMION²⁹ and experimental data (not shown) have demonstrated that the geometry of D1 focuses ions exiting either F1 or F5 into F2, with very little deviation in path length when compared to D2 or D3 under the same field conditions. With respect to D4, the propagation of ions in this region is controlled by electrostatic gates. The lenses in the center of the Y are split (as shown in the inset in Figure 1). By applying the appropriate voltages to the lenses labeled G2a and G2b, both of which are isolated from the resistor chain, it is possible to maintain ions inside the multipass cyclotron region, or let ions out of the cyclotron drift tube (bottom two pulse sequences). Again, SIMION simulations and experimentation show that this has a negligible effect on drift times through this region. Once out of the cyclotron drift tube, ions are focused in F6 prior to entering the D5 region, where they exit into vacuum and are ultimately mass analyzed and detected.

A square wave at a fixed frequency (generated by a Wavetek Model 195 universal waveform generator, Wavetek Dalton Inc.), controls the drift field. This is shown as the third pulse sequence in Figure 1. The wavedriver is arranged such that the drift field is applied across the first lens of an ion funnel to the last lens of a curved region for one-half of the period (the A regions in Figure 1). Under these conditions, the constant field regions are F2 through D2, F3 through D3, F4 through D4, and F5 through D1. For the next half of the period (B), the field is defined by the first lens of a curved region to the last lens of an ion funnel; D1 through F2, D2 through F3, D3 through F4, and D4 through both F5 (and F6). A large positive potential across the 1.27 cm gaps (between adjacent continuous drift field regions), keeps ions from entering the next region.

It is instructive to describe how a packet of ions is propagated around this drift tube. The injection pulse (G1) occurs simultaneously with the A half of the period. During this time, ions enter the D1 region, but can travel no further, because of the large positive potential between the exit of this region and the entrance to F2. Once the drift field wavedriver switches to the B phase, ions can diffuse from D1 into F2, but only those ions that enter F2 before the next A phase are now stable within the instrument. Any ions at the leading edge of the distribution are defocused by the large positive potential and diffuse into surrounding electrodes; ions at the tailing edge are cut off by the switching potential, and diffuse away as well. This process is repeated twice more to guide ions around ¾ of the cyclotron; for each subsequent cycle around the drift tube, 4 more periods are required. For simplicity, this multiple of the wavedriver period is used as the delay time on the split lens G2a/G2b assembly in order to keep ions within the cyclotron for the number of cycles desired. As an example, the pulse sequence shown in Figure 1 is for two ion injections at one cycle at a frequency of 200 Hz.

The result of these voltage applications is the creation of four transmission and four elimination regions that are present at any given time within the instrument.¹ In the present configuration the transmission regions are significantly smaller than elimination regions. Within each application of the drift field (a full A-B-A transition, or the period of the wavedriver), ions must travel ~45.22 cm (the length of one funnel and one curved region) to remain stable. In one full cycle, 180.88 cm are traversed.

All drift regions and ions funnels are maintained at 7 V·cm⁻¹. The length of the linear region (F6 through F7) is 97.58 cm. The current design will allow this length to be reduced to 30.93 cm; the utility of this will be addressed in future publications. Thus, the distance an ion travels for a 1¾ cycle experiment would be 447.09 cm; each additional cycle adds 180.88 cm in distance traveled. F1 is operated at an RF frequency of 320 kHz, 280 V_p-p. F7 is operated at 325 kHz, 95 V_p-p. All other ion funnels (F2 through F6) are maintained at 500 kHz, 130 V_p-p. Since each ion funnel F2–F5 is operated at two different dc potentials, their RF generators must be floated by the dc potential applied to each funnel. The entire drift tube is filled with ~3.00–3.15 Torr of 300 K He buffer gas, and the pressure is monitored by a capacitance manometer.

Electrospray conditions

Substance P (98% purity), melezitose hydrate (99% purity), and raffinose pentahydrate (98% purity) were purchased from Sigma Aldrich and used without purification. A 2.0 × 10⁻⁴ M solution of substance P was prepared in 49:49:2% water: acetonitrile: acetic acid (by volume). Solutions of 5.0 × 10⁻⁴ M concentration (containing each of the oligosaccharides) were prepared in 50:50% water: acetonitrile, 2 mM NaCl. A mixture of the two was prepared by mixing equal volumes of the two solutions, for a final concentration of 2.5 × 10⁻⁴ M for each sugar.

Results and discussion

Illustration of multiple passes of substance P [M+2H]²⁺ and [M+3H]³⁺ ions

Figure 2 illustrates the multipass capability of the cyclotron drift tube for the [M+2H]²⁺ and [M+3H]³⁺ ions of substance P. To obtain these results, we begin by determining the optimal drift field application frequency for transmission of each of the ions. This is done by propagating the ions around ¾ of the cyclotron and monitoring the intensities of the m/z values corresponding to [M+2H]²⁺ or [M+3H]³⁺. The intensities at frequencies spanning 128.2 Hz to 250.0 Hz (39 different frequencies in total) are plotted at the top of Figure 2. The [M+2H]²⁺ ion is optimally transmitted using a drift field frequency of 158.7 Hz; whereas the [M+3H]³⁺ ion is favored at 208.3 Hz. Increasing the number of cycles for which the ions are stored within the cyclotron yields interesting results. While the [M+2H]²⁺ ion remains centered about 158.7 Hz, two maxima appear for the [M+3H]³⁺ ion, 196.1 Hz and 232.6 Hz. Increasing from 1¾ cycles to 3¾ cycles leads to a sharpening of these peaks in frequency space, as more of the ions with mobilities not corresponding to the maxima are lost to the mechanism of operation described above. This finding is consistent with the improved resolution observed in overtone mobility spectrometry with an increased number of drift segments.¹ This illustrates the possibility to stabilize specific structures at applied drift field frequencies while eliminating other species, even for the same ion.

Figure 2.

Intensities of the substance P [M+2H]²⁺ and [M+3H]³⁺ charge states measured with the TOF mass analyzer as a function of frequency, for injected ions experiencing from ¾ of a cycle to 3¾ cycles around the cyclotron drift tube. Frequencies of 128.2 Hz (a period of 7.80 ms) to 250.0 Hz (4.00 ms) were examined, in increments of 0.10 ms period, for a total of 39 mass spectra for each individual number of cycles. The two intense frequencies observed for the ¾ cycles data (158.7 Hz for the [M+2H]²⁺ ion and 208.3 Hz for the [M+3H]³⁺ ion) were those employed in Figure 3.

It is interesting to consider the distributions as a function of frequency for these ions. We begin by noting that since the drift field application frequency, f, is related to the drift time, t (f = 1/t), where t corresponds to the drift time through one of the four 45.22 cm segments of the cycle, then reduced mobilities, K₀, can be obtained from:

$$K_0=\frac{L^{2}f}{V}\times \frac{273.2}{T}\times \frac{P}{760},$$

where L is the length of the drift region, V is the drift voltage, f is the drift field frequency, and T and P are the temperature and pressure at which the experiment was conducted, respectively (for normalization purposes). Although we have not published extensively about substance P, the mobilities of the [M+2H]²⁺ and [M+3H]³⁺ species are well characterized. From the data of Myung et al.³⁰ we derive K₀([M+2H]²⁺) = 3.41 cm²·V⁻¹·sec⁻¹. Drift time distributions for the [M+3H]³⁺ ion shows that there are two resolvable conformers, a compact state (having K₀ = 5.02 cm²·V⁻¹·sec⁻¹),³⁰ and a relatively more stable elongated state (with K₀ = 4.44 cm²·V⁻¹·sec⁻¹).³¹ In the data shown in Figure 2, the peak at 158.7 Hz for the [M+2H]²⁺ ion allows us to determine a value of K₀ = 3.45 cm²·V⁻¹·sec⁻¹, in good agreement with the value determined from Myung’s data.³⁰ The peak at 208.3 Hz for [M+3H]³⁺ yields a value of K₀([M+3H]³⁺) = 4.52 cm²·V⁻¹·sec⁻¹. This value is most consistent with the measured mobility for the elongated state for [M+3H]³⁺. Using the 3¾ cycles data, the peak at 232.6 Hz gives us a value of K₀ = 5.06 m²·V⁻¹·sec⁻¹, in agreement with the mobility calculated for the compact state. The peak at 196.1 Hz yields a value of K₀([M+3H]³⁺) = 4.26 cm²·V⁻¹·sec⁻¹.

With this understanding of which ions are favored as a function of frequency, consider the drift time distributions in Figure 3. In separate experiments, using transmission frequencies of 158.7 and 208.3 Hz we have examined ions for multiple cycles around the cyclotron. The results appear very promising. At 1¾ cycles (4.47 m total length) we determine drift times of 47.04 and 62.88 ms for the [M+3H]³⁺ and [M+2H]²⁺ ions, respectively. The measured fwhms of typical peaks under these conditions are 0.72 and 0.96 ms, respectively. This yields an IMS resolving power of 65 for each peak.

Figure 3.

Isolation and separation of the [M+2H]²⁺ and [M+3H]³⁺ charge states of substance P at 1¾, 5¾, and 10 ¾ cycles with the cyclotron drift tube. Two spectra were collected for each number of cycles; one at a frequency of 158.7 Hz for the isolation of the [M+2H]²⁺ ion, and another at a frequency of 208.3 Hz to isolate the [M+3H]³⁺ ion. The total distance traveled by the ions for each number of cycles is shown, as well as the resolving power for both charge states after 10¾ cycles.

Upon increasing the delay of the G2a/G2b gate we allow the ions to experience 5¾ cycles. Under these conditions, each ion travels 11.71 m. Although peak centers increase to 124.08 and 163.68 ms, there is little change in the fwhm of these peaks. The fwhm of the [M+3H]³⁺ peak is 1.20 ms, and the [M+2H]²⁺ peak is 0.96 ms. Thus, the peaks have moved apart but do not appear to broaden significantly. This provides an important illustration of the separation process that we are utilizing. The widths of peaks are not solely determined by diffusional broadening. If they were dictated only by diffusion, the fwhm of peaks would always increase upon increasing the number of cycles. Instead, ions with mobilities that are not resonant with the drift field frequency wind up in positions that cannot be transmitted around the instrument. The net result is that the ion packet is periodically trimmed. As the ions move through each drift region, populations that have diffused to the leading and trailing edges are eliminated at each new section. We have recently written about this phenomenon in a multidrift region approach called overtone mobility spectrometry.¹ This trimming also leads to substantial losses in signal at multiple cycles, and it becomes apparent that only frequencies for which there exist a stable mobility will have signal after many passes.

The net result of this trimming process is that it allows us to access relatively high resolving powers under relatively moderate experimental conditions. This effect becomes more pronounced with an increasing number of cycles. Figure 3 also shows data acquired for 10¾ cycles. Under these conditions the ions have traveled 20.75 m. The peak centers increase to 220.32 and 289.68 ms. In this case, the fwhm([M+2H]²⁺) = ~0.84–0.96 ms, and fwhm([M+3H]³⁺) = 0.96 ms (see inset). From these values, we determine t/Δt = 230 for [M+3H]³⁺ and ~305–345 for [M+2H]²⁺.

The results for other trapping conditions are shown in Figure 4, which shows a plot of the drift times for the [M+2H]²⁺ and [M+3H]³⁺ ions of substance P for data obtained for 1¾ to 10¾ cycles. The line through the data has a slope that corresponds to the time required for a single pass around the cyclotron drift tube. The intercept corresponds to the time spent traveling ¾ of the cyclotron as well as the linear drift region. The [M+2H]²⁺ data has a slope of 25.21 ms/pass, and the intercept is 37.60 ms. The [M+3H]³⁺ data has a slope of 19.22 ms/pass, and an intercept of 27.98 ms.

Figure 4.

Total drift time as a function of the number of cycles for the [M+2H]²⁺ and [M+3H]³⁺ charge states of substance P through the cyclotron drift tube are shown in the top plot. Ions have experienced from 1¾ to 10¾ cycles. Times are shown as points, with the lines of best fit drawn through each set of times. The slope of each line represents the time the ions spend in one cycle of the drift tube, while the intercept represents the time to traverse the linear region as well as ¾ of the cyclotron region. The bottom plot shows the IMS resolving power as a function of the number of cycles for both the [M+2H]²⁺ and [M+3H]³⁺ charge states of substance P. Lines projecting IMS resolving powers for both ions at higher numbers of cycles are shown.

These values can also be used to determine the mobilities of these two ions. Under the experimental conditions employed, the mobilities of the [M+2H]²⁺ and [M+3H]³⁺ determined from the observed slopes are K₀ = 3.44 and 4.52 cm² V⁻¹ sec⁻¹, respectively. These values are in agreement with the values calculated from the ¾ cycle data (3.45 and 4.52 cm² V⁻¹ sec⁻¹, respectively). The values are also in agreement with prior drift time measurements.^30,31

It is also interesting to examine the resolving power after additional cycles. Figure 4 also shows a plot of the resolving power for peaks measured using ten different cyclotron conditions such that ions experience 1¾ to 10¾ cycles. The resolving power increase with the number of cycles is roughly linear. Note, t/Δt does not increase as $\sqrt{L}$, as is expected for peak shapes dictated by diffusion. As mentioned above, this is because only ions with a mobility that is resonant with the drift field frequency remain stable in this instrument. Thus, as ions are transmitted from region to region, only species that are stable within the next region will remain. Leading and trailing edges of the ion distribution are eliminated. While this effectively trims the ion packet and limits the fwhm of the peak that is observed, the values of t/Δt that are obtained rigorously correspond to values of resolving power; only, in this case, diffusion has a minimal effect on peak shape until ions are released into the final linear drift region. It is interesting to consider projected resolving powers for experiments that utilize even more passes. From Figure 3 we anticipate that the resolving powers associated with the [M+2H]²⁺ ion peak of substance P will exceed 500 after 20 cycles. We also note that the peak widths could be minimized by using a shorter linear drift region (as well as a higher drift field in this region) at the exit of the cyclotron, as this limits broadening due to diffusion.

The effects of curves, fields, and frequencies on separations and measured mobilities

In the present experimental design, only an ion that traverses the central axis of the drift tube exactly will experience a constant drift field. Any ion that diffuses toward the inside of the tube will travel a shorter distance and experience a higher drift field. Likewise, any ion that diffuses toward the outside of the drift tube will traverse a longer distance and experience a lower drift field. We have attempted to minimize this type of effect by incorporating ion funnels immediately before and after each curve. In this way, all ions are focused to the center of the drift region prior to entering each curve. At this early point in development, we cannot entirely rule out the possibility that the use of curved drift regions introduces some systematic errors in these measurements. However, we note that it is comforting that so far, in the systems we have studied, mobilities appear to be in reasonable agreement with accepted values. Thus, it appears that ions experience a drift field and length that corresponds to the center of the drift region.

With this analysis we expect that accurate mobilities are attainable with this approach. However, such accuracy may be somewhat artificial. As long as an ion’s mobility is in resonance with the drift field frequency, it should be transmitted. The ion need not be at the center of a distribution of ions. The requirement is that the structure is stable. Over multiple cycles, all other mobilities will ultimately drift into regions of the drift tube that do not lead to transmission. Therefore, while it is possible to measure which mobilities are stable at a particular number of cycles around the cyclotron, those mobilities may not correspond to the center point of a peak determined by traditional IMS methods. Rather, these ions may correspond to small stable populations that are centered near the leading or trailing sides of large populations.

An example involving the separation of two isomers: raffinose and melezitose

A much more difficult system to separate is the pair of isobaric trisaccharides melezitose and raffinose. Figure 5 shows that such species are readily isolated using the multipass capabilities of the cyclotron drift tube. We begin by recording the ion intensities as a function of drift field frequency around ¾ of the cyclotron for the m/z = 527 ion which corresponds to the [M+Na]⁺ ion of each monomer. Twenty four frequencies were scanned, and this was carried out separately for each trisaccharide. Melezitose possesses a more compact structure, and is therefore observed at higher frequencies, with the highest intensity found at 169.5 Hz. The lower mobility raffinose shows a maximum at 149.3 Hz; however, we used a frequency of 144.9 Hz for the isolation of this sugar, since there was overlap at 149.3 Hz. Using the experimental conditions, these values can be used to define K₀ = 4.05 and 3.47 cm²·V⁻¹·sec⁻¹, respectively, for melezitose and raffinose. This matches well for melezitose, which has K₀ = 4.08 cm²·V⁻¹·sec⁻¹; the agreement is not as good for raffinose, which has K₀ = 3.88 cm²·V⁻¹·sec⁻¹, for the reasons described in the above section (i.e., we did not transmit the center of the ion distribution).

Figure 5.

The top distribution displays the intensity of the [M+Na]⁺ ion of the two trisaccharides melezitose and raffinose (electrosprayed individually), measured with the TOF mass analyzer, through ¾ of the cyclotron drift tube. Frequencies of 137.0 Hz (7.30 ms period) to 200.0 Hz (5.00 ms period) were examined, in increments of 0.10 ms period, for a total of 24 mass spectra. For analysis of the mixture, a frequency of 144.9 Hz was used to isolate the raffinose [M+Na]⁺ ion, while 169.5 Hz was used for melezitose. The second series of distributions shows spectra collected separately at each of these frequencies for 1¾, 3¾, and 6¾ cycles, for the mixture of the two sugars. The total distance traveled shown.

Example data obtained for the separation of the mixture of melezitose and raffinose after multiple cycles is also shown in Figure 5. At 169.5 Hz for melezitose or 144.9 Hz for raffinose we find that 1¾ cycles is sufficient to isolate each ion. Under these conditions, melezitose has a drift time of 58.56 ms and raffinose has a drift time of 68.40 ms. At 3¾ cycles, the ions have traveled 8.09 m, and are further separated. Finally, at 6¾ cycles, the two sugars have now traveled 13.52 m. The drift time increases to 176.64 ms for melezitose, and this ion has a fwhm of 1.20 ms, or R = 147. The drift time of raffinose is 206.64 ms; combined with a fwhm of 0.96 ms, we obtain R = 215 for this peak.

Summary and conclusions

The first data collected with a multipass cyclotron geometry drift tube was presented. By varying the field across regions of the drift tube at a fixed frequency, ions of specific mobilities are isolated and this isolation refined over numerous cycles through the instrument. The operation and precision of the instrument was demonstrated by examining the [M+2H]²⁺ and [M+3H]³⁺ ions of the peptide substance P for up to 10¾ cycles. Additionally, we presented an isolation of a mixture of the isomers melezitose and raffinose. Peak widths do not increase significantly with an increase in the number of cycles. This is a result of the trimming away of ions in the leading or trailing regions of the distribution as species are transmitted to new drift regions. While not the focus of this first result, we note that this approach leads to limitations in sensitivity. We are currently investigating this and working on methods to improve sensitivity. Clearly, many other improvements also remain to be made as well; however, this first prototype appears promising as a means of increasing the resolving power of IMS methods.