Dodging the crisis of folding proteins with knots

Abstract

Proteins with nontrivial topology, containing knots and slipknots, have the ability to fold to their native states without any additional external forces invoked. A mechanism is suggested for folding of these proteins, such as YibK and YbeA, that involves an intermediate configuration with a slipknot. It elucidates the role of topological barriers and backtracking during the folding event. It also illustrates that native contacts are sufficient to guarantee folding in ≈1–2% of the simulations, and how slipknot intermediates are needed to reduce the topological bottlenecks. As expected, simulations of proteins with similar structure but with knot removed fold much more efficiently, clearly demonstrating the origin of these topological barriers. Although these studies are based on a simple coarse-grained model, they are already able to extract some of the underlying principles governing folding in such complex topologies.

During the past 2 decades, a joint theoretical and experimental effort has largely advanced the quantitative understanding of the protein folding mechanism. Most small- and intermediate-size proteins live on a minimally frustrated funnel-like energy landscape, which allows fast and robust folding (1–3). Because proteins have been able to solve the energy problem, the final challenge is the structural complexity of the protein folding motifs. Most proteins avoid complex topologies, but recent discoveries have shown that some proteins are actually able to fold into nontrivial topologies where the main chain folds into a knotted conformation (4–6). Although these “knotted” folding motifs have been observed, we still have to face the challenging question of how the protein overcomes the kinetic barrier associated with the search of the knotted conformation. We suggest a possible mechanism where the knot formation is preceded by a conformation called a “slipknot.” A slipknot is topologically similar to a knot, except that an internal knot is effectively undone as the pathway of the backbone folds back on itself. The fact that such slipknots have already been observed in some protein final structures (7) adds support to this suggestion.

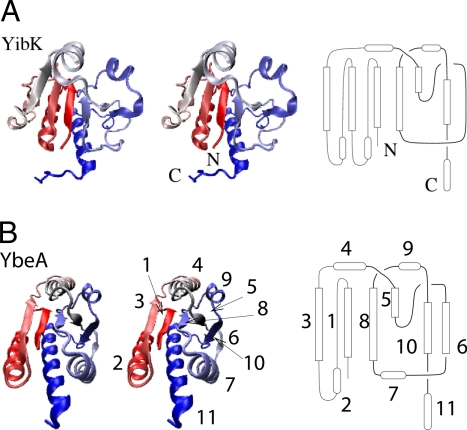
This folding mechanism is explored in the context of the two most experimentally investigated knotted families of proteins, Haemophilus influenzae YibK and Escherichia coli YbeA, which are homodimeric α/β-knot methyltransferases (MTases). A schematic representation of these proteins is shown inFig. 1, [see also supporting information (SI) Fig. S1]. It has been shown experimentally that both these proteins unfold spontaneously and reversibly on addition of chemical denaturant (8–11) and they are able to fold even when additional domains are attached to one or both termini (12). In very recent experimental work (13), based on analysis of the effect of mutations in the knotted region of the protein, a folding model for YibK was also proposed. In this model the threading of the polypeptide chain and formation of the native structure in the knotted region can occur independently as successive events. These results alone, however, are not sufficient to explain the folding mechanism. To complement the experimental information, we have devised a theoretical computational strategy. Simulations are performed for 3 knotted proteins (YibK and YbeA) and 2 proteins with slipknots (AFV3-109 and thymidine kinase) by using structure-based coarse-grained models.

Fig. 1.

Structure of knotted proteins. (A) Stereoview of structure of knotted protein YibK (PDB ID code 1j85) (Left) and schematic of structure (Right). (B) Stereoview of YbeA (PDB ID code 1od6) and it schematic structure (Left). Details of proteins structure are described in SI Text.

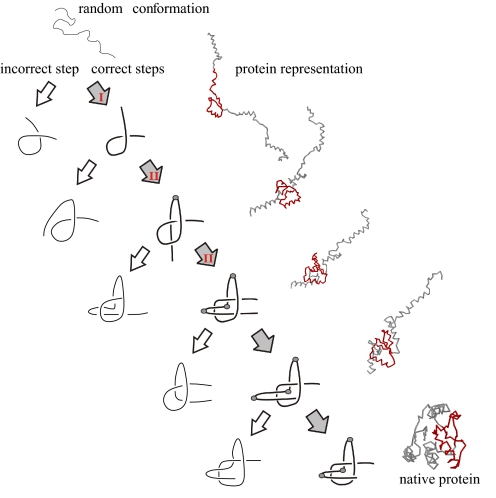
In the present study we consider knots of the simplest type, referred to as a trefoil or 3₁ knot. It is the simplest possible knot, which consists of a loop through which one end of a chain is threaded. In principle, there might be 3 possible mechanisms leading to the creation of such a knot. The most straightforward one would require just 2 steps: creating a loop and threading one end through it. The second mechanism is more complicated and involves an intermediate step with a slipknot. The third and final possibility would involve the creation of an ensemble of loose random knots in the first stage, which might turn into deeper knots after a relatively longer time. Analysis of simulated folding trajectories provides the necessary insight on this complex folding event. The results indicate that the folding of YibK and YbeA proceeds according to the second mechanism, through a slipknot intermediate configuration. This is consistent with earlier theoretical observations (6, 7). Fig. 2 provides a detailed description of the suggested folding mechanism, and its kinetics are presented in Fig. 3.

Fig. 2.

The folding route that leads to the native knotted configuration 3₁ through an intermediate configuration with a slipknot. The pathway is represented by a series of configurations, starting in the top left (a random conformation) and proceeding toward the right bottom. The path involves 5 essential steps, the first three of them correspond to Reidemeister moves I and II (denoted on appropriate arrows). A typical representation of the protein conformations is shown to the right of the associated mechanistic step. Native-like locations of the knot are shown in red. Each step is characterized by the appearance of new structural elements such as loops and hooks. During the folding route incorrect steps may occur. Examples of some incorrect configurations, which are kinetic traps, are represented by thin lines (sketched on the left). These traps act as topological barriers (14) and escaping from them requires a backtracking mechanism similar to the ones we have observed in regular folding (15). For the protein 1o6d, gray dots represent amino acid 102 in the third step plus amino acids 114 and 125 in the following steps. Special emphasis is given to them because they are associated with sharp turns, which are required to achieve the knotted state. This folding process is shown in the attached movie, whose details are described in SI Text.

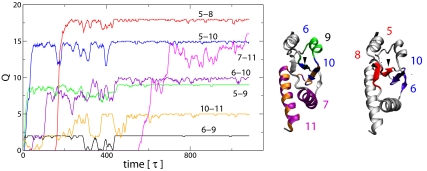
Fig. 3.

Kinetic properties of contacts inside the knotted structure of protein 1o6d. (Left) The time dependence of the number of formed native contacts between relevant structural elements of the protein knot, 1od6. (Right) Schematic representation of knotted part of the protein 1od6. Interacting regions of the protein 1o6d are colored according to the ones used in each trajectory. For clarity, if there are native interactions of one secondary structure element with 2 different parts of the protein, they are shown on 2 separate structures. Backtracking is observed at different levels for all trajectories. The contacts between β-strands 5–8 are red, the ones between β-strands 6–10 are magenta, and the ones for the turn 97–105 are orange. Kinetic studies were performed by using overdamped Langevin dynamics. Time steps have been chosen to have typical folding times of ≈1,000 steps.

Understanding the folding mechanism for these knotted proteins provides the tools to explore additional complex folds. For example, one can extend these studies to proteins that do not fully knot but form a slipknot in the native state (see Fig. 4 and Fig. S2). Some slipknotted proteins have a simple folding motif such as crenarchaeal viruses AFV3–109 (16), but others, such as thymidine kinase (17), are longer and have a more complex folding mechanism.

Fig. 4.

Structure of 2 proteins with slipknots: crenarchaeal viruses AFV3–109 (2j6b) (Left) and a thymidine kinase (1p6x) (Center). (Right) A schematic representation of the structure of 1p6x. Stereoviews of proteins are shown in SI (Fig. S2).

Results

Folding Knotted Proteins.

The folding pathways that lead to the knotted conformation are observed in our simulations through an intermediate configuration containing a slipknot. This route is shown schematically in Fig. 2 and discussed below. Analysis of this suggested folding mechanism requires that we divide this route into a few geometrically distinctive steps. A step may consist, for example, of threading the chain through a loop created in a separate region of the sequence. This representation allows us to describe long folding trajectories, consisting of thousands steps in our simulations, by a sequence of the essential intermediate ensemble of configurations. When projected on a plane, certain transitions between such 2 adjacent configurations can be identified with so-called Reidemeister moves. The Reidemeister moves change a relative location of some strands (when projected on a place), but do not change the type of the knot. There are 3 such moves, denoted I, II, and III, that involve, respectively 1, 2, and 3 strands. They are described in detail in SI Text and Fig. S3.

Folding Proteins in the α/β-Knot Superfamily into a Trefoil Knot.

Our analysis is based on the simulations of the α/β-knotted proteins YibK (PDB ID code 1j85) and YbeA (PDB ID codes 1o6d and 1vho), shown in Fig. 1 and Fig. S1, which are homodimers in their native configuration. According to the experimental results (9, 10) they fold via a few intermediate steps reaching the stable monomer states with considerable structure. Only the last step involves formation of a dimer. This allows us to study these proteins as monomers. Notice that YibK shares only 19% sequence identity with YbeA (10). Folding simulations were performed at temperatures slightly above the folding temperature T_f, starting from random conformations. Simulations were run by using a standard C_α structure-based model (sometimes called Go Model) (18, 19). For each protein we observed at least 10 successful folding trajectories; ≈1–2% of all routes succeeded to reach the native knotted states. These successful trajectories choose between 2 parallel folding trajectories similarly to what has been proposed experimentally (9, 10). Both trajectories are characterized by an intermediate slipknot configuration but, in one case, it is formed early in the folding process whereas, in the other case, it is a late event. Fig. S4 shows the fraction of native contacts Q at the moment when the slipknot is being created, i.e., when its hook-region starts to be threaded through the loop 66–96. In the most common trajectory the structure elements located closer to the N terminus of the protein fold in the final stages of the folding process around Q ≃ 0.8. In the alternative trajectory, the N-terminal folds in the early stages of folding, thus when the slipknot is being created Q ≃ 0.6. In fact, there is also an additional but very rare possibility (which we observed only once) of formation of a knot by threading the C terminus through the loop 66–96 without a slipknot intermediate.

For clarity we now discuss in detail one folding trajectory for 1o6d, shown schematically in Fig. 2. (This is the smallest of all proteins being analyzed and therefore had the largest number of successful runs.) Although we focus on this single example, this trajectory is similar to other proteins with a knot 3₁, such as 1vho and 1j85. This folding route consists of 6 distinctive configurations. During the first transition a loop is created (Reidemeister move I). This loop extends between amino acids 66 and 96 and remains formed during the entire folding event. After this step, a further region of the chain gets close to the loop, requiring a hook formation (Reidemeister move II). This hook is then threaded through the loop (also move II), creating the slipknot in the fourth intermediate. The slipknot is then transformed into a knot by pulling one terminus through the loop, which may be viewed as a 2-step process, with an intermediate 5 and final configuration 6. There are no Reidemeister moves corresponding to these last 2 steps, because they could not happen for a closed chain without cutting it.

As argued above, the creation of a knot requires several turns to occur at the right place and in the right time order. In the trajectory shown in Fig. 2 these turns are represented by gray dots. The first one occurs at amino acid 102, which redirects the protein chain toward the loop 66–96. Then 2 other turns at positions 114 and 125 are needed for the hook formation. This hook is threaded through the loop 66–96. Finally, the terminus 147 is pulled through this loop, which results in the 3₁ knot.

To understand the knot formation, we investigate the order that native contacts are formed and, sometimes, broken and re-formed (backtracking) during the folding event. Correlation between formation of some native contacts with the backtracking of other ones can teach us about topological bottlenecks. This information can be extracted from Fig. 3, where the time dependence of the number of formed native contacts between relevant structural elements of the protein knot is shown (see Table S1). Initially, we focus on the formation of the loop between residues 66 and 96 that requires the creation of contacts between β-strands 5 and 8. This can only be achieved by the preformation of the contacts between 5 and 10, which is followed by a simultaneous destruction of these contacts and formation of the ones between 5 and 8. During this loop formation, contacts between strands 6 and 10 are also formed, which are needed to create the slipknot conformation. The formation and destruction (≈180 time steps) of contacts between strands 5 and 10 is an example of backtracking. Backtracking also plays a role in the formation of contacts between 5 and 9 and between 6 and 9. The order of contact formation is crucial, otherwise knotting is not possible.

Backtracking is also a mechanism to escape from kinetic traps as described in Fig. 2. For example, if 8–11 contacts are formed early, the creation of a loop between residues 66 and 96 becomes impossible. The 8–11 contacts need to be broken before this loop can be created. A similar situation occurs at the final stage of knot creation that involves threading helix 11 through the loop. During this process, contacts between helices 7 and 11 may be accidentally created. They need to be broken until further threading can proceed.

Energetic Heterogeneity Enhancing Folding Ability.

The results above demonstrate that making only the native contacts attractive is sufficient to fold the protein into its native conformation. The percentage of successful trajectories, however, is then very small—only ≈0.1%. Analysis of these data suggests that this success rate can be increased by improving the time order of contact formation and therefore reducing backtracking. We used a different strength for a few selected native interactions to achieve this folding improvement. Backtracking gets reduced but the overall folding mechanism remains the same as described in Fig. 2.

Guided by the results of Fig. 3 that identify the structural regions responsible for enhancing folding, we modified some of our contact interactions. We increased the strength of contacts between β-strands 5 and 8. This modification facilitates the formation of the loop between residues 66 and 96 and also the attachment of the C terminus to this loop, which leads to the slipknot conformation involving the contacts between strands 6 and 10. We also slightly reduced the interaction energy between the C terminus and the loop. Rapid formation of those contacts results in problematically fast blocking of the necessary backtracking and threading of the C terminus across the loop. Simulations with this “optimal” model succeeded in folding into the knotted structure 29 times in 2,500 trials. Further increasing the contact strength in these regions does not keep improving knot formation. Because backtracking is also needed during the knotting process, if those increases are too large, they will lead to more kinetic traps. For further analysis on how this optimal set of contacts have been determined see SI Text.

Extension of the Protein Chain and a Rebuilt Protein Without Knot Structure.

We also analyzed how folding properties of these proteins were affected when additional chains (tails) were attached to one or both termini by following the idea of the experiments reported in ref. 12. Due to computational limitations we restricted our studies to purely flexible homopolymer tails built of no more than 12 residues (Fig. S1).

The addition of these tails not only did not restrict, but sometimes even increased the number of correctly formed knotted native states. The last step in the folding process, which involves pulling the entire tail through the loop, is slower than in the regular protein. Nonetheless, the overall folding time is similar in both cases.

The final test that can clarify the folding ability of the knotted protein (1o6d) and the presence of a topological barrier is to use a modified protein in which the knot is absent. To engineer such a protein with a trivial topology, it is sufficient to change the crossing of protein chain between 78 and 85 and 120–125 aa by using methods from refs. 20 and 21. The folding ability of such an untighted structure increases to a 73% success for equally long folding runs. This means that a simple change of topology eliminates an otherwise very high topological barrier.

Folding Proteins with Slipknots.

So far we have discussed proteins that have a 3₁ knot in the native conformation. Our suggested folding mechanism via a slipknot intermediate configuration gets further support from the fact that, in a different class, proteins actually contain slipknots in their native states (6, 7). Comparing their folding mechanism to our initial results provides further understanding of our proposed model. We focus on a relatively short protein, 2j6b (consisting of 109 aa), and a much longer one, 1p6x (333 aa), which are shown in Fig. 4and Fig. S2. Again, a model that includes only attractive interactions for native contacts is sufficient to fold these proteins. Although both these proteins contain slipknots, their folding trajectories are different. Folding of 2j6b is composed simply by the first 3 steps in Fig. 2. This independently provides strong support for our proposed folding mechanism for the knotted proteins. Formation of a slipknot in 1p6x is more complicated and it is described below.

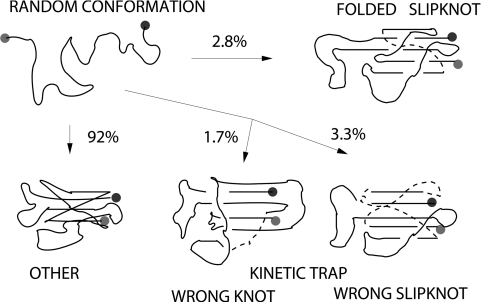
The folding mechanism for the short protein 2j6b involves creation of a loop through which a hook is subsequently threaded. As discussed above, its folding is analogous to the first 3 steps of folding of 1o6d. Again, folding simulations were run at temperatures slightly above T_f. Based on 1,000 trajectories, we found 4 different ensembles of final conformations, shown in Fig. 5. Only 2.8% of these trajectories reached the correct folding basin by using 3 slightly different routes. A few conformations (≈0.5%) in the “OTHER” basin in Fig. 5 have most of the native contacts formed but do not form the slipknot. Interestingly, the typical folding time for these trajectories is much longer than for ones that reach the correct native folding. This indicates that slipknot creation should be a fast process, as long as the correct trajectory is followed. We have also attached a tail to 2j6b to the termini which is closer to the slipknot conformation. Similarly to the knotted proteins, it did not substantially affect its folding properties. These extended proteins were able to fold into slipknot configurations in a similar fashion to the original protein.

Fig. 5.

Schematic representation of the 4 different ensembles of final conformations observed in 1,000 folding runs of the slipknotted protein 2j6b. Simulations were performed at temperatures slightly above T_f. Only the structure in the top right corresponds to the correctly folded protein with the correct slipknot and all native contacts.

We now discuss thymidine kinase (PDB ID code 1p6x), whose structure is described in detail in Materials and Methods. We checked its folding ability at several temperatures above T_f, and for each one we ran 500 trajectories. The highest probability of folding was observed at temperatures 18% above T_f. In a set of 8,000 trajectories, the correctly folded conformation including the slipknot and all native contacts was reached only 11 times. In an additional 12 cases, the slipknot was created but in a structure with an incorrectly folded bundle of 5 helices; in these cases, 92% of native contacts where established. In yet another set of 13 trajectories, although most of the native contacts were formed, a knot instead of a slipknot was observed in the final structure. Knotted structures were reached in 5–20% of the runs at each temperature and they had typically <73% of native contacts. All other final structures were some trivial kinetic traps or misfolded conformations.

Folding of the 1p6x protein, because of its large size and complexity, is more interesting than folding of the previously discussed proteins. It can start from several nucleation sites. One of such site includes a loop similar to the one reached after the first step in Fig. 2. Notice that, in the folding motif, both termini are close to the loop. Also, during folding, both of them have to cross the loop. This implies that, even though in the folding of 1p6x the steps from Fig. 2 are used, it proceeds in a different way than creation of a slipknot in 1o6d (where only one terminus had to be threaded through a similar loop). Therefore, the folding mechanism is similar to the one shown in Fig. 2, but then the second terminus also has to thread through the loop.

For the 11 correctly folded trajectories, we identified 4 possible folding routes (19). They were classified according to the instant during folding in which the slipknot contacts are formed for the first time (see Fig. S5). Three of these 4 possible routes, albeit slightly different, have basically the folding mechanism described in Fig. 2 plus an additional step. As before their folding mechanism leads initially to the knot formation close to the N terminus. This is followed by threading the C terminus through the loop. This final step gives rise to the slipknot conformation. These 3 folding routes share several common features. First, their nucleation sites, although they always include the loop, are composed by different additional regions of the protein (14): bundles of α-helices, a vicinity of the α-helix at the N terminus or a huge loop close to the C terminus. Second, both termini enter the loop in configuration of a loosely packed hairpin. Third, for all folding trajectories, backtracking is related to 2 topological barriers associated with the formation of the knot closest to the N terminus and to the slipknot formation during last stages of folding.

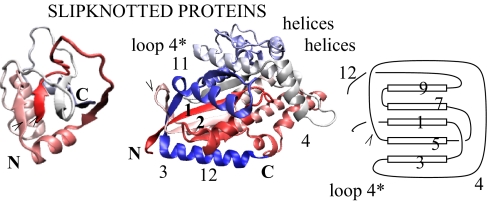
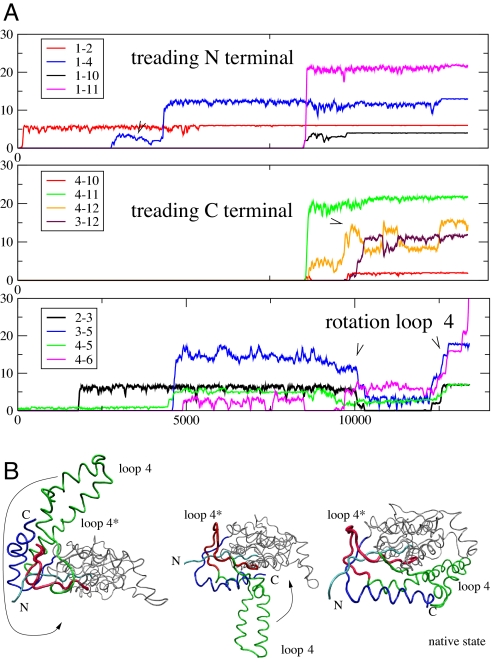
The fourth folding route is different from the ones mentioned above. Similarly to the previous cases, this route involves a creation of a knot close to the N terminus and a slipknot that involves terminal C. At the late stages of folding, however, it also requires a huge rotation of the knotting loop (denoted by loop 4 in Fig. 6). Both the knot and the slipknot are formed almost simultaneously during this surprising rotation of loop 4 by almost 360°, as shown by 3 steps in Fig. 6. This one move makes the protein structure nontrivial. It has to be pointed out that some deviations of this route are also possible, but a critical role is always played by rotation of loop 4. More details about the trajectories described above are given in SI Text. We suggest that this mechanism, involving a rotation of the loop together with the steps from Fig. 2, should be typical in folding bigger and more complicated knotted structures.

Fig. 6.

The folding route for 1p6x (described as the fourth one in the text) that involves a rotation of the loop 4. (A) The 3 figures from the top, respectively: average number of contacts in indicated sets of secondary structure around N terminus, C terminus, and loop 4 during the folding of 1p6x. (B) Steps that lead to a formation of a knot and slipknot structure by the rotation of the loop 4. The steps are connected to A in the following way. In the first image at time 2,000 τ the knot is already partially formed, but not yet a slipknot; thus loop 4 is still above the sheet 1-3-5. Then the backtracking follows, which involves β-strands 3–5, helix 2 and strand 3, and a few others, as seen in the second image. During the rotation of this loop values of rmsd and RG steadily grow. The contacts inside loop 4 break temporarily to provide sufficient space to accommodate N and C termini, which are subsequently threaded through this loop, and which eventually leads to a slipknot conformation. The colors of various elements of the structure in B match corresponding contact numbers in A. This folding process is shown in the attached movie, whose details are described in SI Text.

Discussion and Conclusions

The analysis of folding trajectories for topologically nontrivial proteins allows us to explore possible mechanisms for creation of knots and slipknots. Furthermore, the results emphasize difficulties associated with these processes that commonly lead to kinetic traps. Below we summarize these 2 issues.

Folding Mechanism for Nontrivial Topologies.

Folding into topologically nontrivial configurations is associated to a series of complex events. Transitions between different stages in this process are nontrivial. In many cases they are not successful, which is associated with a presence of so-called topological barriers. When a protein does not manage to overcome such a barrier, it may be captured in an improper configuration—a kinetic trap. Even successful events that overcome such a barrier may require a series of partial unfolding and refolding events, which we call a backtracking. Because backtracking is a stochastic process, it may lead to a broad distribution of timescales for such transitions.

The proteins YibK (PDB ID code 1j85) and YbeA (PDB ID codes 1o6d and 1vho) have the simplest type of knot, 3₁. We determined that, in most cases, folding into this knotted structure goes through an intermediate configuration that contains a slipknot (Fig. 2). A presence of this slipknot was conjectured in refs. 6 and 7, and our results confirm this prediction. A slipknot arises after threading a partially structured region, which we call a hook, through a previously created loop. The appearance of an intermediate slipknot in our simulations also suggests a plausible mechanism for the creation of deep knots (located far from both termini). We also expect that more complicated types of knots [such as 4₁ and 5₂ (5)] are formed through a similar intermediate slipknot configuration. Supporting this suggestion is the fact that the native state of ubiquitin hydrolase UCH-L1 (PDB ID code 2etl) contains a sharp turn close to its C terminus, which might be a remnant of an intermediate slipknot.

Folding into knots and slipknots involves precise geometrical constrains. Knots and slipknots require threading a region of the protein through a loop. Protein chains, however, are not flexible strings because they are composed of helices and β-strands that typically do not freely bend. Because creation of a tight knot requires sharp turns, the protein needs to have properly located regions that allow for bending and motion. Locations of such regions cannot be accidental. For example, these sharp turns should occur around the loop region to facilitate threading. As shown in Fig. 2, loop formation has to precede a sharp turn, otherwise correct loop formation would be impossible and would lead to kinetic trapping. Careful analysis of the protein structure already allows us to identify these bend regions before simulations are performed.

Topological Barriers and Kinetic Traps.

We suggest that the folding mechanism in Fig. 2 provides a route that reduces the topological barriers in the free-energy landscape of knotted proteins. These topological barriers have already been proposed earlier from an analysis of the structure (topology) of various proteins (14). In our folding studies, these topological constraints due to the presence of knots severely restrict possible folding routes. Topological constraints strongly restrict the folding landscape (2, 3) and only allow one or a few similar trajectories leading to the native state. An improper step along each such pathway may lead to a kinetic trap, which corresponds to a local minimum in the folding landscape. For shallow traps, the protein can resolve this kinetic problem with the aid of backtracking.

Our numerical analysis has identified various types of kinetic traps. Recall that the geometry of a knot or a slipknot requires the formation of sharp turns or flexible regions in appropriate places. These sharp turns often arise on prolines or glycines. Turns at amino acids 102, 114, and 125 in 1o6d in Fig. 2 exemplify these regions. Turns are also formed at amino acids Pro and Gly (positions 62 and 63) in the native conformation. These are late turns formed much later than the others during the folding event. During folding, however, these turns may be formed in an incorrect time order and/or may be formed at additional prolines or glycines. In this situation the protein is unable to fold in the correct conformation. For example, when the turn at position 62 and 63 in 1o6d is formed too early, it precludes the correct route toward folding.

The simple appearance of an intermediate configuration with a slipknot during the folding event does not yet guarantee that it will be followed by the formation of a knot. The hook, which is required to move into the previously formed loop, may turn back and leave the loop, as shown in the fourth step of Fig. 2. Successfully crossing of the loop by the terminus is needed to overcome the topological barrier and therefore form the correct knot. Although we have successfully folded these proteins several times, these multiple geometrical requirements are difficult to satisfy, and lead to kinetic traps on many occasions, in particular, if the simulation temperature is too low. These challenges have inspired others to propose alternative mechanisms to facilitate folding such as placing attractive long-range nonnative contacts (22), or chaperones to help push the hook through the loop. We submit that the use of nonnative contacts prevents the crucial formation of an intermediate slipknot conformation. Our studies have the advantage of being based only on interactions associated with native contacts. This allows us to observe and to understand the role of an intermediate slipknot in an unbiased way. Nonetheless, physically motivated, properly placed nonnative contacts, which do not interrupt the slipknot formation, may improve the success rate of folding events. This point is worth further study.

To further understand the effect of the knot, we rebuilt protein 1o6d into a very similar structure, but without knot topology (23). As expected, under similar simulation conditions, the number of successful folding events increases substantially to ≈73%. This shows that knot formation is the main limitation for folding, because in both cases the amino acid sequence is very similar, but the folding success rate is remarkably different. This provides direct evidence that the topological barrier arises as a consequence of knot formation.

Contrary to some previous experimental suggestions (12) that knot formation is preceded by a formation of random knots, we do not observe such a mechanism. Indeed, the analysis of protein conformations during early stages of folding clearly shows a noticeable number of randomly knotted structures. Such behavior agrees with results of simulations in (24) and well-known experimental results that flexible polymers or strings (25) can easily become spontaneously knotted. However, in most cases random knots observed in folding simulations do not lead to deep, but to relaxed knots. Notice that at room temperature knots on a protein chain do not necessarily behave in the same way as in a polymer chain, which was shown in stretching simulations (26). Additionally, our results show that the knotting mechanism is not prevented even when additional tails are attached to the protein, which was also observed in experiment (12). Without an intermediate slipknot it would be hard to explain the creation of knots in this case. These results further support the mechanism described in this article.

Finally, it would be more satisfying to achieve a higher success rate of folding than just 1–2% in our simulations. Such a small success rate may be a consequence of several factors. Our folding routes may be too short. Some preliminary results indicate a higher degree of success for simulations 5 times longer. Also, the simplicity of the model that includes only native interactions and no geometrical details may cause limitations. Even with these limited coarse-grained models, however, we have already been able to provide strong insights about the possible mechanism governing folding in knotted proteins that can now be checked by experiments and more detailed/expensive simulations.

Materials and Methods

Proteins with Knots and Slipknots Studied.

Knots observed in proteins are “open” knots, and so they differ from the mathematical definition of (closed) knots. Nonetheless, when both termini of the protein are located far enough from its entangled core, they usually can be unambiguously joined by an additional interval that transforms them to a closed loop. If such a loop is not homeomorphic to a circle, then the native protein is regarded as representing a nontrivial (open) knot. The families of proteins with the trefoil knot 3₁ studied here are YibK (PDB ID code 1j85) and YbeA (PDB ID codes 1o6d and 1vho). The slipknots are topological configurations more subtle than knots. They exist when a piece of a protein chain gets in and out of a loop formed by some other part of the chain. This means that cutting several residues from one end of the protein would lead to a configuration with an (open) knot, which is absent in the native state. One protein with a slipknot that we study is a highly conserved protein from crenarchaeal viruses AFV3–109 (16) (PBD ID code 2j6b). It consists of n = 109 aa, belongs to the α/β-class, and is built of 5 β-strands, which form the sheet surrounded by a loop from one side and the helices on the other side (Fig. 4). This protein forms a dimer with the shape of a cradle (16). 2j6b contains a slipknot, such that removing 9 aa from the C-terminal side leads to a knotted configuration. The smooth topological representations of 2j6b are shown in Fig. S2http://www.pnas.org/cgi/data/0811147106/DCSupplemental/Supplemental_PDF#nameddest=SF2. The function of 2j6b is still unknown, but it has been suggested that it could interact with nucleic acids (16). The second protein with a slipknot that we study is a thymidine kinase (17) (PDB ID code 1p6x) that belongs to α/β-class, consists of a β-sheet of 5 β-strands that are surrounded by 6 helices, and a bundle of 5 peripheral α-helices (Fig. 4). It contains a slipknot such that, considering only amino acids 26–140, one finds a knot 3₁ made of 3 β-sheets and 3 helices. The slipknot arises when the bundle of helices and 2 β-sheets come back to the structure by the loop between 121 and 132 aa. As was described in ref. 7, the slipknot is very deep on the C-terminal side, but it is shallow on the N-terminal side, with only 10 residues extending out of the knot core. This difference suggests that the knot is most likely formed by the N-terminal segment of the protein passing through a loop in the protein arising during the later stages of the protein folding. Because the N terminus is shorter, the slipknot in thymidine kinase is considerably more shallow than the one in alkaline phosphatase; this knot is also much tighter. We use thymidine kinase to analyze its folding ability and mechanical properties. The analysis of protein structure is described in SI Text.

Reidemeister Moves.

Three Reidemeister moves shown in Fig. S3 describe basic geometric transformations that do not change a type of a knot. They are very useful in a simplified description of proteins with nontrivial topology.

Coarse-Grained Model.

We use the coarse-grained molecular dynamics modeling described in detail in refs (19, 27, 28). The native contacts between the C^α atoms in amino acids i and j separated by the distance r_ij are described by the Lennard–Jones potential V_LJ = 4ε[(σ_ij/r_ij)¹² − (σ_ij/r_ij)⁶]. The length parameter σ_ij is determined pair-by-pair so that the minimum in the potential corresponds to the native distance. The energy parameter ε is taken to be uniform. As discussed in ref. 29, other choices for the energy scale and the form of the potential are either comparable or worse when tested against experimental data on stretching. Implicit solvent features come through the velocity-dependent damping and Langevin thermal fluctuation in the force. We consider the over-damped situation that makes the characteristic time scale, τ, to be controlled by diffusion and not by ballistic-motion, making it on the order of a nanosecond (30). Thermodynamic stability of a protein can be characterized by providing the folding temperature T_f at which half of the native bonds are established on average in an equilibrium run (based on at least 10 long trajectories that start in the native state). The analysis of the knot-related characteristics is made along the lines described in ref. 26.

Koniaris and Muthukumar (KMT) Algorithm.

We determine the sequential extension of a knot, i.e., the minimal segment of amino acids that can be identified as a knot, by using the KMT algorithm (31). It involves removing the C^α atoms one by one, as long as the backbone does not intersect a triangle set by the atom under consideration and its 2 nearest sequential neighbors.