Two-slit diffraction with highly charged particles: Niels Bohr's consistency argument that the electromagnetic field must be quantized

Abstract

We analyze Niels Bohr's proposed two-slit interference experiment with highly charged particles which argues that the consistency of elementary quantum mechanics requires that the electromagnetic field must be quantized. In the experiment a particle's path through the slits is determined by measuring the Coulomb field that it produces at large distances; under these conditions the interference pattern must be suppressed. The key is that, as the particle's trajectory is bent in diffraction by the slits, it must radiate and the radiation must carry away phase information. Thus, the radiation field must be a quantized dynamical degree of freedom. However, if one similarly tries to determine the path of a massive particle through an inferometer by measuring the Newtonian gravitational potential the particle produces, the interference pattern would have to be finer than the Planck length and thus indiscernible. Unlike for the electromagnetic field, Bohr's argument does not imply that the gravitational field must be quantized.

Niels Bohr once suggested a very simple gedanken experiment to prove that, in order to preserve the consistency of elementary quantum mechanics, the radiation field must be quantized as photons.* In the experiment one carries out conventional two-slit diffraction with electrons (or other charged particles), building up the diffraction pattern one electron at a time (as in the experiment of ref. 1). One then tries to determine which slit the electron went through by measuring far away, in the plane of the slits, the Coulomb field of the electron as it passes through the slits (Fig. 1). If the electron passes through the upper slit it produces a stronger field than if it passes through lower slit. Thus, if one can measure the field sufficiently accurately one gains “which-path” information, posing the possibility of seeing interference while at the same time knowing the path the electron takes, a fundamental violation of the principles of quantum mechanics.†

Fig. 1.

Two-slit diffraction with single electrons, in which one measures the Coulomb field produced by the electrons at the far-away detector.

In an experiment with ordinary electrons of charge e the uncertainty principle prevents measurement of the Coulomb field to the required accuracy, as we shall see below, following the prescription of Bohr and Rosenfeld for measuring electromagnetic fields (2, 3). However, as Bohr pointed out, one can imagine carrying out the same experiment with (super) electrons of arbitrarily large charge, Ze, and indeed, for sufficiently large Z, one can determine which slit each electron went through. However, elementary quantum mechanics requires that once one has the capability of obtaining which-path information, even in principle, the interference pattern must be suppressed, independent of whether one actually performs the measurement.

Underlying the loss of the pattern is that the electron not only carries a Coulomb field, but also produces a radiation field as it “turns the corner” when passing through the slits. The larger the charge the stronger is the radiation produced. This radiation must introduce a phase uncertainty to destroy the pattern, and so itself must carry phase information; thus, the electromagnetic field must have independent quantum degrees of freedom. Were the quantum mechanical electrons to emit classical radiation, the emission would produce a well-defined phase shift of the electron amplitudes along the path, which, while possibly shifting the pattern, as in the Aharonov–Bohm effect (4), would not destroy it. In a sense the suppression of the pattern is an extension of the Aharonov–Bohm effect to fluctuating electromagnetic potentials (discussed by Aharonov and Popescu‡).

Our object in this article is to carry out a detailed analysis of the physics implicit in Bohr's suggested experiment. After describing the experiment more fully, we determine the strength of charge needed to measure the Coulomb field at large distances sufficiently accurately. We then analyze how coupling of the particle to the quantized electromagnetic field in diffraction suppresses the interference pattern, with increasing charge, before Coulomb measurements can yield which-path information.

The first experiment that revealed effects of quantization of the electromagnetic field in interference was that of Grangier et al. (5), which showed how interference of single photons differs from classical interference. The loss of particle coherence in interferometry due to photon emission was first demonstrated by Pfau et al. (6), and due to photon scattering by Chapman et al. (7). Various works, both theoretical and experimental, have discussed determining the path of charged particles in the double-slit problem, but none, it seems, in connection with Bohr's proposed experiment. The theoretical possibility of distinguishing paths by measurement of the photon field is discussed in ref. 8, and refs. 9 and 10 discuss determining the path through detection of the electric field inside the loop of the paths. See also Stern et al. (11) on decoherence due to the interaction of charged particles with the gauge field. Experimental attempts to measure which-path information by using interferometers fabricated in high-mobility 2-dimensional electron gases include refs. 12–14.

A natural question to ask is whether, by measuring the Newtonian gravitational field produced by the mass of a particle as it diffracts, one can similarly gain which-path information; as we show, the answer is that one can, for sufficiently large mass. However, one cannot conclude in this case that the gravitational field must also be quantized, since for masses for which one can determine the path, the fringe separation in the diffraction pattern would shrink to below the Planck length, ℓ_pl = (Gℏ/c³)^1/2, where G is Newton's gravitational constant and c is the speed of light. However, position measurements are fundamentally limited in accuracy to scales ≳ℓ_pl (15), and thus distinguishing so a fine pattern cannot be carried out. Unlike in the electromagnetic case, where the interference pattern is suppressed because of decoherence caused by the radiated photons, the pattern in the gravitational case becomes immeasurably fine, not because the particles radiate quantized gravitons.

Measurement of the Coulomb Field

In the experiment sketched in Fig. 1, a charged particle enters the apparatus from the left side, goes through a double slit, and hits the screen (b). The spacing of the slits is d, and L is the distance from the particle emitter (a) to the screen. The Coulomb field of the electron is measured at distance ∼ R in the plane of the slits, sufficiently far away from the apparatus that there can be no backreaction from the distant measurement of the electromagnetic field. Thus, R ≳ cT, where T is the time of the flight of the particle, ≃ L/v, with v the particle velocity. We consider only nonrelativistic particles, in which case the longitudinal Coulomb field of the electron at distance R ∼ cT is larger than the transverse radiation field by a factor ∼ c/v. We assume that the Coulomb field is determined by the charge in the usual manner.

To distinguish whether the particle goes through the upper or lower slit one needs to measure the electric field to at least an accuracy Ze(1/R² − 1/(R + d)²) ∼ Zed/R³ (with d ≪ R). The quantum limit on the measurability of a weak electric field E was obtained by Bohr and Rosenfeld (2, 3). In an early discussion of such a quantum measurement, Landau and Peierls (16) noted that if one attempts to measure the field by its effect on a point charge, radiation recoil introduces uncertainties in the measurement that diverge for short measuring times, and thus concluded that “in the quantum range … the field strengths are not measurable quantities.” To avoid this problem, Bohr and Rosenfeld envisioned measuring the average of the electric field over a region of space–time by using an extended apparatus consisting of an object A of mass M and volume V_A with extended charge Q, tethered by Coulomb forces to a similar object B with background charge −Q. (See Fig. 2.) The background charge is fixed in space, but A is displaced by an electric field from its equilibrium position. The apparatus measures the field by detecting the deflection of A from its equilibrium position. The net equilibrium charge density of the apparatus is zero in the absence of an external field that displaces the object from the background. In their analysis they first assume quantization of the electromagnetic field, and show how vacuum fluctuations of the field in the region limit the accuracy of field measurements. They then go on to show that the accuracy of the measurement of a single field is limited by the uncertainty principle applied to the apparatus, without the need to invoke field quantization. We give a schematic derivation of this result (see also the recent discussions in refs. 17–19).

Fig. 2.

Bohr–Rosenfeld apparatus for measuring the electric field. The positively charged object A slides on the negatively charged fixed object B.

The relative motion of A and B is a harmonic oscillator whose frequency ω is readily derived from the familiar expression for the plasma frequency (ω_p² = 4πne²/m), namely, ω² = 4πQ²/MV_A. When A is displaced relative to B by a distance x, the restoring force acting between them is

Thus, an external field E_x acting on A for time T′ changes the momentum of A by p_x = (E_xQ − 4πQ²x/V_A)T′, from which one would deduce an electric field,

Because p_x and x obey the uncertainty relation, δxδp_x ≳ ℏ, we see, from minimizing the right side of Eq. 2 with respect to δx, that the uncertainty in the measurement of E_x is independent of Q, and given by the Bohr–Rosenfeld relation, $\delta E_x˜\sqrt{\hslash /V_{A}T\text{'}}$. For simplicity we assume cubic geometry of A and B, with V_A = ξ³, the measurement time T′ is at most the time of flight, T, since further increasing the measurement time does not help to distinguish the paths; thus, we take T′ = T. In addition the length ξ of interest is at most the Coulomb pulse width, cT, since a longer size does not help to distinguish the paths either. With ξ = cT, we obtain the limit of accuracy of the measurement of the Coulomb field:

To estimate the critical scale of charge of particles above which one begins to be able to distinguish the path, we take the measuring apparatus to be located from R to R+ξ above the upper slit. Then, when a particle with charge Ze passes through the upper slit, the average Coulomb field in the apparatus is

Similarly, the average electric field when the particle passes through the lower slit is Ze/(R + d)(R + d+ξ), where d is the slit interval. Hence, to distinguish the paths the apparatus needs to distinguish an electric field difference

a decreasing function of ξ. Since to measure the path, one needs ΔE > δE (the measurement uncertainty), or

With ξ ∼ R ∼ cT we find that the scale of critical charge Z₁ above which one can begin to distinguish the path is

where α = e²/ℏc is the fine structure constant. Note that Z₁ ≫ 1, so that one could never detect the path with ordinary electrons or other particles of charge ∼|e|. For illustration, from the parameters corresponding to the experiment of ref. 1: d ∼ 1 μm, and cT ≈ 6 cm, we estimate Z₁ ≃ 7 × 10⁵.

One can in fact, for general Z, determine partial information on the paths, the amount of information increasing with Z. Writing p(D_u,l) as the probability of the particle having taken the lower path and the detector detecting it to have taken the upper path, p(D_u,u) as the probability of the particle having taken the upper path and the detector detecting it to have taken the upper path, etc., one can quantify the information in terms of the distinguishability D (20–23)

Since p(D_u,u) + p(D_l,u) + p(D_l,l) + p(D_u,l) = 1, D ≤ 1.

To calculate D we note that the detector determines the electric field through simultaneous measurement of the position and momentum, which leads to a Gaussian uncertainty of width δE in the measured value of the electric field from the expected value. For the particle taking the upper path, producing an expected (averaged) electric field E_u at the detector, the probability distribution of the measured electric field is

with a similar expression for the field distribution P_l(E) for the lower path in terms of the expected E_l. Since E_u > E_l, we can for simplicity regard the detector as having detected the particle taking the upper path if the measured value of the electric field is greater than (E_u + E_l)/2, and as having taken the lower path otherwise.

With the assumption that the amplitudes for the particle taking the upper and the lower paths are equal in magnitude, which is true if the two slits are located symmetrically, then

with similar equations for p(D_l,l) and p(D_u,l). With ΔE = E_u − E_l, the distinguishability becomes

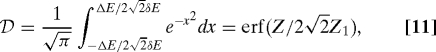where erf(x) is the error function. We plot D in Fig. 3 below for the parameters of ref. 1.

Fig. 3.

Visibility and distingishability vs. charge for the parameters of ref. 1, for which the characteristic charge Z₁ for distinguishing paths by measuring the Coulomb field is ∼7 × 10⁵, and the characteristic charge Z₂ for loss of interference is ∼ 1.5 × 10⁵. Also shown is V² + D² (dotted line).

Loss of Interference

We turn now to the question of how for sufficiently large charge (which should be ≲ Z₁) the interference pattern fades out. The basic physics is that the particle radiates when being accelerated by the slits, and undergoes a random change in its phase because it is coupled to a dynamical degree of freedom, the quantized radiation field. We do not take into account any quantum degrees of freedom associated with the slits, i.e., we assume that they act effectively as a potential on the electron. The pattern on the screen is proportional to ∑_f(|β_u(b,f)+β_l(b,f)|²) where β_u(b,f) is the amplitude for the particle to go through the upper slit to point b on the screen, with the electromagnetic field going from its initial state |0〉 (the vacuum) to final multiphoton state |f〉, and β_l(b,f) is the amplitude for the particle to take the lower trajectory.

The interference pattern thus has the relative intensity,

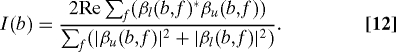Although it is possible to carry out a full quantum calculation of the radiation emitted in diffraction, its essential features are brought out if we make the simplifying assumption that the charged particle follows a single straight trajectory along either the upper or lower path from the emission point a to a given point b on the screen (see Fig. 1). and thus the emitted radiation has only the effect of changing the phase of the electron amplitude. Then

where β_u⁰ is the simple quantum amplitude in the absence of the electromagnetic field, and

where $\overrightarrow{A}(\overrightarrow{r},t)$ is the electromagnetic field operator, and the integral is time ordered (denoted by the subscript “+”) along the path. From Eq. 13,

and

where the angle brackets denote the electromagnetic vacuum expectation value. Thus

where the subscript c denotes the time ordering of the contour integral from emission to the screen along the upper path and then negatively time ordered from the screen back to the emission point along the lower path. This expression is the expectation value of the Wilson loop around the path u − l (24). Since the free quantum electromagnetic field is Gaussianly distributed in the vacuum,

where

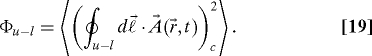Writing

where the visibility V = |〈U_l^†U_u〉| is ≤ 1, and the phase shift ζ is real, we have

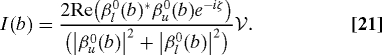The coupling to the radiation field reduces the intensity of the interference pattern by V, as well as shifting it via ζ. By symmetry, the shift vanishes at the center point on the screen (and is otherwise not relevant to the present discussion). Since the Coulomb field does not enter the states of the radiation field in V, Eq. 21 gives a valid description of the interference pattern whether or not an attempt is made to distinguish paths by detecting the Coulomb field at large distances.

The real part of Φ_u−l, entering the visibility, is given by the same integrals as in Eq. 19 without time ordering along the contour, since $\overrightarrow{j}(\overrightarrow{r},t)$ · $\overrightarrow{A}(\overrightarrow{r},t)$ is Hermitian (25):

To estimate the visibility we write the free electromagnetic field operator in terms of photon annihilation and creation operators: $\overrightarrow{A}(\overrightarrow{r},t)$ ≃ ∑_k ∑_λk (2πℏc/kΩ)^1/2(a_k$\overrightarrow{\lambda }$_ke^{i($\overrightarrow{k}$·$\overrightarrow{r}$−ωt)}+h.c.), where $\overrightarrow{\lambda }$ is the photon polarization vector, ω = ck, and Ω is the quantization volume. For nonrelativistic motion (v ≪ c) along a classical trajectory,

With the simplifying assumption that on the upper path the velocity undergoes a sudden change at the slits, from $\overrightarrow{v}$₁ to $\overrightarrow{v}$′₁ (see Fig. 1), and from $\overrightarrow{v}$₂ to $\overrightarrow{v}$′₂ through the lower slit, then in the limit of large time of passage, ωT ≫ 1,

For ω ≲ 1/T, the integral is proportional to T. Near the center of the pattern, $\overrightarrow{v}$′₂ ≃ $\overrightarrow{v}$₁ and $\overrightarrow{v}$′₁ ≃ $\overrightarrow{v}$₂, so that

and

The integral over ω, nominally logarithmically divergent at large ω, is physically cut off by ω_max, the maximum frequency of emitted photons, which from energy conservation cannot exceed mv²/2ℏ = πv/λ, where λ is the de Broglie wavelength of the interfering particle. The lower cutoff is effectively 1/T; hence,

Eq. 27 is essentially the nonrelativistic limit of the result of ref. 26. For L ≫ d, ($\overrightarrow{v}$₁ − $\overrightarrow{v}$₂)² ≃ (2d/T)², and finally,§

Because the path length must be many de Broglie wavelengths, the Z₂ which the visibility becomes < 1/e² obeys,

The visibility and distinguishability are closely related; as Z increases, the interference pattern fades away on the scale Z₂, while the distinguishability of the paths by measurement of the Coulomb field grows on the scale Z₁. Quantitatively,

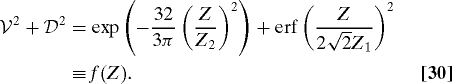Since f(0) = f(∞) = 1, and for $Z_2\&lt;8Z_1/\sqrt{3}$ and 0 < Z < ∞, f(Z) < 1, namely

in agreement with the inequality derived by Jaeger et al. (21) and Englert (22). Fig. 3 shows the visibility and distinguishability as functions of Z, as well as V² + D², for the parameters of the experiment of ref. 1, given above. With these parameters, log(πL/λ) ∼ 20.

A simple interpretation of the decrease in visibility, in terms of the Aharonov–Bohm effect (4), is that the closed electron loop, u − l, encircles a fluctuating electromagnetic field which shifts the interference pattern randomly, thus tending to wash it out. The interpretation of the reduction of the pattern in terms of a random flux requires photon emission processes, and is equivalent to the present discussion. Indeed, for the subset of processes in which there is no photon emission, the modification of the interference pattern is given by 〈U_l^†〉〈U_u〉 (cf. ref. 17), where the brackets denote states with zero photons. Now

the reduction reflects the loss of forward-scattering amplitude owing to photon emission processes. Thus, the zero-photon emission pattern is multiplied by a factor V^1/2; the suppression of the zero-photon pattern at charge $\sqrt{2}Z$ equals the suppression of the total visibility at charge Z. The phase of 〈U_l^†〉〈U_u〉 is essentially proportional to the difference of real parts of the electron self-energy corrections on the upper and lower paths, corrections that do not contribute to the diminution of the interference pattern.

Measuring the Path by Gravity

Finally, we ask if it is possible to detect the path by measuring the fluctuations in the (Newtonian) gravitational potential at large distance as a particle of sufficiently large mass passes through the slits. In this scenario, the Newtonian gravitational field plays the role of the Coulomb field for charged particles. We consider detecting the change of the Newtonian gravitational field by using a modern gravity wave detector, e.g., a highly sensitive laser interferometer (27) (a measurement not equivalent to detecting possible gravitational radiation produced by the mass going through the slits). Fig. 4 sketches such a detector. As before, the x axis lies in the plane of the slits. We assume that the mirrors in the detector are tied down in the lab frame; to a first approximation, the distance between the mirrors (or equivalently the ends of a Weber bar) is a harmonic degree of freedom, with oscillator frequency, ω (which includes the gravitational attraction of the two mirrors).

Fig. 4.

Gravitational field detector.

We derive schematically the response of the detector to a Newtonian gravitational potential ϕ(x,t). In the presence of ϕ, the positions of the mirrors, x_±, obey the Newtonian equations of motion,

with S the equilibrium distance between the mirrors, and the prime denoting differentiation with respect to x. We write x_± = x₀ ± (S+η)/2, where x₀ is the midpoint between the mirrors in equilibrium, and η is the relative displacement of the mirrors caused by the gravitational pulse. Then linearizing in η and ϕ″, we have

For simplicity we assume that ϕ is zero before the gravitational pulse reaches the detector, and is constant in time during the detection. With initial conditions η(0) = η′(0) = 0, we obtain

The accuracy required for the measurement of ϕ″(x₀) is

where m is the mass of the particle, and the measuring apparatus, as before, is at a distance R from the slits. Thus, since 1 − cos ωt ≤ (ωt)²/2, one needs to measure η to an accuracy,

which implies that the mass scale for which one can begin to distinguish the path obeys,

Physically the uncertainty Δη must exceed the Planck length,¶ and thus

the mass scale must be a factor R/d larger than the Planck mass, $\sqrt{\hslash c/G}˜2\times {10}^{-5}$ g. For R/d ∼ 6 × 10⁴ (1), the scale would have to be of order 1 g.

The interference pattern caused by a particle whose mass obeys the condition (39) has a fringe separation,

which implies that when the mass is large enough to allow which-path detection via gravity, the pattern becomes immeasurably fine, of order the Planck length or shorter. This result assures the consistency of quantum mechanics; however, unlike in the electromagnetic case, consistency does not require that the gravitational field be quantized.∥ (Although a decrease of the visibility of the pattern would arise were gravity quantized, as in the electromagnetic situation, detailed calculations of the diminution would depend on the detailed theory of quantized gravity assumed, an issue we do not address here.)

In summary, when one can distinguish the path of a particle by measuring the electromagnetic or gravitational field at large distance, interference disappears. For a large enough charge on the interfering particle, emission of quantized electromagnetic radiation destroys the interference, whereas for a large enough mass, the pattern becomes too fine to be discerned.