The reciprocal coordination and mechanics of molecular motors in living cells

Abstract

Molecular motors in living cells are involved in whole-cell locomotion, contractility, developmental shape changes, and organelle movement and positioning. Whether motors of different directionality are functionally coordinated in cells or operate in a semirandom “tug of war” is unclear. We show here that anterograde and retrograde microtubule-based motors in the flagella of Chlamydomonas are regulated such that only motors of a common directionality are engaged at any single time. A laser trap was used to position microspheres on the plasma membrane of immobilized paralyzed Chlamydomonas flagella. The anterograde and retrograde movements of the microsphere were measured with nanometer resolution as microtubule-based motors engaged the transmembrane protein FMG-1. An average of 10 motors acted to move the microsphere in either direction. Reversal of direction during a transport event was uncommon, and quiescent periods separated every transport event, suggesting the coordinated and exclusive action of only a single motor type. After a jump to 32 °C, temperature-sensitive mutants of kinesin-2 (fla10) showed exclusively retrograde transport events, driven by 7 motors on average. These data suggest that molecular motors in living cells can be reciprocally coordinated to engage simultaneously in large numbers and for exclusive transport in a single direction, even when a mixed population of motors is present. This offers a unique model for studying the mechanics, regulation, and directional coordination of molecular motors in a living intracellular environment.

Force transduction occurs at the surface of the Chlamydomonas flagellum, and this force is used for whole-cell gliding motility (1, 2). This flagellar surface motility can also be visualized through the bidirectional movement of microspheres adherent to the flagellar surface (3). There is only a single flagellar membrane glycoprotein (designated FMG-1) that is in contact with a moving microsphere (4). A number of observations suggest that the cross-linking–induced clustering and movement of FMG-1 within the flagellar membrane is responsible for both gliding motility and microsphere movements (5–9). Another bidirectional motility system [called intraflagellar transport (IFT)] operates on the intracellular side of the flagellar membrane (10). IFT is responsible for the assembly and maintenance of cilia and flagella; anterograde IFT is associated with the kinesin-2 motor, whereas retrograde IFT is associated with the dynein 1b motor. The fla10 mutant of Chlamydomonas is temperature sensitive for kinesin-2; at a nonpermissive temperature, the flagella of fla10 cells eventually lose both IFT and microsphere movement (11), suggesting that both of these processes are dependent on the anterograde motor, kinesin-2. The retrograde motor for microsphere movements has not been clearly identified but may be the dynein 1b motor responsible for retrograde IFT in Chlamydomonas (12). We have taken advantage of the bidirectional transport of polystyrene microspheres (and, by inference, the bidirectional movement of FMG-1) to study the behavior of microtubule-dependent motors in the living cell. This is a unique and noninvasive model system for studying the properties of intracellular motors from outside the living cell.

Transport of cargo in vivo is necessarily bidirectional, and both plus- and minus-end–directed motors are found on cellular cargos. Two scenarios have been proposed for how bidirectional, stop-and-go “saltatory” transport is managed within the cellular milieu. First, oppositely directed motors might engage in a “tug-of-war,” with the stronger or more abundant motor winning (13). Alternatively, the motors might be regulated such that only a single motor direction is active at any given point in time (14).

To sort out these possibilities, others have used subnanometer optical tracking to observe individual steps taken by single molecular motors in living cells (15–19). Some of these data support the concept of coordinated transport as opposed to a tug-of-war (16, 20). However, a molecular tug-of-war process has been shown through computational models to be sensitive to small parameter changes in single-molecule dynamics, thus providing an alternate means for regulation of directional transport by the cell (13).

Mechanical manipulation of the intracellular transport process might provide a better estimate of the number of engaged motors as well as the mechanism of regulation for directional transport and a more detailed understanding of motor function in living cells.

In this article, we report nanometer- and pico-Newton (pN)–resolution measurements of bidirectional transport in living cells. Microspheres were captured in a laser trap and brought into contact with the flagellar surface of Chlamydomonas reinhardtii, strain pf18, cells; pf18 is unable to propagate bends because of a central pair defect but expresses normal gliding motility and microsphere movement (1, 3). We observed the velocities and peak forces of transport in each direction and found that transport in either direction was driven by ≈10 simultaneously engaged motors. Quiescent periods between transport events were largely devoid of steps. A temperature-sensitive mutant of kinesin-2, the presumptive anterograde motor for microsphere movement (11), eliminated nearly all anterograde transport events, leaving only retrograde transport events. These data strongly support models of transport regulation in which kinesin-2 and cytoplasmic dynein are locally and reciprocally regulated to engage in large numbers and for exclusive transport in a single direction.

Results

Intracellular Motor Protein Activities Can Be Visualized by the Observation of Extracellular Microsphere Movements.

C. reinhardtii, strain pf18, cells adhered to the surfaces of flow cells coated with poly-l-lysine. This paralyzed mutant was used so that “swimming” motility would not interfere with our measurements of microsphere movements. Flagella used for the observations in this study were also adherent to the flow cell wall for at least a portion of their length. A 0.9-μm microsphere was positioned over the midpoint of the flagellum using a laser trap (described previously in ref. 21) and carefully brought into contact with the flagellum by raising the piezoelectric microscope stage. Motions of the bead in the focal plane were observed by back focal plane interferometry (22) to resolutions of ≈1 nm.

An example of the raw data is shown in Fig. 1. Both anterograde and retrograde movements of the microsphere are evident. The X and Y data were combined as the root sum-squared magnitudes into a single force magnitude trace (Fig. 1C), because flagella are rarely oriented directly along the X or Y axis.

Fig. 1.

Example of force traces along the X and Y axes (A and B) and combined to give the absolute force magnitude (C). (D) Cell schematic shows the position of the microsphere on the flagellum (F) relative to the cell body. (E) Anterograde and retrograde transport events (a and r, respectively, in C) can be distinguished on a 2D plot of X versus Y.

Anterograde transport events were nearly twice as frequent as retrograde transport events: 64.6% of events were anterograde. The direction of each transport event was independent of previous history; that is, the probability of an anterograde event following a retrograde event, or any other combination, was random (P = 0.3 by χ² test).

The force necessary to stall forward progress of a collection of motors is generally accepted as accurately reflecting the number of engaged motors; the individual motor force should simply be additive. The peak forces reported in Table 1, however, are not all true stalls. Rather, they are the peak force achieved before the microsphere began moving back toward trap center. Nonetheless, assuming motor stall forces of 6 pN for both kinesin (23) and dynein (24), on average, each transport event must be the result of at least 10 simultaneously engaged motors. The initial velocities of the anterograde and retrograde events did not differ significantly from one another in pf18, and neither did the peak forces.

Table 1.

Velocities and forces of transport events in pf18 (control) and fla10 pf1 strains of Chlamydomonas (mean ± SEM)

	pf18		pf1 fla10
	22°C		22°C		32°C
	Velocity (nm/s)	Peak force (pN)	Velocity (nm/s)	Peak force (pN)	Velocity (nm/s)	Peak force (pN)
Anterograde	489 ± 55	58 ± 5	404 ± 104	17 ± 2	—	—
Retrograde	432 ± 53	66 ± 6	677 ± 88	64 ± 6	716 ± 31	44 ± 2

If we define a “stall” as a static bead position for greater than 100 ms, stalls were rare. However, when observed, stall forces too were consistent with 10 engaged motors (56 ± 9 pN in the anterograde direction).

The velocity of transport has sometimes been used as an indicator of the number of engaged motors (16, 20, 25), although this assumption is at odds with in vitro data from purified high-duty cycle motor proteins like kinesin, for which velocity is independent of the number of engaged motors (26, 27), and with the work of Martinez et al. (28). Our data show that the velocity of transport was correlated neither to the stall force (P = 0.46) nor to the peak force achieved (P = 0.65). Thus, force remains the only reliable estimator for the number of engaged motors.

Only a Single Direction of Transport Is Engaged at Any Point in Time.

The “directional ratio” for transport was measured as the fraction of time in a given experiment that the microsphere spent beyond baseline displacement noise in either direction. The directional ratio for anterograde transport averaged ≈18%, and for retrograde transport, it averaged ≈7%. Assuming independence, the probability that an anterograde event and a retrograde event will overlap is thus P = [1–(1–0.18) (1–0.07)], or 0.23; yet, we observed no overlap of events. Instead, events were always separated visually by quiescent periods. These data suggest that the motors are reciprocally regulated and not engaged in a tristable tug-of-war, as suggested by one model (13), or in a bistable interaction of simultaneously engaged and oppositely directed motors (29).

If saltatory movement is the result of a tristable tug-of-war between anterograde and retrograde transporters (with a quasistable zero velocity when the motors are balanced), markedly different behavior would be expected if one could eliminate one or the other of the motors. Specifically, transport in one direction would continue uninterrupted, and there should be no quiescent periods separating events. To this end, we repeated our measurements on a different paralyzed mutant (pf1) crossed with a temperature-sensitive mutant of FLA10, whose gene product is a subunit of kinesin-2 (30) responsible for anterograde IFT and anterograde microsphere movement in Chlamydomonas (11). At a transitional temperature of ≈29 °C, anterograde transport in fla10 is affected such that flagella begin to shorten; 32 °C is nonpermissive in this mutant for maintaining flagella (31).

The results of these experiments are given in Table 1. At room temperature (22 °C), the number of anterograde events, but not the number of retrograde events, in pf1 fla10 was reduced relative to pf18, which is probably reflective of decreased overall cellular concentrations of the FLA10 subunit of kinesin-2, even at permissive temperatures (11). This is mirrored both in directional ratios (≈5% and ≈14% for anterograde and retrograde directions, respectively) and in peak force in the anterograde direction, which falls to 29% of that measured in pf18, implying fewer active motors. Anterograde velocities in pf1 fla10 at 22 °C were unchanged compared with pf18 at 22 °C, whereas retrograde velocities increased significantly; retrograde peak forces were unchanged.

In contrast, when the measurements were repeated within 10 min of a temperature jump to 32 °C, anterograde events were eliminated (as would be expected for a temperature-sensitive mutation in the anterograde motor for microsphere movement), whereas retrograde events persisted at a directional ratio of ≈17%. Retrograde events were still discrete, with quiescent periods in between. After 30 min at 32 °C, all transport events ceased, consistent with the fact that an anterograde motor is necessary to ship retrograde motors back out the flagellum.

Directional Runs Are Terminated Rather than Reversed.

We manually divided each transient into 2 phases: “away” signifying that the bead was being pulled away from trap center and “return” indicating that the bead was returning toward trap center. Thus, “anterograde away” events were always followed by “anterograde return” events unless the bead escaped from the trap. The velocities of return events were significantly higher than those of away events, by a factor of 3.1 ± 0.3 in anterograde transport and 4.8 ± 1.0 in retrograde transport. Further, return velocities were greater than the away velocities of opposite direction; for example, anterograde return velocities were higher than retrograde away velocities. This demonstrates that the return phases of discrete transport events were probably not initiated by the activation or enlistment of oppositely directed motors.

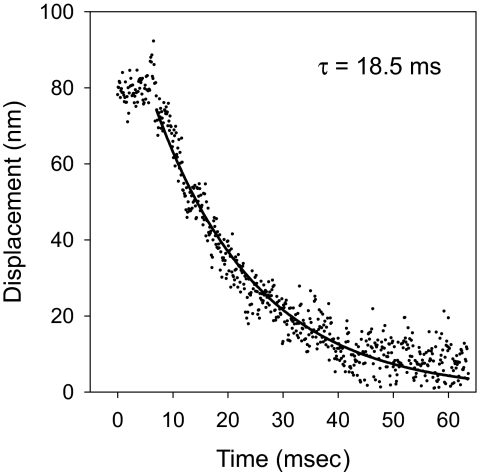
An obvious alternative explanation for returns to trap center following a transport event is that of a passive viscoelastic process driven by the stiffness of the trap (≈0.5 pN/nm in these experiments). Supporting this hypothesis, returns are generally well fitted by a single exponential decay (Fig. 2). We measured a time constant for return of 11 ± 1 ms. Assuming a spring and dashpot model (as in ref. 32, with E = 0), we calculate the effective viscous drag acting on the bead to be ≈0.005 pN·s/nm. Eleven milliseconds is much longer than the expected time constant for the free return of a bead displaced from the trap center (≈0.1 ms); thus, the process is clearly not limited by environmental fluid drag on the microsphere. This is also too long to be attributable to in-plane translation of a patch of FMG-1 through the cell membrane with aqueous solutions on either side (calculated from ref. 33); the patch would have to be larger than the diameter of the flagellum itself to explain the measured viscous drag.

Fig. 2.

“Return” from an anterograde transport event in a pf18 flagellum. The transient is fitted with a model (32) that accounts for the decreasing load from the laser trap as the bead returns to trap center. The time constant (τ) for this particular fit is shown on the graph and is too slow to be accounted for by viscous drag on either the microsphere or the FMG-1 patch in the membrane.

Discussion

Our data are consistent with the conclusion that the anterograde and retrograde motors responsible for microsphere transport on the surface of Chlamydomonas flagella are reciprocally coordinated such that only motors of a single direction are engaged at any given moment. Further, multiple motors (around 10, on average) are rapidly engaged and disengaged within hundreds of milliseconds of one another, giving rise to saltatory transport.

Our data are not consistent with the tug-of-war hypothesis of motor coordination. There was no overlap of anterograde and retrograde events and no direct transition of one into the other; rather, transport events were always separated by quiescent periods with few, if any, engaged motors. Further, the velocity of return events is inconsistent with the activity of the oppositely directed motor. One might argue that the increased velocity of retrograde transport in pf1 fla10, which has reduced expression of kinesin-2, supports a tug-of-war model; however, elimination of the anterograde motors through a jump in temperature left retrograde transport intact and transport remained saltatory. Were the tug-of-war hypothesis true, one would expect retrograde transport to proceed unabated (nonsaltatory) and to higher forces when the anterograde motors were eliminated. In fact, force fell slightly at 32 °C, probably because of the effects of temperature on the kinetics of substeps in the motor cycle.

Why then are retrograde velocities increased in pf1 fla10 at permissive temperatures? The motors clustered below each microsphere are probably neither exclusively kinesin nor exclusively dynein. Thus, even if the oppositely directed motors are inactive during a transport event, it is possible that they will transiently interact with either the membrane receptor or the microtubule, creating a drag on transport. Because kinesin-2 expression in fla10 is reduced even at permissive temperatures, one would expect less drag on retrograde transport, and thus higher velocities. Slowing of molecular motors by the drag of a separate polypeptide has been demonstrated in vitro in myosin (34).

It has been previously shown that at nonpermissive temperatures, the steady-state length of flagella in fla10 mutants is decreased and that both IFT and transport of surface particles, as studied here, eventually cease (11). Indeed, after 30 min at 32 °C, we found no transport events of either directionality. However, within 10 min of a temperature jump to 32 °C, some exclusively retrograde transport remains. These data corroborate previous evidence that (i) kinesin-2 is indeed the anterograde motor for surface transport and (ii) the oppositely directed motors, kinesin and dynein, are cargo for one another. With anterograde transport deactivated by the temperature jump, dynein 1b is no longer delivered to the flagellum tip. Thus, although retrograde transport events may persist for a brief period, all those motors will eventually be returned to the cell body with no mechanism except diffusion for returning them to the flagellum. Our data do not shed light on whether IFT and surface particle transport are different aspects of the same underlying biological process or completely separate processes.

Models for Saltatory Surface Transport.

We envision 3 possible models, illustrated in Fig. 3, that could explain reciprocally coordinated transport of microspheres on Chlamydomonas flagella, and perhaps the collective behavior of other complex mixtures of molecular motors in cells. All begin with clustering of the flagellar membrane adhesion receptor (FMG-1) within the membrane as it binds to the microsphere (9) to form a “patch.” In the first model (Fig. 3A), FMG-1, the motor proteins, and a signaling complex are colocalized in the membrane as a structurally persistent “transport complex” analogous to a focal adhesion. Associated signaling proteins would ensure that motors of only a single direction are activated at any moment in time. The mechanism for engaging and disengaging motors has yet to be determined, but this model is otherwise similar to a model proposed by Gross (35). The transport complex model would help to explain how 2 beads bound to the surface of the same flagellum can be moving in opposite directions to one another at the same time; it also explains how 10 motors could be engaged or disengaged within hundreds of milliseconds of one another.

Fig. 3.

Models explaining reciprocal coordination of flagellar membrane transport. Extracellular cargo (bead)-induced clustering and ligation of the FMG-1 membrane protein initiate transport through a transmembrane signaling pathway (7–9). (A) In the transport complex model, anterograde and retrograde motors are persistently bound, directly or through adaptor proteins, to FMG-1. Associated signaling proteins reciprocally activate and deactivate motors of opposing direction. (B) In the biased accumulation model, the FMG-1 patch becomes transiently adhesive to either anterograde or retrograde motors, but not to both, causing motors of a single direction to accumulate on the patch. (C) In the molecular clutch model, patches of motors moving together in a single direction passively associate with the FMG-1 patch as they pass by, randomly moving the FMG-1 patch until the bonds between them slip or rupture. Double arrowheads indicate the predominant direction in which the patch is transported, whereas smaller single arrowheads indicate the directions of individual motor proteins. Inactive motors are shown in gray.

In a “biased accumulation” model (Fig. 3B), motors are envisioned as being dissociated from the membrane patch. Signaling events cause the FMG-1 patch to become transiently “sticky” to motors of one direction or another, moving singly or in clusters, such that the motors rapidly accumulate within the patch and generate force in a single direction. Although conceptually simpler than the transport complex model, biased accumulation would still require a signaling complex local to the FMG-1 patch. It would also require a large number of molecular motors moving along the outer doublet for them to be able to accumulate in the patch in a short period.

Finally, in a “molecular clutch” model (Fig. 3C), a term introduced by Mitchison and Kirschner (36) in reference to myosin-receptor interactions, after ligation by extracellular cargo, the FMG-1 patch becomes nonspecifically sticky to molecular motors of either direction. Preexisting clusters of molecular motors moving in a single direction, with or without cargo, would stick on the FMG-1 patch and generate force. As force builds, the motor cluster would occasionally slip across the FMG-1 patch because of rupture of intermolecular bonds, eventually departing the patch entirely. This model easily explains the random assortment of transport direction and the quiescent periods between transport events. However, the model may not be fully consistent with saltatory conduction of microspheres along the flagellar membrane when no significant external load is present; without an external load to dislodge the membrane patch from the motors, how would directional events terminate to render transport saltatory? It is possible, however, that oppositely directed motors, or other internal or external loads, might act on the patch, dislodge the motor cluster from FMG-1, and terminate the run. One attractive aspect of this model is that it explains why the retrograde directional ratio increases in fla10 mutants at permissive (reduced kinesin-2 expression) and restrictive (deactivated kinesin-2) temperatures; with reduced numbers of anterograde motor clusters to dislodge the patch, the fraction of time spent moving retrograde might be expected to rise.

Both the molecular clutch and biased accumulation models would likely involve the modification of the phosphorylation state of the motor proteins and/or their receptors on the patch, as reviewed by Hollenbeck (37), to render the patch sticky to motor proteins or their cargo. It has already been established that FMG-1 ligation leading to cargo transport also causes dephosphorylation of 60-kDa protein that coprecipitates with FMG-1 (7). Whether phosphorylation of this protein leads to motor binding or, alternatively, to motor activation (as in the transport complex model) remains to be determined.

Although the molecular clutch model is the simplest model and explains most of the phenomena we observed here, it presupposes the existence of clusters of like-directed molecular motors. The above models also need not be mutually exclusive. Simultaneous visualization of motor proteins, FMG-1, and trap-based force measurements may resolve these models.

In Vivo Velocities.

The velocities measured in vitro for kinesin-2 homo- and heterodimers range between 0.2 and 0.4 μm/s (38–42), consistent with the in vivo velocities measured here using pf18 cells (≈0.4 μm/s) but below those of unrestrained microspheres on Chlamydomonas measured previously by one of us (3). Our measured velocities for retrograde transport are lower than those measured from cytoplasmic dynein in vitro (24, 43). However, Shima et al. (43) found that the velocity of dynein is strongly dependent on the site of cargo attachment; attachment part of the way down the cargo-binding tail (T2 in ref. 43) yields velocities similar to ours; they also found velocity to be dependent on motor density. It is likely that the exact point by which cargo is attached to the motors, which may be a function of adaptor proteins, will have a pronounced effect on in vivo velocities, as will the high spatial density of motors driving transport of membrane patches.

“Return” to trap center from directional transport events was well fitted by a single exponential, suggesting a viscoelastic process. However, this process was too slow to be explained by either viscous drag on the microsphere or in-plane drag on the FMG-1 patch. Three possible explanations emerge. First, intracellular structures in the space between the flagellar membrane and outer doublets may present barriers to free movement of the patch. Second, if the molecular clutch mechanism for transport is correct, the return to trap center would be limited in speed by rupture of intermolecular bonds and slippage of the clutch. A similar phenomenon could occur if deactivated motors in a transport complex underwent transient associations with the outer doublets as the patch moved through the membrane. Finally, if not all the motors turn off simultaneously in a transport complex, those that remain active would suddenly be supporting a load beyond stall and would slip back along the microtubule.

Displacement traces frequently showed evidence of steps that could conceivably represent single steps taken by motor proteins. However, the displacement of the microsphere was measured through the underlying flagellum, which introduced more noise than is present in single-molecule experiments in vitro. Further, with ≈10 motors per patch, one would expect the steps taken by individual motors to get averaged out, partially through their individual mechanical compliance (44, 45). Further, the duration of each step should be quite brief. Thus, we do not stake claim here to compelling measurements of single-molecule steps in this complex system. However, technical advances may yet enable us to study the detailed molecular mechanics of single microtubule-based motors in living cells noninvasively.

Methods

Cells.

C. reinhardtii, strain pf18 mt-, was obtained from the Chlamydomonas Genetics Center (http://www.chlamy.org). C. reinhardtii, strain pf1 fla10, was obtained from the laboratory of Joel Rosenbaum at Yale University (New Haven, CT). Cells were cultured as previously described (7).

Laser Trap.

The laser trap used in these studies has been described in detail elsewhere (21), except that the laser was replaced with a 25-W fiber laser (1,090 nm; SPI). The objective (n.a. 1.3; Olympus Plan Fluorite 100X) was fitted with a heater (Bioptechs) to maintain temperature, when desired, above 22 °C. Cells were imaged using bright-field illumination.

Back focal plane interferometry (22) was used to measure the position of the trapped bead relative to the trap center, thus providing measurements of displacement and force. Vertical displacement of the bead within the trap was also monitored (46). Laser powers of 3 W were used, giving an estimated 400 mW in the specimen plane. The interferometer and the trap stiffness were calibrated for every experimental bead by the step response method (21, 47, 48) and by fits to the power spectral density (21, 22, 48) and adjusted for proximity to the coverslip surface. In these experiments, trap stiffness averaged ≈0.5 pN/nm.

Flow Cell Preparation.

Flow cells were prepared as a sandwich of 22 × 22-mm and 18 × 18-mm coverslips separated by Mylar shims to make a ≈35-μL chamber. The flow cell was coated immediately before use with 1 mg/mL poly-l-lysine for 10 min to promote cell adhesion.

Microspheres were not modified by adsorption or conjugation with any substance. Rather, 0.9-μm polystyrene microspheres were washed 3 times with water and subsequently mixed with a suspension of Chlamydomonas. This suspension was immediately injected into the poly-L-lysine–coated flow cell, which was placed on the piezo-controlled stage of the microscope for trapping.

Experimental Protocol.

Adherent cells were selected for study if part or all of a flagellum was in contact with the coverslip; this increased the rigidity of the system and reduced noise attributable to random movements of the flagella. A microsphere was captured and positioned above the midpoint of the flagellum. Before contact with the flagellum, a calibration trace was collected at a 40-kHz sampling rate that included a number of 200-nm step displacements of the bead. After calibration, the bead was carefully lowered into contact with the flagellum. The moment of contact was determined visually and by monitoring the vertical displacement of the bead out of the laser trap. If transport events were observed, data were collected at a 10-kHz sampling rate for 30–60 seconds. A sketch was made of each cell, showing the orientation of the flagella relative to the cell body and the placement of the microsphere (see Fig. 1D for an example).

Analysis.

Data were analyzed using custom software developed in Borland Delphi. Because flagella were rarely oriented directly along a single axis, the X and Y data were combined as the root sum-squared magnitudes into a single force magnitude trace (Fig. 1C) after first subtracting the mean baseline from each signal. The direction of transport was determined by comparing the X and Y displacements in a given trace with a hand sketch of the cell from that experiment (Fig. 1D). Initial velocities of transport were measured from near baseline until before stall, estimating by eye the range of displacement that was linear with time. Peak forces and stall forces were similarly measured by hand. All statistical comparisons were performed using SPSS software.