Abstract
The synchronization of coupled oscillators plays an important role in many biological systems, including the heart. In heart diseases, cardiac myocytes can exhibit abnormal electrical oscillations, such as early afterdepolarizations (EADs), which are associated with lethal arrhythmias. A key unanswered question is how cellular EADs partially synchronize in tissue, as is required for them to propagate. Here, we present evidence, from computational simulations and experiments in isolated myocytes, that irregular EAD behavior is dynamical chaos. We then show in electrically homogeneous tissue models that chaotic EADs synchronize globally when the tissue is smaller than a critical size. However, when the tissue exceeds the critical size, electrotonic coupling can no longer globally synchronize EADs, resulting in regions of partial synchronization that shift in time and space. These regional partially synchronized EADs then form premature ventricular complexes that propagate into recovered tissue without EADs. This process creates multiple hat propagate “shifting” foci resembling polymorphic ventricular tachycardia. Shifting foci encountering shifting repolarization gradients can also develop localized wave breaks leading to reentry and fibrillation. As predicted by the theory, rabbit hearts exposed to oxidative stress (H2O2) exhibited multiple shifting foci causing polymorphic tachycardia and fibrillation. This mechanism explains how collective cellular behavior integrates at the tissue scale to generate lethal cardiac arrhythmias over a wide range of heart rates.
Keywords: chaos, foci, reentry, fibrillation
The synchronization of cellular oscillations plays an important role in biological systems (1, 2), such as segmentation in development (3, 4), circadian rhythms (5), neural networks (6), insulin secretion in pancreatic β-cells (7), etc. The heart is an excitable medium, in which the normal rhythm is generated by an electrical impulse originating in the sinoatrial node, propagating successively through the atria, atrioventricular node and the His–Purkinje system to the ventricles, producing a coordinated contraction. However, in rapid polymorphic ventricular tachycardia (VT) or fibrillation (VF), because of rotors (spiral or scroll waves) or focal excitations (8, 9), the contraction becomes too uncoordinated to effectively pump blood to the vital organs, causing sudden cardiac death.
It is conventionally accepted that VT or VF are initiated by a triggering event encountering an electrophysiologically vulnerable tissue substrate (8, 9). The triggering events are typically premature ventricular complexes (PVCs), spontaneous excitations arising from the ventricles, which are promoted by cardiac diseases (10). At the cellular level, one type of PVC is caused by early afterdepolarizations (EADs), abnormal voltage oscillations occurring during the repolarizing phase (plateau) of the cardiac action potential (AP). EADs can be induced by drugs (11–13) or genetic modifications that cause an imbalance between the inward depolarizing currents and the outward repolarizing currents, such as in the long QT syndromes (14–16) and in heart failure (17). The underlying molecular mechanisms have been analyzed extensively in both experimental and simulation studies (14–16, 18), but how cellular EADs self-organize at the tissue level to cause PVCs is poorly understood. Typically, PVCs occur irregularly (19, 20), as do EADs recorded from single myocytes in experimental studies (21–23). This irregular behavior has been generally attributed to random fluctuations of underlying ion channels (24). However, for an EAD to propagate in tissue as a PVC, a critical number of cells must exhibit EADs simultaneously, to overcome local source–sink mismatches. That is, an EAD from a single cell cannot emerge if the surrounding cells are all repolarizing because of their electrotonic load. The critical question is: If EADs are random events, how do they occur synchronously in a large enough group of cells to reach the critical size required for successful propagation?
In this study, we demonstrate, using computational simulations, and presenting experimental evidence from isolated myocytes, that the irregularity of EADs is not random, but dynamical chaos. We show that, at the tissue level, electrotonic coupling between cells tends to synchronize chaotic EADs over a characteristic spatial scale, causing islands of long AP durations (APDs) (with EADs) to appear next to islands of short APDs (without EADs). This juxtaposition allows partially synchronized EADs to propagate as PVCs, causing a mixture of focal and reentrant activations resembling polymorphic VT. These insights may be relevant to the genesis of lethal cardiac arrhythmias in diverse clinical settings, including long-QT syndromes and heart failure.
Results
Evidence That Irregular EADs Are Chaotic.
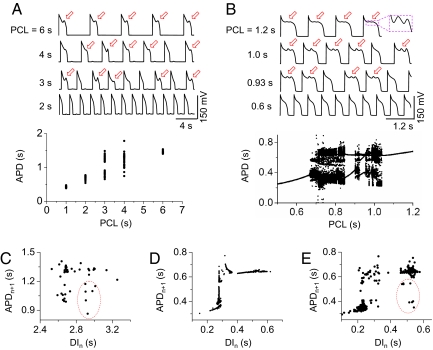
The irregular behavior of EADs has been generally attributed to random fluctuations of underlying ion channels (24). Here, we show in computational simulations and supporting evidence from experiments of isolated myocytes that this irregularity is dynamical chaos, i.e., irregular dynamics from a deterministic system. EADs were induced in patch-clamped isolated rabbit cardiac myocytes by exposure to 1 mM H2O2, which promotes EADs by enhancing inward currents during repolarization, including the late Na+ current and the L-type Ca2+ current (13, 25, 26). At different pacing cycle lengths (PCLs), we observed different EAD patterns with 1 example shown in Fig. 1A. At long PCL (6 s), EADs occur with each AP, and the APD is almost constant. At short PCLs (1 and 2 s), no EADs occur, and APD is also nearly constant. However, at intermediate PCLs (3 and 4 s), EADs occur irregularly, with the APD changing from beat to beat in a random-appearing pattern, as illustrated in the bifurcation diagram. In these experiments, a number of cells failed to provide sufficiently long recordings for a bifurcation diagram as in Fig. 1A. We were able to obtain analyzable records in 3 additional myocytes, all of which produced bifurcation diagrams similar to Fig. 1A [we show one of these in supporting information (SI) Fig. S1].
Fig. 1.
Chaotic EAD dynamics in isolated cardiac myocytes and in an AP model. (A and B) Voltage recordings and bifurcation diagrams (APD vs. PCL) from a paced rabbit ventricular myocyte exposed to 1 mM H2O2 (A), and a ventricular AP model (B), illustrating that irregular EADs occur only at intermediate PCLs. Red arrows indicate EADs. (C) Plot of APDn+1 vs. DIn for PCL = 4 s from the experimental recordings in the rabbit myocyte. (D) Same as C but from the computational simulations for PCL = 0.923 s. (E) Same as D, but with channel noise added to the model. The red circle in E marks the extra data points due to channel noise, which are similar to the data points in the red circle in C. If the points in the red circle in C are removed, the plot resembles D.
We observed similar patterns in computational simulations of a deterministic rabbit ventricular AP model (Fig. 1B) by Mahajan et al. (27) with modifications to generate EADs (see SI Text and Table S1). At long PCLs, every AP has the same number of EADs, and APD remains constant. At short PCLs, no EADs occur, and APD is also constant. However, at intermediate PCLs, both the number of EADs and the APD change from beat to beat, forming chaotic or higher periodic patterns.
To understand the nature of chaos in this system, we plotted the APD of the present beat (APDn+1) versus the diastolic interval (DI) of the preceding beat (DIn) from the isolated rabbit myocyte at PCL = 4 s (Fig. 1C) and from the simulation at PCL = 0.923 s (Fig. 1D). In the computational simulation, APDn+1 is nearly a function of DIn, but the experimental data show a more scattered pattern. However, if we exclude the data points in the red circle, the 2 plots are similar, i.e., APD increases steeply initially and then saturates at longer DIs. To show whether random channel fluctuations in the experimental data caused the discrepancy, we added random ion channel fluctuations into the AP model. The simulation more closely resembles the experimental data, including the points in the red circle (Fig. 1E). As shown in SI Text, in the presence of noise, APD is distributed over a narrow range around its mean for both long and short PCLs but varies dramatically in the chaotic regimes and periodic windows (Fig. S2A). If we sample the simulation data at larger intervals of PCLs, the bifurcation diagram looks very similar to that of the experiment (Fig. S2B). For the parameter settings used, the APD and pacing rates at which irregular EADs occurred in the experimental and simulation data in Fig. 1 differ quantitatively. By using different parameter settings, chaotic EADs could be generated over a wide range of pacing rates, including the experimentally observed range (Fig. S3). In all cases, the mechanism of chaos was the same, as discussed below.
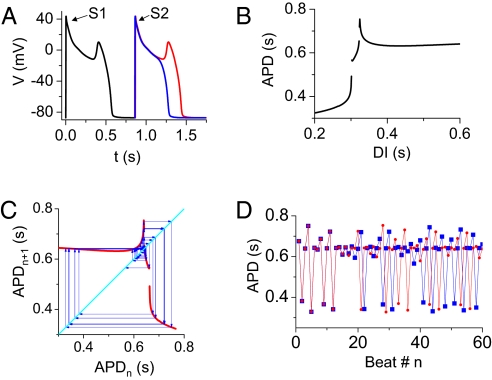
To understand the mechanisms of chaos in this system, we plotted the APD restitution curve (i.e., APDn+1 vs. DIn) in Fig. 2B, obtained by using the premature stimulus protocol illustrated in Fig. 2A. As DI increased, the APD restitution slope increased steeply, at which point an EAD occurred suddenly in the AP (red trace in Fig. 2A). Because of the all-or-none nature of single or multiple EADs, corresponding discontinuities appeared in the APD restitution curve (Fig. 2B). Note that the restitution curve shown in Fig. 2B closely resembles the plot from the chaotic data in Fig. 1D but is not identical because of memory effects in the AP model. When we used the APD restitution curve in Fig. 2B to formulate an iterated map equation, i.e., APDn+1 = f(DIn) = f(PCL − APDn), chaos was readily generated (Fig. 2 C and D). The cause of chaos is the steep increase in slope and the discontinuity in the APD restitution curve. This mechanism is distinct from chaotic APD variation caused by the steep APD restitution slope at short DIs (28).
Fig. 2.
Iterated map model of EAD chaos. (A) Protocol for measuring APD restitution. Voltage traces of the last beat (S1) followed by the premature beat (S2), at coupling intervals of 860 ms (blue, without an EAD) and 865 ms (red, with an EAD). (B) APD restitution curve obtained from the protocol in A. (C) A graphical iteration (cobweb) of APDn+1 = f(DIn) = f (PCL − APDn), [with f(DIn) from B] and PCL = DIn + APDn = 0.964 s. (D) APD vs. beat number n from the iteration in C, for 2 slightly different initial conditions (red circles and blue squares), demonstrating the sensitivity to initial conditions that is characteristic of chaos. We calculated the Lyapunov exponent to be 0.3871.
Partial Regional Synchronization of Chaos Generating the Substrate for Reentry.
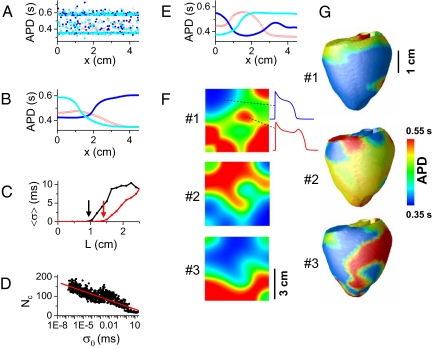
The hallmark of chaos is sensitivity to initial conditions, e.g., for 2 uncoupled identical cells starting with slightly different initial conditions, the beat-to-beat EAD pattern in the 2 cells will rapidly diverge. This effect is illustrated in a 1D array of 300 identical cells with no coupling between the cells, in which APD varies dramatically from cell to cell and also from beat to beat (Fig. 3A and Fig. S4), although the cells started with only slightly different initial conditions. In the same array with diffusive coupling through gap junctions, however, the APD distribution is smoothed, but large APD gradients form (Fig. 3B). In this case, the APs from the neighboring cells are almost, but not precisely, synchronized (Fig. S5) and remain temporally chaotic from beat to beat; we define this as partial regional synchronization of chaos. Chaos synchronization was first demonstrated by Pecora and Carroll (29) in 2 diffusively coupled identical chaotic systems in which the 2 systems maintain the same chaotic motion even with large difference in initial conditions. In cardiac tissue, we showed in a previous study (28) that chaos induced by rapid pacing could be completely synchronized when tissue size is smaller than a critical length, even with large differences in initial conditions. Beyond this critical size, complete synchronization fails because of a spatial instability (28), creating complex spatiotemporal patterns and large APD gradients. The critical size for synchronization depends on both the strength of the chaos (28) and the coupling strength, the latter shown in Fig. 3C by the standard deviation of APD 2 (σ) as a function of cable length. Better coupling can keep a larger tissue synchronized without developing APD heterogeneities. The time required to develop a given degree of macroscopic APD heterogeneity depends on the initial perturbation, such that the number of paced beats required decreases exponentially as the size of the initial perturbation increases (Fig. 3D). Note that APD gradients do not occur in the nonchaotic (or periodic) regimes, even with large differences in initial conditions, as also shown in the previous study (28).
Fig. 3.
Partial regional synchronization of chaotic EADs, causing APD dispersion. (A) APD vs. cell position (cell length Δx = 0.015 cm) for uncoupled cells with slightly different initial conditions (1% random variation in SR Ca2+ concentration), during 3 consecutive beats (red → blue → cyan) after many pacing beats. All cells were paced simultaneously. APD is highly irregular from cell to cell. (B) Same as A, but now with the cells electrotonically coupled (diffusion constant D = 0.001 cm2/ms). APD variation is smoothed by electrotonic coupling. (C) Chaos synchronization fails at a critical length. Average standard deviation of APD (〈σ〉) vs. cable length L for D = 0.001 cm2/ms (red) and D = 0.0005 cm2/ms (black). The critical length at which chaos synchronization fails (arrows) increases with the diffusion constant D. 〈σ〉 was averaged over 100 successive beats (after the first 100 beats) in 64 random trials. (D) The number of beats needed (Nc) to reach a critical degree of APD heterogeneity (σc = 30 ms) decreases as the initial APD heterogeneity σ0 increases (σc and σ0 are the standard deviations of APD in the cable). (E) Same as B, but with identical initial conditions for all cells and stimuli applied to 5 cells at the left end of the cable to initiate propagating waves. (F) APD distributions for 3 consecutive beats in homogeneous 2D tissue (4.5 × 4.5 cm) with stimuli applied uniformly at the left edge of the tissue. Islands of long APD (with EADs) surrounded by regions with short APD (without EADs) develop as a result of the spatial instabilities illustrated in B and E. (G) APD distributions for 3 consecutive beats in an anatomical rabbit ventricle model paced from a single site in the apex, illustrating similar islands of long APD. The AP model is the same as in Fig. 1B, and the stimulation strength is 40 μA/cm2.
If the cable is paced from one end to allow wave propagation, APD gradients also develop along the direction of propagation, even with identical initial conditions in each node (Fig. 3E). Therefore, APD gradients develop in both transverse (as in Fig. 3B) and longitudinal (as in Fig. 3E) direction of propagation when the tissue is larger than the critical size, leading to the emergence of islands of APD heterogeneity in 2D (Fig. 3F) and 3D (Fig. 3G) tissue. The formation of islands of APD heterogeneity is critically important because it can cause localized conduction block and initiation of reentry when APD gradients exceed a critical steepness (30, 31), without the requirement of preexisting tissue heterogeneities or a PVC originating from a location different from the periodic pacing site.
Partial Regional Synchronization of Chaotic EADs Generates Localized PVCs and Mixed Focal-Reentrant Arrhythmias in Homogeneous Tissue.
EADs have been observed to occur over a wide range of takeoff potentials during AP repolarization (15, 16, 32–34). EAD propagation is favored when the takeoff potential is more negative than in the AP model used in Figs. 1–3. To examine the effects of EADs with more negative takeoff potentials, we modified the AP model by incorporating the nonspecific Ca2+-activated cation current, which causes large-amplitude EADs with lower takeoff potentials (Fig. 4A). In this case, partial regional synchronization of chaos gives rise to localized EADs that propagate as PVCs into adjacent recovered regions without EADs. This is illustrated in Fig. 4B, in which a paced 1D cable develops a localized PVC near the middle of the cable after the last pacing beat, which propagates toward both ends of the cable (see AP traces).
Fig. 4.
Partial regional synchronization of chaos generates PVCs initiating reentry. (A) Voltage trace from a single-cell model (see SI Text for details) showing early- and late-phase EADs at PCL = 2.7 s. (B) Space–time plot of voltage in a 1D cable paced at 1 end. A localized EAD that formed at the center of the cable after the fifth paced beat (Middle Inset trace) propagated as a PVC toward both ends (Top and Bottom Inset traces). (C) Voltage snapshots of 2D homogeneous tissue (12 × 12 cm) showing a localized EAD (red area in first image) that initiates reentry (arrow, third image). (D) Voltage trace from the center of the 2D tissue.
Because partial regional synchronization of chaotic EADs in 2D or 3D tissue gives rise to both localized PVCs and large APD dispersion, both triggers and substrates are simultaneously generated by the same dynamical mechanism. Thus, the conditions for reentry can develop without any requirement for preexisting tissue heterogeneity, as illustrated by the voltage snapshots and AP trace from 2D homogeneous tissue in Fig. 4 C and D. Stimulation was uniformly applied at the left edge of the tissue, and after several pacing beats, a localized region of EADs formed that propagated unidirectionally to form reentry in the tissue. Reentry in cardiac tissue can either be stable or it can break up into multiple reentrant waves because of electrical restitution properties (8, 35). However, in this model, both spontaneous EAD-mediated PVCs and reentry-like waves continuously appear and disappear because of dynamical instabilities, maintaining the irregular activations in the tissue (Movie S1).
Multiple Shifting Foci Due to Partial Regional Synchronization of Chaos as a Mechanism of Polymorphic VT and Torsade de Pointes.
Optical mapping experiments in ventricular tissue (11, 12) support multiple foci as a mechanism of polymorphic VT and Torsade de pointes (36). In these studies, foci “shifted,” i.e., varied dynamically in time and space, although the underlying mechanisms were unknown. Here, we show that partial regional synchronization of chaos can explain this behavior. The mechanism is as follows: An EAD-triggered PVC due to partial regional chaos synchronization at one location propagates into recovered cells in an adjacent region, where it induces a new EAD-mediated PVC in that region. This new PVC propagates into less-recovered adjacent tissue, generating an EAD-mediated PVC in this new region, and so forth. This leads to spontaneous formation of multiple foci that vary dynamically in time and space. For example, if we simulate a longer homogeneous cable than the one shown in Fig. 4B, multiple PVCs form in the cable, maintaining the electrical activities in the cable for a long time after the stimulation is stopped, corresponding to a polymorphic VT that spontaneously terminated (see Fig. S6A). The duration of the polymorphic VT depends on the length of the cable and can be prolonged if the cable length is further increased. We also simulated a homogeneous 2D tissue in which we applied only a single stimulation to the lower left corner. Multiple foci developed spontaneously, varying both in time and location (see Fig. S6B and Movie S2). The foci shift around the tissue because they arise from a functional, rather than an anatomically based, mechanism (analogous to spiral wave reentry versus anatomical reentry). We also simulated this behavior in an anatomical model of rabbit ventricle. Two episodes of multiple shifting foci are shown in Fig. 5A (see also Movie S3), manifesting as polymorphic VT on the pseudoelectrocardiogram (Fig. 5B).
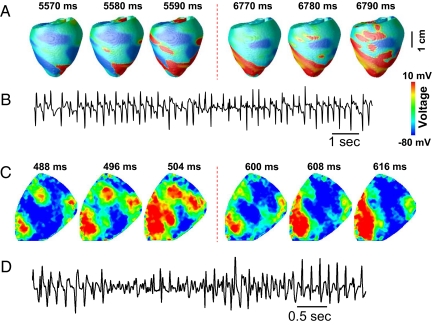
Fig. 5.
Partial regional synchronization of chaos causes multiple foci resembling polymorphic VT. (A) Multiple EAD-induced “shifting” foci are shown in voltage snapshots on the epicardical surface of the anatomic rabbit ventricle model. Note that the positions of the foci in the 2 epochs (from 5,570 to 5,590 ms, and from 6,770 to 6,790 ms) have shifted to new locations. Details of the AP model are provided in the SI Text. (B) Pseudoelectrocardiogram of A, illustrating polymorphic VT resembling Torsade de pointes. (C) Voltage snapshots on the epicardical surface of a rabbit heart during exposure to 0.2 mM H2O2, showing 2 episodes of multiple EAD-induced foci (from 488 to 504 ms with 3 foci and from 600 to 608 ms with 1 focus) similar to the simulation in A. (D) Pseudoelectrocardiogram of C, illustrating polymorphic VT resembling Torsade de pointes.
Similar behavior was observed in intact rabbit hearts exposed to 0.2–1 mM H2O2. Multiple shifting foci were observed that changed timing and location dynamically (Fig. 5C), finally leading to a mixture of nonstationary focal activations and reentry, manifested electrocardiographically as polymorphic VT and VF (Fig. 5D, online Movie S4). This pattern is similar to the simulation shown in Fig. 4C as well as to prior experimental mapping studies in which EAD-mediated polymorphic VT was induced pharmacologically (11, 12). In a total of 8 rabbits, we analyzed 106 VF episodes during H2O2 exposure, of which 91 episodes showed multiple shifting foci mixed with reentry, and 15 episodes showed either pure reentry or a single rapid focal site. To rule out the possibility that the shifting foci were breakthroughs of intramural reentry, we cryoablated the endo- and midmyocardium in 2 hearts, leaving only a thin layer of surviving excitable epicardium. Subsequent H2O2 exposure caused similar behavior (Fig. S7 and Movie S5).
Discussion
In this study, we show in computational simulations and in corroborating evidence from experiments in isolated myocytes, that irregular EAD behavior is chaotic and that partial chaos synchronization at the tissue level gives rise to localized EAD-mediated PVCs. This answers the key question: How do the random cell events occur synchronously in a large enough group of cells to reach the critical size required for successful propagation? In addition, we show that this same dynamics generates tissue heterogeneity to form a substrate for reentry, resulting in arrhythmias similar to those observed experimentally and clinically.
Whereas many interesting dynamical phenomena, including chaos, have been shown to occur in cardiac cells and tissue paced at fast heart rates (37–39), how these relate to arrhythmias arising from normal or slow heart rates, as frequently observed in clinical settings, has been a mystery. Our finding that EADs at slow heart rates exhibit chaotic dynamics provides a framework explaining how arrhythmias can arise spontaneously at normal or slow heart rates. However, the principles of partial chaos synchronization delineated here also apply to chaotic behavior at rapid heart rates, as shown by our previous study (28). It is known that EADs can also occur at faster heart rates, often in association with delayed afterdepolarizations (32, 33); our analysis should apply as well as to this situation. These phenomena will be exacerbated by preexisting tissue heterogeneity in the diseased heart, which is therefore likely to accelerate the development of electrophysiological dispersion by partial chaos synchronization, because the temporal evolution is sensitive to the size of the initial perturbation (Fig. 3D). Thus, these findings provide an explanation for tachyarrhythmias arising spontaneously over a wide range of heart rates relevant to clinical conditions such as long QT syndromes, catecholaminergic polymorphic VT, and heart failure.
An important question is whether a random, rather than a chaotic, mechanism of EADs can produce equivalent results. We cannot exclude this possibility. However, our theoretical analysis demonstrates that the physiological behavior of ionic currents underlying the cardiac action potential has an intrinsic mechanism for generating chaos due to the steep dependence of APD on DI when EADs are present (Fig. 2 B–D). We are not aware of a physiologically plausible mechanism that can generate EADs on a purely random basis without engaging this mechanism of chaos. This leads us to believe that irregular EADs in real cardiac cells are chaotic, and that the dynamics of partial chaos synchronization, in the presence or absence of random fluctuations, plays a critical role in the genesis of cardiac arrhythmias.
Finally, although the synchronization of coupled oscillators has been shown to have important applications in biological systems (1, 2, 4), we show, in this study as well as our previous theoretical study (28), that synchronization of chaotic elements can give rise to spatiotemporal dynamics in cardiac tissue, causing different types of arrhythmias. Our study also raises the possibility that chaos synchronization may have applications in other excitable biological systems, such as neural networks (6) and pancreatic β-cell islets (7).
Materials and Methods
The following is a short summary of the methods and materials used in this study, the detailed description is presented in the SI Text.
Myocyte Experiments.
Ventricular myocytes were enzymatically isolated from adult rabbit hearts. Myocytes were patch-clamped by using the whole-cell configuration of the patch-clamp technique. The voltage signals were measured with an Axopatch 200B patch-clamp amplifier controlled by a computer using a Digidata 1200 acquisition board driven by pCLAMP 8.0 software (Axon Instruments). The action potentials were elicited with 2-ms and 2- to 4-nA square pulses at various PCLs from 300 ms to 6 s. All experiments were performed at 34–36 °C.
Tissue Experiments.
Hearts were quickly removed from anesthetized female New Zealand White rabbits (3–6 years old) and perfused with oxygenated Tyrode's solution at a constant rate of 35 mL/min at 37 °C. The hearts were stained with the voltage-sensitive fluorescent dye RH 237, excited at 532 nm. Epifluorescence was collected by a CCD camera (CA-D1–0128T, Dalsa) through a 715-nm long-pass filter (Nikon). We used Blebbistatin (Biomol) (10 μM) as an excitation–contraction uncoupler for stable optical and microelectrode recordings. H2O2 (0.2–1 mM) was perfused to induce arrhythmias.
Computational Simulations.
AP models in this study were modified from the AP model by Mahajan et al. (27) to generate different EAD behaviors. The 1D cable, 2D tissue, and the anatomical ventricles are monodomain tissue models that are described by reaction-diffusion equations. Details of the AP models, the tissue models, numerical methods, and simulation protocols are presented in SI Text.
Supplementary Material
Acknowledgments.
We thank ATS Medical, Minneapolis, MN, for the unrestricted gift of a cryoablation unit. This work was supported by National Institutes of Health/National Heart, Lung, and Blood Institute Grant P01 HL078931, National Institute of General Medical Sciences Grant T32 GM065823 (to D.X.T.), the Laubisch and Kawata Endowments, and postdoctoral fellowships from the American Heart Association, Western States Affiliate (to D.S. and N.M.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0809148106/DCSupplemental.
References
- 1.Glass L. Synchronization and rhythmic processes in physiology. Nature. 2001;410:277–284. doi: 10.1038/35065745. [DOI] [PubMed] [Google Scholar]
- 2.Strogatz SH, Stewart I. Coupled oscillators and biological synchronization. Sci Am. 1993;269(6):102–109. doi: 10.1038/scientificamerican1293-102. [DOI] [PubMed] [Google Scholar]
- 3.Jiang Y-J, et al. Notch signalling and the synchronization of the somite segmentation clock. Nature. 2000;408:475–479. doi: 10.1038/35044091. [DOI] [PubMed] [Google Scholar]
- 4.Riedel-Kruse IH, Muller C, Oates AC. Synchrony dynamics during initiation, failure, and rescue of the segmentation clock. Science. 2007;317:1911–1915. doi: 10.1126/science.1142538. [DOI] [PubMed] [Google Scholar]
- 5.Winfree AT. When Time Breaks Down. Princeton: Princeton Univ Press; 1987. [Google Scholar]
- 6.Cobb SR, Buhl EH, Halasy K, Paulsen O, Somogyi P. Synchronization of neuronal activity in hippocampus by individual GABAergic interneurons. Nature. 1995;378:75–78. doi: 10.1038/378075a0. [DOI] [PubMed] [Google Scholar]
- 7.Sherman A, Rinzel J. Model for synchronization of pancreatic beta-cells by gap junction coupling. Biophys J. 1991;59:547–559. doi: 10.1016/S0006-3495(91)82271-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Weiss JN, Chen PS, Qu Z, Karagueuzian HS, Garfinkel A. Ventricular fibrillation: How do we stop the waves from breaking? Circ Res. 2000;87:1103–1107. doi: 10.1161/01.res.87.12.1103. [DOI] [PubMed] [Google Scholar]
- 9.Jalife J. Ventricular fibrillation: Mechanisms of initiation and maintenance. Annu Rev Physiol. 2000;62:25–50. doi: 10.1146/annurev.physiol.62.1.25. [DOI] [PubMed] [Google Scholar]
- 10.CAST investigators. Effect of encainide and flecainide on mortality in a random trial of arrhythmia suppression after myocardial infarction. N Engl J Med. 1989;321:406–412. doi: 10.1056/NEJM198908103210629. [DOI] [PubMed] [Google Scholar]
- 11.Asano Y, Davidenko JM, Baxter WT, Gray RA, Jalife J. Optical mapping of drug-induced polymorphic arrhythmias and torsade de pointes in the isolated rabbit heart. J Am Coll Cardiol. 1997;29:831–842. doi: 10.1016/s0735-1097(96)00588-8. [DOI] [PubMed] [Google Scholar]
- 12.Choi BR, Burton F, Salama G. Cytosolic Ca2+ triggers early afterdepolarizations and Torsade de Pointes in rabbit hearts with type 2 long QT syndrome. J Physiol. 2002;543:615–631. doi: 10.1113/jphysiol.2002.024570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Song Y, Shryock JC, Wagner S, Maier LS, Belardinelli L. Blocking late sodium current reduces hydrogen peroxide-induced arrhythmogenic activity and contractile dysfunction. J Pharmacol Exp Ther. 2006;318:214–222. doi: 10.1124/jpet.106.101832. [DOI] [PubMed] [Google Scholar]
- 14.Sanguinetti MC, Tristani-Firouzi M. hERG potassium channels and cardiac arrhythmia. Nature. 2006;440:463–469. doi: 10.1038/nature04710. [DOI] [PubMed] [Google Scholar]
- 15.Clancy CE, Rudy Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature. 1999;400:566–569. doi: 10.1038/23034. [DOI] [PubMed] [Google Scholar]
- 16.Clancy CE, Kass RS. Inherited and acquired vulnerability to ventricular arrhythmias: Cardiac Na+ and K+ channels. Physiol Rev. 2005;85:33–47. doi: 10.1152/physrev.00005.2004. [DOI] [PubMed] [Google Scholar]
- 17.Pogwizd SM, Bers DM. Cellular basis of triggered arrhythmias in heart failure. Trends Cardiovasc Med. 2004;14:61–66. doi: 10.1016/j.tcm.2003.12.002. [DOI] [PubMed] [Google Scholar]
- 18.Knollmann BC, Roden DM. A genetic framework for improving arrhythmia therapy. Nature. 2008;451:929–936. doi: 10.1038/nature06799. [DOI] [PubMed] [Google Scholar]
- 19.Glass L. Multistable spatiotemporal patterns of cardiac activity. Proc Natl Acad Sci USA. 2005;102:10409–10. doi: 10.1073/pnas.0504511102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lerma C, Lee CF, Glass L, Goldberger AL. The rule of bigeminy revisited: Analysis in sudden cardiac death syndrome. J Electrocardiol. 2007;40:78–88. doi: 10.1016/j.jelectrocard.2006.04.011. [DOI] [PubMed] [Google Scholar]
- 21.Gilmour RF, Jr, Moise NS. Triggered activity as a mechanism for inherited ventricular arrhythmias in German shepherd dogs. J Am Coll Cardiol. 1996;27:1526–1533. doi: 10.1016/0735-1097(95)00618-4. [DOI] [PubMed] [Google Scholar]
- 22.Song Y, Thedford S, Lerman BB, Belardinelli L. Adenosine-sensitive afterdepolarizations and triggered activity in guinea pig ventricular myocytes. Circ Res. 1992;70:743–753. doi: 10.1161/01.res.70.4.743. [DOI] [PubMed] [Google Scholar]
- 23.Li GR, Lau CP, Ducharme A, Tardif JC, Nattel S. Transmural action potential and ionic current remodeling in ventricles of failing canine hearts. Am J Physiol. 2002;283:H1031–H1041. doi: 10.1152/ajpheart.00105.2002. [DOI] [PubMed] [Google Scholar]
- 24.Tanskanen AJ, Greenstein JL, O'Rourke B, Winslow RL. The role of stochastic and modal gating of cardiac L-Type Ca2+ channels on early after-depolarizations. Biophys J. 2005;88:85–95. doi: 10.1529/biophysj.104.051508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ward CA, Giles WR. Ionic mechanism of the effects of hydrogen peroxide in rat ventricular myocytes. J Physiol. 1997;500(Pt 3):631–42. doi: 10.1113/jphysiol.1997.sp022048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xie L-H, Chen F, Karagueuzian HS, Weiss JN. Oxidative stress-induced afterdepolarizations and calmodulin kinase II signaling. Circ Res. 2009;104:79–86. doi: 10.1161/CIRCRESAHA.108.183475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mahajan A, et al. A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophys J. 2008;94:392–410. doi: 10.1529/biophysj.106.98160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Xie Y, et al. Dispersion of refractoriness and induction of reentry due to chaos synchronization in a model of cardiac tissue. Phys Rev Lett. 2007;99:118101. doi: 10.1103/PhysRevLett.99.118101. [DOI] [PubMed] [Google Scholar]
- 29.Pecora LM, Carroll TL. Synchronization in chaotic systems. Phys Rev Lett. 1990;64:821–824. doi: 10.1103/PhysRevLett.64.821. [DOI] [PubMed] [Google Scholar]
- 30.Qu Z, Garfinkel A, Weiss JN. Vulnerable window for conduction block in a one-dimensional cable of cardiac cells, 1: Single extrasystoles. Biophys J. 2006;91:793–804. doi: 10.1529/biophysj.106.080945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Laurita KR, Rosenbaum DS. Interdependence of modulated dispersion and tissue structure in the mechanism of unidirectional block. Circ Res. 2000;87:922–928. doi: 10.1161/01.res.87.10.922. [DOI] [PubMed] [Google Scholar]
- 32.Volders PG, et al. Progress in the understanding of cardiac early afterdepolarizations and torsades de pointes: Time to revise current concepts. Cardiovasc Res. 2000;46:376–392. doi: 10.1016/s0008-6363(00)00022-5. [DOI] [PubMed] [Google Scholar]
- 33.Huffaker RB, Weiss JN, Kogan B. Effects of early afterdepolarizations on reentry in cardiac tissue: A simulation study. Am J Physiol. 2007;292:H3089–H30102. doi: 10.1152/ajpheart.01309.2006. [DOI] [PubMed] [Google Scholar]
- 34.Burashnikov A, Antzelevitch C. Late-phase 3 EAD. A unique mechanism contributing to initiation of atrial fibrillation. Pacing Clin Electrophysiol. 2006;29:290–295. doi: 10.1111/j.1540-8159.2006.00336.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Xie F, et al. A simulation study of the effects of cardiac anatomy in ventricular fibrillation. J Clin Invest. 2004;113:686–693. doi: 10.1172/JCI17341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dessertenne F. Ventricular tachycardia with 2 variable opposing foci (translated from French) Arch Mal Coeur Vaiss. 1966;59:263–272. [PubMed] [Google Scholar]
- 37.Guevara MR, Glass L, Shrier A. Phase locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cardiac cells. Science. 1981;214:1350–1353. doi: 10.1126/science.7313693. [DOI] [PubMed] [Google Scholar]
- 38.Chialvo DR, Gilmour RF, Jalife J. Low dimensional chaos in cardiac tissue. Nature. 1990;343:653–657. doi: 10.1038/343653a0. [DOI] [PubMed] [Google Scholar]
- 39.Watanabe M, Otani NF, Gilmour RF. Biphasic restitution of action potential duration and complex dynamics in ventricular myocardium. Circ Res. 1995;76:915–921. doi: 10.1161/01.res.76.5.915. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.