Abstract
We demonstrate single-molecule fluorescence imaging beyond the optical diffraction limit in 3 dimensions with a wide-field microscope that exhibits a double-helix point spread function (DH-PSF). The DH-PSF design features high and uniform Fisher information and has 2 dominant lobes in the image plane whose angular orientation rotates with the axial (z) position of the emitter. Single fluorescent molecules in a thick polymer sample are localized in single 500-ms acquisitions with 10- to 20-nm precision over a large depth of field (2 μm) by finding the center of the 2 DH-PSF lobes. By using a photoactivatable fluorophore, repeated imaging of sparse subsets with a DH-PSF microscope provides superresolution imaging of high concentrations of molecules in all 3 dimensions. The combination of optical PSF design and digital postprocessing with photoactivatable fluorophores opens up avenues for improving 3D imaging resolution beyond the Rayleigh diffraction limit.
Keywords: microscopy, photoactivation, superresolution, computational imaging, PSF engineering
Fluorescence microscopy is ubiquitous in biological studies because light can noninvasively probe the interior of a cell with high signal-to-background and remarkable label specificity. Unfortunately, optical diffraction limits the transverse (x–y) resolution of a conventional fluorescence microscope to approximately λ/(2NA), where λ is the optical wavelength and NA is the numerical aperture of the objective lens (1). This limitation requires that point sources need to be > ≈200 nm apart in the visible wavelength region to be distinguished with modern high-quality fluorescence microscopes. Diffraction causes the image of a single-point emitter to appear as a blob (i.e., the point-spread function or PSF) with a width given by the diffraction limit. However, if the shape of the PSF is measured, then the center position of the blob can be determined with a far greater precision (termed superlocalization) that scales approximately as the diffraction limit divided by the square root of the number of photons collected, a fact noted as early as Heisenberg in the context of electron localization with photons (2) and later extended to point objects (3, 4) and single-molecule emitters (5–8). Because single-molecule emitters are only a few nanometers in size, they represent particularly useful point sources for imaging, and superlocalization of single molecules at room temperature has been pushed to the 1-nm regime (9) in transverse (2-dimensional) imaging. In the third (z) dimension, diffraction also limits resolution to ≈2nλ/NA2 with n the index of refraction, corresponding to a depth of field of ≈500 nm in the visible wavelength region with modern microscopes. Improvements in 3D localization beyond this limit are also possible by using astigmatism (10, 11), defocusing (12), or simultaneous multiplane viewing (13).
Until recently, superlocalization of individual molecules was unable to provide true resolution beyond the diffraction limit (superresolution) because the concentration of emitters had to be kept at a very low value, less than one molecule every (200 nm)2, to prevent overlap of the PSFs. In 2006, three groups independently proposed localizing sparse ensembles of photoswitchable or photoactivatable molecules as a solution to the “high concentration problem” to obtain superresolution fluorescence images (14–16) (denoted PALM, STORM, and F-PALM, respectively). A final image is formed by summing the locations of all single molecules derived from imaging the separate randomly generated sparse collections. Variations on this idea have also appeared, for example, by using accumulated binding of diffusible probes (17) or quantum dot blinking (18). Importantly, several of these techniques have recently been pushed to 3 dimensions by using astigmatism (19), multiplane methods (20), and 2-photon activation by temporal focusing (21) to quantify the z position of the emitters. In the astigmatic case, the depth of field was only ≈600 nm, whereas in the extensively analyzed (13) multiplane approach, the maximum depth of field was ≈1 μm, which has been recently extended to 2.5 μm with bright quantum dot emitters (22).
Here, we present a unique method for 3D superresolution with single fluorescent molecules where the PSF of the microscope has been engineered to have 2 lobes that have a different angle of the line between them depending on the axial position of the emitting molecule. In effect, the PSF appears as a double-helix along the z axis of the microscope; thus, we term it the double-helix PSF (DH-PSF) for convenience (see Fig. 1B Inset). This method is based on earlier work that showed that rotating intensity DH-PSF distributions could be formed by taking superpositions of G-Laguerre (GL) modes that form a cloud along a line in the GL modal plane (23–25). The DH-PSF has been used to localize photon-unlimited point scatterers inside the volume of a glass slide, and to track moving fluorescent microspheres (26). In addition, an information theoretical analysis shows that the DH-PSF provides higher and more uniform Fisher information for 3D position estimation than the PSFs of conventional lenses. Here, we show that a particularly useful photon-limited source, a single-molecule emission dipole, can be imaged far beyond the diffraction limit by using a DH-PSF. In thick samples, we demonstrate superlocalization of single fluorescent molecules with precisions as low as 10 nm laterally and 20 nm axially over axial ranges >2 μm. Further, we also show that 3D superresolution imaging of high concentrations of single molecules in a bulk polymer sample can be achieved by using a photoactivatable 2-dicyanomethylene-3-cyano-2,5-dihydrofuran (DCDHF) fluorophore, a modification of the recently reported azido-DCDHF (27). Two molecules as close as 14 nm (x), 26 nm (y), and 21 nm (z) are resolved by this technique. The ideas presented here should be broadly applicable to superresolution imaging in various fields ranging from single emitters in solid hosts for materials science applications to biological and biomedical imaging studies.
Fig. 1.
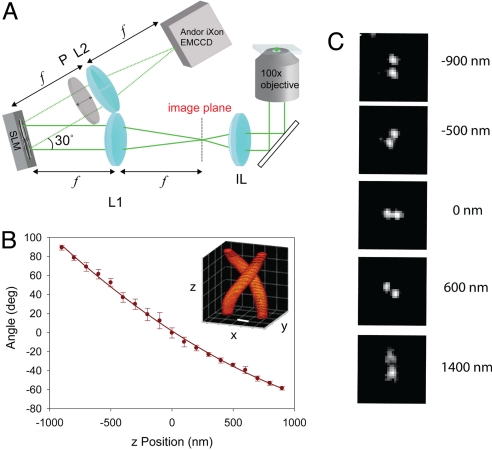
DH-PSF imaging system and z-calibration. (A) Collection path of the single-molecule DH-PSF setup. IL is the imaging (tube) lens of the microscope, L1 and L2 are focal-length-matched achromatic lenses, and SLM is a liquid crystal spatial light modulator. (B) Typical calibration curve of angle between 2 lobes with respect to the horizontal versus axial position measured with a piezo-controlled objective. (Inset) 3D plot of the DH-PSF intensity profile (Scale bar: 400 nm.) (C) Images of a fluorescent bead used for the calibration curve at different axial positions, with 0 being in focus.
Fundamentals of Imaging by Using the DH-PSF
The 3D positions of multiple sparse molecules are estimated with a single wide-field fluorescence image by using the DH-PSF design as follows. The imaging system is composed of a sample located at the objective focal plane of a conventional inverted microscope and an optical signal-processing section as shown in Fig. 1A. The signal-processing section is essentially a 4f imaging system with a reflective phase-only spatial light modulator (SLM) placed in the Fourier plane. Specifically, an achromatic lens L1 placed at a distance f from the microscope's image plane produces the Fourier transform of the image at a distance f behind the lens. The phase of the Fourier transform is modulated by reflection from the liquid crystal of the SLM. Because the SLM is sensitive only to vertically polarized light, a vertical polarizer P is placed immediately after the SLM to block any horizontally polarized light not modulated by the SLM. The final image is produced by another achromatic lens L2 (f = 15 cm) placed at a distance f after the SLM and recorded with an electron-multiplying CCD (EMCCD) camera.
When the SLM is loaded with the DH-PSF phase-mask (26) (see supporting information (SI) Appendix), the Fourier transform of the sample image is multiplied by the DH-PSF transfer function. Equivalently, every object point is convolved with 2 DH-PSF lobes, with the angular orientation of the lobes depending on the axial location of the object above or below focus. The lobes are horizontal when the emitter is in focus. As the emitter is moved toward the objective, the DH-PSF lobes rotate in the counterclockwise direction. However, if the emitter is moved away from the objective the lobes rotate in the clockwise direction. When a sample comprises multiple sparse molecules at different 3D positions, the detected DH-PSF image will exhibit 2 lobes (with different angular orientations) for each molecule. The transverse (x–y) position of a molecule is estimated from the midpoint of the line connecting the positions of the 2 lobes, and the axial position is estimated from the angle of the line connecting the 2 lobes by using a calibration plot that maps angles to axial positions. An example calibration plot of angle versus z position is shown in Fig. 1B. Fig. 1B Inset is a simulation of the 3D shape of the DH-PSF. Fig. 1C also shows actual DH-PSF images taken from a fluorescent bead at different z positions illustrating the type of data used to extract the calibration plot. The beads (pumped with 514 nm) have an emission spectrum with a peak at ≈580 nm.
Single-Molecule Localization by Using the DH-PSF
Although imaging of highly fluorescent beads with the DH-PSF has been recently reported (26), it is critical to demonstrate useful imaging of single molecules because the much lower signal-to-background inherent in a typical single-fluorophore experiment taxes any imaging system and highlights areas for future development. Single-molecule imaging can be impeded by the >75% loss associated with the SLM reflection arising from nonidealities in the device. Nevertheless, we have achieved 3D localization precision that compares well with previous approaches while more than doubling the available depth of field. Fig. 2 shows the results from the localization of one single molecule in a ≈2-μm-thick poly(methyl methacrylate) (PMMA) film. The molecule is a derivative of the previously described class of photoswitchable fluorogenic azido-DCDHF molecules, specifically (E)-2-(4-(4-azido-2,3,5,6-tetrafluorostyryl)-3-cyano-5,5-dimethylfuran-2(5H)-ylidene)malononitrile, abbreviated as DCDHF-V-PF4-azide (see SI Appendix for structure). Although a full photophysical characterization of this molecule is needed, it was chosen for this study because (i) the azido-DCDHF class of fluorophores emit on the order of 106 photons before photobleaching (27) (an order of magnitude more than photoswitchable fluorescent proteins), (ii) the molecule has a suitable emission wavelength for our SLM, and (iii) a relatively small amount of blue light irradiance is necessary for photoactivation. For the data shown, the fluorogenic azide functionalized molecule was previously irradiated with 407-nm light to generate the amine functionalized emissive form (27). For imaging, the molecule was pumped with 514 nm and the fluorescence peaking at 580 nm was recorded for 500 ms per frame to yield images similar to Fig. 2B. The synthesis and optical properties of the molecule can be found in the SI Appendix.
Fig. 2.
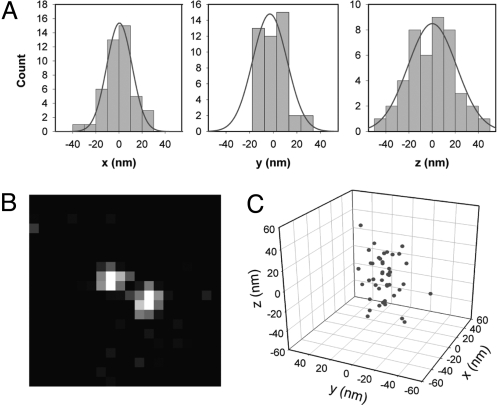
3D localization of a single molecule. (A) Histogram of 44 localizations of one single photoactivated DCDHF-V-PF4 molecule in x, y, and z in a layer of PMMA. The standard deviations of the measurements in x, y, and z are 12.8, 12.1, and 19.5 nm, respectively. The smooth curve is a Gaussian fit in each case. An average of 9,300 photons were detected per estimation on top of background noise fluctuations of 48 photons per pixel. (B) Representative single-molecule image with DH-PSF acquired in one 500-ms frame. (C) Localizations plotted in 3 dimensions.
In this work, the location of each single molecule was determined by using 2 different schemes (see SI Appendix). The first method found the center of each DH-PSF lobe by using a least-squares Gaussian fit, then determined the midpoint between the centroid positions to define the x,y position of the bead, and finally obtained the angle between the centroid positions, which gives the z position of the emitter. The second method, which was considerably more computationally efficient than the first, determined the positions of the lobes of the PSF by using a simple centroid calculation. The first procedure gives better precision measurements than the second, although it is less robust in that it requires a fairly symmetric shape to obtain a good fit. The data in Fig. 2 were analyzed by using the first scheme, and data for the large number of molecules in Figs. 3 and 4 were analyzed by using the second scheme for computational convenience.
Fig. 3.
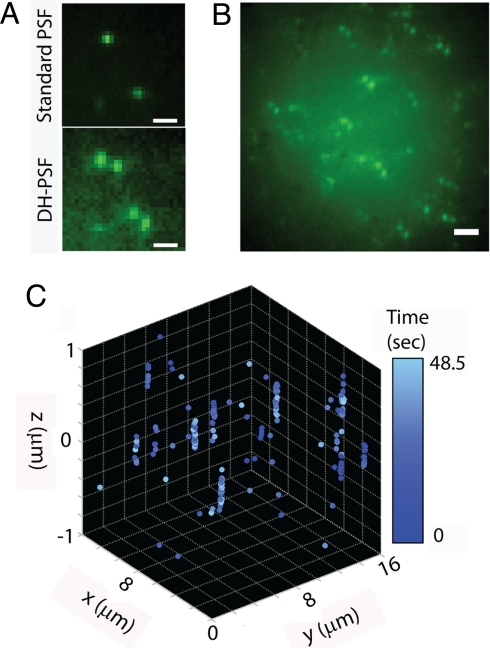
3D superlocalizations of a low concentration of DCDHF-P molecules in a thick PMMA sample. (A) Comparison of the standard PSF (i.e., Upper, SLM off) to the DH-PSF image of 2 molecules (Lower, SLM on). (Scale bar: 1 μm.) (B) Representative image of many single molecules at different x, y, and z positions. (Scale bar: 2 μm.) (C) 4D (x, y, and z, time) representation of single-molecule position determinations during a sequence of 97 frames, with a color map showing the time of acquisition.
Fig. 4.
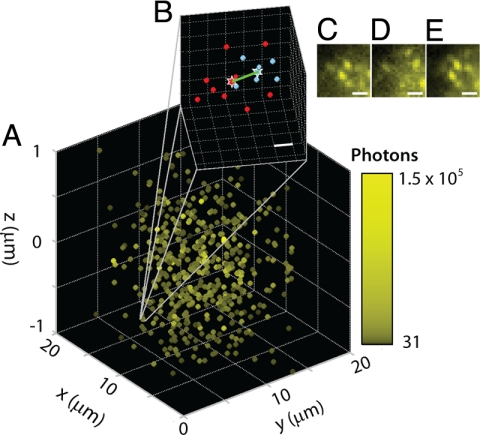
3D superresolution imaging. (A) High concentrations of single molecules of DCDHF-V-PF4-azide in a thick PMMA sample image using the PALM/STORM/F-PALM method with the DH-PSF as described in the text. Color indicates total number of photons used for estimation after background correction. (B) Zoom-in of position estimations for molecules 1 and 2 (blue and red, respectively) separated by 14 nm (x), 26 nm (y), and 21 nm (z); Euclidean distance (green): 36 nm. (Scale bar: 20 nm.) (C) Image from activation cycle 1 showing molecule 1. (D) Image from later in cycle 1 confirming that molecule 1 bleached. (E) Image from activation cycle 2 showing molecule 2. (Scale bar: C–E, 1 μm.)
The 3D position of one single molecule was estimated 44 times and the histograms of the 3 spatial coordinates of the molecule are presented in Fig. 2A. The molecule was found to have a mean z position of 644 nm above the standard focal plane. Each estimation used an average of 9,300 photons with an average rms background fluctuation of 48 photons per pixel. The histograms in Fig. 2A must be regarded as a population of successive position determinations that have a population standard deviation, or localization precision, of 12.8, 12.1, and 19.5 nm in x, y, and z, respectively. The x direction is defined as the orientation of the line between the 2 DH-PSF lobes for a molecule at z = 0 in Fig. 1. These values should be regarded as the expected localization precision for a single measurement (7). As is well known, if all of the 44 position measurements in Fig. 1A are combined, the result will have a far smaller localization precision as would be expected from the scaling of the standard error of the mean (i.e., the inverse of the square root of the number of measurements or 6.6 times smaller), but in many studies, multiple localizations of the same single molecule may not be possible. The localization precision of our method is within the same range as both the astigmatic (19) and multiplane techniques (20), while simultaneously more than doubling the depth of field. It is worth noting that the simple estimators reported here are not statistically efficient because they do not reach the Cramer–Rao bound for the DH-PSF (26). This indicates that the simple estimators are not currently using all of the possible information contained in the images, and that there is room for significant improvement through the choice of a better estimator. Also, the system can be made more photon-efficient by using a custom DH-PSF phase mask, which would take away the need for a polarizer and would avoid the SLM losses. These and other improvements in background minimization and drift correction should allow for improved localization precision in the future.
DH-PSF Imaging of Single Molecules in a Thick Sample
The DH-PSF imaging system can be used to identify the 3D position of many molecules in a single image as long as the PSFs from the different emitters do not appreciably overlap. Fig. 3 demonstrates this capability by using a sample containing a low concentration of the fluorophore DCDHF-P (28) (see SI Appendix for structure) embedded in a ≈2-μm-thick PMMA film. Fig. 3A compares the standard and the DH-PSF images of 2 molecules at different 3D positions selected to be fairly close to the focal plane for purposes of illustration only. Notable in the DH-PSF image is a slightly increased background compared with the standard PSF, a property that arises from the distribution of photons between the DH-PSF lobes over a long axial range. In general, molecules away from the focal plane appear quite blurry in the standard PSF image. In contrast, the DH-PSF image encodes the axial position of the molecules in the angular orientation of the molecules' DH-PSF lobes, which are distinctly above the background with approximately the same intensity through the entire z range of interest. This increased depth-of-field is illustrated directly in Fig. 3B, which shows a representative DH-PSF image of multiple molecules in a volume. Each molecule is seen to exhibit 2 lobes oriented at an angle that is uniquely related to its axial position. This image is obtained by averaging 97 successive frames recorded with a 500-ms exposure time. Fig. 3C shows the 3D positions of molecules extracted from each of these 97 frames as a function of time in the imaging sequence (encoded in the color map). Molecules were localized below the diffraction limit over an axial range of 2 μm. Molecules that were localized more than once are shown as a spread of points, each representing a single localization event. This apparent spread is not due to drift, but is rather an ensemble of multiple position determinations as in Fig. 2A.
Imaging of Molecules Spaced Closer than the Diffraction Limit
When a large concentration of fluorophores is present, repeated photoactivation, image acquisition, localization, and photobleaching of nonoverlapping subsets of fluorescent molecules provides resolutions beyond the classical diffraction limit (superresolution). Fig. 4 shows that 3D superresolution can be achieved with a DH-PSF system. We used the fluorogenic DCDHF-V-PF4-azide (see SI Appendix) as our photoactivatable molecule, again in a thick film of PMMA. Subsets of the molecules were photoactivated with 407-nm light, and then excited with 514-nm light to image the fluorescent emission centered at 578 nm. Accordingly, a DH-PSF mask designed for 578 nm was loaded into the SLM. The power and the duration of the purple 407-nm beam were chosen so that only a sparse subset of molecules activate in each cycle.
Fig. 4A shows the 3D average position of each molecule extracted from 30 activation cycles, with 30 (500 ms) frames per activation. The color map encodes the total number of photons available for position localization. Fig. 4B shows a zoom-in of 2 molecules establishing the superresolving capability of the method: these 2 molecules are separated by 14 nm (x), 26 nm (y), and 21 nm (z), for a Euclidean distance of 36 nm. Fig. 4 C–E shows the corresponding images for these 2 molecules during 2 consecutive activation cycles. The initially emissive first molecule (Fig. 4C) bleaches near the beginning of an activation/imaging cycle (Fig. 4D), and the second molecule starts emitting precisely after the second activation, ≈9.5 s after the first molecule bleached. Because the dark time gap is far larger than the blinking timescale for these molecules (≈100's of milliseconds), and because these molecules are photoactivatable, but not photoswitchable, the molecules that appear in different imaging cycles (Fig. 4 C and E) must be different molecules. In future work, where photoactivatable or photoswitchable molecules are labeling a particular structure, superresolution information can be extracted as long as the labeling density is sufficiently high to satisfy the Nyquist criterion (29).
Conclusion
The DH-PSF provides a powerful new tool for 3D superlocalization and superresolution imaging of single molecules. By encoding the z-position in the angular orientation of 2 lobes in the image, the x, y, and z positions of each single emitter can be determined well beyond the optical diffraction limit. Moreover, the DH-PSF enables 3D imaging with greater depth of field than is available from other imaging methods. Despite losses from the insertion of an SLM into the imaging system, single small molecules can in fact be localized with precision in the 10- to 20-nm range in 3 dimensions with single images. It is expected that future improvements in the phase mask design, the use of a custom phase mask, optimized estimators, background minimization, and a closed-loop drift correction will lead to even further improvements in resolution. With the proofs-of-principle reported here, the path is open to implementation of these ideas in a range of areas of science, including the study of materials for defect characterization, the quantum optical generation of optical fields by using subwavelength localization of properly coupled single emitters, the use of single molecules to characterize nanostructures, and 3D biophysical and biomedical imaging of labeled biomolecules inside and outside of cells.
Methods
Sample Preparation.
Axial position calibration data were obtained at 2 different emission wavelengths, 515 nm and 580 nm, using fluorescent beads (Fluospheres 505/515, 200 nm, biotin labeled, and Fluospheres 565/580, 100 nm, carboxylated, both from Molecular Probes) immobilized in a spin-coated layer of 1% poly(vinyl alcohol) (72,000 g/mol, Carl Roth Chemicals) in water; the polymer solution was cleaned with activated charcoal and filtered before being doped with beads. Single-molecule samples were prepared by doping a nanomolar concentration of DCDHF-P (28) into a 10% solution of poly(methyl methacrylate) (Tg = 105 °C, molecular mass = 75,000 g/mol atactic, polydispersity ≈7.8, Polysciences) in distilled toluene that was spun (at 2,000 rpm for 30 s with an acceleration of 10,000 rpm/s) onto a plasma-etched glass coverslip to form a ≈2-μm-thick layer. The thickness was estimated by finding the axial in-focus position of various single molecules by scanning the z position of the objective. The thick photoactivatable sample was made similarly by using the molecule DCDHF-V-PF4-azide (for synthesis, see SI Appendix), except that a layer of PVA containing 565/580-nm fluorescent beads was spun on top of the PMMA layer to incorporate fiduciary markers in the images.
Imaging.
All epifluorescence images of both fluorescent beads and single molecules were collected with an Olympus IX71 inverted microscope equipped with a 1.4 NA 100× oil-immersion objective, where the setup has been fully described in ref. 30 with the exception of the collection path. The filters used were a dichroic mirror (Chroma Z514RDC or z488RDC) and a longpass filter (Omega XF3082 or Chroma HQ545LP). The objective was fitted with a z-piezo adjustable mount (PIFOC p-721.CDQ stage with E625.CO analog controller, Physik Instrumente) that allowed for control of the z position of the objective. The samples were imaged with either 488 nm (DCDHF-P) or 514 nm (DCDHF-V-PF4-azide) circularly polarized excitation light (Coherent Innova 90 Ar+ laser) with an irradiance of 1–10 kW/cm2. Because some of the fluorogenic DCDHF-V-PF4-azide molecules were already activated, the molecules were first exposed to the 514-nm beam until most of them were bleached, leaving only a sparse subset of them in the fluorescent state. For further superresolution imaging, molecules were photoactivated by using circularly polarized 407-nm (Coherent Innova 300 Kr+ laser) light with an irradiance of <1 kW/cm2, which was chosen such that only a few molecules were turned on at a time. Images were then continuously acquired with 514-nm pumping with 500-ms exposure time. After all of the molecules were bleached, the green beam was blocked and the purple beam was unblocked for 100 ms to photoactivate additional molecules. The green beam was then unblocked for the next 15 s, until all of the activated molecules were bleached again. Each round of one 100-ms activation period and one 15-s imaging period constitutes one activation cycle. Thirty such cycles were required to obtain the data in Fig. 4. Mechanical shutters under computer control were used to define the timing of the imaging and activation beams.
In the collection path, a standard 4f imaging setup was used with a phase-only spatial light modulator (Boulder Nonlinear Systems XY Phase Series) programmed to generate the DH-PSF placed at the Fourier plane. The light exiting the side port of the microscope was collected by a 15-cm focal length achromat lens (Edmund NT32–886) placed 15 cm from the microscope's image plane (25.5 cm from the exit port). The SLM was placed 15 cm from this lens at a slight angle such that the phase-modulated reflected beam would be diverted from the incoming beam by ≈30°. The phase pattern on the SLM was made by using an optimization procedure described in ref. 25 (see SI Appendix). The reflected light passed through a polarizer and was then collected by another achromat lens 15 cm from the SLM. The real image was then focused onto an EMCCD (Andor Ixon+). Bead samples were imaged with no electron multiplication gain, whereas single-molecule samples were imaged with a software gain setting of 250 yielding a calibrated gain of 224.5. The imaging acquisition rate for all single-molecule imaging was 2 Hz.
Analysis.
Movies from the camera were exported by the Andor software as tiff stacks. The images were then analyzed with MATLAB. Two methods were used to determine the center position of each lobe of the DH-PSF (see SI Appendix). In brief, a threshold was applied to remove background, and then the center position of each lobe of the DH-PSF was determined by using either a least-squares Gaussian fit or a simple centroid calculation. The midpoint of the 2 centroids gave the x and y positions of the emitter and the angle of the line connecting the 2 centroids with respect to the horizontal gave the axial position after conversion from degrees to nanometers by using the calibration curve in Fig. 1.
The average number of photons detected in each case was obtained by summing the fluorescence counts in a background corrected image coming from a molecule and then converting the A/D counts into photons. The conversion gain of our camera, 24.7 e− per count, was calibrated by a method described in the SI Appendix and the electron multiplication gain was calibrated to be 224.5 by measuring the increase in detected signal with gain versus that for no gain.
Supplementary Material
Acknowledgments.
This work was supported in part by National Institute of General Medical Sciences Grant R01GM085437 (to W.E.M.), by National Science Foundation Award NIRT-0304650 (to R.P.), and by the Technology Transfer Office of the University of Colorado (R.P.). S.R.P.P. was supported by a CDM Optics PhD fellowship and M.A.T. was supported by a National Science Foundation Graduate Fellowship and a Stanford Graduate Fellowship.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0900245106/DCSupplemental.
References
- 1.Abbe E. Contributions to the theory of the microscope and microscopic detection (translated from German) Arch Mikroskop Anat. 1873;9:413–468. [Google Scholar]
- 2.Heisenberg W. The Physical Principles of Quantum Theory. Chicago: University of Chicago Press; 1930. p. 22. [Google Scholar]
- 3.Bobroff N. Position measurement with a resolution and noise-limited instrument. Rev Sci Instrum. 1986;57:1152–1157. [Google Scholar]
- 4.Gelles J, Schnapp BJ, Sheetz MP. Tracking kinesin-driven movements with nanometre-scale precision. Nature. 1988;4:450–453. doi: 10.1038/331450a0. [DOI] [PubMed] [Google Scholar]
- 5.Ambrose WP, Basché T, Moerner WE. Detection and spectroscopy of single pentacene molecules in a p-terphenyl crystal by means of fluorescence excitation. J Chem Phys. 1991;95:7150. [Google Scholar]
- 6.van Oijen AM, Köhler J, Schmidt J, Müller M, Brakenhoff GJ. 3-dimensional superresolution by spectrally selective imaging. Chem Phys Lett. 1998;292:183–187. [Google Scholar]
- 7.Thompson RE, Larson DR, Webb WW. Precise nanometer localization analysis for individual fluorescent probes. Biophys J. 2002;82:2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ober RJ, Ram S, Ward ES. Localization accuracy in single-molecule microscopy. Biophys J. 2004;86:1185–1200. doi: 10.1016/S0006-3495(04)74193-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yildiz A, et al. Myosin V walks hand-over-hand: Single fluorophore imaging with 1.5-nm localization. Science. 2003;300:2061–2065. doi: 10.1126/science.1084398. [DOI] [PubMed] [Google Scholar]
- 10.Kao HP, Verkman AS. Tracking of single fluorescent particles in three dimensions: Use of cylindrical optics to encode particle position. Biophys J. 1994;67:1291–1300. doi: 10.1016/S0006-3495(94)80601-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Holtzer L, Meckel T, Schmidt T. Nanometric three-dimensional tracking of individual quantum dots in cells. Appl Phys Lett. 2007;90 053902. [Google Scholar]
- 12.Speidel M, Jonas A, Florin E. Three-dimensional tracking of fluorescent nanoparticles with subnanometer precision by use of off-focus imaging. Opt Lett. 2003;28:69–71. doi: 10.1364/ol.28.000069. [DOI] [PubMed] [Google Scholar]
- 13.Ram S, Chao J, Prabhat P, Ward ES, Ober RJ. A novel approach to determining the three-dimensional location of microscopic objects with applications to 3D particle tracking. Proc SPIE. 2007;6443:64430D-1–64430D-7. [Google Scholar]
- 14.Betzig E, et al. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 15.Rust MJ, Bates M, Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM) Nat Methods. 2006;3:793–795. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hess ST, Girirajan TPK, Mason MD. Ultra-high resolution imaging by fluorescence photoactivation localization microscopy. Biophys J. 2006;91:4258–4272. doi: 10.1529/biophysj.106.091116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sharonov A, Hochstrasser RM. Wide-field subdiffraction imaging by accumulated binding of diffusing probes. Proc Natl Acad Sci USA. 2006;103:18911–18916. doi: 10.1073/pnas.0609643104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lidke KA, Rieger B, Jovin TM, Heintzmann R. Superresolution by localization of quantum dots using blinking statistics. Opt Express. 2005;13:7052–7062. doi: 10.1364/opex.13.007052. [DOI] [PubMed] [Google Scholar]
- 19.Huang B, Wang W, Bates M, Zhuang X. Three-dimensional super-resolution imaging by stochastic optical reconstruction microscopy. Science. 2008;319:810–813. doi: 10.1126/science.1153529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Juette MF, et al. Three-dimensional sub-100 nm resolution fluorescence microscopy of thick samples. Nat Methods. 2008;5:527–529. doi: 10.1038/nmeth.1211. [DOI] [PubMed] [Google Scholar]
- 21.Vaziri A, Tang J, Shroff H, Shank CV. Multilayer three-dimensional super resolution imaging of thick biological samples. Proc Nat Acad Sci USA. 2008;105:20221–20226. doi: 10.1073/pnas.0810636105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ram S, Prabhat P, Chao J, Ward ES, Ober RJ. High accuracy 3D quantum dot tracking with multifocal plane microscopy for the study of fast intracellular dynamics in live cells. Biophys J. 2008;95:6025–6043. doi: 10.1529/biophysj.108.140392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Piestun R, Schechner YY, Shamir J. Propagation-invariant wave fields with finite energy. J Opt Soc Am A. 2000;17:294–303. doi: 10.1364/josaa.17.000294. [DOI] [PubMed] [Google Scholar]
- 24.Greengard A, Schechner YY, Piestun R. Depth from diffracted rotation. Opt Lett. 2006;31:181–183. doi: 10.1364/ol.31.000181. [DOI] [PubMed] [Google Scholar]
- 25.Pavani SRP, Piestun R. High-efficiency rotating point spread functions. Opt Express. 2008;16:3484–3489. doi: 10.1364/oe.16.003484. [DOI] [PubMed] [Google Scholar]
- 26.Pavani SRP, Piestun R. Three dimensional tracking of fluorescent microparticles using a photon-limited double-helix response system. Opt Express. 2008;16:22048–22057. doi: 10.1364/oe.16.022048. [DOI] [PubMed] [Google Scholar]
- 27.Lord SJ, et al. A photoactivatable Push-Pull fluorophore for single-molecule imaging in live cells. J Am Chem Soc. 2008;130:9204–9205. doi: 10.1021/ja802883k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Willets KA, Ostroverkhova O, He M, Twieg RJ, Moerner WE. New fluorophores for single-molecule spectroscopy. J Am Chem Soc. 2003;125:1174–1175. doi: 10.1021/ja029100q. [DOI] [PubMed] [Google Scholar]
- 29.Shroff H, et al. Dual-color superresolution imaging of genetically expressed probes within individual adhesion complexes. Proc Nat Acad Sci USA. 2007;104:20308–20313. doi: 10.1073/pnas.0710517105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Deich J, Judd EM, McAdams HH, Moerner WE. Visualization of the movement of single histidine kinase molecules in live caulobacter cells. Proc Nat Acad Sci USA. 2004;101:15921–15926. doi: 10.1073/pnas.0404200101. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.