Invariant phase structure of olivo-cerebellar oscillations and its putative role in temporal pattern generation

Abstract

Complex movements require accurate temporal coordination between their components. The temporal acuity of such coordination has been attributed to an internal clock signal provided by inferior olivary oscillations. However, a clock signal can produce only time intervals that are multiples of the cycle duration. Because olivary oscillations are in the range of 5–10 Hz, they can support intervals of ≈100–200 ms, significantly longer than intervals suggested by behavioral studies. Here, we provide evidence that by generating nonzero-phase differences, olivary oscillations can support intervals shorter than the cycle period. Chronically implanted multielectrode arrays were used to monitor the activity of the cerebellar cortex in freely moving rats. Harmaline was administered to accentuate the oscillatory properties of the inferior olive. Olivary-induced oscillations were observed on most electrodes with a similar frequency. Most importantly, oscillations in different recording sites retained a constant phase difference that assumed a variety of values in the range of 0–180°, and were maintained across large global changes in the oscillation frequency. The inferior olive may thus underlie not only rhythmic activity and synchronization, but also temporal patterns that require intervals shorter than the cycle duration. The maintenance of phase differences across frequency changes enables the olivo-cerebellar system to replay temporal patterns at different rates without distortion, allowing the execution of tasks at different speeds.

Cerebellar involvement in timing is well-established, with evidence encompassing both normal and pathological conditions. Motor coordination in the 7–9 Hz range has been shown to involve the cerebellum (1), and pathologies associated with the cerebellum can either disrupt motor timing (2–4) or exaggerate tremor in this frequency range (5). The cerebellum also plays a pivotal role in timing of sensory and cognitive functions (6–11). The olivo-cerebellar system thus seems to be crucial for accurate timing in the range of tens to hundreds milliseconds. Two mechanisms have been proposed for cerebellar timing. First, parallel fibers have been suggested to activate Purkinje cells (PCs) with accurate delays (12–14) subserving timing. Second, oscillations in the inferior olive (IO) (15–18) have been proposed to act as a clock signal for timing. Both these mechanisms fail to cover the required range of 10–500 ms, the former because the length of a parallel fiber is exhausted within ≈10 ms and therefore can only support shorter time scales, and the latter because an olivary clock signal can only support temporal coordination at multiples of the clock cycle (≈100–200 ms) (19). Time intervals shorter than the cycle duration could be generated by creating phase differences between different subgroups of IO neurons. Although in vitro studies demonstrate that IO oscillations can exhibit rich spatiotemporal dynamics (20, 21), the possibility that different parts of the IO may be coupled at nonzero-phase difference has largely been overlooked (however, see refs. 22 and 23).

To investigate the phase structure of olivary activity in the cerebellar cortex, we chronically implanted arrays of 32 tungsten electrodes in the rat cerebellar vermis and studied the complex spike field oscillations in awake, behaving rats. Harmaline was administered to expose the underlying structure of IO oscillatory activity. Our results indicate that IO oscillations can retain nonzero-phase differences independent of frequency. We suggest that these phase differences endow the olivo-cerebellar system with the capability to time events, both motor and cognitive, across the time range suggested by behavioral observations.

Results

The Effect of Harmaline on Cerebellar Cortical Activity.

Harmaline induced rhythmic activity in the cerebellar cortex of awake rats, which was observed both in single-unit complex spike (CS) activity of Purkinje cells (Fig. 1A, red traces) and in the ensemble activity, characterized by the envelope of the multiunit activity (MUA) (Fig. 1B, red traces). MUA envelope oscillations could be observed on most electrodes (15 of 16 electrodes in this experiment; on average, 10 of 14 electrodes per experiment exhibited oscillatory activity), suggesting that nearby neurons that contributed to the MUA oscillated in-phase. The rhythmic character of the neuronal activity, quantified by the autocorrelation of CS and MUA (Fig. 1 C and D, red curves), was absent before harmaline administration (Fig. 1 C and D, black curves). This absence was true for all electrodes in all experiments. Harmaline was therefore crucial for robust observable oscillations in freely moving animals (24) (see Discussion). The spectrograms of complex spike activity (Fig. 1E) and MUA envelope (Fig. 1F) demonstrated that rhythmic activity started with an initial transient period (T < 20 min.), after which oscillations frequency remained relatively constant. MUA-envelope oscillations could be detected earlier than CS rhythmicity, probably because of integration of activity across several cerebellar units. In this experiment, oscillation frequency was ≈8.6 Hz on all 15 electrodes that exhibit oscillatory activity. Across experiments (n = 13), stable oscillation frequency was in the range of 4–11 Hz with 1 exception (20–30 Hz). Within each experiment, oscillation frequency was similar across electrodes, and occasional epochs of frequency deviation (Fig. 1 E and F, white arrows) occurred simultaneously on all recorded electrodes. These frequency changes were corroborated in the single-unit CS activity [supporting information (SI) Fig. S1].

Fig. 1.

The effect of harmaline on cerebellar-cortical activity. (A) Raw data and complex spikes times (vertical bars) taken before (black) and after (red) harmaline application. (B) Raw data (lower trace) with its corresponding multiunit activity (MUA) envelope (upper trace) before (black) and after (red) harmaline application. Data were collected simultaneously with the data in A. B has the same time scale as A. (C) Autocorrelation of the complex spike train reveals rhythmic activity after harmaline application (red) but not before (black). (D) The same as C for MUA envelope. Note that the activity after harmaline has the same oscillation frequency of the CS activity in C. (E and F) Spectrograms of CS and MUA envelope following harmaline application (T = 0). Note the delay in CS oscillation onset and the transient changes in oscillation frequency (arrows).

Electrode Pairs Exhibit a Variety of Stable Phase Differences.

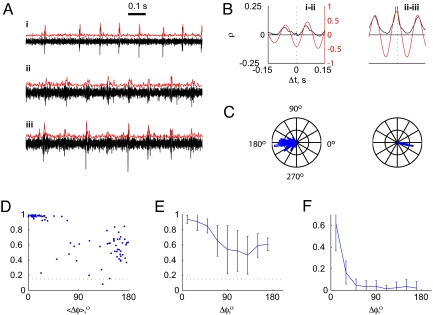
Oscillation frequency in each experiment was similar on all electrodes, but different electrodes oscillated with a variety of phase differences. Raw data segments from 3 electrodes (Fig. 2A, black traces) and their MUA envelopes (red traces) demonstrate that oscillatory activity was not necessarily zero-phase-locked. The bottom 2 electrodes exhibited in-phase oscillations, whereas the top electrode oscillated out-of-phase. The typical phase difference between pairs of electrodes was extracted from the cross-correlation of their MUA envelopes. The cross-correlations between electrode pairs from Fig. 2A are shown in Fig. 2B, exhibiting ≈0° and ≈180° phase differences. All electrodes reverberated at the same frequency, but exhibited a variety of time shifts and a variety of correlation strengths. To examine the stability of phase differences, each experiment was parsed into 10-s segments and phase difference was calculated separately in each segment. Fig. 2C illustrates the phase difference distribution across segments for the 2 electrode pairs shown in Fig. 2B. The phase difference distribution width, quantified by the mean resultant length (MRL) (see Materials and Methods), is shown in Fig. 2D. For phase differences <90° (49 of 91 pairs), pairs had very high MRL values (MRL = 0.91 ± 0.18), indicating that phase differences were extremely tightly maintained throughout the experiment. Even for large phase differences (>90°), MRL values were relatively high (42 of 91, MRL = 0.54 ± 0.17) and differed significantly from chance level (MRL = 0.15 ± 0.1) (Fig. 2D, dotted line). Maximum correlation values between electrode pairs exhibited a similar dependence on phase difference, and the 2 measures were almost indistinguishable. Across all experiments (n = 13), a similar trend was observed (Fig. 2E) with the majority of phase differences in the range of 0–60° (Fig. 2F). These results suggest that oscillations in adjacent parts of the cerebellar cortex (and in this case, in adjacent parts of the IO; see Discussion) are coupled and can maintain a constant nonzero-phase difference.

Fig. 2.

Electrode pairs exhibit a variety of stable relative phase values. (A) Segments of raw data from 3 simultaneously recorded electrodes (black) and their respective envelopes (red). Electrode i is out-of-phase relative to electrodes ii and iii. (B) Cross-correlations between 2 electrode pairs (shown in A) reverberate at the resonant frequency and exhibit different phase differences. Analysis performed on raw (black) and narrow-band (red) envelopes (see Materials and Methods). Cross-correlations are from electrode pairs from A. (C) Circular histograms of phase difference for the same electrode pairs as in B (255 segments from a total of 21.5 min.). (D) MRL of phase-difference distribution in 1 experiment plotted against phase difference. Each dot represents 1 electrode pair. Dotted line indicates chance level. (E) Population summary of MRL as a function of phase difference for all experiments (n = 13). Phase difference was grouped into 20°-wide bins. (F) Probability distribution of phase differences across all pairs, averaged across all experiments (n = 13).

Oscillation Frequency Is Modulated Synchronously.

Changes in the resonant frequency lasting several seconds could be observed even after frequency stabilization. Fig. 3A shows the MUA-envelope spectrograms of 3 simultaneously recorded electrodes. All 3 electrodes display a remarkably similar modulation in the oscillation frequency, characterized by occasional rises in oscillation frequency from a baseline of 9–10 Hz to 11–12 Hz. To quantify this similarity, we first extracted the time course of oscillation frequency from the spectrogram of each electrode (see Materials and Methods). The frequency time courses (FTCs) of all of the electrodes (n = 11) are superimposed in Fig. 3B (black lines) together with their mean (red line), and all FTCs exhibit almost identical temporal dynamics. Global changes in frequency would result in high similarity of individual FTCs to their mean, therefore we defined a global similarity index (GSI) (see Material and Methods) to quantify this similarity. In this experiment, GSIs were in the range of 0.89 ± 0.05, indicating that most frequency fluctuations occurred simultaneously in the entire recorded cerebellar region. Frequency variability as a function of time was quantified in each experiment by the coefficient of variation (CV) of the mean FTC (σ_FTC/〈FTC〉). CV values were in the range of 0.05–0.18, i.e., frequency changes had a SD of 5–18% of the mean oscillation frequency. In all experiments (n = 13), GSIs were on average 0.52 ± 0.1 (Fig. 3C, abscissa), and significantly higher than those obtained by using surrogate FTCs (Fig. 3C, ordinate) (see Materials and Methods). Frequency was thus comodulated and seems to be related to the behavioral state of the rat (see SI Text, Fig. S2). Oscillation frequency can therefore be viewed as uniform in the recorded cerebellar area.

Fig. 3.

Oscillation frequency is modulated synchronously. (A) Spectrograms of MUA envelopes from 3 different electrodes during the same experiment, demonstrating that frequency changes happen simultaneously. (B) Frequency time courses (FTCs, black lines) from all resonant electrodes (n = 11) and the global mean FTC (red line). (C) The mean global similarity index (GSI) for each experiment ± 1 SD (abscissa) are plotted against the GSI obtained by using bootstrap methods with surrogate FTCs in the same experiment (ordinate), indicating that in all experiments the common modulation is much higher than expected by chance.

Phase Differences Are Retained Across Frequency Changes.

The lag in activity between electrode pairs can be interpreted either as phase or as time differences. This distinction becomes significant, if one of these parameters is invariant to frequency changes. Invariance of phase difference to frequency changes has been shown to exist in other oscillating neural systems (25) and enables a system to scale time patterns across varying speeds. Phase and time differences between electrode pairs were calculated throughout the experiments. In Fig. 4A, the MUA-envelope spectrograms of 2 electrodes are shown. Both envelopes have a similar pattern of frequency change across time. Fig. 4B demonstrates similar FTCs for all oscillatory electrodes (black lines; n = 10; red line shows mean FTC; GSI = 0.78). The FTC was segmented into regions of low and high frequency (9.3 ± 0.2 Hz and 10.7 ± 0.2 Hz in this experiment). The mean phase difference between each pair of electrodes was extracted in the low-frequency range (Δφ, LF) and the high-frequency range (Δφ, HF) and these mean phase differences were plotted against each other (Fig. 4C). The regression line through all electrode pairs (green line) demonstrates that phase difference is well-maintained across ≈15% frequency change (slope 0.92; statistically indistinguishable from 1). Time delays between electrode pairs in the 2 frequency ranges demonstrate that time differences are less well-maintained (Fig. 4D) (slope 0.81 differs significantly from 1).

Fig. 4.

Phase is retained across large frequency changes. (A) Spectrograms of MUA envelopes from 2 simultaneously recorded electrodes exhibit similar, almost binary, frequency transitions. (B) FTCs of all 10 oscillatory electrodes from the same experiment (black lines), and the global mean FTC (red). (C) Summary of phase differences for electrode-pairs in the low-frequency range (LF, 9.1–9.5 Hz; abscissa) vs. the high-frequency range (HF, 10.5–10.9 Hz; ordinate). Dotted red line is the identity line, Green line is the linear regression through all data points, whose slope value is 0.92 (statistically indistinguishable from 1). Phases were extracted from cross-correlations of narrow-band envelopes. (D) Summary of delays between electrode-pairs in the LF (abscissa) vs. HF (ordinate). Delay is further away from the diagonal (slope 0.81, significantly different from 1). (E) Population summary (n = 10) of delay and slope changes. Each star summarizes the slope ratio (HF/LD) of delays (ordinate) vs. the slope ratio of phases (abscissa). Values closer to 1 indicate better maintenance of value. In all experiments, phase was better-maintained than delays.

Population data are summarized in Fig. 4E (n = 11; 2 experiments were excluded because of negligible frequency changes). Each experiment is represented by the slope of the phase difference plot (such as in Fig. 4C) and by the slope of the delay plot (such as in Fig. 4D). All of the points in the graph are below the diagonal, indicating that phase differences (abscissa) are maintained much better than delays (ordinate). Invariant time delays would have resulted in phase-difference slopes >1, which are never observed in our data (see also SI Text). In 6 of 11 experiments the phase was almost perfectly maintained (statistically indistinguishable from 1). In the other 5 experiments, the phase differences were less than perfectly maintained. However, in all experiments, phase differences were bettermaintained than time differences. The ability of the olivo-cerebellar system to maintain phase differences relatively well during significant frequency changes has important implications for the pattern generation capabilities.

Discussion

By recording multiunit activity in the cerebellar cortex of rats, we unravel the phase structure of harmaline-induced oscillations. Changes in oscillation frequency were global in the recorded region, but oscillation in different electrodes retained phase differences. Remarkably, phase differences were well maintained across changes in oscillation frequency. Thus, oscillations of IO neurons can subserve time intervals shorter than the cycle duration. This ability allows the olivo-cerebellar system to support timing in the range implicated by behavioral studies (19).

Harmaline-induced oscillatory activity in the cerebellar cortex has previously been shown to depend on intact olivo-cerebellar connectivity (24), manifesting itself as rhythmic CS activity. Indeed, harmaline acts directly on IO neurons, inducing rhythmic activity by shifting the activation curve of their low-threshold Ca²⁺ conductance (16). Hence, harmaline does not change the basic electrotonic coupling between IO neurons, but only their propensity to oscillate and produce spikes. Although CSs are the major source of cerebellar cortical oscillations, other neuronal populations may also be involved.

Previous work on CSs in the cerebellar cortex has described zero-phase synchrony between PC pairs (26–29). Our study extends these results to stable, nonzero-phase differences. Reports of nonzero-phase relationships have been presented in only a few studies (22, 23, 30). The issue of phase maintenance was not addressed in these studies, and the range of resulting time differences was relatively short.

Without harmaline, IO oscillations are nonstationary and intermittent (31), with only a minority of subthreshold oscillation cycles producing output spikes (18). Recordings in the cerebellar cortex therefore pose severe limitations on the detection of nonzero-phase differences. Cross-correlations between PCs using short time windows would not yield enough spikes to detect phase locking. Using large time windows would violate the stationarity requirement for cross-correlation analysis. Furthermore, phase-difference invariance implies that the time lag of cross-correlation peak would move with frequency changes, and the resulting cross-correlation would be smeared. This smearing may give rise to the impression that no rhythmicity exists except for zero-phase locking (32). The enhanced regularity and high firing rate imposed by harmaline help to uncover a phenomenon that most likely occurs during normal behavior. Indeed, temporal delays between groups of synchronous PCs have been shown to exist in animals performing a repetitive motor task (30), suggesting a role for such nonzero-phase differences.

The 2 significant aspects of our results are the maintenance of nonzero phase between areas of the cerebellar cortex and their invariance to frequency changes. We suggest that these results should be interpreted within the framework of olivary timing, proposed by Llinás (33). The phase structure revealed in our work enables the cerebellum to create complex output patterns. A synchronized clock signal works with a fixed quantum of time—the cycle duration. Thus, a synchronized clock can produce time sequences that are limited to the cycle duration and its multiples. By combining several clocks with nonzero-phase differences, the temporal patterns within each cycle are almost unlimited, and the system can support much shorter time intervals (19). The shortest interval is set by the accuracy of the olivary spike-production mechanism and the longest by the cycle duration or multiples thereof.

Our results are supported by in vitro studies that have demonstrated a wide repertoire of olivary oscillations, including stationary phase-locked oscillations, breakdown into smaller groups of phase-locked oscillators (20), and traveling waves (21). Phase differences can appear in vitro within the same olivary area, at distances as small as 100 μm (21). In contrast, reports of nonzero-phase difference have only been reported anecdotally in vivo (22, 24, 34) and never been studied systematically. Nonetheless, kinematic studies in harmaline-treated rats suggest that IO coupling is required to maintain tight, nonzero-phase differences between muscle pairs, further supporting our results (35). The mechanism of phase-difference maintenance still requires elucidation, but probably relies on direct or indirect coupling between oscillating IO neurons. Our recording electrodes were placed in vermal regions of lobule V and VI (and occasionally perhaps in lobule IV), which are all connected to the medial accessory olive and do not cross IO anatomical boundaries (36). This connectivity provides the anatomical substrate necessary for direct and indirect coupling between the IO neurons. It should be noted that indirect coupling of olivary neurons probably underlies the larger phase differences observed in our data. In such cases, decoupling can occur at several sites, and this decoupling may be the source for the decrease in the synchronization measure (MRL) observed when phase differences were large.

A system that maintains phase differences across frequency changes has important implications for temporal sequence generation. For example, complex motor behavior—from walking to playing the piano—can be performed accurately at different speeds. Such complex motor behaviors require undistorted scaling of temporal patterns. We propose that the olivo-cerebellar system may underlie this ability through phase-difference invariance to frequency changes.

Materials and Methods

Microelectrode Arrays.

Custom-made arrays of 32 Isonel-coated tungsten microwires (35 μm in diameter) were arranged in a 4 × 8 matrix. Electrodes were spaced 250 μm on both axes such that the entire array spanned 1.75 mm × 0.75 mm. Electrode resistance before implantation was ≈200 KΩ.

Surgical Procedure.

All procedures were approved by Bar Ilan University institutional animal care and use committee and were performed in accordance with the National Institutes of Health guidelines. The surgical procedures have previously been described in detail (37, 38). In brief, adult Long-Evans male rats weighing 420–540 g (Harlan and Taconic) were initially sedated by 5% isoflurane and then injected i.m. with ketamine HCl and xylazene HCl (100 mg/kg and 10 mg/kg, respectively). Supplementary injections of ketamine and xylazene were given as required.

The rat's head was fixed in a stereotaxic frame (Kopf Instruments). A midline incision was made to expose the skull surface up to the occipital ridge posteriorly. Connective tissue was removed and the skull surface cleaned with 3% hydrogen peroxide. Four stainless-steel screws (Small Parts) were tapped into the skull to serve as ground electrodes and as anchors for the dental cement. A craniotomy, slightly larger than the electrode array, was performed above the occipital bone. The vermal portion of lobule V/VI was exposed, and dura was removed. The ground wire was rolled around all 4 screws and an electrode array oriented in the rostro-caudal or medio-lateral axis was slowly lowered into the brain while monitoring the neural activity by using a neural recorder system (Plexon Inc.). Electrodes were fixed at depths of 0.8–2 mm below the surface by using a high viscosity cyanoacrylate (RX-gel; Pacer Technology). The array, anchoring screws, and the ground electrode were covered with dental cement, leaving only the connector exposed. Rats were allowed ≥2 weeks of recovery before recording.

Anatomical location of electrodes within the cerebellar cortex was verified post mortem after electrical lesions were created at the electrode tips (Fig. S3).

Data Acquisition.

Activity was recorded from rats 2–10 weeks postsurgery by using a multichannel acquisition processor system (Plexon Inc.). Channels were filtered before sampling between 0.15–9 kHz, and ≤16 channels at a time were recorded continuously at 40 kHz. Activity was then recorded in awake animals, before and after harmaline HCl injection (Sigma-Aldrich) (12–15 mg/kg, i.p. injection under light isoflurane anesthesia). Unless otherwise stated, results presented are from harmaline-injected animals taken after the effect of harmaline stabilized (10–20 min).

Data Analysis.

All data analysis was performed on MATLAB 7 (MathWorks).

Complex spike analysis.

Spikes were detected by using a median threshold (39). Extracellular complex spikes were identified by their wide waveform (2–8 ms) and their low firing rate before harmaline administration (<2 Hz) and were analyzed as such only if their shape was retained during the harmaline condition. When multiple spike shapes were detected on the same electrode, clustering was performed by using the projection on the first 2 principal components of the aligned spikes.

Extraction of multiunit envelopes.

After harmaline application, the amplitude envelope of the voltage signal in many electrodes oscillated at slow rates. The carrier frequency range of this slow rate differed across experiments and exhibited some variability within an experiment. The original voltage signal was band-pass filtered in the carrier frequency range and the amplitude envelope extracted by low-pass filtering (0–250 Hz) its absolute value. In some cases, bands were wide and could potentially violate the band-limitation requirement (40), and therefore, oscillation phase in different frequency bands was compared to ensure that no distortions were introduced.

Definition of oscillatory channels and spectral analysis.

Envelopes were analyzed for rhythmic activity by calculating the power spectrum by using Welch's averaged periodogram method [digital prolate spheroidal sequence (DPSS) window, NW = 3]. Further analysis was performed only on oscillatory channels, in which the envelope power spectrum after harmaline application exhibited a peak >3 dB above the power in adjacent frequency bins. Coherence between pairs of envelopes and spectrograms were calculated by using Welch's algorithm with similar parameters to power-spectrum calculation.

Phase difference extraction and stability.

To extract phase differences between channel pairs, the 2 envelopes were filtered to create narrow-band signals (41) (see Fig. S4). Band-filtered envelopes were then parsed into 10-s windows with 5-s overlap. The cross-correlation of pairs of segments was calculated, and the phase difference was extracted from the cross-correlation by taking the angle of its Hilbret transform at Δt = 0.

To quantify the stability of phase differences across all measurements, standard methods from circular statistics (42) were used. The mean phase difference and mean resultant length (MRL), a.k.a. phase-locking index factor (PLF) (43), were calculated. The MRL of phase-difference values {ϕ_k}_k=1^N, where 0 ≤ ϕ_k < 2π, is defined as:

MRL values range from 0 (uniform distribution of phase differences on the unit circle) to 1 (constant phase difference). Noise levels of the MRL were assessed by using bootstrap statistics. Surrogate data were created with Fourier amplitude similar to the original envelopes but with random phase, and the above procedure for calculating MRL was repeated 200× to yield bootstrap statistics.

Global nature of frequency changes.

Bootstrap statistics were used to validate the global nature of oscillation frequency dynamics. Frequency time courses (FTCs) of all resonant electrodes were averaged to yield the mean FTC. The percent variance in each FTC explained by the mean FTC was used as a global similarity index (GSI). To ensure that obtained GSI values were significant, the procedure was repeated with surrogate FTCs. Surrogate FTCs were created by shifting cyclically each FTC by a random time interval and repeating all of the computation of mean FTC and GSIs. These surrogate FTCs retain all of the statistics of the original FTCs and do not violate the null hypothesis that modulations in each channel were independent. This procedure was repeated 2000× to yield bootstrap statistics for each experiment.