Converging Neuronal Activity in Inferior Temporal Cortex during the Classification of Morphed Stimuli

Abstract

How does the brain dynamically convert incoming sensory data into a representation useful for classification? Neurons in inferior temporal (IT) cortex are selective for complex visual stimuli, but their response dynamics during perceptual classification is not well understood. We studied IT dynamics in monkeys performing a classification task. The monkeys were shown visual stimuli that were morphed (interpolated) between pairs of familiar images. Their ability to classify the morphed images depended systematically on the degree of morph. IT neurons were selected that responded more strongly to one of the 2 familiar images (the effective image). The responses tended to peak ∼120 ms following stimulus onset with an amplitude that depended almost linearly on the degree of morph. The responses then declined, but remained above baseline for several hundred ms. This sustained component remained linearly dependent on morph level for stimuli more similar to the ineffective image but progressively converged to a single response profile, independent of morph level, for stimuli more similar to the effective image. Thus, these neurons represented the dynamic conversion of graded sensory information into a task-relevant classification. Computational models suggest that these dynamics could be produced by attractor states and firing rate adaptation within the population of IT neurons.

Introduction

The inferior temporal (IT) cortex is thought to play an important role in visual categorization (Wilson and DeBauche 1981; Sigala and Logothetis 2002; Sigala 2004; Afraz et al. 2006; Op de Beeck et al. 2008). IT neurons can be selective for complex visual stimuli including people, places, and objects (Desimone et al. 1984; Kobatake and Tanaka 1994; Allred et al. 2005; Hung et al. 2005; Kiani et al. 2007; Peissig et al. 2007). In some cases this selectivity corresponds more strongly to exemplar-specific than to category-specific information (Vogels 1999; Rolls et al. 1977; Thomas et al. 2001; Freedman et al. 2003). However, IT neurons can also be sensitive to the features that distinguish categories and are influenced by experience (Sigala and Logothetis 2002; Sigala 2004). At the population level, neural responses may reflect performance in behavioral classification tasks (Vogels 1999; Allred and Jagadeesh 2007; Kiani et al. 2007; Koida and Komatsu 2007; Liu and Jagadeesh 2008). Single IT neurons encode different kinds of information about visual stimuli in their temporal firing pattern, suggesting that the dynamics of visual responses may reflect different kinds of processing of a visual image (Sugase et al. 1999; Matsumoto, Okada, Sugase-Miyamoto, Yamane 2005; Brincat and Connor 2006). These results suggest that IT can represent both stimulus-specific information and categories. To further understand this dual representation, we recorded IT activity in monkeys performing a visual categorization task and examined the dynamic conversion of incoming information from complex visual stimuli into categories.

One way to extract relatively stable features from the flow of sensory information to form associations and categorize information is through the operation of attractor-based neural networks (Hopfield 1982; Amit et al. 1997). An attractor network has several preferred activity states, such that relevant external inputs cause network activity to change dynamically and approach one of these preferred states, usually the one most closely correlated with some aspects of the inputs. Attractor networks have been proposed to account for numerous cerebral functions with discrete end values, including spatial orientation, sensory pattern recognition, categorical perceptual judgments, and execution of movement trajectories (Lukashin et al. 1996; Wyttenbach et al. 1996; Bartlett and Sejnowski 1998; Fdez Galan et al. 2004; Wills et al. 2005; Wong and Wang 2006). In principle, attractor dynamics might also be expressed in IT cortex, where associative long-term visual memories are stored, to extract visual category information. However, it is unclear which aspects of IT activity might represent category boundaries and whether these boundary representations are interpretable in terms of the basins of an IT attractor network (Sakai and Miyashita 1991; Amit et al. 1997). In this paper we present evidence of converging neural activity in macaque IT cortex representing the conversion of graded visual information into a category. We then simulate a local neural network to assess the possible relevance of attractor states and spike-rate adaptation to the observed neural dynamics. These simulations support a contribution by distributed local attractor networks, modulated by firing rate adaptation, to drive neural response convergence to reflect perceptually relevant categories.

Materials and Methods

We recorded from 154 IT neurons in 2 adult rhesus macaques (Monkey G: 58 neurons; Monkey L: 96 neurons) using standard recording techniques (Allred et al. 2005). Experimental design was identical to that in Liu and Jagadeesh (2008), which contains a discussion of an overlapping data set.

Experimental Procedure

Surgery on each animal was performed to implant a head restraint, a cylinder to allow neural recording, and a scleral search coil to monitor eye position(Fuchs and Robinson 1966; Judge et al. 1980). Materials for these procedures were obtained from Crist Instruments (Hagerstown, MD) or produced in-house at the University of Washington. Responses of single IT neurons were collected while monkeys performed a delayed-match to sample task (Liu and Jagadeesh 2008). Spikes were recorded using the Alpha–Omega spike sorter (Nazareth: Israel). Coded spikes were stored on a PC at a rate of 1000Hz using CORTEX, a program for neural data collection and analysis developed at the National Institutes of Health (Bethesda, MD). Eye movements were monitored and recorded (at 500 Hz) using an eye coil based system from DNI (Newark, DE). All animal handling, care, and surgical procedures were performed in accordance with guidelines established by the National Institutes of Health and approved by the Institutional Animal Care and Use Committee at the University of Washington.

Chamber Placement

The chambers were placed over the right hemisphere, using stereotaxic coordinates. Neural recordings were targeted near the center of the chamber (Monkey L: 17L, 17.5 A; G: 16 L, 17.5A); this location is in between the perirhinal sulcus and the anterior middle temporal sulcus, in reference to reconstructions from the structural MRI. Recording depths ranged from 27 to 32 mm for Monkey L and 30 to 33 mm for Monkey G. Depth measurements are from the dural surface, measured during an early recording session. The recording locations are identical to those in Liu and Jagadeesh (2008).

Recording Procedures

To isolate neurons, we moved the electrode while monkeys performed the passive fixation task with a set of 24 images arranged in 12 pairs (Supplementary Fig. 1). When the experimenter judged that a neuron responded better to one of the 2 images in the 12 pairs of images, she recorded from that neuron while the monkey performed the 2-alternative-forced-choice delayed-match-to-sample (2AFC-DMS) task with that stimulus pair.

We repeatedly sampled a single location until we could no longer isolate cells with selectivity for one of the 12 pairs used in the experiment. We moved the electrode location only when selectivity was not detectable over 2–3 days of recording, and moved only slightly across the surface (less than 1 mm). The range of sampled cites spanned a 4 mm diameter circle centered on the stereotaxis locations above. Using this procedure, we found potential selectivity for the 12 image pairs in 75% of the attempted sessions; thus, the cells included in this sample were found frequently. The recorded neurons might include samples from both TE and perirhinal cortex. No anatomical confirmation of recording sites is available from these monkeys because the monkeys continue to be used in other experiments.

Stimuli

Images consisted of photographs of people, animals, natural and man-made scenes, and objects (Supplementary Fig. 1). All images were 90 × 90 pixels, and were drawn from a variety of sources, including the World Wide Web, image databases, and personal photo libraries. Image pairs were organized prior to recording sessions into 12 pairs of stimuli. From these predefined lists of image pairs, selective neurons were found (see Recording Procedures) for a total of 12 unique image pairs used in the analysis. At the viewing distance used, stimuli were presented on a computer monitor with 800 × 600 resolution (refresh rate 100 Hz), and images subtended 4°. Cells selective for each of the 12 image pairs were found, and the distribution of the cells for each image pair is shown in Supplementary Figure 1 above each image pair.

Effective and Ineffective Images

Based on the average response over trials during the sample presentation epoch, offset by a latency (i.e., over the 75- to 375-ms period) we assigned the image in the pair that provided a stronger response to be the “Eff” image, whereas the other was deemed the “Ineff” image. Because we recorded from multiple neurons with the same stimulus sets, either of the 2 images in a pair could serve as the Eff image during a particular recording session. Across the sample included in the study, each image in the pair was the Eff image in approximately half the sessions using that pair.

Image Morphing and Ranking

Each of the 12 pairs of images was morphed using MorphX (http://www.norrkross.com/software/morphx/MorphX.php), a freeware, open source program for morphing between 2 photographic images. We constructed 9 intermediate images in between the 2 original images, as described in Liu and Jagadeesh (2008); the images and their morph variants are presented in Figure 2 of Liu and Jagadeesh (2008). These 9 intermediate images, along with the 2 images in the pair were used as samples in the 2AFC-DMS task described above. The particular pair used in a recording session depended on observing selectivity for one of the images in the pair.

Figure 2.

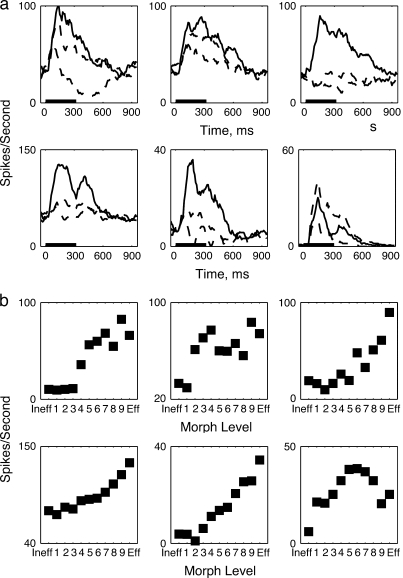
Single cells show a variety of neural responses to different morphed images. (a) Response time course of 6 different cells to the 2 end point images Eff (black) and Ineff (black dashed) and to the midlevel morph (blue dashed). (b) Firing rates to the Eff and Ineff and 9 morph variants computed over time period 100–200 ms. The black horizontal line shows the period of sample presentation (320 ms).

The morphing algorithm used by MorphX cannot be presumed to be linear; nevertheless we assigned a level to each morph variant corresponding to the ordering of each morph variant between the 2 original images from which they were morphed; There are 11 possible sample images (the 2 original images and 9 morph variants). The original image that produced a weaker response in the cell in a particular session (Ineff, as defined above) was assigned morph level 0; the original image that produced a stronger response in the experiment (Eff, as defined above) was assigned morph level 10. The 9 intermediate morph variants were assigned levels 1–9. Of these, morph variants 1–4 were closer to the Ineff image, and therefore, images 0–4 are collectively referred to as the Ineff morphs. Morph variants 6–9 were closer to the Eff image, and therefore, images 6–10 are considered Eff morphs. Morph variant level 5 was a priori defined as the midpoint of the morph continuum between the 2 images. These designations matched the behavioral reward contingencies, described below.

Behavioral Tasks

Two-Alternative-Forced-Choice Delayed-Match-to-Sample

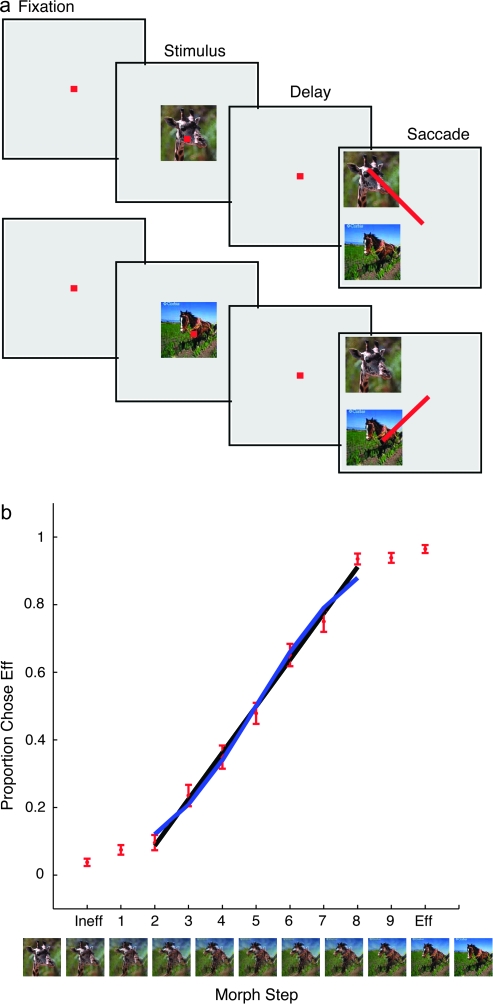
On each day, the monkey performed the 2AFC-DMS task (Liu and Jagadeesh 2008) with 2 sample images and 9 morph variants of those images. In each trial, one sample image (or one of its morph variants) was presented, followed by a delay and then followed by a pair of choice images (“choice array”). The monkey's task was to saccade to the image in the choice that most resembled the sample image. An example image pair and associated trials are illustrated in Figure 1. In each trial a red fixation spot (0.3° x 0.3°) appeared at the center of the monitor, and was the cue for the trial to begin. After the monkey acquired fixation, there was a variable delay (250–500 ms) before the onset of the sample image. The sample was presented for 320 ms. After a delay period (700–1100 ms), the choice array (which consisted of both sample images from which the morph variants were created, the Eff and Ineff image) was presented. The choice images were presented 5° up (or down) and to the left of the fixation spot. Location of individual choice images was randomized between the 2 positions (up and down), so the monkey could not determine the location of correct saccade before choice array onset. The different morph variants were presented as samples in random order, until 5–17 trials were recorded for each image.

Figure 1.

(a) Classification task. After the monkey achieved fixation on a fixation point, a sample, chosen at random among the 9 morphed images or the pair of photographs from which the morphs were made, was presented for 320 ms. Then, after a delay, the photographs appeared together as possible choices (targets). The monkey's task was to pick the target choice that more closely resembled the sample, and make a saccade to it. (b) Behavioral performance. The data are plotted as the proportion of times the monkey chose one of the images (the “effective” image for the cell (see Methods), or Eff) of the 2 original photographs, as a function of the different samples. The trend is linear in the central region between morphs 2 and 8, but performance levels off at the extremes and their nearest neighbors, images Ineff (0) to 2 and 8 to Eff (10). The data are fit with a sigmoid (blue line) and a line (black line). Error bars are standard errors of the mean across different sessions. Images are examples used in one session, where the giraffe was the Ineff image, and the horse the Eff image.

When the original image pairs were presented as the sample, the monkey's task was to pick the identical sample image from the choice array (Fig. 1a). When the morph variants were presented, the monkey's task was to classify the morphed sample as one image in the choice pair by judging the similarity between the morphed image and the original images (which were presented as choices). The monkey was rewarded for picking image 0 (the Ineff) image when morph variants 0–4 were presented as the sample image and the monkey was rewarded for picking image 10 (the Eff) when morph variants 6–10 were presented. For morph variant 5, the monkey was rewarded randomly, resulting in 50% reward for either choice.

The monkeys were trained over a period of 6 months before the recording sessions began, with the 12 pairs of images and their morphed exemplars, as described in Liu and Jagadeesh (2008), so that both the morphed images and image pairs (Supplementary Fig. 1) were not novel to the animal before the beginning of the recording session.

Analysis of Neural Data

Neurons were included in the population for analysis based on post hoc analysis of selectivity for the image pair selected during the recording session (averaged responses over the sample presentation period to the effective image, Eff, are to be at least 110% of those to Ineff), yielding a neural population of 132 experiments. Four experimental sessions were also discarded because of poor performance by the monkey, resulting in a neural population of 128 experiments. Choosing different populations of cells (all 154) or only cells which pass a selectivity criterion (P value between the 2 original images < 0.01) does not change the results shown in the neural data figures.

Average spike rates (Figs 2 and 3) were calculated by aligning action potentials to the onset of the sample stimulus presentation, and analyzing the data from 100 ms before the onset of the image to the period 1000 ms after the onset of the image. The peristimulus time histogram (PSTH) for each cell was calculated by averaging the rate functions across the repeated trials of presentation of the same stimulus. The population PSTH was calculated by averaging the PSTHs across the set of 128 selective cells. All completed trials were included in the analyses; trials were excluded if the monkey did not make a choice from the 2 possible choice stimuli. Both correct and incorrect trials were included.

Figure 3.

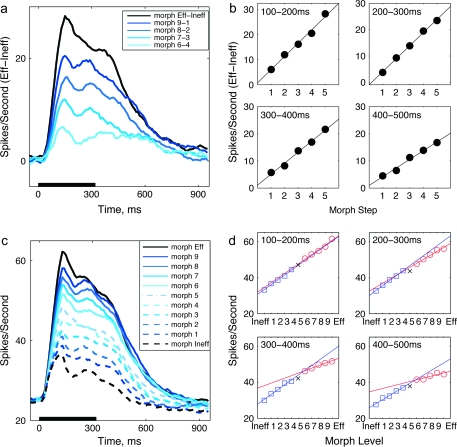
Time course of population responses to morphed images. (a) Time course of average differences between the responses to images Eff and Ineff (black) and to morphs successively different from the images (Eff & Ineff) between which they were morphed, averaged across the population of cells n=128. In both panels, as in Figure 2 spike counts are binned into 100 ms bins, which slide every 10 ms from stimulus onset, and are averaged across 15–20 trials per unit and morph step. (b) Mean response difference between Eff and Ineff morphs in successive 100 ms epochs after sample onset. (c) Time course of firing rate to Eff and Ineff, and each morph variant, as in (a). (d) Mean response to Eff and Ineff image and morph variants in successive 100 ms epochs as a function of morph level.

All the tests of significance were performed on firing rate functions FR(t). FR(t) was calculated for each neuron, for each sample image, by averaging firing rate across multiple presentations of each sample in overlapping time bins (also called epochs) of 100 ms, shifted in time steps of 10 ms (Zoccolan et al. 2007). This procedure smoothes the data. The average FR(t) was plotted at the middle of the 100-ms bin. Therefore, average responses at time 0 consist of the average of responses from -50 to 50 ms after stimulus onset. To calculate the dependence of the neural responses on morph level, we performed a regression analysis for each cell for each epoch. We regressed the spike rate in an epoch against the morph level, separately for Eff and Ineff images (Fig. 4). To compare the response to Eff with its 4 variants and also Ineff with the other 4 ineffective variants (Fig. 5), we applied an unbalanced 2-way ANOVA. In this ANOVA, we treated the cell as one factor (128 level), and stimulus as the second factor (2 level: Eff vs. 9, Eff vs. 8, Eff vs. 7, Eff vs. 6, Ineff vs. 1, Ineff vs. 2, Ineff vs. 3, Ineff vs. 4). Morphs 2 levels apart were also compared using an unbalanced one-way ANOVA, considering again “stimulus” and “cell” as 2 factors with 2 levels (2 vs. image Ineff, 4 vs. 2, 6 vs. 4, 8 vs. 6 and Eff vs. 8) and 128 levels, respectively (Fig. 5).

Figure 4.

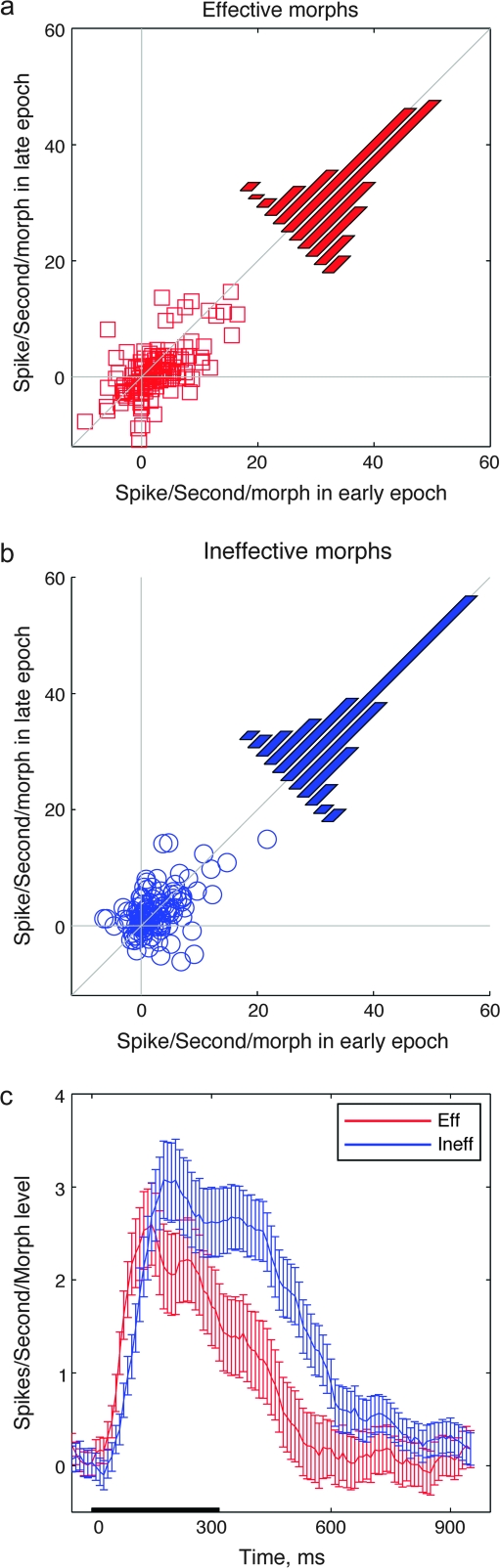
(a, b) Scatter plots of slope of linear regression (in Spikes/Second/Morph Level) in late versus early epoch (100–200 ms vs. 400–500 ms after sample onset) for each individual cell in the population. Histograms are the distributions of slopes for individual cells in early and late epochs. n = 128 experiments. (a) Slope of Eff image and Eff morphs (Eff, 6–9), (b) slope of Ineff image, and Ineff morphs (Ineff, 1–4). (c) Time course of slope (across population) as a function of time. One hundred millisecond bins, stepped 10 ms.

Figure 5.

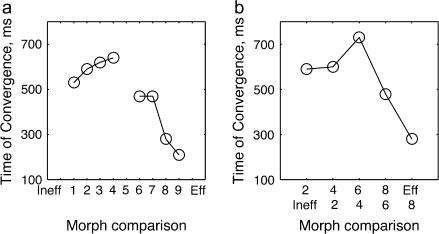
(a) The times of convergence to the Eff (or Ineff) response for each morph variant. This graph shows the time at which the responses to the morph variants were first no longer significantly different form those to Eff (or Ineff) stimulus (taken from the ANOVA, when P > 0.01). (b) The same ANOVA-based analysis as in a, but comparing the response to morphs 2 level apart, that is, to morph 2 versus Ineff, 4 versus 2, 6 versus 4, 8 versus 6, and Eff versus 8.

Network Simulations

General Characteristics of the Autoassociative Network

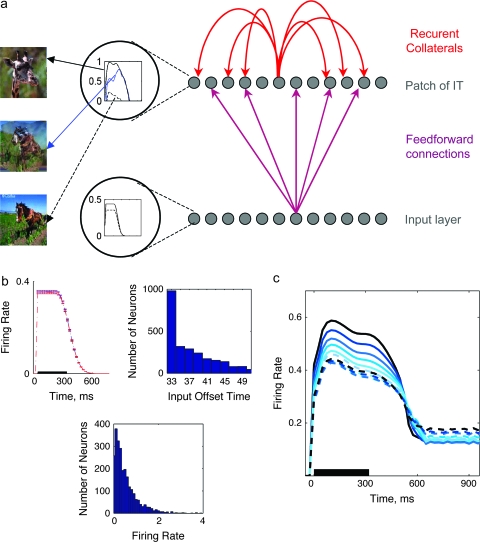
In line with previous work modeling IT networks (see e.g., Parga and Rolls 1998; Roudi and Treves 2008), we have considered a simple autoassociative network model comprised of 2 layers, shown schematically in Figure 6, which simulates a cortical patch as a local recurrent network. The first layer functions as an input stage that projects afferent inputs to the second layer; this layer is analogous to the input from earlier visual areas to the second, recurrent layer. Units in the second layer receive inputs both from the first layer, as well as from units in the same layer, and provide outputs to one another (recurrent connections). The second layer is analogous to the cortical patch containing the neurons recorded in this study (neurons recorded from inferotemporal cortex, IT). In our simulation, we consider the dynamics of local interconnected networks in IT, and thus the simulation is focused on the second, output, layer of units with recurrent connections. The units in the network are labeled with an index i, i = 1…N = 2500, but the connectivity between the units, or the probability that 2 units are connected, does not depend on their indexes. In a classic Hopfield model the connectivity is complete, which means every unit in the network receives input from all other units (Hopfield 1982). The connectivity can be sparse, but still independent of the index, as in (Sompolinsky 1986) or in the highly diluted limit considered by (Derrida et al. 1987). This type of model has been thoroughly analyzed in terms of its storage capacity, yielding a relation between the maximum number p_c of patterns that can be turned into dynamical attractors, i.e. that can be associatively retrieved, and the number C of connections per receiving unit. Typically the relationship includes, as the only other crucial parameter, the sparseness of firing a, and for sparsely coded patterns (values of a close to 0) it takes the form (Treves and Rolls 1991).

(1)

where k is a numerical factor of order 0.1–0.2. Representing the firing rate of unit i by a variable r_i, which can be taken as an average over a short time window, the sparseness a of the representation can be measured, by extending the binary notion of the proportion of neurons that are firing, as

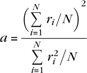(2)

Figure 6.

(a) Schematic view of the simulated network, including an input layer, which projects its activity to an output layer (recurrent connections) through sparse FF connections. Different units in first layer receive input, generated using a common truncated logarithmic distribution (b, bottom middle), with durations drawn at random from a logarithmic distribution (b, top right); one example is shown in circle at bottom. The units in this layer are active at a certain level for a specific duration, with a gradual transition to zero (example shown in circle at top). (b) Simulated input activity pattern: the average activity across all of the input units, for one pattern, is shown in top left; distribution of input offset times in top right, and firing rates in bottom middle. (c) Average network activity, in response to morphs obtained between 2 nonstored patterns, including a linear decay of firing frequency. Because there are no stored patterns, no attractors appear in this simulation.

Specific Model

In our model, units receive feedforward (FF) projections from an input layer of another 2500 units. Each unit in the (output) patch receives C_ff= 750 FF connections from the input array, and C_rc= 500 recurrent collateral (RC) connections from other units in the patch. Both sets of connections are assigned to each receiving unit at random. Weights are originally set at a uniform constant value, to which is added a random component of similar mean square amplitude, to generate an approximately exponential distribution of initial weights onto each unit. Once a pattern is imposed on the input layer, the activity circulates in the network for 80 simulation time steps, each taken to correspond to ca 12.5 ms (Treves 2004). Each updating of unit i amounts to summing all excitatory inputs.

(3)

The first 2 terms enable the memories encoded in the weights to determine the dynamics; the third term is unrelated to the memory patterns, but is designed to regulate the activity of the network, so that at any moment in time, $x\equiv (1/N){\displaystyle {\sum }_i{r}_i}$and $y\equiv (1/N){\displaystyle {\sum }_i{r}_i^2}$both approach the prescribed value a (the pattern sparseness mentioned above).

The simulation assumes a threshold-linear activation function for each unit. This assumption enables the units to assume real continuously variable firing rates, similar to what is found in the brain (Treves et al. 1999).

(4)

where Th is a threshold below which the input elicits no output and g is a gain parameter. In the simulations, induced activity in each unit is followed by a competitive algorithm that normalizes the mean activity of the (output) units, and also sets their sparseness to a constant a = 0.2 (Treves and Rolls 1991). The algorithm represents a combination of subtractive and divisive feedback inhibition, and operates by iteratively adjusting the gain g and threshold Th of the threshold-linear transfer function. In Eq. 3, M can be any value between 0 and 1, and corresponds to the proportional contribution of collaterals in driving the activity of each unit. But, as previously shown (Treves 2004; Menghini et al. 2007) the best performance is obtained when collaterals are suppressed during pattern storage, in line with the Hasselmo argument about the role of cholinergic modulation of recurrent connections (Barkai and Hasselmo 1994). The suppression of collaterals during training provides a mechanism for ensuring that during storage, the firing rate of output units, r_i, follows external inputs relayed by afferents to the network. Without this suppression, afferent inputs are represented less accurately in the pattern to be stored in the network, which ends up largely reflecting the previously stored patterns. Therefore, in this simulation, M = 0 during storage and M = 1 during testing, corresponding to suppression of collaterals during “training,” and to allowing their full influence during testing.

FF connections, playing the role of afferent signals to IT, are set once, as mentioned above, and kept fixed during the simulation. Recurrent connections, which are the storage site for the memory patterns, have their baseline weight modified according to a model “Hebbian” rule. The specific covariance “Hebbian” learning rule we consider prescribes that the synaptic weight between units i and j, w_ij, be given as

(5)

where represents the activity of unit i in memory pattern μ, and c_ij is a binary variable equal to 1 if there is a connection running from neuron j to neuron i, and 0 otherwise. $\overline{\mathrm{\eta }}$ is the mean activity of unit j over all memory patterns.

Input Patterns

Each η^μ is the projection to the second layer of the input signal from the first layer, ${\mathrm{\eta }}_{\text{in}}^{\mathrm{\mu }}$, which is drawn independently from a fixed distribution, with the constraints η > 0, <η> = <η²> = a, where < > stands for the average over the distribution. p uncorrelated patterns were generated using a common truncated logarithmic distribution (Fig. 6a, middle panel) obtained by setting for each input unit.

(6)

If x < a, and η = 0 if x > a, where x is a random value with a uniform distribution between 0 and 1.

The parameters used in the simulations are listed in Table 1.

Table 1.

Default values used in all simulations

Size and sparseness	Others
Input array	Nin = 2500	Adaptation time constants	β1 = 0.1
Output array	Nout = 2500	[(time step)−1]	β2 = 0.2
FF connections	Cff = 750		γ = 2 × 10−4
Recurrent connections	Crc = 500	Initial neuronal gain	g = 1
Output sparseness	aout = 0.2	Initial neuronal threshold	Th = 0.05
Input sparseness	aout = 0.5

When a_out = 0.2, theoretical calculations indicate that the storage capacity of the model is around 0.2–0.4 times the number C_rc of recurrent connections per neuron (in our simulations C_rc = 500), Thus, although finite size effects make the notion of storage capacity less well defined for a network that is small, it is expected to be able to retrieve on the order of 100–200 patterns. To assess the storage capacity of our model, for each value of p we gave the trained network a full cue, corresponding to one of the stored patterns, and after 80 synchronous updates we measured the final overlap of the network state with the presented pattern. If the final overlap is larger than 0.8, retrieval was deemed successful. Repeating this process for 4 different seeds of the random number generator and p different patterns, the maximum value of p at which success still reaches 50% is around 250 patterns, higher than but consistent with the theoretical expectation. We then ran simulations in which we stored 20 or 160 patterns, which correspond to conditions where the network is far below its storage capacity and near its storage capacity.

Different units in the first layer receive inputs of variable duration, drawn at random, for each unit from a logarithmic distribution. Inputs were not removed sharply, but gradually, with a linear decay to zero. The distribution of input offset latency is shown in Figure 6a (middle panel). The output of units in this layer is a step-like function, active at a certain level for a specific duration (Fig. 6a, middle), with a gradual transition to zero. The average activity across all input units, for one pattern, is shown in Figure 6a (right panel).

Once either p = 20 or 160 original patterns had been stored, the network was tested with intermediate morphs. Original patterns were then combined into pairs, and 9 “morphed” intermediate versions of each pair of patterns were set by gradually changing their correlation level with the 2 original patterns. This was achieved simply by taking one of the original patterns and setting the firing rate of a randomly chosen 10%, 20%, 90% of the input units to their firing rate in the second original pattern. To simulate experimental procedures, for each output unit we assign a pair of patterns to which the unit has a different response during stimulus onset (a pair of “effective” and “ineffective” stimuli). In some simulations, intermediate morphs were produced not between 2 stored patterns, but between one pattern that was stored and one other pattern which was not stored in the network. It should be noted that only the original patterns (either 20 or 160) were stored in the network and not the intermediate morphs. The reason for this choice is that in the experiment there seems to be no reason for the monkey to deposit strong memory traces of the intermediate morphs, which are ambiguous and nonmeaningful and, moreover, the monkey does not have to recognize each individual morph image separately.

To test the network, we measured the time evolution of all output units, over 80 time steps, after presenting a morphed pattern (or the original images from which the patterns were morphed) in the input layer.

Implementation of Firing Rate Decay

Spike-frequency adaptation, a gradual reduction of the firing frequency in response to a constant input, is a prominent feature of several types of neurons that generate action potentials, and it is observed in pyramidal cells in cortical slice preparations (Mason and Larkman 1990; Connors et al. 1982; Foehring et al. 1991; Lorenzon and Foehring 1992; Barkai and Hasselmo 1994), or in vivo intracellular recordings (Ahmed et al. 1998). The biophysical mechanisms of spike-frequency adaptation have been extensively studied in vertebrate and invertebrate systems and often involve calcium-dependent potassium conductances (Meech 1978; Sah 1996). However, little is known about its computational role in processing behaviorally relevant natural stimuli, beyond filtering out slow changes in stimulus intensity. Recent studies have sought to attach computational significance to this ubiquitous phenomenon in cortical circuits. Spike-frequency adaptation might be a determining factor in setting the oscillation frequency of cortical circuits (Crook et al. 1998; van Vreeswijk and Hansel 2001; Fuhrmann et al. 2002) for the temporal decorrelation of the inputs (Goldman et al. 2002; Wang et al. 2003), and in balancing coding and prediction (Treves 2004).

We implemented adaptation by subtracting from the input activation of each unit a term proportional to the recent activation of the unit. The term is a difference of 2 exponentials with different time constants:

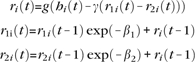where r_i(t) is the activity of unit i at time t, h_i(t) is the summed input to the unit at time t, and β₁ = 0.1 β₂ = 0.2, and γ = 2 × 10^-4 are time constants. The input to each unit is then affected by its firing rate at all previous time steps. The exponential decay makes its activity at the last time step more influential than the others. The difference of the 2 exponentials means that the effect of adaptation appears only after the second iteration. Note that this formulation reduces the effectiveness of adaptation when t is small.

Results

We recorded the responses of 154 IT cells in 2 macaque monkeys while the monkeys performed a 2AFC-DMS task. In a previous report, we compared the discrimination capacity of single neurons calculated in a fixed response epoch for morphed photographic images to behavior with those same images during the sessions in which the neurons were recorded (Liu and Jagadeesh 2008). In this report, we examined the changing dynamics of neural responses during a fixed presentation of a static images morphed between 2 exemplars. The subset of cells in which one of the 2 choice images produced a response at least 10% greater than the other (n = 128) are presented in this analysis. Data are combined for the 2 monkeys, and no detectable differences between the 2 monkeys were found.

The behavior in the task was linear for intermediate morphs but essentially categorical for the morphs most similar to the choice images. Figure 1b shows the proportion of trials in which the monkey chose the effective image (Eff) by making a saccade to it, across all sessions and all stimuli. The trend is linear in the central region, morph levels 2 to 8, but levels off at the extremes and their nearest neighbors, morph levels Ineff and 1 and morph levels 9 and Eff. The central region can in fact be fitted by a 1-parameter sigmoid (df = 6, χ2 = 0.43) but is even better fit by a straight line (df = 6, χ2 = 0.33). Is a similar pattern evident in the responses of individual IT units?

Most cells were also modulated by the degree of morph. Immediately after stimulus onset (100–200 ms after stimulus onset) the response of 93/128 cells decreased as the response was morphed away form the Eff image, and the response of 100/128 cells increased as the response was morphed away from the Ineff image, as tested by the slope of the linear regression of the responses for each cell. The pattern of modulation differed among individual neurons, however. Six example cells are shown in Figure 2a,b. By definition, the average response to the Eff stimulus (solid line) was greater than the average response to the Ineff stimulus (dashed line) (Fig. 2a). Most cells’ responses increased systematically between the Eff and Ineff image with the mean response to the mid-morph stimulus lying somewhere between the 2 extremes (Fig. 2b). Eff images were defined on the basis of the response during the stimulus epoch (75–375 ms after stimulus onset). Immediately after stimulus onset (100–200 ms), 124/128 cells had bigger responses to the Eff image (level 10) than the Ineff image (level 0), replicating the response difference based on the longer epoch in which the Eff and Ineff image were defined. In the epoch immediately after the stimulus onset, 99/128 cells had smaller responses to the middle morph image (level 5) than to the Eff image (level 10); 106/124 cells had bigger responses to the middle morph image (level 5) than to the Ineff image (level 0) The responses of a smaller number (n = 35) of individual cells to the intermediate morphs, on the other hand, did not vary linearly along the morphing dimensions and did not increase monotonically with morph level (Fig. 2a,b, bottom right). The range of firing rates across the morphs and the time course of the responses was also variable, from 10–20 Hz for some cells, and up to 120 Hz for others.

Classification ability depended linearly on morph level for intermediate morph levels but not morph levels close to either familiar images, which were classified nearly perfectly (Fig. 1b). A hallmark of this behavior might be reflected in the neural responses, if neural responses were also linearly dependent on morph level, except for those morph exemplars that were similar to the Eff or Ineff image. Some neurons did appear to follow this pattern, whereas others did not. One cell shown in Figure 2b produced responses that roughly follow the pattern seen in the behavior (Fig. 2b, top left), whereas others produced linear responses for all morph levels (Fig. 2b, top right, bottom left and middle).

In order to further examine the relationship between these neural responses and the morph level of the stimulus, we calculated population averages across the neurons (n = 128). Because the behavioral response is symmetric around morph level 5 (Fig. 1b), we initially took such symmetry for granted and compared average responses to morphed images “equidistant” to morph level 5 by calculating the difference between them (Kreiman et al. 2000; Allred and Jagadeesh 2007; Liu and Jagadeesh 2008). However, averaged across the population, firing rate differences did not replicate the plateaus shown in the behavior for morph levels close to the Eff or Ineff images (Fig. 3a). Instead, average firing rate differences decreased smoothly, almost linearly, with decreasing distance along the morph continuum, throughout the response to the sample stimulus (morph level main factor, 50–550 ms (P < 0.02), nonparametric 2-way ANOVA (Friedman test)).

Symmetry in responses to Eff and Ineff morphs is not preordained, however: subtracting the response to Ineff images from the response to Eff images might obscure the time course of the separate responses to Eff and to Ineff images. If either the Eff or Ineff responses were strongly dependent on morph level, the difference between the firing rates might mask the lack of dependence on morph level of the other images. Image Eff, moreover, had been selected from the pool of image pairs for being visibly effective for that particular cell, across the group of images used, all of which were generically effective for some IT cells; although the “ineffective” image, Ineff, produced a smaller response, but was not necessarily ineffective in driving the cell. Frequently, cells responded to “ineffective” images producing responses substantially higher than the baseline response. Therefore, the apparent linear trend in Figure 3a could result from a strong quasi-linear dependence of either the Eff or Ineff images on morph level, masking the other half of the dependence.

The asymmetry between responses to Eff morphs and Ineff morphs is visible when responses to each individual morph level are plotted separately (Fig. 3c). The Ineff morph responses were linearly dependent on the morph level throughout and after the sample presentation nearly until the responses return to baseline. The Eff morph responses, in contrast, are linearly scaled as a function of morph level only for a brief time at the first peak of the response, centered around 120-ms poststimulus onset. By 200 ms post-stimulus (average response in the 150- to 250-ms epoch) the dependence of Eff morph responses was decreasing, and in the linear regression as a function of morph level, the slope decreases more rapidly than the one describing the dependence of Ineff morph responses on morph level. There is a second, lower response peak around 270 ms, where levels Eff, 9 and 8 are together but significantly above levels 7 and 6, and at 320 ms, at the end of the sample presentation time, all morph levels 6 to 10 are within the 95% confidence interval of each other. The response to morph level 5, which was not consistently classified as either stimulus choice and was randomly rewarded is different from the response to both the Ineff and Eff variants until 700-ms poststimulus, late in the delay period. There are 3 behaviorally defined groups in the morph continuum, the Ineff group, which must be classified as the Ineff choice, the Eff group, which must be classified as the Eff choice, and the image corresponding to morph level 5, which belongs to neither Eff nor Ineff group, and can be classified as either Eff or Ineff, with random reward for each possible choice. These 3 groups remain distinct until at least 700 ms after stimulus onset; the Eff group of stimuli, the morph level 5 (middle morph stimulus), and the Ineff group of stimuli, even as the responses to the individual images in the Eff group become indistinguishable.

The flattening of the linear relationship with respect to stimulus morph level can be seen in Figure 3d, where the average firing rates to the 11 morph variants are shown, over 4, 100-ms time periods. The data for Eff and Ineff morphs are fit with separate lines. The slope of the linear fit for the Eff morphs gradually drops off compared with the slope for Ineff images. For the first 2 time windows (100–200 ms and 200–300 ms) the slopes are not significantly different from each other (P = 0.85 and P = 0.20, for the 2 windows respectively), but are both significantly different from zero (Eff: t-test, P = 0.02 and P = 0.01, Ineff 0.02 and 0.01, for the 2 time windows, respectively). During the later epoch (400–500 ms) the slope of the linear fit for the Eff morphs was not significantly different from zero (ttest, P = 0.34 400–500 ms) and is significantly different from the slopes for Ineff morphs (P = 0.01). Thus across the entire population of neural data, unlike the behavioral data, the response “plateau” appears to extend over the whole Eff range, and does not extend over the Ineff range. Note, however, that the notion of a response plateau is an oversimplification, which does not really describe the response of individual cells (see below).

Morph level is a main factor affecting the Eff responses from 70–220 ms after stimulus onset (unbalanced one-way ANOVA shows that for Eff stimuli, the P < 0.05), whereas the Ineff morphs responses remain significantly different from each other for the entire sample presentation and into the delay period (70- to 590-ms poststimulus onset, P < 0.05). Responses to the Eff images, as a group, remain significantly above those to Ineff images (2-way ANOVA, P < 0.05) until 900 ms, when responses to both Eff and Ineff images are back at spontaneous level. The similarity of the firing rates for the Eff image and its 4 nearing morphs could be a hallmark of the morphs having been attracted to the basin of attraction of image Eff. These data show that subtracting the response to Eff images, in Figure 3a, had obscured the time course of the convergence among responses to Eff images. This can be interpreted, presumably, as an indication that there is no convergence of neural responses to Ineff images, at least on average across the cells in our dataset, whereas there is, on average, a convergence of neural responses to Eff images.

In going from single neurons to the population average, it is important to take into account the potential differences among responses of individual cells (Fig. 2). Is the population average a faithful representation of most cells or does it reflect the behavior of a few highly active cells? To address this concern, we applied the same analysis used for the population average in Figure 3d to each individual cell. We fit with a line the firing rate of individual neural response as a function of morph level for 4 different response epochs of 100–200 ms, 200–300 ms, 300–400 ms, and 400–500 ms. In each epoch the linear regression was applied separately for Eff and Ineff images, giving a fit slope for the 2 subgroups of stimuli. Slope is expressed in units of spikes/second/morph level and reports how well the response to the Eff and Ineff images was modulated as a function of morph level. Figure 4 shows scatter plots of the slopes in the late time window (400–500 ms) with respect to the early one (100–200 ms), for Eff (Fig. 4a) and Ineff (Fig. 4b) morphs, respectively, for each individual cell in the population. Across the population of neurons, the slope is significantly higher in the early epoch than in the late epoch (sign test, P < 0.0001) for the Eff images (Fig. 4a). Most of the points lie below the diagonal line indicating equal slopes. This effect is not found for Ineff morphs, for which individual neurons are uniformly distributed around the diagonal (Fig. 4b, sign test, P = 0.1329). Furthermore, slopes for both the Eff and Ineff morphs are significantly different from zero in the early time window (sign test, P < 0.0001, population significance), whereas in the late time window, only slopes for the Ineff morphs are significantly greater than 0 (sign test, P < 0.0001). Figure 4c shows time course of averaged slope (over all cells) for Eff (red curve) and Ineff (blue curve) morph stimuli. In the time bin 380–480 ms after stimulus onset, Eff responses no longer depend on the morph level of the individual stimulus (t-test, difference from 0, P > 0.05). At those same time periods, Ineff responses still depend significantly on the morph level (t-test, difference from 0, P < 0.0001) and Eff and Ineff response slopes are different from each other (paired t-test, P < 0.01). Ineff slopes remain significantly different from zero until the 700- to 800-ms time bin, when they are no longer significantly different from 0 (t-test, difference from 0, P > 0.05). Thus, the pattern of response dynamics seen in the population average in Figure 3c,d is present in the individual cells (Fig. 4a-c). Both the individual cells’ responses and the average population show that response to the Eff morphs and the Ineff morphs depends on morph level in the period immediately following the onset of the stimulus. Over time, however, the responses evolve so that neural responses to different Eff images all converge to similar values. The responses to Ineff variants remain separated, however, and the response remains dependent on the morph level.

The response to the Eff and Ineff images (morph levels 0 and 10) were used to classify the 2 images, raising the possibility that these images might skew the regression analysis. Therefore, we performed the linear regression shown in Figure 4 for each cell, after first eliminating the Eff and Ineff images from the regression (i.e., morph levels 0 and 10). The analysis on this limited data set confirms the analysis shown in Figure 4. In the time bin 430–530 ms after stimulus onset, the responses to Eff morphs no longer depend on the morph level of the individual stimulus (t-test, difference from 0, P > 0.05). At those same time periods, the responses to Ineff morphs still depend significantly on the morph level (t-test, difference from 0, P < 0.0001). The Ineff slopes remain significantly different from zero until the 660- to 770-ms time bin, when they are no longer significantly different from 0 (t-test, difference from 0, P > 0.05).

The simple regressions used in this analysis do not completely represent the patterns seen in individual cells. Among several alternative analyses, one may fit regression lines only to parts of the entire morph range. The behavioral data raises the expectation that convergence might be expected only for morph levels 8–10 (the original, and the 2 variants close to it), suggesting the possibility that only some of the stimuli for which a particular behavioral classification was required consistently converge to the same node. Stimuli closer to the response boundary may not always converge to the same node (different stimuli may behave differently, and the same stimuli may behavior differently in different trials or different sessions). To address this question, linear regression can be performed with data for morphs 0–2 and 8–10, corresponding to the “plateaus” seen in the behavioral data, corresponding to stimuli for which the behavior was roughly similarly (each was classified consistently, respectively, as the Ineff or Eff image). This regression analysis changes the time course of dependence on morph level for the Eff and Ineff images. Eff responses converge faster, resulting in zero slopes sooner after the onset of the image. In addition, the Eff slopes actually turn negative, with greater morph levels resulting in a slightly smaller response at response onsets. Ineff slopes remain significantly different from zero until late in the delay period, with the difference between Eff and Ineff slopes increasing.

Part of the variability among cells may be due to the diversity of image pairs used in the experiment, but the significant trends shown in Figure 4 are replicated for individual images, with the similarity to the population increasing with the number of recorded units for each image.

Although the monkeys were trained before the beginning of the recording session, improvements can be seen in behavioral performance over the course of the multiple recording sessions in the study. Behavioral performance was significantly better during the second half of the recording sessions compared with the first indicating that the monkeys’ performance continued to improve over the course of the sessions (Supplementary Fig. 2A, paired ttest, P < 0.01 for morph levels 1–4 and 6–9). Performance for the 2 original images was stable over the course of the recording sessions (P = 0.52). An improvement in behavioral performance might suggest that neural representations were also changing over the course of the study. To examine whether the dynamics of the response as shown in Figure 4 changed over the course of the study, we separately examined the neural response dependence on morph level (shown for the entire data set in Fig. 4c) for the first and second half of the sessions (Supplementary Fig. 2b,c). The results suggest that the dynamics of the response convergence (the pattern of results shown in Fig. 4) changed over the course of the recording sessions. The difference in slope for Eff stimuli at stimulus onset compared with stimulus offset was significant only during the 2nd half of the sessions (n = 62 first half, n = 66 second half, Eff slope at 100–200 ms compared with slope at 400–500 ms, P = 0.0160, early sessions, P = 0.0959). Furthermore, the difference between slopes for Eff and Ineff images was significantly different only in the second half of the sessions (slope at 400–500 ms, compare Eff vs. Ineff slopes, P = 0.0105, early sessions P = 0.2374). The trends were compatible with storage of the patterns (as described in the network model) improving over sessions.

Neural responses evolve, or change dynamically over the course of the presentation of the constant, unchanging stimulus to show convergence to different response levels. Does the dynamics of this response evolution depend on the morph level? To address this question, we performed an analysis of variance to examine how separated responses to different morphed images remained as a function of time (Supplementary Fig. 3). The times of convergence to the Eff (or Ineff) stimulus for each morph variant are shown in Figure 5a. This graph shows the time at which the responses to the morph variants were no longer significantly different form the Eff (or Ineff) stimulus (P value of ANOVA < 0.01 Supplementary Fig. 3a,b). The response to the Ineff variants remains different from the Ineff until long after the stimulus presentation, until approximately 600 ms after stimulus onset. Eff variants, on the other hand, take progressively shorter times to converge to the Eff response as the morph level increases (indicating higher similarity to the Eff stimulus).

Figure 5a illustrates the timing of convergence of the response to each morph toward that to the Eff or Ineff image. We can also assess convergence between pairs of other morph levels. The analysis comparing how quickly different pairs of morph levels converge is shown in Figure 5b, using the same analysis of variance used in Figure 5a, but comparing other pairs of morphed stimuli (Supplementary Fig. 3c). We compared the response to morphs 20% apart, by running an unbalanced one-way ANOVA analysis for responses to morphs 2 versus image Ineff, 4 versus 2, 6 versus 4, 8 versus 6 and Eff versus 8. The data in Figure 5b shows that the Ineff morphs remained separated for durations longer than the presentation of the sample stimulus (greater than 500 ms) (Fig. 5b, left 2 points). The pair of morphed stimuli that lie across the behaviorally defined classification border (morphs 4 and 6, remain separated for over 700 ms). The Eff morphs, on the other hand, converged to one another at durations close to sample duration, or even shorter (Fig. 5b, right 2 points).

Simulation Results

What is the neural mechanism underlying this convergence? Can the observed convergence express the outcome of visual signal processing within IT cortex, or must it be driven by afferent inputs that have already converged before reaching IT, or top-down, by signals from more advanced processing stages (Bar et al. 2006)? If the convergence can result from local processing within IT, what is the contribution of network interactions, that is, of dynamical attractor states determined by the structure of recurrent connections in IT? Or, could the convergence reflect, in part, simple firing rate decay of individual IT neurons, expressed as a gradual decay, rather than network dynamics? Firing rate adaptation effects are conceptually quite different from those arising out of genuine network interactions, but may in practice be difficult to distinguish. If firing rate adaptation progressively suppresses the responses to Eff and to its closest morphs 9, 8, … effectively squashing them onto each other, the functional consequences may resemble the convergence posited to result, in network models that do not include firing rate adaptation, from synaptically mediated attractor dynamics. We addressed these possibilities by simulating a simple local network model of cortical activity, with and without firing rate decay, to assess the relative contribution of attractor dynamics and of adaptation. Note that this simulation does not rule out all forms of adaptation, and a sufficiently complicated form might replicate response dynamics in this individual data set, even if the simple form does not.

Our model simulates a single hypothetical local network within the IT cortex. The network includes an input station, simulating afferent inputs from earlier visual areas, which projects its activity to an output layer, simulating an IT patch, through sparse FF connections. The units in the output layer receive both FF and recurrent connections at random, with unstructured baseline weights (see Fig. 7a and Methods).

Figure 7.

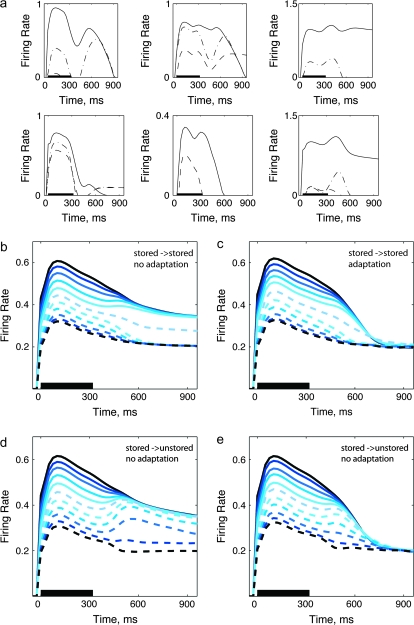
(a) Sample of single units from the model; Eff: solid, Ineff: dashed, mid-morph: dashed-dots (b) Simulation: 160 stored patterns, tested with morphs between stored patterns, no adaptation. (c) Simulation: 160 stored patterns, tested with morphs between stored patterns, adaptation. (d) Simulation: 160 stored patterns, tested with morphs between one stored and one unstored pattern, no adaptation. (e) Simulation: 160 stored patterns, tested with morphs between one stored and one unstored pattern, adaptation

Simulation 1

In simulation 1 we assessed the effect of firing frequency adaptation on responses, modeled as a decay term, a linear decay as a function of the recent activity of the cell. Can convergence result from such firing rate adaptation over time?

The simulated network is a simple approximation of inputs and recurrent connections to a patch of cortex. It consists of 2500 units that receive FF projections from an input layer containing another 2500 units (Fig. 6a). Each unit in the (output) patch receives approximately 750 FF connections from the input layer, and 500 recurrent connections from other units in the output patch (Fig. 6a). The connections are assigned at random and, because there is no storage of activity patterns in this first version of simulation, weights are not modified to reflect memory storage. The weights are instead set to a random value and then normalized to generate an approximately exponential distribution of initial weights onto each unit (see Methods, and Fig. 6b). Once a pattern is imposed on the input layer, the activity circulates in the network for 80 simulation time steps, corresponding to ca 12.5 ms (Fig. 6c) (Treves 2004). The details of the network, including signals receiving by each unit and their activity functions, together with the default values for parameters used in the model are reported in Methods.

The input patterns simulate the hypothetical input produced by 20 unrelated visual images, and morph variants of them. Inputs consisted of 20 uncorrelated input patterns combined into pairs. Nine “morphed” intermediate versions of each pair of patterns were set by gradually changing the correlation of one original pattern with the other pattern. To simulate experimental procedures, for each output unit we assign a pair of patterns to which the unit has a different response during stimulus onset (a pair of “Eff” and “Ineff” stimuli). Then, the response of individual output units to these selected patterns and to their morphs was monitored. The duration of the inputs was variable, to simulate the potentially variable duration of different input streams. Input offset time for each unit is driven from a sharp logarithmic distribution, peaked at time ca. 300 ms (Fig. 6c).

In the first simulation, we examined the effect of firing rate decay. Firing rate decay was modeled (see Methods) by subtracting from the sum of FF inputs and recurrent connections to each output unit a fraction of its own recent output activity. The trace of its “recent” activity is calculated with a convolution kernel, expressed as a difference of 2 exponentials, with inverse time constants β1 = 2β2 = 0.2 (time steps)^-1. This form of firing rate decay applies to all output units from the second time step, for all the succeeding 100 time steps.

The average network dynamics shows that linear decay of responses over time produced by adaptation does not produce a response convergence similar to that observed (Fig. 6c). In the early phase of the simulated neural response, during which the network is mostly driven by afferent inputs, average network responses to all morphing levels are well separated. Then, as the afferents are gradually removed, the population response to all the morph levels decrease, but there is no tendency for the Eff responses to group or squeeze together (Fig. 3b).

Convergence might require “memories” to be stored within the network. Unlike the simple local network above, with no stored patterns, in autoassociative networks memories can be stored as stable network activity states, called attractors (Hopfield 1982; Treves and Rolls 1992; Amit 1994; Brunel 1996). A stored pattern, may be then be retrieved when a noisy or occluded version of it (a partial cue) is provided as input. This ability is due to the formation of dynamical attractors that capture network activity, if an input is sufficiently close to one of the patterns stored. The formation of the attractor landscape is achieved by creating overlapping patterns of synaptic modifications adhering to the Hebbian paradigm (Hebb 1949) such that each synapse is involved in the storage of multiple related memories. Inevitably, this common synaptic representation implies interactions between memories stored in the same network. The putative presence of long-term memories in IT and the observation of increasing stimulus selectivity, through learning, in individual neurons (Sakai and Miyashita 1991) suggest that attractor dynamics may be plausibly expressed in IT cortex, where visual object memories are likely stored, and may drive the extraction of visual category information. Therefore, in our next simulation, we considered an autoassociative network, with memory patterns stored in RC connections through a realistic synaptic modification mechanism.

Simulation 2

Does the addition of stored patterns produce convergence in the network? The properties of the network were identical to those used in simulation 2; the only addition is that in simulation 2 the recurrent weights are modified to store memory patterns before testing the response of the network to patterns and their morphs. First we produced 200 uncorrelated patterns, using a common truncated logarithmic distribution, from which the firing rate of each unit is driven independently (see methods). Then we stored in the network P = 160 of these patterns, by modifying the RC weights of the output layer with a “Hebbian” learning rule (see Methods). Either 2 stored patterns or a stored pattern and a novel one, from other 40 unused patterns, are then combined into pairs, and 9 “morphed” intermediate versions of each pair of patterns are presented as the input. As indicated in the Methods, this results in a network that is below its storage capacity

In the first simulation with stored representations, we analyzed network activity in response to stimuli obtained by morphing between 20 sets of 2 stored patterns (40 out of 160 stored patterns). Single units show a variety of behaviors in response to morphs (Fig. 7a), resembling the diversity observed with real cells. Averaged population activity qualitatively mirrors the convergence seen in the population average of IT neural responses, for Eff morphs (Fig. 3c). Figure 7b shows the mean responses in the simulation, after averaging over all units. In the first phase, whereas sufficiently many units in the network still receive afferent inputs, all the morphs are well separated. Rather abruptly, as the average ratio of RC to FF activation increases beyond a critical level, network activity was determined by the attractors embedded in the RCs. The responses to the Eff morphs are all attracted to the full memory pattern Eff. However, in this simulation, unlike in the data, the responses to the Ineff morphs are also attracted to a basin of attraction for the Ineff morphs, a feature not seen in the data (Fig. 3c). Adding adaptation to this simulation (as described for the first simulation), does not produce the lack of convergence for Ineff morphs seen in the neural data (Fig. 7c).

Testing with morphs between 2 stored patterns corresponds to the assumption that both images used in the real experiment had memory representations in the local network that includes the particular unit being recorded from. The experimental procedure for picking image pairs for each cell, on the other hand, might introduce a bias, where the Eff image is more likely to be represented by a “neural assembly” to which the unit belongs, than the Ineff image, which might have its own representation elsewhere over IT (Haxby et al. 2001; Kiani et al. 2007). To model this situation, we tested network activity in response to morphs obtained between an (Eff) stored pattern and one that had not been stored. Figure 7d shows that the convergence of the mean responses, again averaged over all units, is now limited to the Eff patterns. We found that the morph level, above which responses converge, is strongly dependent on the storage load. With low load (Supplementary Fig. 4, 20 stored patterns), all morphs converge to the stored pattern Eff, whereas when many patterns are stored (Fig. 7d, 160 stored patterns), the basin of attraction effectively shrinks, and only the morphs closer to the Eff pattern showed convergence.

Simulation 3

We then combined stored attractors with firing rate decay over time. In this version of simulation, we used the same network as in Simulation 2, with 160 stored patterns, and applied firing rate adaptation, modeled as in simulation 1. We again monitored the firing activity of output units in response to intermediate morphs produced between one stored pattern and one novel pattern. In this way we could assess the effect of response decay on the simulation in Figure 7d (or Fig. 7b). Introducing this form of firing rate adaptation did not change the qualitative behavior of the network (Fig. 7e or Fig. 7c): in the first phase of the response, when the network is mostly driven by afferent inputs, different morphs are linearly separated; in the second, “memory” phase, when afferent inputs have been largely removed, the network activity converges to either one or 2 attractor states, depending on whether both patterns are stored (Fig. 7c) or only one is stored (Fig. 7e). Adaptation however introduces a third phase, in that after some time it brings the network out of the current attractor state and makes single units fire in a somewhat erratic manner to the different morphs and brings all responses close together. This disorderly behavior imitates the population average of neural responses (Fig. 3c). The simulation also shows a crossover between the responses to Eff and to morphs 9, 8 and those to morphs 7, 6, which is an effect of adaptation (Fig. 7e,c). This crossover is also visible in the experimental data, in that around 450-ms poststimulus onset the average firing rate of the response to stimulus Eff drops below the responses to the rest of the Eff images (Fig. 3c).

The simulations can thus replicate the linear dependence of the response on morph level at stimulus onset (Fig. 3c,d) for both Eff and Ineff images, and the selective convergence of the Eff responses, whereas the Ineff morphs remain separated long after the stimulus has been turned off. The simulation best matches the data if we assume that 1) many patterns are stored in the network (close to storage capacity), that 2) the sampled cells belong to the representation of only one of the 2 images that are morphed into one another, and if we add some degree of response adaptation. Even with these characteristics, the simulation cannot replicate another feature of the data: the gradual convergence over time among Eff responses (Fig. 3c). In addition, compared with the real data the onset transient is less peaked in the simulation, and the delay activity returned to a common value for both sets of morph sooner (Fig. 7e) than in the real data (Fig. 3c).

Discussion

We recorded from individual neurons in IT cortex while monkeys performed a classification task on morphed visual images. We report here a population of IT neurons whose responses evolve gradually over the course of a trial, first representing parametrically the morphed image and later converging to represent one of the 2 categories. Below we discuss the results in the context of the attractor network simulations, which highlight key features of the IT dynamics and provide insights into local network properties that might underlie them. We then discuss related studies and reconsider the role of IT in visual classification.

Attractor Network Simulation

The convergence of IT activity from a stimulus-based representation to a category-based representation was asymmetric, in that only responses to the morphed images that resemble the effective stimulus for an individual cell converge, whereas responses to morphed images that resemble the ineffective stimulus remain segregated by morph level. An asymmetric convergence may result from multiple mechanisms, of course. We have tried to assess 2 possible underlying mechanisms, a gradual decay of the response over time and attractor dynamics in the local recurrent networks. With our first simulation, we could rule out the possibility that the convergence was the result of simple linear decay of neural responses. A linear decay of responses had an equivalent effect at each individual morph level, and did not produce a change from the linear dependence visible at stimulus onset (simulation 1, Fig. 6), whereas the operation of a simple attractor network produced qualitatively similar convergence to that observed in the neural data, allowing a more detailed interpretation of the observations.

To obtain asymmetric convergence, we had to consider morphs between a “learned” input pattern, used in training the network, and a novel pattern (simulation 2, Fig. 7d). Convergence to a category representation occurred only for the learned pattern and not for the novel pattern. This simulation suggests that the convergence asymmetry depends critically on the memory representation of a pattern in the network. Neurons that contribute to the memory representation of a pattern show convergence to the associated category, whereas neurons that do not contribute to the memory representation do not show such convergence. Our selection of neurons for inclusion in the population likely included a bias in the contribution of each neuron to the memory representation of each of the 2 exemplar images used in a given experiments. All of the images we used were likely to be represented in the activity of subpopulations of neurons in IT cortex. However, we chose pairs of images such that one (the Eff image) elicited stronger responses than the other (the Ineff image) for a given neuron. This selection implies that although the neuron might play a primary role in representing the Eff image, the Ineff image might often be represented elsewhere. Accordingly, the attractor dynamics would not be expected to manifest in the response to the Ineff images and its variants because they are not represented in the local network that includes the recorded cell.

Unlike the neural data, our network stimulations show an abrupt convergence as soon as a threshold number of output units stop receiving afferent inputs. In the model, afferent inputs keep the output responses to different morphs separate, and afferent inputs must subside for the responses to converge. The convergence was abrupt even though a range of durations for afferent input was a feature of the model. This second feature of the model contrasts with the gradual convergence seen in the real data. A plausible explanation is that gradual convergence results from a distribution of local ensembles, each of which engages in its own response dynamics.

In the model most afferent inputs must subside in order for convergence to occur. This contrast with the real data, in which convergence begins during the response to the sample image, suggests that afferent inputs to those putative local networks also follow a variety of time courses, often decaying after a transient period of elevated strength, well before visual stimulus offset.

When a pair including a nonstored pattern is used to test the model, responses to morphs 2,3 also converge toward the response to the effective pattern, indicating a very wide “basin of attraction” for the latter. This is in contrast with the real data, which suggests narrower basins of attraction. In the model, the width of the attractor basins can be modulated by various factors, including the storage load. It would be interesting to design experiments that can test whether such width can be also modulated in real neuronal circuits.

The initial simulation dismissed the alternative explanation of the convergence in terms of linear firing rate decay. However, although linear decay of the response cannot produce the observed asymmetric convergence, it might destroy attractor effects once applied to single cells. To test this possibility, adaptation was added to the attractor simulation (Fig. 7c,e). The addition of adaptation did not change the qualitative behavior of the network, and also produced a more realistic simulation of the real data; adaptation pulls units out of a fixed level of delay activity, producing greater variability in their responses at the end of the stimulus presentation and during the delay period (compare Fig. 7e and Fig. 3c).

Not all forms of adaptation were excluded, of course, by the simulation of linear decay as a potential mechanism for the convergence seen in Figure 3c. Mechanisms that produce second-order firing rate adaptation, leading to nonlinear decay of the response, might replicate the convergence, without requiring attractor dynamics. For example, adaptation with a time constant of decay that depends on the size of the onset transient, along with modulation of this relationship (between transient and time constant) that further depends on the transient response level might replicate some of the dynamics seen in this individual data set. We cannot discard this possibility. However, we note that attractor dynamics are a plausible mechanism to hypothesize in IT cortex (Sakai and Miyashita 1991), and thus a plausible mechanism to produce the convergence seen in the neural data. In addition, adaptation dynamics may be determined by characteristics other than the firing rate of the adapting neuron (Priebe and Lisberger 2002; Sawamura et al. 2005).

The biological plausibility of implementing attractors in cortical networks is based on 2 reasonable assumptions: the presence of RC connection and synaptic plasticity (Braitenburg and Schuz 1991). Typically, the exact details of the plasticity process, that is, the modification of connection weights that leads to the formation of attractors, are not crucial in mathematical models of the operation (rather than formation) of autoassociative networks, but it is a widely held hypothesis that in cortical or hippocampal network's attractors could be formed by tuning the synaptic efficacy of its RCs with synaptic plasticity mechanisms akin to LTP and LTD (McNaughton and Morris 1987). Associative long-term memories in IT, hypothesized to acquire stimulus selectivity through learning, by individual neurons (Sakai and Miyashita 1991) suggest that attractor dynamics may be plausibly expressed in IT cortex, where visual memories are stored, and drive the extraction of visual category information.

In our model, the intermediate morph stimuli do not contribute to synaptic modifications during learning. In other words, there is no attractor individually assigned to each morph level. In this sense our model is different from those discussing “attractor collapse”, in which each intermediate morph patterns contribute equally to synaptic modification (Blumenfeld et al. 2006). Stimuli and task demands, in other experimental studies, may also differ in many ways from our experimental setting. In one particular study (Blumenfeld et al.), a fundamental difference is that they used faces as visual stimuli, which allows them to generate a whole morphing stream equally meaningful for the subjects—each individual morph image has a specific identity and is perceptually recognizable as a face, and the subject should report whether each morph face is a Friend or non-Friend. In our study, instead, the intermediate morph images are rather ambiguous and nonmeaningful, and the monkey is not asked to recognize each morph independently. It seems more justified to assume a synaptic plasticity effect for perceptually meaningful faces than for nonmeaningful images, which in our experiment which must be classified in 2 groups by the monkey, based on their similarity to either Eff or Ineff. Even if we take synaptic plasticity into account for intermediate morphs—and one could easily implement it in the current model, having the morphs stored in the network by changing the weights with a β factor an order of magnitude weaker than the original patterns—we still believe that the storage of the 2 end point images (Eff and Ineff) would dominate the ensuing attractor dynamics.

The simulations show that a very simple model of an IT patch, with memory attractors stored on recurrent connections by associative plasticity, responds with a convergent dynamics similar to that seen in the data. Furthermore, the simulations suggest that such local networks may be loaded with memories close to their storage capacity, which would be consistent with the expectation of an efficient utilization of the available memory resources—the synaptic weights (Braitenburg and Schuz 1991).

Although the network simulation suggests that attractor dynamics could explain the dynamics of the responses seen in IT, the simulation cannot address the question of whether this attractor network plays out in IT itself, or if it is inherited from another visual area with all of the dynamics preserved. For example, some simulations of learned categories suggest that an interactive feedback between IT and prefrontal cortex might provide initial information separating the categories. Over time, this feedback information changes synaptic weights in IT, enhancing the representation of features that differentiate between the categories (Sigala and Logothetis 2002; Sigala 2004; Szabo et al. 2006). Alternatively stimulus frequency has been proposed as a method for adjusting synaptic weights to produce categorical boundaries (Rosenthal et al. 2001). These computations could play a role in the dynamics reproduced here with attractor networks, and could precede the attractor dynamics demonstrated here.

IT Neurons and Visual Classification

Previous studies provided mixed evidence for the role of IT in the classification of visual stimuli. Several studies suggest that IT neurons can encode known categories that reflect the identities of visual images (Sugase et al. 1999; Matsumoto, Okada, Sugase-Miyamoto, Yamane 2005; Matsumoto, Okada, Sugase-Miyamoto, Yamane, et al. 2005; Kiani et al. 2007). In contrast, other studies showed that IT neurons do not encode recently learned categories of visual images, instead maintaining similar selectivity to the images before and after category training (Kubota and Niki 1971; Rolls et al. 1977; Vogels 1999; Freedman et al. 2003; Thomas et al. 2001; Freedman and Miller 2008). Thus, these studies imply a stable visual code in IT, highlighting the need for contributions from other brain areas including the prefrontal cortex (PFC) and basal ganglia for correct classification behavior (White and Wise 1999; Asaad et al. 2000; Freedman et al. 2002, 2003; Shohamy et al. 2004; Muhammad et al. 2006; Nomura et al. 2007).

A critical difference between our study and previous studies relating learned classifications to IT activity is the kind of visual images used. In our task, the morphed stimuli are basically noisy variants of the original images. In contrast, other studies have used images that are more complicated and rules that are more abstract (e.g., cat vs. dog or tree in Vogels 1999; Freedman et al. 2003). This difference suggests that IT may not participate in classification when categories are defined by abstract rules but might when classification reduces to visual noise removal, or to a perceptually based classification of the image. This idea further suggests that category learning might co-occur with perceptual learning, which would improve the ability to discriminate the noisy images and thus produce classification responses that might not have been present earlier in training (Tomita et al. 1999; Sigala and Logothetis 2002; Sigala 2004; Bar et al. 2006; Szabo et al. 2006).

A study using a task similar to ours measured functional magnetic resonance imaging (fMRI) responses in human subjects categorizing images of morphed faces (Rotshtein et al. 2005). In that study, a blood oxygenation level–dependent (BOLD) signal in the inferior occipital gyrus reflected distance along the morphing dimension. In contrast, a BOLD signal in the fusiform face gyrus (FFG) of IT cortex reflected face identity, comparable to the convergent activity from our data. A signal reflecting face identity, similar to the convergent activity seen in the IT data, was present in the FFG. The fMRI paradigm cannot afford the temporal resolution of single unit recordings, and thus, the timing of the identity signal in FFG could be quite late, perhaps appearing after the offset of the visual stimulus during the decision making process. In the present study, however, the time for convergence of IT responses appears to be short, and to increase smoothly with increasing morphing distance, with the closest morphs being indistinguishable from the Eff image during the presentation of the visual stimulus. These features may be more consistent with a local IT mechanism, than with a (cascade of) top-down signals; however they are in agreement with the idea that both bottom-up signals from the retina and also top-down signals from the prefrontal cortex may trigger the retrieval of associative codes in IT, which may serve as a neural basis for conscious recall (Miyashita and Hayashi 2000). Furthermore, a top-down signal might be required at some point in the production of the network, and then no longer necessary after the network is stable (Bar 2003; Szabo et al. 2006). The stimuli used in this study were highly familiar, and thus, classification information might have been stored as a result of that familiarity (Liu and Jagadeesh 2008).

In the network simulation, attractors must be stored in the network to reproduce the dynamics seen in the neural data. The monkeys in this study were well-trained before the beginning of the recording session, allowing for the relevant information to be stored in the image before the beginning of the recording session. However, during the course of the recording sessions, the animals showed improvement in their performance with the more difficult morph variants, as seen as well in a perceptually demanding motion task (Law and Gold 2008). This improvement in behavioral performance was paralleled by an increase in the convergence of Eff images seen in Figure 4 for the whole data set. Convergence was more rapid for Eff images, and the Eff and Ineff difference appeared only in the latter half of the sessions (Supplementary Fig. 2). This property suggests that attractor dynamics may improve as images are stored in the network through repeated exposure and training, a question to address in future experiments.

As well as the time course and mechanism of storage of patterns into IT, several other predictions cannot be fully addressed by this report. For example, all of the data presented were collected with familiar images during the performance of a demanding task. Both these factors may influence the dynamics of response seen.

The data also cannot address the size and shape of attractor basins, and assumptions have been made about their shape in the regression analysis shown in Figure 4. In particular, the behavioral classification rule (images 0–4, rewarded for being classified as Ineff; 5 randomly rewarded, 6–10, rewarded for being classifed as Eff) has been used to divide the images into groups that were presumed to converge to different nodes. In fact, the behavioral results suggest that this assignment is an incomplete description of the data, because only the 3 most similar images in each group consistently result in the same behavioral classification. Using only these images to define the groups belonging to different attractors enhances the convergence for Eff images. However, fundamentally, we cannot be sure which images would be predicted to belong to which classification groups, and thus to converge to a particular attractor basin. These groups could change based on the stimulus, the session, and the trial, adding unpredictability to the population convergence zones. Finally, although we used the experimental manipulation of the classification rule to define the groups, we cannot know that this experimental manipulation drove the dynamics seen in these data. Further experiments, for example, changing the classification rule, or the size of the classification groups might address whether response dynamics depends on those features in the data.

Our results also point at the distinction between firing rate convergence, whether induced by attractor states or not, and delay activity, a form of short-term memory commonly observed in monkey prefrontal cortex (Kubota and Niki 1971; Miller et al. 1996) and in IT cortex (Miyashita and Chang 1988; Erickson and Desimone 1999). Delay activity is interpreted as the maintenance of behaviorally relevant information during a delay period, to be used after the delay to execute a task. It is also a salient property of the same recurrent network models that naturally express attractor dynamics. The distinction between sustained delay activity and convergent activity, and the potential role of the latter in perceptual classification, will likely benefit from theoretically guided experimental investigations.

An attractor network belongs to the same general class of classification mechanisms based simply on the distance, in a multidimensional feature space, between the exemplar and a prototype, which in the attractor network is the stored pattern. Unlike FF multilayer network models like MAX or Radial Basis Function networks (Riesenhuber and Poggio 1999) or ALCOVE (Kruschke 1992) which have been considered to account for responses in IT (Zoccolan et al. 2007; Op de Beeck et al. 2008), and in which individual units respond to a stimulus with an activation level which does not vary in time, recurrent attractor models do show temporal dynamics similar to that observed in the neural data, and such dynamics are the very mechanism underlying classification in those models (Rosenthal et al. 2001). Thus, attractor network based simulations of the properties of IT cortex might produce additional insights into the dynamic processing of visual information in IT.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/.

Funding

Whitehall Foundation, McKnight Foundation and NIH-NCRR to BJ and Human Frontier Science Foundation (RGP0047/2004-C) to B.J. and A.T.